УДК 22.151.0
Решение задачи о трисекции угла способом деления дуги на три равные части
А. Сатмаматов, М.Раманкулов
Трисекция угла является одной из задач классической геометрии. Суть задачи состоит в том, чтобы с помощью циркуля и линейки построить угол, который был бы в три раза меньше данного угла [1, с.12; 2, с. 254; 3, с.313-317; 4, с. 238-239].
Задача была известна ещё Архимеду. К ней обращались многие ученые, в том числе хорезмиец Гясетдин Джемшид аль Каши в XIII веке, немец Альбрехт Дюрер и француз Франсуа Виет в XVI веке, итальянец Лоренц Маскерони в XVIII веке и т.д., которые приходили к выводу о её неразрешимости.
Задача была объектом исследования и математиков XVIII и XX веков - П.Ванцеля, С.О.Шатуновского, Н.Ф.Четверухина и др.
Необходимо отметить, что до настоящего времени ученые-математики пытались решить задачу главным образом с помощью аналитических методов. Однако ни алгебраические уравнения (аль Каши), ни тригонометрические уравнения (Виет), ни другие методы и способы теоретической математики не способствовали достижению желаемого результата. Задача продолжала оставаться нерешенной. В 1997-2003 годы математик Джим Лой, собрав, обсудив и критически оценив свыше 80 способов решения задачи, отмечает принципиальную невозможность точного разделения угла на три секции (Trisection of an Angle.htm). Ученые убедились в том, что, вооружившись исключительно циркулем и линейкой, невозможно построить любой угол, кроме стандартных, и провести прямую, имеющую длину, выраженную иррациональным числом. Поэтому они стали говорить о необходимости снять задачу трисекции угла с проблематики геометрии.
Мы тоже поставили своей целью решить задачу трисекции угла графическим способом - с помощью циркуля и линейки. Предварительные результаты проведенных в этом направлении исследований опубликованы нами в статьях [6, с.11-114; 7, с.15-17]. Решение задачи предполагает:
постановку задачи;
выполнение построения;
доказательство правильности решения на конкретных примерах;
демонстрацию способности выбранной методики решения к экстраполяции на другие задачи на построение.
Задача постулирует построение угла, который был бы в три раза меньше, чем угол АОВ. В качестве примера мы выбрали угол в 60°.
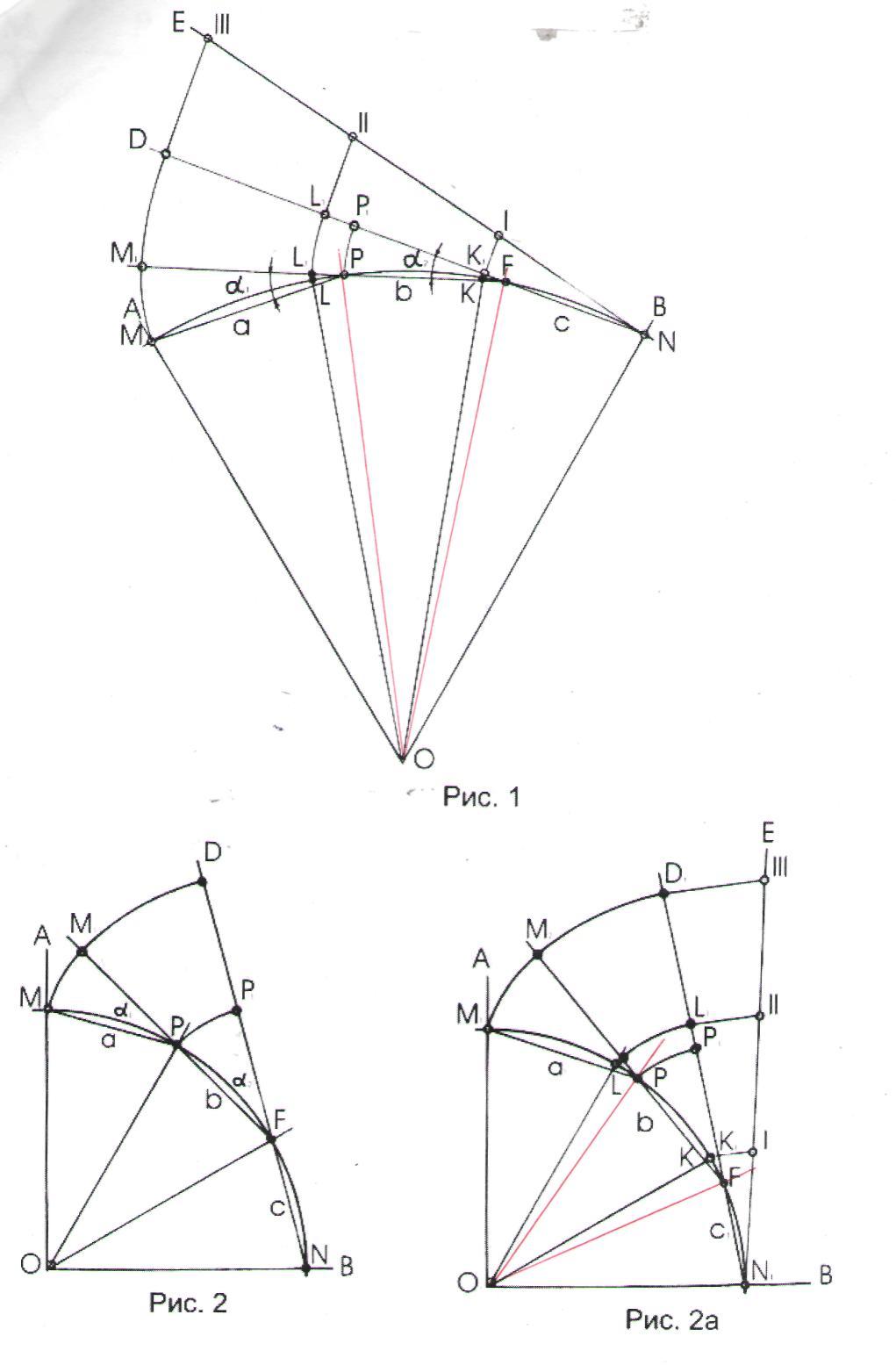
Дан угол АОВ (рис. 1). Лучи АО и ВО являются сторонами данного угла 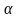 . Угол
. Угол 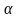 составляет 1/6 часть окружности. Вокруг центра О проведем дугу с произвольным радиусом R и отметим две точки М и N как точки пересечения проведенной дуги со сторонами данного угла.
составляет 1/6 часть окружности. Вокруг центра О проведем дугу с произвольным радиусом R и отметим две точки М и N как точки пересечения проведенной дуги со сторонами данного угла.
На дуге с радиусом R берем еще две точки Р и F. Проведем хорды через точки 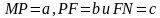 . Длины этих хорд не равны, т.е.
. Длины этих хорд не равны, т.е.  .
.
Общую длину а + (b + с) можно определить путем простого сложения на чертеже. При сложении применяются переместительный закон: а + b = b + а и сочетательный закон: (а + b) + с = а + (b + с).
Для получения общей суммы длин трех хорд a, b и с используем метод Маскерони [1] или обычный метод геометрического построения (вращения).
Через точки N и F, F и Р проведем прямые линии. В результате образуется угол ах между прямыми NF и FP и угол 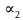 между прямыми РМ1 и РМ . Приняв за центр точку Р, проводим дугу с радиусом R1 = РМ, которая пересечет прямую, проходящую через точки F и Р в точке М1. Видно, что РМ = РМ1 и FP = FP1. Приняв за центр точку F, проводим дугу с радиусом R2 = FМ1 и R3 = FP, которая пересекает прямую, проходящую через точки N и F в точках D и Р1. Здесь также видно, что FM1 =FD1 и FP=FP1, где отрезок DN является истинной длиной слагаемых трех хорд а, b и с .
между прямыми РМ1 и РМ . Приняв за центр точку Р, проводим дугу с радиусом R1 = РМ, которая пересечет прямую, проходящую через точки F и Р в точке М1. Видно, что РМ = РМ1 и FP = FP1. Приняв за центр точку F, проводим дугу с радиусом R2 = FМ1 и R3 = FP, которая пересекает прямую, проходящую через точки N и F в точках D и Р1. Здесь также видно, что FM1 =FD1 и FP=FP1, где отрезок DN является истинной длиной слагаемых трех хорд а, b и с .
Далее разделим отрезок DN на три равные части методом Фалеса. Для этого через точку N дополнительно проведем прямую NE произвольным направлением немного большей длины, чем отрезок DN . Разделив отрезок NE на три равные части, обозначим их цифрами I, II, и III. Затем вернем их на отрезок DN и обозначим буквами D, L1, К1, N , в результате чего отрезок DN делится на три равные части: DL1 = L1K1=K1N. Далее нужно будет вернуть эти точки на дугу данного угла, что осуществляется обратным вращением по ступеням. Таким образом, на дуге данного угла появляются новые точки L и К, разделяющие данную дугу на три равные части.
Следовательно, длины хорд ML = LK = KN. Соединив точку О с точками К и L легко убедиться, что угол АОВ в 60° разделена на три равные части.
Данная методика нами была использована при делении разных углов на три равные части. Она оказалась пригодной для решения любой из задач трисекции угла, особенно углов до 90°.
Задача разделения угла в 90° осуществляется построением угла в 30°, т.е. угла равнобедренного треугольника. Угол в 90° как обычно делится на три равные части с помощью радиуса данной дуги (рис.2). На рис.2 видим, что точки М и N являются точками пересечения дуги со сторонами данного угла в 90°. На дуге отметим ещё две точки Р и F, полученные вращением точки О вокруг точек М и N . Проводим хорду MP = a, PF = b и FN = с. Эти хорды а = b = с между собой равны, т.е. MP = PF = FN , и являются ломаными отрезками. Спрямляя ломаные отрезки, мы можем расположить их на одной прямой линии. Используя способ вращения, вокруг точки Р вращаем точку М с радиусом R1 = РМ на угол  до пересечения с прямой, проведенной через хорду b, и отметим точку М1 ; приняв за центр точку F, проводим дугу с радиусом R2 = FM1, вращая точку М1, на угол
до пересечения с прямой, проведенной через хорду b, и отметим точку М1 ; приняв за центр точку F, проводим дугу с радиусом R2 = FM1, вращая точку М1, на угол  , определим точки пересечения с прямой, проходящей через хорды с, и получим точку D. В результате мы имеем сумму трёх хорд, т.е. DN = a + (b + c). Отрезок DN является натуральной длиной всех слагаемых хорд а, b и с . DN=DP1 + P1F + FN. Возвращение точек D и Р, к первоначальному положению приводит к делению угла в 90° на три равные части.
, определим точки пересечения с прямой, проходящей через хорды с, и получим точку D. В результате мы имеем сумму трёх хорд, т.е. DN = a + (b + c). Отрезок DN является натуральной длиной всех слагаемых хорд а, b и с . DN=DP1 + P1F + FN. Возвращение точек D и Р, к первоначальному положению приводит к делению угла в 90° на три равные части.
1. Попытаемся разделить угол в 90° избранным нами способом построения (рис.2а). Сначала построим угол AОВ в 90° и проводим дугу с радиусом R1, равным радиусу R (рис.2), т.е. R1 = R. Отметим две точки Р и F, лежащие на этой дуге, проведем хорды a1, b1 и c1, которые 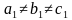 . Длины хорд между собой неравны, т.е. al=M1P, b1=PF, c1=FN1 (M1P ≠ PF ≠ FN1). Как видно из рис.2а, a1, b1 и c1 представляют собой ломаные отрезки. Спрямляя эти ломаные отрезки, расположим их на одной прямой линии (рис.2а). Спрямление хорд a1, b1 и c1 осуществлено по уже известным правилам, как это было на рис.2. Сопоставляя рис.2 и рис.2а, мы убедимся, что отрезки DN = D1N1.
. Длины хорд между собой неравны, т.е. al=M1P, b1=PF, c1=FN1 (M1P ≠ PF ≠ FN1). Как видно из рис.2а, a1, b1 и c1 представляют собой ломаные отрезки. Спрямляя эти ломаные отрезки, расположим их на одной прямой линии (рис.2а). Спрямление хорд a1, b1 и c1 осуществлено по уже известным правилам, как это было на рис.2. Сопоставляя рис.2 и рис.2а, мы убедимся, что отрезки DN = D1N1.
Далее разделим отрезок D1N1 на три равные части методом Фалеса. Для этого через точку N1 дополнительно проведем прямую N1E произвольным направлением немного большей длины, чем отрезок D1N1. Разделив отрезок N1E на три равные части, обозначим их цифрами I, II, и III. Затем вернем их на отрезок D1N1 и обозначим буквами D1L1 K1N1,, в результате чего отрезок D1N1 делится на три равные части: D1L1 = L1K1 = K1N1. Теперь нужно будет вернуть эти точки на дугу данного угла, что осуществляется обратным вращением по ступеням. Таким образом, на дуге данного угла появляются новые точки L и К , разделяющие данную дугу на три равные части.
Следовательно, длины хорд M1L = LK = KN1. Соединив точку О с точками К и L, легко убедимся, что угол AОВ разделена на три равные части.
2. Пусть требуется разделить дугу на три равные части.
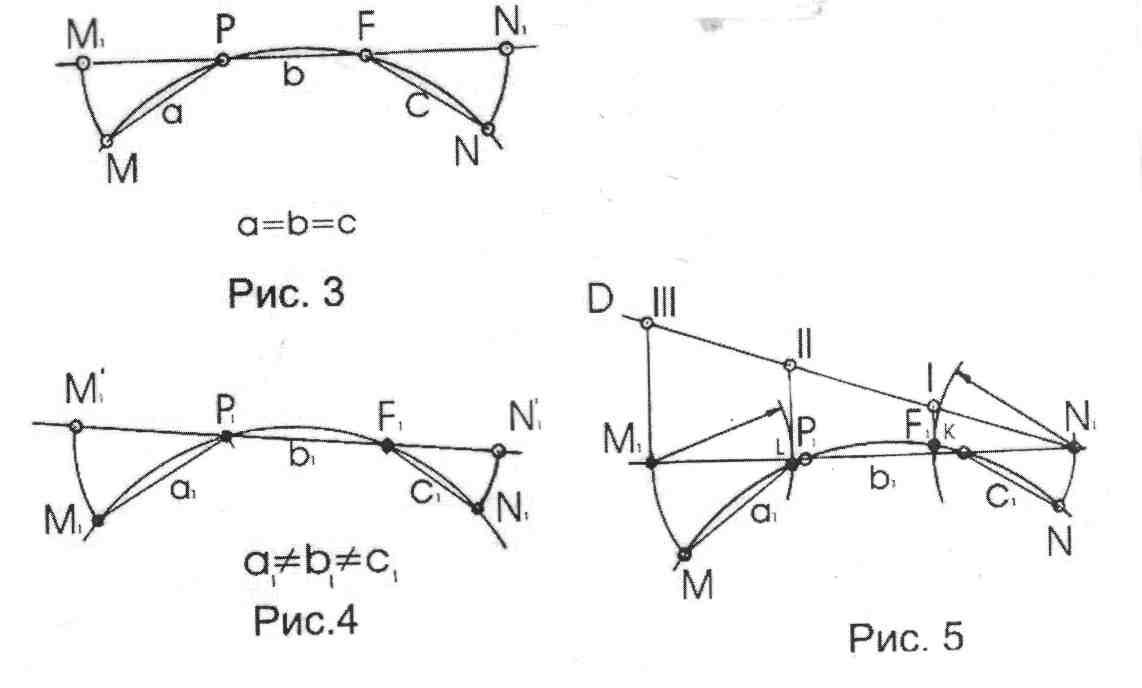
Сначала построим две одинаковые дуги MN и M1N1. Первая дуга разделена на три равные части с одинаковым расстоянием. Вторая дуга также разделена на три части, но не с одинаковым расстоянием (рис.3) и (рис.4). На рис.3 проведенные хорды а = b = с. Из рис.4 видно, что проведенные хорды 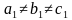 .
.
Следовательно, на рис.3 хорды MP = PF = FN. Из рис.4 видно, что хорды M1P1 ≠ P1F1 ≠ F1N1. В обоих случаях эти хорды являются ломаными. Мы будем их спрямлять. Для этого через хорды b и b1 проведена прямая линия. Вокруг точки Р и F (рис.3) вращаем точки М и N до пересечения с прямой, проходящей через хорды b, и определим точки М' и N' в новом положении. Теперь также на рис.4 вокруг точки Р1 и F1 вращаем точки М1 и N1 до пересечения с прямой, проходящей через хорды b1, и определим точки (М'1 и N'1) в новом положении. Если сопоставить спрямленные хорды из рис.3 М' и N' и из рис.4 М'1 и N'1, то они будут между собой равны M'N' = М'1N'1.
Этим мы доказываем, что независимо от длины хорд одинаковых дуг сумма длин трёх хорд остается постоянной, т.е. а + (b + с) = a1 + (b1 +с1).
Согласно постановке задачи приступим к делению дуги М'1N'1 на три равные части построением (рис.5). На рис.5 данная дуга разделена на три равные части. Здесь нами применен тот же способ построения, что и при решении задачи для любого угла (см.рис.1 и рис.2).
Основная задача нашего исследования состоит в установлении разрешимости задачи и определении числа её решений. При построении мы ограничивались лишь отысканием одного способа решения, причём предполагаем, что все этапы построения действительно выполнимы (рис.1).
Есть основание считать, что задача трисекция угла допускает решение графическим способом.
Литература
Адлер А. Теория геометрических построений. Изд. 3-е. - Ленинград, 1940.
Александров А. Д., Нецветаев Н. Ю. Геометрия. - Москва, 1990.
Аргунов Б. И., Балк М. Б. Элементарная геометрия. - Москва, 1966.
Бекбоев И. Б., Борубаев А. А., Айылчиев А. А. Геометрия: Учебник для 7-9 кл. - Бишкек, 2000.
Сатмаматов А., Ахмедов А. А. Приближённое графико-аналитическое решение задачи о трисекции угла // Вестник Ошского государственного университета. Серия психолого-педагогических наук. - №8. - Ош, 2005.
Сатмаматов А. К приближённому решению задачи о трисекции угла // Естественные и технические науки. - № 2 (16). - Москва, 2005.
Сатмаматов А., Ахмедов А. А. Деление окружности на девять равных частей // Известия Ошского технологического университета. - №1. - Ош, 2005.
Решение задачи о трисекции угла. Кыргызпатент. Свидетельство №837. 2006 г.
Решение задачи о трисекции угла способом движения. Кыргызпатент. Свидетельство №1694. 2011 г.
3







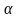 . Угол
. Угол 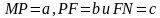 . Длины этих хорд не равны, т.е.
. Длины этих хорд не равны, т.е.  .
.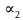 между прямыми РМ1 и РМ . Приняв за центр точку Р, проводим дугу с радиусом R1 = РМ, которая пересечет прямую, проходящую через точки F и Р в точке М1. Видно, что РМ = РМ1 и FP = FP1. Приняв за центр точку F, проводим дугу с радиусом R2 = FМ1 и R3 = FP, которая пересекает прямую, проходящую через точки N и F в точках D и Р1. Здесь также видно, что FM1 =FD1 и FP=FP1, где отрезок DN является истинной длиной слагаемых трех хорд а, b и с .
между прямыми РМ1 и РМ . Приняв за центр точку Р, проводим дугу с радиусом R1 = РМ, которая пересечет прямую, проходящую через точки F и Р в точке М1. Видно, что РМ = РМ1 и FP = FP1. Приняв за центр точку F, проводим дугу с радиусом R2 = FМ1 и R3 = FP, которая пересекает прямую, проходящую через точки N и F в точках D и Р1. Здесь также видно, что FM1 =FD1 и FP=FP1, где отрезок DN является истинной длиной слагаемых трех хорд а, b и с . до пересечения с прямой, проведенной через хорду b, и отметим точку М1 ; приняв за центр точку F, проводим дугу с радиусом R2 = FM1, вращая точку М1, на угол
до пересечения с прямой, проведенной через хорду b, и отметим точку М1 ; приняв за центр точку F, проводим дугу с радиусом R2 = FM1, вращая точку М1, на угол  , определим точки пересечения с прямой, проходящей через хорды с, и получим точку D. В результате мы имеем сумму трёх хорд, т.е. DN = a + (b + c). Отрезок DN является натуральной длиной всех слагаемых хорд а, b и с . DN=DP1 + P1F + FN. Возвращение точек D и Р, к первоначальному положению приводит к делению угла в 90° на три равные части.
, определим точки пересечения с прямой, проходящей через хорды с, и получим точку D. В результате мы имеем сумму трёх хорд, т.е. DN = a + (b + c). Отрезок DN является натуральной длиной всех слагаемых хорд а, b и с . DN=DP1 + P1F + FN. Возвращение точек D и Р, к первоначальному положению приводит к делению угла в 90° на три равные части.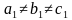 . Длины хорд между собой неравны, т.е. al=M1P, b1=PF, c1=FN1 (M1P ≠ PF ≠ FN1). Как видно из рис.2а, a1, b1 и c1 представляют собой ломаные отрезки. Спрямляя эти ломаные отрезки, расположим их на одной прямой линии (рис.2а). Спрямление хорд a1, b1 и c1 осуществлено по уже известным правилам, как это было на рис.2. Сопоставляя рис.2 и рис.2а, мы убедимся, что отрезки DN = D1N1.
. Длины хорд между собой неравны, т.е. al=M1P, b1=PF, c1=FN1 (M1P ≠ PF ≠ FN1). Как видно из рис.2а, a1, b1 и c1 представляют собой ломаные отрезки. Спрямляя эти ломаные отрезки, расположим их на одной прямой линии (рис.2а). Спрямление хорд a1, b1 и c1 осуществлено по уже известным правилам, как это было на рис.2. Сопоставляя рис.2 и рис.2а, мы убедимся, что отрезки DN = D1N1.



















