Mavzu: Ko`p o`lchovli tasodifiy miqdorlar.
REJA:
Kirish
Asosiy qism
Ko‘p o‘lchovli tasodifiy miqdorlar va ularning birgalikdagi taqsimot funksiyasi.
Tasodifiy miqdorlarning bog‘liqsizligi. Shartli taqsimot qonunlari.
Ikki o`lchovli tasodifiy miqdorlarning sonli xarakteristikalari. Ba’zi muhim ikki o‘lchovlik taqsimotlar
Xulosa
Foydalanilgan adabiyotlar
Kirish.
Ehtimollar nazariyasi “tasodifiy tajribalar”, ya’ni natijasini oldindan
aytib bo‘lmaydigan tajribalardagi qonuniyatlatni o‘rganuvchi matematik
fandir. Bunda shunday tajribalar qaraladiki, ularni o‘zgarmas (ya’ni, bir
xil) shartlar kompleksida hech bo‘lmaganda nazariy ravishda ixtiyoriy
sonda takrorlash mumkin, deb hisoblanadi. Bunday tajribalar har birining
natijasi tasodifiy hodisa ro‘y berishidan iboratdir. Insoniyat faoliyatining
deyarli hamma sohalarida shunday holatlar mavjudki, u yoki bu tajribalarni
bir xil sharoitda ko‘p marta takrorlash mumkin bo‘ladi. Ehtimollar
nazariyasini sinovdan-sinovga o‘tishida natijalari turlicha bo‘lgan tajribalar
qiziqtiradi. Biror tajribada ro‘y berish yoki bermasligini oldindan aytib
bo‘lm aydigan hodisalar tasodifiy hodisalar deyiladi. Masalan, tanga
tashlash tajribasida har bir tashlashga ikki tasodifiy hodisa mos keladi: tanganing gerb tomoni tushishi yoki tanganing raqam tomoni tushishi.
Albatta, bu tajribani bir marta takrorlashda shu ikki tasodifiy hodisalardan
faqat bittasigina ro‘y beradi. Tasodifiy hodisalarni biz tabiatda, jamiatda,
ilmiy tajribalarda, sport va qimoro‘yinlarida kuzatishimiz mumkin. Umumlashtirib aytish mumkinki, tasodifiyat elementlarisiz rivojlanishni
tasavvur qilish qiyindir. Tasodifiyatsiz umuman hayotning va biologik
turlarning yuzaga kelishini, insoniyat tarihini, insonlarning ijodiy
faoliyatini, sotsial-iqtisodiy tizim larning rivojlanishini tasavvur etib
bo‘lmaydi. Ehtimollar nazariyasi esa aynan mana shunday tasodifiy
bog‘liqliklarning matematik modelini tuzish bilan shug‘illanadi.
Tasodifiyat insoniyatni doimo qiziqtirib kelgandir. Shu sababli ehtimollar
nazariyasi boshqa matematik fanlar kabi amaliyot talablariga mos ravishda
rivojlangan. Ehtimollar nazariyasi boshqa matematik fanlardan farqli o‘laroq nisbatan qisqa, ammo o‘ta shijoatlik rivojlanish tarixiga ega. Endi qisqacha tarixiy ma’lumotlarni keltiramiz. Ommaviy tasodifiy hodisalarga mos masalalarni sistematik ravishda o‘rganish va ularga mos matematik apparatning yuzaga kelishi XVII asrga to‘g‘ri keladi. XVII asr boshida, mashhur fizik Galiley fizik o‘lchashlardagi xatoliklarni tasodifiy deb hisoblab, ularni ilmiy tadqiqot qilishga uringan. Shu davrlarda kasallanish, o‘lish, baxtsiz hodisalar statistikasi va shu kabi ommaviy tasodifiy hodisalardagi qonuniyatlarni tahlil qilishga asoslangan sug‘urtalanishning umumiy nazariyasini yaratishga ham urinishlar bo‘lgan. Ammo, ehtimollar nazariyasi matematik ilm sifatida murakkab tasodifiy jarayonlarning o‘rganishdan emas, balki eng sodda qimor o‘yinlarini tahlil qilish natijasida yuzaga kela boshlagan. Shu boisdan ehtimollar nazariyasining paydo bo‘lishi XVII asr ikkinchi yarmiga mos keladi va u Paskal (1623 1662), Ferma (1601-1665) va Gyuygens (1629-1695) kabi olimlarning qimor o‘yinlarini nazariyasidagi tadqiqotlari bilan bog‘liqdir. Ehtimollar nazariyasi rivojidagi katta qadam Yakov Bernulli (1654-1705) ilmiy izlanishlari bilan bog‘liqdir. Unga, ehtimollar nazariyasining eng muhim qonuniyati, deb hisoblanuvchi “katta sonlar qonuni” tegishlidir. Ehtimollar nazariyasi rivojidagi yana bir muhim qadam Muavr (1667-1754) nomi bilan bog‘liqdir. Bu olim tomonidan normal qonun (yoki normal taqsimot) deb ataluvchi muhim qonuniyat mavjudligi sodda holda asoslanib berildi.
Ehtimollar nazariyasining muhim tusunchalaridan biri tasodifiy miqdor tushunchasidir. Tasodifiy tajriba natijasida u yoki bu qiymatni qabul qilishi oldindan ma’lum bo‘lmagan miqdor tasodifiy miqdor deyiladi. Tasodifiy miqdorlar lotin alifbosining bosh harflari 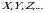 (yoki grek alifbosining kichik harflari
(yoki grek alifbosining kichik harflari 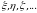 ) bilan qabul qiladigan qiymatlari esa kichik harflar
) bilan qabul qiladigan qiymatlari esa kichik harflar 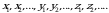 bilan belgilanadi.
bilan belgilanadi.
Tasodifiy miqdorlarga misollar keltiramiz: 1) 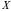 -tavakkaliga olingan mahsulotlar ichida sifatsizlari soni; 2)
-tavakkaliga olingan mahsulotlar ichida sifatsizlari soni; 2) 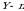 ta o‘q uzilganda nishonga tekkanlari soni; 3)
ta o‘q uzilganda nishonga tekkanlari soni; 3) 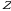 -asbobning beto‘htov ishlash vaqti; 4)
-asbobning beto‘htov ishlash vaqti; 4) 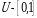 kesmadan tavakkaliga tanlangan nuqtaning koordinatalari; 5)
kesmadan tavakkaliga tanlangan nuqtaning koordinatalari; 5) 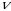 -bir kunda tug‘iladigan chaqaloqlar soni va h.k..
-bir kunda tug‘iladigan chaqaloqlar soni va h.k..
Agar tasodifiy miqdor (tasodifiy miqdor) chekli yoki sanoqli qiymatlar qabul qilsa, bunday tasodifiy miqdor diskret tipdagi tasodifiy miqdor deyiladi.
Agar tasodifiy miqdor qabul qiladigan qiymatlari biror oraliqdan iborat bo‘lsa uzluksiz tipdagi tasodifiy miqdor deyiladi.
Demak, diskret tasodifiy miqdor bir-biridan farqli alohida qiymatlarni, uzluksiz tasodifiy miqdor esa biror oraliqdagi ixtiyoriy qiymatlarni qabul qilar ekan. Yuqoridagi 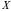 va
va  tasodifiy miqdorlar diskret,
tasodifiy miqdorlar diskret, 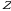 esa uzluksiz tasodifiy miqdor bo‘ladi.
esa uzluksiz tasodifiy miqdor bo‘ladi.
Endi tasodifiy miqdorni qat’iy ta’rifini keltiramiz.
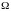 elementar hodisalar fazosida aniqlangan
elementar hodisalar fazosida aniqlangan 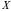 sonli funksiya tasodifiy miqdor deyiladi, agar har bir
sonli funksiya tasodifiy miqdor deyiladi, agar har bir 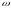 elementar hodisaga
elementar hodisaga 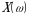 sonni mos qo‘ysa, yani
sonni mos qo‘ysa, yani 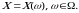
Masalan, tajriba tangani 2 marta tashlashdan iborat bo‘lsin. Elementar hodisalar fazosi 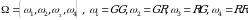 bo‘ladi.
bo‘ladi. 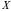 -gerb chiqishlari soni bo‘lsin, u holda
-gerb chiqishlari soni bo‘lsin, u holda 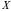 tasodifiy miqdor qabul qiladigan qiymatlari:
tasodifiy miqdor qabul qiladigan qiymatlari: 
Ko‘p o‘lchovli tasodifiy miqdorlar va ularning birgalikdagi taqsimot
funksiyasi
Bir o‘lchovli tasodifiy miqdorlardan tashqari, mumkin bo‘lgan qiymatlari 2 ta, 3 ta, ...,  ta son bilan aniqlanadigan miqdorlarni ham o‘rganish zarurati tug‘iladi. Bunday miqdorlar mos ravishda ikki o‘lchovli, uch o‘lchovli, … ,
ta son bilan aniqlanadigan miqdorlarni ham o‘rganish zarurati tug‘iladi. Bunday miqdorlar mos ravishda ikki o‘lchovli, uch o‘lchovli, … ,  o‘lchovli deb ataladi.
o‘lchovli deb ataladi.
Faraz qilaylik, 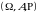 ehtimollik fazosida aniqlangan
ehtimollik fazosida aniqlangan 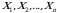
tasodifiy miqdorlar berilgan bo‘lsin.
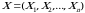 vektorga tasodifiy vektor yoki
vektorga tasodifiy vektor yoki  -o‘lchovli tasodifiy miqdor deyiladi. Ko‘p o‘lchovli tasodifiy miqdor har bir elementar hodisa
-o‘lchovli tasodifiy miqdor deyiladi. Ko‘p o‘lchovli tasodifiy miqdor har bir elementar hodisa  ga
ga  ta
ta 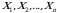 tasodifiy miqdorlarning qabul qiladigan qiymatlarini mos qo‘yadi.
tasodifiy miqdorlarning qabul qiladigan qiymatlarini mos qo‘yadi.
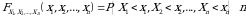 o‘lchovli funksiya
o‘lchovli funksiya
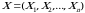 tasodifiy vektorning taqsimot funksiyasi yoki
tasodifiy vektorning taqsimot funksiyasi yoki 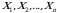
tasodifiy miqdorlarning birgalikdagi taqsimot funksiyasi deyiladi.
Qulaylik uchun 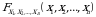 taqsimot funksiyani
taqsimot funksiyani 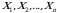
indekslarini tushirib qoldirib, 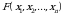 ko‘rinishida yozamiz.
ko‘rinishida yozamiz.
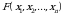 funksiya
funksiya 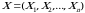 tasodifiy vektorning taqsimot
tasodifiy vektorning taqsimot
funksiyasi bo‘lsin. Ko‘p o‘lchovli 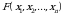 taqsimot funksiyaning asosiy
taqsimot funksiyaning asosiy
xossalarini keltiramiz:
1. 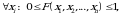 ya’ni taqsimot funksiya chegaralangan.
ya’ni taqsimot funksiya chegaralangan.
2. 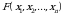 funksiya har qaysi argumenti bo‘yicha kamayuvchi emas va chapdan uzluksiz.
funksiya har qaysi argumenti bo‘yicha kamayuvchi emas va chapdan uzluksiz.
3. Agar biror 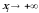 bo‘lsa, u holda
bo‘lsa, u holda
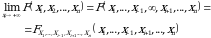 (1.1)
(1.1)
4. Agar biror 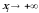 bo‘lsa, u holda
bo‘lsa, u holda 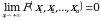 . 3-xossa yordamida keltirib chiqarilgan (1.1) taqsimot funksiyaga marginal(xususiy) taqsimot funksiya deyiladi.
. 3-xossa yordamida keltirib chiqarilgan (1.1) taqsimot funksiyaga marginal(xususiy) taqsimot funksiya deyiladi. 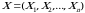 tasodifiy vektorning barcha marginal taqsimot funksiyalari soni
tasodifiy vektorning barcha marginal taqsimot funksiyalari soni
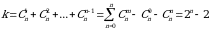 ga tengdir.
ga tengdir.
Masalan, 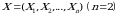 ikki o‘lchovlik tasodifiy vektorning marginal taqsimot funksiyalari soni
ikki o‘lchovlik tasodifiy vektorning marginal taqsimot funksiyalari soni 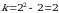 ta bo‘lib, ular quyidagilardir:
ta bo‘lib, ular quyidagilardir:
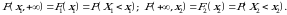
Ikki o‘lchovli diskret tasodifiy miqdor va uning taqsimot qonuni
 ikki o‘lchovli tasodifiy miqdor taqsimot qonunini
ikki o‘lchovli tasodifiy miqdor taqsimot qonunini
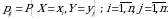 (1.2)
(1.2)
formula yordamida yoki quyidagi jadval ko‘rinishida berish mumkin:
bu yerda barcha 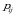 ehtimolliklar yig‘indisi birga teng, chunki
ehtimolliklar yig‘indisi birga teng, chunki
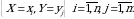 birgalikda bo‘lmagan hodisalar to‘la guruppani tashkil etadi
birgalikda bo‘lmagan hodisalar to‘la guruppani tashkil etadi  (1.2) formula ikki o‘lchovli diskret tasodifiy miqdorning taqsimot qonuni, yuqoridagi jadval esa birgalikdagi taqsimot jadvali deyiladi.
(1.2) formula ikki o‘lchovli diskret tasodifiy miqdorning taqsimot qonuni, yuqoridagi jadval esa birgalikdagi taqsimot jadvali deyiladi.
 ikki o‘lchovli diskret tasodifiy miqdorning birgalikdagi taqsimot qonuni berilgan bo‘lsa, har bir komponentaning alohida (marginal) taqsimot qonunlarini toppish mumkin. Har bir
ikki o‘lchovli diskret tasodifiy miqdorning birgalikdagi taqsimot qonuni berilgan bo‘lsa, har bir komponentaning alohida (marginal) taqsimot qonunlarini toppish mumkin. Har bir  uchun
uchun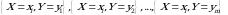 hodisalar birgalikda bo‘lma-gani sababli:
hodisalar birgalikda bo‘lma-gani sababli: 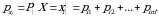
Demak,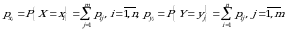
Ikki o‘lchovli tasodifiy miqdorning taqsimot funksiyasi va uning xossalari
Ikki o‘lchovli tasodifiy miqdor taqsimot funksiyasini  orqali belgilaymiz.
orqali belgilaymiz.
Ikki o‘lchovli  tasodifiy miqdorning taqsimot funksiyasi,
tasodifiy miqdorning taqsimot funksiyasi,  va
va 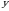 sonlarning har bir jufti uchun
sonlarning har bir jufti uchun 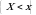 va
va 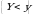 hodisalarning birgalikdagi ehtimolligini aniqlaydigan
hodisalarning birgalikdagi ehtimolligini aniqlaydigan  funksiyasidir: ya’ni
funksiyasidir: ya’ni
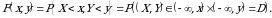 (1.3)
(1.3)
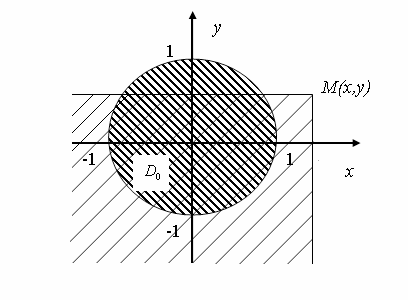
(3) tenglikning geometrik tasviri rasmda keltirilgan.

 ikki o‘lchovlik diskret tasodifiy miqdor taqsimot funksiyasi quyidagi yig‘indi orqali aniqlanadi:
ikki o‘lchovlik diskret tasodifiy miqdor taqsimot funksiyasi quyidagi yig‘indi orqali aniqlanadi:
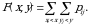 (1.4)
(1.4)
Ikki o‘lchovlik tasodifiy miqdor taqsimot funksiyasining xossalari:
1.  taqsimot funksiya chegaralangan:
taqsimot funksiya chegaralangan: 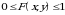 .
.
2.  funksiya har qaysi argumenti bo‘yicha kamayuvchi emas:
funksiya har qaysi argumenti bo‘yicha kamayuvchi emas:
agar 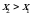 bo‘lsa,
bo‘lsa, 
agar 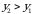 bo‘lsa,
bo‘lsa, 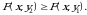
3.  funksiyaning biror argumenti
funksiyaning biror argumenti 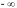 bo‘lsa(limit ma’nosida), u holda
bo‘lsa(limit ma’nosida), u holda  funksiya nolga teng,
funksiya nolga teng, 
4. Agar  funksiyaning bitta argumenti
funksiyaning bitta argumenti 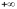 bo‘lsa(limit ma’nosida), u holda
bo‘lsa(limit ma’nosida), u holda
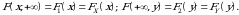 (1.5)
(1.5)
5. Agar ikkala argumenti 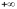 bo‘lsa(limit ma’nosida), u holda
bo‘lsa(limit ma’nosida), u holda
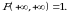
6.  funksiya har qaysi argumenti bo‘yicha chapdan uzluksiz, ya’ni
funksiya har qaysi argumenti bo‘yicha chapdan uzluksiz, ya’ni
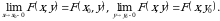
Tasodifiy miqdorlarning bog‘liqsizligi
 va
va  tasodifiy miqdorlar bog‘liqsiz deiladi, agar
tasodifiy miqdorlar bog‘liqsiz deiladi, agar 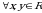 , uchun
, uchun 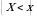 va
va 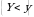 hodisalar bog‘liqsiz bo‘lsa.
hodisalar bog‘liqsiz bo‘lsa.
Endi tasodifiy miqdorlar bog‘liqsizligining zarur va yetarli shartini keltiramiz.
Teorema.  va
va  tasodifiy miqdorlar bog‘liqsiz bo‘lishi uchun
tasodifiy miqdorlar bog‘liqsiz bo‘lishi uchun
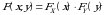 (2.1)
(2.1)
tenglik bajarilishi zarur va yetarlidir.
Isboti. Zarurligi. Agar  va
va  tasodifiy miqdorlar bog‘liqsiz bo‘lsa,
tasodifiy miqdorlar bog‘liqsiz bo‘lsa, 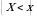 va
va 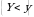 hodisalar ham bog‘liqsiz bo‘ladi. U holda
hodisalar ham bog‘liqsiz bo‘ladi. U holda 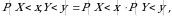 ya’ni
ya’ni 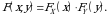
Yetarliligi. (2.1) tenglik o‘rinli bo‘lsin, u holda 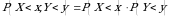 bo‘ladi. Bu tenglikdan
bo‘ladi. Bu tenglikdan  va
va  tasodifiy miqdorlar bog‘liqsizligi kelib chiqadi.
tasodifiy miqdorlar bog‘liqsizligi kelib chiqadi.
1-natija.  va
va  uzluksiz tasodifiy miqdorlar bog‘liqsiz bo‘lishi uchun
uzluksiz tasodifiy miqdorlar bog‘liqsiz bo‘lishi uchun
 (2.2)
(2.2)
tenglik bajarilishi zarur va yetarlidir.
Isboti. Zarurligi. Agar  va
va  tasodifiy miqdorlar bog‘liqsiz bo‘lsa, u holda (1) tenglik o‘rinli bo‘ladi. Bu tenglikni
tasodifiy miqdorlar bog‘liqsiz bo‘lsa, u holda (1) tenglik o‘rinli bo‘ladi. Bu tenglikni  bo‘yicha, keyin esa
bo‘yicha, keyin esa 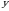 bo‘yicha differensiyallab,
bo‘yicha differensiyallab, 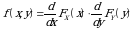 tengliklarni, ya`ni
tengliklarni, ya`ni  hosil qilamiz.
hosil qilamiz.
Yetarliligi. (2.2) tenglik o‘rinli bo‘lsin. Bu tenglikni  bo‘yicha va
bo‘yicha va 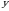
bo‘yicha integrallaymiz:
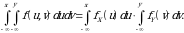
Bu esa 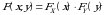 tenglikning o`zidir. Teoremaga ko`ra
tenglikning o`zidir. Teoremaga ko`ra  va
va  tasodifiy miqdorlar bog‘liqsizligi kelib chiqadi.
tasodifiy miqdorlar bog‘liqsizligi kelib chiqadi.
2-natija.  va
va  diskert tasodifiy miqdorlar bog‘liqsiz bo`lishi uchun ixtiyoriy
diskert tasodifiy miqdorlar bog‘liqsiz bo`lishi uchun ixtiyoriy 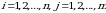 larda
larda
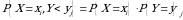 (2.3)
(2.3)
tengliklarning bajarilishi zarur va yetarlidir.
Shartli taqsimot qonunlari
 ikki o‘lchovlik tasodifiy miqdorni tashkil etuvchi
ikki o‘lchovlik tasodifiy miqdorni tashkil etuvchi  va
va  tasodifiy miqdorlar bog‘liq bo‘lsa, ularning bog‘liqligini xarakterlovchi shartli taqsimot qonunlari tushunchalari keltiriladi.
tasodifiy miqdorlar bog‘liq bo‘lsa, ularning bog‘liqligini xarakterlovchi shartli taqsimot qonunlari tushunchalari keltiriladi.
 ikki o‘lchovli diskret tasodifiy miqdor birgalikdagi taqsimot qonuni
ikki o‘lchovli diskret tasodifiy miqdor birgalikdagi taqsimot qonuni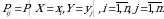 bo‘lsin. U holda
bo‘lsin. U holda
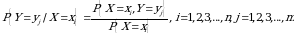 (2.4)
(2.4)
ehtimoliklar to‘plami, ya’ni 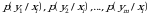 lar
lar  tasodifiy miqdorning
tasodifiy miqdorning 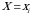 dagi shartli taqsimot qonuni deyiladi. Bu yerda
dagi shartli taqsimot qonuni deyiladi. Bu yerda
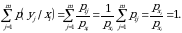
Xuddi shunday,
 (2.5)
(2.5)
ehtimolliklar to‘plami, ya’ni  lar
lar  tasodifiy miqdorning
tasodifiy miqdorning 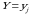 dagi shartli taqsimot qonuni deyiladi.
dagi shartli taqsimot qonuni deyiladi.
Misol.  ikki o‘lchovlik tasodifiy miqdorni birgalikdagi taqsimot jadvali berilgan:
ikki o‘lchovlik tasodifiy miqdorni birgalikdagi taqsimot jadvali berilgan:
| 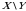
| 1 | 2 | 3 |
| 0,1 | 0,12 | 0,08 | 0,40 |
| 0,2 | 0,16 | 0,10 | 0,14 |
Quyidagilarni toping: a)  va
va  tasodifiy miqdorlarning alohida taqsimot qonunlari; b)
tasodifiy miqdorlarning alohida taqsimot qonunlari; b)  tasodifiy miqdorning
tasodifiy miqdorning  dagi shartli taqsimot qonuni
dagi shartli taqsimot qonuni
a) 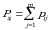 va
va 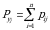 tengliklardan:
tengliklardan:
| 
| 0,1 | 0,2 | |  | 0,60 | 0,40 |  | 1 | 2 | 3 |
|  | 0,28 | 0,10 | 0,54 |
b) (5) formulaga asosan: 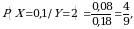
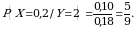
 tasodifiy miqdorning Y=2 dagi shartli taqsimot qonuni quyidagiga teng:
tasodifiy miqdorning Y=2 dagi shartli taqsimot qonuni quyidagiga teng:
Endi (X,Y) ikki o‘lchovli tasodifiy miqdor uzluksiz bo‘lgan holni ko‘ramiz.  tasodifiy miqdorning birgalikdagi zichlik funksiyasi,
tasodifiy miqdorning birgalikdagi zichlik funksiyasi, 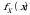 va
va  lar esa
lar esa  va
va  tasodifiy miqdorlarning alohida zichlik funksiyalari bo‘lsin.
tasodifiy miqdorlarning alohida zichlik funksiyalari bo‘lsin.
 tasodifiy miqdorning
tasodifiy miqdorning 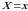 bo‘lgandagi shartli zichlik funksiyasi
bo‘lgandagi shartli zichlik funksiyasi
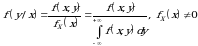 (2.6)
(2.6)
ifodaga orqali aniqlanadi.
Shartli zichlik funksiyasi zichlik funksiyasining
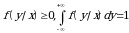
kabi xossalariga egadir.
Xuddi shunday,  tasodifiy miqdorning
tasodifiy miqdorning 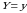 bo‘lgandagi shartli zichlik funksiyasi
bo‘lgandagi shartli zichlik funksiyasi
 (2.7)
(2.7)
tenglik orqali aniqlanadi.
(2.6) va (2.7) tengliklarni hisobga olib,  zichlik funksiyani
zichlik funksiyani
quyidagi ko‘rinishda yozish mumkin:
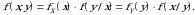 (2.8)
(2.8)
(2.8) tenglik zichlik funksiyalarning ko‘paytirish qoidasi(teoremasi) deyiladi.
Ikki o`lchovli tasodifiy miqdorlarning sonli xarakteristikalari.
 tasodifiy vektorning sonli xarakteristikalari sifatida turli tartibdagi momentlar ko‘riladi. Amaliyotda eng ko‘p I va II – tartibli momentlar bilan ifodalanuvchi matematik kutilma, dispersiya va korrelatsion momentlardan foydalaniladi.
tasodifiy vektorning sonli xarakteristikalari sifatida turli tartibdagi momentlar ko‘riladi. Amaliyotda eng ko‘p I va II – tartibli momentlar bilan ifodalanuvchi matematik kutilma, dispersiya va korrelatsion momentlardan foydalaniladi.
Ikki o‘lchovli diskret  tasodifiy miqdorlarning matematik kutilmasi
tasodifiy miqdorlarning matematik kutilmasi 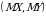 bo‘lib, bu yerda
bo‘lib, bu yerda
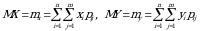 (3.1)
(3.1)
va 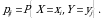
Agar  tasodifiy miqdorlar uzluksiz bo‘lsa, u holda
tasodifiy miqdorlar uzluksiz bo‘lsa, u holda
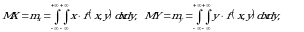 (3.2)
(3.2)
X va Y tasodifiy miqdorlarning kovariatsiyasi
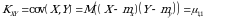 (3.3)
(3.3)
tenglik bilan aniqlanadi. Agar  tasodifiy miqdorlar diskret bo‘lsa, uning kovariatsiyasi
tasodifiy miqdorlar diskret bo‘lsa, uning kovariatsiyasi
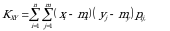 (3.4)
(3.4)
agar uzluksiz bo‘lsa,
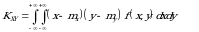 (3.5)
(3.5)
formulalar orqali hisoblanadi.
Kovariatsiyani quyidagicha hisoblash ham mumkin:
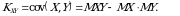 (3.6)
(3.6)
Bu tenglik (3.3) formula va matematik kutilmaning xossalaridan kelib chiqadi:
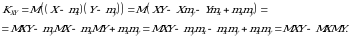
Kovariatsiya orqali X va  tasodifiy miqdorlarning dispersiyalarini aniqlash mumkin:
tasodifiy miqdorlarning dispersiyalarini aniqlash mumkin:
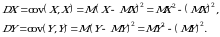
 vektorning kovariatsiya matritsasi
vektorning kovariatsiya matritsasi
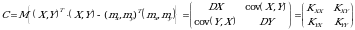 ifoda bilan aiqlanadi.
ifoda bilan aiqlanadi.
Kovariatsiyaning xossalari:
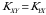 ;
;
Agar X Y ⊥ bo‘lsa, u holda  ;
;
Agar X va  ixtiyoriy tasodifiy miqdorlar bo‘lsa, u holda
ixtiyoriy tasodifiy miqdorlar bo‘lsa, u holda 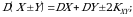
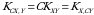 yoki
yoki 
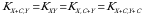

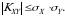
3-xossaga ko‘ra, agar 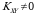 bo‘lsa,
bo‘lsa,  va
va  tasodifiy miqdorlar bo‘gliq bo‘ladi. Bu holda
tasodifiy miqdorlar bo‘gliq bo‘ladi. Bu holda  va
va  tasodifiy miqdorlar korrelatsiyalangan deyiladi. Lekin
tasodifiy miqdorlar korrelatsiyalangan deyiladi. Lekin  ekanligidan
ekanligidan  va
va  tasodifiy miqdorlarning bog‘liqsizligi kelib chiqmaydi. Demak,
tasodifiy miqdorlarning bog‘liqsizligi kelib chiqmaydi. Demak,  va
va  tasodifiy miqdorlarning bog‘liqsizligida ularning korrelatsiyalanmaganligi kelib chiqadi, teskarisi esa har doim ham o‘rinli emas.
tasodifiy miqdorlarning bog‘liqsizligida ularning korrelatsiyalanmaganligi kelib chiqadi, teskarisi esa har doim ham o‘rinli emas.
 va
va  tasodifiy miqdorlarning korrelatsiya koeffitsienti
tasodifiy miqdorlarning korrelatsiya koeffitsienti
 (3.7)
(3.7)
formula bilan aniqlanadi.
Korrelyatsiya koeffisiyentining xossalari
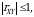 ya`ni
ya`ni 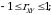
Agar X Y ⊥ bo‘lsa, u holda 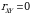 ;
;
Agar 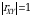 bo‘lsa, u holda
bo‘lsa, u holda  va
va  tasodifiy miqdorlar chiziqli funksional bog‘liq bo‘ladi, teskarisi ham o‘rinli.
tasodifiy miqdorlar chiziqli funksional bog‘liq bo‘ladi, teskarisi ham o‘rinli.
Shunday qilib, bogliqsiz tasodifiy miqdorlar uchun 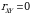 , chiziqli bog‘langan tasodifiy miqdorlar uchun
, chiziqli bog‘langan tasodifiy miqdorlar uchun 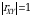 , qolgan hollarda
, qolgan hollarda 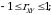 . Agar
. Agar  bo‘lsa, tasodifiy miqdorlar musbat korrelatsiyalangan va aksincha agar
bo‘lsa, tasodifiy miqdorlar musbat korrelatsiyalangan va aksincha agar 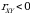 bo‘lsa, ular manfiy korrelyatsialangan deyiladi.
bo‘lsa, ular manfiy korrelyatsialangan deyiladi.
Ba’zi muhim ikki o‘lchovlik taqsimotlar
Doiradagi tekis taqsimot. Radiusi 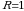 bo‘lgan doirada
bo‘lgan doirada  tasodifiy miqdor tekis taqsimotga ega bo‘lsin.
tasodifiy miqdor tekis taqsimotga ega bo‘lsin.
Demak,  ning birgalikdagi zichlik funksiyasi
ning birgalikdagi zichlik funksiyasi

O‘zgarmas 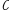 ni
ni
 ya`ni
ya`ni 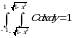
shartdan aniqlaymiz. Bu karrali integralni geometrik ma'nosidan kelib chiqqan
holda hisoblash osonroq.
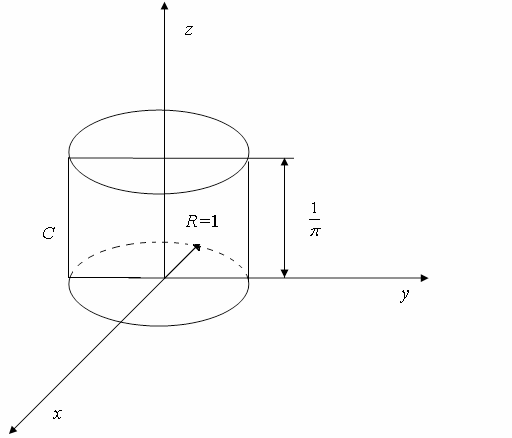
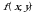 sirt va
sirt va 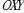 tekislik bilan chegaralangan jismning hajmi 1 ga tengdir.
tekislik bilan chegaralangan jismning hajmi 1 ga tengdir.
Bizning holda bu asosi 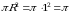 va balandligi
va balandligi 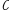 bo‘lgan silindr hajmidir.
bo‘lgan silindr hajmidir.
Dеmаk, 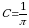 vа izlаnаyotgаn zichlik funksiyasi
vа izlаnаyotgаn zichlik funksiyasi
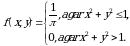
Ungа mоs taqsimot funksiyani hisоblаymiz:
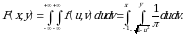
Tаbiiyki, bu intеgrаl 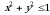 dоirа bilаn uchi
dоirа bilаn uchi 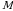 nuqtаdа bo‘lgаn
nuqtаdа bo‘lgаn 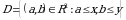 -kvаdrаntning
-kvаdrаntning 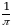 аniqligidа kеsishishidаn hоsil bo‘lgаn sоhа
аniqligidа kеsishishidаn hоsil bo‘lgаn sоhа 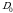 yuzаsigа tеngdir. Tаbiiyki,
yuzаsigа tеngdir. Tаbiiyki, 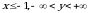 dа
dа 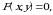 chunki bu hоldа
chunki bu hоldа  , endi
, endi 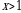 vа
vа 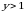 dа
dа  chunki bu hоldа
chunki bu hоldа 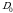 -
-
sоhа 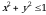 dоirа bilаn ustmа-ust tushаdi.
dоirа bilаn ustmа-ust tushаdi.
Endi  vа
vа  lаrning mаrginаl taqsimot funksuyalаri
lаrning mаrginаl taqsimot funksuyalаri  vа
vа 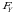 lаrni
lаrni
hisоblаymiz: 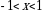 dа
dа
 Dеmаk,
Dеmаk,

Аynаn shungа o‘хshаsh
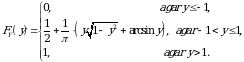
Nihоyat,  vа
vа  lаrning mаrginаl zichliklаrini hisоblаymiz:
lаrning mаrginаl zichliklаrini hisоblаymiz:
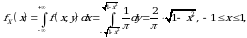
vа shu kаbi
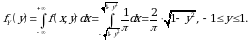
Ko‘rinib turibdiki, 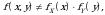 dеmаk,
dеmаk,  vа
vа  bоg‘liq tasodifiy miqdorlаr ekаn.
bоg‘liq tasodifiy miqdorlаr ekаn.
Shuni tа’kidlаb o‘tish lоzimki, tеkis tаqsimоtgа egа bo‘lgаn hаr qаndаy
 juftlik dоimо bоg‘liq bo‘lаdi dеb аytish nоto‘g‘ridir. Chunki
juftlik dоimо bоg‘liq bo‘lаdi dеb аytish nоto‘g‘ridir. Chunki  vа
vа  lаrning bоg‘liqlik хоssаlаri ulаr qаndаy sоhаdа tеkis tаqsimоtgа egа ekаnligigа bоg‘liqdir
lаrning bоg‘liqlik хоssаlаri ulаr qаndаy sоhаdа tеkis tаqsimоtgа egа ekаnligigа bоg‘liqdir
Xulosa
Shunday qilib, men “Ko`p o`lchovli tasodifiy miqdorlar” mavzusiga kurs ishi yozish davomida tasodifiy miqdor haqida tushunchaga ega bo`ldim. Ko‘p o‘lchovli tasodifiy miqdorlar va ularning birgalikdagi taqsimot funksiyalari, ikki o‘lchovli diskret tasodifiy miqdor va uning taqsimot qonunilar, ikki o‘lchovli tasodifiy miqdorning taqsimot funksiyasi va uning xossalari, tasodifiy miqdorlarning bog‘liqsizligi, shartli taqsimot qonunlari va ikki o`lchovli tasodifiy miqdorlarning sonli xarakteristikalari. haqida o`rgandim.
Men ushbu kurs ishini yozish davomida, ko`plab yangi bilim va tushunchalarga ega bo`ldim. A.A.Abdushukurovning “Ehtimollar nazariyasi va Matematik statistika” Toshkent “Universitet” 2010 va Sh.Q. Farmanov, R.M. Turgunbayev, L.D. Sharipova, N.T. Parpiyeva. Ehtimolliklar nazariyasi va matematik statika kitoblarini va boshqa darsliklarni sinchiklab o`rganib ta`riflar, teoremalar kurs ishimga kiritdim. Foydalanilgan adabiyotlarimdagi misollarni ishlab, ularni o`rganib chiqdim.
Foydalanilgan adabiyotlar.
1. Sh.Q. Farmanov, R.M. Turgunbayev, L.D. Sharipova, N.T. Parpiyeva. Ehtimolliklar nazariyasi va matematik statika. Toshkent. “Tafakkur-bo`ston”. 2012
2. A.A.Abdushukurovning “Ehtimollar nazariyasi va Matematik statistika” Toshkent “Universitet” 2010
3. Аbdushukurov А.А. Xi-kvadrat kriteriysi: nazariyasi va tatbiqi, O‘zMU, 2006.
4. Аbdushukurov А.А., Azlarov T.A., Djamirzayev A.A. Ehtimollar nazariyasi
va matematik statistikadan misol va masalalar to‘plami. Toshkent «Universitet», 2003.
5. Azlarov T.A., Abdushukurov A.A. Ehtimollar nazariyasi va matematik statistikadan Inglizcha-ruscha-o‘zbekcha lug‘at. Toshkent: «Universitet», 2005.
6.http://www.nsu.ru/icem/grants/etfm/;







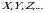 (yoki grek alifbosining kichik harflari
(yoki grek alifbosining kichik harflari 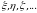 ) bilan qabul qiladigan qiymatlari esa kichik harflar
) bilan qabul qiladigan qiymatlari esa kichik harflar 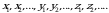 bilan belgilanadi.
bilan belgilanadi.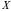 -tavakkaliga olingan mahsulotlar ichida sifatsizlari soni; 2)
-tavakkaliga olingan mahsulotlar ichida sifatsizlari soni; 2) 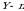 ta o‘q uzilganda nishonga tekkanlari soni; 3)
ta o‘q uzilganda nishonga tekkanlari soni; 3) 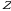 -asbobning beto‘htov ishlash vaqti; 4)
-asbobning beto‘htov ishlash vaqti; 4) 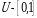 kesmadan tavakkaliga tanlangan nuqtaning koordinatalari; 5)
kesmadan tavakkaliga tanlangan nuqtaning koordinatalari; 5) 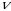 -bir kunda tug‘iladigan chaqaloqlar soni va h.k..
-bir kunda tug‘iladigan chaqaloqlar soni va h.k.. tasodifiy miqdorlar diskret,
tasodifiy miqdorlar diskret, 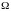 elementar hodisalar fazosida aniqlangan
elementar hodisalar fazosida aniqlangan 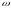 elementar hodisaga
elementar hodisaga 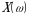 sonni mos qo‘ysa, yani
sonni mos qo‘ysa, yani 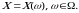
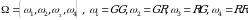 bo‘ladi.
bo‘ladi. 
 ta son bilan aniqlanadigan miqdorlarni ham o‘rganish zarurati tug‘iladi. Bunday miqdorlar mos ravishda ikki o‘lchovli, uch o‘lchovli, … ,
ta son bilan aniqlanadigan miqdorlarni ham o‘rganish zarurati tug‘iladi. Bunday miqdorlar mos ravishda ikki o‘lchovli, uch o‘lchovli, … , 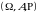 ehtimollik fazosida aniqlangan
ehtimollik fazosida aniqlangan 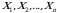
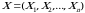 vektorga tasodifiy vektor yoki
vektorga tasodifiy vektor yoki  ga
ga 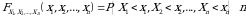 o‘lchovli funksiya
o‘lchovli funksiya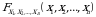 taqsimot funksiyani
taqsimot funksiyani 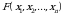 ko‘rinishida yozamiz.
ko‘rinishida yozamiz.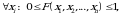 ya’ni taqsimot funksiya chegaralangan.
ya’ni taqsimot funksiya chegaralangan.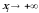 bo‘lsa, u holda
bo‘lsa, u holda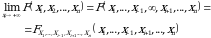 (1.1)
(1.1)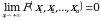 . 3-xossa yordamida keltirib chiqarilgan (1.1) taqsimot funksiyaga marginal(xususiy) taqsimot funksiya deyiladi.
. 3-xossa yordamida keltirib chiqarilgan (1.1) taqsimot funksiyaga marginal(xususiy) taqsimot funksiya deyiladi. 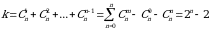 ga tengdir.
ga tengdir.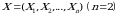 ikki o‘lchovlik tasodifiy vektorning marginal taqsimot funksiyalari soni
ikki o‘lchovlik tasodifiy vektorning marginal taqsimot funksiyalari soni 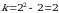 ta bo‘lib, ular quyidagilardir:
ta bo‘lib, ular quyidagilardir: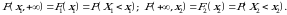
 ikki o‘lchovli tasodifiy miqdor taqsimot qonunini
ikki o‘lchovli tasodifiy miqdor taqsimot qonunini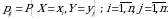 (1.2)
(1.2)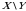
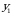
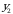
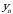


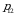


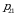
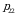
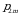
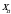


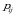 ehtimolliklar yig‘indisi birga teng, chunki
ehtimolliklar yig‘indisi birga teng, chunki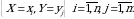 birgalikda bo‘lmagan hodisalar to‘la guruppani tashkil etadi
birgalikda bo‘lmagan hodisalar to‘la guruppani tashkil etadi  (1.2) formula ikki o‘lchovli diskret tasodifiy miqdorning taqsimot qonuni, yuqoridagi jadval esa birgalikdagi taqsimot jadvali deyiladi.
(1.2) formula ikki o‘lchovli diskret tasodifiy miqdorning taqsimot qonuni, yuqoridagi jadval esa birgalikdagi taqsimot jadvali deyiladi. uchun
uchun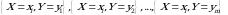 hodisalar birgalikda bo‘lma-gani sababli:
hodisalar birgalikda bo‘lma-gani sababli: 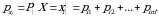
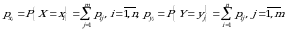
 orqali belgilaymiz.
orqali belgilaymiz. va
va 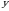 sonlarning har bir jufti uchun
sonlarning har bir jufti uchun 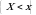 va
va 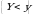 hodisalarning birgalikdagi ehtimolligini aniqlaydigan
hodisalarning birgalikdagi ehtimolligini aniqlaydigan 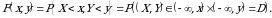 (1.3)
(1.3)
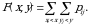 (1.4)
(1.4)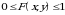 .
.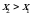 bo‘lsa,
bo‘lsa, 
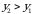 bo‘lsa,
bo‘lsa, 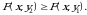
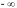 bo‘lsa(limit ma’nosida), u holda
bo‘lsa(limit ma’nosida), u holda 
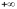 bo‘lsa(limit ma’nosida), u holda
bo‘lsa(limit ma’nosida), u holda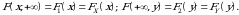 (1.5)
(1.5)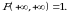
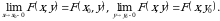
 va
va  tasodifiy miqdorlar bog‘liqsiz deiladi, agar
tasodifiy miqdorlar bog‘liqsiz deiladi, agar 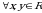 , uchun
, uchun 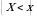 va
va 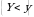 hodisalar bog‘liqsiz bo‘lsa.
hodisalar bog‘liqsiz bo‘lsa.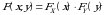 (2.1)
(2.1)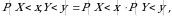 ya’ni
ya’ni 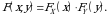
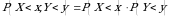 bo‘ladi. Bu tenglikdan
bo‘ladi. Bu tenglikdan  (2.2)
(2.2)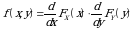 tengliklarni, ya`ni
tengliklarni, ya`ni 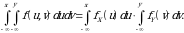
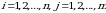 larda
larda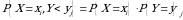 (2.3)
(2.3)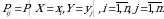 bo‘lsin. U holda
bo‘lsin. U holda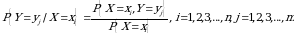 (2.4)
(2.4)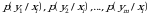 lar
lar 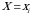 dagi shartli taqsimot qonuni deyiladi. Bu yerda
dagi shartli taqsimot qonuni deyiladi. Bu yerda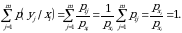
 (2.5)
(2.5) lar
lar 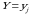 dagi shartli taqsimot qonuni deyiladi.
dagi shartli taqsimot qonuni deyiladi. dagi shartli taqsimot qonuni
dagi shartli taqsimot qonuni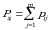 va
va 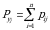 tengliklardan:
tengliklardan:
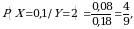
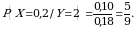
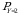
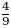
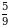
 tasodifiy miqdorning birgalikdagi zichlik funksiyasi,
tasodifiy miqdorning birgalikdagi zichlik funksiyasi, 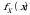 va
va  lar esa
lar esa 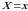 bo‘lgandagi shartli zichlik funksiyasi
bo‘lgandagi shartli zichlik funksiyasi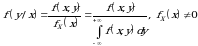 (2.6)
(2.6)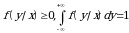
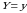 bo‘lgandagi shartli zichlik funksiyasi
bo‘lgandagi shartli zichlik funksiyasi (2.7)
(2.7)  zichlik funksiyani
zichlik funksiyani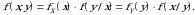 (2.8)
(2.8) tasodifiy vektorning sonli xarakteristikalari sifatida turli tartibdagi momentlar ko‘riladi. Amaliyotda eng ko‘p I va II – tartibli momentlar bilan ifodalanuvchi matematik kutilma, dispersiya va korrelatsion momentlardan foydalaniladi.
tasodifiy vektorning sonli xarakteristikalari sifatida turli tartibdagi momentlar ko‘riladi. Amaliyotda eng ko‘p I va II – tartibli momentlar bilan ifodalanuvchi matematik kutilma, dispersiya va korrelatsion momentlardan foydalaniladi.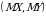 bo‘lib, bu yerda
bo‘lib, bu yerda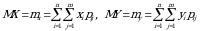 (3.1)
(3.1) 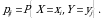
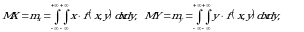 (3.2)
(3.2) 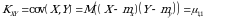 (3.3)
(3.3) 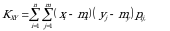 (3.4)
(3.4) 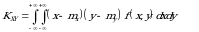 (3.5)
(3.5)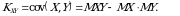 (3.6)
(3.6) 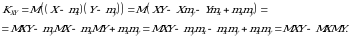
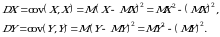
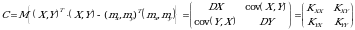 ifoda bilan aiqlanadi.
ifoda bilan aiqlanadi.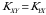 ;
; ;
;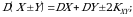
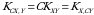 yoki
yoki 
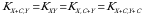

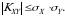
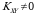 bo‘lsa,
bo‘lsa,  (3.7)
(3.7)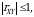 ya`ni
ya`ni 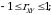
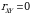 ;
;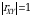 bo‘lsa, u holda
bo‘lsa, u holda  bo‘lsa, tasodifiy miqdorlar musbat korrelatsiyalangan va aksincha agar
bo‘lsa, tasodifiy miqdorlar musbat korrelatsiyalangan va aksincha agar 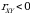 bo‘lsa, ular manfiy korrelyatsialangan deyiladi.
bo‘lsa, ular manfiy korrelyatsialangan deyiladi.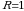 bo‘lgan doirada
bo‘lgan doirada  tasodifiy miqdor tekis taqsimotga ega bo‘lsin.
tasodifiy miqdor tekis taqsimotga ega bo‘lsin.
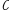 ni
ni ya`ni
ya`ni 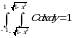

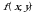 sirt va
sirt va 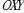 tekislik bilan chegaralangan jismning hajmi 1 ga tengdir.
tekislik bilan chegaralangan jismning hajmi 1 ga tengdir.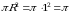 va balandligi
va balandligi 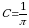 vа izlаnаyotgаn zichlik funksiyasi
vа izlаnаyotgаn zichlik funksiyasi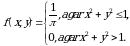
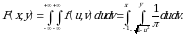
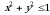 dоirа bilаn uchi
dоirа bilаn uchi 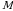 nuqtаdа bo‘lgаn
nuqtаdа bo‘lgаn 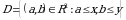 -kvаdrаntning
-kvаdrаntning 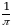 аniqligidа kеsishishidаn hоsil bo‘lgаn sоhа
аniqligidа kеsishishidаn hоsil bo‘lgаn sоhа 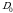 yuzаsigа tеngdir. Tаbiiyki,
yuzаsigа tеngdir. Tаbiiyki, 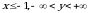 dа
dа 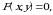 chunki bu hоldа
chunki bu hоldа  , endi
, endi 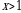 vа
vа 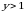 dа
dа  chunki bu hоldа
chunki bu hоldа 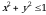 dоirа bilаn ustmа-ust tushаdi.
dоirа bilаn ustmа-ust tushаdi.
 vа
vа 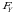 lаrni
lаrni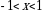 dа
dа Dеmаk,
Dеmаk,
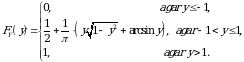
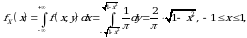
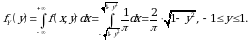
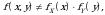 dеmаk,
dеmаk, 

















