| Всякая кривая второго порядка относительно декартовых координат задается уравнением: 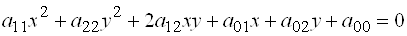 , (18) , (18)
Где aik– константы. Это уравнение задает окружность, эллипс, параболу или гиперболу в зависимости от соотношений между его коэффициентами. Например, если в уравнении: a11= a22 и a12=0, то оно является уравнением окружности. Если уравнение (18) разлагается на два линейных множителя, то в этом случае оно определяет пару прямых, которые могут пересекаться, быть параллельными или совпадать. 2.Окружность и её уравнение. Определение. Окружностью называется геометрическое место точек плоскости, равноудаленных от некоторой фиксированной точки плоскости, называемой ее центром. Каноническое уравнение окружности имеет вид: 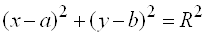 , (19) , (19)
Где(a,b)– координаты центра, а R– радиус окружности. Пример 1. Найти центр и радиус окружности 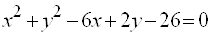 . . Решение. Выделяя полные квадраты по x и по y, приведем уравнение к виду 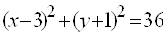 , , откуда, сравнивая с (19), находим C(3; -1)и R = 6. Пример 2. Составить уравнение окружности, проходящей через три точки 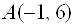 , , 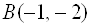 , , 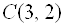 . . Решение. Центр окружности находится в точке пересечения перпендикуляров, проведенных через середины хорд. Точка М1(-1;2) – середина хорды АВ, а  М1( 1;4) – середина АС и 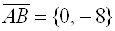 , , 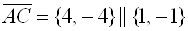 . . Уравнения перпендикуляров к хордам АВ и АС, проходящих через их середины, имеют вид: 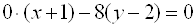 и и 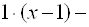 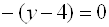 или или 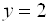 и и 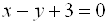 . . Точка пересечения этих прямых Р(-1;2). Для нахождения радиуса найдем расстояние между точками 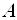 и и 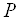 : : 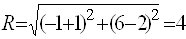 . . Запишем уравнение окружности: 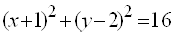 . . 3. Эллипс и его уравнение. Определение. Эллипсом называется геометрическое место всех точек плоскости, сумма расстояний которых до двух данных точек плоскости, называемых фокусами, есть величина постоянная. Каноническое уравнение эллипса: 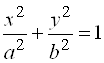 , ,
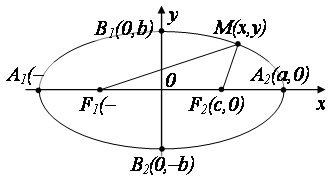
Где а– большая полуось, в– малая полуось, 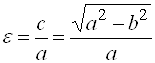 – эксцентриситет эллипса. – эксцентриситет эллипса. Прямую, на которой расположены фокусы эллипса F1 u F2, называют фокальной осью, а 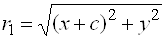 и и 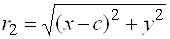 – фокальными радиусами. – фокальными радиусами. Прямые x= 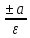 называют директрисами эллипса. называют директрисами эллипса. Пример 3. Убедитесь, что уравнение определяет эллипс. Найдите полуоси, координаты фокусов, эксцентриситет, уравнения директрис. Решение. Приведем уравнение к каноническому виду , откуда  , ,  . Из условия . Из условия  найдем найдем  , то есть . , то есть . Тогда , а уравнение директрис x= (±25)/ . . Пример 4. Доказать, что уравнение определяет эллипс. Найти координаты его центра симметрии. Решение. Преобразуем данное уравнение, выделив полные квадраты по  и по и по  : : . Обозначим  , где , где  – новые переменные. Тогда уравнение примет вид – новые переменные. Тогда уравнение примет вид   или, приводя к каноническому виду, . или, приводя к каноническому виду, . Сравнивая полученное уравнение с уравнением (20) убеждаемся, что кривая – эллипс. Центр его симметрии находится в точке (-2;2). 4. Гипербола и её уравнение. Определение. Гиперболой называется геометрическое место точек плоскости, разность расстояний которых до двух данных точек  и и  плоскости, называемых фокусами, есть величина постоянная. плоскости, называемых фокусами, есть величина постоянная. Каноническое уравнение гиперболы: , (21) Где  . . Точки  , ,  называются вершинами гиперболы, прямые называются вершинами гиперболы, прямые  являются асимптотами гиперболы, являются асимптотами гиперболы,  – действительная полуось, – действительная полуось,  – мнимая полуось, – мнимая полуось,  – эксцентриситет гиперболы, прямые – эксцентриситет гиперболы, прямые  – ее директрисы. – ее директрисы. Пример 5. Написать уравнение гиперболы и ее асимптот, если фокусы гиперболы находятся в точках и длина вещественной оси равна 6. Решение. По условию  , тогда из формулы , тогда из формулы  найдем найдем  . Каноническое уравнение гиперболы: . Каноническое уравнение гиперболы:  уравнения асимптот: уравнения асимптот:  . . Пример 6. Написать уравнение гиперболы, проходящей через точку  , асимптоты которой , асимптоты которой  . . Решение. Из уравнения асимптот следует, что  . Уравнение гиперболы будем искать в виде . Так как точка . Уравнение гиперболы будем искать в виде . Так как точка  лежит на гиперболе, то лежит на гиперболе, то  . Решая систему найдем . Решая систему найдем  , ,  . Получаем или . . Получаем или . Пример 7. Доказать, что уравнение  определяет гиперболу. Написать уравнения ее асимптот. определяет гиперболу. Написать уравнения ее асимптот. Решение. Выделим полные квадраты по  и по и по  : : или . Обозначая  и деля обе части уравнения на 9, получим каноническое уравнение и деля обе части уравнения на 9, получим каноническое уравнение  , откуда следует, что , откуда следует, что  , центр находится в точке то есть , центр находится в точке то есть  . Учитывая, что асимптоты проходят через точку . Учитывая, что асимптоты проходят через точку  и и  , запишем их уравнения: , запишем их уравнения: или . 5. Парабола и её уравнение. Определение. Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки  плоскости, называемой фокусом, и данной прямой, называемой директрисой. плоскости, называемой фокусом, и данной прямой, называемой директрисой. Каноническое уравнение параболы  , (22) , (22)
Где  (параметр параболы) – расстояние между фокусом и директрисой, а уравнение ее директрисы (параметр параболы) – расстояние между фокусом и директрисой, а уравнение ее директрисы  . . Так как уравнение параболы содержит  , то она симметрична относительно оси , то она симметрична относительно оси  . Ось симметрии параболы называется осью параболы. . Ось симметрии параболы называется осью параболы. Вершиной параболы называется точка пересечения параболы с ее осью симметрии. Пример 8. Парабола с вершиной в начале координат проходит через точку  и симметрична относительно оси и симметрична относительно оси  . Написать ее каноническое уравнение. . Написать ее каноническое уравнение. Решение. Подставляя координаты точки  в уравнение (22), найдем, что в уравнение (22), найдем, что  . Значит, уравнение параболы . Значит, уравнение параболы  . . Пример 9. Доказать, что уравнение определяет параболу. Найти значение ее параметра и координаты вершины. Решение. Выделяя полный квадрат, получим   . Если положить . Если положить  то уравнение примет вид то уравнение примет вид  . Сравнивая его с каноническим уравнением (22), находим . Сравнивая его с каноническим уравнением (22), находим  , откуда , откуда  . Вершина параболы находится в точке . Вершина параболы находится в точке  , ,  , то есть , то есть  . . Для самостоятельного решения. 1. Найти координаты центра и радиус окружности . Ответ:  , ,  . . 2. Составить уравнение окружности, если она проходит через точки  и и  , а центр ее лежит на прямой , а центр ее лежит на прямой  . . Ответ: . 3. Найти площадь четырехугольника, две вершины которого лежат в фокусах эллипса , а две другие совпадают с концами его малой оси. Ответ: 16. 4. Составить уравнение хорды параболы  , которая проходит через ее вершину перпендикулярно прямой , которая проходит через ее вершину перпендикулярно прямой  . . Ответ: . 5. На параболе  найти точку найти точку  , ближайшую к прямой , ближайшую к прямой  , и вычислить расстояние , и вычислить расстояние  от точки от точки  до прямой. до прямой. Ответ: . 6. Найти площадь треугольника, образованного асимптотами гиперболы  и прямой . и прямой . Ответ: 12. 7. Дана окружность . Найти уравнение радиусов, проведенных из центра в точки пересечения окружности с осью ординат, а также угол между этими радиусами. Ответ: . | 






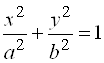 ,
, 
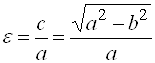 – эксцентриситет эллипса.
– эксцентриситет эллипса.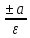 называют директрисами эллипса.
называют директрисами эллипса.


















