Россия, с.Столбово
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 08.04.2024 16:43
Сорокина Елена Васильевна
учитель математики
55 лет
2 674
18 377 
Местоположение
Специализация
Магический квадрат
Категория:
Математика
03.11.2020 11:41
Просмотр содержимого документа
«Документ Microsoft Word»
Аннотация
Цель данной работы - выяснить различные варианты составления магических квадратов, изучив которые можно заполнить квадрат любого размера, а так же рассмотреть возможные области их применения.
В ходе работы были использованы следующие методы:
поисковый метод (использование справочной и учебной литературы, а также информационных ресурсов глобальной сети Интернет);
практический метод (составление магических квадратов на основе полученных знаний);
исследовательский метод (составление психологического портрета личности по квадрату Пифагора).
В работе исследуется происхождение и формулируется определение магических квадратов, рассмотрены различные виды квадратов, способы их составления, а так же показана область применения этих загадочных фигур.
В ходе работы над проектом, я не только расширила свои знания по данной теме и повысила свои вычислительные навыки, но и научилась составлять магический квадрат Пифагора, с помощью которого можно познать характер человека, состояние его здоровья, потенциальные возможности, раскрыть достоинства и недостатки.
Во время летних каникул мне часто приходилось решать кроссворды. В одном журнале меня заинтересовала задача на логическое мышление - заполнение магического квадрата. Необходимо было заполнить квадрат числами от 1 до 9 так, чтобы сумма чисел по столбцам, по строкам и по диагоналям была одинакова.
Как это сделать, я не знала, поэтому решила обратиться за помощью к папе. Мы перебирали различные варианты, и, наконец, задача решена. И вот мой квадрат заполнен. Но метод перебора мне не понравился: он отнимает много времени, хотя и позволяет тренировать свои вычислительные навыки. Я предположила, что существует специальный прием, который помогает быстро заполнить магический квадрат. Это и побудило меня заняться данным проектом.
История появления магических квадратов.
Магический квадрат - квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
Страна, в которой был впервые придуман магический квадрат, точно неизвестна, неизвестен век, даже тысячелетие нельзя установить точно. Первые упоминания о магических квадратах были у древних китайцев. И, вероятно, самым старым из дошедших до нас магических квадратов является таблица Ло Шу. Она имеет размер 3*3 и заполнена натуральными числами от 1 до 9. В этом магическом квадрате сумма чисел в каждой строке, столбце и диагонали равна 15. Согласно одной из легенд прообразом Ло Шу стал узор из связанных черных и белых точек, украшавший панцирь огромной священной черепахи, всплывшей из вод реки Хуанхэ.
Из Китая магические квадраты распространились сначала в Индию, а затем и в другие страны. В начале XVI века знаменитый немецкий художник Альбрехт Дюрер увековечил магический квадрат в искусстве, изобразив его на гравюре «Меланхолия». Дата создания гравюры (1514 год) указана числами, стоящими в двух центральных клетках нижней строки.
В IX веке. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры. Получение магических квадратов считалось популярным развлечением среди математиков. Ими создавались огромные квадраты, например, 45*45, содержащий числа от 1 до 2025, Были придуманы способы построения магических квадратов любого размера, однако до сих пор не найдена формула, по которой можно было бы найти количество магических квадратов данного размера.
В наше время магические квадраты продолжают привлекать к себе внимание не только специалистов, но и любителей математических игр и развлечений. За последнее столетие значительно возросло число книг по занимательной математике, в которых содержатся головоломки и задачки, связанные с необычными квадратами.
Виды магических квадратов и способы их заполнения.
В ходе своей работы, я пришла к выводу, что магических квадратов 2*2 не существует. Квадрат размером 2*2 должен был бы состоять из чисел 1,2,3,4, а его постоянная была бы равна 5. У такого квадрата по две строки, столбца и диагонали. Чтобы квадрат стал магическим, надо представить число 5 в виде суммы двух данных чисел шестью различными способами, но это сделать не возможно! Ведь таких комбинаций всего две: 1+ 4 и 2+3. Как ни расставляй числа в клетках таблицы, их сумма будет равна 5 либо в каждой строке, либо в обоих столбцах, либо по диагоналям, но никак не одновременно.
Существует единственный магический квадрат 3*3, так как остальные магические квадраты 3*3 получаются из него либо перестановкой строк или столбцов либо путем поворота исходного квадрата на 900 или на 1800
Общий метод построения квадратов неизвестен. Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата. Квадраты могут быть:
- нечетными, то есть состоять из нечетного числа клеток,
- четно-четные, то есть порядок равен удвоенному четному;
- четно-нечетные, то есть порядок равен удвоенному нечетному.
Магические квадраты нечетного порядка.
| 1. Метод достроения. Рассмотрю на примере квадрата 5*5. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) Построю квадрат с 25 клетками и временно дострою его до симметричной ступенчатой ромбовидной фигуры. Достроенные клеточки обозначу символом *
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2) В полученной фигуре располагаю по порядку косыми рядами сверху-вниз-направо 25 целых чисел от 1 до 25.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3). Каждое число, расположенное вне исходного (выделенного) квадрата, следует перенести вдоль того же ряда или столбца ровно на столько клеток от той клетки, которую оно занимает, каков порядок квадрата, в моем примере – на пять. | 1 - вниз под 13 2 - вниз под 14 6 - вниз под 18 21 - вправо за 13 22 - вправо за 14 16 - вправо за 8 | 5 - влево перед 13 4 - влево перед 12 10-влево перед 18 25 - вверх над 13 24 - вверх над 12 20 - вверх над 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4) Таким образом, все ячейки квадрата заполнены. Сумма чисел в столбцах, строках и диагоналях равна 65.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Магические квадраты четно-четного порядка.
| 1. Порядок 2n . Этот метод удобно рассматривать на примере магического квадрата 8*8. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) Исходный квадрат разделю на соответствующее число квадратов порядка 4. В данном случае таких квадратов будет 4. В каждом подквадрате отмечу диагональные элементы символом. Остальные элементы построчно заполню порядковыми целыми числами в направлении слева-направо и сверху-вниз. Числа, приходящиеся на выделенные диагональные элементы, должны быть пропущены. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2) Отмеченные * диагональные элементы квадрата заполняю пропущенными целыми числами в порядке возрастания в направлении справа-налево и снизу-вверх, причем числа, приходящиеся на недиагональные элементы, должны быть пропущены. Сумма чисел по строкам, столбцам и диагоналям равна 260.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. Метод Раус – Бола. Для примера возьму квадрат 8-го порядка. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) Квадрат заполняется слева направо и сверху вниз числами от 1 до n2 в их естественном порядке. Разделить заполненный числами от 1 до 64 квадрат на четыре равных квадрата порядка 4. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2) В каждой строке и столбце верхнего левого квадрата порядка 4 отметить 2 (8=2*2*2) клетки (всего 8 клеток). Это можно сделать, применив "шахматный" порядок. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3) Для каждой из отмеченных клеток отметить симметричную ей относительно вертикальной оси клетку.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4) Содержимое каждой из отмеченных клеток переставить с содержимым соответствующей центрально-симметричной ей клетки. После этих перестановок получится магический квадрат. Сумма его элементов равна 260.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Магические квадраты четно-нечетного порядка.
| Диагональный метод. Для примера возьму квадрат 10*10. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) Разделить заполненный числами от 1 до 100 квадрат на четыре квадрата порядка 5 осями симметрии.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2) В левом верхнем квадрате закрашу разным цветом три группы клеток, при этом в каждой строке и в каждом столбце отмечу по две клетки из первой группы и по одной — из второй и третьей групп. Одинаковым цветом выделю клетки, расположенные вдоль диагонали квадрата и прямых, ей параллельных. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3) Клетки, симметричные клеткам первой группы относительно вертикальной оси, закрашу таким же цветом.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4) Число, стоящее в каждой из отмеченных в пункте 2 клеток, переставлю с числом из соответствующей центрально-симметричной клетки.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5) Содержимое каждой клетки второй группы обменяю с содержимым симметричной ей относительно горизонтальной оси клетки.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6) Содержимое каждой клетки третьей группы обменяю с содержимым симметричной ей относительно вертикальной оси клетки. Получится четно-нечетный магический квадрат с суммой, равной 505.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Применение магических квадратов.
Когда я рассмотрела способы составления магических квадратов, меня заинтересовала область их применения. Она показалась мне довольно таки интересной. Сегодня очень актуальным становится вопрос о защите информации. Например, на уроке информатики мы изучали тему кодирование. С помощью магических квадратов так же можно закодировать информацию. Например, зашифровать текст. Расположив буквы согласно числам магического квадрата, получаем фразу «БУДУ В СЕМЬ» или «КЛЮЧИ ПОД КОВРИКОМ».
Так же очень популярна японская головоломка судоку, прародителем которой можно считать Магический квадрат. Она помогает нам развивать логическое мышление и вычислительные навыки. В настоящее время много газет печатают эти головоломки вместе с кроссвордами и другими логическими задачами. Не меньшую популярность завоевали судоку и в сети Интернет.
Англичане используют площадку для игры в шаффлборд, размеченную в виде магического квадрата.
Ну, и, конечно же, в нумерологии. Еще великий ученый Пифагор, считал, что всем на свете управляют числа. Поэтому сущность человека заключается тоже в числе - дате его рождения. Он создал метод построения квадрата, по которому можно познать характер человека, состояние его здоровья и его потенциальные возможности, раскрыть достоинства и недостатки и тем самым выявить, что следует предпринять для его совершенствования. Во времена Пифагора магические квадраты на каждого человека создавались индивидуально. Сейчас есть специальная программа, где вводится дата рождения человека, а на экран выводится готовый магический квадрат. Составлю магический квадрат для себя.
Я родилась 28 июля 1998 года.
1) Складываем числа дня месяца и года рождения, получаем первое рабочее число 44.
2) Далее складываем цифры первого рабочего числа и получаем второе рабочее число 8.
3) Из первого рабочего числа вычитаем удвоенную первую цифру дня рождения, так получается третье рабочее число: 44-(2+2)=40
4) четвертое рабочее число получаем из суммы цифр третьего рабочего числа: 4+0=4
| 1 | 4444 | 7 |
| 2 | - | 888 |
| - | - | 99 |
Теперь выпишу два ряда цифр. Первый состоит из цифр даты рождения: 28.07.1998. Второй - рабочих чисел: 44.8.40.4. Запишу их в квадрат.
«1» – стремлюсь из любого положения извлечь максимальную выгоду, «2» - я человек чувствительный к изменениям в атмосфере, «4444»- у меня отличное здоровье, «7»- для того, чтобы достичь желаемого, я должна много трудиться, «888» – означает, что в жизни, я добьюсь выдающихся результатов, «99»- умна от рождения, знания даются легко.
Чтобы быть более уверенной я использую данный квадрат в качестве талисмана.
Безусловно, не следует слепо верить всему магическому. Возможно, некоторые черты характера и заложены в дате рождения человека, но человек всегда может найти способы что-то изменить в своей судьбе.
Просмотр содержимого документа
«тезисы»
Просмотр содержимого документа
«аннотация»
Просмотр содержимого документа
«выступление»
Просмотр содержимого документа
«текст работы»
Муниципальное бюджетное общеобразовательное учреждение
«Столбовская средняя общеобразовательная школа»
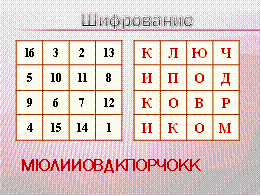
Магический квадрат
Автор: Чарикова Регина Михайловна,
ученица 5 класса
Руководитель: Сорокина Е.В., учитель математики
Столбово, 2016
Оглавление.
Введение…………….……………………………..……………….…………….3
I. Теоретическая часть…………………….………………………..……….......3
1.1. История появления магических квадратов………………..........................3
1.2. Способы заполнения магических квадратов……………………………..5
II. Практическая часть………………..………………………………………….7
2.1. Заполнение магических квадратов изученными способами………………7
Выводы……………………………………………………..………………….....8
Список литературы…………..…...……..............................................................9
Приложения……………………………………………………………….……..10
Введение
Однажды учитель математики предложил мне решить следующую задачу.
Задача: заполнить квадрат 3 на 3 натуральными числами от 1 до 9 включительно, так, чтобы были использованы все цифры и сумма чисел на всех строках, столбцах и диагоналях была одинакова.
Перебирая различные варианты, я пришла к нужному. Меня заинтересовала предложенная задача. Но метод перебора не понравился: он отнимает очень много времени, хотя и позволяет тренировать свои вычислительные навыки. Это побудило меня заняться исследовательской работой.
Цель работы: выяснить различные варианты составления магических квадратов, изучив которые можно заполнить квадрат любого размера.
I. Теоретическая часть.
1.1. История появления магических квадратов.
Магический квадрат, квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
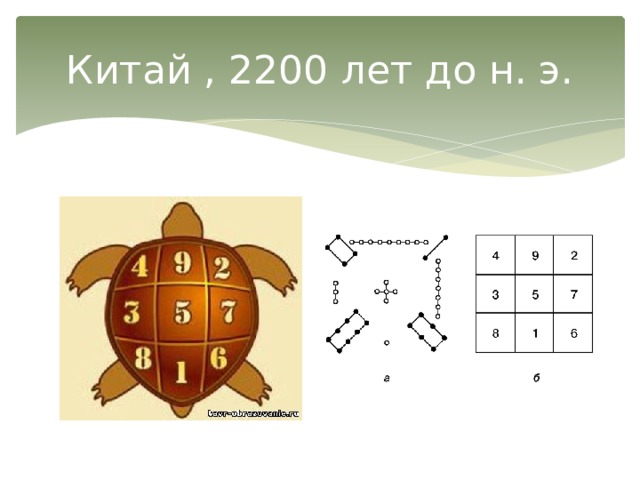
Магический квадрат - древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (около 2200 лет до нашей эры) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы (приложение 1), и эти знаки известны под названием ло-шу и равносильны магическому квадрату размера 3 на 3.
В 11 веке о магических квадратах узнали в Индии, а затем в Японии, где в 16 веке магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 веке византийский писатель Э.Мосхопулос.
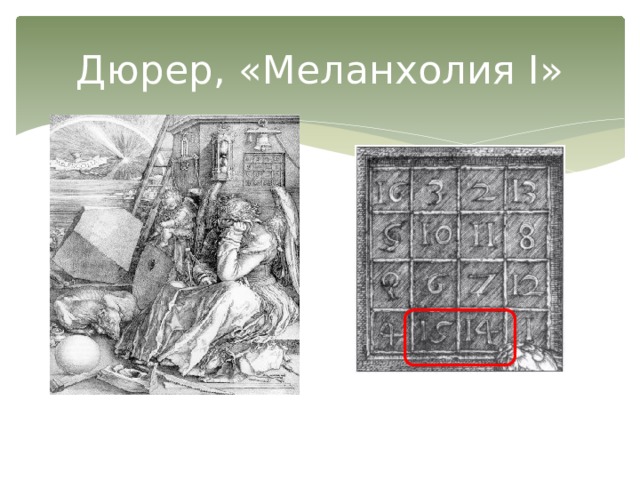
Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера (приложение 2), изображенный на его знаменитой гравюре Меланхолия I. Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки (приложение 3).
Магическим квадратам приписывали различные мистические свойства. В 16 веке Корнелий Генрих Агриппа построил квадраты третьего, четвертого, пятого, шестого, седьмого, восьмого и девятого порядков, которые были связаны с астрологией семи планет.
Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.
В девятнадцатом и двадцатом веках интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры.
На сегодняшний день квадрата размерностью два на два не существует, квадрат три на три только один, квадратов размерностью четыре на четыре около восьмиста, а квадратов пять на пять – около четверти миллиона.
Основная терминология
Каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n2 клеток и называется квадратом n-го порядка.
В большинстве магических квадратов используются первые n последовательных натуральных чисел.
Две диагонали, проходящие через центр квадрата, называются главными диагоналями.
Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы, некоторые из которых мы рассмотрим ниже.
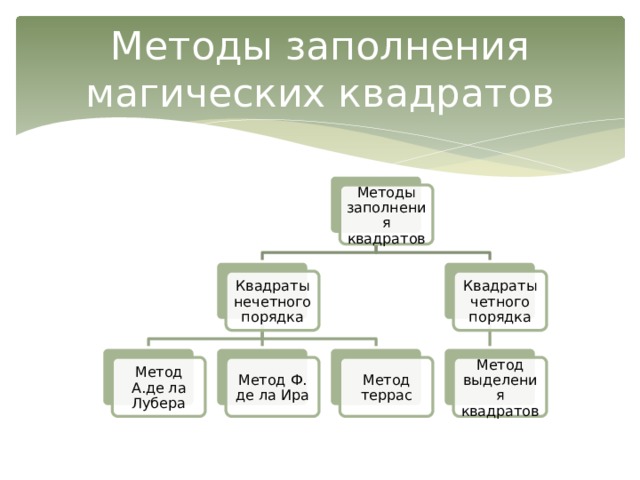
1.2. Способы заполнения магических квадратов
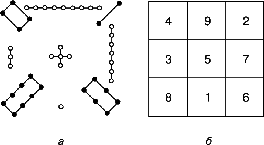
Задачу, которая решалась методом перебора (заполнение магического квадрата третьего порядка) можно решить следующим способом:
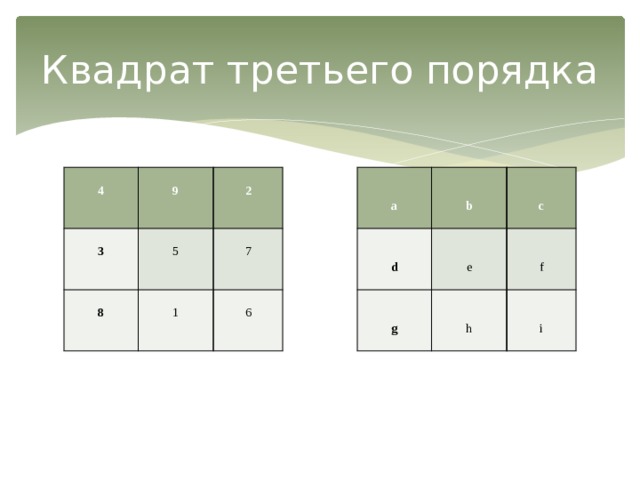
Допустим, мы расставили девять чисел согласно требуемым условиям: заполнить квадрат 3 на 3 натуральными числами от 1 до 9 включительно, так, чтобы были использованы все цифры и сумма чисел на всех строках, столбцах и диагоналях была одинакова (приложение 4).
Тогда должны быть равны суммы
a+b+c = d+e+f = g+h+i = a+d+g = b+e+h = c+f+i = a+e+i = c+e+g = S.
Число S называется константой магического квадрата. Чтобы найти её, надо сложить все числа разделить на размер квадрата
3S= a+b+c + d+e+f + g+h+i = 1+2+3+4+5+6+7+8+9=45.
Отсюда S=15.
Найдём теперь центральный элемент, e. Для этого рассмотрим четыре суммы: центральные вертикаль и горизонталь и обе диагонали.
4S = a+e+i + b+e+h + c+e+g + d+e+f = 3S+3e.
Отсюдаe=S/3=5.
Остальные числа расставляем в соответствии с условиями задачи.
Магические квадраты нечетного порядка можно построить с помощью метода французского геометра 17 в. А.де ла Лубера. Рассмотрим этот метод на примере квадрата 5-го порядка (приложение 5). Число 1 помещается в центральную клетку верхней строки. Все натуральные числа располагаются в естественном порядке циклически снизу вверх в клетках диагоналей справа налево. Дойдя до верхнего края квадрата (как в случае числа 1), продолжаем заполнять диагональ, начинающуюся от нижней клетки следующего столбца. Дойдя до правого края квадрата (число 3), продолжаем заполнять диагональ, идущую от левой клетки строкой выше. Дойдя до заполненной клетки (число 5) или угла (число 15), траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.
Метод Ф.де ла Ира (1640–1718) основан на двух первоначальных квадратах. В клетку первого квадрата вписываются числа от 1 до 5 так, что число 3 повторяется в клетках главной диагонали, идущей вправо вверх, и ни одно число не встречается дважды в одной строке или в одном столбце. То же самое мы проделываем с числами 0, 5, 10, 15, 20 с той лишь разницей, что число 10 теперь повторяется в клетках главной диагонали, идущей сверху вниз. Поклеточная сумма этих двух квадратов образует магический квадрат.
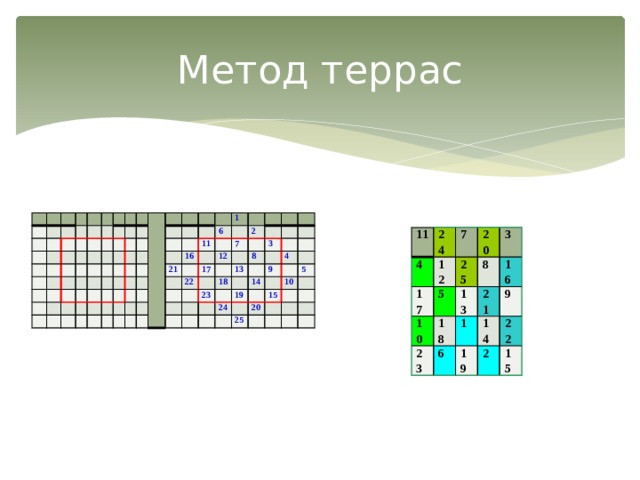
Метод террас(или метод достраивания до ромбовидной фигуры), применяется для построения магических квадратов нечётного порядка: пятого, седьмого и т. д.
Рассмотрим его на примере магического квадрата 3 порядка (приложение).
С четырёх сторон к исходному квадрату 3х3 добавляются террасы. В полученной фигуре располагают числа от 1 до 9 в естественном порядке косыми рядами снизу вверх. Числа в террасах, не попавшие в квадрат, перемещаются как бы вместе с террасами внутрь него так, чтобы они примкнули к противоположным сторонам квадрата (числа, не попавшие в заштрихованный квадрат, сдвигаем на n=3 единицы: 1 – вниз, 3 – влево, 9 – вверх, 7 – вправо).
Числа, не попавшие в выделенный квадрат, сдвигаем на n=5 единиц: 1,2,6 – вниз, 4,5,10– влево, 24,25,20 – вверх, 16,21,20 – вправо.
Методом террас можно построить не только традиционный магический квадрат нечётного порядка, но и квадрат, заполненный любыми другими числами, лишь бы разность между каждым последующим и предыдущим числом была постоянной.
Так, в приложении 5 изображен нетрадиционный магический квадрат пятого порядка, заполненный чётными числами от 2 до 50, построенный методом террас.
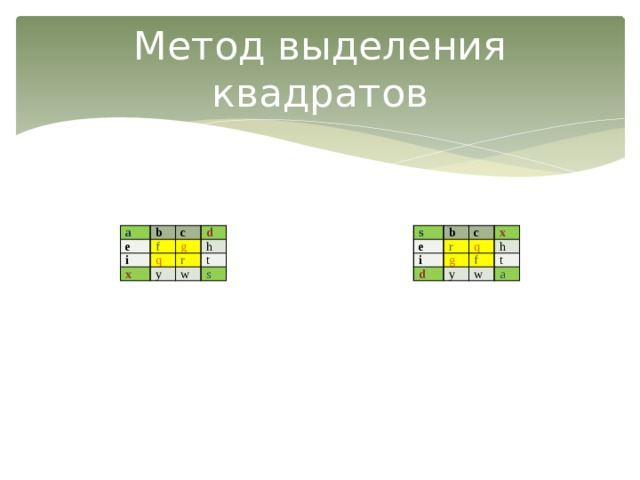
Для заполнения квадратов четного порядка можно применить следующий метод:
В квадрат вписываются натуральные числа в порядке возрастания. Затем выделяются квадраты из чисел по углам и в центре (получается квадрат размерностью на два меньше). Необходимо поменять местами числа, стоящие на краю диагонали. С квадратом, получившимся внутри, при необходимости, можно применить тот же алгоритм.
Рассмотрим этот метод на примере квадрата четвертого порядка (приложение 6) .
Допустим, что мы заполнили квадрат четыре на четыре числами от 1 до 16 в порядке возрастания построчно. Выделяем диагональные числа :a, d, s, x, и квадрат в центре размером два на два, в который вошли числа : f,g,r,q.
Меняем местами числа, стоящие на концах диагоналей по парам :
a-s, x-d, f-r, g-q
Константа полученного квадрата равна 34.
Этот метод можно назвать методом выделение квадратов.
II. Практическая часть
2.1. Заполнение магических квадратов изученными способами
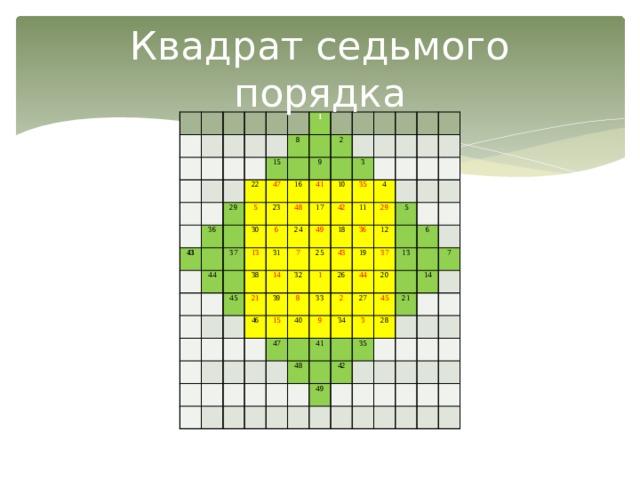
Заполним квадрат седьмого порядка методом террас (приложение 8)
Начертим квадрат 7 на 7
Достроим его до ромбовидной формы.
Впишем в порядке возрастания по диагоналям получившейся фигуры натуральные числа от 1 до 49
Перенесем каждое число, оказавшееся за пределом первоначального квадрата на 7 клеток.
Получили квадрат, константа которого равна 175.
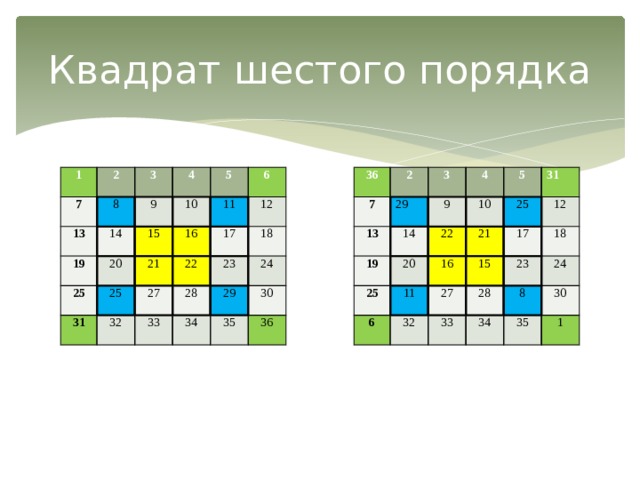
Заполним квадрат шестого порядка методом выделения квадратов (приложение 8).
В квадрат шестого порядка впишем натуральные числа от 1 до 36 в порядке возрастания построчно сверху вниз.
Выделим числа, стоящие по углам и квадрат в середине четвертого порядка.
Выделим числа, стоящие по углам и квадрата четвертого порядка и в нем же квадрат в центре второго порядка.
Поменяем местами числа, стоящие на концах диагоналей получившихся трех квадратов.
Получили квадрат шестого порядка с константой 111.
Выводы
1. Магический квадрат - древнекитайского происхождения.
2. Универсального способа заполнения магических квадратов нет.
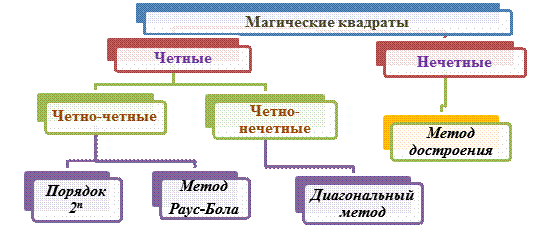
3. Способ заполнения магического квадрата, зависит от его порядка.
4. Для квадратов нечетного порядка существуют способы: метод Ф.де ла Ира (на двух квадратах), метод А.де ла Лубера (сиамский метод) и достраивание до симметричной ступенчатой ромбовидной фигуры.
5. Для квадратов, четного порядка можно применять метод выделения квадратов.
Список литературы
Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др. «Математика. 5 класс», Москва, Просвещение , 2010 год.
Интернет ресурсы:
http://wikipedia.org.ru
http://www.informio.ru
Приложение 1
Приложение 2
Приложение 3
Приложение 4
|
a
| b | c |
|
d
| e | f |
|
g
| h | i |
|
4
| 9 | 2 |
|
3
| 5 | 7 |
|
8
| 1 | 6 |
Приложение 5
Приложение 6
| a | b | c | d |
| e | f | g | h |
| i | q | r | t |
| x | y | w | s |
| s | b | c | x |
| e | r | q | h |
| i | g | f | t |
| d | y | w | a |
Приложение 7
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
| 8 |
| 2 |
|
|
|
|
|
|
|
|
|
| 15 |
| 9 |
| 3 |
|
|
|
|
|
|
|
| 22 | 47 | 16 | 41 | 10 | 35 | 4 |
|
|
|
|
|
| 29 | 5 | 23 | 48 | 17 | 42 | 11 | 29 | 5 |
|
|
|
| 36 |
| 30 | 6 | 24 | 49 | 18 | 36 | 12 |
| 6 |
|
| 43
|
| 37 | 13 | 31 | 7 | 25 | 43 | 19 | 37 | 13 |
| 7 |
|
| 44 |
| 38 | 14 | 32 | 1 | 26 | 44 | 20 |
| 14 |
|
|
|
| 45 | 21 | 39 | 8 | 33 | 2 | 27 | 45 | 21 |
|
|
|
|
|
| 46 | 15 | 40 | 9 | 34 | 3 | 28 |
|
|
|
|
|
|
|
| 47 |
| 41 |
| 35 |
|
|
|
|
|
|
|
|
|
| 48 |
| 42 |
|
|
|
|
|
|
|
|
|
|
|
| 49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 8
| 1
| 2 | 3 | 4 | 5 | 6 |
| 7
| 8 | 9 | 10 | 11 | 12 |
| 13
| 14 | 15 | 16 | 17 | 18 |
| 19
| 20 | 21 | 22 | 23 | 24 |
| 25
| 25 | 27 | 28 | 29 | 30 |
| 31
| 32 | 33 | 34 | 35 | 36 |
| 36
| 2 | 3 | 4 | 5 | 31 |
| 7
| 29 | 9 | 10 | 25 | 12 |
| 13
| 14 | 22 | 21 | 17 | 18 |
| 19
| 20 | 16 | 15 | 23 | 24 |
| 25
| 11 | 27 | 28 | 8 | 30 |
| 6
| 32 | 33 | 34 | 35 | 1 |
Приложение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6 |
| 2 |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| 11 |
| 7 |
| 3 |
|
| |
|
|
|
|
|
|
|
|
|
|
| 16 |
| 12 |
| 8 |
| 4 |
| |
|
|
|
|
|
|
|
|
|
| 21 |
| 17 |
| 13 |
| 9 |
| 5 | |
|
|
|
|
|
|
|
|
|
|
| 22 |
| 18 |
| 14 |
| 10 |
| |
|
|
|
|
|
|
|
|
|
|
|
| 23 |
| 19 |
| 15 |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 24 |
| 20 |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 25 |
|
|
|
|
| 11 | 24 | 7 | 20 | 3 |
| 4 | 12 | 25 | 8 | 16 |
| 17 | 5 | 13 | 21 | 9 |
| 10 | 18 | 1 | 14 | 22 |
| 23 | 6 | 19 | 2 | 15 |
| 6 | 32 | 18 | 44 | 30 |
| 40 | 16 | 42 | 28 | 4 |
| 14 | 50 | 26 | 2 | 38 |
| 48 | 24 | 10 | 36 | 12 |
| 22 | 8 | 34 | 20 | 46 |
12
Просмотр содержимого презентации
«Чарикова Регина_презентация квадрат магический»
Магический квадрат
Выполнила Чарикова Регина
Руководитель Сорокина Елена Васильевна
Цель:
- выяснить различные варианты составления магических квадратов, изучив которые можно заполнить квадрат любого размера.
Китай , 2200 лет до н. э.
Дюрер, «Меланхолия I»
Квадрат третьего порядка
4
9
a
3
8
2
b
5
d
1
g
7
e
c
6
h
f
i
Методы заполнения магических квадратов
Методы заполнения квадратов
Квадраты нечетного порядка
Квадраты четного порядка
Метод А.де ла Лубера
Метод Ф. де ла Ира
Метод террас
Метод выделения квадратов
Метод террас
21
16
1
11
6
17
22
12
7
2
13
3
23
8
18
9
4
24
14
19
20
25
5
15
10
11
4
24
17
7
12
10
25
5
20
3
23
8
13
18
16
21
1
6
9
14
19
22
2
15
Метод выделения квадратов
s
a
b
e
e
b
i
c
c
i
r
f
x
d
x
d
g
q
q
g
h
f
y
y
r
h
w
t
t
w
s
a
Квадрат седьмого порядка
22
15
1
36
29
43
8
5
47
9
44
37
30
2
23
16
13
48
6
41
38
24
3
31
10
17
45
7
42
49
21
35
14
32
11
25
18
46
4
39
29
43
8
1
36
15
40
26
5
19
12
47
33
37
44
2
9
6
13
20
48
34
27
41
45
3
28
42
7
14
21
49
35
Квадрат шестого порядка
36
1
2
7
2
7
8
29
3
13
13
3
14
4
19
9
19
4
9
14
10
20
20
10
25
22
15
5
25
5
25
31
16
21
31
25
11
21
6
11
6
16
32
12
12
22
32
15
27
27
17
17
23
28
18
18
33
28
33
23
34
24
34
24
8
29
35
30
30
35
36
1
Выводы :
- 1. Универсального способа заполнения магических квадратов нет.
- 2. Способ заполнения магического квадрата, зависит от его порядка.
Используемые ресурсы:
- 1. Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др. «Математика. 5 класс», Москва, Просвещение , 2010 год.
- 2. Интернет ресурсы:
- http://wikipedia.org.ru
- http://www.informio.ru
Спасибо за внимание!
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
