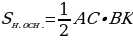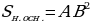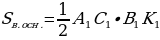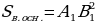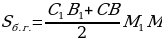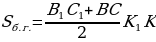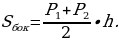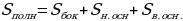СТАХАНОВСКОЕ ОТДЕЛЕНИЕ МЕДИЦИНСКОГО КОЛЛЕДЖА
ГОСУДАРСТВЕННОГО УЧРЕЖДЕНИЯ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
«ЛУГАНСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ ИМЕНИ СВЯТИТЕЛЯ ЛУКИ»
Методическая разработка
открытого лекционного занятия
по учебной дисциплине «Математика»
для студентов I курса
Тема «Пирамида»

Преподаватель: Мягких М.И.
2021
Тема «Пирамида»
Количество часов: 2
Тип занятия: комбинированный
1. Мотивация.
Т
 ема «Пирамида» учит думать, помогает рассуждать логично и последовательно, развивает умение выделять главное, заставляет анализировать ситуацию и делать выводы, способствует поиску различных путей решения одной задачи.
ема «Пирамида» учит думать, помогает рассуждать логично и последовательно, развивает умение выделять главное, заставляет анализировать ситуацию и делать выводы, способствует поиску различных путей решения одной задачи.
Разве эти умения не нужны человеку в повседневной жизни, профессиональной деятельности?
Вот что говорили про математику выдающиеся личности: «Математика – гимнастика ума» (Александр Суворов), «Математику только затем учить надо, что она ум в порядок приводит» (Михаил Ломоносов).
2. Учебные цели (с определением уровня усвоения).
Ознакомиться, иметь представление о пирамиде, её видах и свойствах (β-І)
Знать, усвоить нахождение площади боковой и полной поверхностей, основных элементов пирамиды (β-ІІ)
3. Цели развития личности (воспитательные цели) умение анализировать, сравнивать, обобщать, делать выводы, развивать внимание, формировать коммуникативную компетенцию студентов, последовательность действий при решении задач в зависимости от конкретных условий.
4. Междисциплинарная интеграция.
| № п/п | Название учебной дисциплины | Тема | Знать |
| 1. | История | Ранние цивилизации, их отличительные черты. Расцвет цивилизаций бронзового века и железный век Востока. | Определение пирамиды и её элементы. |
| 2. | Основы философии | Философия Древнего Востока. | Определение пирамиды и её элементы. |
5. Внутридисциплинарная интеграция.
| № п/п | Название учебной дисциплины | Тема | Знать |
| 1. | Математика | Правильные многогранники | Определение, элементы, свойства и формулы пирамиды. |
| 2. | Математика | Объём пирамиды | Определение, элементы, виды, свойства и формулы пирамиды. |
6. План и организационная структура лекции.
|
№ п/п |
Основные этапы лекции и их содержание | Учебные цели в уровнях | Методы и способы активизации студентов. Материалы методического обеспечения. | Время в мин. |
| I. | Подготовительный этап | 25 |
| 1. | Организация занятия. Проверка готовности студентов к занятию. | 3 |
| 2. | Постановка учебных целей, мотивация, актуализация темы. | 2 |
| 3. | Контроль уровня знаний студентов. | β-І, β-ІІ | Устный фронтальный опрос (кроссворд). Устный индивидуальный опрос («Математическое лото»). СВРС | 20 |
| II. | Основной этап | 50 |
| 4. | Постановка проблемы «Можно ли в наше время построить пирамиду Хеопса?». История Египетских пирамид. | β-І | Информационное сообщение студента. | 5 |
| 5. | План: |
|
|
|
|
| 1. Понятие, основные элементы пирамиды. | β-І | Методы: беседа, объяснение. Игра «да» - «нет» | 6 |
|
| 2. Виды пирамид: 2. 1.Прямоугольная и правильная пирамиды. | β-І, β-ІІ | Методы: беседа, объяснение, решение задач. 1. Ответить на вопрос: В чём сходство и отличие между правильной и прямоугольной четырёхугольными пирамидами?
2. Выполнить задание: Используя фигуру пирамиды сделать измерения и вычисления (работа в парах). 3. Решить задачи: 3.1 Найти площадь полной поверхности пирамиды. 3.1 Найти боковое ребро пирамиды. | 20 |
|
| 2.2. Усечённая пирамида. | β-І, β-ІІ | Методы: беседа, объяснение, решение задач. 1. Выполнить задание на соответствие («Логические пары»). 2. Решить задачи: 2.1 Найти площадь полной поверхности пирамиды. 2.2 Найти площадь боковой поверхности пирамиды. | 19 |
| 6. | Закрепление изученного материала. Поэтапное закрепление материала. |
|
| III. | Заключительный этап | 5 |
| 7. | Решение поставленной проблемы. |
| «Мозговой штурм» | 2 |
| 8. | Подведение итогов. Общие выводы. Выставление оценок. | 2 |
| 9. | Домашнее задание. Учебник Л.С. Атанасян «Геометрия» Тема Пирамида Страницы 69-73 | 1 |
7. Материалы методического обеспечения занятия:
1. Конспект лекции.
2. Дидактический материал.
3. Демонстрационный материал.
4. Мультимедийная презентация.
5. Вопросы.
6. Задачи.
7. Опорный конспект.
8. Литература.
Атанасян Л.С. и др. Геометрия. 10(11) кл. - М.:Просвещение, 2017.
9. Материалы методического обеспечения занятия.
I. Подготовительный этап.
1. Решить кроссворд.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1. | п | р | и | з | м | а |
|
|
|
|
|
|
| 2. | о | с | н | о | в | а | н | и | я |
|
|
|
|
|
|
|
|
| 3. | в | ы | с | о | т | а | |
|
|
|
|
|
|
|
|
|
|
| 4. | г | р | а | н | и |
|
|
|
|
|
| 5. | п | р | я | м | о | й |
|
|
|
|
|
|
|
|
|
| 6. | д | и | а | г | о | н | а | л | ь |
|
|
|
|
|
|
|
|
| 7. | р | ё | б | р | а |
|
|
|
| 8. | в | е | р | ш | и | н | а | м | и |
|
|
|
|
|
|
| 9. | н | а | к | л | о | н | н | о | й |
|
|
|
|
|
|
|
| 10. | п | о | л | н | о | й |
|
|
|
|
|
|
|
| 11. | п | р | а | в | и | л | ь | н | а | я |
|
|
|
|
|
|
| 12. | б | о | к | о | в | о | й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммы, имеющие общие стороны с этими многоугольниками.
2. Многоугольники А1А2...Аn и В1В2…Вn.
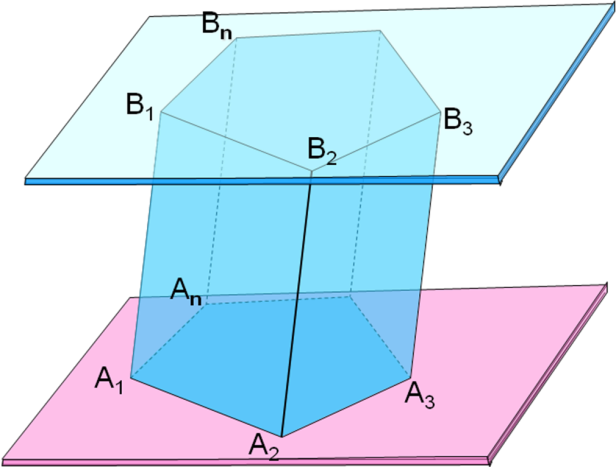
3. Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания.
4. Параллелограммы А1А2В2В1, А2А3В3В2,…, АnA1B1Bn – боковые…
5. Если боковые рёбра призмы перпендикулярны к основаниям, то призма называется…
6. Отрезок, соединяющий две вершины, не принадлежащие одной грани призмы.
7. Стороны граней.
8. Концы рёбер называются…
9. Если боковые рёбра призмы не перпендикулярны к основаниям, то призма называется…
10. Сумма площадей всех граней призмы – площадь … поверхности.
11. Прямая призма, основания которой правильные многоугольники.
12. Сумма площадей боковых граней призмы – площадь … поверхности.
2. «Математическое лото».
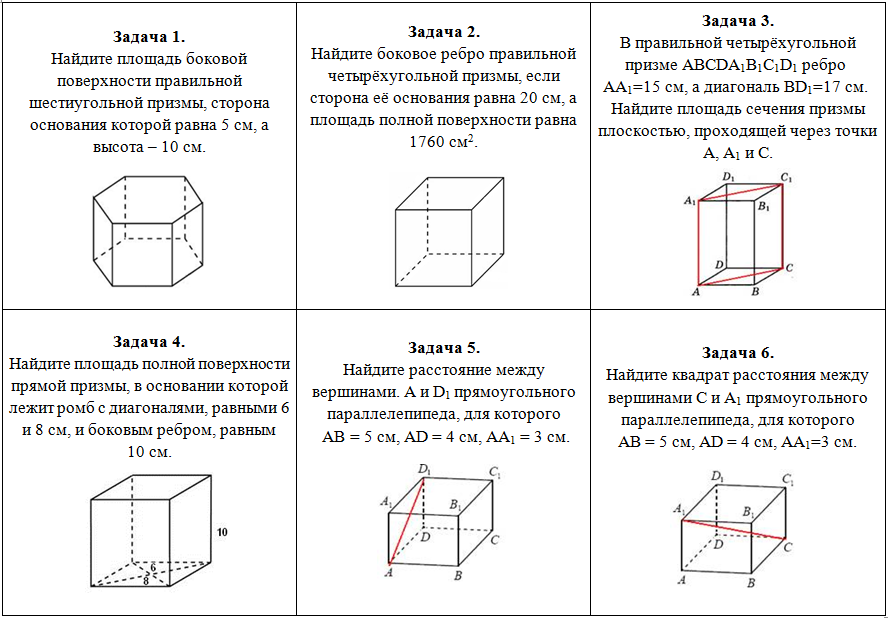
З адача 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5 см, а высота – 10 см.
адача 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5 см, а высота – 10 см.
Решение. Площадь боковой поверхности такой фигуры состоит из 6-ти площадей прямоугольников с основанием 5 см и высотой 10 см. Следовательно, площадь боковой поверхности равна 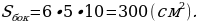
Ответ: 300 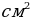 .
.
Задача 2. Найдите боковое ребро правильной четырёхугольной призмы, если сторона её основания равна 20 см, а площадь поверхности равна 1760 см2.
Решение. В основании правильной четырёхугольной призмы лежит квадрат. Следовательно, площадь нижней и верхней граней равна
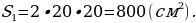
Тогда площадь боковой поверхности будет
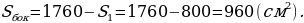
В то же время, площадь боковой поверхности – это сумма площадей четырёх боковых граней с основанием 20 см и высотой h, имеем:
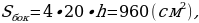
откуда
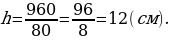
Ответ: 12 см.
Задача 3. В правильной четырёхугольной призме ABCDA1B1C1D1 ребро AA1 равно
15 см, а диагональ BD1 равна 17 см. Найдите площадь сечения призмы плоскостью, проходящей через точки A, A1 и C.
Р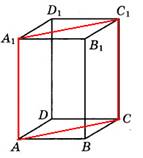 ешение. Найдём площадь сечения, показанную на рисунке красными линиями. Данное сечение представляет собой прямоугольник, одна сторона которого AA1=15 см. Диагональ этого сечения AC1=BD1=17 см. Найдём вторую сторону прямоугольника из прямоугольного треугольника AA1C1 по теореме Пифагора:
ешение. Найдём площадь сечения, показанную на рисунке красными линиями. Данное сечение представляет собой прямоугольник, одна сторона которого AA1=15 см. Диагональ этого сечения AC1=BD1=17 см. Найдём вторую сторону прямоугольника из прямоугольного треугольника AA1C1 по теореме Пифагора:
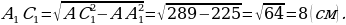
и площадь сечения равна 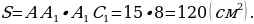
Ответ: 120 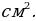
Задача 4. Найдите площадь полной поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8 см, и боковым ребром, равным 10 см.
Р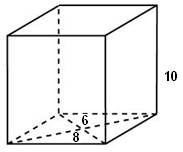 ешение. Диагонали ромба всегда пересекаются под прямым углом и делятся точкой пересечения пополам. Для того, чтобы найти сторону ромба можно рассмотреть прямоугольный треугольник с катетами 6 : 2 = 3 см и 8 : 2 = 4 см и по теореме Пифагора вычислим:
ешение. Диагонали ромба всегда пересекаются под прямым углом и делятся точкой пересечения пополам. Для того, чтобы найти сторону ромба можно рассмотреть прямоугольный треугольник с катетами 6 : 2 = 3 см и 8 : 2 = 4 см и по теореме Пифагора вычислим: 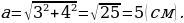
Теперь найдём площадь поверхности призмы. Площади 4-х боковых граней будут равны
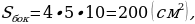
а площади нижней и верхней граней
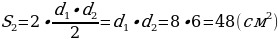
Таким образом, площадь поверхности призмы равна
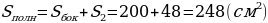 .
.
Ответ: 248 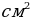 .
.
Задача 5. Найдите расстояние между вершинами А и D1 прямоугольного параллелепипеда, для которого AB = 5 см, AD = 4 см, AA1 = 3 см.
Р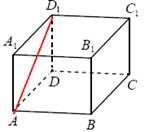 ешение. Так как параллелепипед прямоугольный, то треугольник ADD1 – прямоугольный с катетами AD = 4 см и DD1=AA1=3 см. По теореме Пифагора найдём гипотенузу AD1:
ешение. Так как параллелепипед прямоугольный, то треугольник ADD1 – прямоугольный с катетами AD = 4 см и DD1=AA1=3 см. По теореме Пифагора найдём гипотенузу AD1:
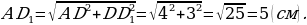
Ответ: 5 см.
З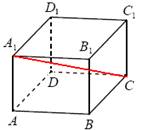 адача 6. Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5 см, AD = 4 см, AA1=3 см.
адача 6. Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5 см, AD = 4 см, AA1=3 см.
Решение. В задаче даны все три стороны прямоугольного параллелепипеда, тогда квадрат расстояния между точками A1 и C (диагональ параллелепипеда) можно найти по формуле 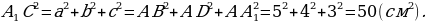
Ответ: 50 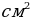 .
.
II. Основной этап.
1. Игра «да» - «нет».
1. Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину? (да)
2. Основание – многоугольник, которому принадлежит вершина
пирамиды? (нет)
3. Боковые грани пирамиды – это четырёхугольники? (нет)
4. Вершина пирамиды – точка, соединяющая боковые рёбра, и не лежащая в плоскости основания? (да)
5. Боковые ребра пирамиды – отрезки, соединяющие вершину пирамиды с вершинами основания? (да)
6. Если в основании пирамиды лежит четырёхугольник, то она называется тетраэдром? (нет)
7. Высотой пирамиды называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания? (да)
8. Площадью боковой поверхности пирамиды называется сумма площадей всех её граней? (нет)
9. Площадью полной поверхности пирамиды называется сумма площадей всех боковых граней и основания?(да).
2. В чём сходство и отличие между правильной (рис.A) и прямоугольной (рис.B) четырёхугольными пирамидами?
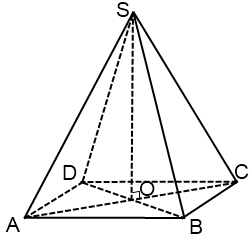
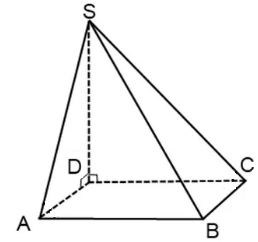
Рис. A Рис. B
Сходства. Вершина - точка, соединяющей боковые рёбра и не лежащая в плоскости основания.
Отличия.
|
| Правильная четырёхугольная пирамида | Прямоугольная четырёхугольная пирамида |
| Основание | Правильный четырёхугольник | Четырёхугольник |
| Высота | Отрезок, соединяющий вершину пирамиды с центром основания | Боковое ребро, перпендикулярное основанию |
| Боковые грани | Равные равнобедренные треугольники | Треугольники |
| Боковые рёбра | Равные отрезки, соединяющие вершину пирамиды с вершинами основания | Отрезки, соединяющие вершину пирамиды с вершинами основания |
3. Используя фигуру правильной пирамиды, сделать соответствующие измерения и вычисления.
| Сторона основания | Площадь основания | Боковые рёбра | Площадь боковой грани | Площадь боковой поверхности | Площадь полной поверхности |
| 6 см | 36 см2 | 7 см | 18,97 см2 | 75,88 см2 | 111,88 см2 |
4. Чему равна площадь поверхности правильного тетраэдра с ребром 1 м?
Р ешение.
ешение.
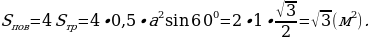
Ответ: 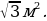
5. В основании правильной египетской пирамиды - квадрат со стороной 230 м, высота пирамиды 138 м. Найдите боковое ребро пирамиды.
Решение.
1 . АС
. АС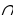 BD = O.
BD = O.
2. ΔAOD – прямоугольный.
По теореме Пифагора AD2 = OD2 +OA2;
2302 = 2OD2; 52900=2OD2; OD2 =26450.
3. Пирамида правильная = SO ⊥ (ABC)
4. Δ SOD – прямоугольный, по теореме Пифагора DS2 = DO2 +OS2 = 26450 + 1382 =
=26450+19044 = 45494;
DS ≈ 213 (м).
Ответ: 213 метров
6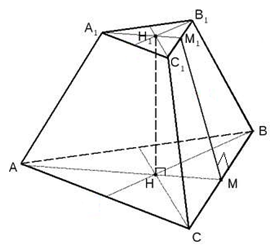 . «Логические пары».
. «Логические пары».
| 1. А1В1С1 | a. высота |
| 2. АВС | b. боковое ребро |
| 3. Н1Н | c. верхнее основание |
| 4. М1М | d. нижнее основание |
| 5. АА1С1С | e. апофема |
| 6. АА1 | f. боковая грань |
О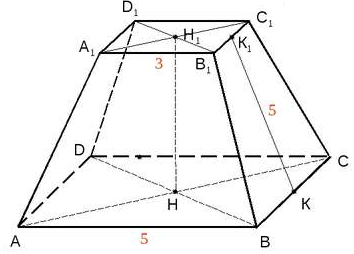 твет: 1-с; 2-d; 3-a; 4-e; 5-f; 6-b.
твет: 1-с; 2-d; 3-a; 4-e; 5-f; 6-b.
7. АВСDA1B1C1D1 – правильная усечённая пирамида. К1К – апофема. Найдите площадь полной поверхности усечённой пирамиды.
Решение.
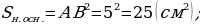
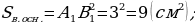
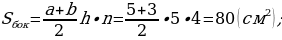
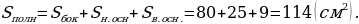
О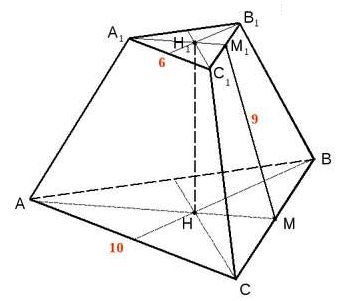 твет: 114 см2.
твет: 114 см2.
8. АВСА1В1С1 – правильная усечённая пирамида. М1М – апофема. Найдите площадь боковой поверхности усечённой пирамиды.
Решение.
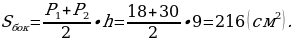
Ответ: 216 см2.
9. Содержание лекционного материала.
План:
1. Понятие, основные элементы пирамиды.
2. Виды пирамид:
2.1 Прямоугольная и правильная пирамиды.
2.2 Усечённая пирамида.
1. Понятие, основные элементы пирамиды.
Рассмотрим многоугольник A1A2…An и точку P, не лежащую в плоскости этого многоугольника. Соединив точку P отрезками с вершинами многоугольника, получим n треугольников (рис. 1): PA1A2, PA2A3,…, PAnA1.

Рис. 1
Многогранник составленный из n-угольника A1A2…An и n треугольников PA1A2, PA2A3,…, PAnA1, называется пирамидой.
Многоугольник A1A2…An называется основанием, а треугольники PA1A2, PA2A3,…, PAnA1 – боковыми гранями пирамиды. Точка P называется вершиной пирамиды, а отрезки PA1, PA2,…, PAn – её боковыми рёбрами. Пирамиду с основанием A1A2…An и вершиной P обозначают так: PA1A2…An – и называют n-угольной пирамидой.
Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 1 отрезок PH является высотой пирамиды.
В зависимости от количества сторон основания различают треугольные, четырёхугольные, …, n-угольные пирамиды (рис. 2). Треугольную пирамиду называют также тетраэдром.
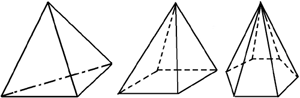
Рис. 2
Площадью боковой поверхности пирамиды называется сумма площадей её боковых граней, а площадью полной поверхности пирамиды называется сумма площадей всех её граней (т.е. основания и боковых граней).
2. Виды пирамид:
2.1 Прямоугольная и правильная пирамиды.
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию (рис. 3). Тогда это ребро и есть высота пирамиды.
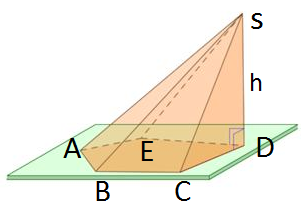
Рис. 3
Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой (рис.4).

Рис. 4
Докажем, что все боковые рёбра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Рассмотрим правильную пирамиду PA1A2…An (см. рис. 5).

Рис. 5
Сначала докажем, что все боковые рёбра этой пирамиды равны. Любое боковое ребро представляет собой гипотенузу прямоугольного треугольника, одним катетом которого служит высота PO пирамиды, а другим – радиус описанной около основания окружности (например, боковое ребро PA1 – гипотенуза треугольника ОPA1, в котором OP=h, OA1=R). По теореме Пифагора любое боковое ребро равно 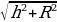 , поэтому PA1=PA2 =… = PAn.
, поэтому PA1=PA2 =… = PAn.
Мы доказали, что боковые рёбра правильной пирамиды PA1A2…An равны друг другу, поэтому боковые грани – равнобедренные треугольники. Основания этих треугольников также равны друг другу, так как A1A2…An – правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников, что и требовалось доказать.
Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой. На рисунке 5 отрезок РЕ – одна из апофем. Все апофемы правильной пирамиды равны друг другу.
Докажем теорему о площади боковой поверхности правильной пирамиды.
Теорема
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Доказательство
Боковые грани правильной пирамиды – равные равнобедренные треугольники, основания которых – стороны основания пирамиды (а), а высоты равны апофеме (h). Тогда площадь одной боковой грани равна 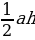 . Боковая поверхность пирамиды состоит из n таких граней. Поэтому если периметр основания пирамиды равен P, то площадь её боковой поверхности
. Боковая поверхность пирамиды состоит из n таких граней. Поэтому если периметр основания пирамиды равен P, то площадь её боковой поверхности
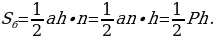
Теорема доказана.
Тетраэдр называется правильным, если все его грани – равносторонние треугольники (см. рис. 6).
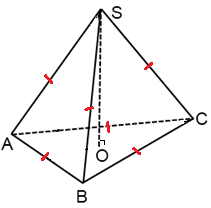
Рис. 6
Формулы для правильных пирамид
|
| Правильная треугольная пирамида 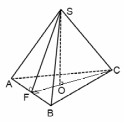
| Правильная четырёхугольная пирамида 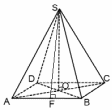
|
| Площадь основания | 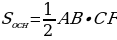
| 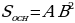
|
| Площадь боковой грани | 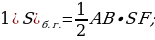
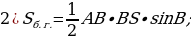
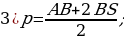
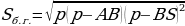 . .
| 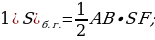
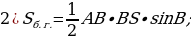
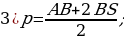
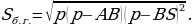
|
| Площадь боковой поверхности | 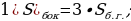
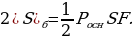
| 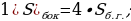
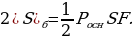
|
| Площадь полной поверхности | 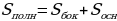
| 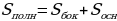
|
2 .2 Усечённая пирамида.
.2 Усечённая пирамида.
Возьмём произвольную пирамиду PA1A2…An и проведём секущую плоскость β, параллельную плоскости α основания пирамиды и пересекающую боковые рёбра в точках В1, В2,… Вn (рис.7). Плоскость β разбивает пирамиду на два многогранника.
Многогранник, гранями которого являются n – угольники A1A2…An и В1В2,… Вn, расположенные в параллельных плоскостях, и n четырёхугольники A1A2В2В1, A2A3В3В2,…АnA1B1Bn, называется усечённой пирамидой.
Рис.7
Многоугольник A1A2…An называется нижним основанием, а многоугольник В1В2,… Вn - верхним основанием усечённой пирамиды.
Четырёхугольники A1A2В2В1, A2A3В3В2,…АnA1B1Bn называются боковыми гранями усечённой пирамиды, а отрезки A1B1, A2B2, …, AnBn её боковыми рёбрами.
Усечённую пирамиду с основаниями A1A2…An и В1В2,… Вn обозначают так: A1A2…AnВ1В2,… Вn.
Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усечённой пирамиды. На рисунке 7 отрезок СН является высотой усечённой пирамиды.
Докажем, что боковые грани усечённой пирамиды – трапеции.
Рассмотрим, например, боковую грань A1A2В2В1(см. рис. 7). Стороны A1A2 и В1В2 параллельны, поскольку принадлежат прямым, по которым плоскость PA1A2 пересекается с параллельными плоскостями α и β. Две другие стороны А1В1 и А2В2 этой грани не параллельны – их продолжения пересекаются в точке P. Поэтому данная грань – трапеция. Аналогично можно доказать, что и остальные боковые грани – трапеции.
Усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усечённой пирамиды – правильные многоугольники, а боковые грани – равные равнобедренные трапеции. Высоты этих трапеций называются апофемами.
Площадью боковой поверхности усечённой пирамиды называется сумма площадей её боковых граней, а площадью полной поверхности усечённой пирамиды называется сумма площадей всех её граней (т.е. оснований и боковых граней).
Докажем теорему о площади боковой поверхности правильной усечённой пирамиды.
Теорема
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
Д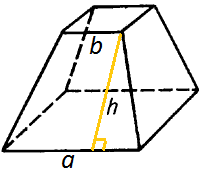 оказательство
оказательство
Боковые грани правильной усечённой пирамиды – равные равнобедренные трапеции, основания которых – стороны нижнего и верхнего оснований пирамиды (а и b), а высоты равны апофеме (h).
Найдём площадь одной из граней правильной
n-угольной усечённой пирамиды (рис.8). Рис. 8
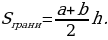
Боковая поверхность пирамиды состоит из n таких граней.
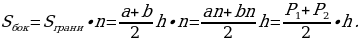
Теорема доказана.
Формулы для правильных усечённых пирамид
|
| Правильная треугольная усечённая пирамида 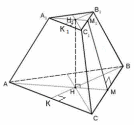
| Правильная ч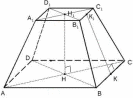 етырёхугольная усечённая пирамида етырёхугольная усечённая пирамида |
| Площадь нижнего основания | 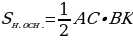
| 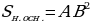
|
| Площадь верхнего основания | 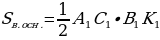
| 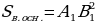
|
| Площадь боковой грани | 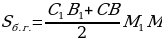
| 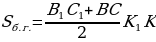
|
| Площадь боковой поверхности | 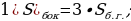
2) 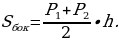 | 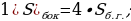
2)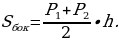 |
| Площадь полной поверхности | 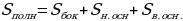
| 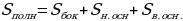
|








 ема «Пирамида» учит думать, помогает рассуждать логично и последовательно, развивает умение выделять главное, заставляет анализировать ситуацию и делать выводы, способствует поиску различных путей решения одной задачи.
ема «Пирамида» учит думать, помогает рассуждать логично и последовательно, развивает умение выделять главное, заставляет анализировать ситуацию и делать выводы, способствует поиску различных путей решения одной задачи.

 адача 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5 см, а высота – 10 см.
адача 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5 см, а высота – 10 см.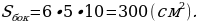
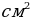 .
.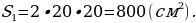
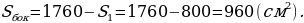
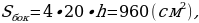
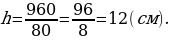
 ешение. Найдём площадь сечения, показанную на рисунке красными линиями. Данное сечение представляет собой прямоугольник, одна сторона которого AA1=15 см. Диагональ этого сечения AC1=BD1=17 см. Найдём вторую сторону прямоугольника из прямоугольного треугольника AA1C1 по теореме Пифагора:
ешение. Найдём площадь сечения, показанную на рисунке красными линиями. Данное сечение представляет собой прямоугольник, одна сторона которого AA1=15 см. Диагональ этого сечения AC1=BD1=17 см. Найдём вторую сторону прямоугольника из прямоугольного треугольника AA1C1 по теореме Пифагора: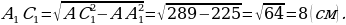
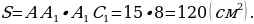
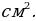
 ешение. Диагонали ромба всегда пересекаются под прямым углом и делятся точкой пересечения пополам. Для того, чтобы найти сторону ромба можно рассмотреть прямоугольный треугольник с катетами 6 : 2 = 3 см и 8 : 2 = 4 см и по теореме Пифагора вычислим:
ешение. Диагонали ромба всегда пересекаются под прямым углом и делятся точкой пересечения пополам. Для того, чтобы найти сторону ромба можно рассмотреть прямоугольный треугольник с катетами 6 : 2 = 3 см и 8 : 2 = 4 см и по теореме Пифагора вычислим: 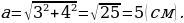
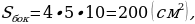
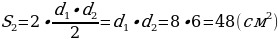
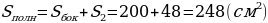 .
. ешение. Так как параллелепипед прямоугольный, то треугольник ADD1 – прямоугольный с катетами AD = 4 см и DD1=AA1=3 см. По теореме Пифагора найдём гипотенузу AD1:
ешение. Так как параллелепипед прямоугольный, то треугольник ADD1 – прямоугольный с катетами AD = 4 см и DD1=AA1=3 см. По теореме Пифагора найдём гипотенузу AD1: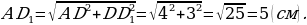
 адача 6. Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5 см, AD = 4 см, AA1=3 см.
адача 6. Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5 см, AD = 4 см, AA1=3 см.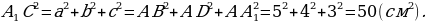



 ешение.
ешение.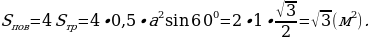
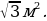
 . АС
. АС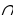 BD = O.
BD = O. . «Логические пары».
. «Логические пары».  твет: 1-с; 2-d; 3-a; 4-e; 5-f; 6-b.
твет: 1-с; 2-d; 3-a; 4-e; 5-f; 6-b. 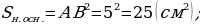
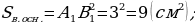
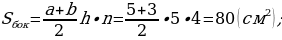
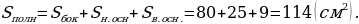
 твет: 114 см2.
твет: 114 см2.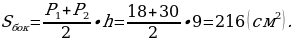




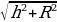 , поэтому PA1=PA2 =… = PAn.
, поэтому PA1=PA2 =… = PAn.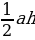 . Боковая поверхность пирамиды состоит из n таких граней. Поэтому если периметр основания пирамиды равен P, то площадь её боковой поверхности
. Боковая поверхность пирамиды состоит из n таких граней. Поэтому если периметр основания пирамиды равен P, то площадь её боковой поверхности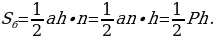



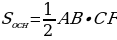
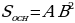
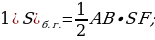
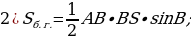
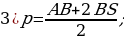
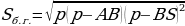 .
.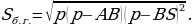
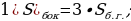
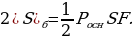
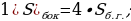
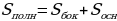
 .2 Усечённая пирамида.
.2 Усечённая пирамида.  оказательство
оказательство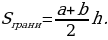
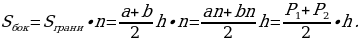

 етырёхугольная усечённая пирамида
етырёхугольная усечённая пирамида