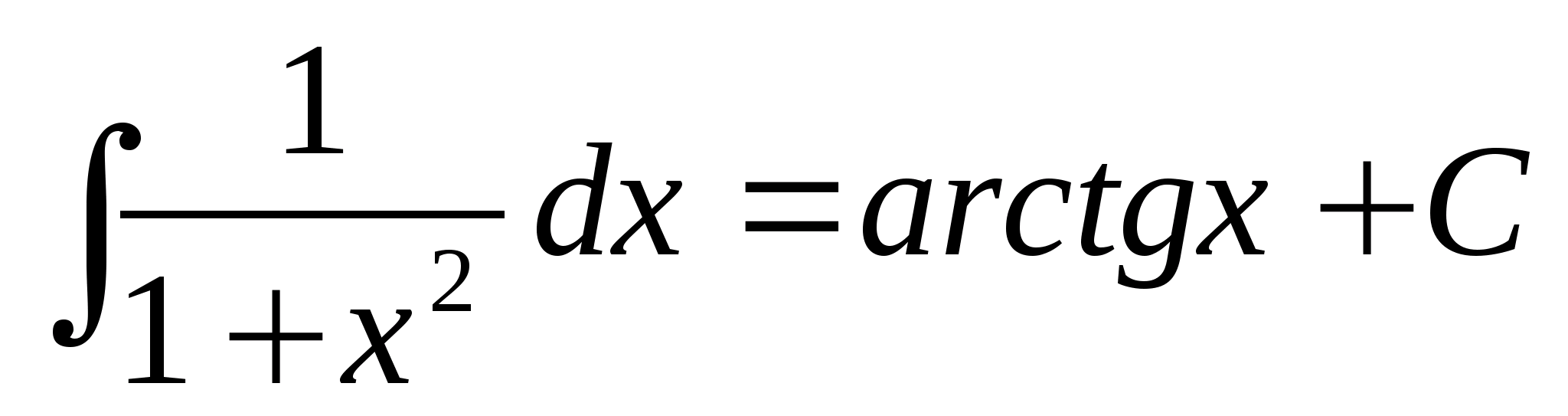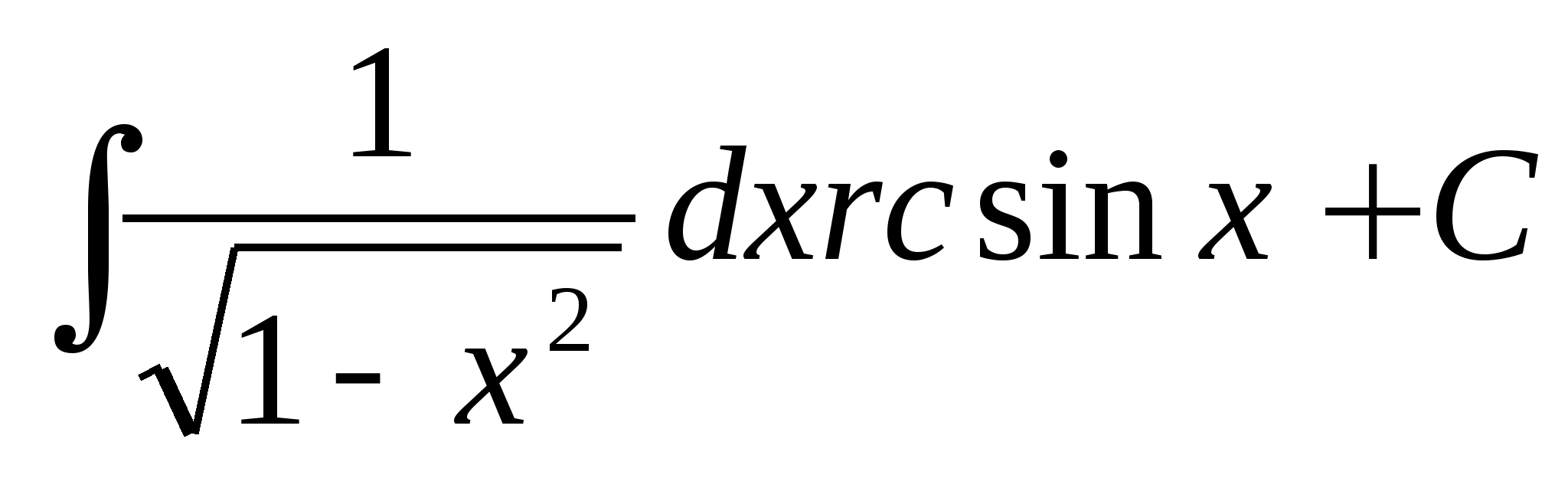СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Методические указания по выполнению ЛПЗ
Просмотр содержимого документа
«Методические указания по выполнению ЛПЗ»
Министерство общего и профессионального образования Ростовской области
Государственное бюджетное профессиональное образовательное учреждение
Ростовской области «Сальский аграрно-технический колледж»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКИХ ЗАНЯТИЙ
по предмету «Математика»
для специальности 38.02.01 Экономика и бухгалтерский учет (по отраслям)
Гигант
2022
| Одобрено предметной (цикловой) комиссией математических и общих естественнонаучных дисциплин Протокол № ___ от ________ 20___г. Председатель:_______ Кудрявцева Е.П. | УТВЕРЖДАЮ Зам. директора по учебной работе ___________________ И.А. Хара «_____» ______________20___г. |
Автор: Ромащенко Т.А.
Рецензент: Калашникова Г.И.
АННОТАЦИЯ
на «Методические указания по выполнению практических занятий»
по ОУП «Математика»
для специальности:38.02.01 Экономика и бухгалтерский учет (по отраслям).
Автор: Ромащенко Т.А., преподаватель ОУП «Математика».
Адрес учебного заведения: Ростовская обл., Сальский р-н, п. Гигант, ул. Крупской,6.
«Методические указания» включают в себя:
оглавление;
предисловие;
содержание методических указаний;
правила выполнения ПЗ;
практические занятия № 1 – 25;
литературу.
Настоящий сборник ПЗ предназначен в качестве методического пособия для проведения практических занятий по программе предмета «Математика».
Методические указания содержат теоретический материал, необходимый по ходу выполнения работы, формулы, примеры подобных заданий с образцами решений и варианты заданий для самостоятельного выполнения.
Настоящий сборник может быть использован в качестве основного или дополнительного материала при проведении ПЗ.
ОГЛАВЛЕНИЕ
| Предисловие …………………………………………………………………………… |
| Содержание методических указаний…………………………………………………. |
| Правила выполнения ЛПЗ……………………………………………………………... |
Практическая работа № 1………………………………………………………………
Практическая работа № 2………………………………………………………………
Практическая работа № 3………………………………………………………………
Практическая работа № 4………………………………………………………………
Практическая работа № 5………………………………………………………………
Практическая работа № 6………………………………………………………………
Практическая работа № 7………………………………………………………………
Практическая работа № 8………………………………………………………………
Практическая работа № 9………………………………………………………………
Практическая работа № 10……………………………………………………………..
Практическая работа № 11……………………………………………………………..
Практическая работа № 12……………………………………………………………..
Практическая работа № 13……………………………………………………………..
Практическая работа № 14……………………………………………………………...
Практическая работа № 15………………………………………………………………
Практическая работа № 16………………………………………………………………
Практическая работа № 17………………………………………………………………
Практическая работа № 18………………………………………………………………
Практическая работа № 19………………………………………………………………
Практическая работа № 20………………………………………………………………
Практическая работа № 21………………………………………………………………
Практическая работа № 22………………………………………………………………
Практическая работа № 23………………………………………………………………
Практическая работа № 24………………………………………………………………
Практическая работа № 25………………………………………………………………
Литература……………………………………………………………………………….
ПРЕДИСЛОВИЕ
Назначение методических указаний
Настоящий сборник ПЗ предназначен в качестве методического пособия для проведения практических работ по программе ОУП «Математика», рекомендуется использовать студентами различных специальностей и с разным уровнем начальной подготовки. Данный материал содержит описания практических работ:
Арифметические действия над числами, нахождение приближенных значений величин и погрешностей вычислений, сравнение числовых выражений
Вычисление и сравнение корней
Нахождение значений степеней с рациональными показателями
Нахождение значений логарифма по произвольному основанию
Решение показательных уравнений.
Решение логарифмических уравнений
Перпендикуляр и наклонная к плоскости.
Теорема о трех перпендикулярах.
Размещения, сочетания и перестановки.
Бином Ньютона и треугольник Паскаля
Векторы. Действия с векторами.
Основные тригонометрические тождества, формулы сложения, удвоения, преобразование суммы тригонометрических функций в произведение, преобразование произведения тригонометрических функций в сумму.
Простейшие тригонометрические уравнения и неравенства.
Построение и чтение графиков функций
Преобразования графика функции
Вычисление площадей и объемов.
Правила и формулы дифференцирования, таблица производных элементарных функций.
Нахождение наибольшего, наименьшего значения и экстремальных значений функции
Исследование функции с помощью производной.
Интеграл и первообразная
Теорема Ньютона-Лейбница
Применение интеграла к вычислению физических величин и площадей
Вычисление вероятностей
Решение систем уравнений
Использование свойств и графиков функций для решения уравнений и неравенств.
Содержание методических указаний:
тема, наименование работы;
цель работы, требования к умениям и навыкам;
методические указания (практические работы):
краткие теоретические сведения
примеры подобных заданий с образцами решений
варианты заданий для самостоятельного выполнения
содержание отчёта.
ПРАВИЛА ВЫПОЛНЕНИЯ ПЗ
Студент должен прийти на практическое занятие подготовленным к выполнению работы. Студент, не подготовленный к работе, не может быть допущен к ее выполнению.
Каждый студент после выполнения работы должен представить отчет о проделанной работе, содержание которого определено в конце каждой работы.
Отчет о проделанной работе следует выполнять в тетради для практических работ.
Чертежи и схемы, необходимые для выполнения работы, следует выполнять карандашом с помощью чертежных инструментов (линейки, циркуля и т.д.).
Вычисления производить с точностью до двух значащих цифр.
Если студент не выполнил практическую работу или часть работы, то он может выполнить работу или оставшуюся часть во внеурочное время, согласованное с преподавателем.
Оценку по практической работе студент получает с учетом срока выполнения работы, если:
- задачи решены правильно и в полном объеме;
- студент может пояснить выполнение любого этапа работы;
- отчет выполнен в соответствии с требованиями к выполнению работы;
- грамотно, чётко и ответил на контрольные вопросы к защите работы.
В случае отсутствия на занятиях при выполнении практической работы, студент должен:
- получить указания у преподавателя;
- выполнить работу во внеурочное время согласно методическому указанию.
Зачет по работе студент получает при условии выполнения всех предусмотренных программой работ после сдачи отчетов по работам.
Практическая работа № 1.
Тема 1. Развитие понятия о числе
Наименование работы: Арифметические действия над числами, нахождение приближенных значений величин и погрешностей вычислений, сравнение числовых выражений
Цель работы, требования к умениям и навыкам:применить на практике теоретические знания по нахождению приближенных значений величин и погрешности вычислений (абсолютная и относительная); сравнивать числовые выражения.
Методические рекомендации.
Если х - точное значение числа,
а – приближённое значение, то х ≈ а.
ОПР.
Разность х – а между точным и приближённым значением числа называется погрешностью приближения.
ОПР.
Модуль разности между точным и приближённым значением числа называется абсолютной погрешностью приближения ∆а = │х – а│.
ОПР.
Некоторая цифра приближённого числа считается верной, если его абсолютная погрешность
∆а не превышает единицы того разряда, в котором стоит эта цифра. В противном случае цифра называется сомнительной.
Пример.
а = 945,673 ± 0,03
6 – цифра десятых долей, ∆а = 0,03
Проверяем: 0,03
7 – цифра сотых долей
Проверяем: 0,03
ОПР.
Значащими цифрами десятичной дроби называют все её цифры, кроме нулей, расположенных левее первой, отличной от нуля цифры
ОПР.
Значащими цифрами целого числа называют все его цифры, кроме нулей, расположенных в конце числа, если они стоят взамен неизвестных или отброшенных цифр.
0,712 - 3 значащие цифры.
45,03 – 4 значащие цифры
0,0016 - 2 значащие цифры
ОПР.
Относительной погрешностью приближённого значения числа а называется отношение абсолютной погрешности этого числа к модулю приближённого значения.Ϭ = ∆а* 100%
│а│
Правила подсчёта цифр:
При сложении и вычитании приближённых чисел в результате сохраняют столько десятичных знаков, сколько их в наименее точном числе.
При умножении и делении приближённых чисел в результате сохраняют столько значащих цифр, сколько их в числе с наименьшим количеством значащих цифр.
При возведении в степень в результате сохраняют столько значащих цифр, сколько их в основании степени.
При извлечении корня сохраняют столько значащих цифр, сколько их в подкоренном выражении.
При выполнении промежуточных действий оставляют на один знак больше, чем требуют правила, а в результате запасной знак округляют.
Если в вычислениях точность задана заранее, то вычисления ведут с запасным знаком, который в результате округляют
2.Задания для самостоятельной работы.
1 вариант.
1 задание. Установить число значащих цифр в числе:а) 649 ;б) 0,01405; в) 347|51≈ ; г) 24321≈
2 задание. Определить верные и сомнительные цифры чисел
а) а = 85,263 ± 0,0084 б) х = 729,3 ± 1
3 задание. Вычислить значение выражений с оценкой погрешностей, если все числа даны с верными
цифрами.
а) 645,27 + 102,234 + 715,645 + 10,2 б) 96,891 – 4,25
33,3 + 0,426
4 задание. Округлить число до единиц и найти абсолютную и относительную погрешности
приближения : 23,263
2 вариант.
1 задание. Установить число значащих цифр в числе:а) 43,08; б) 0,0298 ; в) 353|617≈ ; г) 25|213 ≈
2 задание. Определить верные и сомнительные цифры чисел
а) х = 14,28 ± 0,05 б) а = 749,3 ± 1
3 задание. Вычислить значение выражений с оценкой погрешностей, если все числа даны с верными
цифрами.
а) 12030 + 645,29 + 748,5 + 1625,375 б) ( 0,17 + 0,2445 ) · 0, 56
1,424
4 задание. Округлить число до единиц и найти абсолютную и относительную погрешности
Приближения: 0,892
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа №2
Тема 2. Корни, степени и логарифмы
Наименование работы: Вычисление и сравнение корней
Цель работы, требования к умениям и навыкам:закрепить и проверить теоретические знания в ходе выполнения упражнений, выработать навыки применения теоретических знаний на практике.Применять определения и свойства степени с действительными показателями при выполнении тождественных преобразований над степенными выражениями.
М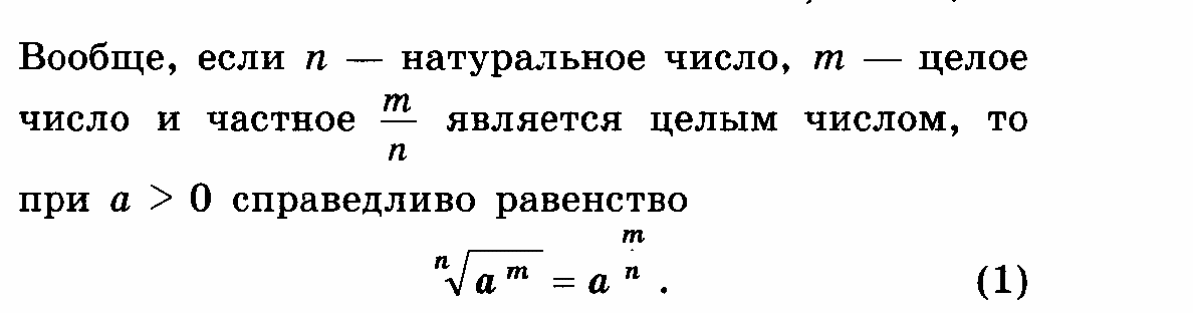
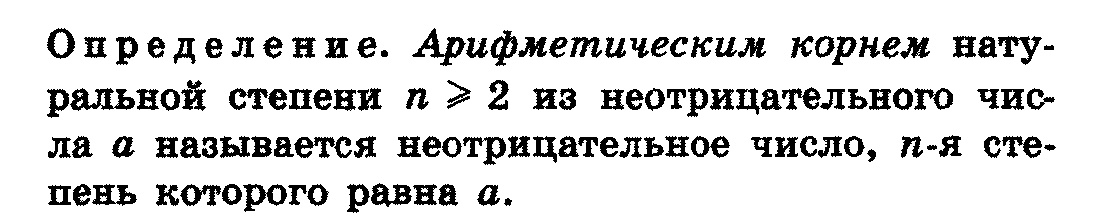
 етодические рекомендации.
етодические рекомендации.
.
![]()
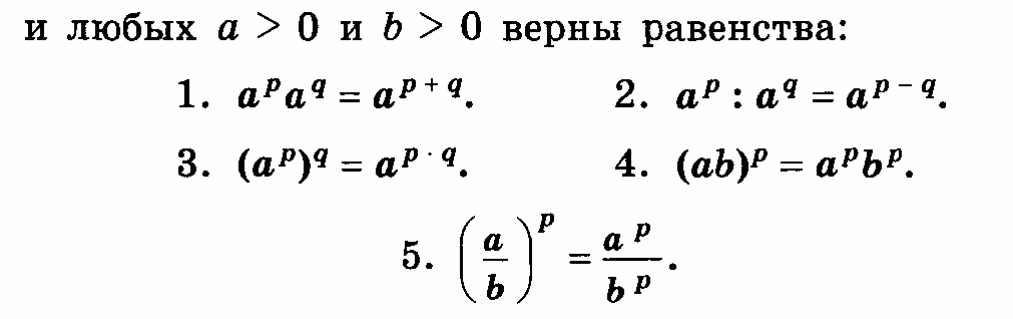
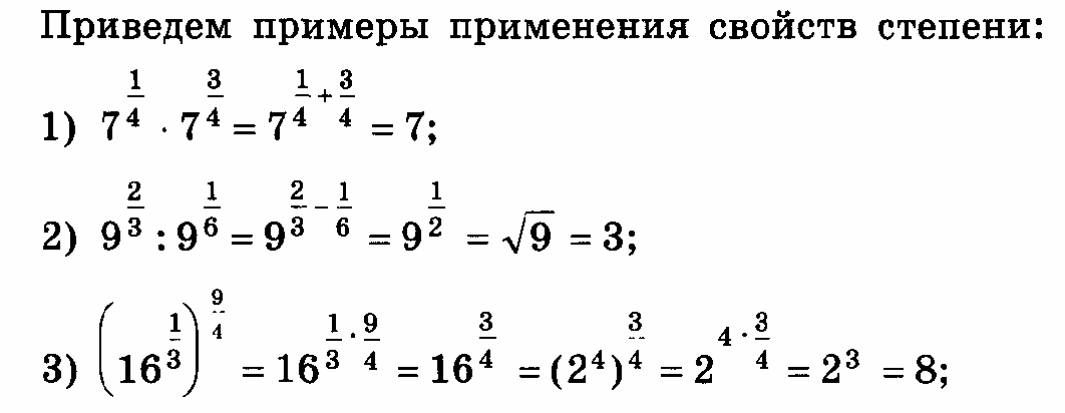
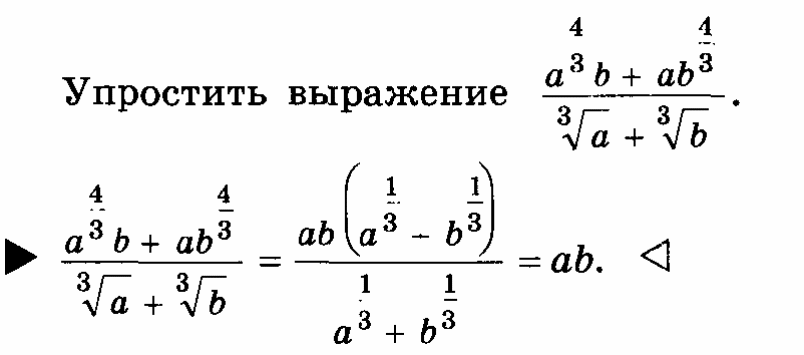
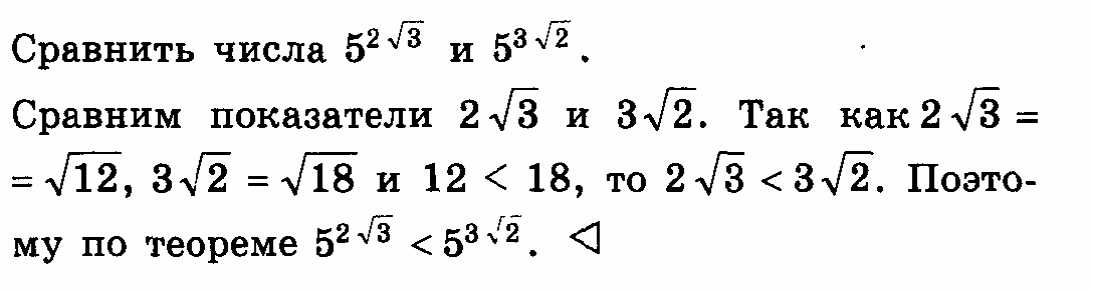
2.Задания для самостоятельной работы.
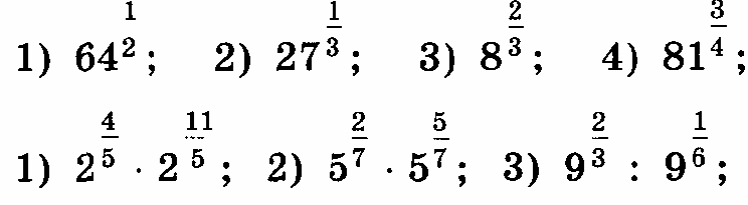
Вычислить:
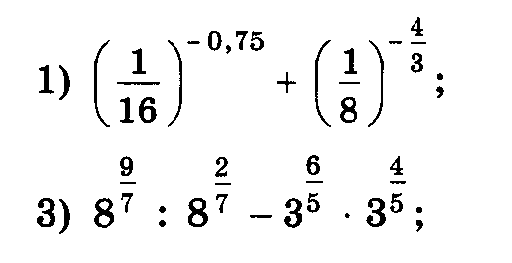
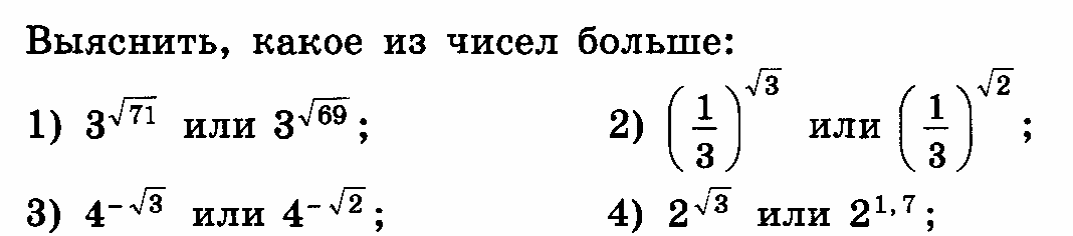
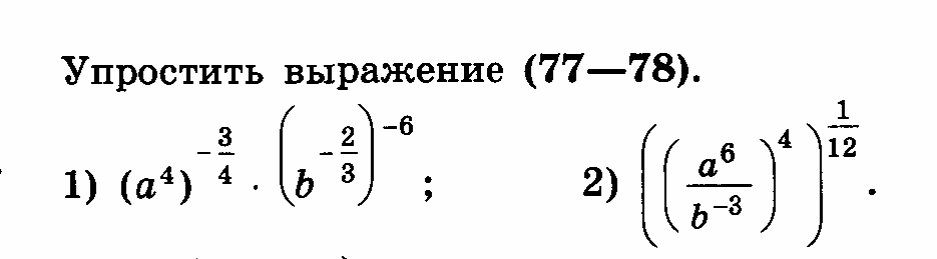
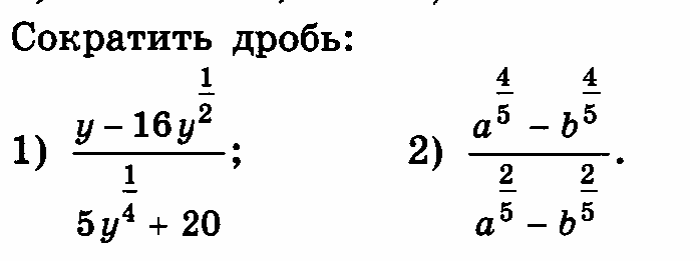
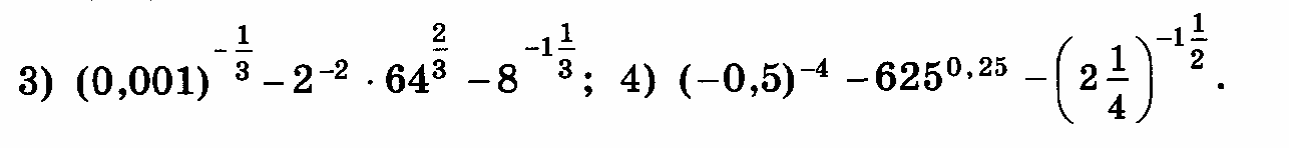
Вычислить:
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа №3
Тема 2. Корни, степени и логарифмы
Наименование работы: Нахождение значений степеней с рациональными показателями.
Цель работы, требования к умениям и навыкам: Сформировать умения и навыки по применению определений и свойств степени с произвольными показателями при выполнении тождественных преобразований над степенными выражениями.
Методические указания.
Краткие теоретические сведения
1.Степень с рациональным показателем и её свойства.
Определения:
Пусть, a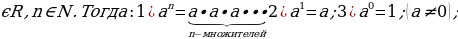
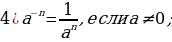
Пусть, 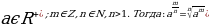 .
.
2.Действия со степенями.
Пусть,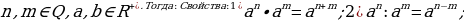
3) 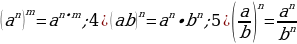
3. Степень с действительным показателем и её свойства.
Определение. Пусть действительное число 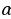 записано в виде бесконечной десятичной дроби и пусть
записано в виде бесконечной десятичной дроби и пусть 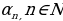 - последовательность его десятичных приближений с недостатком. Тогда для любого действительного числа
- последовательность его десятичных приближений с недостатком. Тогда для любого действительного числа 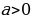 степень
степень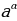 определяется равенством
определяется равенством 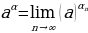 . Степени с действительными показателями обладают всеми свойствами степеней с рациональными показателями.
. Степени с действительными показателями обладают всеми свойствами степеней с рациональными показателями.
Выполнить упражнения:
Пример 1: Упростить: 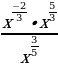 ;
;
Решение. Используя свойства степени с рациональным показателем, получим
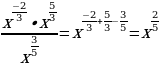 .
.
Пример 2. Упростить: 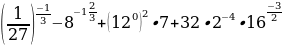 .
.
Решение. Используя определение и свойства степени с рациональным показателем, получим
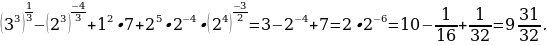
Пример 3. Вычислить значение выражения: 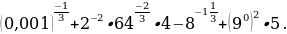
Решение. Используя определения и свойства степени с рациональным показателем, получим
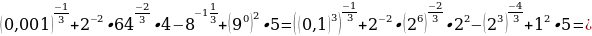
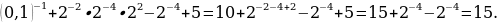
2.Задания для самостоятельной работы.
Вариант 1.
1.Найти значение выражения: а) 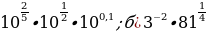 в)
в) 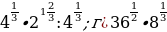
2.Вычислить значение выражения: а)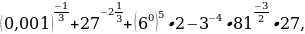
Б) 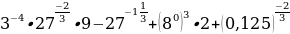
Вариант 2.
1.Найти значение выражения: а) 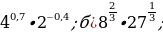 в)
в) 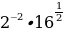 ; г)
; г) 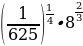
2.Вычислить значение выражения: а)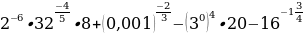 ;
;
б) 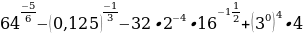
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 4
Тема 2. Корни, степени и логарифмы
Наименование работы: Нахождение значений логарифма по произвольному основанию
Цель работы, требования к умениям и навыкам: Сформировать умения и навыки по применению определения, свойств и теорем логарифмирования к выполнению преобразований и вычислений логарифмических выражений.
Задание: 1. Изучить методические указания к работе,записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
1.Определение логарифма. Основное логарифмическое тождество.
Определение. Логарифмом числав по основанию а называется показатель степени с, в которую нужно возвести основание а, чтобы получить число в. При этом пишут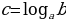 т.е.
т.е. 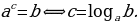 В этой записи подразумеваются следующие ограничения:
В этой записи подразумеваются следующие ограничения:  Из равенства
Из равенства подставив вместо с его запись через логарифм, получаем
подставив вместо с его запись через логарифм, получаем
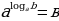 . Эта формула называется основным логарифмическим тождеством.
. Эта формула называется основным логарифмическим тождеством.
2.Свойства логарифмов.
Не существует логарифма отрицательного числа и нуля.
Логарифм числа по тому же основанию равен единице 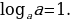
Логарифм единицы по любому основанию равен нулю 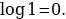
3.Теоремы логарифмирования.
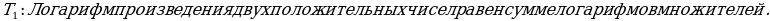
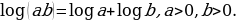
 : Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя.
: Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. 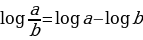 .
.
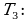 Логарифм степени положительного числа равен произведению показателя степени на логарифм основания.
Логарифм степени положительного числа равен произведению показателя степени на логарифм основания. 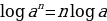 .
.
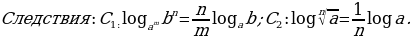
4. Формула перехода от одного основания логарифма к другому:
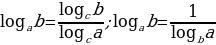 .
.
5. Виды логарифмов:а) обыкновенный 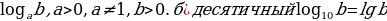 . в)натуральный
. в)натуральный 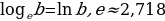 .
.
Выполнить упражнения:
Пример 1. Найти значение выражения 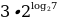 .
.
Решение. Для вычисления используем основное логарифмическое тождество (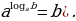 Получим
Получим 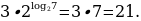
Пример 2. Вычислить значение выражения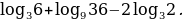
Решение. Для вычисления используем теоремы логарифмирования и следствия:
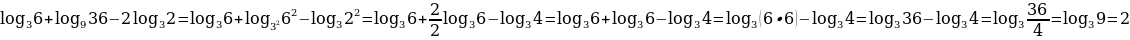 .
.
Пример 3. Вычислить: 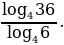
Решение. Для вычисления используем формулу перехода от одного основания логарифма к другому 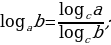 в данном случае с = 4, в = 36, а = 6. Тогда получим
в данном случае с = 4, в = 36, а = 6. Тогда получим 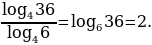
Пример 4. Вычислить: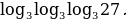
Решение. Применяя последовательно определение логарифма, получим
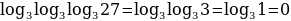 .
.
2.Задания для самостоятельной работы.
Вариант 1.
1. Вычислить: а) 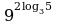 ; б)
; б) 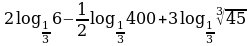 ; в)
; в) 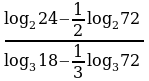

2. Найти х по данному логарифму :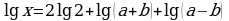
3.Решить уравнение: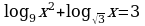
4. При каких значениях х имеет смысл выражение: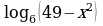
Вариант 2.
1. Вычислить: а) 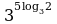 ; б)
; б) 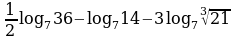 ; в)
; в) 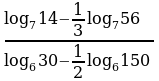

2. Найти х по данному логарифму :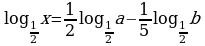
3.Решить уравнение: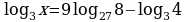
4. При каких значениях х имеет смысл выражение: 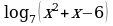
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 5
Тема 2. Корни, степени и логарифмы
Наименование работы: Решение показательных уравнений.
Цель работы, требования к умениям и навыкам:Сформировать знания, умения и навыки по решению показательных уравнений. Применять определение степени и свойства степени при нахождении корней уравнений.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
1.Определение. Уравнение, содержащее неизвестную величину в показателе степени, называется показательным.
Уравнение вида 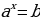 называется простейшим показательным. Очевидно, что если
называется простейшим показательным. Очевидно, что если 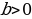 , то простейшее уравнение имеет единственное решение
, то простейшее уравнение имеет единственное решение 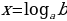 . Если
. Если 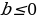 , то уравнение решенийне имеет, т.к. показательная функция не может принимать отрицательные значения или быть равной нулю.
, то уравнение решенийне имеет, т.к. показательная функция не может принимать отрицательные значения или быть равной нулю.
При решении показательных уравнений вида 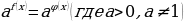 используется следующее свойство: (
используется следующее свойство: (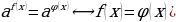 .
.
Преобразование показательного уравнения к виду 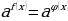 выполняется многими способами.
выполняется многими способами.
2.Способы решения показательных уравнений.
2.1. Способ уравнивания оснований.
Решить уравнения:
Пример 1. 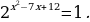
Решение . По определению нулевого показателя получим 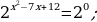 отсюда следует
отсюда следует 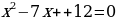 , решая квадратное уравнение, получим
, решая квадратное уравнение, получим 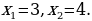 Ответ:
Ответ: 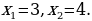
Пример 2.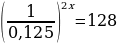
Решение. Выполняя преобразования в левой и правой частях уравнения, используя определения и свойства степени, получим: 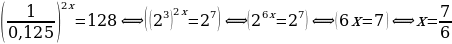 Ответ:
Ответ: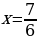 .
.
Пример 3. 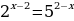
Записав уравнение 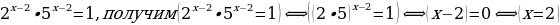 .
.
Ответ: 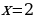 .
.
Пример 4.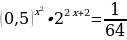 .
.
Решение. 
 . Ответ:
. Ответ: 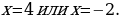
 Способ вынесения общего множителя за скобки.
Способ вынесения общего множителя за скобки.
Пример 5. 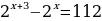 .
.
Решение. Вынесем общий множитель 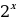 за скобки, выполняя последовательно действия, получим:
за скобки, выполняя последовательно действия, получим:
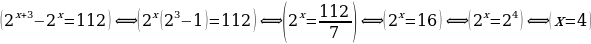 .
.
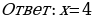 .
.
Пример 6. 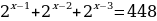 .
.
Решение.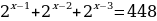 . Вынесем общий множитель
. Вынесем общий множитель 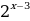 за скобки и получим:
за скобки и получим:
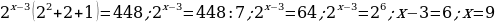 .
.
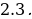 Преобразование к квадратному уравнению.
Преобразование к квадратному уравнению.
Пример 7. 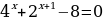 .
.
Решение.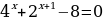 . Выполним преобразование, используя свойства степени:
. Выполним преобразование, используя свойства степени: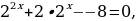 пусть
пусть 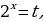 тогда уравнение примет вид:
тогда уравнение примет вид: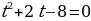 . Решая квадратное уравнение относительно
. Решая квадратное уравнение относительно 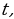 получим корни
получим корни 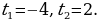 Учитывая замену переменной, получим
Учитывая замену переменной, получим 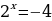 , но это уравнение корней не имеет, т.к.
, но это уравнение корней не имеет, т.к. 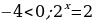 , отсюда
, отсюда 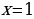 . Ответ:
. Ответ: 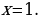
Пример 8. 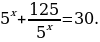
Решение.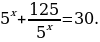 Выполним преобразования (приведём к общему знаменателю), в результате получим:
Выполним преобразования (приведём к общему знаменателю), в результате получим: 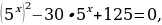 пусть
пусть 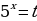 , тогда уравнение примет вид:
, тогда уравнение примет вид: 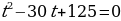 . Решая квадратное уравнение относительно
. Решая квадратное уравнение относительно 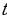 , получим корни
, получим корни 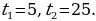 Учитывая замену переменной, получим
Учитывая замену переменной, получим 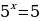 , отсюда
, отсюда 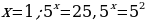 , отсюда
, отсюда 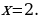 Ответ:
Ответ: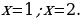
2.Задания для самостоятельной работы.
Вариант 1. Решите уравнения:
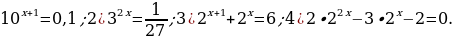
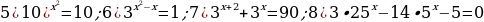 .
.
Вариант 2. Решите уравнения:
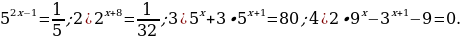
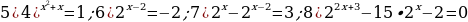 .
.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 6
Тема 2. Корни, степени и логарифмы
Наименование работы: Решение логарифмических уравнений
Цель работы, требования к умениям и навыкам:Сформировать знания, умения и навыки по решению логарифмических уравнений. Применять определение логарифма, его свойства и теоремы логарифмирования при нахождении корней уравнений.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Логарифмические уравнения.
Определение. Уравнения, содержащие переменную под знаком логарифма или в основании логарифма, называются логарифмическими.
Уравнение вида 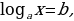 где
где 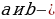 заданные числа, называется простейшим логарифмическим. Очевидно, что если,
заданные числа, называется простейшим логарифмическим. Очевидно, что если, 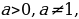 то такое уравнение при любом
то такое уравнение при любом 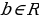 имеет единственное решение:
имеет единственное решение: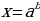 . Логарифмические уравнения, как и показательные, рассматриваются только на множестве действительных чисел. Общего метода решения логарифмические уравнения не имеют, но обычно используются способы, основанные на определении логарифма, свойствах логарифмов, замене переменных, приведении уравнения к виду
. Логарифмические уравнения, как и показательные, рассматриваются только на множестве действительных чисел. Общего метода решения логарифмические уравнения не имеют, но обычно используются способы, основанные на определении логарифма, свойствах логарифмов, замене переменных, приведении уравнения к виду 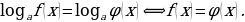
1) Логарифмом числа в по основаниюа называется показатель степени с, в которую нужно возвести основание а, чтобы получить число в. При этом пишут 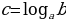 т.е.
т.е. 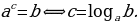
2)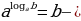 основное логарифмическое тождество.
основное логарифмическое тождество.
3)Логарифм произведения двух положительных чисел равен сумме логарифмов множителей:
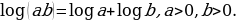
4) Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя: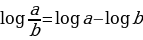
5) Логарифмстепениположительногочисларавенпроизведениюпоказателястепениналогарифмоснованиястепени: 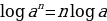 .
.
Решитьуравнения:
Пример 1. 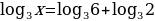 .
.
Решение.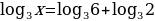 . Вправойчастиуравнениясделаемпреобразование, используясвойство, иполучим:
. Вправойчастиуравнениясделаемпреобразование, используясвойство, иполучим: 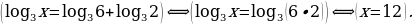 Ответ:
Ответ: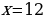
Пример 2.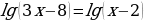
Решение.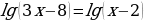 , учитываяравенствологарифмовиравенствоихоснований, получим:
, учитываяравенствологарифмовиравенствоихоснований, получим: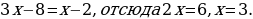 Ноданноерешениетребуетпроверки, т.к. несуществуетлогарифмаотрицательногочислаинуля.
Ноданноерешениетребуетпроверки, т.к. несуществуетлогарифмаотрицательногочислаинуля.
Проверка: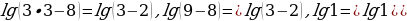 (получимверноеравенство), следовательно,
(получимверноеравенство), следовательно, 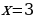 –кореньуравнения. Ответ:
–кореньуравнения. Ответ: 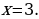
Пример3.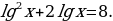
Решение. 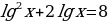 данноеуравнениепреобразуемкквадратному, выполнивподстановку: пусть
данноеуравнениепреобразуемкквадратному, выполнивподстановку: пусть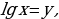 тогдаполучимквадратноеуравнение:
тогдаполучимквадратноеуравнение: 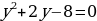 , решаяего, получим
, решаяего, получим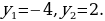 Тогда
Тогда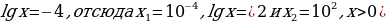 (условиесуществованиялогарифмавыполнено) Ответ:
(условиесуществованиялогарифмавыполнено) Ответ: 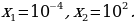
Пример 4.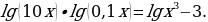
Решение.Используятеоремылогарифмирования, выполнимпреобразованияи, решая, получим:
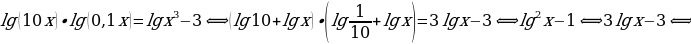
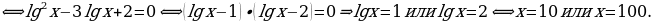 Ответ:
Ответ: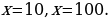
2.Задания для самостоятельной работы.
Решите уравнения:
Вариант 1.
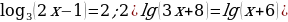 . .
. .
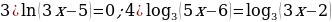
Вариант 2.
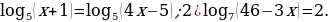
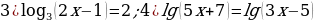 .
.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 7
Тема 3. Прямые и плоскости в пространстве
Наименование работы: Перпендикуляр и наклонная к плоскости.
Цель работы, требования к умениям и навыкам:Рассмотреть связь между перпендикуляром, наклонной и проекцией наклонной, систематизировать и закрепить эти понятия в ходе решения типовых задач по этой теме.
Задание: 1. Изучить методические указания к работе, записать указанные задачи с чертежами и решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Н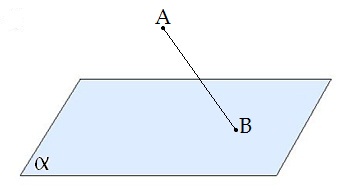 аклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий даную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
аклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий даную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
Конец отрезка, лежащий в плоскости, называется основанием наклонной.
AB - наклонная. B - основание наклонной.
Перпендикуляром, проведенным из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости.
Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
AC - перпендикуляр.
C - основание перпендикуляра.
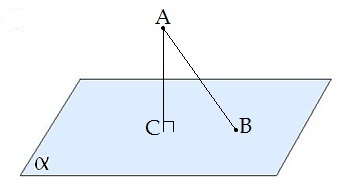
Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к плоскости.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
C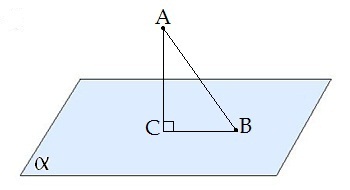 B - проеция наклонной AB на плоскость α.
B - проеция наклонной AB на плоскость α.
Треугольник ABC прямоугольный.
Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость.
CBA - угол между наклонной AB и плоскостью α.
Е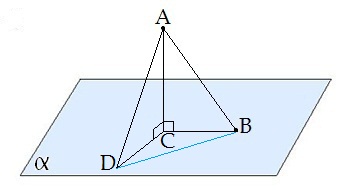 сли ADAB, то DCBC
сли ADAB, то DCBC
Если из данной точки к данной плоскости провести несколько наклонных, то большей наклонной соответствует большая проекция.
DAB - угол между наклонными
DCB - угол между проекциями наклонных
Отрезок DB - расстояние между основаниями наклонных.
Применение знаний при решении типовых заданий.
Задача 1
Из точки К, на расстоянии 9 см, к плоскости 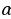 опущен перпендикуляр КС и проведена наклонная КМ, равная 15 см.
опущен перпендикуляр КС и проведена наклонная КМ, равная 15 см.
Найти проекцию наклонной. ( Устно, менять условие, найти наклонную, найти перпендикуляр)
Решение:
Р ассмотрим прямоугольный треугольник КСМ: (КС-перпендикуляр, по условию), по теореме Пифагора:
ассмотрим прямоугольный треугольник КСМ: (КС-перпендикуляр, по условию), по теореме Пифагора:
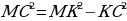
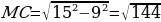 =12 (см)
=12 (см)
Ответ: Проекция наклонной МС=12 см.
Задача2
К плоскости α проведена наклонная AB (A∈α). Длина наклонной равна 8 см, наклонная с плоскостью образует угол 60°. Вычисли, на каком расстоянии от плоскости находится точка B.
Р
В
ешение: Рассмотрим треугольник АВО: прямоугольный, ВО- р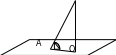 асстояние от точки В до плоскости
асстояние от точки В до плоскости 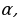 перпендикулярно АО. Следовательно угол В=30
перпендикулярно АО. Следовательно угол В=30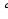 , а АО =4 см, как катет лежащий против угла в 30
, а АО =4 см, как катет лежащий против угла в 30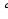 .
.
По теореме Пифагора:
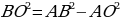
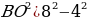
В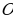 =
=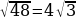 (см)
(см)
Ответ: 4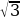 см.
см.
Задача 3
АВ перпендикулярно плоскости α. Наклонная AС образует с плоскостью α , угол 60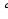 , а наклонная АD равна
, а наклонная АD равна 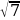 . Длина проекции наклонной ВD равна 2 см.
. Длина проекции наклонной ВD равна 2 см.
Вычисли длину наклонной АС.
Решение:
А
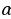
В
С
D
Решение:
Рассмотрим 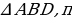 о теореме Пифагора:
о теореме Пифагора: 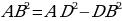 ;
;
АВ=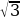 .
.
Угол АСВ = 60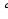 (по условию), следовательно
(по условию), следовательно САВ=30
САВ=30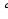 .
.
Рассмотрим 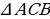 ,
, 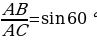 ;
;
АС =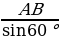 ;
;
АС = 2.
Ответ: 2см.
Задача 4
О трезок АB длиной 6
трезок АB длиной 6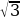 м, пересекает плоскость β в точке O. Расстояние от концов отрезка до плоскости соответственно равны 3 м и 6 м. Найди острый угол, который образует отрезок АB с плоскостью β.
м, пересекает плоскость β в точке O. Расстояние от концов отрезка до плоскости соответственно равны 3 м и 6 м. Найди острый угол, который образует отрезок АB с плоскостью β.
Решение:
Пусть АО=х, тогда ОВ=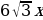 .
.
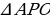 подобен
подобен 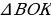 (угла при вершине О, равны как вертикальные, углы Р и К , равны 90
(угла при вершине О, равны как вертикальные, углы Р и К , равны 90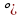 .
.
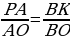 ;
;
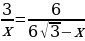 ;
;
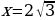 ;
;
Рассмотрим 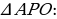
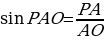
sinРАО =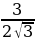
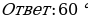
2.Задания для самостоятельной работы.
Вариант 1
на «3»:
Прямая a пересекает плоскость β в точке C, и образует с плоскостью угол 30°.В∈a, точка А - проекция точки В на плоскость β. ВC=12 см. Найдите ВА.
Прямая a пересекает плоскость β в точке C, и образует с плоскостью угол 30°.P∈a, точка N - проекция точки P на плоскость β. PN=5 см. Найдите PC.
на «4»:
К плоскости α проведена наклонная AС (A∈α). Длина наклонной равна 24 см, наклонная с плоскостью образует угол 60°. Вычислите, на каком расстоянии от плоскости находится точка С.
К плоскости α проведена наклонная AC (A∈α). Длина наклонной равна 16 см, наклонная с плоскостью образует угол 60°. Вычислите, на каком расстоянии от плоскости находится точка C.
на «5»:
Наклонная AК с плоскостью α образует угол 30 , а наклонная КC с плоскостью α образует угол 45
, а наклонная КC с плоскостью α образует угол 45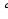 .Длина перпендикуляра КB равна 12 см.
.Длина перпендикуляра КB равна 12 см.
Вычислите длины наклонных.
Наклонная AD с плоскостью α образует угол 30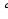 , а наклонная DC с плоскостью α образует угол 45
, а наклонная DC с плоскостью α образует угол 45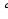 .Длина перпендикуляра DB равна 32 см.
.Длина перпендикуляра DB равна 32 см.
Вычислите длины наклонных.
Вариант 2
на «3»:
К плоскости α проведена наклонная, длина которой равна 25 см, проекция наклонной равна 15 см . На каком расстоянии от плоскости находится точка, из которой проведена наклонная?
Прямая a пересекает плоскость β в точке C, и образует с плоскостью угол 30°.P∈a, точка F - проекция точки P на плоскость β. PC=14 см. Найдите PF.
на «4»:
К плоскости α проведена наклонная AB (A∈α). Длина наклонной равна 12 см, наклонная с плоскостью образует угол 45°. Вычисли, на каком расстоянии от плоскости находится точка B.
К плоскости α проведена наклонная AB (A∈α). Длина наклонной равна 12 см, наклонная с плоскостью образует угол 60°. Вычислите, на каком расстоянии от плоскости находится точка B.
на «5»:
5)Проекции наклонных AD и DC на плоскости α равны соответственно 8 см и 4 см, а угол между ними равен 120°.Вычислите расстояние между концами проекций наклонных.
6) Наклонная AD с плоскостью α образует угол 30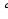 , а наклонная DC с плоскостью α образует угол 45
, а наклонная DC с плоскостью α образует угол 45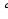 .Длина перпендикуляра DB равна 22 см.Вычислите длины наклонных.
.Длина перпендикуляра DB равна 22 см.Вычислите длины наклонных.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 8
Тема 3. Прямые и плоскости в пространстве
Наименование работы: Теорема о трех перпендикулярах.
Цель работы, требования к умениям и навыкам:совершенствовать умения учащихся применять теоретические знания к решению задач на доказательство и вычисления, развивать пространственное воображение, развивать умение строить аргументированное и логически верное решение задачи, способствовать дальнейшему развитию навыков самоконтроля.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Прямая теоремаТеорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
Рассмотрим следующий рисунок.
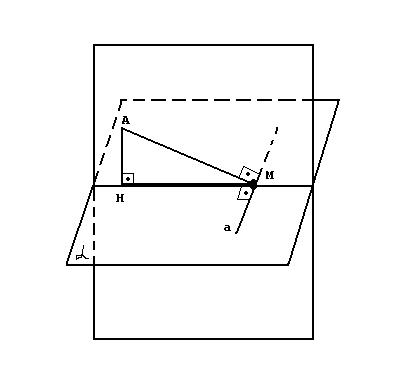
AH - перпендикулярен плоскости α. AM это наклонная в плоскости α; a - прямая, проведенная в плоскости α через точку М перпендикулярно к проекции HM наклонной. Теперь, докажем, что прямая а перпендикулярна АМ. Для этого рассмотрим плоскость AMH.
По условию прямая а перпендикулярна НМ. Также прямая а перпендикулярна АН, так как АН перпендикулярна плоскости α. Прямые НМ и АН принадлежат плоскости АНМ и пересекаются. Из этих трех пунктов следует, что прямая а перпендикулярна плоскости АМН, значит, она перпендикулярна любой прямой, которая принадлежит плоскости АМН.
Так как прямая АМ принадлежит плоскости АМН, значит прямая a и прямая АМ перпендикулярны между собой. Что и требовалось доказать.
Так как в теореме присутствуют три перпендикуляра, АН, НМ и АМ, теорема называется теоремой о трех перпендикулярах. Все три прямых угла показаны на рисунке, который приведен в начале доказательства. Помимо основной теоремы о трех перпендикулярах, существует и обратная теорема о трех перпендикулярах.
Обратная теоремаПрямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.
Задача. Отрезок AD перпендикулярен к плоскости равнобедренного треугольника АВС. Известно, что АВ = АС = 5см, ВС = 6 см, AD = 12 см. Найти расстояние от точки А до прямой ВС.
Решение.
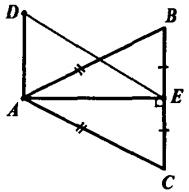
Пусть точка Е это середина ВС. Тогда ВС будет перпендикулярным АЕ. То есть АЕ будет расстояние от точки А до прямой ВС.
ЕА является проекцией DE на плоскость АВС. АЕ перпендикулярен ВС, а следовательно по теореме о трех перпендикулярах DE будет перпендикулярен BC. Получаем, что DE - это расстояние от точки D до отрезка BC. Теперь будем определять AE.
ВЕ = (1/2)*ВС = 3 см.
Так как треугольник АВЕ прямоугольный, то можем по теореме Пифагора найти АЕ.
АЕ^2 = AB^2-BE^2 = 25-9 = 16, следовательно, АЕ = 4 см.
Ответ. 4 см.
2.Задания для самостоятельной работы.
Вариант 1
Через вершину В прямоугольника АВСД проведен перпендикуляр МВ к плоскости прямоугольника. Определите вид ∆ АМД и найдите его площадь, если стороны прямоугольника АВ = 3 и АД = 8, а ВМ = 4
К плоскости треугольника из центра вписанной в него окружности восставлен перпендикуляр длиной 3. Найдите расстояние от конца этого перпендикуляра до сторон треугольника, если длины сторон треугольника 13, 14 и 15
Катеты прямоугольного треугольника равны 18 и 32. Из точки М, делящей гипотенузу пополам, восставлен к плоскости треугольника перпендикуляр МК, равный 12. Найдите расстояние от точки К до каждого катета.
Вариант 2
Из вершины равностороннего треугольника АВС восставлен перпендикуляр АД к плоскости треугольника. Найдите расстояние от точки Д до стороны ВС, если
АД = 13, ВС = 6.
Точка М лежит вне плоскости ромба АВСД на равном расстоянии от его сторон. Найдите расстояние от проекции точки М на эту плоскость до сторон ромба, если сторона ромба равна 12, а острый угол 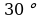
Через вершину А прямоугольного треугольника АВС в прямым углом В проведён перпендикуляр АД к плоскости треугольника. Найдите длину наклонной ДС, если её проекция равна ℓ, 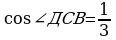 ,
, 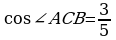 .
.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 9
Тема 4. Комбинаторика
Наименование работы: Размещения, сочетания и перестановки.
Цель работы, требования к умениям и навыкам:Проконтролировать умения и навыки по решению комбинаторных задач на подсчет размещений, сочетаний и перестановок.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Человеку часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия.
Например, сколькими способами можно расположить 50 человек в очереди в кассу за билетами в кино, сколькими способами могут быть распределены золотая, серебряная и бронзовая медали на чемпионате Европы по футболу?
Задачи такого типа называются комбинаторными.
Введем некоторые важные обозначения:
множества будем обозначать заглавными буквами;
множества состоят из элементов, которые будем обозначать малыми буквами. Так, запись аА обозначает, что элемент а принадлежит множеству А. Такие множества будем изображать перечислением элементов, заключая их в фигурные скобки. Например, {а, b, х, у}.
3) Количество элементов в множестве называется мощностью и записывается как |A|.
Комбинаторные соединения
Некоторая совокупность элементов данного n-множества называется выборкой. Число элементов в выборке называется длиной выборки.
Пример 1. Пусть дано множество Х – множество цифр, т.е. ![]() . Это множество состоит из 10 элементов. Любой набор цифр, состоящий, например, из 4 цифр будет являться выборкой длины 4.
. Это множество состоит из 10 элементов. Любой набор цифр, состоящий, например, из 4 цифр будет являться выборкой длины 4.
Замечание. Некоторую совокупность элементов из данного конечного множества можно выбирать по-разному:
если при составлении выборки учитывается порядок следования элементов в выборке, тогда выборка называется упорядоченной; если же при составлении выборки не учитывается порядок следования элементов в ней, то выборка называется неупорядоченной;
если при составлении выборки в нее может быть включен один и тот же элемент множества несколько раз, то выборка называется выборкой с повторениями; если же элементы множества входят в выборку только по одному разу, то выборка называется выборкой без повторений.
Пример 2.Пусть дано множество Х – множество цифр, т.е. ![]() . Составить из цифр пятизначное число, цифры в котором не повторяются.
. Составить из цифр пятизначное число, цифры в котором не повторяются.
Этим пятизначным числом может быть, например, число 54321. Переставим цифры в данном числе, например, так 45321, в результате получим другое число (другую выборку). Таким образом, при изменении порядка следования элементов в выборке, изменяется сама выборка, поэтому каждое пятизначное число является упорядоченной выборкой. Так как оба составленных числа не имеют в своем составе одинаковых цифр, то обе эти выборки являются выборками без повторений. Однако пятизначное число, например, 554331 является упорядоченной выборкой, но с повторениями.
Пример 3.Пусть имеются открытки 6 видов. Составить из этих открыток набор, состоящий из 4 открыток.
Каждый набор из 4 открыток будет являться выборкой. Если мы поменяем в наборе местами две открытки, то от этого набор открыток не измениться, т.е. выборка останется прежней. Таким образом, при изменении порядка следования элементов в выборке выборка не меняется, следовательно, в данном случае выборка неупорядоченная. Если в составленном наборе будут одинаковые открытки, то он будет выборкой с повторениями, если же все открытки в наборе будут различными, то набор будет являться выборкой без повторений.
Основные виды комбинаторных соединений: размещения, перестановки и сочетания.
Определение 1.Размещением без повторений из m элементов данного n- множества называется упорядоченная выборка без повторений длины m из элементов данного множества.
Таким образом, если характер выборки: 1) упорядоченная; 2) без повторений, то выборка является размещением без повторений. Число размещений без повторений из m элементов данного n-множества обозначается ![]() , и вычисляется по формуле:
, и вычисляется по формуле: ![]() =
= ![]() (2)
(2)
Замечание. Символ ![]() читается как n – факториал и означает произведение первых n натуральных чисел:
читается как n – факториал и означает произведение первых n натуральных чисел: ![]() .
.
Задача 1.Сколько различных четырехбуквенных слов можно составить из букв слова ученик, написанных на отдельных карточках?
Решение. 1) Множество из которого производится выборка – множество букв слова ученик, в котором n = 6 букв.
2) Составляют четырехбуквенные слова, поэтому каждое такое слово есть выборка длиной m = 4.
3) Определим характер выборки: 1) так как составляем слова, в которых порядок букв существенен, то выборка является упорядоченной; 2) так как все буквы данного слова различные, то выборка происходит безповторений.
3) По характеру выборки делаем вывод что, каждое составленное слово является размещением без повторений. По формуле (2) найдем число размещений без повторений из 6 элементов по 4: ![]() =
=![]() =
= ![]() = 360.
= 360.
Ответ: из букв слова ученик можно составить 360 четырехбуквенных слов.
Определение 2.Перестановкой без повторений из n элементов данного n- множества называется упорядоченная выборка без повторений длины n из элементов данного множества.
Таким образом, если характер выборки: 1) упорядоченная; 2) без повторений, и выбирают все элементы n-множества, то выборка является перестановкой без повторений. Число перестановок без повторений из n элементов обозначается ![]() , и вычисляется по формуле:
, и вычисляется по формуле: ![]() (3)
(3)
Задача 2.Сколькими способами очередей можно составить из 10 человек.
Решение. 1) Множество из которого выбирают, состоит из n = 10 элементов;
2)Выбирают все 10 человек, поэтому длина выборки m = 10, т.е. m = n.
Определим характер выборки: выбираем упорядоченно и без повторений.
По характеру выборки делаем вывод, что каждая составленная очередь это перестановка без повторений. По формуле (3) вычислим число перестановок без повторений из n элементов: ![]() .
.
Ответ: можно составить 3628800 очередей.
Используя формулу (3) можно вычислить, сколько четырехзначных цифр можно составить из цифр 1,2,3,4: ![]() . В слове мама тоже четыре буквы, поставим задачу: сколько различных четырёхбуквенных слов можно составить из букв слова мама. В отличие от предыдущего случая таких слов будет не 24, а всего 6 (мама, маам, ммаа, амам, аамм, амма). Дело в том, что в слове мама есть одинаковые буквы, т.е. при составлении слов происходит упорядоченная выборка с повторениями. Однако в отличие от размещения с повторениями, в этом случае элементы множества повторяются не произвольно, а в определенном составе: 2 раза буква м и 2 раза буква а.
. В слове мама тоже четыре буквы, поставим задачу: сколько различных четырёхбуквенных слов можно составить из букв слова мама. В отличие от предыдущего случая таких слов будет не 24, а всего 6 (мама, маам, ммаа, амам, аамм, амма). Дело в том, что в слове мама есть одинаковые буквы, т.е. при составлении слов происходит упорядоченная выборка с повторениями. Однако в отличие от размещения с повторениями, в этом случае элементы множества повторяются не произвольно, а в определенном составе: 2 раза буква м и 2 раза буква а.
Определение 3.Сочетанием без повторений из m элементов данного n- множества называется любое подмножество из m элементов данного n- множества.
Таким образом, если характер выборки: 1) неупорядоченная; 2) без повторений, то выборка является сочетанием без повторений. Число сочетаний без повторений из m элементов данного n- множества обозначается ![]() , и вычисляется по формуле:
, и вычисляется по формуле:![]() =
= ![]() (5)
(5)
Задача 3. Сколько различных хорд можно провести через 6 точек, лежащих на данной окружности?
Решение. 1) Будем выбирать из множества, состоящего из n = 6 элементов.
2) Хорда определяется двумя точками, поэтому будем из 6 элементов составлять выборку длиной m = 2.
3) Определим характер выборки: порядок выбора точек для построения каждой хорды не имеет значения, поэтому имеем неупорядоченную выборку; так как одну и туже точку в выборку из двух точек брать нельзя (т.к. через одну прямую проходит множество прямых), то выборка – без повторений. Таким образом, имеем сочетание без повторений.
По формуле (5) находим: ![]() =
= ![]() =15.
=15.
Ответ: через 6 точек, лежащих на окружности можно провести 15 хорд.
2.Задания для самостоятельной работы.
Вариант 1
Сколькими способами можно разместить 5 человек за столом, на котором поставлено 5 приборов?
Комитет из 20 членов избирает председателя и секретаря. Сколькими способами это можно сделать?
На плоскости отмечено 10 точек так, что никакие три из них не лежат на одной прямой. Сколько существует треугольников с вершинами в этих точках?
Сколькими способами Дима сможет покрасить пять елок в серебристый, зеленый и синий цвета, если количество краски у него неограничено, а каждую елку он красит только в один цвет?
б) У Димы есть пять шариков: красный, зеленый, желтый, синий и золотой. Сколькими способами он сможет украсить ими пять елок, если на каждую требуется надеть ровно один шарик?
Вариант 2
В пассажирском поезде 17 вагонов. Сколькими способами можно распределить по вагонам 17 проводников, если за каждым вагоном закрепляется один проводник?
Сколько существует возможностей для присуждения первого, второго и третьего мест семнадцати участницам соревнований по икебане
Хоккейная команда насчитывает 18 игроков. Одиннадцать из них входят в основной состав. Подсчитайте количество возможных основных составов.
У людоеда в подвале томятся 25 пленников.
а) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин? Порядок важен.
б) А сколько есть способов выбрать троих, чтобы отпустить на свободу?
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическое занятие № 10
Тема 4 Комбинаторика
Наименование работы: Бином Ньютона и треугольник Паскаля.
Цель, приобретаемые умения и навыки: Обеспечить усвоение формулы бинома Ньютона, выявить свойства формулы бинома Ньютона, рассмотреть и закрепить применение формулы бинома Ньютона на частных примерах, установить связь треугольника Паскаля с биномиальными коэффициентами разложения бинома Ньютона.
Методические указания
Краткие теоретические сведения.
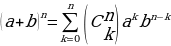 формула бинома Ньютона.
формула бинома Ньютона.
ПримерЗаписать разложение бинома Ньютона 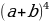 , не вычисляя биномиальные коэффициенты.
, не вычисляя биномиальные коэффициенты.
Решение:
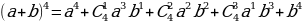
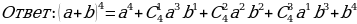
Определение: Треугольник Паскаля - это треугольник, составленный из чисел, являющихся коэффициентами в формуле бином Ньютона.
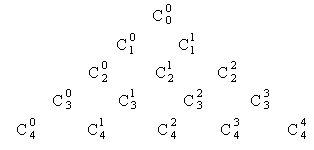
Каждый крайний элемент равен 1, а каждый не крайний элемент равен сумме двух своих верхних соседей.
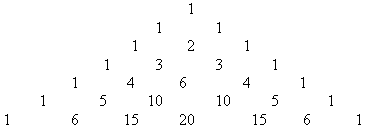
Треугольник можно продолжать до бесконечности, но на практике чаще составляют таблицу для первых 10 степеней.
Треугольник Паскаля для n от 1 до 10.
| n | k1 | k2 | k3 | k4 | k5 | k6 | k7 | k8 | k9 | k10 | k11 |
| 1 | 1 | 1 |
|
|
|
|
|
|
|
|
|
| 2 | 1 | 2 | 1 |
|
|
|
|
|
|
|
|
| 3 | 1 | 3 | 3 | 1 |
|
|
|
|
|
|
|
| 4 | 1 | 4 | 6 | 4 | 1 |
|
|
|
|
|
|
| 5 | 1 | 5 | 10 | 10 | 5 | 1 |
|
|
|
|
|
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 |
|
|
|
|
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
|
|
|
| 8 | 1 | 8 | 28 | 70 | 70 | 56 | 28 | 8 | 1 |
|
|
| 9 | 1 | 9 | 36 | 126 | 126 | 126 | 84 | 36 | 9 | 1 |
|
| 10 | 1 | 10 | 45 | 210 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
2.Задания для самостоятельной работы.
Вариант 1.
1.Записать разложение бинома Ньютона 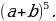
2.Записать разложение бинома Ньютона 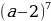
3.Записать разложение бинома Ньютона по треугольнику Паскаля 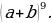
Вариант 2.
1. Записать разложение бинома Ньютона 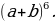
2. Записать разложение бинома Ньютона 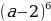
3. Записать разложение бинома Ньютона по треугольнику Паскаля 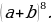
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы
Практическая работа №11
Тема 5. Координаты и векторы
Наименование работы: Векторы. Действия с векторами.
Цель работы, требования к умениям и навыкам:Научиться выполнять действия над векторами, заданными своими координатами на плоскости и в пространстве. Выполнять действия над векторами в координатной форме; решать задачи на применение свойств векторов.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
Выполнить самостоятельную работу по вариантам.
Сделать отчет
Методические указания.
Краткие теоретические сведения.
1.Векторы. Координаты вектора.
Определение 1. Вектором называется направленный отрезок. Обозначения: 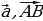 .
.
Система координат на плоскости (пространстве).
Рассмотрим декартову систему координат, базис которой образуют на плоскости (пространстве) два ортогональных единичных вектора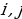 (три попарно ортогональных единичных вектора
(три попарно ортогональных единичных вектора 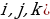 . Тогда любой векторaможет быть представлен в виде:
. Тогда любой векторaможет быть представлен в виде: 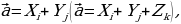 (формула разложения вектора по ортам на плоскости и в пространстве).
(формула разложения вектора по ортам на плоскости и в пространстве).
Определение 2. Числа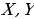 называются декартовыми координатами вектора a на плоскости (числа
называются декартовыми координатами вектора a на плоскости (числа 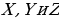 называются декартовыми координатами вектора a в пространстве).
называются декартовыми координатами вектора a в пространстве).
2.Нахождение модуля (длины) вектора. Расстояние между двумя точками.
В прямоугольной декартовой системе координат на плоскости даны точки 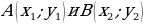 , тогда вектор AB будет иметь координаты
, тогда вектор AB будет иметь координаты 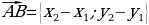 , его длину можно вычислить по формуле:
, его длину можно вычислить по формуле: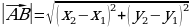 (по этой же формуле можно вычислить расстояние между двумя точками и длину отрезка).
(по этой же формуле можно вычислить расстояние между двумя точками и длину отрезка).
Если точки заданы в пространстве, то 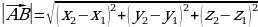 .
.
Если координаты одной из точек совпадают с началом координат, то вектор 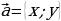 или
или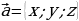 и длина его может быть вычислена по формуле:
и длина его может быть вычислена по формуле: 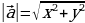 или для пространства
или для пространства 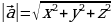
3.Действия над векторами в координатной форме.
3.1.Сложение (вычитание) векторов: если векторы заданы своими координатами на плоскости
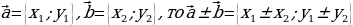 ,
,
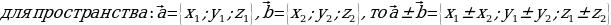 .
.
3.2.Умножение вектора на число: вектор a на плоскости имеет координаты 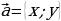 , то
, то
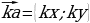 .
.
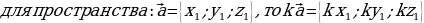 .
.
Пример 1. Дано: 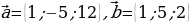
Найти: 1) 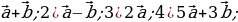
Решение: 1) 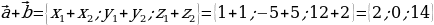 ;
;
2)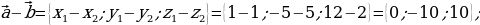
3) 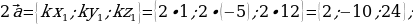
4) 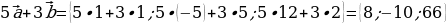 .
.
Пример 2. Найти длину вектора АВ, если 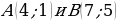
Решение. По формуле 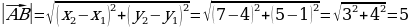
Пример 3. Найти длину вектора 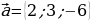
Решение: По формуле 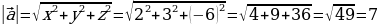
2.Задание для самостоятельной работы.
Вариант 1.
1. Дано: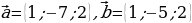
Найти: 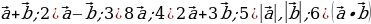
2. Дано: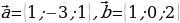
Найти: 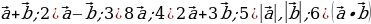
Вариант 2.
1. Дано: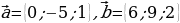
Найти: 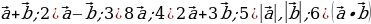
2. Дано: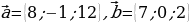
Найти: 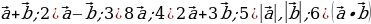
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 12
Тема 6. Основы тригонометрии
Наименование работы: Преобразование тригонометрических выражений
Цель работы, требования к умениям и навыкам:Закрепить умение использовать основные тригонометрические формулы при тождественных преобразованиях в процессе решения примеров на упрощение тригонометрических выражений, на доказательство тригонометрических тождеств. Применять основные тригонометрические тождества, формулы сложения, удвоения, преобразования суммы тригонометрических функций в произведение, формулы преобразования произведения тригонометрических функций в сумму для преобразования тригонометрических выражений.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
1.Основные тригонометрические тождества.
1.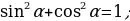 2.
2. 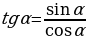 ; 3.
; 3. 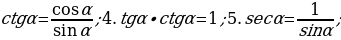
6. 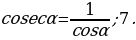 1+
1+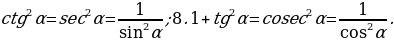
2.Таблица значений тригонометрических функций некоторых углов.
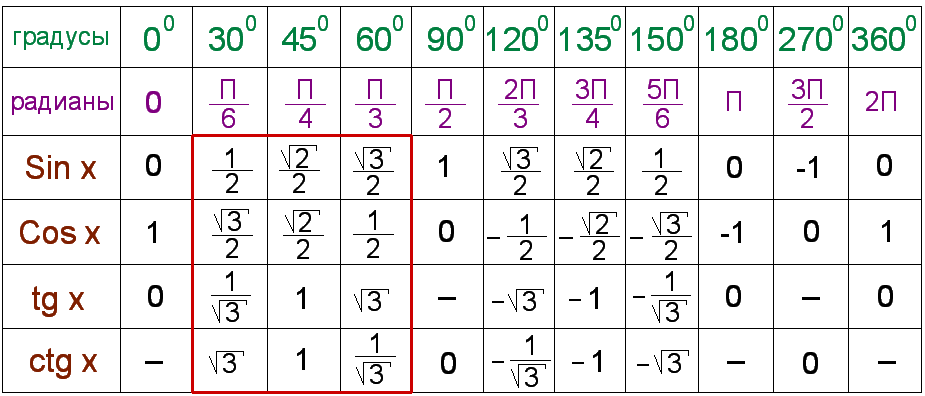
Пример 1. Найдите значение выражения:
а) 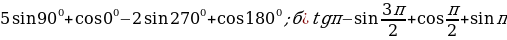 .
.
Решение: Используя таблицу значений тригонометрических функций некоторых углов, получим:
а) 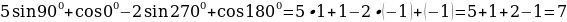 .
.
б) 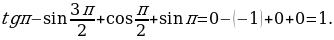
Пример 2. Дано: 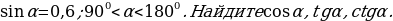
Решение: Т.к. 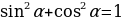 и
и 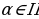 четверти, то косинус будет отрицателен, тогда
четверти, то косинус будет отрицателен, тогда
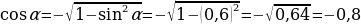 .
.
Для нахождения 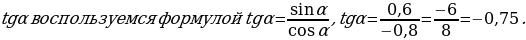
Для нахождения 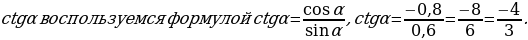
3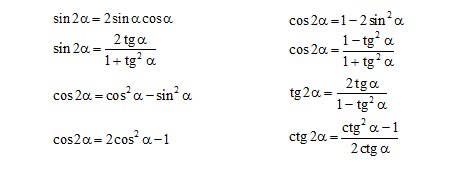 . Тригонометрические формулы.
. Тригонометрические формулы.
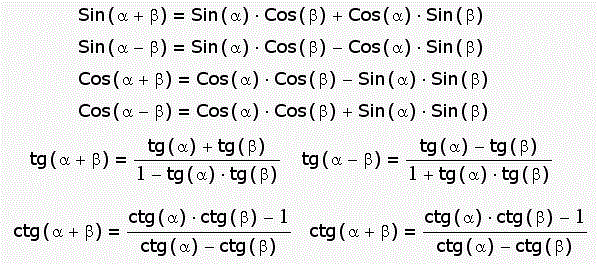
Вычислить:
Пример 3. а)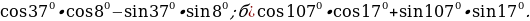
Решение: а) 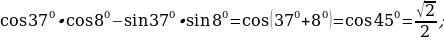
б)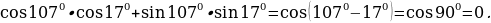
Пример 4. 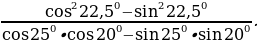
Решение: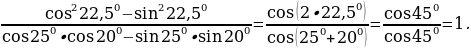
Пример 5. Найдите значение выражения: 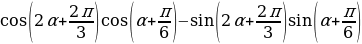
при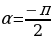 .
.
Решение: 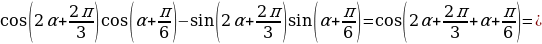
=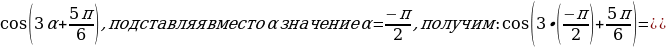
= 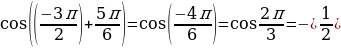 .
.
Пример 6. Найдите значение выражения :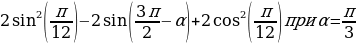 .
.
Решение: Учитывая, что 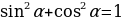 справедливо при любом значении
справедливо при любом значении 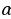 , и применяя правило формул приведения к выражению
, и применяя правило формул приведения к выражению 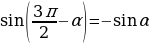 , получим:
, получим:
2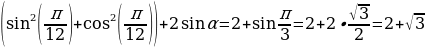 .
.
2.Задания для самостоятельной работы.
Вариант 1.
1.Доказать тождество: 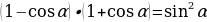 ;
;
2. Упростить выражение: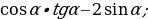
3. Упростить выражение и найти его числовое значение при заданном значении 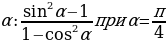 .
.
4. Найдите значение выражения: 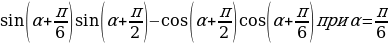 .
.
5. Найдите значение выражения: 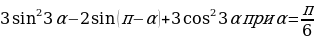 .
.
Вариант 2.
1.Доказать тождество: 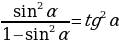 ;
;
2. Упростить выражение: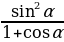
3. Упростить выражение и найти его числовое значение при заданном значении 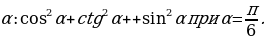
4. Найдите значение выражения: 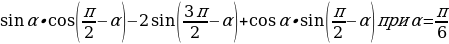 .
.
5.Упростите выражение: 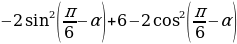 .
.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 13
Тема 6. Основы тригонометрии
Наименование работы: Простейшие тригонометрические уравнения и неравенства.
Цель работы, требования к умениям и навыкам:Закрепление умения решать задачи с использованием тригонометрических уравнений.Применять формулы решения простейших тригонометрических уравнений
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
1.Определение. Простейшими тригонометрическими уравнениями называются уравнения 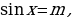
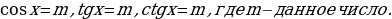
Решить простейшее тригонометрическое уравнение 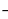 значит найти множество всех значений аргумента (дуг или углов), при которых данная тригонометрическая функция принимает заданное значение
значит найти множество всех значений аргумента (дуг или углов), при которых данная тригонометрическая функция принимает заданное значение 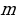 .
.
Решить уравнения: 1) 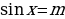
Если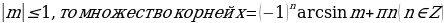
Если 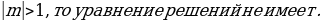
Частные случаи: 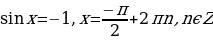
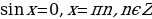
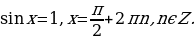
2) 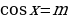
Если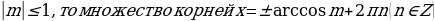
Если 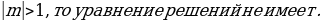
Частные случаи: 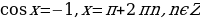
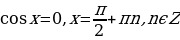
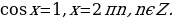
3) 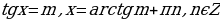
Частный случай: 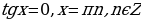 .
.
4) 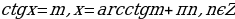
Частный случай: 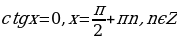 .
.
2. Виды тригонометрических уравнений и методы их решения.
2.1 Уравнения вида 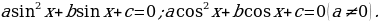 Такие уравнения называют квадратными относительно одной тригонометрической функции одного аргумента. Эти уравнения сводятся к простейшим тригонометрическим уравнениям путём решения их как алгебраических уравнений второй степени относительно заданной тригонометрической функции.
Такие уравнения называют квадратными относительно одной тригонометрической функции одного аргумента. Эти уравнения сводятся к простейшим тригонометрическим уравнениям путём решения их как алгебраических уравнений второй степени относительно заданной тригонометрической функции.
Пример 1. Решить уравнение 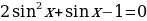 .
.
Решение. Это уравнение является квадратным относительно 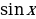 , его корни
, его корни 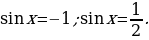
Уравнение:  .
.
Ответ: 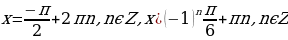 .
.
Пример 2. Решить уравнение 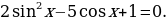
Решение. Заменив 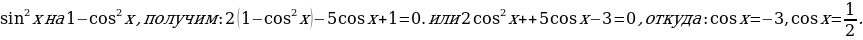 Уравнение
Уравнение 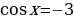 не имеет корней, из второго уравнения находим корни
не имеет корней, из второго уравнения находим корни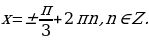
Ответ: 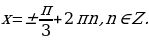
2.2 Однородные тригонометрические уравнения.
Однородными тригонометрическими уравнениями называются уравнения, в которых неизвестная величина имеет одну и ту же степень и в одной из частей уравнения находится число 0.
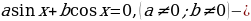 однородное тригонометрическое уравнение первой степени. Оно приводится к линейному уравнению относительно
однородное тригонометрическое уравнение первой степени. Оно приводится к линейному уравнению относительно 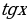 (путём деления обеих его частей на
(путём деления обеих его частей на 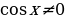 ) или относительно
) или относительно 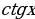 (посредством деления на
(посредством деления на 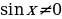 ). Рассмотрим уравнение
). Рассмотрим уравнение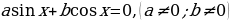 . Разделим обе части на
. Разделим обе части на 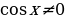 , получим
, получим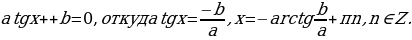
В процессе решения обе части уравнения были разделены на 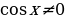 . Поэтому следует проверить, не являются ли корнями уравнения те значения
. Поэтому следует проверить, не являются ли корнями уравнения те значения 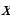 , при которых
, при которых 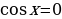 . Если
. Если 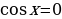 , то из уравнения следует, что и
, то из уравнения следует, что и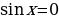 , так как
, так как 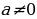 . Но равенство
. Но равенство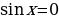 и
и 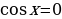 одновременно не могут выполняться ни при каком значении
одновременно не могут выполняться ни при каком значении 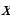 , так как
, так как 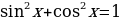 . Таким образом, при переходе от уравнения
. Таким образом, при переходе от уравнения 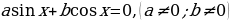 к уравнению
к уравнению 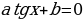 корни не теряются и посторонние не появляются, т.е. уравнения равносильны.
корни не теряются и посторонние не появляются, т.е. уравнения равносильны.
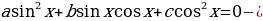 однородное уравнение второй степени.
однородное уравнение второй степени.
Если 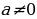 , то разделим обе части на
, то разделим обе части на 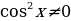 , тогда получим:
, тогда получим: 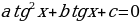 .
.
Если 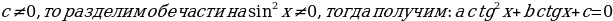 .
.
Пример 3.Решить уравнение 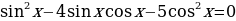 .
.
Решение. Данное уравнение равносильно уравнению 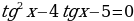 . Решая это квадратное уравнение относительно
. Решая это квадратное уравнение относительно 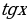 , находим
, находим 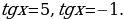 Откуда получаем следующие корни:
Откуда получаем следующие корни: 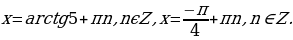
Ответ: 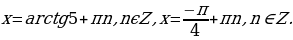
2.3Тригонометрические уравнения, решаемые разложением на множители.
При решении уравнений этого вида нужно пользоваться всеми известными способами разложения на множители: вынесение общего множителя за скобки, группировка, применение формул сокращенного умножения.
Пример 4. Решить уравнение 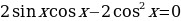 .
.
Решение. Вынесем общий множитель за скобки, получим: 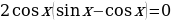 . Произведение двух множителей равно нулю тогда и только тогда, когда один из множителей равен нулю, а другой при этом имеет смысл.
. Произведение двух множителей равно нулю тогда и только тогда, когда один из множителей равен нулю, а другой при этом имеет смысл. 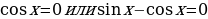 , а)
, а) 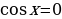 ,
, 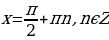 ;
;
б)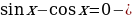 однородное уравнение первой степени относительно
однородное уравнение первой степени относительно 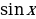 и
и 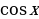 . Разделим на
. Разделим на 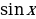 , так как
, так как 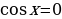 . Получим
. Получим 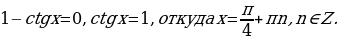
Ответ: 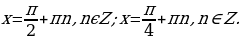
Пример 5. Решить уравнение 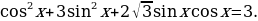
Решение. Преобразуем обе части уравнения:
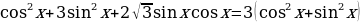 ,
,
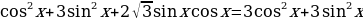 ,
,
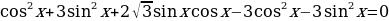 ,
,
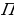 осле приведения подобных членов получим уравнение
осле приведения подобных членов получим уравнение 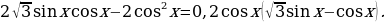
Полученное уравнение равносильно совокупности двух уравнений: 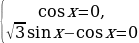
а)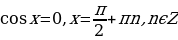 .
.
б) 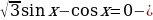 однородное тригонометрическое уравнение первой степени. Разделим обе части уравнения на
однородное тригонометрическое уравнение первой степени. Разделим обе части уравнения на 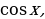 причем
причем 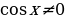 . Получим уравнение
. Получим уравнение 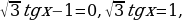
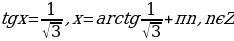 .
.
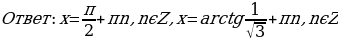 .
.
Опр.
Неравенства, содержащие переменную под знаком тригонометрической функции, называются тригонометрическими.
При решении тригонометрических неравенств используют единичную окружность.
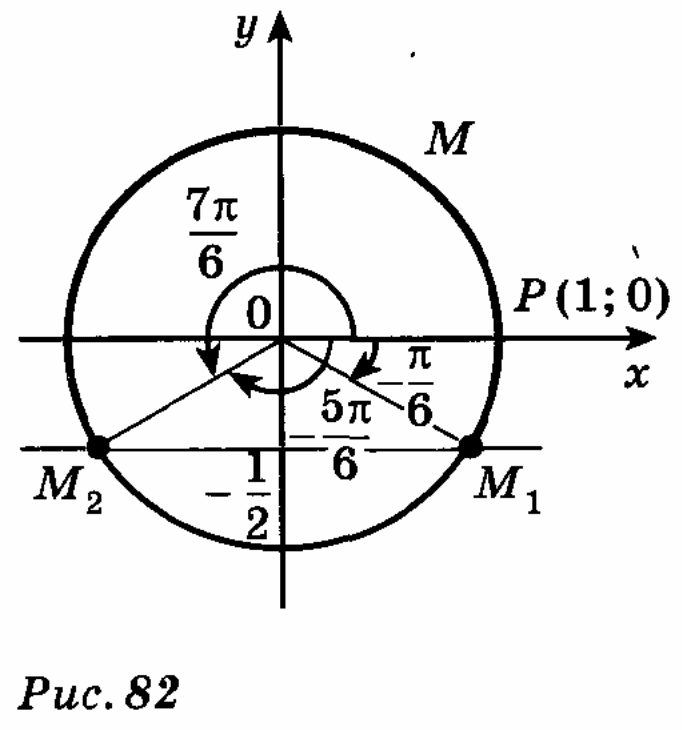
ЗадачаРешить неравенство cosx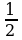
П о определению cosx – это абсцисса точки единичной окружности. Абсциссу, равную
о определению cosx – это абсцисса точки единичной окружности. Абсциссу, равную 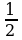 , имеют две точки единичной окружности М1 и М2 . Абсциссу, большую
, имеют две точки единичной окружности М1 и М2 . Абсциссу, большую  имеют все точки М дуги единичной окружности, лежащие правее прямой М1М2 . Таким образом, решениями неравенства cosx
имеют все точки М дуги единичной окружности, лежащие правее прямой М1М2 . Таким образом, решениями неравенства cosx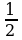 являются все числа х из промежутка
являются все числа х из промежутка 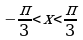 .
.
Все решения данного неравенства – множество интервалов 
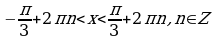
Ответ: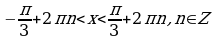

2.Задания для самостоятельной работы.
1 вариант.
1) Решить уравнение
1.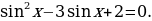
2. 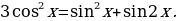
3. 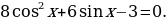
4. 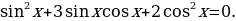
2) Решить неравенства:
1) 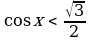 ; 2)
; 2) 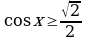 ; 3)
; 3) 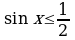 ; 4)
; 4) 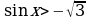 5)
5) 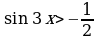
2 вариант.
1) Решить уравнение
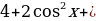 5
5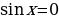 .
.
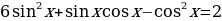 .
.
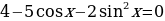 .
.
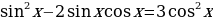 .
.
2) Решить неравенства:
1) 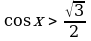 ; 2)
; 2) 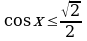 ; 3)
; 3) 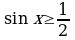 ; 4)
; 4) 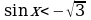 5)
5) 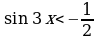
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 14
Тема 7. Функции и графики.
Наименование работы: Построение и чтение графиков функций
Цель работы, требования к умениям и навыкам:Использовать свойства функций для построения графиков, заданных различными способами.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
1. Опр.
Функция вида 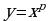 , где
, где 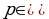 R (любое действительное число), называется степенной.
R (любое действительное число), называется степенной.
Степенная функция с натуральным показателем.
Функция у = хn, где n - натуральное число, называется степенной функцией с натуральным показателем.
При n = 1 получаем функцию у = х.
При n = 2 получаем функцию у = х2.
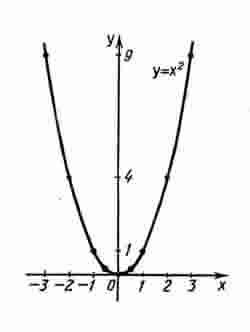
Функция у = х2.
Перечислим свойства функции у = х2.
1) Область определения функции - вся числовая прямая.
2) у = х2 - четная функция (f ( - х) = ( - х)2 = х2 = f (x)).
3) На промежутке [0; + ∞) функция возрастает (если 0 ≤ х12 , то х1222, а это и означает возрастание функции).
4) На промежутке ( - ∞ ; 0] функция убывает ( если x12 ≤ 0, то х12 х22 , а это и означает убывание функции).
Графиком функции у = х2 является парабола (см. рис).
При n = 3 получаем функцию у = х3.
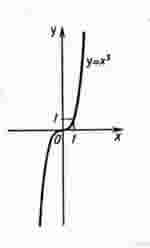
Функция у = х3.
Перечислим свойства функции у = х3.
1) Область определения функции - вся числовая прямая.
2) у = х3 - нечетная функция (f (- х) = (- х)3= - х3 = - f (x))
3) Функция у = х3 возрастает на всей числовой прямой.
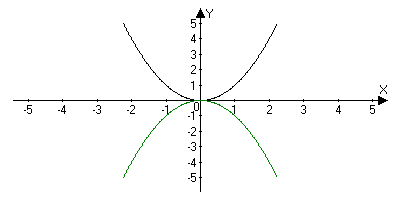
График функции у = х3 изображен на рисунке. Он называется кубической параболой.
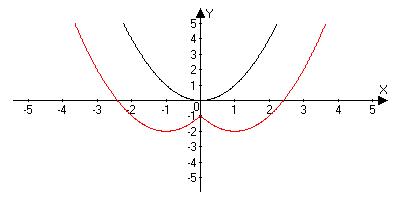
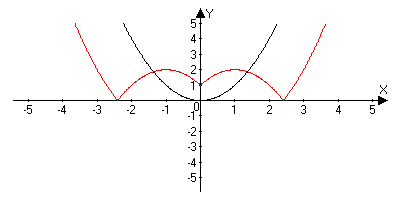
Пусть n - произвольное четное натуральное число, большее двух: n = 4, 6, 8, ... . В этом случае функция у = хn обладает теми же свойствами, что и функция у = х2. График такой функции напоминает параболу у = х2, только ветви графика при |x| 1 тем круче идут вверх, чем больше n, а при |x|
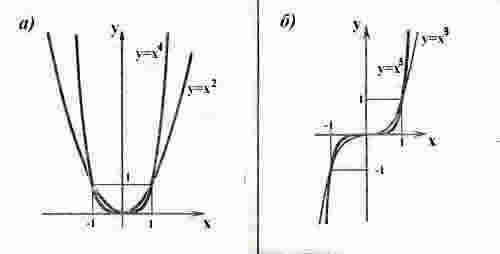
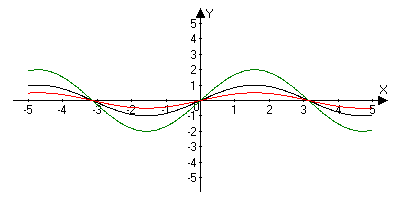
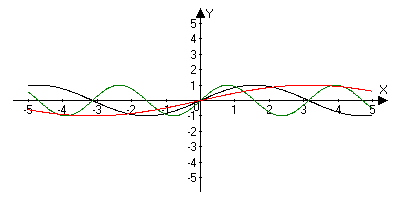
Пусть n - произвольное нечетное число, большее трех: n = 5, 7, 9, … . В этом случае функция у = хn обладает теми же свойствами, что и функция у = х3. График такой функции напоминает кубическую параболу (только ветви графика тем круче идут вверх, вниз, чем больше n) (рис. б). Отметим также, что на промежутке (0; 1) график степенной функции у = хn тем медленнее отдаляется от оси х с ростом х, чем больше n.
Степенная функция с целым отрицательным показателем.
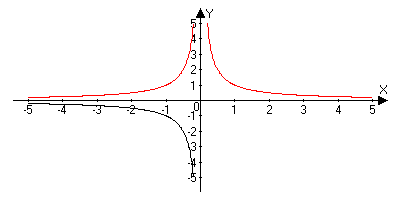
Рассмотрим функцию у = х -n, где n - натуральное число.
При n = 1 получаем у = х -1 или у = 1/х. Свойства этой функции рассмотрены выше.
Пусть n - нечетное число, большее единицы, n = 3, 5, 7, …
В этом случае функция у = х -n обладает в основном теми же свойствами, что и функция у = 1/х. График функции у = х -n (n = 3, 5, 7, …) напоминает график функции у = 1/х (рис. а).
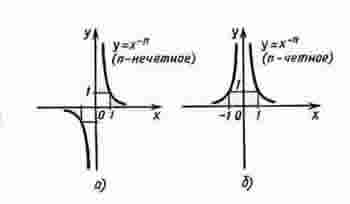
Пусть n - четное число, например n = 2.
Перечислим некоторые свойства функции у = х -2, т. е. функции у = 1/х2.
1) Функция определена при всех x ≠ 0
2) y =1/х2 - четная функция.
3) y = 1/х2 убывает на (0; + ∞) и возрастает на ( - ∞; 0).
Теми же свойствами обладают любые функции вида у = х -n при четном n, большем двух.
График функции у = 1/х2 изображен на рисунке б. Аналогичный вид имеет график функции у = х -n, если n = 4, 6, ...
Функция у = х1/2.
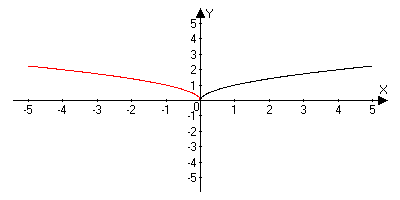
Перечислим свойства функции у = ![]() .
.
1) Область определения - луч [0; + ∞). Это следует из того, что выражение ![]() определено лишь при х ≥ 0.
определено лишь при х ≥ 0.
2) Функция у = ![]() ни четна, ни нечетна.
ни четна, ни нечетна.
3) Функция у = ![]() возрастает на луче [0; + ∞).
возрастает на луче [0; + ∞).
График функции у = ![]() изображен на рисунке а..
изображен на рисунке а..
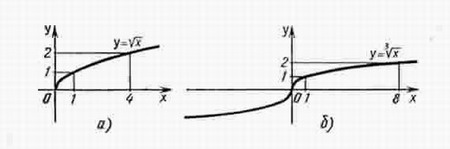
Функция у = х1/3.
Перечислим свойства функции у = ![]() .
.
1) Область определения функции - вся числовая прямая.
2) Функция у = ![]() нечетна.
нечетна.
3) Функция у = ![]() возрастает на всей числовой прямой.
возрастает на всей числовой прямой.
График функции у = ![]() изображен на рисунке б.
изображен на рисунке б.
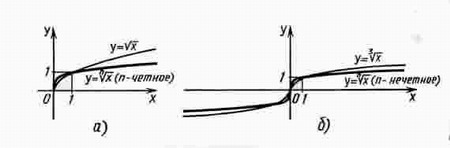
Функция у = х1/n.
При четном n функция y = ![]() обладает теми же свойствами, что и функция у =
обладает теми же свойствами, что и функция у = ![]() , и график ее напоминает график функции у =
, и график ее напоминает график функции у = ![]() .
.
При нечетном n функция у = ![]() обладает теми же свойствами, что и функция у =
обладает теми же свойствами, что и функция у = ![]() , и график ее напоминает график функции у =
, и график ее напоминает график функции у = ![]() .
.
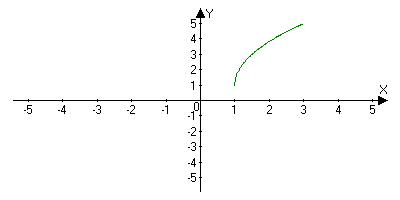
Степенная функция с положительным дробным показателем.
Рассмотрим функцию у = хr, где r - положительная несократимая дробь.
Перечислим некоторые свойства этой функции.
1) Область определения - луч [0; + ∞).
2) Функция ни четная, ни нечетная.
3) Функция у = хr возрастает на [0; + ∞).
На рисунке а изображен график функции у = х2,5 .
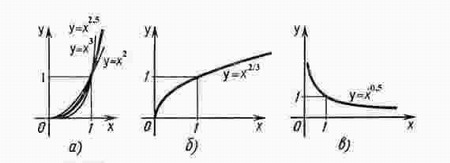
Он заключен между графиками функций у = х2 и у = х3, заданных на промежутке [0; + ∞).
Подобный вид имеет график любой функции вида у = хr, где r 1.
На рисунке б изображен график функции у = х2/3. Подобный вид имеет график любой степенной функции у = хr, где 0
Степенная функция с отрицательным дробным показателем.
Рассмотрим функцию у = х -r, где r - положительная несократимая дробь.
Перечислим свойства этой функции.
1) Область определения - промежуток (0; + ∞).
2) Функция ни четная, ни нечетная.
3) Функция у = х -r убывает на (0; + ∞)
Построим график функции у = х -1/2 (рис. в). Подобный вид имеет график любой функции у = хr, где r - отрицательная дробь.
Показательная функция.
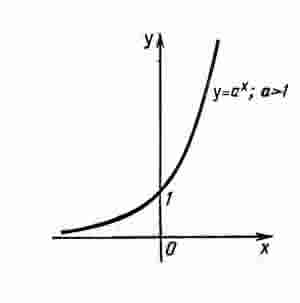
Показательная функция задается формулой у = ах, где а 0 и а ≠ 1.
Перечислим свойства функции у = ахпри а 1.
1) Область определения функции - вся числовая прямая.
2) Область значений функции - промежуток (0; + ∞).
3) Функция не является ни четной, ни нечетной. Это следует из того,
что а -х ≠ ах и а -х ≠ - ах.
4) Функция возрастает на всей числовой прямой.
График функции у = ах при а 1 выглядит так, как показано на рисунке. Отметим, что эта функция принимает любые положительные значения.
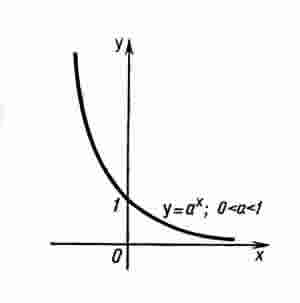
Свойства функции у = ах при 0 1) Область определения функции - вся числовая прямая.
2) Область значений - (0; + ∞).
3) Функция не является ни четной, ни нечетной.
4) Функция убывает на всей числовой прямой.
График функции у = ах при 0
Логарифмическая функция.
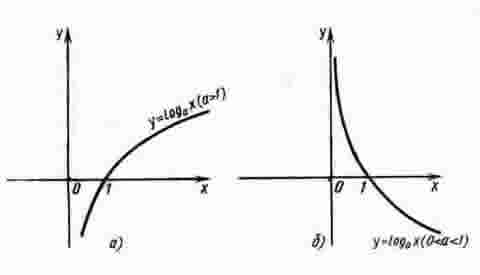
Логарифмическая функция у = loga x обладает следующими свойствами :
1) Область определения - (0; + ∞).
2) Область значений - ( - ∞; + ∞)
3) Функция ни четная, ни нечетная.
4) Функция возрастает на промежутке (0; + ∞) при a 1, убывает на (0; + ∞) при 0
График функции у = loga x может быть получен из графика функции у = ах с помощью преобразования симметрии относительно прямой у = х. На рисунке а построен график логарифмической функции для а 1, а на рисунке б - для 0
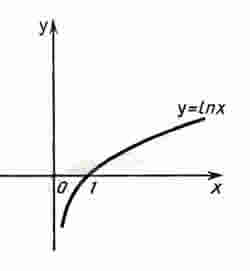
Функция у = ln х.
Среди показательных функций у = ах, где а 1, особый интерес для математики и ее приложений представляет функция, обладающая следующим свойством: касательная к графику функции в точке (0; 1) образует с осью х угол 45°. Основание а такой функции ах принято обозначать буквой е, т. е. у = ех. Подсчитано, что е = 2, 7182818284590..., и установлено, что е - иррациональное число. Логарифмическую функцию, обратную показательной функции у = ех, т. е. функцию у = logе x, принято обозначать у = ln х
(ln читается "натуральный логарифм"). График функции у = ln х изображен на рисунке.
2.Задания для самостоятельной работы.
1 вариант.
1. Изобразить схематически график функции, указать её область определения и множество значений: а) 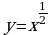 б)
б) 
 в)
в) 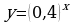
2. Построить график функции ( таблицу) : а) 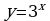 б)
б) 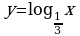
3. Решить графически уравнение: 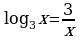
4. Решить графически неравенство: 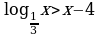
5. Сравнить числа: а) 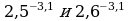 ; б)
; б) 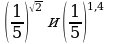 ; в)
; в) 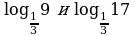
2 вариант.
1. Изобразить схематически график функции, указать её область определения и множество значений:
а) 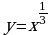 б)
б) 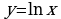 в)
в) 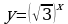
2. Построить график функции ( таблицу): а) 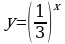 б)
б) 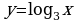
3. Решить графически уравнение: 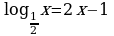
4. Решить графически неравенство: 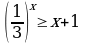
5. Сравнить числа: а) 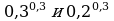 ; б)
; б) 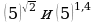 ; в)
; в) 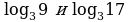
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 15
Тема 7. Функции и графики.
Наименование работы: Преобразования графика функции
Цель работы, требования к умениям и навыкам: закрепитьумение выполнять преобразованиеграфиковфункций
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Геометрические преобразования графиков функции| № | Функция | Преобразование | Графики |
| 1 | y = −ƒ(x) | Сначала строим график функции ƒ(x), а затем симметрично отображаем его относительно оси OX. | y = − (x2) y = x2 → − (x2)
|
| 2 | y = ƒ(−x) | Сначала строим график функции ƒ(x), а затем симметрично отображаем его относительно оси OY. | y = √ (−x) y =√(x) → √ (−x)
|
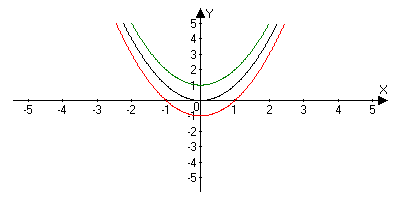
| 3 | y = ƒ(x) +A A - const | Сначала строим график функции ƒ(x), а затем, если А0 поднимаем полученный график на А единиц вверх по оси OY. Если А | y = x2 → x2 +1 y = x2 → x2 –1
|
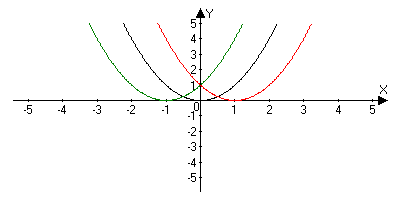
| 4 | y = ƒ(x −а) | Сначала строим график функции ƒ(x), а затем, если а0, то график функции смещаем на а единиц вправо, а если а "−" − → "+" − ← | y = x2 → (x + 1)2 y = x2 → (x -1)2
|
| 5 | y = K ƒ(x ) k − const k0 | Сначала строим график функции ƒ(x), а затем, если K0, то растягиваем полученный график в K раз вдоль оси OY. А если 0 ↕ ↓ ↑ | y = sin(x) → 2sin(x) y = sin(x) → Ѕ sin(x)
|
| 6 7
| y = ƒ(к x ) k − const k0 y = A ƒ(к x+а) +В A, к, а, В − const | Сначала строим график функции ƒ(x), а затем, если к 1, то сжимаем полученный график в к раз вдоль оси OХ. А если 0 к 1 − →← 0 ƒ( x ) → ƒ(к x ) → ƒ(к( х + а ∕ к )) →A ƒ(к( х + а ∕ к )) → A ƒ(к( х + а ∕ к )) +В | y = sin(x) → sin(2x) y = sin(x) → sin (Ѕ x)
y = 2√(2x-2)+1 y =√x →√2x→√2(x -1) → 2√2(x -1) →2√2(x-1)+1
|
| 8 | y = │ƒ(x)│ | Сначала строим график функции ƒ(x), а затем часть графика, расположенную выше оси ОХ оставляем без изменения, а часть графика, расположенную ниже оси ОХ, заменяем симметричным отображением относительно ОХ. | y =│x -3│ y = x -3→│x -3│
|
| 9 | y = ƒ(│x│) | Сначала строим график функции ƒ(x), а затем часть графика, расположенную правее оси ОУ, оставляем без изменения, а левую часть графика заменяем симметричным отображением правой относительно ОУ. | y = (│x│−1)2 −2 y = x2→(x -1)2→ (x -1)2 − 2→(│x│−1)2 −2
|
| 10 | y = │ƒ(│x│)│ | ƒ(x) → ƒ(│x│) →│ƒ(│x│)│ | y= │(│x│−1)2 - 2│ y= x2 → (x-1)2 →(x-1)2 - 2→(│x│−1)2 - 2→│(│x│−1)2 - 2│
|
2.Задания для самостоятельной работы.
1 вариант
1. Построить графики функций.
а) 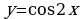 в)
в) 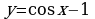
б) 
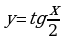 г)
г) 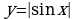
2. Найти все корни уравнения, принадлежащие отрезку [0; 3π] :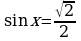
3. Найти все решения неравенства, принадлежащие отрезку [0; 3π] :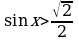
2 вариант
1. Построить графики функций.
а) 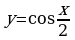 в)
в) 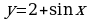
б) 
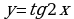 г)
г) 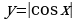
2. Найти все корни уравнения, принадлежащие отрезку [0; 3π] :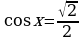
3. Найти все решения неравенства, принадлежащие отрезку [0; 3π] :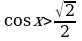
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 16
Тема 8. Многогранники и круглые тела
Наименование работы: Вычисление площадей и объемов.
Цель работы, требования к умениям и навыкам:Отрабатывать навыки применения формул для вычисления площадей поверхностей, объёмов многогранников
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Определение 1. Число, характеризующее величину внутренней области многогранника, называется объёмом многогранника.
Определение 2. Смежными многогранниками называются такие многогранники, которые имеют одну или несколько общих граней, причём остальные точки каждого из многогранников расположены вне другого.
Объём обладает следующими свойствами:
Два равных многогранника имеют один и тот же объём, независимо от их расположения в пространстве.
Объём многогранника, представляющего собой сумму двух смежных многогранников, равен сумме объёмов этих многогранников.
Если из двух многогранников первый содержится целиком внутри второго, то объём первого многогранника не превосходит объёма второго.
Многогранники, имеющие равные объёмы, называются равновеликими.
За единицу объёма принимается объём куба, ребро которого равно единице длины (мм; см; дм и т.д.).
Формулы объемов многогранников:
1. Объём призмы: 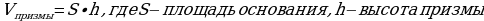 .
.
2.Объём прямоугольного параллелепипеда: 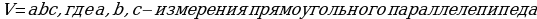 .
.
3.Объём куба 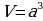 .
.
Решение задач.
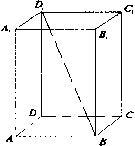 1.Измерения прямоугольного параллелепипеда относятся , как 2 : 7 : 26; диагональ параллелепипеда равна 81см. Найдите объём параллелепипеда.
1.Измерения прямоугольного параллелепипеда относятся , как 2 : 7 : 26; диагональ параллелепипеда равна 81см. Найдите объём параллелепипеда.
Решение. 1) Пусть 1часть равна х, тогда а = 2х, в = 7х, с = 26х. По свойству диагоналей прямоугольного параллелепипеда будем иметь: 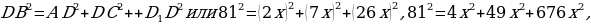
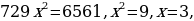 тогда
тогда 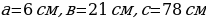 .
.
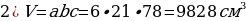 .
.
Ответ: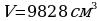 .
.
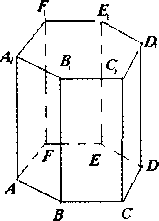 2.Основанием шестиугольной призмы служит правильный шестиугольник со стороной, равной 25см. Высота призмы равна 40см. Найти объём призмы.
2.Основанием шестиугольной призмы служит правильный шестиугольник со стороной, равной 25см. Высота призмы равна 40см. Найти объём призмы.
Решение. 1) Объём призмы: 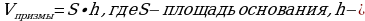 высота призмы. По условию – основание призмы правильный шестиугольник со стороной a = 25см.
высота призмы. По условию – основание призмы правильный шестиугольник со стороной a = 25см. 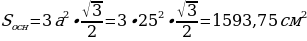 .
.
2) 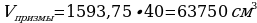 .
.
Ответ: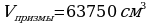 .
.
3.Найти сторону куба , объём которого равен 64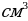 .
.
Решение.Объём куба 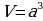 , где а - ребро куба. По условию
, где а - ребро куба. По условию 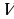 = 64
= 64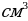 , следовательно,
, следовательно, 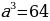 , тогдаа =
, тогдаа = 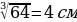 .
.
Ответ: а = 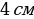 .
.
2.Задания для самостоятельной работы.
1 вариант
Изобразите многогранник, выполнив чертёж схематически. На чертеже введите обозначения и покажите известные элементы многогранника.
Вычислите площадь полной поверхности многогранника.
Вычислите объём многогранника.
Запишите результаты решения, проверьте единицы измерения величин.
| Многогранник | Дано: | Вариант 1 |
| Куб | а | 2 см |
| Прямоугольный параллелепипед
| а | 2 см |
| в | 5 см | |
| с | 1 см | |
| Правильная четырёхугольная пирамида | АВ | 2 см |
| h апофема | 3 см | |
| Правильная четырёхугольная усечённая пирамида | АВ | 2 см |
| А1В1 | 4 см | |
| h апофема | 3 см |
2 вариант
1) Изобразите многогранник, выполнив чертёж схематически. На чертеже введите обозначения и покажите известные элементы многогранника.
2) Вычислите площадь полной поверхности многогранника.
Вычислите объём многогранника.
Запишите результаты решения, проверьте единицы измерения величин.
| Многогранник | Дано: | Вариант 2 |
| Куб | а | 3 см |
| Прямоугольный параллелепипед
| а | 3 см |
| в | 4 см | |
| с | 2 см | |
| Правильная четырёхугольная пирамида | АВ | 3 см |
| h апофема | 4 см | |
| Правильная четырёхугольная усечённая пирамида | АВ | 1 см |
| А1В1 | 3 см | |
| h апофема | 4 см |
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 17
Тема 9. Начала математического анализа
Наименование работы: Правила и формулы дифференцирования, таблица производных элементарных функций.
Цель работы, требования к умениям и навыкам:формирование умения находить производные и дифференциалы функций, используя правилаиформулыдифференцирования
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Опр.Производной функции f(x) в точке х называется предел разностного отношения 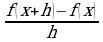 при
при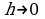 .
.
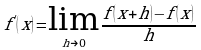 .
.
Опр.Операция нахождение производной называется дифференцированием.
Это правило является основным, т.к. выведено из самого определения. Однако при дифференцировании сложных функций, суммы, произведения, частного применение общего правила представляет большие трудности. Поэтому применяют правила дифференцирования.
Правила
1. 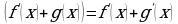 - Производная суммы равна сумме производных.
- Производная суммы равна сумме производных.
2. 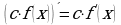 - Постоянный множитель можно вынести за знак производной.
- Постоянный множитель можно вынести за знак производной.
3. 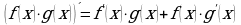 - Производная произведения.
- Производная произведения.
4. 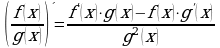 Производная частного
Производная частного
Формулы дифференцирования
С′ = 0 11. 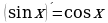
( х ) ′ = 1 12. 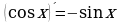
( х 2) ′ = 2х 13. 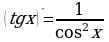
( х 3) ′ = 3х2
( х р ) ′ = р х р – 114. 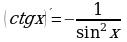
( е х ) ′ = е х 15.
15. 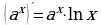
7. 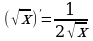 16.
16. 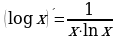
8. 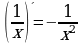 17.
17. 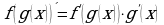
9. 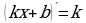 18.
18. 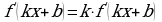
10. 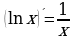
При решении задач на нахождение уравнения касательной к графику функции в точке используется геометрический смысл производной 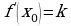
Уравнение касательной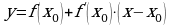
Примеры:
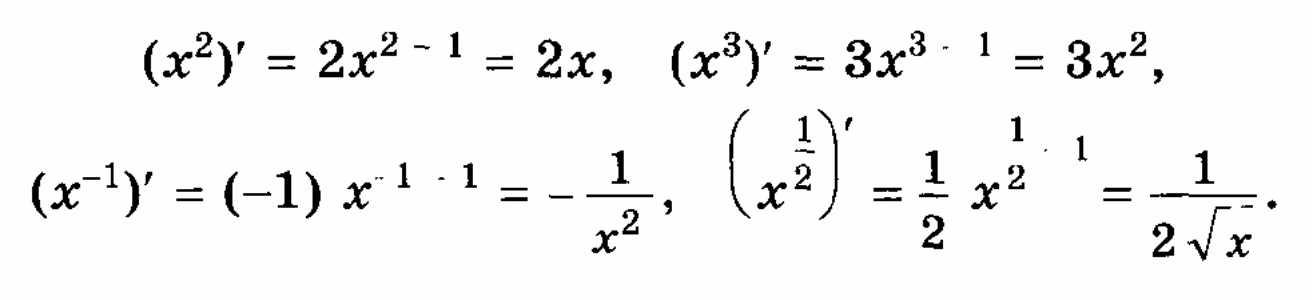

Задача 5
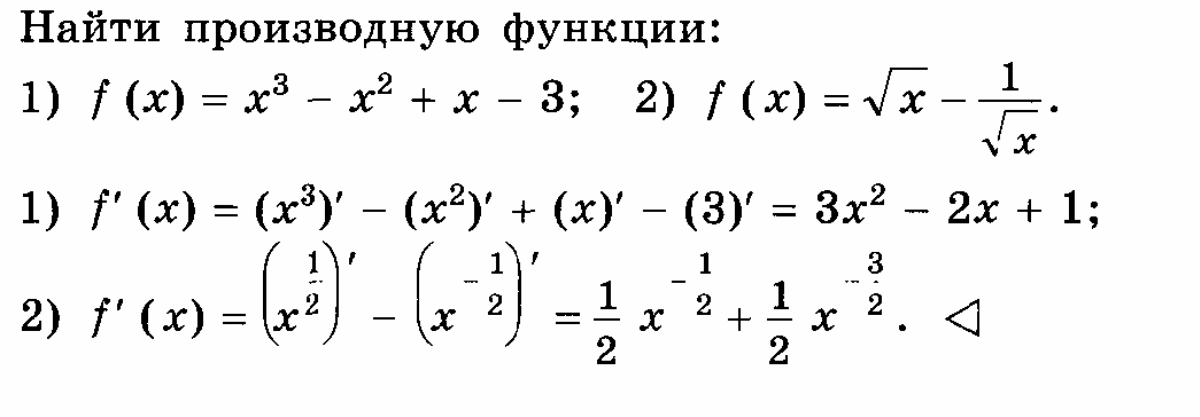
2.Задания для самостоятельной работы.
1 вариант
Задание 1. Найти производную функции.
а) 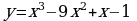 б)
б)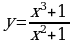 в)
в) 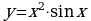
г)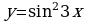 д)
д)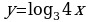 е)
е) 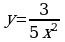
Задание 2. Решить уравнение f′(x) = 0, если 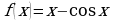
Задание 3. Написать уравнение касательной к графику функции у = f(x) в точке с абсциссой х0
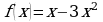 х0= 2
х0= 2
2 вариант
Задание 1. Найти производную функции.
а) 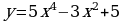 б)
б)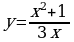 в)
в) 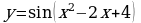
г)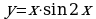 д)
д)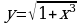 е)
е) 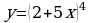
Задание 2. Решить уравнение f′(x) = 0, если 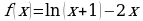
Задание 3. Написать уравнение касательной к графику функции у = f(x) в точке с абсциссой х0
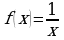 х0= 3.
х0= 3.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 18
Тема 9. Начала математического анализа
Наименование работы: Нахождение наибольшего, наименьшего значения и экстремальных значений функции
Цель работы, требования к умениям и навыкам:Систематизировать навыки и умения применять знания о производной при решениизадач
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
На практике часто приходится решать задачи на нахождение наибольшего или наименьшего значения функции на отрезке.

Наибольшее f(b), наименьшее f(x2)
x1, x2 – стационарные точки
Для нахождения наибольшего и наименьшего значений функции на отрезке [a; b] нужно:
1) найти значение функции на концах отрезка, т.е . f(a) и f( b) ;
2) найти её значения в тех критических точках, которые принадлежат интервалу (a;b)
3) из найденных значений выбрать наибольшее и наименьшее.
Замечание: Если на (a, b) нет стационарных точек, то наибольшее и наименьшее значения функция принимает на концах отрезка [a; b].
Пример:

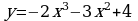 на [-2; 1]
на [-2; 1]
1) 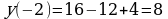
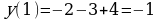
2) 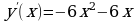
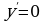 при
при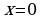 и
и 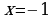
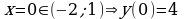
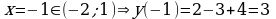
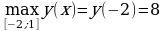
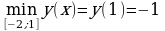
Для нахождения наибольшего и наименьшего значений функции на интервале ( a ; b ) , нужно:
Если функция дифференцируема на интервале ( a ; b ) и имеет только одну стационарную точку х0: это либо точку максимума, либо точку минимума, тогда
если х0 - точка максимума, то функция в этой точке принимает наибольшее значение;
если х0 - точка минимума, то функция в этой точке принимает наименьшее значение;
Задача
Число 36 записать в виде произведения 2-х положительных чисел, сумма которых наименьшая.
Решение
Пусть первый множитель равен х, тогда второй множитель равен 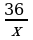 .
.
Сумма этих чисел равна 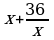 . По условию задачи х – положительное число. Таким образом задача свелась к нахождению такого значения х, при котором функция
. По условию задачи х – положительное число. Таким образом задача свелась к нахождению такого значения х, при котором функция 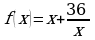 принимает наименьшее значение на интервале х 0.
принимает наименьшее значение на интервале х 0.
Найдём производную :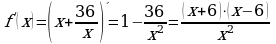
Стационарные точки: х1= 6 и х2 = - 6. На интервале х 0 есть только одна стационарная точка х= 6.
При переходе через точку х = 6 производная меняет знак с « - » на « + » , и поэтому точка х = 6 – точка минимума. Следовательно, наименьшее значение на интервале х 0 функция 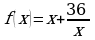 принимает в точке х = 6 . это значение
принимает в точке х = 6 . это значение 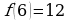
Ответ: 36 = 6 · 6
Пример
1) 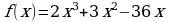 на [-4; 3]
на [-4; 3]
1) 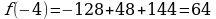
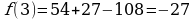
2) 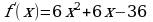
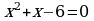
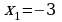
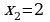 - (-4; 3)
- (-4; 3)
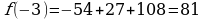
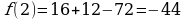
Ответ: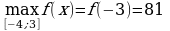
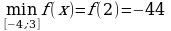
2.Задания для самостоятельной работы.
1 вариант.
Задание 1.
Найти наибольшее и наименьшее значение функции на отрезке:
а) у = х3 – 6х на отрезке [-3; 4] б) у = х2– 4х + 3 на отрезке [0; 3]
Задание 2.
Найти наибольшее и наименьшее значение функции на интервале : у = 1 – х4 + х5 на (-3; 3)
Задание 3.
Разложить число 100 на 2 слагаемых так, чтобы их произведение было наибольшим.
2 вариант.
Задание 1.
Найти наибольшее и наименьшее значение функции на отрезке:
а) 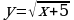 на отрезке [-1; 4] б) у = sinx + cosx на отрезке [0;
на отрезке [-1; 4] б) у = sinx + cosx на отрезке [0; 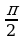 ]
]
Задание 2.
Найти наибольшее и наименьшее значение функции на интервале: 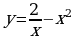 при х
при х
Задание 3.
Найти такое число, которое будучи сложенное со своим квадратом даёт наименьшую сумму.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 19
Тема 9. Начала математического анализа
Наименование работы: Исследование функции с помощью производной.
Цель работы, требования к умениям и навыкам:закрепить умение исследоватьфункциюспомощьюпроизводной и строить её график; · развивать вычислительные навыки
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
1.Исследование функций с помощью производных.
Определение 1. Функция 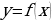 монотонно убывает, если большему значению аргумента
монотонно убывает, если большему значению аргумента  соответствует меньшее значение функции. Условие убывания функции на интервале
соответствует меньшее значение функции. Условие убывания функции на интервале 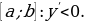
Определение 2. Функция 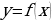 монотонно возрастает, если большему значению аргумента
монотонно возрастает, если большему значению аргумента 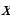 соответствует большее значение функции
соответствует большее значение функции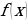 . Условие убывания функции на интервале
. Условие убывания функции на интервале 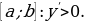
Определение 3. Функция 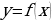 имеетмаксимум (минимум) при
имеетмаксимум (минимум) при 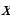 =
= 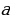 , если при всех
, если при всех 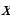 достаточно близких к
достаточно близких к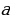 , выполняется неравенство:
, выполняется неравенство: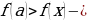 максимум,
максимум, 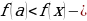 минимум.
минимум.
Признаки максимума:
1.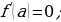
2.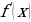 при переходе аргумента через
при переходе аргумента через 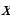 =
= 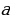 меняет знак с плюса на минус (с возрастания на убывание).
меняет знак с плюса на минус (с возрастания на убывание).
Признаки минимума:
1.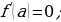
2.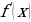 при переходе аргумента через
при переходе аргумента через 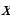 =
= 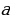 меняет знак с минуса на плюс (с убывания на прибавление). Говорят, что функция имеет экстремум в некоторой точке
меняет знак с минуса на плюс (с убывания на прибавление). Говорят, что функция имеет экстремум в некоторой точке 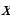 =
= 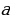 , если она имеет в этой точке максимум или минимум. Точки, в которых функция
, если она имеет в этой точке максимум или минимум. Точки, в которых функция 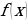 достигает экстремума, называютсякритическими точками первого рода.
достигает экстремума, называютсякритическими точками первого рода.
Пример 1. Исследовать функцию 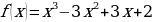 на монотонность и экстремумы.
на монотонность и экстремумы.
Решение. Найдём производную: 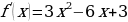 . Найдём точки – «претенденты» на экстремум:
. Найдём точки – «претенденты» на экстремум: 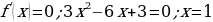 . Определим знаки производной на промежутках
. Определим знаки производной на промежутках  :
:
+ 1 +
Т.е. функция  возрастает на всей прямой, и
возрастает на всей прямой, и  - не экстремум. Данный пример показывает, что не все точки, в которых производная равна нулю, являются точками экстремума.
- не экстремум. Данный пример показывает, что не все точки, в которых производная равна нулю, являются точками экстремума.
Пример 2. Найти интервалы возрастания и убывания функции 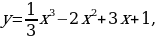 и её экстремумы.
и её экстремумы.
Решение. Производная рассматриваемой функции существует при любом х и равна у' =х2 - 4х + 3 . Приравняв производную нулю и решив полученное квадратное уравнение, найдем две критические точки 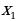 = 1 и х2 = 3.
= 1 и х2 = 3.
Ось х разбивается этими точками на три интервала: 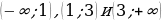 причем на каждом из них у' сохраняет знак.
причем на каждом из них у' сохраняет знак.
Определим эти знаки, например, вычислив у' в произвольных точках указанных интервалов, получим: 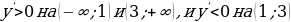
Отсюда функция 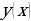 возрастает на интервалах
возрастает на интервалах 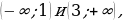 убывает на интервале
убывает на интервале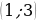 в точке
в точке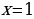 достигает максимального значения
достигает максимального значения 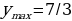 , а в точке
, а в точке 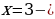 минимального значения
минимального значения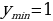 .
.
2. Схема исследования функции.
Найти область определения D(f), указать промежутки непрерывности.
Найти область значений E(f). Определить четность и периодичность функции.
Найти «нули» функции (если это возможно).Указать промежутки знакопостоянства функции (т.е. промежутки между двумя соседними нулями или точками разрыва) и определить знаки функции на этих промежутках (если это возможно).
Найти производную функции.
Найти точки, которые могут оказаться экстремумами
Найти промежутки монотонности и точки экстремума.
По результатам проведенной работы построить график.
Пример 3. Исследовать функцию и построить ее график: 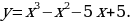
Решение 1. Область определения функции - множество всех действительных чисел: 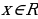 или
или 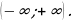 Функция непрерывна на всей области определения, так как является суммой элементарных функций.
Функция непрерывна на всей области определения, так как является суммой элементарных функций.
Область значений, также, множество всех действительных чисел: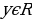 .
.
При ,
, ; при
; при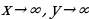 .
.
Нули функции:х3 - х2 - 5х + 5 = 0,х2 (х -1) - 5(х -1) = 0, (х - 1)(х2 - 5) = 0,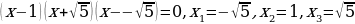 .
.
В этих точках график функции пересекает ось Ох.
Точка пересечения графика функции с осью Оу: х = 0, у = 5.
Функция ни четная и ни нечетная.
Функция непериодическая.
Промежутки возрастания и убывания.
Производная функции равна: у' = Зх2 - 2х - 5 .
Критические точки: 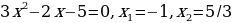 .
.
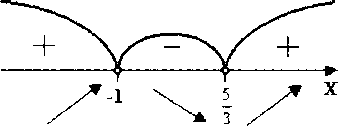
При 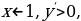 значит, функция возрастает на этом промежутке.
значит, функция возрастает на этом промежутке.
При 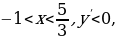 значит, функция убывает на этом промежутке.
значит, функция убывает на этом промежутке.
При 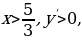 значит, функция возрастает на этом промежутке.
значит, функция возрастает на этом промежутке.
9.Максимумы и минимумы функции (экстремумы функции).
В точке 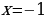 функция имеет максимум:
функция имеет максимум: 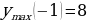 .
.
В точке 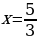 функция имеет минимум:
функция имеет минимум: 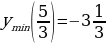 .
.
Г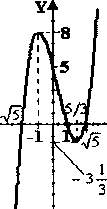 рафик функции.
рафик функции.
2.Задания для самостоятельной работы.
Вариант 1.
Задание 1.
Исследовать функцию с помощью производной и построить её график.
а) 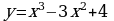 б)
б) 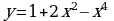
Вариант 2.
Задание 1.
Исследовать функцию с помощью производной и построить её график.
а) 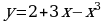 б)
б) 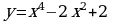
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 20
Тема 9. Начала математического анализа
Наименование работы: Интеграл и первообразная.
Цель работы, требования к умениям и навыкам: закрепить умения и навыки вычисления неопределенного интеграла различными способами
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Зная производную или дифференциал функции, можно найти саму эту функцию (восстановить функцию). Такое действие, обратное дифференцированию, называется интегрированием.
Первообразной функцией по отношению к данной функции ![]() называется такая функция
называется такая функция ![]() , производная от которой равна данной функции, т.е.
, производная от которой равна данной функции, т.е. ![]()
Для данной функции ![]() первообразных функций бесчисленное множество, т.к. любая из функций
первообразных функций бесчисленное множество, т.к. любая из функций ![]() , также является первообразной для
, также является первообразной для ![]() .
.
Совокупность всех первообразных ![]() для данной функции
для данной функции ![]() называется ее неопределенным интегралом обозначается символом:
называется ее неопределенным интегралом обозначается символом:
![]() , где
, где
![]() называется подынтегральным выражением, функция
называется подынтегральным выражением, функция ![]() - подынтегральной функцией.
- подынтегральной функцией.
Геометрический смысл неопределенного интеграла. Геометрически, неопределенный интеграл представляет собой семейство интегральных кривых на плоскости, полученных путем параллельного переноса графика функции ![]() вдоль оси ординат (рис. 3).
вдоль оси ординат (рис. 3).
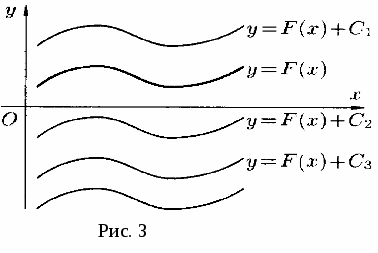
Основные свойства неопределённого интеграла
Свойство 1. Производная неопределенного интеграла равна подынтегральной функции:
![]()
Свойство 2. Дифференциал неопределенного интеграла равен подынтегральному выражению:
![]()
Свойство 3. Интеграл от дифференциала функции равен этой функции плюс const:
![]()
Свойство 4. Линейность интеграла.
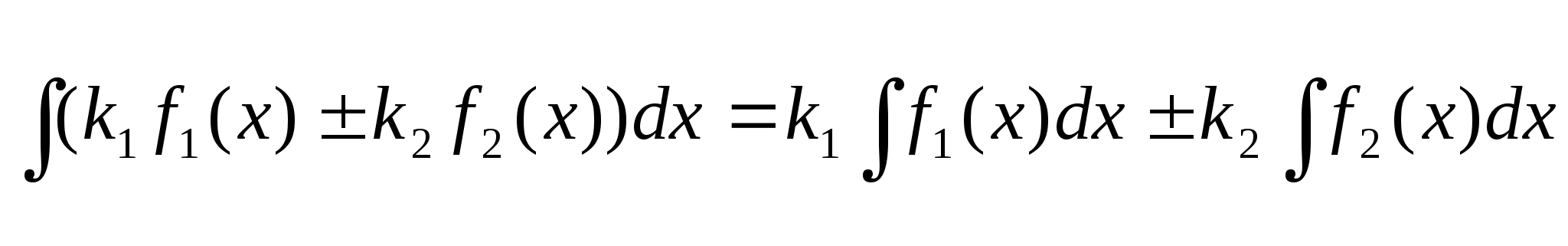
Таблица основных интегралов
| Функция | Интеграл |
| степенная | |
| | |
| | |
| показательная | |
| | |
| тригонометрические | |
| | |
| | |
| | |
| обратные тригонометрические | |
| |
Основные методы интегрирования
Непосредственное интегрирование – это метод, основанный на применении тождественных преобразований подынтегральной функции, а также основных свойств неопределенного интеграла и табличных интегралов. Наиболее часто используются следующие преобразования подынтегральной функции:
деление числителя на знаменатель почленно;
применение формул сокращенного умножения;
применение тригонометрических тождеств.
Замена переменной (метод подстановки) – это метод, заключающийся во введении новой переменной с целью преобразования данного интеграла в табличный. Чаще всего этот метод используется, если в подынтегральном выражении содержится сложная функция, тогда ее промежуточный аргумент и надо обозначить как новую переменную, например ![]() . Далее необходимо выполнить следующие действия:
. Далее необходимо выполнить следующие действия:
найти дифференциал новой переменной ![]() ;
;
записать прежний интеграл, используя только переменную ![]() , если подстановка сделана правильно, то полученный интеграл
, если подстановка сделана правильно, то полученный интеграл ![]() должен быть табличным;
должен быть табличным;
используя таблицу интегралов, записать решение для подынтегральной функции ![]() ;
;
осуществить обратную подстановку, заменив переменную ![]() .
.
Метод интегрирования по частям – это метод, заключающийся в использовании формулы:
![]() .
.
Этот метод применяется в том случае, если интеграл ![]() является более простым для решения чем
является более простым для решения чем ![]() . Как правило, этим методом решаются интегралы вида
. Как правило, этим методом решаются интегралы вида ![]() , где
, где ![]() - многочлен, а
- многочлен, а ![]() - одна из следующих функций:
- одна из следующих функций: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
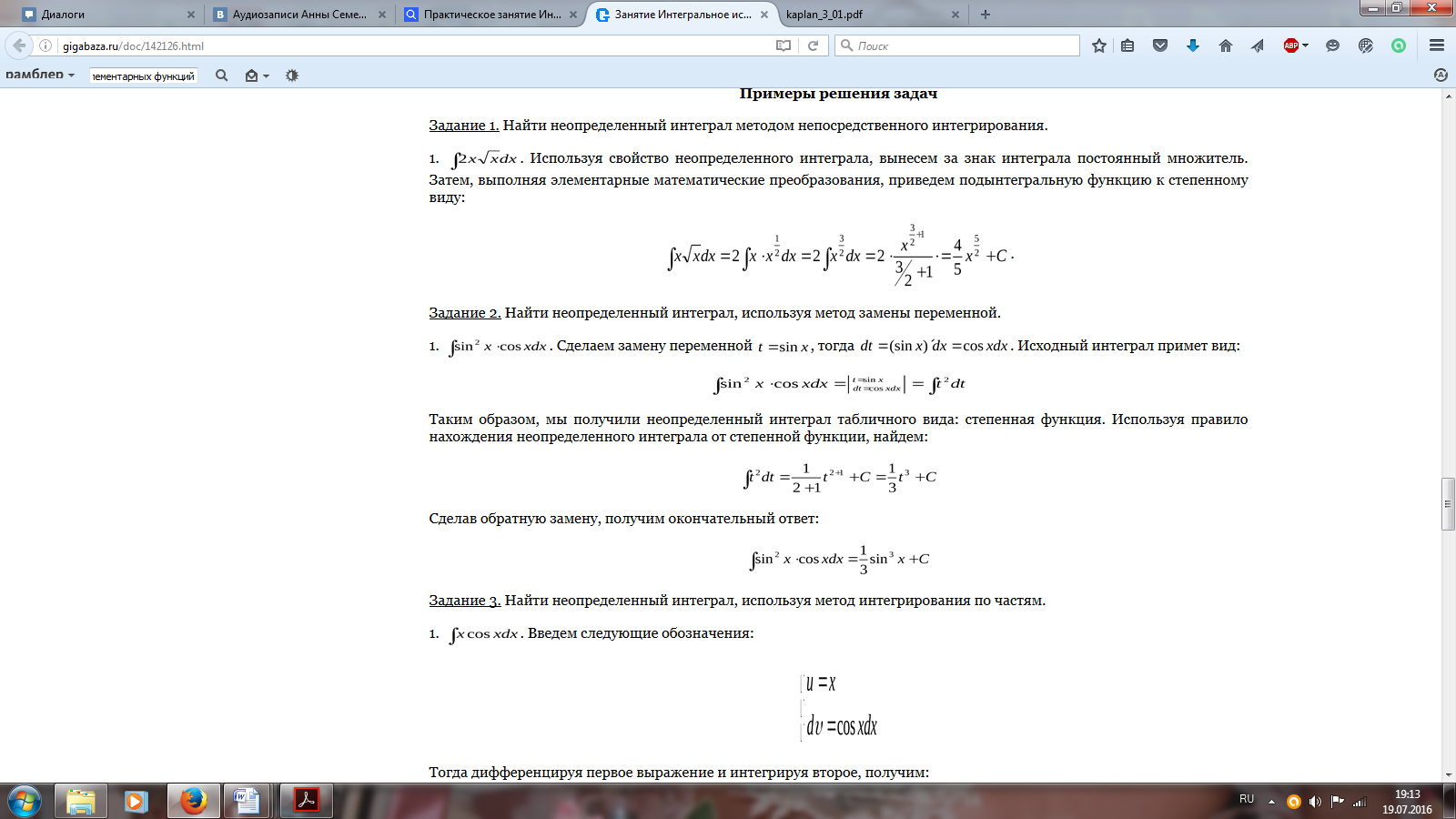
2.Задания для самостоятельной работы.
Вариант 1.
Вычислить интегралы:
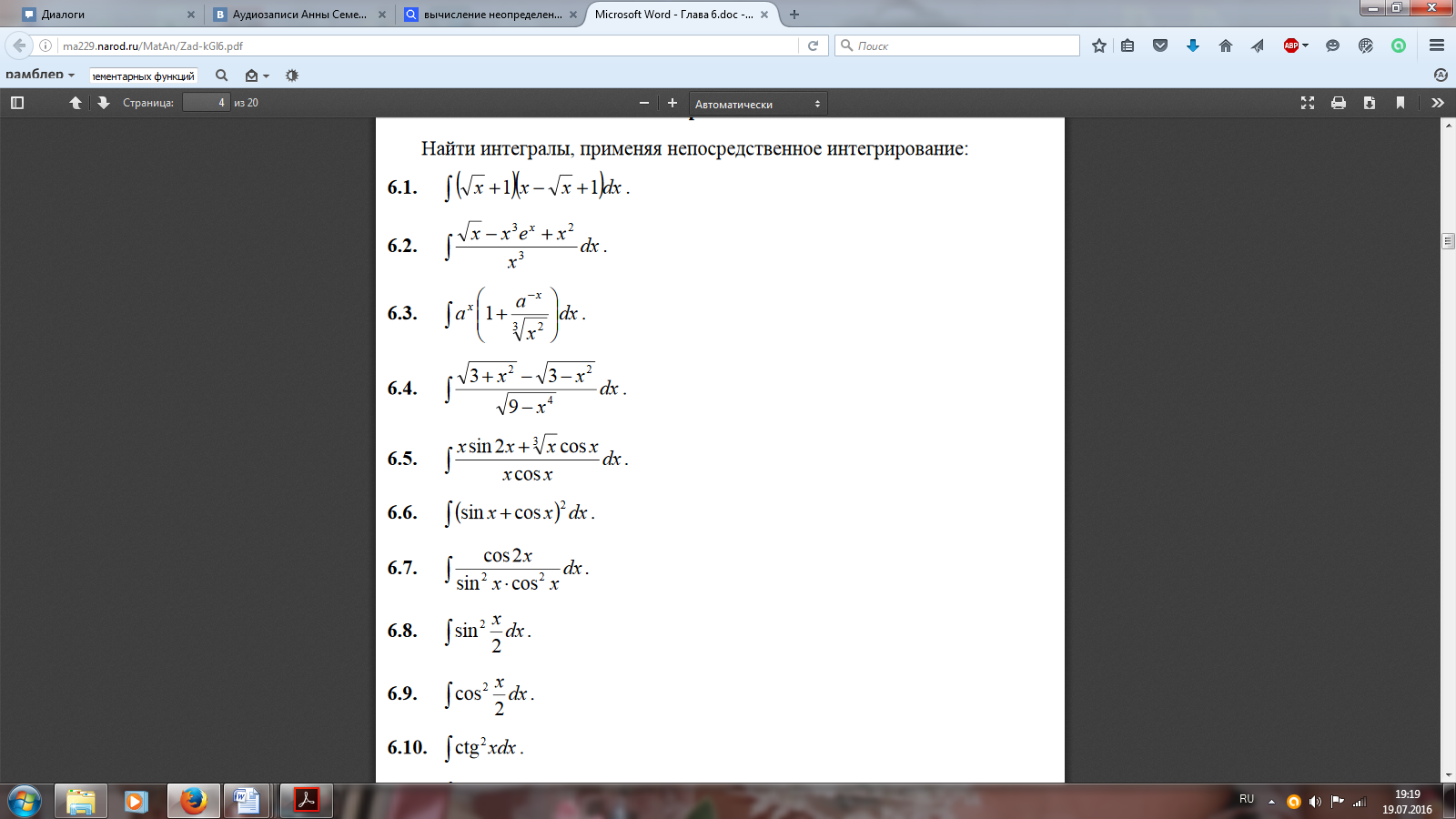
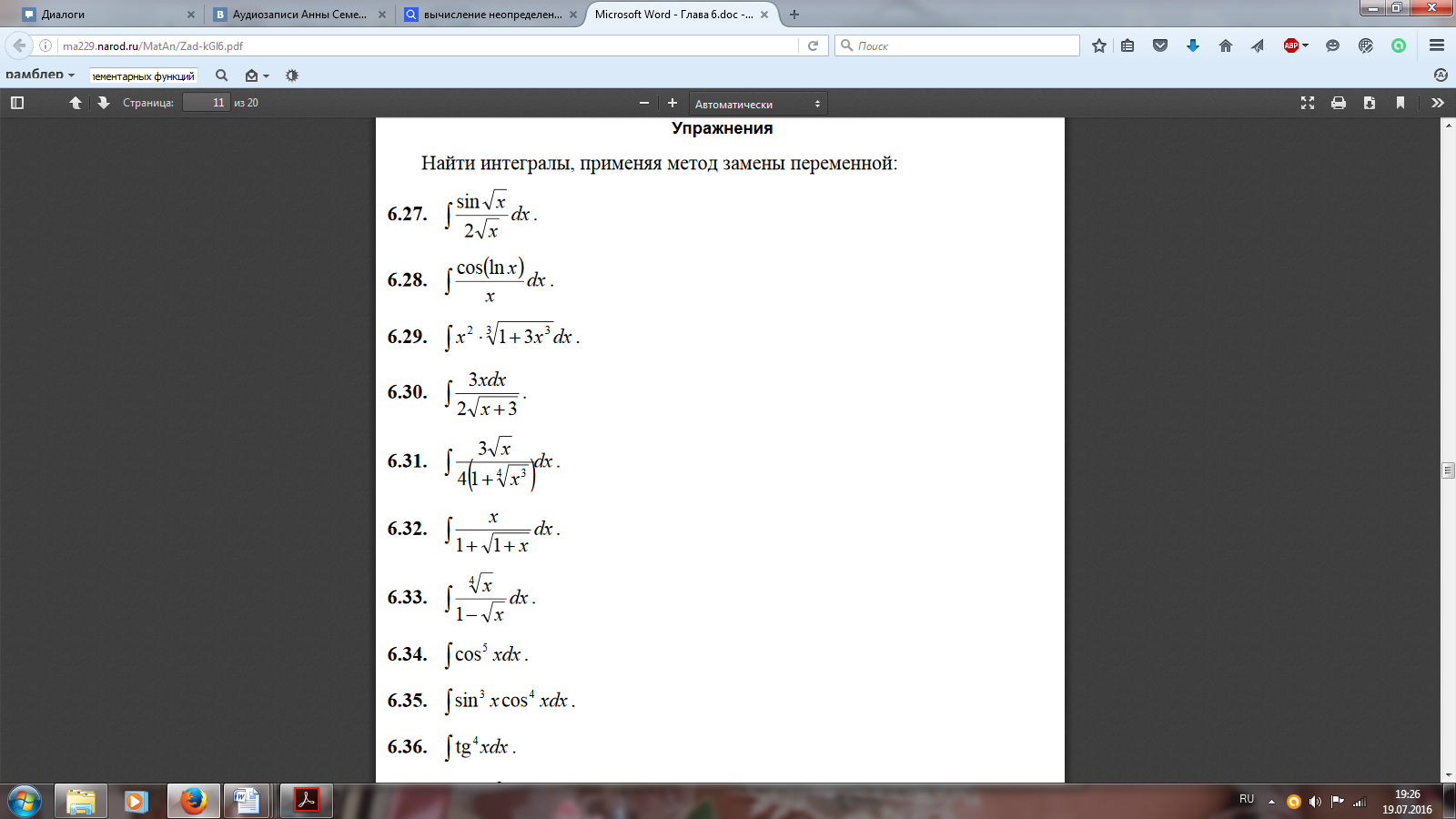
Вариант 2.
Вычислить интегралы:


3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 21
Тема 10. Интеграл и его применение
Наименование работы: Теорема Ньютона-Лейбница
Цель работы, требования к умениям и навыкам:закрепления умения пользоваться таблицей интегралов, правилами интегрирования, отработка навыков вычисленияопределенныхинтегралов
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Опр.
Если F(x) - первообразная функции f(x) , то разность F(b) - F(а) называется определённым интегралом от функции f(x) на отрезке [a ;b] и обозначают 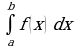
а – нижний предел интегрирования
b - верхний предел интегрирования
f(x)- подынтегральная функция
Правило вычисления определённого интеграла:
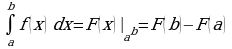 Формула Ньютона – Лейбница
Формула Ньютона – Лейбница


Примеры:
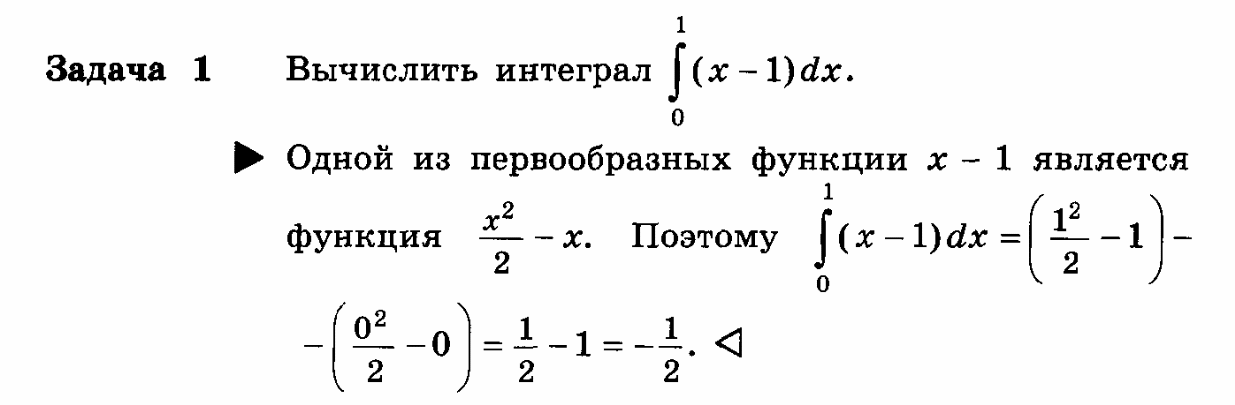
Задача 2
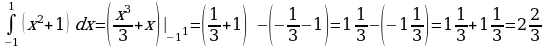
2.Задания для самостоятельной работы.
1 вариант
Вычислить определённый интеграл с помощью основных свойств и формулы Ньютона-Лейбница
1) 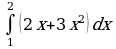 ; 2)
; 2) 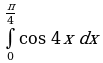 ; 3)
; 3) 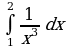 ; 4)
; 4) 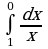 ; 5)
; 5) 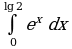 ; 6)
; 6) 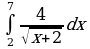
2 вариант
Вычислить определённый интеграл с помощью основных свойств и формулы Ньютона-Лейбница
1) 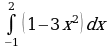 ; 2)
; 2) 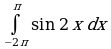 ; 3)
; 3) 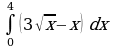 ; 4)
; 4) 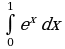 ; 5)
; 5) 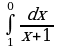 ; 6)
; 6) 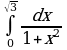
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 22
Тема 10. Интеграл и его применение
Наименование работы: Применение интеграла к вычислению физических величин и площадей
Цель работы, требования к умениям и навыкам:расширить кругозор, знания о возможном примененииинтегралаквычислению различных величин; закрепить навыки использовать интеграл для решения прикладных задач
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Фигура, изображённая на рисунке является криволинейной трапецией
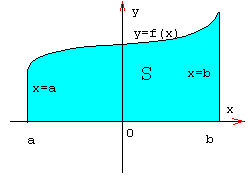
Определение
Криволинейной трапецией называется фигура, ограниченная сверху графиком непрерывной функции y=f(x), снизу отрезком [a;b] оси Ох, а с боков отрезками прямых х=а, х=b
Площадь криволинейной трапеции можно вычислить с помощью определённого интеграла
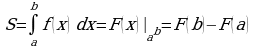
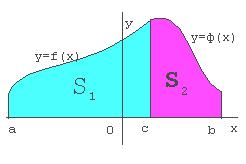
Возможно такое расположение:
S = S1 +S2
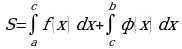
Возможен следующий случай, когда f(x)b]
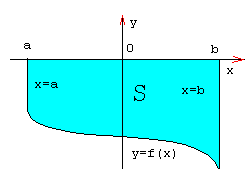
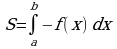
Возможно и такое расположение 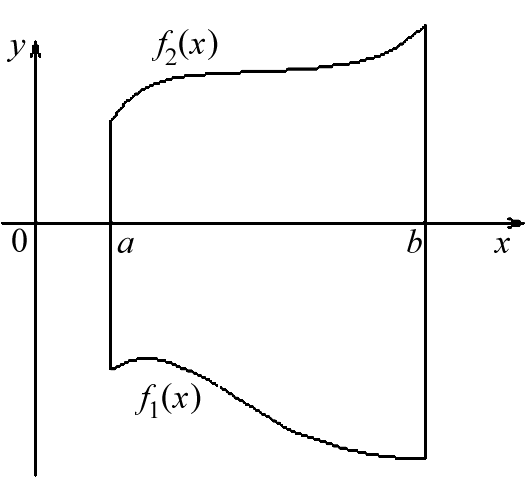 S=
S=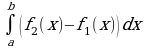
Задачи на вычисление площадей плоских фигур можно решать по следующему плану:
по условию задачи делают схематический чертёж;
представляют искомую фигуру как сумму или разность площадей криволинейных трапеций. Из условия задачи и чертежа определяют пределы интегрирования для каждой составляющей криволинейной трапеции.
записывают каждую функцию в виде 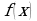
вычисляют площадь каждой криволинейной трапеции и искомой фигуры.
Задача
Н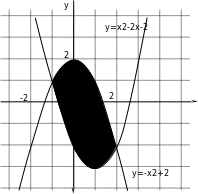 айти площадь фигуры, ограниченной линиями.
айти площадь фигуры, ограниченной линиями.
S = 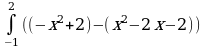 dx =
dx =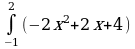 dx =
dx =
= (-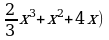 |
|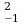 =-
=- 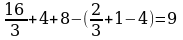 (кв. ед.)
(кв. ед.)
С помощью определённого интеграла можно решать различные задачи физики, геометрии и т.д., которые трудно или невозможно решить методами элементарной математики.
1. Нахождение пути, пройденного телом при прямолинейном , неравномерном движении.
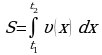 - путь, пройденный телом за время от t1 до t2 ,
- путь, пройденный телом за время от t1 до t2 ,
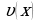 - скорость неравномерного движения
- скорость неравномерного движения
Задача
Скорость движения материальной точки задаётся формулой 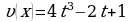 м/с. Найти путь, пройденный телом за первые 4 с от начала движения.
м/с. Найти путь, пройденный телом за первые 4 с от начала движения.
Решение
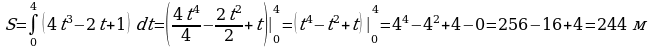
Ответ: 244 м
Вычисление работы, затраченной на растяжение и сжатие пружины.
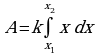 - работа силы упругости, где k – коэффициент упругости пружины, х1 – начальное положение пружины, х2 – конечное положение пружины .
- работа силы упругости, где k – коэффициент упругости пружины, х1 – начальное положение пружины, х2 – конечное положение пружины .
F = k ·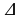 x - закон Гука, где k – коэффициент упругости пружины,
x - закон Гука, где k – коэффициент упругости пружины, 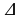 x - изменение длины пружины.
x - изменение длины пружины.
Задача
Какую работу совершает сила в 10 Н при растяжении пружины на 2 см?
Решение
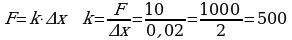 H/м
H/м
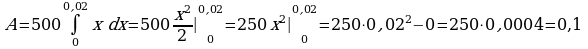 Дж.
Дж.
Ответ:А = 0,1Дж
Определение объёма тела вращения.
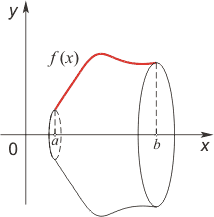



 - объём тела вращения , где S(x) – площадь сечения фигуры плоскостью перпендикулярной оси Ох
- объём тела вращения , где S(x) – площадь сечения фигуры плоскостью перпендикулярной оси Ох
2.Задания для самостоятельной работы.
1 вариант
Найти площадь фигуры, ограниченной линиями
параболой у = (х + 1)2 , прямой у = 1 – х и осью Ох.
Скорость прямолинейно движущегося тела  = ( 4t – t2 ) м/с. Вычислить путь, пройденный телом за первые 5 сек.
= ( 4t – t2 ) м/с. Вычислить путь, пройденный телом за первые 5 сек.
Вычислить работу силы F при сжатии пружины на 0,08 м, если для её сжатия на 0,02 м требуется сила в 10 Н.
Фигура, ограниченная прямыми у = - х + 3, х = 0, х = 3, у = 0 вращается вокруг оси Ох. Найти объём полученного тела вращения.
2 вариант
Найти площадь фигуры, ограниченной линиями
параболой у = 4 - х2 и осью Ох.
Найти путь, пройденный телом от начала движения до остановки, если его скорость определяется по формуле  = ( 6t – 2t2 ) м/с.
= ( 6t – 2t2 ) м/с.
Вычислить работу, производимую при сжатии пружины на 4 см, если при растяжении её на 1 см нужна сила в 10 Н.
Фигура, ограниченная кривой у = 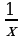 и прямыми х = 2, х = 3 . Найти объём тела, полученного при вращении кривой вокруг оси Ох.
и прямыми х = 2, х = 3 . Найти объём тела, полученного при вращении кривой вокруг оси Ох.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 23
Тема 11. Элементы теории вероятностей и математической статистики
Наименование работы: Вычисление вероятностей
Цель работы, требования к умениям и навыкам:проверка знания основных формул теории вероятности и умения вычислять вероятности событий.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Опр.Событие – это любое явление, которое происходит или не происходит или результат испытаний, наблюдений и явлений. События обозначают заглавными латинскими буквами А, В, С, …
Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи.
Долю успеха того или иного события называют вероятностью этого события и обозначают Р(А)
Опр. Если в некотором испытании существует правновозможных попарно несовместных исходов итиз них благоприятствуют событию А, то вероятностью наступления события А называют отношение 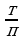 и записывают Р(А) =
и записывают Р(А) = 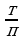
Пример Найти вероятность появления при одном бросании игральной кости числа очков, большего 4.
Решение: А – « появление числа очков, большего 4» п = 6 - число всех исходов, т = 2 – благоприятствующих событию А ( 5, 6 ) Р(А) = 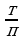 =
= 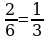 Ответ: Р(А) =
Ответ: Р(А) = 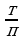 =
= 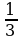
Опр. Суммой (объединением) двух событий A и B (обозначается A+B, A B) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.
B) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.
Пример
В коробке лежат 8 зеленых, 7 синих и 15 красных карандашей. Вычислить вероятность того, что взятый наугад карандаш будет, синим или зеленым.
Решение:
А: взяли синий карандаш
В: взяли зеленый карандаш
С: взяли синий или зеленый карандаш
Событие С равно сумме событий А и В: С = А + В
Вероятность события А равна ![]()
Вероятность события В равна ![]()
Вероятность события С равна ![]()
Опр.Произведением (пересечением) двух событий A и B (обозначается A×B, AиB) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.
Пример
В одной коробке находится 4 белых и 8 черных шаров, а в другой – 3 белых и 9 черных. Из каждой коробки вынули по шару. Вычислить вероятность того, что оба шара окажутся белыми.
Решение:
А: из первой коробки вынули белый шар
В: из второй коробки вынули белый шар
С: из коробок вынули белые шары
Вероятность события А равна ![]()
Вероятность события В равна ![]()
Вероятность события С равна ![]()
Ответ:Р ( С )  0,083
0,083
2.Задания для самостоятельной работы.
1 вариант.
1. Среди 170 деталей, изготовленных на станке, оказалось 8 деталей, не отвечающих стандарту. Найдите вероятность выбора детали, не отвечающей стандарту.
2. Контролёр, проверяя качество 500 изделий, установил, что 10 из них относится ко 2-му сорту, а остальные к 1-му. Найдите вероятность: а) выбора изделия 1-го сорта; б) выбора изделия 2-го сорта.
3. Какова вероятность того, что сумма очков, выпавших на 2-х брошенных костях, равна 6 ?
4. На складе имеется 50 деталей, изготовленных тремя бригадами. Из них 25 изготовлено первой бригадой, 15- второй и 10 – третьей. Найти вероятность того, что на сборку поступила деталь, изготовленная второй или третьей бригадой.
5. Игральную кость бросают трижды. Какова вероятность того, что ни разу не выпадет цифра 5?
6. Из колоды карт (36 листов ) наугад вынимается одна карта. Какова вероятность того, что эта карта: 1) валет; 2) король чёрной масти; 3) с чётным числом красной масти; 4) не с числом?
7. Брошены 3 монеты: копейка, пятак и 10 гривенник. Какова вероятность того, что: 1) на копейке появится орёл, а на пятаке и гривеннике – решки; 2) на всех монетах выпадут решки?
2 вариант.
1. Пусть имеется 80 деталей, среди которых 60 исправных, а 20 бракованных. Найти вероятность того, что взятая наугад деталь окажется исправной.
2. В партии из 100 деталей имеется 5 бракованных. Определить вероятность того, что взятая на удачу деталь окажется стандартной.
3. Какова вероятность того, что сумма очков, выпавших на 2-х брошенных костях, равна 5 ?
4. В коробке находятся 250 лампочек, из них 100 по 100 Вт, 50 - по 60 Вт, 50 – по 25 Вт и 50 – по 15 Вт. Вычислить вероятность того, что мощность любой взятой наугад лампочки не превысит 60 Вт.
5. Игральную кость бросают трижды. Какова вероятность того, что ни разу не выпадет цифра 6?
6. Из колоды карт (36 листов ) наугад вынимается одна карта. Какова вероятность того, что эта карта: 1) валет; 2) король чёрной масти; 3) с чётным числом красной масти; 4) не с числом?
7. Брошены 3 монеты: копейка, пятак и 10 гривенник. Какова вероятность того, что: 1) на копейке появится орёл, а на пятаке и гривеннике – решки; 2) на всех монетах выпадут решки?
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 24
Тема 12. Уравнения и неравенства
Наименование работы: Решение систем уравнений
Цель работы, требования к умениям и навыкам:Сформировать умения и навыки по решению систем уравнений с помощью формул Крамера. Вычислять определители второго и третьего порядков; решать системы двух уравнений с двумя неизвестными, используя формулы Крамера.
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Определение 1. Определителем второго порядка, составленного из чисел 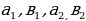 , называется число, определяемое равенством
, называется число, определяемое равенством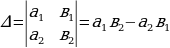 .
.
Числа 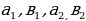 , называются элементами определителя.
, называются элементами определителя.
При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего вправый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.
Примеры.
1.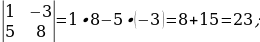 2.
2. 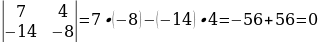 .
.
Определение 2. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы третьего порядка следующим образом:
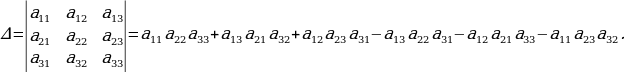
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят со знаком «+», располагаются так:
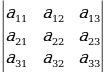 , образуя два треугольника, симметричных относительно главной диагонали.
, образуя два треугольника, симметричных относительно главной диагонали.
Элементы, произведения которых входят в определитель со знаком  , располагаются аналогичным образом относительно побочной диагонали:
, располагаются аналогичным образом относительно побочной диагонали: 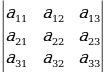 .
.
3.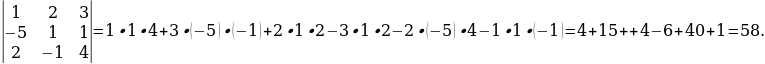
Формулы Крамера решения систем двух уравнений с двумя неизвестными.
Рассмотрим систему двух линейных уравнений с двумя неизвестными в общем виде:
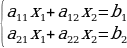
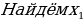 следующим образом: чтобы исключить
следующим образом: чтобы исключить 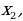 умножим первое уравнение на
умножим первое уравнение на 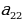 и из полученного уравнения вычтем второе, умноженное на
и из полученного уравнения вычтем второе, умноженное на 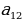 :
: 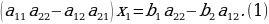
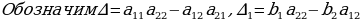 . Для определения
. Для определения  поступим так: умножим второе уравнение на
поступим так: умножим второе уравнение на  и из полученного уравнения вычтем первое, умноженное на
и из полученного уравнения вычтем первое, умноженное на 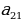 :
:
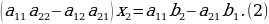
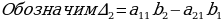 . Из (1) и (2) видно, что если
. Из (1) и (2) видно, что если 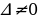 , то система имеет единственное
, то система имеет единственное 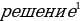 , определяемое формулой
, определяемое формулой 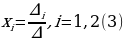
Если 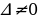 , система имеет единственное решение, определяемое по формуле:
, система имеет единственное решение, определяемое по формуле: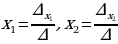 .
.
Если 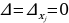 , система имеет бесконечно много решений.
, система имеет бесконечно много решений.
Если 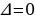 , а хотя бы один из
, а хотя бы один из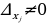 ,система не имеет решений.
,система не имеет решений.
Если говорить строго, то из (1) и (2) следует, что если решение существует, то оно единственным образом выражается через коэффициенты системы и свободные члены. Чтобы доказать существование, надо подставить две формулы (3) в систему и убедиться в том, что оба уравнения обращаются в верные равенства.
Примеры: Решить систему уравнений с помощью формул Крамера.
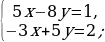
Решение: 1. Составим определители 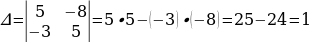
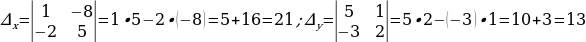 .
.
Так как 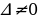 , система имеет единственное решение, определяемое по формулам:
, система имеет единственное решение, определяемое по формулам: 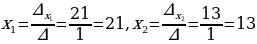 . Таким образом, пара чисел (21; 13) – решение системы. Ответ: (21; 13)
. Таким образом, пара чисел (21; 13) – решение системы. Ответ: (21; 13)
Решение: 2. Рассмотрим систему 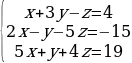 и применим к ней правило Крамера. Найдём все нужные определители:
и применим к ней правило Крамера. Найдём все нужные определители:
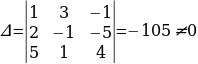 , следовательно, система имеет единственное решение.
, следовательно, система имеет единственное решение.
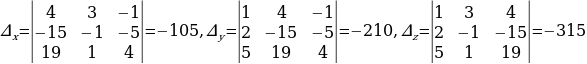 .
.
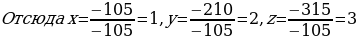 . Ответ:
. Ответ: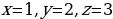 .
.
Решение: 3. 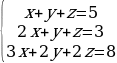 . Здесь
. Здесь 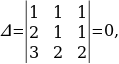 поскольку имеет два одинаковых столбца. Следовательно, система не имеет единственного решения. Найдём
поскольку имеет два одинаковых столбца. Следовательно, система не имеет единственного решения. Найдём 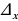 ,
, 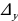 и
и 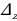 :
:
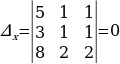 ,
, 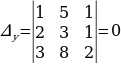 ,
, 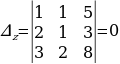 , поэтому система имеет бесконечно много решений.
, поэтому система имеет бесконечно много решений.
 4.
4. 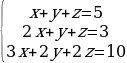 . Для этой системы
. Для этой системы 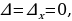 но
но 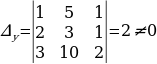 , следовательно, решений нет.
, следовательно, решений нет.
2.Задания для самостоятельной работы.
Вариант 1.
1.Вычислить определители: а) 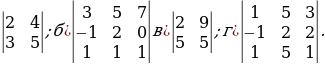
2.Решите систему уравнений по формулам Крамера: 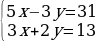 .
.
Вариант 2.
1.Вычислить определители: а) 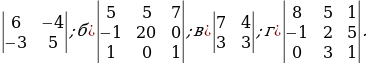
2.Решите систему уравнений по формулам Крамера: 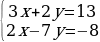 .
.
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
Практическая работа № 25
Тема 12. Уравнения и неравенства
Наименование работы: Использование свойств и графиков функций для решения уравнений и неравенств.
Цель работы, требования к умениям и навыкам:Закрепить умение применять свойствафункций и их графиков при решенииуравнений или неравенств
Задание: 1. Изучить методические указания к работе, записать указанные примеры с решениями.
2. Выполнить самостоятельную работу по вариантам.
3. Сделать отчёт.
Методические указания
Краткие теоретические сведения.
Графическое решение систем уравнений
Решить графически систему уравнений - это значит найти координаты общих точек графиков уравнений, построенных в одной системе координат.
Пример

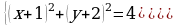
1.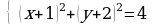 - уравнение окружности с центром в точке с координатами (-1;-2) и радиусом r = 2
- уравнение окружности с центром в точке с координатами (-1;-2) и радиусом r = 2
2. у = 0 – уравнение оси Ох
А(-1;0)

Общая точка:
А(-1:0), значит
х = -1, у = 0.
Проверка:
х=-1, у=0, то система примет вид:
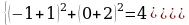 ,
, 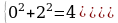 ,
, 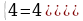
Значит, (-1;0) решение системы
Ответ: (-1;0)
Графическое решение системы неравенств
Решить графически систему неравенств – это значит найти область решений, координаты которой будут удовлетворять обеим неравенствам.
Пример
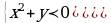
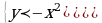
у = х2 - квадратичная функция, график – парабола, ветви направлены вниз
у = 2х - линейная функция, график – прямая
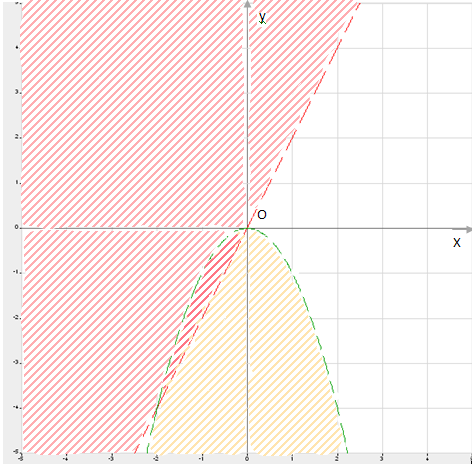
1. А(0;-1), неравенство примет вид:
0-1
2. В(-1;0), неравенство примет вид:
0+20(истинно), значит координаты всех точек области над прямой без границы являются решениями второго неравенства.
Вывод: Т.о, координаты всех точек во внутренней области параболы, но лежащие выше прямой без границы являются решениями системы неравенств.
2.Задания для самостоятельной работы.
1 вариант.
1. Решить систему уравнений: а) 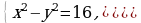 б)
б) 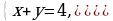
2. Решить систему неравенств: 
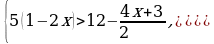
3. Решить графически систему уравнений: 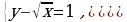
4. Решить графически систему неравенств: 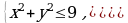
2 вариант.
1. Решить систему уравнений: а) 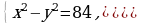 б)
б) 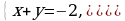
2. Решить систему неравенств: 
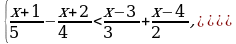
3. Решить графически систему уравнений: 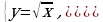
4. Решить графически систему неравенств: 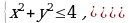
3.Содержание отчёта.
3.1 Название работы.
3.2 Выполнение работы.
ЛИТЕРАТУРА
Основная литература
Башмаков М.И., Математика, ЭБС «КНОРУС»,2022
Башмаков М.И., Математика: Практикум, ЭБС «КНОРУС»,2022
Дополнительная литература
Башмаков М.И., Математика: алгебра и начала математического анализа, геометрия - М.: Издательский центр «Академия», 2017.
Григорьев С.Г., Задулина С.В. Математика. М.: Издательский центр «Академия», 2005г.
Математика - А.А. Дадаян, М.: ФОРУМ: ИНФРА-М. 2006
Интернет- ресурсы
http://www.allenq.ru/edu/
http://www.metod-kopilka.ru/
http://www.klyaksa. net/
http://www.fcior.edu.ru (Информационные, тренировочные и контрольные материалы).
http://www.school-collection.edu.ru (Единая коллекции цифровых образовательных ресурсов).
РЕЦЕНЗИЯ
на методические указания
по выполнению практических занятий
по предмету «Математика»
(Наименование)
для специальности 38.02.01 Экономика и бухгалтерский учет (по отраслям).
( Код, наименование)
разработчик Ромащенко Т.А.
(Ф.И.О.)
На рецензию представлены методические указания по выполнению практических занятий по ОУП «Математика».
Методические указания по ОУП «Математика» составлены на основании рабочей программы общеобразовательного учебного предмета и в соответствии с Положением по планированию, организации и проведению и практических занятий.
В методических указаниях по каждой практической работе отражены:
тема, наименование работы;
цель работы, требования к умениям и навыкам;
методические указания (практические работы):
краткие теоретические сведения
примеры подобных заданий с образцами решений
варианты заданий для самостоятельного выполнения
содержание отчёта.
Данные методические указания позволяют не только формировать умения применять полученные знания на практике, но и развивать такие профессионально значимые качества, как самостоятельность, ответственность, точность, творческая инициатива.
Заключение: данные методические указания рекомендуются к использованию при подготовке квалифицированных специалистов среднего звена.
Рецензент: Калашникова Г.И.
(фамилия, имя, отчество)
преподаватель ГБПОУ РО «САТК»
(место работы, должность, образование)
Подпись _______________ Дата __________ Телефон _______________
© 2022, Ромащенко Татьяна Александровна 260 4
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Полезное для учителя