Брянский Государственный Университет
им. академика И.Г.Петровского
Кафедра методики обучения математике
и информационных технологий
Курсовая работа
Тема: «Методика обучения учащихся решению задач на построение методом вспомогательного треугольника»
Выполнила студентка
5 курса ФМФ ОЗО: Чмыхова Я.Ю.
Руководитель: Яцковская Г.А.
Брянск – 2006
Содержание
Введение…………………………………………………………………………3
Глава I. Методика обучения решению задач на построение методом вспомогательного треугольника…………………………………………….5
Методика решения задач на построение…………………………………..5
Метод вспомогательного треугольника…………………………………..10
Количественный анализ задач на построение в учебниках геометрии
для VII – IX классов………………………………………………………..15
Глава II. Методические разработки по обучению учащихся решению
задач на построение методом вспомогательного треугольника…17
2.1 Погорелов А. В. Геометрия 7 – 11. № 46*………………………………..17
2.2 Атанасян. Л.С. Геометрия 7 – 9. № 393………………………………….19
2.3 Шарыгин И.Ф. Геометрия 7 – 9. № 20 п. 6.2…………………………….21
Заключение…………………………………………………………………...25
Методика обучения учащихся решению задач на построение методом подобия (дополнение)………………………………………………………..27
Список литературы……………………………………………………..…...32
Введение
Центральным видом учебной деятельности, в процессе которой учащиеся усваивают математические теории, у них развиваются самостоятельность мышления и творческие способности, является решение задач.
Органической частью обучения всем учебным предметам, особенно предметам, естественно – математического цикла, в том числе геометрии и черчения, является решение различных графических задач.
В данной работе рассмотрим000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 частный вид класса графических задач – задачи на построение.
Разработкой методов их решения занимались ещё со времён Древней Греции. Ещё в 4 веке до нашей эры математики школы Пифагора решили задачу о построении правильного пятиугольника. В течение многих веков математики проявляли живой интерес к задачам на построение.
Интерес к ним обусловлен не только их красотой и оригинальностью методов их решения, но и большой практической ценностью. Проектирование строительства, архитектура, конструирование различной техники основаны на геометрических построениях. Совершенствование конструкций сопровождается усложнением их геометрических построений, общим расширением применяемого в производстве математического аппарата, включением в него различных методов.
Задачи на построение – это задачи, решаемые различными инструментами (линейка, циркуль и т.д.), которые предполагаются абсолютно точными.
Геометрические задачи на построение играют важную роль в обучении, и эта роль сводится к следующему:
эти задачи помогают учащимся обстоятельно и глубоко разобраться в известном им геометрическом материале;
они способствуют развитию пространственных представлений у учащихся;
они приучают учащихся логически рассуждать;
эти задачи успешно формируют у учащихся алгоритмическую культуру;
посредством этих задач реализуются межпредметные связи геометрии со смежными дисциплинами и особенно с черчением;
эти задачи дисциплинируют внимание учащихся, приучают их проявлять настойчивость, инициативу и изобретательность в достижении намеченной цели.
Требования к математической подготовке учащихся общеобразовательной школы предполагают, что в результате изучения курса геометрии(VII – IX классы) все учащиеся должны овладеть умениями выполнять основные построения циркулем и линейкой, решать несложные комбинированные задачи, сводящиеся к выполнению основных построений. При этом вопрос о существовании и количестве решений не ставится и задача считается решенной, если указана последовательность выполняемых операций и доказано, что получаемая фигура удовлетворяет условию задачи.
Любая задача на построение с помощью циркуля и линейки может быть решена при помощи и других наборов инструментов: одним циркулем, линейкой с двумя параллельными краями, которая может быть заменена угольником; линейкой и окружностью, заданной в плоскости чертежа с отмеченным центром.
В данной работе рассмотрим задачи на построение, которые будут решаться циркулем и линейкой, по той причине, что именно такие задачи рассматриваются в школьном курсе геометрии и являются основными, обеспечивающими межпредметную связь геометрии с другими науками, а также один из методов решения этих задач – метод вспомогательного треугольника.
Глава I. Методика обучения учащихся решению задач на построение методом вспомогательного треугольника.
Методика решения геометрических задач на построение.
Задачи на построение – это задачи, которые значительно чаще других поражают своей красотой и во многих случаях простотой найденного решения, что вызывает к ним повышенный интерес. Чтобы ученик мог приступить к решению таких задач, он в первую очередь должен изучить «простейшие задачи на построение». В существующих учебниках по геометрии для массовых общеобразовательных школ к числу задач такого рода относят следующие: деление данного отрезка пополам, деление данного угла пополам, построение угла равного данному, построение прямой проходящей через данную точку и перпендикулярной к данной прямой; построение на данной прямой отрезка, равного данному; построение треугольника по стороне и двум прилежащим к ней углам, по трем сторонам, по двум сторонам и углу между ними, а также построение прямоугольных треугольников по: а) двум катетам, б) гипотенузе и катету, в) катету и прилежащему к нему острому углу, г) гипотенузе и острому углу.
Решение математических задач вызывает у учащихся большие трудности. Одной из основных причин такого положения является нарушение следующих психолого–педагогических требований к алгоритмизации учебного процесса:
1. при формировании любого действия (умения) необходимо четко выделить этапы его выполнения,
2. выделенные этапы действия следует сформулировать в общем виде,
3. этапы действия желательно выделять с участием учащихся,
4. каждый этап действия следует сформировать отдельно от других этапов на специальных упражнениях,
5. при первоначальном формировании действия, выделенные этапы (алгоритм) должен проговариваться вслух.
Учитывая малый объём отводимого времени и при этом недопустимость упрощённости при изучении материала, учитель из Курской области В.В.Блудов останавливается на некоторых моментах, которые, по его мнению, учитель (особенно начинающий) должен продумать и чётко спланировать.
Приступая к решению комбинированных задач необходимо познакомить учеников с наиболее употребительной схемой (Платона), состоящей из четырёх разделов – анализ, построение, доказательство, исследование, в противном случае они не смогут решать задачи, предложенные в учебниках.
Конечно, эта схема не является, безусловно, необходимой и неизменной, не всегда удобно и целесообразно строго разделять её этапы и в точности осуществлять их в указанном порядке. Но по большей части указанная схема серьёзно помогает при решении конструктивных задач. Рассмотрим каждый этап этой схемы.
АНАЛИЗ. Это подготовительный и в тоже время наиболее важный этап решения задачи на построение, т.к. именно он даёт ключ к решению задачи. Цель анализа состоит в установлении таких зависимостей между элементами искомой фигуры и элементами данных фигур, которые позволили бы построить искомую фигуру. Это достигается с помощью чертежа – наброска, изображающие данные и искомые примерно в том расположении, как это требуется условием задачи. Этот чертёж можно выполнить «от руки». Построение вспомогательного чертежа сопровождается словами: «предположим, что задача уже решена». Наносятся данные на чертёж:
а) выбирают одну из точек за искомую; б) определяют условия, которым удовлетворяет искомая точка; в) определяют фигуры, на которых лежит искомая точка; г) делают вывод, что искомая точка является пересечением найденных фигур.
2. ПОСТРОЕНИЕ. Данный этап решения состоит в том, чтобы указать последовательность основных построений (или ранее решенных задач), которые достаточно произвести, чтобы искомая фигура была построена. Построение обычно сопровождается графическим оформлением каждого его шага с помощью инструментов, принятых для построения.
3. ДОКАЗАТЕЛЬСТВО. Доказательство имеет целью установить, что построенная фигура действительно удовлетворяет всем поставленным в задаче условиям. Доказательство обычно проводится в предположении, что каждый шаг построения действительно может быть выполнен.
4. ИССЛЕДОВАНИЕ. При построении обычно ограничиваются отысканием, одного какого – либо решения, причём предполагается, что все шаги построения действительно выполнимы. Для полного решения задачи нужно ещё выяснить следующие вопросы: 1) всегда ли (т.е. при любом ли выборе данных) можно выполнить построение избранным способом; 2) можно ли и как построить искомую фигуру, если избранный способ нельзя применить; 3) сколько решений имеет задача при каждом возможном выборе данных. Рассмотрение всех этих вопросов и составляет исследование. Таким образом, исследование имеет целью поставить условия разрешимости и определить число решений.
Иногда ставится также задача: выяснить, при каких условиях искомая фигура будет удовлетворять тем или иным дополнительным требованиям.
В качестве образца можно рассмотреть пример:
Построить треугольник по двум сторонам а и b и высоте h, опущенной на прямую, содержащую сторону b.
В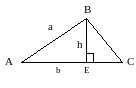 .В.Блудов предлагает ученикам данные отрезки выбрать примерно в таком же отношении как они изображены на доске.
.В.Блудов предлагает ученикам данные отрезки выбрать примерно в таком же отношении как они изображены на доске.
а
h

b


Рис.1
Анализ: предположим, что ∆ АВС искомый. АС =b, АВ = а, ВЕ = h , причём высота ВЕ проведена к прямой, содержащей сторону АС. Построение треугольника сводится к построению трёх точек – его вершин. Т.к. построение стороны АС = b данном случае затруднения не вызывает, то задача сводится к нахождению вершины В. Поскольку ВЕ – высота треугольника, то т. В находится на расстоянии h от прямой АС. Геометрическое место точек, удовлетворяющих этому условию, есть пара прямых параллельных АС и отстоящих от неё на расстоянии, равном h.
В тоже время т.В находится на расстоянии а от точки А. Геометрическое место точек, удовлетворяющих этому условию, есть окружность с центром в точке А и радиусом АВ = а. Искомая нами точка должна удовлетворять одновременно этим двум условиям. Отсюда,
Построение:
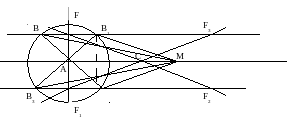
Рис.2
на произвольной прямой выбираем произвольно точку А. От точки А на выбранной прямой откладываем отрезок АС = b (таких отрезков два, пересечение прямой и окружности радиуса b с центром в точке А. Выбираем, для определённости, одну из них, отмечая в дальнейшем, что другой вариант не дает новых решений). Через точку А проводим прямую, перпендикулярную прямой АС. Отложим отрезки АF и AF1, равные h (F и F1 – точки пересечения прямой FF1 и окружности с центром в точке А и радиусом, равным h). Строим прямые, параллельные АС и проходящие через точки F и F1; для чего проводим лучи FM и F1M и за точку М откладываем соответственно отрезки MF2 = F1M и MF3 = FM. Тогда FF3 ║АС и F1F2 ║ АС.
Проводим радиусом, равным а, окружность с центром в точке А. Эта окружность пересекает прямые FF3 и F1F2 в четырёх точках В, В1, В2, В3. Таким образом, мы получили четыре треугольника: АВС, АВ1С, АВ2С, АВ3С.
Доказательство: каждый полученных треугольников имеет стороны равные данным а и b , и высоту равную h , проведенную к прямой, содержащей сторону, равную b, что следует из построения. Следовательно, каждый из них удовлетворяет условию задачи и является искомым. Однако, можно заметить, что ∆АВС = ∆ АВ3С и ∆ АВ1С= ∆АВ2С. Доказательство можно провести, выяснив равенство прямоугольных треугольников АВЕ и АВ3Е (по катету и гипотенузе), откуда ΔВАЕ = ΔВ3АЕ. Тогда по двум сторонам и углу между ними равны ∆АВС и ∆АВ3С. Аналогично доказывается равенство ∆АВ1С и ∆АВ2С.
Исследование: раздел, который, как правило, вызывает наибольшие затруднения.
Чтобы более наглядно подвести к пониманию сути исследования, предлагается выполнить построение, выбрав длины данных отрезков в несколько ином отношении.
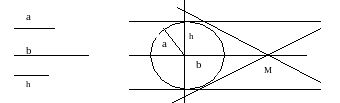
Рис.3
Следует вывод, что в определенной ситуации, точки В, удовлетворяющей поставленным условиям, нет, а значит, задача в этих условиях решения не имеет.
1.2 Метод вспомогательного треугольника.
Само название «Метод вспомогательного треугольника» говорит о том, что решение задач на построение этим методом подразумевает выделение вспомогательного треугольника, который можно построить по данным задачи. При помощи некоторого дополнительного построения (продление отрезка, геометрическое преобразование и т.д.) получают треугольник, который даёт возможность получить решение задачи. Обычно такой треугольник обладает двумя важными для решения задачи свойствами:
его элементы некоторым образом связаны с элементами, фигурирующими в условии задачи;
для его элементов легче найти характеристики, позволяющие получить решение, чем для фигур непосредственно заданных условием.
Задачи на построение методом вспомогательного треугольника имеют такую же схему решения, как и любая другая задача на построение, т.е.: анализ, построение, доказательство, исследование.
На этапе анализа предполагаем, что задача решена, делаем рисунок и на него наносим все данные. Далее выбираем вспомогательный треугольник, который можно построить по данным задачи, потом определяем, какую точку ещё надо построить, или, иначе, какую точку выберем за искомую. Затем выделяем два условия, которым должна удовлетворять искомая точка. На основании этих условий определяем две фигуры, на которых лежит искомая точка, и делаем вывод, что искомая точка является пересечением найденных фигур.
На этапе построения задаём данные фигуры, делаем чертёж с помощью инструментов и описываем последовательность построений.
На этапе доказательства устно проверяем, всем ли данным задачи удовлетворяет построенная фигура. Для чего смотрим на то, что дано, и на каком шаге построения это учитывалось.
В задачах на построение методом вспомогательного треугольника можно выделить задачи, в которых:
1) вспомогательный треугольник виден сразу,
2) вспомогательный треугольник получается в результате параллельного переноса,
3) вспомогательный треугольник получается методом спрямления.
Сущность задач, в которых вспомогательный треугольник виден сразу, можно пояснить на примере решения следующей задачи: № 39 (Погорелов).
Постройте треугольник по стороне и проведенным к ней медиане и высоте.
Решение
Анализ.
Предположив, что задача решена, делаем от руки чертёж искомой фигуры и наносим на него все данные.
В




С
А
D
K

По данным задачи мы можем построить вспомогательный ∆ ВКД, для этого: возьмём произвольную прямую l; построим перпендикуляр р, который пересекает l в т.Д. Точка В лежит на прямой р и отстоит от т.Д на расстоянии h, т.е. точка В принадлежит окр.(Д; h). Окружность пересекает перпендикуляр в двух точках, выберем точку В т.к. другой вариант новых решений не даёт. Точка К лежит на прямой l и т.К принадлежит окр.(В; m).
Для построения ∆АВС нам необходимо построить вершины А и С. Т.к. ВК – медиана, проведённая к стороне b, то точка К делит b пополам. Разделим отрезок b пополам. Определим условия, которым должны удовлетворять т.А и т.С. Точка А должна лежать на ДК и отстоять от точки К на расстоянии 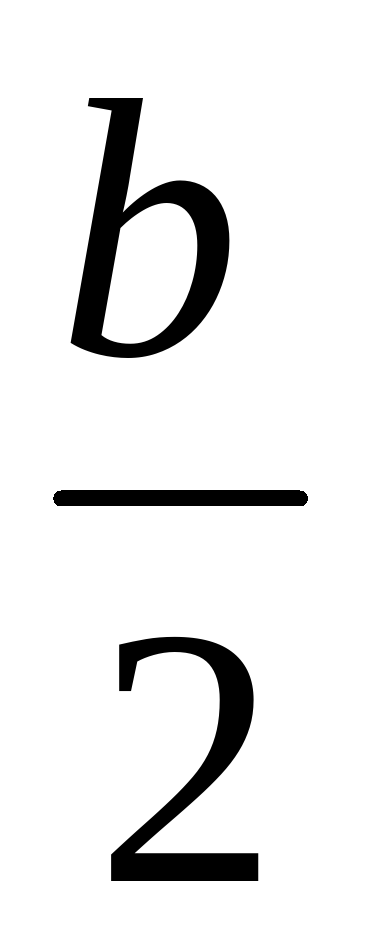 .
.
Точка С должна лежать на ДК и отстоять от точки К на расстоянии 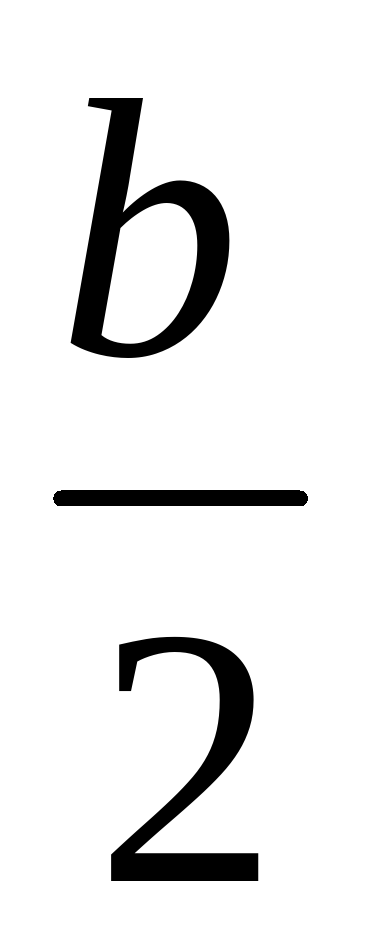 .
.
Точка А – есть точка пересечения прямой ДК и окр.(К; 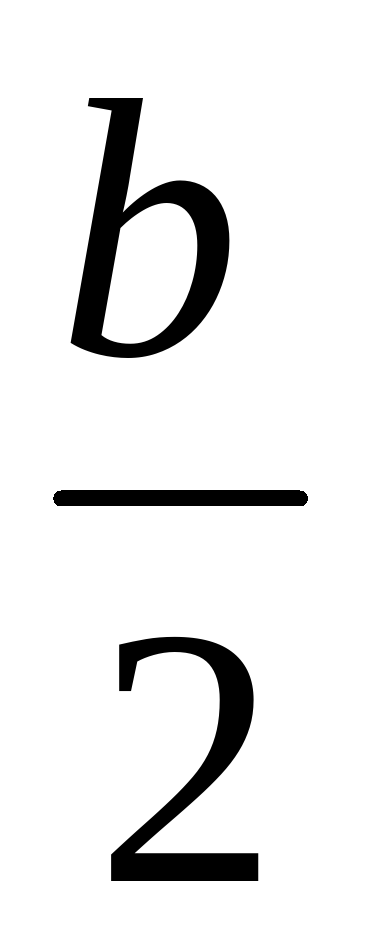 ).
).
Точка С - есть точка пересечения прямой ДК и окр.(К; 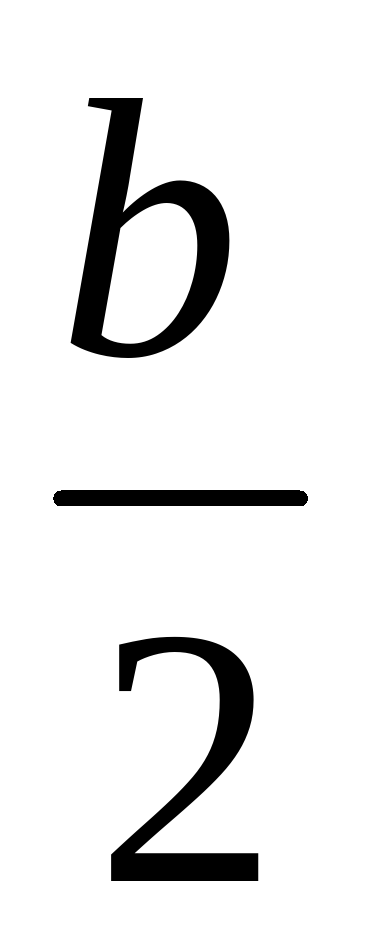 ).
).
Таким образом, мы получили ∆АВС – искомый.
Анализ задачи на доске представляется краткой записью:
Δ ВКД – вспомогательный
С

 : С
: С ДК; СК =
ДК; СК = 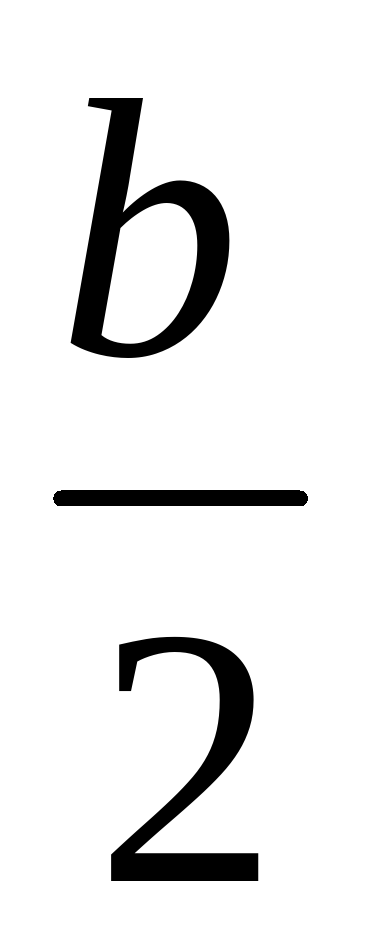
С окр. (К;
окр. (К; 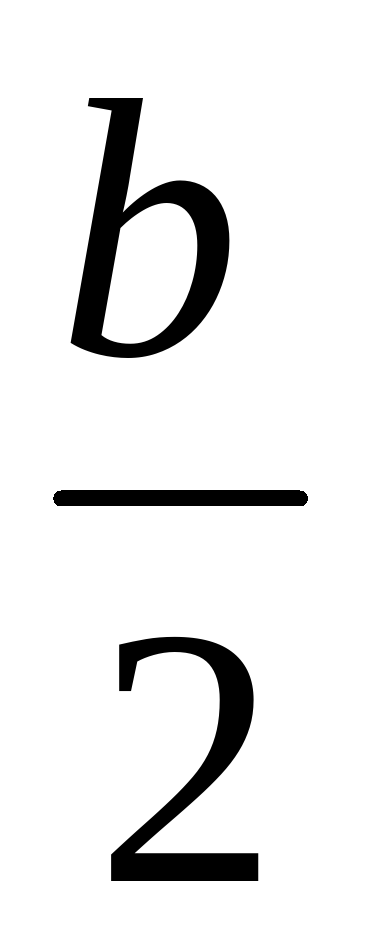 )
)
Построение.
Дано:
| 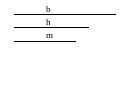 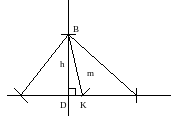
| Строим вспомогательный треугольник ВКД, а) строим произвольную прямую l
б) строим перпендикуляр к l, который пересекает l в точке Д, в) строим т.В: В р; т. В р; т. В  окр.(Д; h) окр.(Д; h) г) строим т. К: К  l; К l; К  окр.(В; m) окр.(В; m) 2. Разделим отрезок b пополам. 3. Строим т.А: А  ДК; А ДК; А окр.(К; окр.(К; 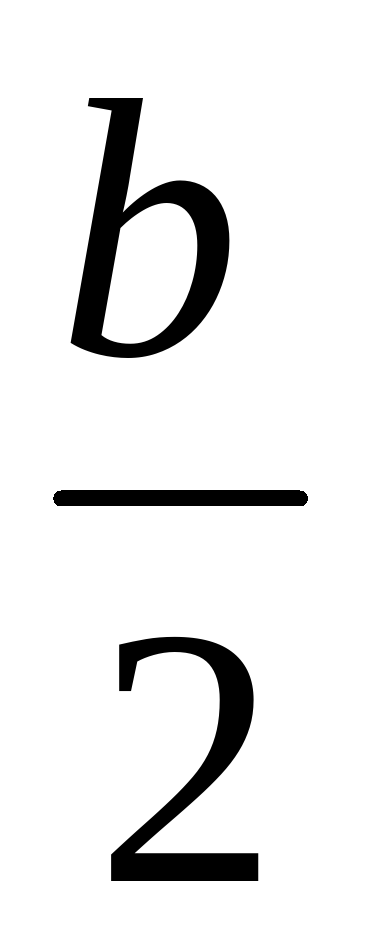 ) ) 4  . Строим т.С: С . Строим т.С: С  ДК; С ДК; С  окр.(К; окр.(К; 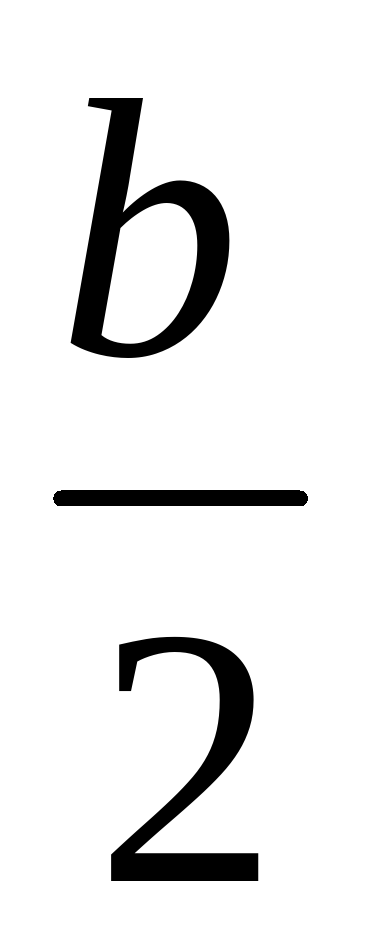 ) )
5. ∆АВС – искомый.
|
Доказательство:
По условию задачи нам была дана сторона b и проведённые к ней медиана m и высота h:
ВД = h (по построению 1(в))
ВК = m (по построению 1(г))
АС = b (по построению2,3,4)
Пример задачи, в которой вспомогательный треугольник получается в результате параллельного переноса. №72* (Погорелов)
Постройте трапецию по основаниям и диагоналям.
А
a
С
В
нализ.





d2
d2
d1
А
D
b

По данным задачи сразу не видно, какой вспомогательный треугольник необходимо построить. Поэтому выполним следующее дополнительное построение: через вершину С проведём прямую параллельную диагонали ВД. Теперь по данным задачи можно построить треугольник АСК по трём сторонам (АС = d1, СК = d2, АК = а + b).
Для построения трапеции АВСД нам необходимо построить вершины В и Д. Проведём через вершину С прямую m параллельно прямой АК. Определим условия, которым должна удовлетворять искомая точка В и точка Д. Точка В принадлежит прямой m и т.В принадлежит окр. (С; а). Точка Д принадлежит прямой АК и т. Д принадлежит окр. (А; b).
Точка В – есть точка пересечения прямой m и окр.(С; а).
Точка Д – есть точка пересечения прямой АК и окр.(А;b).
Таким образом мы получили трапецию АВСД – искомую.
Краткая запись условия:
ΔАСК – вспомогательный Д: Д АК; АД = b
АК; АД = b
т.В и т.Д – искомые Д окр.(А;b)
окр.(А;b)
АК = а +b В: ВС ||АК; ВС = а
В  окр.(С;а)
окр.(С;а)
Построение:
Дано: 1. строим вспомогательный
 треугольник АСК(по трём
треугольник АСК(по трём
сторонам)
2. т. В: ВС || АК; В окр.(С;а)
окр.(С;а)
3. т. Д: Д АК; Д
АК; Д окр.(А;в)
окр.(А;в)
4. АВСД – искомая трапеция.

Доказательство:
ВС = а (по построению 2)
АД = b (по построению 3)
АС = d1
ВД = d2 (по построению 1)
Пример задачи, в которой вспомогательный треугольник получается методом спрямления. № 47* (Погорелов)
Постройте треугольник, если заданы сторона, прилежащий к ней угол и разность двух других сторон.
Решение
Анализ.
Предполагаем, что задача решена, делаем чертёж и наносим на него все данные.
B
Краткая запись:
 1. АС – ВС = АД = d
1. АС – ВС = АД = d
2. Δ АВД – вспомогательный
3. т.С - искомая
D
d
A
C

По данным задачи мы можем построить вспомогательный треугольник АВД по двум сторонам и углу между ними. Для построения Δ АВС нам необходимо построить вершину С. Определим условия, которым должна удовлетворять т.С. Т.к. ВС = ДС, то Т. С лежит на серединном перпендикуляре к стороне ВД. Точка С принадлежит прямой АД. Построим серединный перпендикуляр k к стороне ВД.
Точка С – есть точка пересечения прямой k и прямой АД.
Таким образом, мы получили треугольник АВС – искомый.
Построение:
Дано:
d
a
 1. Строим Δ АВД по двум
1. Строим Δ АВД по двум
 сторонам и углу между ними
сторонам и углу между ними
 АВ = а, АД = d,
АВ = а, АД = d,  А = α
А = α
α

B
 2. Строим серединный
2. Строим серединный 
a
перпендикуляр k к стороне
α
ВД
A
C

3. С: С

АД; С

k С = АД k
D
d
4. Δ АВС – искомый.
Доказательство:
АВ = а (по построению 1)
АД = d (по построению 1)
А = α (по построению 1)
1.3 Количественный анализ задач на построение в учебниках геометрии для VII – IX классов.
Во всех действующих учебниках по геометрии задачи на построение рассматриваются как самостоятельные в конце VII класса.
Осуществляются следующие элементарные построения: деление отрезка пополам; откладывание угла, равного данному; построение биссектрисы угла; построение перпендикуляра к прямой из данной точки, не лежащей на этой прямой. В качестве метода решения задач на построение в ряде учебников рассматривается метод геометрического места точек. Этим небольшим списком круг задач на построение в учебниках для VII класса практически исчерпывается.
В VII – IX классах встречаются задания на построение фигур по некоторым данным элементам.
Таблица (количественный анализ задач на построение в учебниках геометрии для VII – IX классов).
| учебники | класс | Общее число задач на построение | Номера задач на построение методом вспомогательного треугольника |
| Атанасян Л.С. и др. «Геометрия 7-9» (1991) | VII
| 83
| №№ 286, 287, 288, 289, 293, 294, 295, 313*, 316*, 319*, 320*, 321*, 351, 359, 360, 361, 362 |
| VIII
| 47
| №№ 393, 397, 413, 414, 624, 625, 827, 900 |
|
IX |
34 |
№№ 1228, 1229 |
| Погорелов А.В. «Геометрия 7 - 11» (1993)
| VII
| 42
| § 5 №№ 22, 30, 31, 32, 36, 37, 38, 39,40, 46*, 47*, 48* |
|
VIII
|
35
|
§ 6 №№ 22, 23, 38, 39, 53, 71*, 72* |
|
IX |
10 | _____ |
|
Шарыгин И.Ф. «Геометрия 7 - 9» (2001)
|
VII
|
51
| п. 4.2 №№ 7,11
|
| VIII
| 45
| п. 5.3 №№ 7, 13, 14 п. 6.2 №№ 20,21 п. 8.1 №№ 18, 19 |
| IX | 35 | __________
|
Рассматривая наиболее распространённые учебники А.В.Погорелова, Л.С.Атанасяна и др., можно отметить, что в них достаточно высок процент заданий на построение для VII класса, причём рассматриваются стандартные и элементарные задачи на построение. Однако, в последующих классах процент геометрических заданий на построение падает.
Глава II. Методические разработки по обучению учащихся решению задач на построение методом вспомогательного треугольника.
2.1 Погорелов А.В. «Геометрия 7 - 11», № 46*
Постройте треугольник, если заданы: сторона, прилежащий к ней угол и сумма двух других сторон.
| Деятельность учителя | Деятельность учащихся |
ЭТАП. АНАЛИЗ ЗАДАЧИ С чего начинаем работу над задачей на построение? С чего начинаем анализ задачи?
 Каким методом будем решать задачу? (т.к. к моменту решения этой задачи уже были задачи, решаемые другим методом, то данный вопрос правомерен).
Выделите вспомогательный треугольник. Если построим вспомогательный треугольник, то какие вершины искомого треугольника будут определены, а какие останется построить? Итак, какую точку выберем за искомую? Что делаем дальше при анализе задачи?
Назовите условия, которым удовлетворяет искомая точка В.
Какой вывод делаем из выделенных условий? Назовите эти фигуры.
Итак, назовите план построения. 1. ΔАВ1С – вспомогательный 2. т.В: В  р; В р; В  АВ1 АВ1 В = р ∩ АВ1 |
С анализа задачи.
Предположим, что задача решена, делаем чертёж и наносим данные на чертёж.
Методом вспомогательного треугольника, т.к. из рисунка видно, что можно построить ∆АВ1С по двум сторонам и углу между ними.

Будут определены вершины А и С, останется построить вершину В.
Точку В.
Выбираем два условия, которым должна удовлетворять искомая точка. Точка В лежит на луче АВ1 Т.к. точка В равноудалена от точек В1 и С, то т.В лежит на серединном перпендикуляре к стороне В1С. Определяем фигуры, на которых лежит искомая точка. т.В лежит на луче АВ1 т. В лежит на прямой, перпендикулярной к В1С. 1) Строим ∆АВ1С; 2) Строим серединный перпендикуляр к В1С; 3) Строим т. В. |
II ЭТАП. ПОСТРОЕНИЕ.
Дано:
Построение:
1) А = α
А = α
2) АС = b
АВ + ВС = s
3) р – серединный перпендикуляр к В1С
4)В: В = АВ1∩ р
5)∆АВС – искомый.
III.ЭТАП. ДОКАЗАТЕЛЬСТВО.
А = α (по построению 1)
АС = b (по построению 2)
АВ + ВС = ѕ (по построению 2,3,4)
Следовательно, по первому признаку ∆ АВС – искомый.
IV. ЭТАП. ИССЛЕДОВАНИЕ.
При всяких ли данных возможно решение?
Задача невозможна, если b ≥ ѕ, т.к. из неравенства треугольника мы знаем, что любая сторона треугольника меньше суммы двух других сторон, т.е. нет такого треугольника, у которого сумма двух сторон была бы меньше или равна третьей стороне.
Сколько существует решений?
В том случае, когда задача возможна, она имеет только одно решение, т.е. существует только один треугольник, удовлетворяющий требованиям задачи, т.к. пересечение перпендикуляра р с прямой В1С может быть только в одной точке.
2.2 Атанасян Л.С. «Геометрия 7 - 9», № 351.
Постройте треугольник по двум сторонам и высоте к третьей стороне.
| Деятельность учителя | Деятельность учащихся |
| 1.ЭТАП. АНАЛИЗ ЗАДАЧИ С чего начинаем работу над задачей на построение? С чего начинаем анализ задачи? A D
Каким методом будем решать задачу? (Есть ли треугольник, который можно построить?).
Если построим вспомогательный треугольник ВДС, то какие вершины искомого треугольника будут определены, а какие останется построить? Итак, какую точку выберем за искомую? Что делаем дальше при анализе задачи?
Назовите условия, которым удовлетворяет искомая точка А.
Какой вывод делаем из выделенных условий? Назовите эти фигуры.
Итак, назовите план построения. ΔВДС – вспомогательный т.А: А  СД; А СД; А  окр.(В; с) окр.(В; с)
|
С анализа задачи.
Предполагаем задачу решенной, делаем чертёж и наносим данные на чертёж.
Методом вспомогательного треугольника, т.к. из рисунка видно, что можно построить прямоугольный треугольник ВДС по гипотенузе и катету.
Будут определены вершины В и С, останется построить вершину А.
Точку А.
Выбираем два условия, которым должна удовлетворять искомая точка. точка А лежит на луче ДС точка A отстоит от т.В на расстояние с.
Нужно определить фигуры, на которых лежит искомая точка А.
прямая ДС окружность (В; с)
Строим ∆ВДС Строим точку А. |
II. ЭТАП. ПОСТРОЕНИЕ.
Дано:
Построение
∆ВДС:
1)строим произвольную прямую n
2)строим m – перпендикуляр к n
m ∩ n = Д
3) строим ДВ = h
4) строим т.С: С принадлежит n
С принадлежит окр.(В; а)
5) строим т.А:
А принадлежит ДС
А принадлежит окр.(В; с)
III.ЭТАП. ДОКАЗАТЕЛЬСТВО.
ВД = h (по построению 1 - 3)
ВС = а (по построению 4)
АВ = с ( по построению 5)
Значит, ∆АВС – искомый.
IV ЭТАП. ИССЛЕДОВАНИЕ.
1.Вспомогательный треугольник строится по гипотенузе а и катету h, значит, его всегда можно построить при условии, что катет меньше гипотенузы, если пренебречь положением треугольника на плоскости, то такой треугольник единственный.
2. Точку А можно построить, при условии, что сh. При этом условии окр.(В;с) пересекает прямую ДС в двух точках А и А1.
3. Таким образом задача имеет два различных решения.
2.3 Шарыгин И.Ф. «Геометрия 7- 9» № 20 п. 6.2
Постройте трапецию по четырём её сторонам.
| Деятельность учителя | Деятельность ученика |
| 1.ЭТАП. АНАЛИЗ ЗАДАЧИ Какого вида эта задача? С чего начинаем решать задачу на построение? С чего начинаем анализ задачи?
Можете ли вы сказать каким методом будем решать задачу? Выполним следующее дополнительное построение: через вершину В проведём прямую ║ СД. Какой теперь метод выберем?
Если построим вспомогательный треугольник ВДС, то какие вершины искомой трапеции будут определены, а какие останется построить? Итак, какие точки выберем за искомые? Что делаем дальше при анализе задачи?
Назовите эти условия .
Какой вывод делаем из выделенных условий?
Итак, назовите план построения. ΔАВК – вспомогательный С: ВС || АК; ВС = b С  окр.(В;в) окр.(В;в) 3. Д: Д АК, АД = d, АК, АД = d,
Д окр. (А;d) окр. (А;d)
|
Задача на построение. С анализа условия задачи.
Предположим, что задача решена, делаем чертёж и наносим на него все данные задачи.
…
Метод вспомогательного треугольника. Можно построить треугольник АВК по трём сторонам, т.к. ВК = СД = с, т.к. ВСДК – параллелограмм.
Будут определены вершины А и В, останется построить вершины С и Д. Точки С и Д.
Для каждой искомой точки определяем два условия, которым она удовлетворяет.
т.С: ВС ║ АД; ВС = b т.С принадлежит окр. (В; b) т.Д: Д принадлежит АК; АД = d Д принадлежит окр.(А; d)
т.С принадлежит прямой ВС ║ АД С принадлежит окр.(В; b) т.Д лежит на прямой АК = d – b т.Д принадлежит окр.(А; d)
строим ∆АВК ВС ║ АК, ВС = b АД = d Трапеция АВСД – искомая. |
II.ЭТАП. ПОСТРОЕНИЕ
∆АВК:
Строим произвольную прямую m , отмечаем т.А
АК = d – b
АВ = а
КВ = с
Строим через т.В прямую k ║ m
Строим т.С: С принадлежит k, С принадлежит окр.(В; b)
Строим т.Д: Д принадлежит АК, Д принадлежит окр.(А; d)
АВСД – искомая трапеция.
III.ЭТАП.ДОКАЗАТЕЛЬСТВО.
АВ = а (по построению 3)
ДС = с (по построению 4, т.к. ВК = ДС по свойству параллелограмма)
ВС = b (по построению 6)
АД = d (по построению 7)
IV.ЭТАП.ИССЛЕДОВАНИЕ.
При любых заданных отрезках задача имеет единственное решение.
Заключение.
Задачи на построение являются важным средством формирования у учащихся геометрических представлений в целом. В процессе геометрических построений учащиеся в практическом плане знакомятся со свойствами геометрических фигур и отношений, учатся пользоваться чертежными инструментами, приобретают графические навыки. В правильности многих математических утверждений в большинстве случаев школьники убеждаются также в процессе геометрических построений.
«Решить задачу на построение – это значит, свести её к последовательному выполнению множества простейших построений».[3, 289]
Однако, на практике расчленение каждой задачи на простейшие построения нецелесообразно. Обычно сводят построение искомой фигуры к основным построениям; способы решения таких задач приводятся в школьных учебниках геометрии.
Поскольку задания на построения составляют базу для работы, развивающей навыки построения фигур, способствующей формированию умения читать и понимать чертеж, устанавливать связи между его частями, то недостаточность таких заданий обусловливает плохое развитие пространственного мышления ученика, низкий уровень его графической культуры. Эти недостатки не позволяют ученику эффективно изучать те разделы математики, где самостоятельно и хорошо понятая интерпретация является важным моментом, которого иногда не хватает школьнику при изучении математики.
До сих пор для многих учителей характерна недооценка роли задач на построение, в которых формируются умения и навыки построения с чертёжными инструментами, где эти умения являются решающими для развития пространственного мышления ребенка.
Для решения задачи на развитие пространственного мышления необходимо методически реализовать и поддержать содержательно транзитивную связь:
Требования к математической подготовке учащихся общеобразовательной школы предполагают, что в результате изучения курса геометрии(VII – IX кл.) все учащиеся должны овладеть умениями выполнять основные построения циркулем и линейкой, решать несложные комбинированные задачи, сводящиеся к выполнению основных построений. При этом вопрос о существовании и количестве решений не ставится и задача считается решённой, если указана последовательность выполняемых операций и доказано, что получаемая фигура удовлетворяет условию задачи. Количество выделяемого времени на изучение вопроса «Геометрические построения», соответствуют предъявленным требованиям – это 12-14 часов в 7 классе и эпизодические встречи во всех остальных.
Методика обучения учащихся решению задач на построение методом подобия
Построение треугольника подобного данному, при заданном коэффициенте подобия называется подобным преобразованием многоугольника.
Общий метод такого преобразования состоит в следующем: пользуясь некоторыми данными задачи, строят фигуру подобную искомой, а затем переходят к искомой. Этот метод удобен тогда, когда только одна данная величина есть длина, а остальные величины – или углы, или отношения линий.
При обучении решению задач на построение методом подобия полезно предложить учащимся упражнения на формирование отдельных этапов схемы (подготовительные упражнения).
Каких данных достаточно, чтобы построить треугольник, подобный данному?
На какой прямой расположены точки, гомотетичные точкам данной прямой, если данная прямая: а) не проходит через центр гомотетии, б) проходит через центр гомотетии?
Как построить фигуру, гомотетичную данной, если заданы центр гомотетии и точка искомой прямой, а данная прямая не проходит через центр гомотетии?
а) Дан угол АВС, точка К внутри него, прямая а. Построить точку К1, гомотетичную точке К относительно центра В и лежащую на прямой а.
б) Дан угол АВС, треугольник МДК и прямая а. Построить треугольник М1Д1К1, гомотетичный треугольнику МДК относительно центра В, чтобы вершина К1 лежала на прямой а.
Построить треугольник, подобный данному, если известны:
а) стороны (АВ,АС,ВС)
б) медиана
в) биссектриса
г) высота искомого треугольника.
Обучение полезно начинать с решения опорных задач.
Построить треугольник, подобный некоторому треугольнику, если известно: а) отношение двух сторон и угол между ними, б) два угла.
Построить отрезок х, чтобы , где а, в ,с длины данных отрезков.
Все задачи на построение, решаемые методом подобия, можно разделить на две группы. К первой группе относятся задачи, где требуется одну фигуру вписать в другую. В общем случае мы строим фигуру, подобную искомой, удовлетворяющую части условий. Дальнейший анализ ведем по схеме ТУФ (точка, условие, фигура), от фигуры переходим к точке.

Рассмотрим их на примере решения двух задач.
Задача 1. В данный равносторонний треугольник впишите другой равносторонний треугольник, чтобы стороны его были перпендикулярны сторонам данного треугольника.
Начнем решение задачи с ее анализа. Предположим, что задача решена, сделаем чертеж и нанесем на него все данные.
А
С

Очень трудно подобрать точки Д и М так, чтобы третья вершина – точка К – лежала бы на стороне ВС. Построим равносторонний треугольник, стороны которого перпендикулярны сторонам треугольника АВС, у которого две вершины лежат на сторонах треугольника АВС. Для этого достаточно взять какую – то точку Д1 на стороне АВ, из нее опустить перпендикуляр на сторону АС, получим точку М1; Д1М1 – сторона равностороннего треугольника, построим третью его вершину – точку К1.
Как получить из треугольника М1Д1К1 треугольник МДК, чтобы вершина К оказалась на прямой а? нужно построить треугольник гомотетичный треугольнику М1Д1К1 относительно центра А. построим точку К как пересечение прямых АК1 и ВС, затем через нее проведем прямые параллельные сторонам треугольника М1Д1К1, на пересечении этих прямых со сторонами АВ и АС получим точки Д и М.
Построение:
1. строим треугольник М1Д1К1; Д1  АВ,
АВ,
М1  АС, Д1К1 = М1Д1
АС, Д1К1 = М1Д1
2.строим точку К: К = АК1 ВС
строим КД: КД || К1Д1; Д  АВ
АВ
строим ДМ: ДМ  АС; М
АС; М  АС
АС
треугольник МДК – искомый.
Доказательство: треугольник МДК – равносторонний, так как он гомотетичен равностороннему треугольнику М1Д1К1; ДМ  АС (построение 4), МК
АС (построение 4), МК  ВС, т.к. КМС = 90º - 60 º = 30 º, а С = 60 º, аналогично, ДК
ВС, т.к. КМС = 90º - 60 º = 30 º, а С = 60 º, аналогично, ДК  АВ; все три вершины лежат на сторонах треугольника АВС.
АВ; все три вершины лежат на сторонах треугольника АВС.
Перейдем ко второй группе задач, решаемые построением фигуры подобной данной, а затем и самой фигуры. Для этого достаточно знать отношения двух сторон и угол между ними, или два угла, или отношения трех сторон. Запомним, что углы и отношения определяемых элементов позволяют построить фигуру, подобную искомой, а на коэффициент подобия указывает какая – то конкретная длина. Это может быть высота, сторона, медиана, периметр, сумма двух сторон и т.д.
Задача 2. Постройте треугольник по углу, противолежащей стороне и отношению длин двух других сторон. (m:n)
А нализ. Пусть задача решена. Сделаем чертеж и нанесем на него все данные.
Проведем прямую параллельно одной из сторон треугольника АВС, например, стороне АВ, получим точки пересечения со сторонами АС и ВС – точки А1 и В1. Обозначим А1В1 = n, А1С = m, т.к. m:n = в:c по теореме Фалеса. Треугольник А1В1С подобен треугольнику АВС по отношению двух сторон и углу между ними. За коэффициент подобия можно взять отношение любых соответствующих элементов, обычно этот выбор связан с условием, которое еще не было использовано. В нашей задаче еще дана сторона ВС. Значит, за коэффициент подобия можно взять отношение . Задача свелась к построению треугольника АВС, подобного треугольнику А1В1С, если известна сторона ВС, равная а. Для этого нужно увеличить сторону В1С до размера а, для этого от С на продолжении СВ1 отложим отрезок, равный а, получим точку В. Через точку В проведем прямую, параллельную А1В1 до пересечения с А1С, получим точку А.
Построение:

треугольник А1В1С; А1 = ; А1В1 = n, А1С = m
B: В  В1С, ВС = а
В1С, ВС = а
А: АВ || А1В1, А  СА1
СА1
треугольник АВС – искомый.
Доказательство проведено во время анализа.
Литература:
Базовые методики обучения математике: Учеб. пособие для студентов физико – математических факультетов пединститутов и педуниверситетов / Малова И.Е., Горохова С.К., Малинникова Н.А., Пуличева Г.Е., Скоробогатая М.А., Яцковская Г.А. – Брянск: Издательство БГПУ, 2001.
Белошистая А.В. Задачи на построение в школьном курсе геометрии //Математика в школе. № 9, 2002.
Геометрия: Учеб. Для 7-9 кл. сред. шк. / Л.С.Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др. – 2-е изд. – М.: Просвещение, 1991.
Киселев А.П. Элементарная геометрия. Книга для учителя. – М.: Просвещение, 1980.
Методические рекомендации по обучению учащихся решению задач на построение в школьном курсе геометрии / И.Е. Малова – Брянск, 1989.
Погорелов А.В. Геометрия: Учеб. Для 7-11 кл. сред.шк. – 4-е изд. – М.: Просвещение, 1993.
Шарыгин И.Ф. Геометрия. 7-9 кл.: Учеб. для общеобразоват. учеб. завед. – 5-е изд. – М.: Дрофа, 2001.
31





 .В.Блудов предлагает ученикам данные отрезки выбрать примерно в таком же отношении как они изображены на доске.
.В.Блудов предлагает ученикам данные отрезки выбрать примерно в таком же отношении как они изображены на доске. 











 : С
: С




















