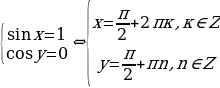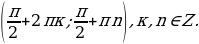МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Хакасский государственный университет им. Н.Ф. Катанова»
(ФГБОУ ВО «ХГУ им. Н.Ф. Катанова»)
Институт естественных наук и математики
Кафедра математики, физики и информационных технологий
Направление подготовки 44.03.05 – Педагогическое образование
Профили Математика и Физика
МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ И ИХ СИСТЕМ
Реферат
Выполнила: Токоякова
Кристина Владимировна
Группа МФ-41
Курс 4
Форма обучения очная
Абакан 2023
Оглавление
Введение 3
1. Понятие «тригонометрическое уравнение» и понятия, с ним связанные 5
2. Методы решения тригонометрических уравнений 7
2.1. Метод замены переменной (универсальная подстановка) 8
2.2. Метод разложения на множители 12
2.3. Метод решения однородных тригонометрических уравнений 13
2.4. Метод введения вспомогательного аргумента 16
3. Отбор корней в тригонометрических уравнениях, принадлежащих указанному числовому промежутку 18
4. Решение систем тригонометрических уравнений 23
Заключение 27
Список литературы 28
Введение
«Уравнения для меня важнее,
потому что политика – для настоящего,
а уравнения для вечности»
Альберт Эйнштейн
В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд» [8].
В настоящее время изучению тригонометрических функций и тригонометрических уравнений уделяется большое внимание в школьном курсе алгебры и начал анализа.
Актуальность состоит в том, что тригонометрические уравнения одна из самых сложных тем в школьном курсе. Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Тригонометрические уравнения и их системы из года в год встречаются среди заданий ЕГЭ для 11 класса. Именно задачи такого типа развивают сообразительность, смекалку, догадливость, находчивость в учениках. Самое важное отличие тригонометрических уравнений от алгебраических состоит в том, что в алгебраических уравнениях имеют конечное число корней, а в тригонометрических – бесконечное.
Актуальность темы – систематизация знаний о различных методах решения тригонометрических уравнений и их систем.
Цель курсовой работы заключается в овладении методами решения основных типов тригонометрических уравнений и их систем.
Для осуществления обозначенной цели служат следующие задачи:
Изучить понятие «тригонометрическое уравнение» и понятия, с ним связанные;
Рассмотреть отбор корней тригонометрических уравнений, принадлежащих указанному числовому промежутку;
Изучить методы решения тригонометрических уравнений и их систем.
Объектом исследования являются тригонометрические уравнения и их системы.
Предмет исследования – изучение методов решения тригонометрических уравнений и их систем.
Понятие «тригонометрическое уравнение» и понятия, с ним связанные
Тригонометрические уравнения - обязательная тема любого экзамена по математике. Основные приемы их решения - замена переменной и разложение на множители. Для успешного решения тригонометрических уравнений нужно хорошо знать тригонометрические формулы, причем не только основные, но и дополнительные (преобразование суммы тригонометрических функций в произведение и произведения в сумму, формулы понижения степени и другие).
Определение 1.1. Тригонометрическим уравнением называется уравнение вида
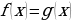 , (1.1)
, (1.1)
где 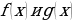 – тригонометрические выражения.
– тригонометрические выражения.
Замечание. Областью допустимых значений (ОДЗ) тригонометрического уравнения (1.1) называется пересечение областей (множеств) определения функций 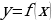 и
и  , т.е.
, т.е. 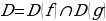 .
.
Всякое число 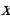 , взятое из ОДЗ уравнения (1.1), называется допустимым значением данного уравнения.
, взятое из ОДЗ уравнения (1.1), называется допустимым значением данного уравнения.
Замечание. Число  , взятое из ОДЗ уравнения (1.1), называется решением или корнем данного уравнения, если при подстановке его вместо неизвестного
, взятое из ОДЗ уравнения (1.1), называется решением или корнем данного уравнения, если при подстановке его вместо неизвестного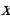 уравнение (1.1) превращается в верное числовое равенство
уравнение (1.1) превращается в верное числовое равенство  .
.
Решить уравнение 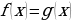 – это значит найти все корни или доказать, что это уравнение не имеет корней.
– это значит найти все корни или доказать, что это уравнение не имеет корней.
Из данного определения следует, что уравнение 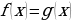 не имеет корней только в двух случаях:
не имеет корней только в двух случаях:
если ОДЗ уравнения есть пустое множество;
если ОДЗ уравнения есть непустое множество D, но ни для одного элемента  этого множества не выполняется числовое равенство
этого множества не выполняется числовое равенство  .
.
Замечание. Тригонометрические уравнения 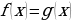 и
и 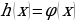 называются равносильными или эквивалентными, если любой корень первого уравнения является корнем второго уравнения, а любой корень второго уравнения – корнем первого уравнения.
называются равносильными или эквивалентными, если любой корень первого уравнения является корнем второго уравнения, а любой корень второго уравнения – корнем первого уравнения.
Из данного определения, в частности, следует, что если каждое из этих уравнений не имеет корней, то рассматриваемые уравнения также будут равносильными.
Кроме того, тригонометрические уравнения 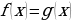 и
и 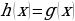
называются равносильными на множестве 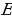 , если любой корень первого уравнения, принадлежащий множеству
, если любой корень первого уравнения, принадлежащий множеству 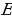 , является корнем второго уравнения и, наоборот, любой корень второго уравнения, принадлежащий множеству Е, является корнем первого уравнения.
, является корнем второго уравнения и, наоборот, любой корень второго уравнения, принадлежащий множеству Е, является корнем первого уравнения.
Замена одного уравнения другим, ему равносильным называется равносильным переходом, который обозначают так:  .
.
Замечание. Тригонометрические уравнения 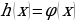 называется следствием тригонометрического уравнения
называется следствием тригонометрического уравнения 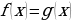 , если любой корень второго уравнения является корнем первого уравнения.
, если любой корень второго уравнения является корнем первого уравнения.
Замена одного тригонометрического уравнения его следствием обозначается так:  .
.
Если уравнение 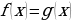 не имеет корней, то любое уравнение
не имеет корней, то любое уравнение 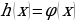 есть его следствие.
есть его следствие.
Из последнего замечания также очевидно, что если 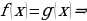
 , то множество
, то множество 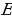 решений уравнения
решений уравнения 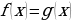 является подмножеством
является подмножеством 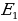 решений уравнения
решений уравнения 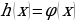 , т.е.
, т.е. 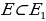 [8].
[8].
Методы решения тригонометрических уравнений
Для решения тригонометрических уравнений используется четыре основных методов решения. Все эти методы своеобразно превосходны и применимы для различных видов тригонометрических уравнений. Основная задача при решении тригонометрического уравнения заключается в том, чтобы правильно преобразовать его, свести к какому-нибудь наиболее стандартному виду, подобрать оптимальный способ решения для определенного случая. То есть, в большинстве своем, главная проблема заключается в том, что уравнения надо обязательно сначала привести к какому-то виду, прежде чем применить необходимый метод решения.
Итак, рассмотрим 4 основных методов решения тригонометрических уравнений.
Метод замены переменной (универсальная подстановка)
Суть метода заключается в том, чтобы данное тригонометрическое уравнение свести к уравнению вида
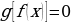 (2.1.1)
(2.1.1)
где  – одна из тригонометрических функций или тригонометрическое выражение, содержащее аргумент, а
– одна из тригонометрических функций или тригонометрическое выражение, содержащее аргумент, а 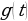 – рациональная, дробно-рациональная или иная другая элементарная функция. Сначала делается замена
– рациональная, дробно-рациональная или иная другая элементарная функция. Сначала делается замена  и решается алгебраическое (рациональное, иррациональное и т.д.) уравнение
и решается алгебраическое (рациональное, иррациональное и т.д.) уравнение
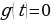 (2.1.2)
(2.1.2)
Уравнение (2.1.2) может не иметь решений, тогда и уравнение (2.1.1) также не имеет решений. Если уравнение (2.1.2) имеет конечное число решений  , то уравнение (2.1.1) будет равносильно совокупности уравнений
, то уравнение (2.1.1) будет равносильно совокупности уравнений
 (2.1.3)
(2.1.3)
Множество всех полученных решений совокупности (2.1.3) простейших тригонометрических уравнений является множеством решений исходного тригонометрического уравнения (2.1.1).
Пример. Решить уравнение
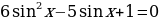
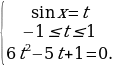
Далее находим корни квадратного уравнения 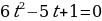 :
:
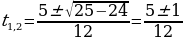 ;
;
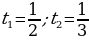
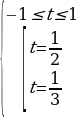
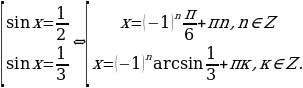
Ответ: 
Теперь рассмотрим универсальную подстановку.
Ранее рассматривали подстановки, которые сводили тригонометрические уравнения типа  и подобные им к решению обычного рационального алгебраического уравнения. Здесь же будем находить решения уравнения вида
и подобные им к решению обычного рационального алгебраического уравнения. Здесь же будем находить решения уравнения вида
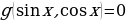 (2.1.4)
(2.1.4)
где 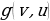 – дробно-рациональная функция переменных
– дробно-рациональная функция переменных 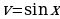 ,
, 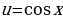 .
.
Подстановка вида  , называемая универсальной тригонометрической подстановкой позволяет тригонометрическое уравнение (2.1.4) превратить в дробно-рациональное уравнение вида
, называемая универсальной тригонометрической подстановкой позволяет тригонометрическое уравнение (2.1.4) превратить в дробно-рациональное уравнение вида
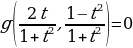 (2.1.5)
(2.1.5)
Действительно, по формулам половинных углов найдем:

(2.1.6)
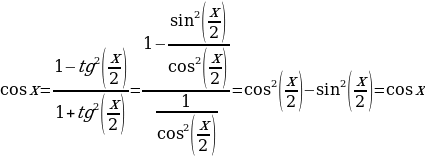
Вычислив корни  , уравнения (2.1.5), получим простейшие тригонометрические уравнения
, уравнения (2.1.5), получим простейшие тригонометрические уравнения  , решения которых находятся по формулам
, решения которых находятся по формулам 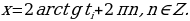 .
.
Замечание. Хотя указанный способ решения тригонометрических уравнений довольно прост, он не всегда рационален, поскольку подстановка  приводит к довольно громоздким вычислениям. Кроме того, замена левых частей формул (2.1.6) (тригонометрических функций
приводит к довольно громоздким вычислениям. Кроме того, замена левых частей формул (2.1.6) (тригонометрических функций 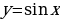 и
и 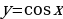 ) их правыми частями приводит к возможной потере корней исходного уравнения (2.1.5). Поэтому необходимо еще проверить, будут ли значения
) их правыми частями приводит к возможной потере корней исходного уравнения (2.1.5). Поэтому необходимо еще проверить, будут ли значения 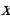 , при которых функция
, при которых функция  не определена, т.е.
не определена, т.е.
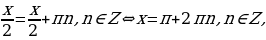 корнями исходного уравнения [12].
корнями исходного уравнения [12].
Пример. Решить уравнение
 .
.
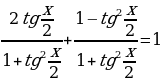
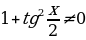
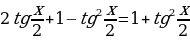
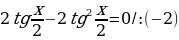
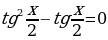
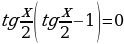
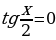
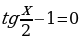
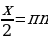
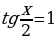

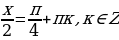
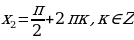
Ответ: 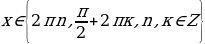 .
.
Метод разложения на множители
Суть метода заключается в следующем: если левая часть 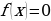 , где
, где 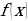 – тригонометрическое выражение (функция), зависящее от одного аргумента, может быть представлена в виде произведения
– тригонометрическое выражение (функция), зависящее от одного аргумента, может быть представлена в виде произведения 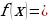
 , то корнями данного уравнения будут все решения совокупности уравнений
, то корнями данного уравнения будут все решения совокупности уравнений
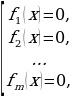
принадлежащие области определения функции 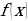 . Отметим, что областью определения функции
. Отметим, что областью определения функции 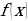 называется множество
называется множество 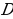 значений переменной
значений переменной 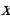 , при которых одновременно определены функции
, при которых одновременно определены функции 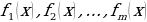 , т.е. множество
, т.е. множество 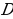 есть пересечение множеств
есть пересечение множеств 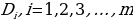 :
:
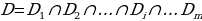 [8].
[8].
Пример. Решить уравнение
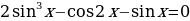


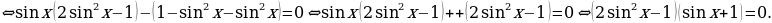

Ответ: 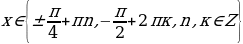 .
.
Метод решения однородных тригонометрических уравнений
Однородным относительно синуса и косинуса называют уравнения вида
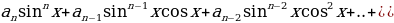
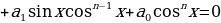 (2.3.1)
(2.3.1)
Если 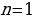 , то уравнение (2.3.1) принимает вид
, то уравнение (2.3.1) принимает вид 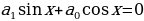 и называется однородным уравнением первого порядка.
и называется однородным уравнением первого порядка.
При 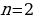 из уравнения (2.3.1) получаем уравнение
из уравнения (2.3.1) получаем уравнение 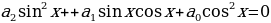 , которое называется однородным уравнением второго порядка, а при
, которое называется однородным уравнением второго порядка, а при 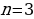 – уравнение
– уравнение 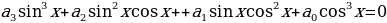 , которое называется однородным уравнением третьего порядка.
, которое называется однородным уравнением третьего порядка.
Общий метод решения основан на сведении таких уравнений к обычным рациональным уравнениям с помощью рационализирующей подстановки 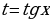 . Однако следует помнить, что введение подстановки
. Однако следует помнить, что введение подстановки 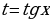 приводит к сужению ОДЗ исходного уравнения и, как следствие, возможно потеря корней исходного уравнения. Поэтому алгоритм решения однородных уравнений (2.3.1) будет состоять в следующем.
приводит к сужению ОДЗ исходного уравнения и, как следствие, возможно потеря корней исходного уравнения. Поэтому алгоритм решения однородных уравнений (2.3.1) будет состоять в следующем.
Сначала проверяем, не являются ли корни уравнения 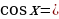
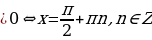 , корнями исходного уравнения. Очевидно, что это будет выполняться при
, корнями исходного уравнения. Очевидно, что это будет выполняться при  .
.
Разделим обе части уравнения (2.3.1) на  .
.
В результате приходим к равносильному уравнению 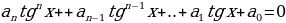 , которое заменой
, которое заменой 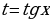 сводится к рациональному решению
сводится к рациональному решению  .
.
Находим решения 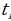 полученного рационального уравнения. Если рациональное уравнение решений не имеет, то и исходное тригонометрическое уравнение (2.3.1) тоже решений не имеет. В противном случае получаем простейшие тригонометрические уравнения
полученного рационального уравнения. Если рациональное уравнение решений не имеет, то и исходное тригонометрическое уравнение (2.3.1) тоже решений не имеет. В противном случае получаем простейшие тригонометрические уравнения 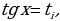
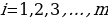 , из решения которых находим
, из решения которых находим 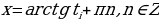 .
.
Замечание. В ряде случаев к уравнению вида (2.3.1) сводятся и более общие уравнения, например:
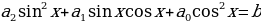 (2.3.2)
(2.3.2)
где b – произвольное число. Действительно, представив уравнение (2.3.2) как 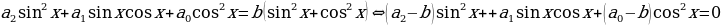 , получаем однородное уравнение
, получаем однородное уравнение  , где
, где 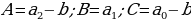 [8].
[8].
Пример. Решить уравнение
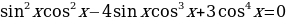
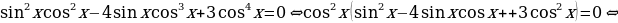

Найдем корни уравнения  .
.
Далее получим корни уравнения  .
.

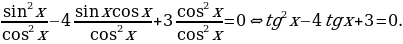
Замена 
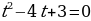
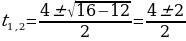
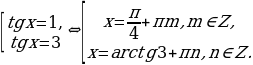

Метод введения вспомогательного аргумента
Рассмотрим линейное относительно синуса и косинуса тригонометрическое уравнение
 , (2.4.1)
, (2.4.1)
где 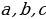 – произвольные числа, причем
– произвольные числа, причем  . Одним из способов решения данного уравнения является сведение его к решению равносильной системы рациональных уравнений с помощью подстановки
. Одним из способов решения данного уравнения является сведение его к решению равносильной системы рациональных уравнений с помощью подстановки 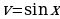 ,
, 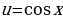 ,
, 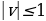 ,
, 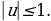 Однако такой подход не всегда эффективен, поскольку приводит к увеличению объема вычислений. Рациональнее использовать так называемый метод введения вспомогательного аргумента.
Однако такой подход не всегда эффективен, поскольку приводит к увеличению объема вычислений. Рациональнее использовать так называемый метод введения вспомогательного аргумента.
Суть метода заключается в следующем. Поскольку уравнение (2.4.1) рассматривается при условии, что  , то обе его части можно разделить на число
, то обе его части можно разделить на число 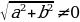 . В результате получаем равносильное уравнение
. В результате получаем равносильное уравнение 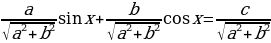 . Очевидно, что существует некоторый угол
. Очевидно, что существует некоторый угол  , для которого
, для которого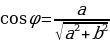 ;
; 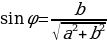 .
.
Тогда последнее уравнение принимает вид 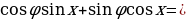
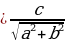 .
.
Видно, что тригонометрическое выражение, стоящее в левой части уравнения, есть синусы суммы двух углов: 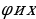 , т.е.
, т.е. 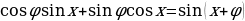 . Следовательно,
. Следовательно, 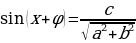 . Если
. Если
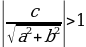 , то полученное уравнение, а следовательно, и исходное уравнение решений не имеет. Если
, то полученное уравнение, а следовательно, и исходное уравнение решений не имеет. Если 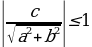 , то по формуле корней для простейшего тригонометрического уравнения получаем
, то по формуле корней для простейшего тригонометрического уравнения получаем

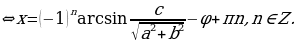
Еще раз подчеркнем, что угол  находят из системы выражений
находят из системы выражений 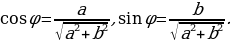 .
.
При этом, поскольку 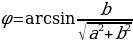 и
и  , условие
, условие
 и
и 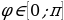 может быть выполнено только при
может быть выполнено только при 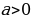 [8].
[8].
Пример. Решить уравнение


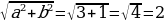
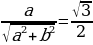 ;
; 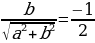 ;
; 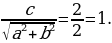
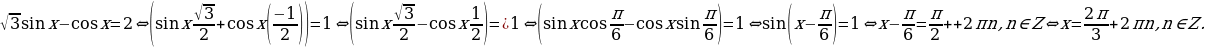
Ответ: 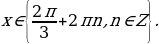
3. Отбор корней в тригонометрических уравнениях, принадлежащих указанному числовому промежутку
При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим.
Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.
Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.
Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения [8].
Рассмотрим все эти способы на одном примере.
Пример. a) Решите уравнение 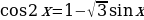 ;
;
б) Укажите корни этого уравнения, принадлежащие отрезку 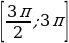 .
.
Решение:
а)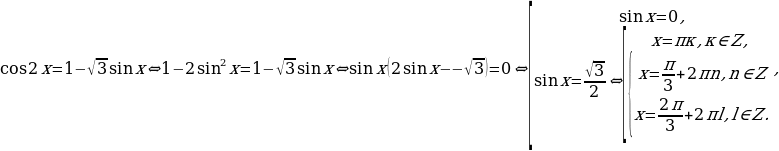
б) Рассмотрим три способа отбора корней данного уравнения, принадлежащих отрезку 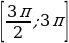 .
.
1 способ. Найдем корни, принадлежащие отрезку 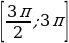 перебором по целочисленному параметру.
перебором по целочисленному параметру.
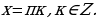
Очевидно, что при всех целых отрицательных 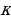 корни вида
корни вида 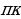 отрицательны и не принадлежат отрезку
отрицательны и не принадлежат отрезку 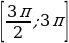 .
.
Если  , то
, то 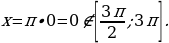
Если  , то
, то 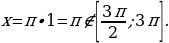
Если 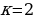 , то
, то 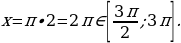
Если 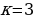 , то
, то 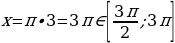 .
.
Если  , то
, то 
На этом переборе остановим, так как при всех целых 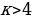 корни этой серии примают значения большие, чем
корни этой серии примают значения большие, чем 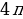 , и не принадлежат отрезку
, и не принадлежат отрезку 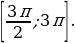
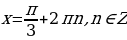
При всех целых отрицательных κ корни вида 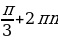 отрицательны и не принадлежат отрезку
отрицательны и не принадлежат отрезку 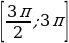 .
.
Если 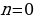 , то
, то 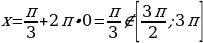 .
.
Если 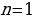 , то
, то 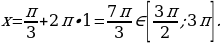
Если 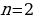 , то
, то  .
.
Перебор прекращен, так как при всех целых 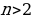 корни этой серии примают значения большие, чем
корни этой серии примают значения большие, чем  , и не принадлежат отрезку
, и не принадлежат отрезку 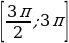 .
.
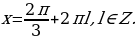
При всех целых отрицательных κ корни вида  отрицательны и не принадлежат отрезку
отрицательны и не принадлежат отрезку 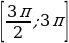 .
.
Если  , то
, то 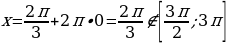 .
.
Если 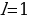 , то
, то 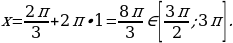
Если 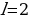 , то
, то 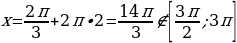 .
.
Перебор прекращен, так как при всех целых 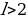 корни этой серии примают значения большие, чем
корни этой серии примают значения большие, чем 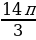 , и не принадлежат отрезку
, и не принадлежат отрезку 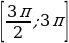 .
.
Итак, корни данного уравнения, принадлежащие отрезку 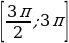 :
: 
2 способ. Найдем корни, принадлежащие отрезку 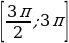 , решая двойное неравенство относительно целочисленного параметра.
, решая двойное неравенство относительно целочисленного параметра.
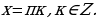
По условию 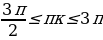 , т.е.
, т.е. 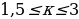 .
.
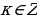 , следовательно,
, следовательно, 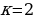 или
или 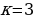 .
.
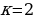 ,
, 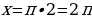 .
.
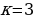 ,
, 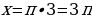 .
.
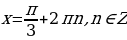 .
.
По условию 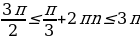 , т.е.
, т.е. 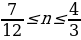 .
.
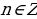 , следовательно,
, следовательно, 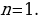
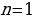 ,
,  .
.
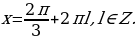
По условию 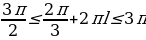 , т.е.
, т.е.  .
.
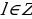 , следовательно,
, следовательно, 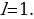
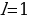 ,
, 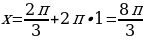 .
.
Корни данного уравнения, принадлежащие отрезку 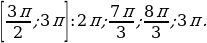
3 способ. Найдем корни, принадлежащие отрезку 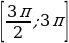 , с помощью единичной (тригонометрической) окружности.
, с помощью единичной (тригонометрической) окружности.
Построим единичную окружность. Отметим на окружности концы промежутка точки  и
и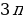 . Выделим на окружности отрезок (дугу)
. Выделим на окружности отрезок (дугу) 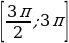 , обходя окружность против часовой стрелки от меньшего числа
, обходя окружность против часовой стрелки от меньшего числа  к большему числу
к большему числу 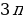 .
.

Дуга на рисунке выделена жирной линией, концы дуги — точки  и
и 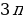 закрашены, так как эти числа входят в данный промежуток. Покажем на выделенной дуге точки, которые соответствуют корням данного уравнения (отмечены на рисунке большими закрашенными точками).
закрашены, так как эти числа входят в данный промежуток. Покажем на выделенной дуге точки, которые соответствуют корням данного уравнения (отмечены на рисунке большими закрашенными точками).
Вычислим значения корней, принадлежащих промежутку 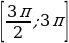 , двигаясь по дуге от корня к корню против часовой стрелки.
, двигаясь по дуге от корня к корню против часовой стрелки.
Получим следующие значения: 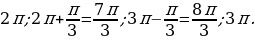
Корни данного уравнения, принадлежащие отрезку 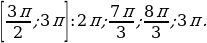
Ответ: а) 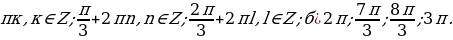
Решение систем тригонометрических уравнений
При решении систем тригонометрических уравнений используются те же подходы, что и при решении систем обычных алгебраических уравнений. Для простоты изложения ограничимся тригонометрическими системами с двумя неизвестными 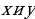 . Решения таких систем обычно записываются в виде упорядоченных пар
. Решения таких систем обычно записываются в виде упорядоченных пар 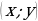 или в виде системы.
или в виде системы.
Итак, рассмотрим сначала систему тригонометрических уравнений
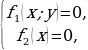 (4.1)
(4.1)
где 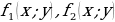 – тригонометрические функции двух неизвестных
– тригонометрические функции двух неизвестных 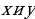 .
.
Для системы (4.1) справедливы следующие утверждения о равносильных преобразованиях.
При изменении порядка следования уравнений системы (4.1) вновь полученная система равносильна заданной.
При замене одного из уравнений системы (4.1) равносильным уравнением вновь полученная система равносильна заданной.
Если в одном из уравнений системы (4.1) одно из неизвестных, например 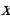 , выразить через другое неизвестное
, выразить через другое неизвестное 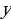 и подставить это выражение вместо
и подставить это выражение вместо 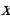 в другое уравнение, то получим систему уравнений, равносильную заданной.
в другое уравнение, то получим систему уравнений, равносильную заданной.
Если первое уравнение системы (4.1) заменить тригонометрическим уравнением, равным сумме первого уравнения, умноженного на некоторое число  , и второго уравнения, умноженного на некоторое действительное число
, и второго уравнения, умноженного на некоторое действительное число  , то полученная система тригонометрических уравнений будет равносильна заданной, т.е.
, то полученная система тригонометрических уравнений будет равносильна заданной, т.е.
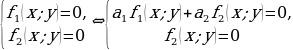
Из утверждения 4 вытекают два важных следствия.
Следствие 1. Если первое уравнение системы тригонометрических уравнений (4.1) заменить суммой или разностью первого и второго уравнений системы, то вновь полученная система тригонометрических уравнений будет равносильна заданной.
Следствие 2. Если первое уравнение системы тригонометрических уравнений (4.1) равносильно совокупности уравнений, т.е.

То система (4.1) равносильна совокупности следующих систем уравнений:
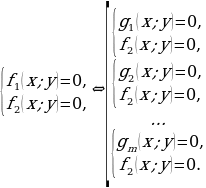
Для преобразования уравнений системы (4.1) используются все те методы решения, которые были рассмотрены выше. Приведем примеры использования методов подстановки, разложения на множители и ряда других [8].
Рассмотрим некоторые примеры.
Пример 1. Решить систему уравнений.
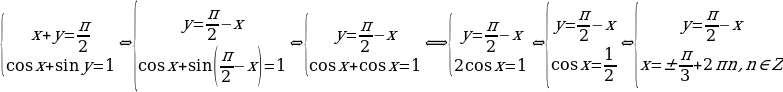
Если 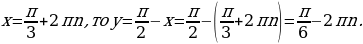
Если 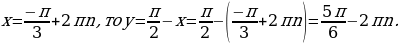
Ответ: 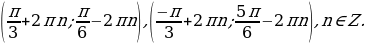
Пример 2. Решить систему.
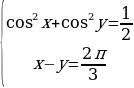
Решение. Сначала преобразуем первое уравнение системы:

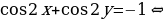
 .
.
Таким образом, система равносильна следующей системе:
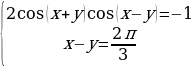
Подставляем 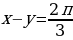 в первое уравнение:
в первое уравнение:
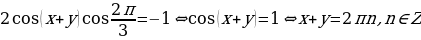 .
.
В результате приходим к системе:
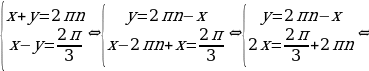
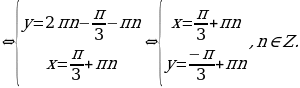
Ответ: 
Пример 3. Решить систему
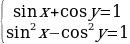
Решение. Замена 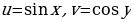 приводит к алгебраической системе относительно u и v:
приводит к алгебраической системе относительно u и v:

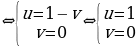
Обратная замена приводит к двум простейшим тригонометрическим уравнениям:
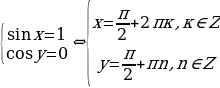
Ответ: 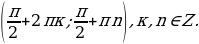
Заключение
В реферате рассмотрены необходимые для овладения навыков решения тригонометрических уравнений и их систем теоретические основы. Изучена история тригонометрии, изучены понятие «тригонометрическое уравнение» и понятия с ним связанные, выделены четыре метода решения тригонометрических уравнений: метод замены переменной (универсальная подстановка), метод разложения на множители, метод решения однородных тригонометрических уравнений, метод введения вспомогательного аргумента. Рассмотрели отбор корней в тригонометрических уравнениях, принадлежащих указанному числовому промежутку. Теоритические сведения были проиллюстрированы примерами.
Считаю, что цель и задачи были достигнуты.
Список литературы
Бескин Н. М. Вопросы тригонометрии и ее преподавания /
Н. М. Бескин. - М.: Учпедгиз, 1950. – 140 с. – Текст: непосредственный
Гешелин А.М. Избранные вопросы тригонометрии / А.М.Гешелин - М.: ОБЛОНО, 2019. – 194 c. – Текст: электронный
Карасев В.А. 12 уроков по тригонометрии / В.А. Карасев. - М.: Илекса, 2018. - 867 c. – Текст: электронный
Борзенко А. А. Виды тригонометрических уравнений и методы их решения / А. А. Борзенко // Научный альманах. – 2020. – № 11-2(73). – С. 14-19. –Тулемисова Д. З. Тригонометрические уравнения / Д. З. Тулемисова, Н. В. Суханова // Молодежь в мире науки : материалы IV внутривузовской студенческой научно-практической конференции, Сургут, 25 ноября 2016 года. – Сургут: Сургутский государственный педагогический университет, 2017. – С. 75-77. [Электронный ресурс]. – URL: https://elibrary.ru/item.asp?id=44545622
Хедырова Н. И. Системы тригонометрических уравнений / Н. И. Хедырова, С. А. Третьяков // Актуальные проблемы научного знания. Новые технологии ТЭК: Материалы III Международной научно-практической конференции, Сургут, 17–18 мая 2019 года / Ответственный редактор М.В. Баделина. – Сургут: Тюменский индустриальный университет, 2019. – С. 213-218. [Электронный ресурс]. – URL: https://elibrary.ru/item.asp?id=42413415
Никитина Е. А. Тригонометрические уравнения / Е. А. Никитина, Г. Х. Воистинова // Наука через призму времени. – 2020. – № 2(35). – С. 51-53. [Электронный ресурс]. – URL: https://elibrary.ru/item.asp?id=42367795
Старова О.А. Тригонометрия / О.А. Старова // Издательская группа «ОСНОВА». – 2012. – № 4(16). – Текст: электронный
Граськин С.С. Тригонометрия: теория и практика решения задач: учеб. Пособие / С.С. Граськин. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2009. – 325 с. – Текст: электронный
Контрольные вопросы
Что называется тригонометрическим уравнением?
Как расшифровывается ОДЗ?
Что значит решить уравнение 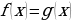 ?
?
В каких случаях уравнение 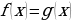 не имеет корней?
не имеет корней?
Какие четыре основных метода вы знаете для использования решения тригонометрических уравнения?
В чём заключается суть метода замены переменной?
В чём заключается суть метода разложения на множители?
Какого вида уравнения называют однородным относительно синуса и косинуса?
В чём состоит суть метода введения вспомогательного аргумента?
Какими следующими способами можно осуществлять отбор корней в тригонометрическом уравнении?
Какие подходы используются при решении систем тригонометрических уравнений?
Глоссарий
Тригонометрическое уравнение – это уравнение, в котором присутствуют тригонометрические функции (такие как синус, косинус, тангенс и др.) от неизвестной переменной.
Тригонометрические функции – математические функции, которые описываю отношения между сторонами и углами в прямоугольных треугольниках.
Синус – тригонометрическая функция, определяемая как отношение противоположной стороны к гипотенузе в прямоугольном треугольнике.
Косинус – тригонометрическая функция, определяемая как отношение прилежащей стороны к гипотенузе в прямоугольном треугольнике.
Тангенс – тригонометрическая функция, определяемая как отношение синуса к косинусу.
Котангенс – тригонометрическая функция, определяемая как отношение косинуса к синусу.
Система тригонометрических уравнений – набор уравнений, содержащих тригонометрические функции, такие как синус, косинус, тангенс и их обратные функции.
Тригонометрическая (единичная) окружность – окружность радиусом, равным одному и с центром в начале координат.







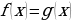 , (1.1)
, (1.1)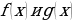 – тригонометрические выражения.
– тригонометрические выражения.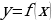 и
и  , т.е.
, т.е. 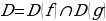 .
.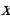 , взятое из ОДЗ уравнения (1.1), называется допустимым значением данного уравнения.
, взятое из ОДЗ уравнения (1.1), называется допустимым значением данного уравнения. , взятое из ОДЗ уравнения (1.1), называется решением или корнем данного уравнения, если при подстановке его вместо неизвестного
, взятое из ОДЗ уравнения (1.1), называется решением или корнем данного уравнения, если при подстановке его вместо неизвестного .
.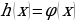 называются равносильными или эквивалентными, если любой корень первого уравнения является корнем второго уравнения, а любой корень второго уравнения – корнем первого уравнения.
называются равносильными или эквивалентными, если любой корень первого уравнения является корнем второго уравнения, а любой корень второго уравнения – корнем первого уравнения.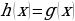
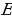 , если любой корень первого уравнения, принадлежащий множеству
, если любой корень первого уравнения, принадлежащий множеству  .
. .
.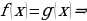
 , то множество
, то множество 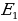 решений уравнения
решений уравнения 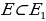 [8].
[8].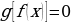 (2.1.1)
(2.1.1) – одна из тригонометрических функций или тригонометрическое выражение, содержащее аргумент, а
– одна из тригонометрических функций или тригонометрическое выражение, содержащее аргумент, а 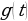 – рациональная, дробно-рациональная или иная другая элементарная функция. Сначала делается замена
– рациональная, дробно-рациональная или иная другая элементарная функция. Сначала делается замена 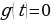 (2.1.2)
(2.1.2) , то уравнение (2.1.1) будет равносильно совокупности уравнений
, то уравнение (2.1.1) будет равносильно совокупности уравнений (2.1.3)
(2.1.3)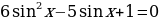
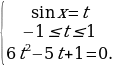
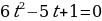 :
: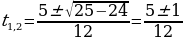 ;
;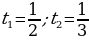
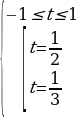
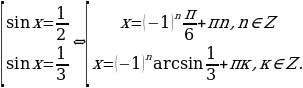

 и подобные им к решению обычного рационального алгебраического уравнения. Здесь же будем находить решения уравнения вида
и подобные им к решению обычного рационального алгебраического уравнения. Здесь же будем находить решения уравнения вида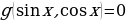 (2.1.4)
(2.1.4)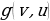 – дробно-рациональная функция переменных
– дробно-рациональная функция переменных 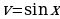 ,
, 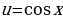 .
.  , называемая универсальной тригонометрической подстановкой позволяет тригонометрическое уравнение (2.1.4) превратить в дробно-рациональное уравнение вида
, называемая универсальной тригонометрической подстановкой позволяет тригонометрическое уравнение (2.1.4) превратить в дробно-рациональное уравнение вида 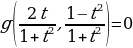 (2.1.5)
(2.1.5)
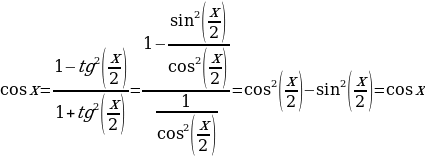
 , уравнения (2.1.5), получим простейшие тригонометрические уравнения
, уравнения (2.1.5), получим простейшие тригонометрические уравнения  , решения которых находятся по формулам
, решения которых находятся по формулам 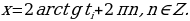 .
.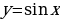 и
и 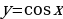 ) их правыми частями приводит к возможной потере корней исходного уравнения (2.1.5). Поэтому необходимо еще проверить, будут ли значения
) их правыми частями приводит к возможной потере корней исходного уравнения (2.1.5). Поэтому необходимо еще проверить, будут ли значения  не определена, т.е.
не определена, т.е.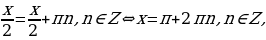 корнями исходного уравнения [12].
корнями исходного уравнения [12]. .
.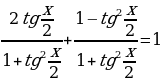
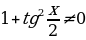
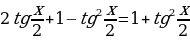
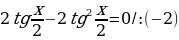
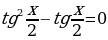
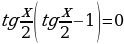
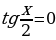
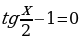
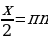
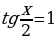

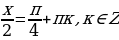
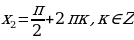
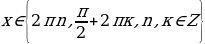 .
.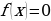 , где
, где 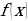 – тригонометрическое выражение (функция), зависящее от одного аргумента, может быть представлена в виде произведения
– тригонометрическое выражение (функция), зависящее от одного аргумента, может быть представлена в виде произведения 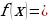
 , то корнями данного уравнения будут все решения совокупности уравнений
, то корнями данного уравнения будут все решения совокупности уравнений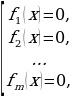
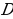 значений переменной
значений переменной 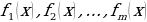 , т.е. множество
, т.е. множество 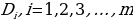 :
: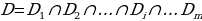 [8].
[8].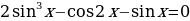


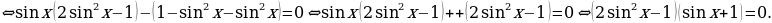

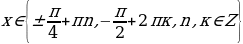 .
.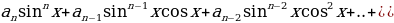
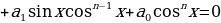 (2.3.1)
(2.3.1)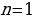 , то уравнение (2.3.1) принимает вид
, то уравнение (2.3.1) принимает вид 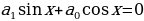 и называется однородным уравнением первого порядка.
и называется однородным уравнением первого порядка.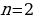 из уравнения (2.3.1) получаем уравнение
из уравнения (2.3.1) получаем уравнение 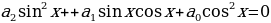 , которое называется однородным уравнением второго порядка, а при
, которое называется однородным уравнением второго порядка, а при 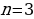 – уравнение
– уравнение 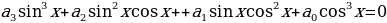 , которое называется однородным уравнением третьего порядка.
, которое называется однородным уравнением третьего порядка.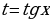 . Однако следует помнить, что введение подстановки
. Однако следует помнить, что введение подстановки 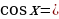
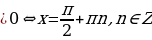 , корнями исходного уравнения. Очевидно, что это будет выполняться при
, корнями исходного уравнения. Очевидно, что это будет выполняться при  .
. .
. 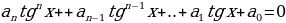 , которое заменой
, которое заменой  .
.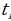 полученного рационального уравнения. Если рациональное уравнение решений не имеет, то и исходное тригонометрическое уравнение (2.3.1) тоже решений не имеет. В противном случае получаем простейшие тригонометрические уравнения
полученного рационального уравнения. Если рациональное уравнение решений не имеет, то и исходное тригонометрическое уравнение (2.3.1) тоже решений не имеет. В противном случае получаем простейшие тригонометрические уравнения 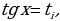
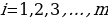 , из решения которых находим
, из решения которых находим 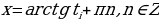 .
.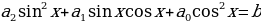 (2.3.2)
(2.3.2)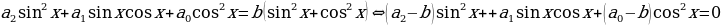 , получаем однородное уравнение
, получаем однородное уравнение  , где
, где 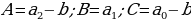 [8].
[8].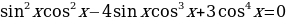
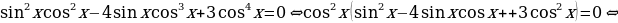

 .
. .
.
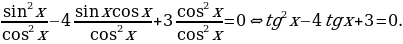

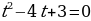
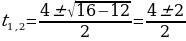
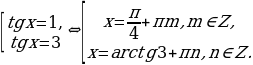

 , (2.4.1)
, (2.4.1)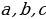 – произвольные числа, причем
– произвольные числа, причем  . Одним из способов решения данного уравнения является сведение его к решению равносильной системы рациональных уравнений с помощью подстановки
. Одним из способов решения данного уравнения является сведение его к решению равносильной системы рациональных уравнений с помощью подстановки 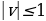 ,
, 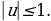 Однако такой подход не всегда эффективен, поскольку приводит к увеличению объема вычислений. Рациональнее использовать так называемый метод введения вспомогательного аргумента.
Однако такой подход не всегда эффективен, поскольку приводит к увеличению объема вычислений. Рациональнее использовать так называемый метод введения вспомогательного аргумента. 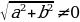 . В результате получаем равносильное уравнение
. В результате получаем равносильное уравнение 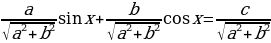 . Очевидно, что существует некоторый угол
. Очевидно, что существует некоторый угол  , для которого
, для которого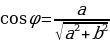 ;
; 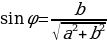 .
. 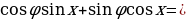
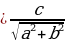 .
.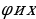 , т.е.
, т.е. 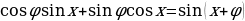 . Следовательно,
. Следовательно, 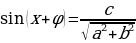 . Если
. Если 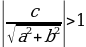 , то полученное уравнение, а следовательно, и исходное уравнение решений не имеет. Если
, то полученное уравнение, а следовательно, и исходное уравнение решений не имеет. Если 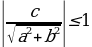 , то по формуле корней для простейшего тригонометрического уравнения получаем
, то по формуле корней для простейшего тригонометрического уравнения получаем 
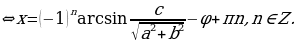
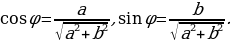 .
.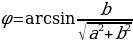 и
и  , условие
, условие  и
и 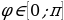 может быть выполнено только при
может быть выполнено только при 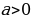 [8].
[8].

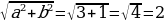
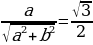 ;
; 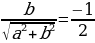 ;
; 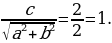
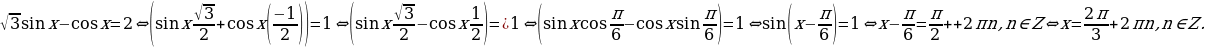
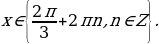
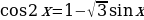 ;
;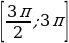 .
.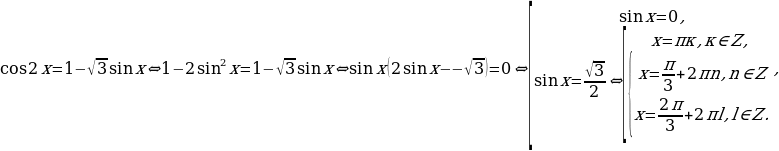
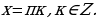
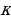 корни вида
корни вида 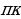 отрицательны и не принадлежат отрезку
отрицательны и не принадлежат отрезку  , то
, то 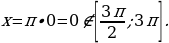
 , то
, то 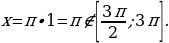
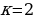 , то
, то 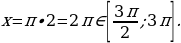
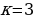 , то
, то 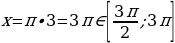 .
. , то
, то 
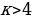 корни этой серии примают значения большие, чем
корни этой серии примают значения большие, чем 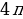 , и не принадлежат отрезку
, и не принадлежат отрезку 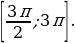
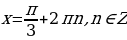
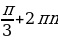 отрицательны и не принадлежат отрезку
отрицательны и не принадлежат отрезку 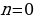 , то
, то 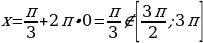 .
.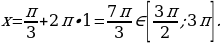
 .
.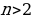 корни этой серии примают значения большие, чем
корни этой серии примают значения большие, чем  , и не принадлежат отрезку
, и не принадлежат отрезку 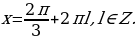
 отрицательны и не принадлежат отрезку
отрицательны и не принадлежат отрезку  , то
, то 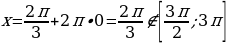 .
.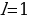 , то
, то 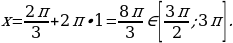
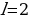 , то
, то 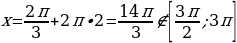 .
.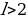 корни этой серии примают значения большие, чем
корни этой серии примают значения большие, чем 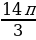 , и не принадлежат отрезку
, и не принадлежат отрезку 
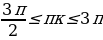 , т.е.
, т.е. 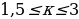 .
.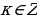 , следовательно,
, следовательно, 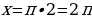 .
.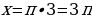 .
.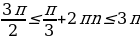 , т.е.
, т.е. 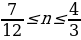 .
.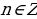 , следовательно,
, следовательно, 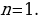
 .
.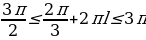 , т.е.
, т.е.  .
.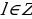 , следовательно,
, следовательно, 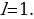
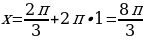 .
.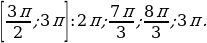
 и
и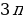 . Выделим на окружности отрезок (дугу)
. Выделим на окружности отрезок (дугу) 
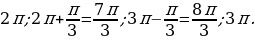
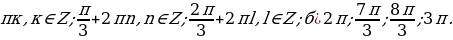
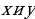 . Решения таких систем обычно записываются в виде упорядоченных пар
. Решения таких систем обычно записываются в виде упорядоченных пар 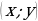 или в виде системы.
или в виде системы.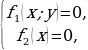 (4.1)
(4.1)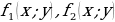 – тригонометрические функции двух неизвестных
– тригонометрические функции двух неизвестных 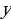 и подставить это выражение вместо
и подставить это выражение вместо  , и второго уравнения, умноженного на некоторое действительное число
, и второго уравнения, умноженного на некоторое действительное число  , то полученная система тригонометрических уравнений будет равносильна заданной, т.е.
, то полученная система тригонометрических уравнений будет равносильна заданной, т.е.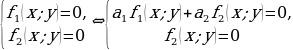

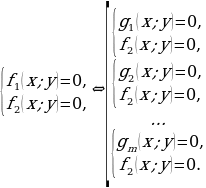
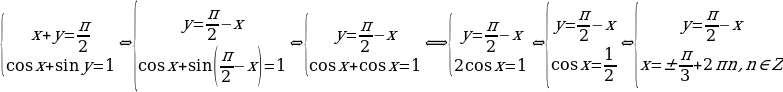
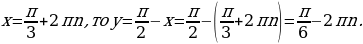
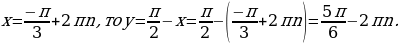
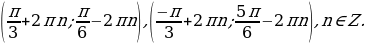
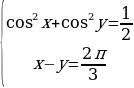

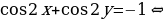
 .
.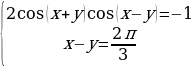
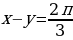 в первое уравнение:
в первое уравнение: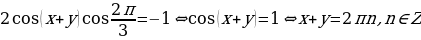 .
.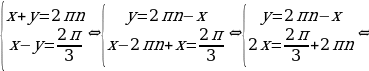
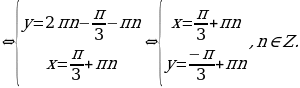

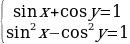
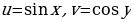 приводит к алгебраической системе относительно u и v:
приводит к алгебраической системе относительно u и v: