4
Некоторые методы решения сложных задач на колебания математического маятника.
Последние годы абитуриенты России всё чаще и чаще сталкиваются с задачами на различные колебательные процессы. Часть из них позволяют при решении использовать модель математического маятника.
Анализируя множество сводящихся к колебаниям математического маятника задач, предлагавшихся на вступительных экзаменах в ведущие технические ВУЗы страны, а также на физических олимпиадах, я пришёл к выводу, что все они сводятся к конечному набору простых проблем, довольно быстро решаемых стандартным набором методов.
Разбиение сложных задач на ряд простых, а также методика решения последних успешно применялись мною в одиннадцатых классах, на протяжении нескольких последних лет. Именно практическое апробирование позволяет мне предложить данные методы для широкого использования в практике.
Задача.
Определите период малых колебаний маятника, представляющего собой шарик массы m, шарнирно укреплённый с помощью лёгкого равностороннего треугольника со стороной L на бруске массой M, который скатывается, двигаясь поступательно, по наклонной плоскости с углом у основания . Коэффициент трения между бруском и наклонной плоскостью . Центр масс бруска движется в плоскости колебаний.
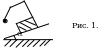
Решение задачи можно разбить на несколько этапов, превратив каждый из них в отдельную задачу.
Определите период малых колебаний шарика массой m, шарнирно укреплённого с помощью лёгкого равностороннего треугольника со стороной L к неподвижному потолку.

Очевидно, что колебания этого шарика возможны в плоскости, перпендикулярной плоскости рисунка.
Вид с боку выглядит так:

Так как треугольник практически невесом, то конструкция является моделью математического маятника, период колебаний которого, как известно, вычисляется по формуле T= 2 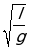 ,где l -длина математического маятника. В данном случае за длину маятника надо принять длину отрезка, соединяющего шарик с потолком на рисунке 3. Этот отрезок является высотой и медианой треугольника, т. е. обозначив его длину за l и, назвав приведённой длиной маятника, мы получаем, что
,где l -длина математического маятника. В данном случае за длину маятника надо принять длину отрезка, соединяющего шарик с потолком на рисунке 3. Этот отрезок является высотой и медианой треугольника, т. е. обозначив его длину за l и, назвав приведённой длиной маятника, мы получаем, что 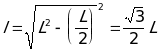 . Тогда период колебаний
. Тогда период колебаний 
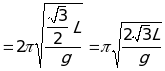 .
.
Определите период малых колебаний маятника, состоящего из шарика массы m, закреплённого с помощью лёгкого стержня длины l на бруске массы M, способного без трения двигаться по горизонтальной поверхности.
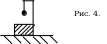
Упростим систему, перенеся брусок в верхнюю точку стержня.
Получим рисунок 5.
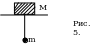
Данная система будет совершать колебания с той же частотой и амплитудой, что и показанная на рисунке 4. Масса M будет двигаться горизонтально, а m совершать колебания в плоскости рисунка.
Очевидно, что тела системы совершают колебания относительно центра масс, вертикальные колебания которого незначительны, поэтому шарик m, будет двигаться как материальная точка маятника. Однако за счёт жёсткой связи брусок M будет совершать колебания с тем же периодом, что и шарик m.
Итак, пусть l*- расстояние от m до центра масс, т. е. это приведённая длина математического маятника. Тогда 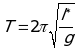 . l*найден из известных формул определения центра масс:
. l*найден из известных формул определения центра масс: 
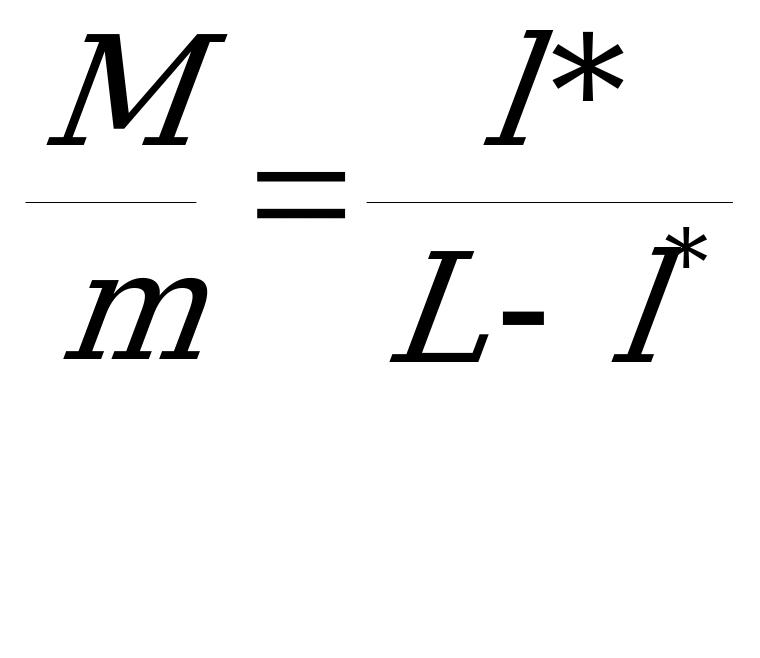 откуда.
откуда.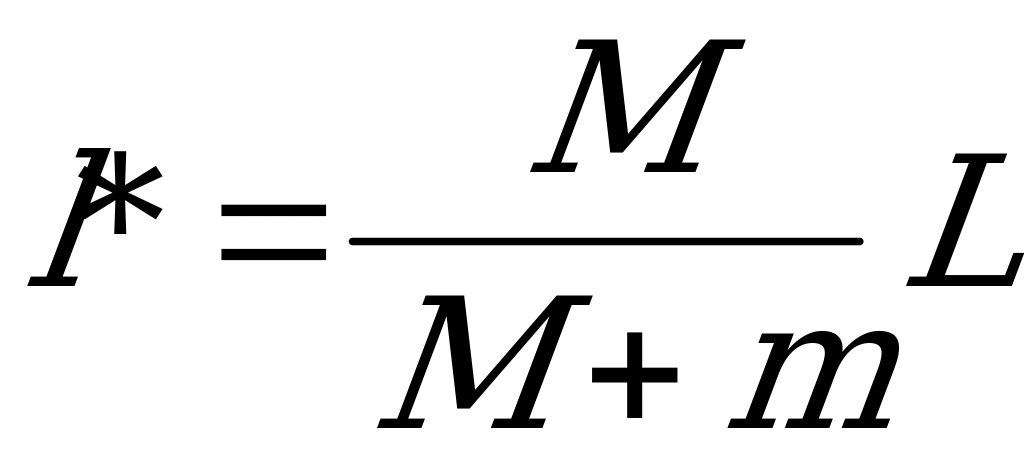
Период колебаний будет равен: 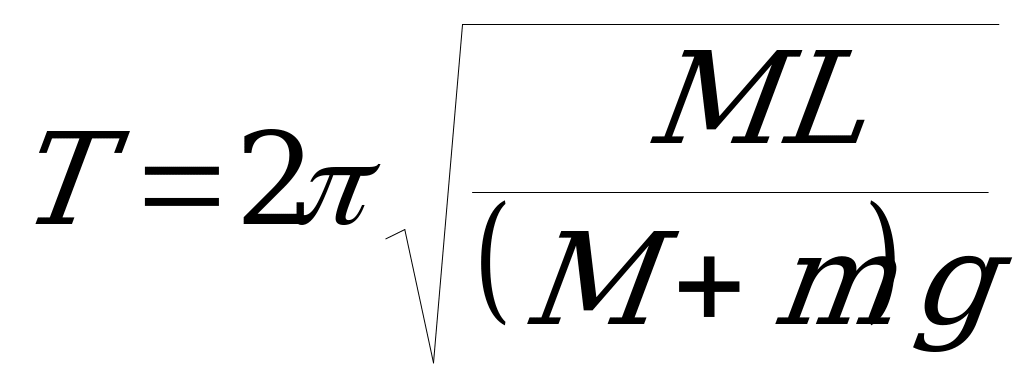 .
.
Найдите период колебаний математического маятника длины l и массы m, если точка его подвеса движется под углом к горизонту с ускорением a.
Для начала преобразуем формулу периода  в вид, помогающий легко решить данную задачу. g - это ускорение свободного падения, которое можно найти как
в вид, помогающий легко решить данную задачу. g - это ускорение свободного падения, которое можно найти как 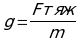 .Но сила тяжести, действующая на материальною точку маятника, численно равна силе натяжения нити FH в положении, когда маятник покоится, поэтому:
.Но сила тяжести, действующая на материальною точку маятника, численно равна силе натяжения нити FH в положении, когда маятник покоится, поэтому:  . Тогда
. Тогда  .
.
Теперь наша задача сводится к нахождению силы натяжения нити в положении равновесия.
Рассмотрим положение равновесия маятника, описанного в задаче.
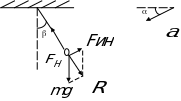
Рис. 6
Нить находится под углом к вертикали. Перейдём в систему отчёта, связанную с точкой подвеса. Тогда на материальною точку маятника действуют: сила тяжести, сила натяжения нити и сила инерции, направленная в сторону, противоположенную ускорению 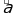 :
: 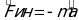 . Равнодействующая сил
. Равнодействующая сил 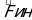 и
и  равна -
равна - .
.
Найдя R, мы найдём FH.
Угол между 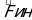 и
и  равен 90+. Тогда, используя теорему косинусов, получим
равен 90+. Тогда, используя теорему косинусов, получим
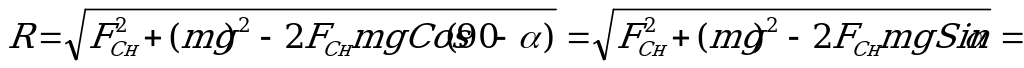
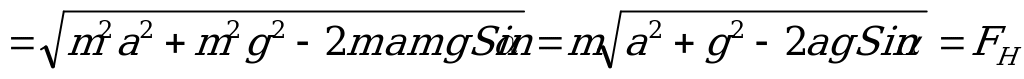
И период маятника: 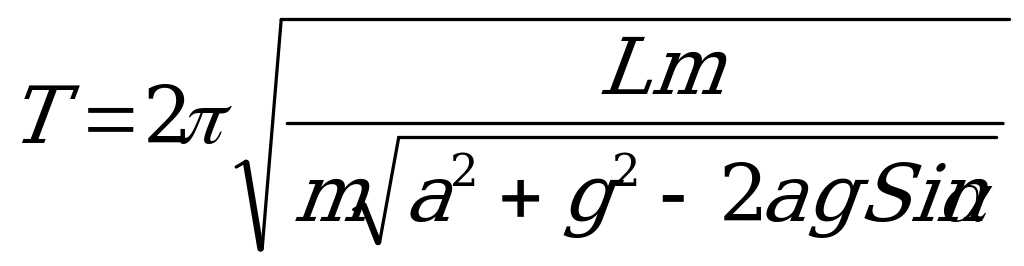 =2
=2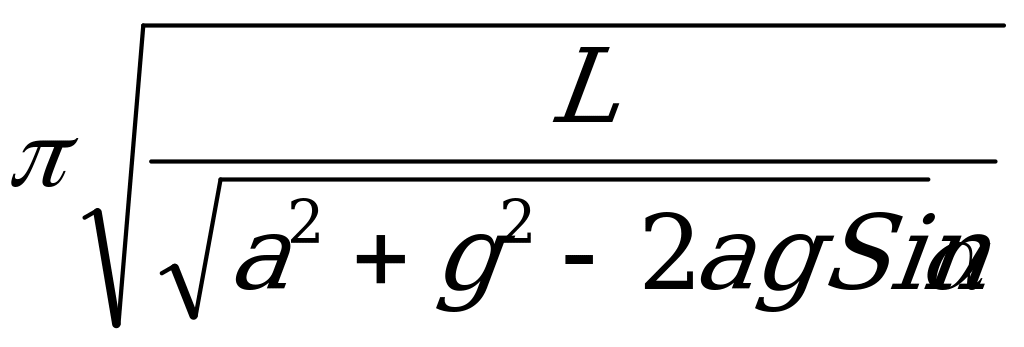
4) Теперь вернёмся к задаче, сформулированной в самом начале.
Система будет двигаться вниз по наклонной плоскости с ускорением, которое находится по второму закону Ньютона: a=g(Sin -μCosα).
-μCosα).
В случае возникновения колебаний системы период вычислим по формуле: (*)Т=2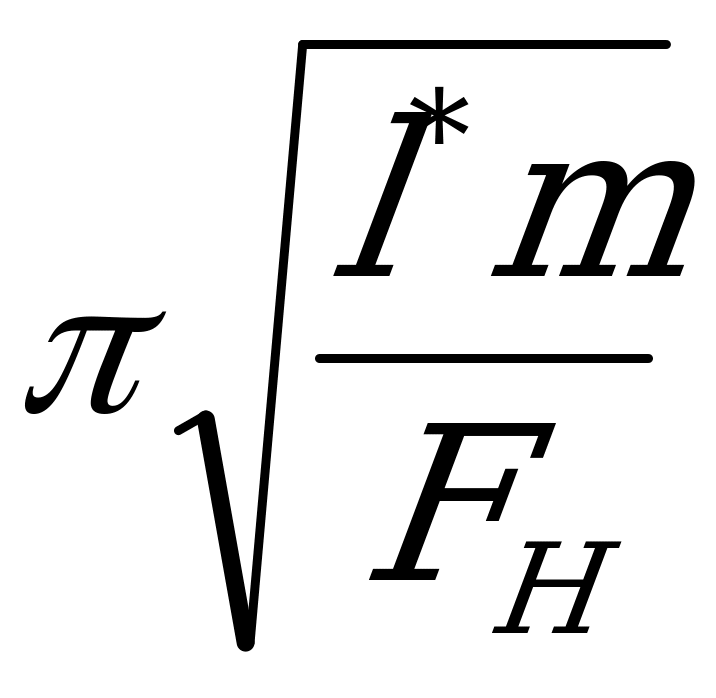 , где l* определяется из решения задач 1) и 2), а FH из задачи 3). Подставляя полученные данные в формулу (*), получаем:
, где l* определяется из решения задач 1) и 2), а FH из задачи 3). Подставляя полученные данные в формулу (*), получаем:
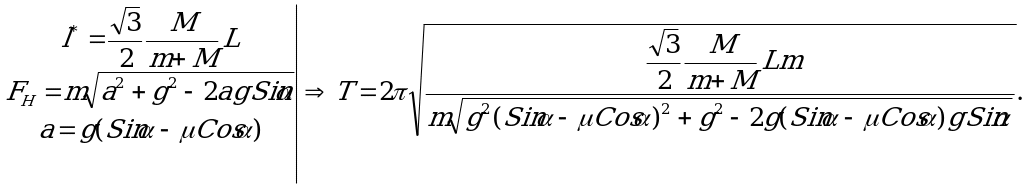
И после преобразований:
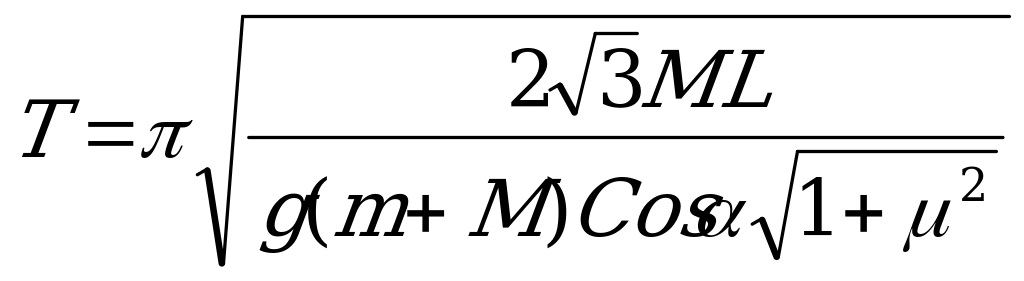 .
.
В заключении хочется отметить, что сложные, «неподъёмные» на первый взгляд задачи из других курсов физики поддаются решению с помощью предложенной методики, которая легко осваивается выпускниками за 2-3 урока и находит широкое применение на практике.









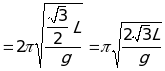 .
.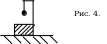
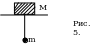

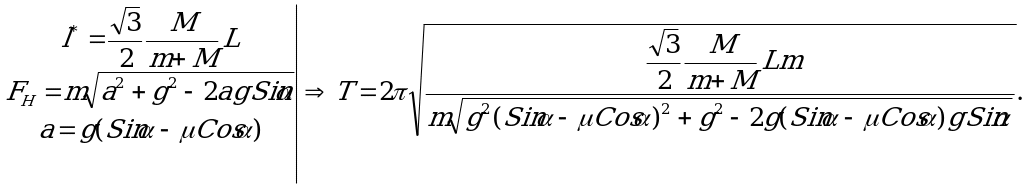
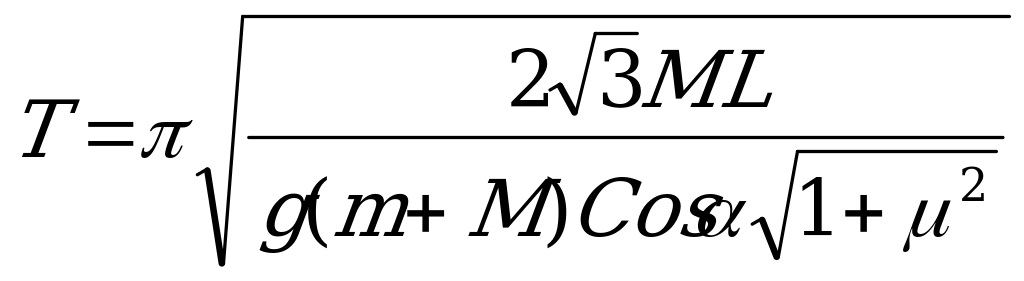 .
.

















