Презентации по физике "Введение в квантовую физику"

Санкт-Петербургский университет ГПС МЧС РФ

Кафедра физики и теплотехники

В.С.ЗВОНОВ

ВВЕДЕНИЕ В КВАНТОВУЮ ФИЗИКУ

2012 г.

Макс Планк

Свет – волна или частица?

Что такое свет?

• Такими вопросами задавались философы, ученые уже долгое время, но никто конкретно не мог представить точную картину.

Две теории сущности света

Корпускулярная теория

Волновая теория

В 17 веке почти одновременно возникли и начали развиваться две совершенно разные теории представления о том, что же такое свет и какова его природа.

Волновая теория света связана с такими именами, как

В 1678 году Гюйгенс – сторонник волновой теории света, предположил, что

• свет – это поток волн, распространяющихся в особой, гипотетической среде – эфире, заполняющем все пространство и проникающем внутрь всех тел.

Ряд открытий сторонниками волновой теории

• Дифракции света –
• это огибание светом препятствий
• это явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий.

Ряд открытий сторонниками волновой теории

• интерференции света - усиление или ослабление освещенности при наложении световых пучков друг на друга.

Ряд открытий сторонниками волновой теории

• Герц в конце XIX века обнаружил удивительное явление, когда

• при освещении электродов, электрическая искра возникает лучше

Ряд открытий сторонниками волновой теории

• Максвел во второй половине XIX века показал, что свет есть частный случай электромагнитных волн

Ряд открытий сторонниками волновой теории

• приводит к тому, что в конце 18 века корпускулярная теория света остается в тени

Волновая теория

1

Корпускулярная теория

2

• Можно сказать, что сторонники волновой теории одержали победу в борьбе за представления о сущности света!

Ньютон, Планк и Эйнштейн были представителями от

• корпускулярной теории света, согласно которой свет – это поток частиц, идущих от источника во все стороны

Сенсация

• Макс Планк делает предположение, а что если

• Свет излучается атомами

не волнами, а порциями энергии - квантами

• В дальнейшем кванты света стали называть фотонами

• Электромагнитная волна не только излучается, но и поглощается в виде потока квантов.
• Электромагнитное излучение ( в том числе и свет) представляет собой поток фотонов.

Мне кажется, что понять квантовую механику, о которой пойдет речь, не сложнее, чем создать такую вот фигуру:

Свет - это волна или частица?

Итак, что же такое свет – частица или волна? Квантовая теория отвечает на этот вопрос так: ни то, ни другое .

Когда мы описываем поведение фотона как поведение частицы или волны, мы навязываем классическое описание этому объекту, имеющему существенно неклассическую природу.

Свет-это волна или частица?

Свет может характеризоваться только с той его стороны (корпускулярной или волновой), проявление которой определяется внешними условиями, создаваемыми экспериментальными средствами наблюдения .

Такая постановка вопроса позволяет рассматривать и тот случай, когда один и тот же исследуемый объект (свет)обладает не совместимыми по классическим представлениям корпускулярными и волновыми свойствами.

В квантовой теории эти свойства не исключают, а дополняют друг друга, так как в “чистом” виде они могутпроявиться лишь в разных опытах, производимых при взаимоисключающих условиях .

Свет- это и волна, и частица

Действительно, нет необходимости пытаться представить себе, как это фотон может быть сразу и волной, и частицей.

Свет обладает потенциальной возможностью проявлять и волновые, и корпускулярные свойства, но эти дополняющие друг друга свойства в чистом виде проявляются лишь при взаимоисключающих условиях эксперимента.

Адекватный способ описания света определяется выбранным способом наблюдения, а вопрос о том, что же существует “на самом деле” – волна или частица, - лишен содержания.

Принцип дополнительности

Этот методологический принцип, выдвинут датским физиком Н. Бором в 1927 году в связи с интерпретацией квантовой механики.

Нильс Бор

1885-1962

Он формулируется так: в процессе познания для воспроизведения целостности объекта необходимо применять взаимоисключающие, "дополнительные" классы понятий, каждый из которых применим в своих особых условиях.

Парадоксы квантовой физики

Примем сейчас фотонную теорию света и постараемся с ее помощью понять факты,

до сих пор объяснявшиеся волновой теорией.

Этим самым мы подчеркнем трудности, которые делают обе теории несовместимыми.

1. Как мы помним, луч однородного света, проходящий

через маленькое отверстие, образует светлые и темные кольца.

Возможно, что между краем отверстия и фотоном существует некоторое

взаимодействие, которое и служит причиной появления дифракционных колец.

2. Возьмем два маленьких отверстия.

Однородный свет, проходя через оба отверстия,

образует на экране светлые и темные полосы.

Как следует понимать этот эффект с точки зрения квантовой теории света?

Если фотон ведет себя подобно корпускуле в классической физике, он должен пройти только через одно из двух отверстий.

Но в этом случае явления дифракции кажутся совершенно непонятными.

Корпускулярно-волновой дуализм

В 1924 году Луи де Бройль выдвинул гипотезу, что корпускулярно-волновой дуализм не является особенностью только оптических явлений (т.е.электромагнитных волн), а носит универсальный характер.

Он предположил, что материальные частицы должны проявлять волновые свойства.

Луи де Бройль

(1892-1987)

Аналогия между светом и частицей

Если свет может быть и частицей, и волной, то

любая частица может быть волной!

Экспериментальное подтверждение гипотезы де Бройля.

Длина волны электрона.

Если электрон – волна, то он должен проявлять свои волновые свойства. Самые яркие явления, характеризующие существование и распространение волны, - это явления интерференции и дифракции, где наблюдаемой величиной по сути дела является длина волны λ.

Девисон и Джермер

(1А = 10 -10 м ) Ангстрем – единица измерения длины

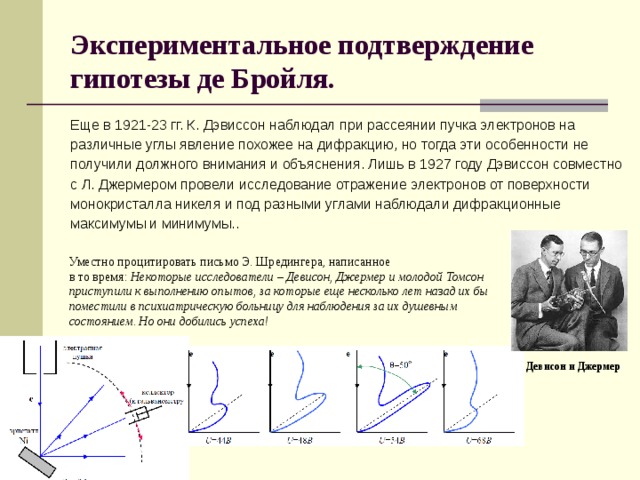
Экспериментальное подтверждение гипотезы де Бройля.

Еще в 1921-23 гг. К. Дэвиссон наблюдал при рассеянии пучка электронов на

различные углы явление похожее на дифракцию, но тогда эти особенности не

получили должного внимания и объяснения. Лишь в 1927 году Дэвиссон совместно

с Л. Джермером провели исследование отражение электронов от поверхности

монокристалла никеля и под разными углами наблюдали дифракционные

максимумы и минимумы..

Уместно процитировать письмо Э. Шредингера, написанное

в то время: Некоторые исследователи – Девисон, Джермер и молодой Томсон приступили к выполнению опытов, за которые еще несколько лет на з ад их бы поместили в психиатрическую больницу для наблюдения за их душевным состоянием. Но они добились успеха!

Девисон и Джермер

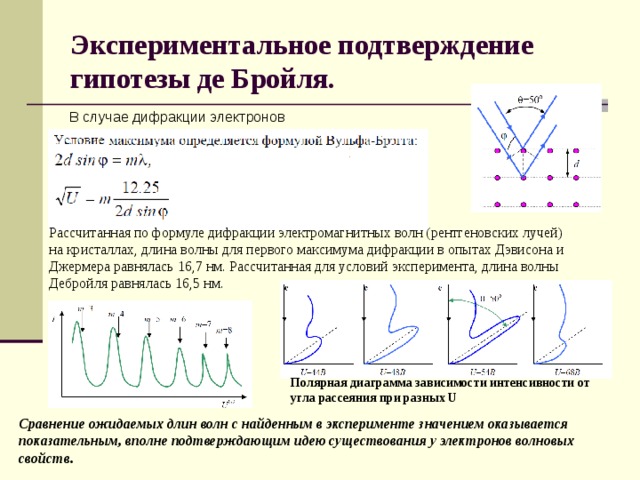
Экспериментальное подтверждение гипотезы де Бройля.

В случае дифракции электронов

Рассчитанная по формуле дифракции электромагнитных волн (рентгеновских лучей)

на кристаллах, длина волны для первого максимума дифракции в опытах Дэвисона и

Джермера равнялась 16,7 нм. Рассчитанная для условий эксперимента, длина волны

Дебройля равнялась 16,5 нм.

Полярная диаграмма зависимости интенсивности от угла рассеяния при разных U

Сравнение ожидаемых длин волн с найденным в эксперименте значением оказывается показательным, вполне подтверждающим идею существования у электронов волновых свойств.

Экспериментальное подтверждение гипотезы де Бройля.

  В 1913 г. русский физик Г.В. Вульф и английские ученые отец и сын Генри и Лоуренс Брэгги, независимо друг от друга, предложили простой метод расчета дифракции рентгеновских лучей в кристаллах.

Они полагали, что дифракцию рентгеновских лучей можно рассматривать как результат отражения рентгеновских лучей от плоскостей кристалла .

Это отражение, в отличие от обычного, происходит лишь при таких условиях падения лучей на кристалл , которые соответствуют максимуму интерференции для лучей, отраженных от разных плоскостей .

Лоренс Брэгг

Генри Брэгг

оптическая разность хода между лучами 1`и 2`

Г.В. Вульф

Нобелевскую премию за это открытие получили отец и сын Брэгги

Дифракция атомов и молекул, нейтронов.

Частицы более тяжелые, чем электроны, также обладают волновыми свойствами, которые характеризуются определенными длинами волн де Бройля.

Следовательно, можно попытаться наблюдать их дифракцию.

О. Штерн в 1930 году наблюдал дифракцию легких атомов и молекул: He и H 2 , измеряя скорости молекул при разной температуре.

Легкие атомы и молекулы нужны для того, чтобы их длина волны де Бройля была достаточна велика для наблюдения явления дифракции. Так при комнатной температуре длина волны атома гелия равна ~ 0 . 1 нм , т.е. порядка постоянной кристаллической решетки.

Отто Штерн

Многочисленные эксперименты убедительно показывают,

что какие бы частицы мы не брали, все они проявляют в определенных условиях волновые свойства.

Хотя, несомненно, остаются частицами .

Дифракция атомов и молекул, нейтронов.

В 1991 году в журнале Phys. Rev. Lett. 66, 2689–2692 (1991) в статье

O. Carnal и J. Mlynek описан проведенный авторами известный интерференционный опыт Юнга, но не со световыми лучами, а с потоком атомов гелия.

Опыты проводили при двух температурах T = 295 K и 83 K. Зная температуру, можно оценить среднюю кинетическую энергию атомов и длину волны де Бройля. Для приведенных температур λ = 0.056 нм и 0.103 нм, соответственно. Двойная щель - два источника когерентных волн в опыте Юнга. На экране волны от них, складываясь, дают чередование темных и светлых полос. Среднее расстояние между максимумами 7.7±0.5 мкм, что в пределах погрешности эксперимента совпадает с теоретическим значением Δ = L'·λ/d = 8.2 мкм.

Наиболее впечатляющий на сегодняшний день эксперимент был недавно проведен Hackermueller L., Hornberger K., Brezger B., Zeilinger A. and Arndt M. Decoherence of matter waves by thermal emission of radiation // Nature 427, 711 (2004). . В этом исследовании пучок фуллеренов (молекул C -70 , содержащих 70 атомов углерода) рассеивался на дифракционной решетке, состоящей из большого числа узких щелей.

При этом имелась возможность вести контролируемый нагрев летящих в пучке молекул C-70 посредством лазерного луча, что позволяло менять их внутреннюю температуру (иначе говоря, среднюю энергию колебаний атомов углерода внутри этих молекул). Квантовая теория блестяще подтвердила результаты эксперимента.

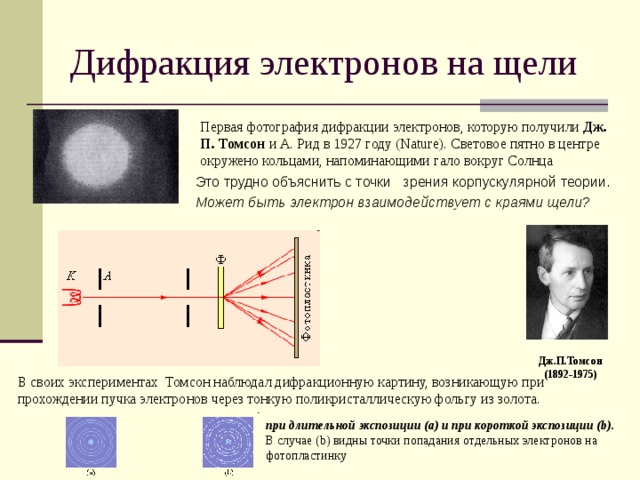
Дифракция электронов на щели

Первая фотография дифракции электронов, которую получили Дж. П. Томсон и А. Рид в 1927 году (Nature). Световое пятно в центре окружено кольцами, напоминающими гало вокруг Солнца

Это трудно объяснить с точки зрения корпускулярной теории.

Может быть электрон взаимодействует с краями щели?

Дж.П.Томсон

(1892-1975)

В своих экспериментах  Томсон наблюдал дифракционную картину, возникающую при прохождении пучка электронов через тонкую поликристаллическую фольгу из золота.

при длительной экспозиции (a) и при короткой экспозиции (b).

В случае (b) видны точки попадания отдельных электронов на фотопластинку

Дифракция электронов на двух щелях

В 1961 г. К. Йенсен выполнил эксперимент по наблюдению интерференции электронов по схеме классических для оптики опытов Юнга с двумя щелями.

Картина полос интерференции электронов и света (электромагнитных волн) имеет удивительное сходство. Этот эксперимент К. Йенсена, по мнению многих физиков, является одним из самых красивых!

Если в опыте по наблюдению дифракции электронов на двух щелях закрыть одну из щелей, то интерференционные полосы исчезнут, и фотопластинка зарегистрирует распределение электронов, продифрагировавших на одной щели (см на рис. график В).

В этом случае все электроны, долетающие до фотопластинки, проходят через единственную открытую щель. Если же открыты обе щели, то появляются интерференционные полосы, и тогда возникает вопрос, через какую из щелей пролетает тот или иной электрон?

Психологически очень трудно смириться с тем, что ответ на этот вопрос может быть только один: электрон пролетает через обе щели.

Открыты две щели

Поштучный поток электронов тоже дает интерференцию при длительной экспозиции т. е. электрон интерферирует сам с собой.

Открыта одна щель

http://ufn.ru/ufn49/ufn49_8/Russian/r498e.pdf

Дифракция одиночных электронов

Возьмем пулемет и мысленно проведем эксперимент, показанный на рис. Пулемет выпускает пули, направление полета которых заранее неизвестно. То ли направо они полетят, то ли налево….

Мысленно проведем три опыта:

первый — когда открыта первая щель, а вторая закрыта; второй — когда открыта вторая щель, а первая закрыта, третий опыт — когда обе щели открыты.

Результат нашего первого «эксперимента» показан на том же рисунке, на графике. Ось вероятности в нем отложена вправо, а координата — это и есть положение точки X . Пунктирная линия показывает распределение вероятности P 1 попавших в детектор пуль при открытой первой щели, кривая из точек — вероятность попадания в детектор пуль при открытой второй щели и сплошная линия — вероятность попадания в детектор пуль при обеих открытых щелях, которую мы обозначили как P 12 . Сравнив величины P 1 , P 2 и P 12 , мы можем сделать вывод, что вероятности просто складываются,

P 1 + P 2 = P 12

Представим тот же опыт с электронами

Результаты подсчетов в случае, когда одна из щелей закрыта, вполне предсказуемы и очень похожи на итоги пулеметной стрельбы (линии из точек и штрихов на рисунке). А вот в случае, когда обе щели открыты, мы получаем совершенно неожиданную кривую P 12 , показанную сплошной линией. Она явно не совпадает с суммой P 1 и P 2 ! Получившуюся кривую называют интерференционной картиной от двух щелей.

Странная картина получается: на кривой P 12 при двух открытых щелях есть точки, в которые попадает значительно меньше электронов, чем при любой из открытых щелей. И наоборот, есть точки, вероятность попадания электронов в которые более чем вдвое превышает вероятность попадания электронов, прошедших через каждую щель по отдельности.

Вероятность и волновая функция

С точки зрения волновой теории , максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля. В области максимумов, зарегистрированных на фотопластинке, попадает большее число электронов. Но процесс попадания электронов в различные места на фотопластинке не индивидуален. Принципиально невозможно предсказать, куда попадет очередной электрон после рассеяния, существует лишь определенная вероятность попадания электрона в то или иное место. Таким образом, описание состояния микрообъекта и его поведения может быть дано только на основе понятия вероятности .

Необходимость вероятностного подхода к описанию микрообъектов является важнейшей особенностью квантовой теории.

В квантовой механике для характеристики состояний объектов в микромире вводится понятие волновой функции Ψ (пси-функции).

Квадрат модуля волновой функции |Ψ| 2 пропорционален вероятности нахождения микрочастицы в единичном объеме пространства. Конкретный вид волновой функции определяется внешними условиями, в которых находится микрочастица. Математический аппарат квантовой механики позволяет находить волновую функцию частицы, находящейся в заданных силовых полях. Безграничная монохроматическая волна де Бройля есть волновая функция свободной частицы, на которую не действуют никакие силовые поля.

Соотношение неопределенности Гейзенберга

Более 85 % всех электронов, прошедших через щель, попадут в центральный дифракционный максимум. Угловая полуширина θ 1 этого максимума находится из условия

D sin θ 1  = λ.

Это формула волновой теории. С корпускулярной точки зрения можно считать, что при пролете через щель электрон приобретает дополнительный импульс в перпендикулярном направлении.

Пренебрегая 15 % электронов, которые попадают на фотопластинку за пределами центрального максимума, можно считать, что максимальное значение p y поперечного импульса равно

Дифракция электронов на щели. График справа – распределение электронов на фотопластинке

Квантовая механика вкладывает в это простое на вид соотношение, являющееся следствием волновых свойств микрочастицы, чрезвычайно глубокий смысл. Прохождение электронов через щель является экспериментом, в котором y – координата электрона – определяется с точностью Δy = D . Величину Δy называют неопределенностью измерения координаты. В то же время точность определения y – составляющей импульса электрона в момент прохождения через щель – равна py или даже больше, если учесть побочные максимумы дифракционной картины. Эту величину называют неопределенностью проекции импульса и обозначают Δp y . Таким образом, величины Δy и Δp y связаны соотношением

которое называется соотношением неопределенностей Гейзенберга

Соотношение неопределенности Гейзенберга

Величины Δy и Δp y нужно понимать в том смысле, что микрочастицы в принципе не имеют одновременно точного значения координаты и соответствующей проекции импульса.

Оно является проявлением двойственной корпускулярно-волновой природы материальных микрообъектов. Соотношение неопределенностей позволяет оценить, в какой мере можно применять к микрочастицам понятия классической механики. Оно показывает, в частности, что к микрообъектам неприменимо классическое понятие траектории, так как движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Принципиально невозможно указать траекторию, по которой в рассмотренном мысленном эксперименте двигался какой-то конкретный электрон после прохождения щели до фотопластинки.

Однако, при определенных условиях соотношение неопределенностей не противоречит классическому описанию движения тел, в том числе и микрочастиц. Например, электронный пучок в кинескопе телевизора при вылете из электронной пушки имеет диаметр D порядка 10 –3  см. В современном телевизоре ускоряющее напряжение U ≈ 15 кВ. Легко подсчитать импульс электрона:                          

Этот импульс направлен вдоль оси трубки. Из соотношения неопределенностей следует, что электронам при формировании пучка сообщается неконтролируемый импульс Δp, перпендикулярный оси пучка: Δp ≈ h / D ≈ 6,6·10 –29  кг·м/с.

Пусть до экрана кинескопа электроны пролетают расстояние L ≈ 0,5 м. Тогда размытие Δl пятна на экране, обусловленное волновыми свойствами электрона, составит

Поскольку Δl 

Соотношение неопределенности Гейзенберга

Δp x ·Δx ≥ h

h

Это соотношение имеет

более сложное содержание.

h

• Если частица находится в стационарном состоянии, то определение энергии с точностью Δ E должно занять время, по меньшей мере Δ t ~ h / Δ E . Т.е. здесь мы связаны с процессом измерения или наблюдения: чем меньше время наблюдения, тем меньше точность определения энергии.
• Если система (или частица) находится в нестационарном состоянии, например возбужденном состоянии, то имеем следующую интерпретацию: неопределенность энергии Δ E - разброс энергии этого состояния, его энергетическая ширина, а неопределенность времени Δ t = τ - время жизни этого нестационарного возбужденного состояния.

Соотношение позволяет говорить о виртуальных состояниях и возбуждениях.

Система за короткое время имеет большой разброс в энергии и может бывать во всех энергетических состояниях, т.е. состояниях с любой энергией. Это не реальные возбуждения, это состояния “временные”, связанные с временным нарушением закона сохранения энергии.

Дифракция отдельных электронов на двух щелях и волновая функция

Прямые измерения с “единичными” электронами - пучками

малой интенсивности - были проведены в 1949 г. Л.М. Биберманом, Н.Г Сушкиным и акад. В.А.Фабрикантом.

Если закрывать одну или другую щель, то получаем на экране расширенное изображение щели – пунктир на рисунке. Но когда падают одиночные электроны на обе открытые щели, то получаем интерференционную картину.

Однако электрон не делится: он проходит либо через одну, либо через другую щель. Если поставим счетчик на фиксирующем экране, то он “срабатывает” в определенном месте от “целого” электрона и никакой интерференции не увидим. Просто следующий электрон будет зафиксирован в другом месте, за ним другой снова в другом месте и т.д.

И там, где амплитуда волнового поля максимальна, там чаще будут регистрироваться электроны, там вероятность нахождения электрона максимальна. Вероятность всегда связывают с квадратом модуля амплитуды волны | A| 2 .

Исходя из этого М. Борном была предложена статистическая интерпретация волн де Бройля.

Волны де Бройля следует рассматривать как волны вероятности :

Интенсивность волн де Бройля в данный момент времени и в данном месте определяет вероятность обнаружить частицу в данное время и в данном месте . А интенсивность волн пропорциональна квадрату амплитуды волны.

Макс Борн

(1882-1970)

Волновая функция и уравнение Шредингера

Итак, при прохождении щелей однозначно предсказать, куда попадет электрон, невозможно. Можно лишь определить вероятность этого попадания. Пусть дает амплитуду волн де Бройля или, иначе говоря, - волновая функция, описывающая поведение частицы.

Для свободной частицы – это плоская волна:

В нашем обыденном мире энергия переносится двумя способами:

материей при движении с места на место  — в такой передаче энергии

участвуют частицы — или волнами.

Но если мы с материальной частицей связали волну, то она должна подчиняться обычному волновому уравнению.

Эрвин Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя.

- уравнение Шредингера

Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица.

Э.Шредингер

(1887-1961)

Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.

Бог не играет в кости?

Альберту Эйнштейну принадлежат слова о том, что Бог не играет в кости. Что имел в виду великий ученый?

А в 1925 году Вернер Гейзенберг создает квантовую механику, которая ниспровергла детерминистическую картину мира. Квантовая механика вернула неопределенность в поведение микрочастиц.

Невозможность одновременного знания положения и скорости частицы влечет за собой и исчезновение понятия траектории. Можно сказать, что в какой-то степени частица находится сразу во многих местах, она «размазана» по всему пространству или его части. Но если мы измерим положение частицы с помощью детектора, то ее положение «схлопывается» в одну точку (вернее, в достаточно малую область пространства). Но какая это будет точка, заранее неизвестно: квантовая механика позволяет узнать лишь вероятности схлопывания положения частицы в ту или иную точку. А это означает, что детерминистическая картина больше не имеет места! Даже если мы владеем полной информацией о частице, мы не можем однозначно предсказывать ее будущее, мы можем предсказывать лишь вероятности того или иного будущего!

Для Эйнштейна (как и ранее для творцов классической механики) выражением религиозности и всемогущества Творца был не вероятностный мир со случайными исходами, а закономерный детерминистический мир, где все движется по установленному Богом распорядку. И до конца своей жизни Эйнштейн пытался построить какую-то более фундаментальную теорию, стоящую за квантовой механикой, которая была бы детерминистической и похожей на механику классическую. Надо сказать, не прекращаются такие попытки и сейчас. Кстати, друг и оппонент Эйнштейна, сторонник квантовой механики Нильс Бор остроумно ответил ему: «Эйнштейн, перестань указывать Богу, что Он должен делать со Своими игральными костями!»

Бог не играет в кости?

Н.Бор и А.Эйнштейн решают, играет ли Бог в кости

БЛАГОДАРЮ ЗА ВНИМАНИЕ

Профессор Звонов Валерий Степанович Санкт-Петербургский университет государственной противопожарной службы МЧС России кафедра Физики и теплотехники

[email protected]

«Введение в квантовую механику »

Профессор Звонов Валерий Степанович Санкт-Петербургский университет государственной противопожарной службы МЧС России кафедра Физики и теплотехники

ВОПРОСЫ ?

Профессор Звонов Валерий Степанович Санкт-Петербургский университет государственной противопожарной службы МЧС России кафедра Физики и теплотехники