Путь в графе. Цепи и циклы. Связные графы.

Путь в графе.

Цепи и циклы.

Связные графы.

Повторение

• Что называется графом?
• Что называется вершиной графа?
• Какая вершина называется изолированной?
• Что называется ребром графа?
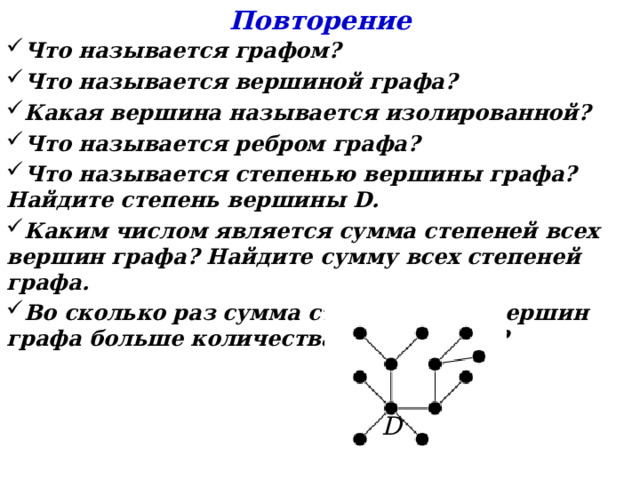
• Что называется степенью вершины графа? Найдите степень вершины D .
• Каким числом является сумма степеней всех вершин графа? Найдите сумму всех степеней графа.
• Во сколько раз сумма степеней всех вершин графа больше количества рёбер графа?

D

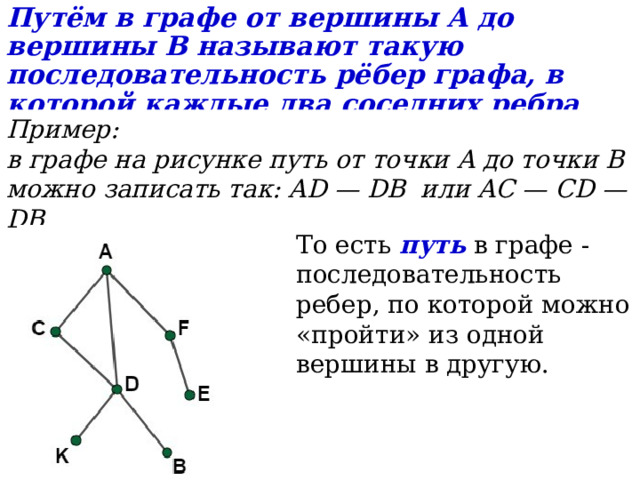
Путём в графе от вершины А до вершины B называют такую последовательность рёбер графа, в которой каждые два соседних ребра имеют общую вершину.

Пример:

в графе на рисунке путь от точки A до точки B можно записать так: AD — DB  или AC — CD — DB.

То есть путь в графе - последовательность ребер, по которой можно «пройти» из одной вершины в другую.

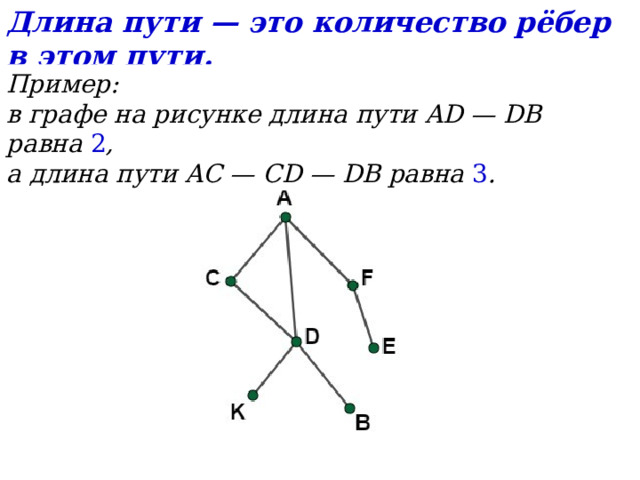
Длина пути — это количество рёбер в этом пути.

Пример:

в графе на рисунке длина пути AD — DB равна  2 ,

а длина пути AC — CD — DB равна  3 .

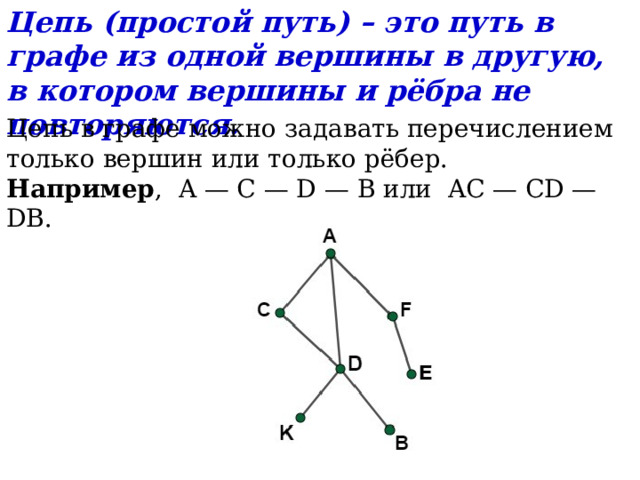
Цепь (простой путь) – это путь в графе из одной вершины в другую, в котором вершины и рёбра не повторяются.

Цепь в графе можно задавать перечислением только вершин или только рёбер.

Например ,  A — C — D — B или  AC — CD — DB.

Если граф состоит из одной-единственной цепи, то такой граф также называют цепью.

Граф без рёбер, состоящий из единственной вершины, также считают цепью.

Цепью также называется граф, у которого вершины последовательно соединены рёбрами.

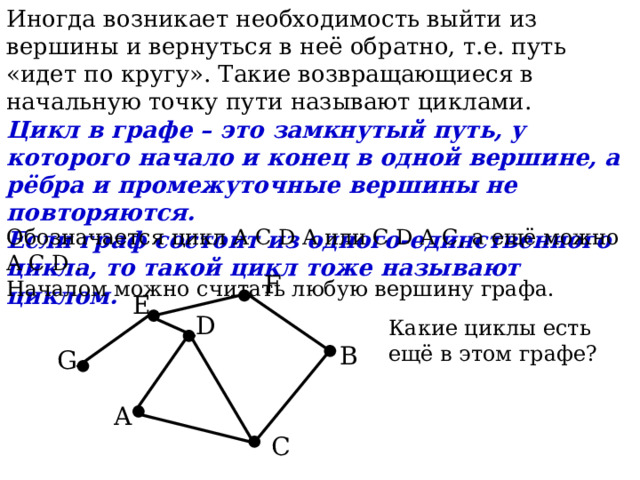
Иногда возникает необходимость выйти из вершины и вернуться в неё обратно, т.е. путь «идет по кругу». Такие возвращающиеся в начальную точку пути называют циклами.

Цикл в графе – это замкнутый путь, у которого начало и конец в одной вершине, а рёбра и промежуточные вершины не повторяются.

Если граф состоит из одного-единственного цикла, то такой цикл тоже называют циклом.

Обозначается цикл A C D A или C D A C, а ещё можно A C D .

Началом можно считать любую вершину графа.

F

E

D

Какие циклы есть ещё в этом графе?

B

G

A

C

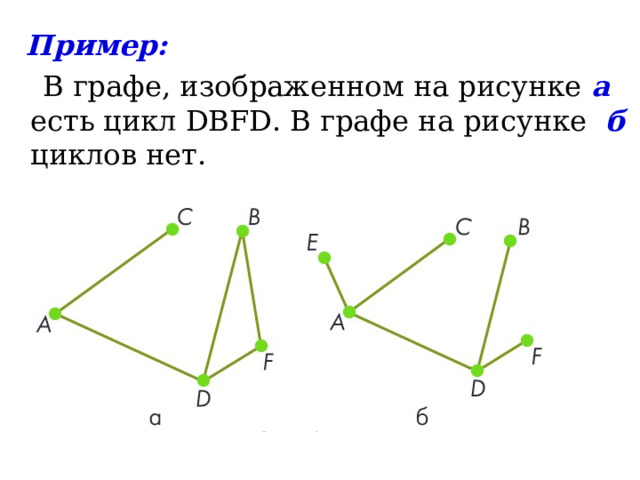
Пример:

В графе, изображенном на рисунке а есть цикл DВFD. В графе на рисунке б циклов нет.

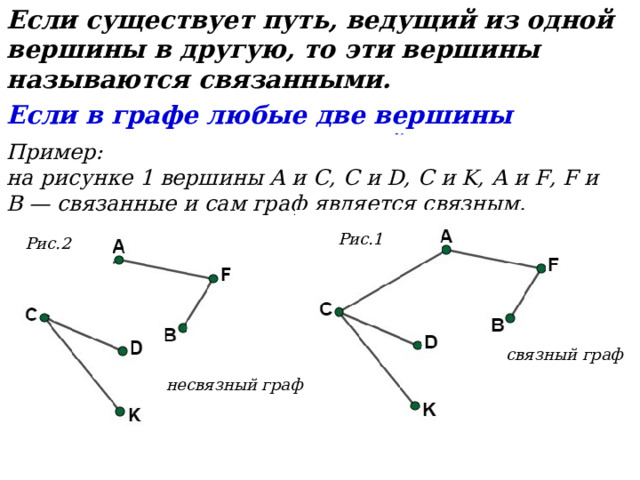
Если существует путь, ведущий из одной вершины в другую, то эти вершины называются связанными.

Если в графе любые две вершины соединены путем, то такой граф называется связным.

Пример:

на рисунке 1 вершины A и C, C и D, C и K, A и F, F и B — связанные и сам граф является связным.

Рис.1

Рис.2

связный граф

несвязный граф

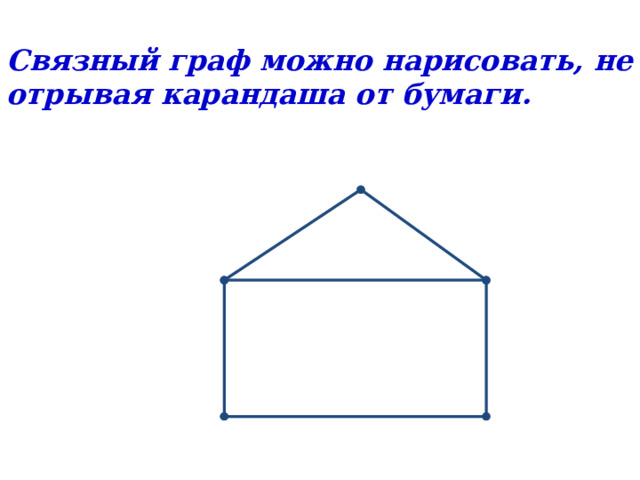
Связный граф можно нарисовать, не отрывая карандаша от бумаги.

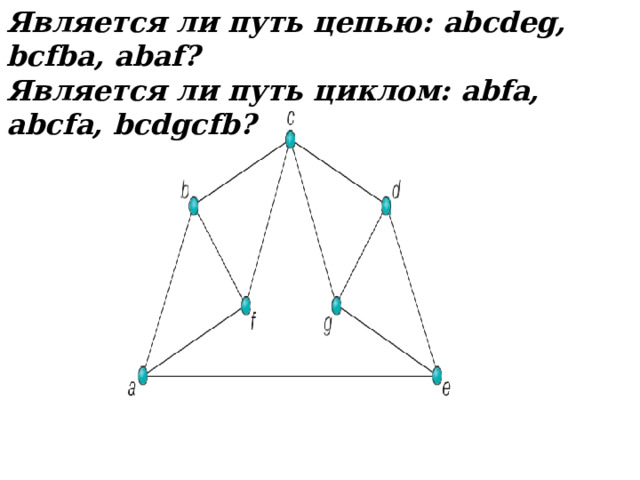
Является ли путь цепью: abcdeg, bcfba, abaf ?

Является ли путь циклом: abfa, abcfa, bcdgcfb ?

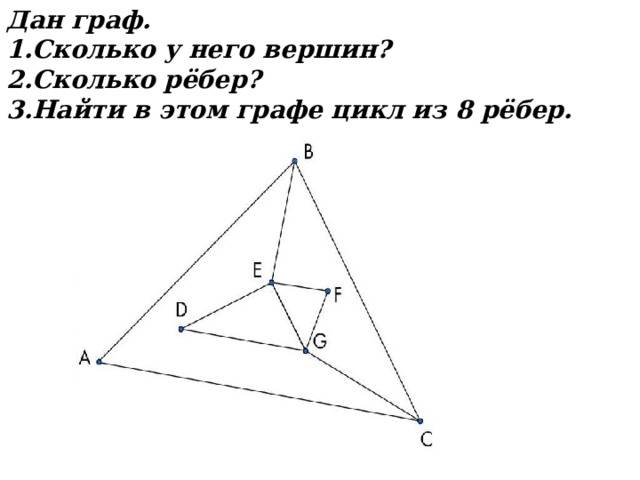
Дан граф.

• Сколько у него вершин?
• Сколько рёбер?
• Найти в этом графе цикл из 8 рёбер.

Использованные источники:

https://www.yaklass.ru/p/veroyatnost-i-statistika/7-klass/teoriia-grafov-7271003/tcepi-i-tcikl-puti-v-grafe-7276192/re-3ae2a5c5-5835-4b64-a9e1-e24e8be59997