«Симметрия» в задачах с параметром
Определенную группу задач с параметром составляют задачи, в формулировке которых ключевым является слово «единственное». В этих задачах требуется найти все значения параметра, при которых уравнение (неравенство, система) имеет единственное решение. Эти задачи имеют особенность: их условия не изменяются при замене знака одной или нескольких переменных («симметрия» относительно знака) или при перестановке нескольких переменных («симметрия» относительно перестановки переменных). Эта особенность – ключ к решению задачи.
Пример 1.
Найти все значения параметра a, при которых уравнение
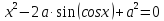 имеет единственное решение.
имеет единственное решение.
Решение.
Если число x0 является решением данного уравнения, то и число 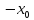 также является его решением. Поэтому для единственности решения необходимо, чтобы x0 =
также является его решением. Поэтому для единственности решения необходимо, чтобы x0 = 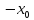 , то есть
, то есть 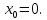
При 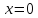 исходное уравнение примет вид:
исходное уравнение примет вид: 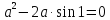 ,
, 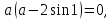
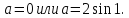 Эти значения 0 и 2sin1 являются допустимыми значениями параметра. Проверим, являются ли условия
Эти значения 0 и 2sin1 являются допустимыми значениями параметра. Проверим, являются ли условия 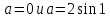 достаточными для единственности решения.
достаточными для единственности решения.
Пусть 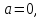 тогда исходное уравнение примет вид:
тогда исходное уравнение примет вид: 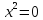 , x = 0 – единственный корень. Следовательно,
, x = 0 – единственный корень. Следовательно, 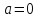 удовлетворяет условию задачи.
удовлетворяет условию задачи.
Пусть 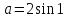 . Тогда исходное уравнение примет вид:
. Тогда исходное уравнение примет вид:
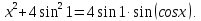
Оценим обе части полученного уравнения. Так как 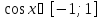 при любом х, а на отрезке
при любом х, а на отрезке 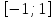 функция sin t является возрастающей, то
функция sin t является возрастающей, то
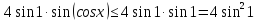 при любом х.
при любом х.
Левая часть 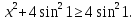
Поэтому уравнение 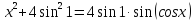 равносильно системе:
равносильно системе:
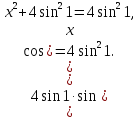
Единственным решением этой системы является х = 0. Значит, 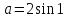 также удовлетворяет условию задачи.
также удовлетворяет условию задачи.
Ответ: 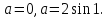
Пример 2.
Найти все значения параметра 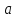 , при которых система
, при которых система
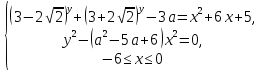
имеет единственное решение.
Решение.
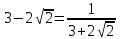 , так как
, так как
Следовательно,  .
.
Поэтому, если пара  является решением исходной системы, то и пара
является решением исходной системы, то и пара  также является ее решением. Значит, для того чтобы решение было единственным, необходимо равенство
также является ее решением. Значит, для того чтобы решение было единственным, необходимо равенство  , то есть
, то есть  При y = 0 исходная система примет вид:
При y = 0 исходная система примет вид:
Решая второе уравнение системы, имеем:
 или
или 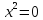 ,
,
 или х = 0.
или х = 0.
Подставим х = 0 в первое уравнение: 
Итак, допустимые значения параметра: 

Проверим, какие из этих допустимых значений удовлетворяют условию задачи.
При  исходная система примет вид:
исходная система примет вид:
Оценим обе части первого уравнения системы.  как сумма взаимно обратных положительных величин.
как сумма взаимно обратных положительных величин.
Поэтому последняя система равносильна следующей:

Значит, при  исходная система имеет единственное решение (0; 0).
исходная система имеет единственное решение (0; 0).
Пусть  . Тогда исходная система примет вид:
. Тогда исходная система примет вид:

Следовательно, при  система имеет единственное решение (-3; 0).
система имеет единственное решение (-3; 0).
При  исходная система примет вид:
исходная система примет вид:
Система не имеет решения.
Ответ: 

Пример 3.
Найти значения параметра t, при которых система имеет два решения.
Решение.
Если  – решение системы, то
– решение системы, то  ,
, 
 также будут решениями системы. Два решения будут в случае
также будут решениями системы. Два решения будут в случае  или
или  .
.
При x = y исходная система примет вид:  Из уравнения
Из уравнения  найдем допустимые значения параметра t: t =
найдем допустимые значения параметра t: t =  1; t = 3.
1; t = 3.
При  исходная система примет вид:
исходная система примет вид:  Из уравнения
Из уравнения
 найдем допустимые значения параметра t: t = 1; t =
найдем допустимые значения параметра t: t = 1; t =  3.
3.
Выполним проверку.
При t =  1 исходная система примет вид:
1 исходная система примет вид:  Система не имеет решения при t =
Система не имеет решения при t =  1. Значение t =
1. Значение t =  1 не удовлетворяет условию задачи.
1 не удовлетворяет условию задачи.
При t = 3 исходная система примет вид:  Прибавим к первому уравнению системы второе уравнение, умноженное на 2. Затем вычтем из первого уравнения второе уравнение, умноженное на 2.
Прибавим к первому уравнению системы второе уравнение, умноженное на 2. Затем вычтем из первого уравнения второе уравнение, умноженное на 2.
Система примет вид: 
 или
или 
При t = 3 исходная система имеет два решения: 
При t =  3 исходная система примет вид: Система не имеет решений при t =
3 исходная система примет вид: Система не имеет решений при t =  3. Значит, t =
3. Значит, t =  3 не удовлетворяет условию задачи.
3 не удовлетворяет условию задачи.
При t = 1 исходная система примет вид:
 или
или
 или
или 
При t = 1 система (исходная) имеет два решения: 
Ответ: t = 1, t = 3.
Пример 4.
Найти значения параметра 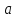 , при которых система имеет единственное решение.
, при которых система имеет единственное решение.
Решение.
Пусть 
 решение системы, тогда
решение системы, тогда  также
также  решение системы.
решение системы.
Система будет иметь единственное решение при  , то есть
, то есть 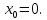
При 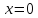 исходная система примет вид:
исходная система примет вид:  откуда найдем допустимые значения параметра
откуда найдем допустимые значения параметра 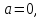

Проверка.
При 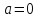 исходная система примет вид:
исходная система примет вид:


 или
или  или
или 
 три решения.
три решения.
Значит, 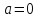 не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
При  исходная система примет вид:
исходная система примет вид:  Из первого уравнения системы
Из первого уравнения системы  , из второго уравнения
, из второго уравнения  Следовательно,
Следовательно,  , тогда
, тогда  Система имеет единственное решение (0; 1).
Система имеет единственное решение (0; 1).
Ответ:  .
.
Пример 5.
При каких значениях параметра 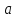 уравнение имеет единственное решение.
уравнение имеет единственное решение.
Решение.
Если 
 решение данного уравнения, то и
решение данного уравнения, то и  также является его решением в силу четности функции в левой части уравнения. Следовательно,
также является его решением в силу четности функции в левой части уравнения. Следовательно, 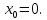
При 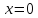 исходное уравнение примет вид:
исходное уравнение примет вид:  Таким образом, 0 и
Таким образом, 0 и 
 допустимые значения параметра.
допустимые значения параметра.
Проверка. При 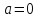 уравнение примет вид:
уравнение примет вид: 


 (три решения). Следовательно,
(три решения). Следовательно, 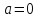 не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
При  исходное уравнение примет вид:
исходное уравнение примет вид:  Левая часть уравнения
Левая часть уравнения  правая
правая  Следовательно, решением уравнения является решение системы:
Следовательно, решением уравнения является решение системы:  х=0 – единственное решение.
х=0 – единственное решение.
Ответ: 
Пример 6.
Найти значения параметра  при которых система имеет два решения.
при которых система имеет два решения.
Решение.
Если  – решение данной системы, то
– решение данной системы, то  ,
, 
 также являются решениями этой системы. Два решения будут, если
также являются решениями этой системы. Два решения будут, если  или
или  .
.
При x = y система примет вид: 
Допустимое значение параметра 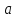 равно 2,5.
равно 2,5.
При  система примет вид:
система примет вид:  и не имеет решения.
и не имеет решения.
Проверка: при 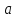 = 2,5 исходная система примет вид:
= 2,5 исходная система примет вид:

 два решения.
два решения.
Ответ: 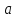 = 2,5.
= 2,5.
Пример 7.
Найти все значения параметра  при каждом из которых уравнение
при каждом из которых уравнение  имеет единственный корень.
имеет единственный корень.
Решение.

Уравнение не изменится, если заменить  числом
числом  . Следовательно, уравнение имеет четное число ненулевых решений, а нечетное число решений будет только тогда, когда одно из них 0.
. Следовательно, уравнение имеет четное число ненулевых решений, а нечетное число решений будет только тогда, когда одно из них 0.
Подставим 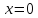 в исходное уравнение:
в исходное уравнение:
 ;
; 
Следовательно,  или
или 
Если  , то исходное уравнение примет вид:
, то исходное уравнение примет вид: 
Если
Если
Значит, исходное уравнение имеет три решения: -2; 0; 2.
Если  , то исходное уравнение примет вид:
, то исходное уравнение примет вид: 









2
-2
x+2
x-2
При  , имеем: , нет корней.
, имеем: , нет корней.
При ,
 единственное решение.
единственное решение.
При  , имеем: , нет корней.
, имеем: , нет корней.
Значит, если  то уравнение имеет единственное решение.
то уравнение имеет единственное решение.
Если
Если
Ответ:  ,
, 
Пример 8.
Найти все значения параметра  при каждом из которых уравнение
при каждом из которых уравнение  имеет ровно три корня.
имеет ровно три корня.
Решение.
Уравнение не изменится, если заменить  числом
числом  . Следовательно, уравнение имеет четное число ненулевых решений, а три решения уравнение имеет только тогда, когда одно из них 0.
. Следовательно, уравнение имеет четное число ненулевых решений, а три решения уравнение имеет только тогда, когда одно из них 0.
Подставим 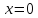 в исходное уравнение:
в исходное уравнение:
 ;
;
 или
или 



При  исходное уравнение примет вид:
исходное уравнение примет вид: 
Если
Если
Итак, при  уравнение имеет три корня:
уравнение имеет три корня:  ; 0; 2.
; 0; 2.
Если  , то исходное уравнение примет вид:
, то исходное уравнение примет вид: 









2
-2
x+2
x-2
При  , имеем: , нет корней.
, имеем: , нет корней.
При ,
 единственное решение.
единственное решение.
При  , имеем: , нет корней.
, имеем: , нет корней.
Значит, если  то уравнение имеет единственное решение.
то уравнение имеет единственное решение.
Ответ: 







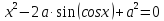 имеет единственное решение.
имеет единственное решение.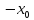 также является его решением. Поэтому для единственности решения необходимо, чтобы x0 =
также является его решением. Поэтому для единственности решения необходимо, чтобы x0 = 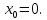
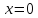 исходное уравнение примет вид:
исходное уравнение примет вид: 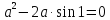 ,
, 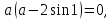
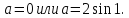 Эти значения 0 и 2sin1 являются допустимыми значениями параметра. Проверим, являются ли условия
Эти значения 0 и 2sin1 являются допустимыми значениями параметра. Проверим, являются ли условия 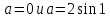 достаточными для единственности решения.
достаточными для единственности решения.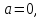 тогда исходное уравнение примет вид:
тогда исходное уравнение примет вид: 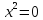 , x = 0 – единственный корень. Следовательно,
, x = 0 – единственный корень. Следовательно, 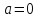 удовлетворяет условию задачи.
удовлетворяет условию задачи.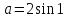 . Тогда исходное уравнение примет вид:
. Тогда исходное уравнение примет вид: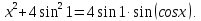
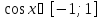 при любом х, а на отрезке
при любом х, а на отрезке 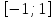 функция sin t является возрастающей, то
функция sin t является возрастающей, то 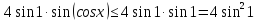 при любом х.
при любом х. 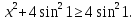
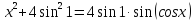 равносильно системе:
равносильно системе: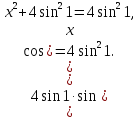
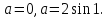
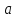 , при которых система
, при которых система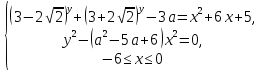
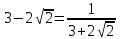 , так как
, так как 
















