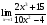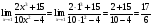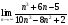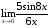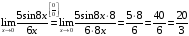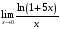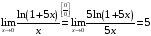ГОБПОУ «Конь-Колодезский аграрный техникум»
Систематизированный курс лекций
УД ЕН.01 Математика
по специальности 38.02.01 Экономика и бухгалтерский учёт
(отрасль – «Сельское хозяйство)
Составитель: Ярцева Ольга Алексеевна,
преподаватель математики
2017г.
Краткая аннотация
Систематизированный курс лекций по учебной дисциплине ЕН.01 Математика разработан на основе ФГОС СПО по специальности 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство), утверждённого приказом Министерства образования и науки РФ от «28» июля 2014 года №832, рабочей программы учебной дисциплины ЕН.01 Математика, доработанной в соответствии с требованиями Профессионального стандарта по профессии «Бухгалтер», утвержденным приказом Министерства труда и социальной защиты Российской Федерации от 22.12.2014 г. №1061н. Курс лекций содержит теоретические сведения, необходимые для успешного освоения учебной дисциплины, изучения основных понятий в области математики, список рекомендованных источников.
Содержание
Лекция №1. «Функции одной независимой переменной. Пределы.
Непрерывность функции. Производная, геометрический смысл.
Исследования функций»……………………………………………………………….4
Лекция №2. «Неопределённый интеграл. Непосредственное
интегрирование. Замена переменной. Определённый интеграл.
Вычисление определённого интеграла. Геометрический смысл
определённого интеграла»…………………………………………………………….9
Лекция №3 «Функции нескольких переменных. Приложение интеграла
к решению прикладных задач. Частные производные»…………………………….12
Лекция №4 «Задачи, приводящие к дифференциальным
уравнениям. Дифференциальные уравнения с разделяющимися
переменными. Общие и частные решения. Однородные
дифференциальные уравнения первого порядка. Линейные однородные
уравнения второго порядка с постоянными коэффициентами»……………………15
Лекция №5 «Числовые ряды. Сходимость и расходимость числовых
рядов. Признак сходимости Даламбера. Знакопеременные ряды.
Абсолютная и условная сходимость рядов. Функциональные ряды.
Разложение элементарных функций в ряд Маклорена»……………………………19
Лекция №6 «Элементы множества. Задание множеств. Операции над
множествами. Отношения. Свойства отношений»…………………………………21
Лекция №7 «Графы. Основные определения. Элементы графов. Виды графов
и операции над ними»…………………………………………………………………24
Лекция №8 «Понятие события и вероятности события. Достоверные
и невозможные события. Классическое определение вероятностей.
Теорема сложения вероятностей. Теорема умножения вероятностей»……….…..26
Лекция №9 «Определение матрицы и ее обозначения. Виды матриц.
Определитель матрицы. Линейная функция и ее график. Уравнение с одной переменной. Корни уравнения. Линейные уравнения. Метод Гаусса решения систем линейных уравнений. Использование системы линейных уравнений
при решении экономических задач. (Метод Крамера. Матричный метод.
Метод Гаусса)»……………………………………………………………..………….28
Лекция №10 «Понятия комплексного числа. Действительная и мнимая части комплексного числа. Аргумент и модуль комплексного числа. Абсцисса и
ордината комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Правила выполнения операций с комплексными числами»……………………………………………………………………………….33
Список использованной литературы………………………………………………...37
Лекция №1
Тема: «Функции одной независимой переменной. Пределы. Непрерывность функции. Производная, геометрический смысл. Исследования функций»
уметь:
- вычислять пределы функции с использованием первого и второго замечательных пределов;
- исследовать функцию на непрерывность с помощью производной;
- вычислять производные функций с помощью таблицы производных и формул производных: суммы, произведения и частного.
знать:
- основные способы вычисления пределов функций;
- формулы первого и второго замечательных пределов;
- алгоритм исследования функции на непрерывность с помощью производной;
- таблицы производных и формул производных: суммы, произведения и частного.
Понятие функции одной переменной.
Рассмотрим два числовых множества X и Y. Правило f, по которому каждому числу х принадлежит Х ставится в соответствие единственное число y из множества Y, называется числовой функцией, заданной на множестве Х и принимающей значения во множестве Y.
Таким образом, задать функцию, значит задать три объекта:
1) множество Х (область определения функции);
2) множество Y (область значений функции);
3) правило соответствия f (сама функция).
Например, поставим в соответствие каждому числу его куб. Математически это можно записать формулой y=x2. В этом случае правило f есть возведение числа х в третью степень. В общем случае, если каждому х по правилу f соответствует единственный y, пишут y = f(x). Здесь "х" называют независимой переменной или аргументом, а "y" -зависимой переменной (т.к. выражение типа x2 само по себе не имеет определенного числового значения пока не указано значение х) или функцией от х. О величинах х и y говорят, что они связаны функциональной зависимостью.
Зная все значения х и правило f можно найти все значения у. Например, если х=2, то функция f(x)=x2 принимает значение у= f(2) =22 =4.
Способы задания функции одной переменной
Существуют несколько способов задания функции.
Аналитический способ. Функция f задается в виде формулы y=f(x). Например, y=3cos(x)+2x2.
Этот способ является преобладающим в математических исследованиях и подробно
рассматривается в классическом курсе математики. В географических исследованиях соответствие между переменными величинами x и y не всегда удается записать в виде формулы. Во многих случаях формула бывает неизвестна. Тогда для выражения функциональной зависимости используются другие способы.
Графический способ. На метеорологических станциях можно наблюдать работу приборов-
самописцев, регистрирующих величины атмосферного давления, температуры воздуха, его влажности в любой момент времени суток. По полученному графику можно определить значения указанных величин в любой момент времени. Имея перед собой график, мы как бы "видим функцию".
Табличный способ. Этот способ является наиболее простым. В одной строке таблицы
записываются все значения аргумента (числа), а в другой – значения f(x), соответствующие каждому х. Например, зависимость температуры воздуха (Т) от времени суток (t) в определенный день можно представить таблицей.
Уже известные для нас элементарные функции:
у = С, у = х, у = кх + в, у = 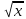 , y = x2 , y = x3, y = sinx, y =cosx, y = tgx, y = ctgx и т.п.
, y = x2 , y = x3, y = sinx, y =cosx, y = tgx, y = ctgx и т.п.
Число А называют пределом функции f(x) при 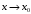 (и пишут
(и пишут 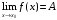 ), если для любого
), если для любого  найдется число
найдется число 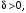 зависящее от , такое, что для всех
зависящее от , такое, что для всех 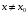 , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 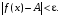
Теоремы о пределах:
1. 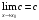 (c=const).
(c=const).
2. Если 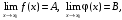 то:
то:
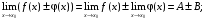
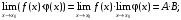
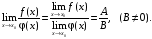
Первый замечательный предел: 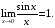
Второй замечательный предел (число е = 2,718…):
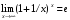 или
или 
Пример 1. Вычислить предел 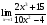
Решение:
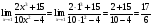
Пример 2. Вычислить предел 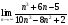
Решение:

Пример 3. Вычислить предел 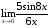
Решение:
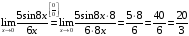
Пример 4. Вычислить предел 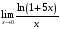
Решение:
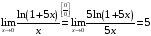
Формулы дифференцирования

 в частности,
в частности, 
 в частности,
в частности, 
 в частности,
в частности, 
Правила дифференцирования
1)  ;
;
2)  , в частности
, в частности  ;
;
3)  ;
;
4)  , если
, если ;
;
5)  , если
, если  и
и  .
.
Возрастание и убывание функций
Теорема 1. (необходимые условия). Если дифференцируемая на интервале (а;b) функция  возрастает (убывает), то
возрастает (убывает), то 
 для любого
для любого  .
.
Теорема 2. (достаточные условия). Если функция  дифференцируема на интервале (a;b) и
дифференцируема на интервале (a;b) и 
 для любого
для любого  , то эта функция возрастает (убывает) на интервале (a;b).
, то эта функция возрастает (убывает) на интервале (a;b).
Теоремы 1 и 2 позволяют довольно просто исследовать функцию на монотонность (функция, убывающая или возрастающая, называется монотонной).
Пример 5. Исследовать функцию  =x3-3x-4 на монотонность.
=x3-3x-4 на монотонность.
Решение:



 + - +
+ - +

-1 1
 при
при 
 при
при 
Ответ: данная функция возрастает при  и убывает
и убывает 
Пример 6. Исследовать функцию  на монотонность.
на монотонность.
Решение:

Так как у’0 в области определения, то функции является возрастающей на каждом интервале области определения.
Контрольные вопросы
Понятие функции одной независимой переменной.
Способы задания функции.
Понятие предела функции.
Основные способы вычисления пределов функций.
Алгоритм исследования функции на непрерывность с помощью производной.
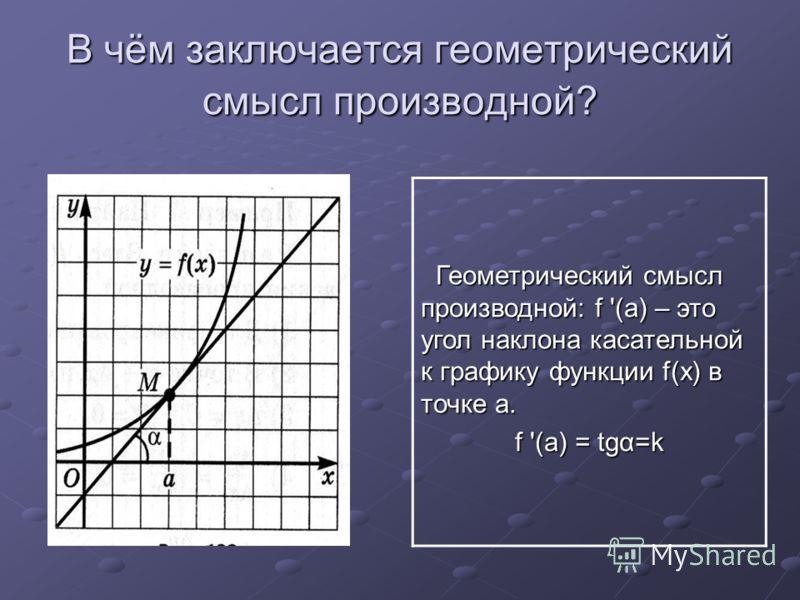
Понятие производной функции. Геометрический смысл производной функции.
Лекция №2
Тема: «Неопределённый интеграл. Непосредственное интегрирование. Замена переменной. Определённый интеграл. Вычисление определённого интеграла. Геометрический смысл определённого интеграла»
уметь:
- интегрировать простейшие определённые интегралы, используя таблицу простейших интегралов и формулу Ньютона – Лейбница;
- вычислять площади плоских фигур;
знать:
- формулы таблицы простейших неопределённых интегралов;
- формулу Ньютона – Лейбница.
Функция  , определенная на интервале
, определенная на интервале  , называется первообразной для функции
, называется первообразной для функции  , определенной на том же интервале
, определенной на том же интервале  , если
, если 
Если  — первообразная для функции
— первообразная для функции  , то любая другая первообразная
, то любая другая первообразная  для функции
для функции  отличается от
отличается от  на некоторое постоянное слагаемое, т. е.
на некоторое постоянное слагаемое, т. е.  где
где  .
.
Неопределенным интегралом от функции  называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:
называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:  где
где 
Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:

Свойства неопределенного интеграла:
1.
2. 
3.
4. 
Таблица основных неопределённых интегралов
Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] называется приращение какой-нибудь её первообразной на этом отрезке.
Если функция f (x) интегрируема на отрезке [a; b], то она ограничена на этом отрезке.
Если функция непрерывна на отрезке, то она интегрируема на нем.
Геометрический смысл определенного интеграла – площадь криволинейной трапеции.
Вычисление площади плоской фигуры
Найдем площадь S криволинейной трапеции, ограниченной кривой  осью
осью  и двумя прямыми
и двумя прямыми  и
и  , где
, где  ,
,  .
.
Так дифференциал переменной площади S есть площадь прямоугольника с основанием dx и высотой  , т. е.
, т. е.  , то, интегрируя это равенство в пределах от a до b, получим
, то, интегрируя это равенство в пределах от a до b, получим


Пример1. Вычислить площадь фигуры, ограниченной указанными линиями 

 и
и 
Решение:
Выполним построение фигуры. Строим прямую  по двум точкам А(4;0) и В(0;2) (рис.6). Выразив у через х, получим
по двум точкам А(4;0) и В(0;2) (рис.6). Выразив у через х, получим  По формуле (1), где
По формуле (1), где  ,
,  и
и  , находим
, находим
(кв. ед.)
Пример2. Скорость движения точки изменяется по закону  м/с. Найти путь, пройденный точкой за 10 с от начала движения.
м/с. Найти путь, пройденный точкой за 10 с от начала движения.
Решение:
Согласно условию,  ,
,  ,
,  . По формуле (6) находим
. По формуле (6) находим
(м).
Контрольные вопросы
Понятие неопределённого интеграла.
Понятие определённого интеграла.
В чём заключается геометрический смысл определённого интеграла?
Площадь каких фигур можно вычислить с помощью формулы Ньютона-Лейбница?
Лекция №3
Тема: «Функции нескольких переменных. Приложение интеграла к решению прикладных задач. Частные производные»
знать:
- формулы для вычисления некоторых физических величин;
уметь:
- вычислять определенные интегралы;
- применять полученные знания и умения при решении задач прикладного характера.
Если каждой паре независимых друг от друга чисел (х,у) из некоторого множества по какому-либо правилу ставится в соответствие одно значение переменной z, то она называется функцией двух переменных. z=f(x,y,)
Область определения функции z - совокупность пар (х,у), при которых функция z существует.
Множество значений (область значений) функции – все значения, которые принимает функция в ее области определения.
График функции двух переменных - множество точек P, координаты которых удовлетворяют уравнению z=f(x,y)
Обозначение определенного интеграла ввел Ж.Фурье.
Формула Ньютона-Лейбница носит название “основной формулы интегрального исчисления”. Она позволяет сводить сложное вычисление определенных интегралов, т.е. нахождение пределов интегральных сумм, к более простой операции отыскания первообразных.

Дальнейшее развитие интегрального исчисления связано с именем Леонарда Эйлера. Он составил полный курс математического анализа, состоящий из шести книг, три из которых посвятил интегральному исчислению.
Наряду с Эйлером выдающихся результатов в области математического анализа добился крупнейший математик 18 века – Лагранж. Он в 18-летнем возрасте уже занял должность профессора в артиллерийской школе города Турина (Италия), а через пять лет был избран членом Берлинской Академии наук.
Теория интеграла была за тем развита Риманом, который впервые определил необходимые и достаточные условия интегрируемости ограниченной функции. Ему принадлежит общее определение определенного интеграла, поэтому интегральную сумму стали называть “римановской”.
Большой вклад в развитие математического анализа в 19 веке внесли российские ученые Остроградский и Чебышев. Работы Чебышева в последствии продолжил его ученик – Ляпунов, Стеклов, Бернштейн и другие. Проблемы теории интегрального исчисления до сих пор волнуют умы математиков всех стран. Дело Чебышева и Остроградского продолжают ученые современной России.
Применение определенного интеграла не ограничивается вычислением площади фигуры.
Определенный интеграл помогает решать ряд физических и общетехнических задач, поэтому знания, полученные вами на этом уроке, помогут в вашей дальнейшей учебе и практической деятельности.
Задача о вычислении пути
Согласно физическому смыслу первой производной, производная функции в точке есть мгновенная скорость точки, т.е.  . Отсюда,
. Отсюда, . Интегрируя полученное равенство в пределах от t1 до t2 получаем
. Интегрируя полученное равенство в пределах от t1 до t2 получаем

Контрольные вопросы:
Что можно вычислить с помощью определенного интеграла?
Лекция №4
Тема: «Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения. Однородные дифференциальные уравнения первого порядка. Линейные однородные уравнения второго порядка с постоянными коэффициентами»
уметь:
-решать дифференциальные уравнения с разделяющимися переменными; однородные дифференциальные уравнения первого порядка;
-линейные дифференциальные уравнения первого порядка с постоянными коэффициентами;
знать:
- основные понятия дифференциального исчисления;
- алгоритм решения дифференциальных уравнений с разделяющимися переменными.
- понятие дифференциальных уравнений в частных производных;
- методы решения простейших дифференциальных уравнений в частных производных.
Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.
Дифференциальное уравнение первого порядка содержит:
независимую переменную х;
зависимую переменную у;
первую производную у′ функции.
Решить дифференциальное уравнение – это значит, найти множество функций
у = f(x) + C, которые удовлетворяют данному уравнению.
Пример 1. Решить дифференциальное уравнение ху′ = у.
В первую очередь нужно переписать производную с помощью дифференциалов:
y′ =  . Теперь подставляем в уравнение, получаем
. Теперь подставляем в уравнение, получаем
х· = y.
= y.
Пробуем разделить переменные, то есть в левой части уравнения оставить только «угреки», а в правой «иксы» или наоборот.
 =
=
Переменные разделены.
Затем интегрируем полученное дифференциальное уравнение:
 =
=
ln =ln
=ln +C, где С=const.
+C, где С=const.
ln - ln
- ln =C
=C
ln =С
=С
 =еС
=еС
у=х· еС – общее решение дифференциального уравнения.
Пример 2. Найти частное решение дифференциального уравнения ху′ = у, удовлетворяющего начальному условию у(1) = 2.
По условию требуется найти частное решение дифференциального уравнения, удовлетворяющего начальному условию. Такая постановка вопроса называется задачей Коши.
Общее решение данного уравнения у нас уже имеется у=х· еС (пример 1).
Найдем частное решение. По условию у(1) = 2, получим
2 = 1· еС
еС=2
еС - тоже некоторая константа, которую обозначим через С.
С=2
Итак, в общее решение подставляем С=2, получим
у=х· е2 – частное решение дифференциального уравнения ху′ = у.
Решение простейших линейных дифференциальных уравнений относительно частных производных.
Дифференциальное уравнение первого порядка в частных производных — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных U = U(x, y) и их частные производные,  .
.
Дифференциальные уравнения в частных производных можно решить по принципу разделения переменных для нахождения общего решения. Затем, для нахождения частного решения уравнение можно решить по принципу задачи Коши, рассмотренной в предыдущем практическом занятии (ПЗ №3), то есть сначала нужно найти общее решение дифференциального уравнения, затем подставив начальные условия (х0,у0), найти значение константы С. Записав общее решение с полученной константой, получим искомое частное решение дифференциального уравнения.
Уравнение с частными производными имеет бесчисленное множество решений. Кроме произвольных постоянных, в решение уравнений с частными производными могут входить произвольные функции тех же аргументов, от которых зависит искомая функция.
Рассмотрим функцию двух переменных:

Требуется найти частные производные первого порядка  ,
,  и составить полный дифференциал
и составить полный дифференциал  .
.
Поменяем букву «зет» на букву «эф»:
Дана функция двух переменных  . Требуется найти частные производные первого порядка
. Требуется найти частные производные первого порядка  ,
,  и составить полный дифференциал
и составить полный дифференциал  .
.
Найдем частные производные первого порядка:

Полный дифференциал составим по формуле:
 , или, то же самое:
, или, то же самое: 
В данном случае: 
Пример 1
Решить дифференциальное уравнение 
Уже известен ответ:  , точнее, надо еще добавить константу:
, точнее, надо еще добавить константу:
Общий интеграл  является решением дифференциального уравнения
является решением дифференциального уравнения  .
.
Таким образом, дифференциальное уравнение  является полным дифференциалом функции
является полным дифференциалом функции  .
.
Рассмотрим алгоритм решения уравнения в полных дифференциалах.
Итак, требуется решить дифференциальное уравнение:

1) Докажем, что уравнение  является уравнением в полных дифференциалах. Как это сделать? Уравнение в полных дифференциалах имеет вид
является уравнением в полных дифференциалах. Как это сделать? Уравнение в полных дифференциалах имеет вид  . Характерное и очень удобное равенство смешанных производных второго порядка:
. Характерное и очень удобное равенство смешанных производных второго порядка:  . Вот его и надо проверить:
. Вот его и надо проверить:


 , значит, данное уравнение является уравнением в полных дифференциалах.
, значит, данное уравнение является уравнением в полных дифференциалах.
Проверка выглядит примерно так:
Проверим, является ли уравнение  уравнением в полным дифференциалах:
уравнением в полным дифференциалах:
 , значит, данное ДУ является уравнением в полных дифференциалах
, значит, данное ДУ является уравнением в полных дифференциалах
Контрольные вопросы
Понятие дифференциального уравнения. Привести пример.
Алгоритм решения дифференциального уравнения.
Понятие задачи Коши.
Понятие дифференциального уравнения. Привести пример.
Понятие дифференциального уравнения в частных производных. Привести пример.
Понятие задачи Коши.
Лекция №5
Тема: «Числовые ряды. Сходимость и расходимость числовых рядов. Признак сходимости Даламбера. Знакопеременные ряды. Абсолютная и условная сходимость рядов. Функциональные ряды. Разложение элементарных функций в ряд Маклорена»
уметь:
определять сходимость числовых и функциональных рядов по признаку Даламбера;
применять признак Лейбница для знакопеременных рядов;
разлагать элементарные функции в ряд Маклорена.
знать:
- основные понятия по теме «Ряды»,
- признаки сходимости числовых и функциональных рядов,
- признак Даламбера.
В «бесконечной» сумме а1+а2+а3… процесс сложения никогда не кончается, за каждым слагаемым всегда стоит следующее.
Ряд 1+х+х2+х3+…=
Сумма этого ряда была определена впервые в III в. до н.э. (из истории математики). Архимед применил суммирование бесконечной геометрической прогрессии со знаменателем 1/4.
После Архимеда вплоть до XVI в. рядами не занимались. С XVI в. началось изучение изменяющихся процессов. Для знакочередующегося ряда
 +
+  -
-  +
+  ….
….
Г. Лейбниц находит сумму. Она равна  .
.
Ряд называется числовым, если все его члены являются числами.
Ряд является функциональным, если все члены ряда – функции.
Если сходится ряд, получившийся из заданного ряда отбрасыванием нескольких его членов, то сходится и сам заданный ряд. Если у сходящегося ряда отбросить несколько членов, то получится также сходящийся ряд.
Если ряд а1+а2+а3… сходится и его сумма равна S, то ряд са1+са2+са3… гдеc – какое-либо фиксированное число, также сходится, и его сумма равна cS.
Необходимый признак сходимости ряда
Если ряд сходится, то предел его общего члена равен нулю при n→∞.
Этот признак не является достаточным, т.е. из того, что  , еще не следует, что ряд сходится.
, еще не следует, что ряд сходится.
Признак Даламбера заключается в следующем:
Если для числового ряда
 существует такое число q{\displaystyle q}, {\displaystyle 00˂q˂1, что, начиная с некоторого номера, выполняется неравенство
существует такое число q{\displaystyle q}, {\displaystyle 00˂q˂1, что, начиная с некоторого номера, выполняется неравенство
 ,{\displaystyle \left|{\frac {a_{n+1}}{a_{n}}}\right|\leqslant q,}то данный ряд абсолютно сходится; если же, начиная с некоторого номера
,{\displaystyle \left|{\frac {a_{n+1}}{a_{n}}}\right|\leqslant q,}то данный ряд абсолютно сходится; если же, начиная с некоторого номера ˃1, {\displaystyle \left|{\frac {a_{n+1}}{a_{n}}}\right|\geq 1}то ряд расходится.
˃1, {\displaystyle \left|{\frac {a_{n+1}}{a_{n}}}\right|\geq 1}то ряд расходится.
Пример 1. Исследовать на сходимость ряд  .
.
Решение:
Применим признак Даламбера; имеем 
 ,
,
Так как D
Контрольные вопросы
Что такое ряд?
Понятие сходящегося ряда.
Понятие расходящегося ряда.
Необходимый признак сходимости.
Признак Даламбера.
Лекция №6
Тема: «Элементы множества. Задание множеств. Операции над множествами. Отношения. Свойства отношений».
знать:
- понятие множества и подмножества;
- основные способы задания множеств;
- операции над множествами;
- свойства отношений.
уметь:
- приводить примеры множества;
- выполнять операции над множествами (
Понятие множества является одним из основных понятий математики. Оно не имеет точного определения и, как правило, объясняется с помощью примеров.
Дадим следующее интуитивное определение понятия множества:
Множество – определенная совокупность объектов.
Объекты, из которых состоит множество, называются элементами множества.
Пример Множество домов на данной улице, множество натуральных чисел, множество студентов группы и т. д.
Множества обычно обозначают заглавными латинскими буквами А, В, С, D, X, Y…, элементы множества строчными латинскими буквами – a, b, c,d, x, y…
Для обозначения того, что объект x является элементом множества A, используют символику: x А (читается: x принадлежит А), запись x
А (читается: x принадлежит А), запись x А обозначает, что объект x не является элементом множества A (читается: x не принадлежит А).
А обозначает, что объект x не является элементом множества A (читается: x не принадлежит А).
множества можно изображать с помощью кругов, которые называются кругами эйлера или диаграммами венна, универсальное множество принято обозначать прямоугольником.
Способы задания множеств
Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:
1) Перечислением всех элементов множества в фигурных скобках.
Пример A = {оля, маша, саша}
2) С помощью характеристического свойства его элементов.
Характеристическое свойство – это свойство, которым обладают все элементы данного множества и только они. Этот способ применим для конечных и бесконечных множеств.
Рекурсивное задание множества.
Этот способ заключается в следующем:
Указываются некоторые исходные элементы, входящие в множество.
Описывается механизм, позволяющий получить новые элементы из имеющихся.
Объявляется, что в множестве нет никаких других объектов кроме тех, которые можно получить из исходных.
Операции над множествами:
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}
Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).
Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
Отношения. Свойства отношений
При помощи отношений в математике отображают некоторые связи между элементами множеств. Простейшими примерами отношений, уже рассмотренных раньше, являются отношения принадлежности х  X элемента х множеству X и отношения включения А
X элемента х множеству X и отношения включения А  В, А
В, А  В подмножества А в подмножество В.
В подмножества А в подмножество В.
По количеству элементов, между которыми определены связи, отношения делятся на унарные (одноместные), бинарные (двухместные), тернарные (трехместные) и n-арные (n-местные).
В унарном отношении участвует один элемент. Эти отношения называются свойствами и отождествляются с подмножеством элементов, которые этим свойством обладают. Так, например, в множестве всех положительных чисел отношение или свойство «быть четным» отождествляется с подмножеством чисел 2, 4, 6, ...
В бинарных отношениях участвуют пары элементов множеств, так называемые упорядоченные пары , 2, у2 .Упорядоченность понимается как то, что в записи х, у на первом месте всегда стоит х , а на втором у. Иными словами, х предшествует у.
Определение 15.1. Прямым (декартовым) произведением множеств А и В, обозначаемым АхВ, называется множество упорядоченных пар, такое, что первая координата каждой пары — элемент А, а вторая координата — элемент В.
Например, А - {1, 2}, В = {а, Ь, с).
Тогда А х В - {1, а , 1, Ь , 1, с , а , Ь , с }. Декартово произведение В х А - { 1 , 2 , с, 1 , а, 2 , Ь, 2 , с, 2 }. Декартово произведение А х А - {, , , } называется декартовым квадратом множества А.
Если множество А включает т различных элементов, а множество В — п элементов, то произведения множеств А х В и В х А имеет тхп элементов. Пусть А-{ 1}, а В = {1,2,3}. Тогда А х В -{ 1, 1 , , }. Если А -0, а В - {1,2,3}. Тогда Ах В = В х А = 0.
В целях наглядного представления декартовых произведений удобно использовать язык геометрии. Для этого множества X, Y представляются осями координат. Элементы х и у — соответственно абсциссами и ординатами. Само произведение X х Y — точками плоскости Х0Y. В качестве примера на рис.1 показано декартово произведение множеств X = {1, 2, 3}, Y = {1, 2}.
Контрольные вопросы
Элементы множества.
Задание множеств.
Операции над множествами.
Понятие отношения множеств. Свойства отношений.
Лекция №7
Тема: «Графы. Основные определения. Элементы графов. Виды графов и операции над ними»
Графом G(V, Е) называется совокупность двух множеств — непустого множества V (множества вершин) и множества Е неупорядоченных пар различных элементов
множества V (Е — множество ребер).
Соединения между узлами графа называются ребрами. Если узлы графа не нумерованы, то ребра являются неориентированными. У графа с нумерованными узлами ребра ориентированы. Ребрам могут быть присвоены определенные веса или метки. Число вершин графа A обозначим р, а число ребер – q:
p : = p ( A ) : = | V |, q : = = q ( A ) : = | E |;
Более простое определение графа - совокупность точек и линий, в которой каждая линия соединяет две точки. Для ориентированного графа E x - конечный набор ориентированных ребер. Ребром может быть прямая или кривая линия. Ребра не могут иметь общих точек кроме вершин (узлов) графа.
Замкнутая кривая в E может иметь только одну точку из множества V, а каждая незамкнутая кривая в E имеет ровно две точки множества V. Если V и E конечные множества, то и граф им соответствующий называется конечным. Граф называется вырожденным, если он не имеет ребер.
Параллельными ребрами графа называются такие, которые имеют общие узлы начала и конца. Если ребро соединят две вершины, то говорят, что оно им инцидентно; вершины, соединенные ребром называются смежными.
Две вершины, соединенные ребром, могут совпадать; такое ребро называется петлей. Число ребер, инцидентных вершине, называется степенью вершины. Если степень вершины равна 0, то получается изолированная графа. Если два ребра инцидентны одной и той же паре вершин, они называются кратными; граф, содержащий кратные ребра, называется мультиграфом.
Виды графов и операции над ними:
Для рассмотрения видов граф и операций над ними необходимо познакомиться с такими понятиями как подграфы, маршрут, цепь, цикл.
Граф G'(V',Е') называется подграфом графа G(V,Е) (обозначается G' Ì G), если V' Ì V и/или Е' Ì Е. Если V' = V, то G ' называется остовным подграфом G. Если V' Ì V & Е' Ì Е & (V' ¹ V Ú Е' ¹ Е), то граф G ' называется собственным подграфом графа G. Подграф G'(V' , Е') называется правильным подграфом графа G(V,Е), если G ' содержит все возможные ребра G.
Маршрутом в графе называется чередующаяся последовательность вершин и ребер в которой любые два соседних элемента инцидентны. Это определение подходит также для псевдо-, мульти- и орграфов. Для «обычного» графа достаточно указать только последовательность вершин или только последовательность ребер.Если v0 = vk, то маршрут замкнут, иначе открыт. Если все ребра различны, то маршрут называется цепью. Если все вершины (а значит, и ребра) различны, то маршрут называется простой цепью. В цепи v0, e1, v1, e2, v2,…,ek, vk,вершины v0 и vk, называются концами цепи. Говорят, что цепь с концами и и v соединяет вершины и и v. Цепь, соединяющая вершины и и v, обозначается (и, v). Очевидно, что если есть цепь, соединяющая вершины и и v, то есть и простая цепь, соединяющая эти вершины.
Замкнутая цепь называется циклом; замкнутая простая цепь называется простым циклом. Число циклов в графе G обозначается z(G). Граф без циклов называется ациклическим.
Элементы графа – любое чередование вершин и рёбер графа, в котором каждому ребру предшествует смежная ей вершина, называющаяся контуром графа.
Контрольные вопросы
Что такое граф?
2.Что относится к элементам графа?
3.Перечислить виды графов.
Какие операции можно выполнять над графами?
Лекция №8
Тема: «Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятностей. Теорема сложения вероятностей. Теорема умножения вероятностей»
уметь:
- находить вероятность, в простейших задачах используя классическое определение вероятности;
- решать задачи с применением теоремы сложения вероятностей для несовместных событий.
знать:
- основные понятия теории вероятностей и математической статистики.
Опр. Событие – это любое явление, которое происходит или не происходит или результат испытаний, наблюдений и явлений. События обозначают заглавными латинскими буквами А, В, С, …
Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи.
Долю успеха того или иного события называют вероятностью этого события и обозначают Р(А)
Опр . Если в некотором испытании существует п равновозможных попарно несовместных исходов и т из них благоприятствуют событию А, то вероятностью наступления события А называют отношение  и записывают Р(А) =
и записывают Р(А) = 
Опр. Суммой (объединением) двух событий A и B (обозначается A+B, A B) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.
B) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.
Опр. Произведением (пересечением) двух событий A и B (обозначается A×B, A и B) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.
Типовые задачи:
Задача1. Найти вероятность появления при одном бросании игральной кости числа очков, большего 4.
Решение : А – « появление числа очков, большего 4» п = 6 - число всех исходов, т = 2 – благоприятствующих событию А ( 5, 6 ) Р(А) =  =
=  Ответ: Р(А) =
Ответ: Р(А) =  =
= 
Задача2. В коробке лежат 8 зелёных, 7 синих и 15 красных карандашей. Вычислить вероятность того, что взятый наугад карандаш будет синим или зелёным.
Решение:
А: взяли синий карандаш
В: взяли зелёный карандаш
С: взяли синий и зелёный карандаш
Событие С равно сумме событий А и В: С = А + В
Вероятность события А равна 
Вероятность события В равна 
Вероятность события С равна
Задача 3. В одной коробке находится 4 белых и 8 черных шаров, а в другой – 3 белых и 9 черных. Из каждой коробки вынули по шару. Вычислить вероятность того, что оба шара окажутся белыми.
Решение:
А: из первой коробки вынули белый шар
В: из второй коробки вынули белый шар
С: из коробок вынули белые шары
Вероятность события А равна 
Вероятность события В равна 
Вероятность события С равна
Ответ: Р ( С )  0,083
0,083
Контрольные вопросы
С помощью какой формулы можно вычислить вероятность появления случайного события?
Приведите пример достоверного события.
Чему равна вероятность невозможного события?
Лекция №9
Тема: «Определение матрицы и ее обозначения. Виды матриц. Определитель матрицы. Линейная функция и ее график. Уравнение с одной переменной. Корни уравнения. Линейные уравнения. Метод Гаусса решения систем линейных уравнений. Использование системы линейных уравнений при решении экономических задач. (Метод Крамера. Матричный метод. Метод Гаусса)»
уметь:
- вычислять определители 2-го и 3-го порядка;
- выполнять операции над матрицами;
- решать системы линейных уравнений;
- решать экономические задачи методом Крамера, методом Гаусса;
- вычислять себестоимость продукции с помощью обратной матрицы.
знать:
- понятие определителей 2-го и 3-го порядка;
- понятие матрицы, квадратной матрицы;
- правила вычисления определителей 2-го и 3-го порядка.
- основные методы решения систем линейных уравнений, в частности метод Крамера, метод Гаусса;
- понятие обратной матрицы.
Определение 1. Определителем второго порядка  называется выражение
называется выражение 
Определение 2. Определителем третьего порядка  называется выражение
называется выражение 
Есть другие способы для нахождения определителя третьего порядка.
1. 
 =
=
где  - элементы определителя,
- элементы определителя,
 - миноры элементов а1, b1, c1
- миноры элементов а1, b1, c1

Минором Мij какого – либо элемента аij определителя  порядка n называется определитель порядка n – 1, полученный из
порядка n называется определитель порядка n – 1, полученный из  вычерчиванием i– й строки и j – го столбца.
вычерчиванием i– й строки и j – го столбца.
2. 
Определитель III порядка можно найти по схеме:
+ -
















+ + +





 3.
3.  =
= 

- - -
Пример 1.
1. Найти определитель

Решение: Воспользуемся формулой (2) теоремы 1.
Проверим, найдём этот же определитель способом 3.

Метод Крамера.
Пример 1. Решить систему линейных уравнений методом Крамера:
.
Найдем определитель системы
 =
=  = 4 – 3 + 15 – 10 + 2 - 9 = -1
= 4 – 3 + 15 – 10 + 2 - 9 = -1
Так как  , система имеет единственное решение, которое определяется по
, система имеет единственное решение, которое определяется по
формулам Крамера:
х =  , у =
, у =  , z =
, z = 
Найдем определители  и подставим полученные значения в формулы Крамера:
и подставим полученные значения в формулы Крамера:
Ответ: x = 2, у = -1, z = 1.
Метод Гаусса.
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) или близкой к трапециевидной (прямой ход метода Гаусса)
Пример 2. Решить систему линейных уравнений, применяя обратный ход метода Гаусса:

Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y:

Теперь нам известны значения уже двух переменных - z и y. Подставляем их в первое уравнение и получаем значение переменной x:

Таким образом, получили решение системы уравнений:

Пример 3. Предприятие выпускает продукцию трех видов: Р1,Р2,Р3 и использует сырье двух типов: S1 и S2. Нормы расхода сырья характеризуются матрицей
, где каждый элемент aij (i=1,2,3; j=1,2) показывает, сколько единиц продукции j- типа расходуется на производства единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой С=(100 80 130), стоимость единицы каждого типа сырья (ден. ед.) – матрицей-столбцом
В =  .
.
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Решение. Затраты 1 –го сырья составляют S1=2∙100+5∙80+1∙130=730 ед., поэтому матрица-строка затрат сырья S может быть записана как произведение
S=C·A=(100 80 130)· = (730 980)
= (730 980)
Тогда общая стоимость сырья Q=730∙30+980∙50=70900 ден. ед. может быть записана в матричном виде Q=S∙B=(CA)B=(70900).Общую стоимость сырья можно вычислить и в другом порядке: вначале вычислим матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу
R=A·B = , а затем общую стоимость сырья
Q = C·R = (100 80 130)· = (70900)
Контрольные вопросы
Определение матрицы.
Какую матрицу называют квадратной порядка n?
Определение определителя 2-го порядка.
Определение определителя 3-го порядка.
Сформулируйте правило вычисления определителя 2-го порядка.
Сформулируйте правило вычисления определителя 3-го порядка.
В чем заключается метод Крамера?
В чем заключается метод Гаусса?
Понятие обратной матрицы.
Как вычислить себестоимость продукции с помощью обратной матрицы?
Лекция №10
Тема: «Понятия комплексного числа. Действительная и мнимая части комплексного числа. Аргумент и модуль комплексного числа. Абсцисса и ордината комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Правила выполнения операций с комплексными числами».
Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными. Примеры иррациональных чисел – это ,
, ,
, .
.
Вывод: Для перечисленных выше множеств чисел справедливо следующее высказывание: . Его можно проиллюстрировать с помощью кругов Эйлера.
Опр. Комплексным числом  называется число вида
называется число вида  , где
, где  и
и  – действительные числа,
– действительные числа,  –мнимая единица. Число
–мнимая единица. Число  называется действительной частью (
называется действительной частью ( ) комплексного числа
) комплексного числа  , число
, число  называется мнимой частью (
называется мнимой частью ( ) комплексного числа
) комплексного числа  .
.
 – это ЕДИНОЕ ЧИСЛО, а не сложение.
– это ЕДИНОЕ ЧИСЛО, а не сложение.
Решая квадратное уравнение x2 = – 1. Оно на множестве действительных чисел решений не имеет, так как среди действительных чисел нет такого числа, квадрат которого отрицателен.
Таким образом, действительных чисел явно недостаточно, чтобы построить такую теорию квадратных уравнений, в рамках которой каждое квадратное уравнение было бы разрешимо. Это приводит к необходимости расширять множество действительных чисел до множества, в котором было бы разрешимо любое квадратное уравнение. Такое множество называется множеством комплексных чисел и обозначается С.
Мы пришли к введению понятия мнимой единицы i= . Т.е. множество действительных чисел расширяется до множества комплексных чисел за счет мнимой единицы.
. Т.е. множество действительных чисел расширяется до множества комплексных чисел за счет мнимой единицы.
Давайте подробнее поговорим о ней и попробуем вычислить: i2 , i4, i3, i5.
i2=-1, тогда i4=-1∙(-1)=1
i3=( )3=-1∙
)3=-1∙ =-
=- =-i, i5=(
=-i, i5=( )5=
)5=  =i
=i
Действительное число а может быть также записано в форме комплексного числа: a+ 0 i или a – 0 i. Например, записи 5 + 0 i и 5 – 0 i означают одно и то же число 5 .
Комплексное число 0+ bi называется чисто мнимым числом. Запись bi означает то же самое, что и 0+ bi.
Два комплексных числа a+ bi и c+ di считаются равными, если a= c и b= d.
Действия с комплексными числами в алгебраической форме
Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.
Сложение комплексных чисел
Пример 1
Сложить два комплексных числа Z1=2+5i Z2=4-3i
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части: Z=6+2i
Пример 2
Самостоятельно: Z1=-4+10i Z2=5+3i Ответ: Z=1+13i
Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
 – от перестановки слагаемых сумма не меняется.
– от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 3
Найти разности комплексных чисел и, если, Z1=10-25i Z2=1-3i
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
Z=10-25i -(1-3i)=9-22i
Пример 4
Самостоятельно: Z1=-5+10i Z2=1+3i Ответ: Z=-6+7i
Умножение комплексных чисел
Правило умножения. Комплексные числа перемножаются как двучлены, при этом учитывается, что  .
.
Пример 5
Найти произведение комплексных чисел Z1=1-i Z2=3+6i Ответ: Z=9+3i
Z1∙Z2= Z2∙Z1 – от перестановки множителей произведение не меняется.
Пример 6
Самостоятельно: Z1=5-2i Z2=1-4i Ответ: Z=-3-22i
Пример 7
Самостоятельно: ( 2+ 8i )( 2 – 8i )= 2 2 + 82
Вывод: ( a+ bi )( a – bi )= a 2 + b 2. Следовательно, произведение двух сопряжённых комплексных чисел равно действительному положительному числу.
Деление комплексных чисел
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Пример 8 Найти  =
=
(Умножаем числитель и знаменатель на (4 -i))
Пример 9 Найти
Пример 10 Вычислить: -(2+7i)(1-i)=-8-7i
-(2+7i)(1-i)=-8-7i
Пример 11 Вычислить: =-1
=-1
Комплексное число z = a + bi изображается на координатной плоскости точкой М( a;b ) или вектором ОМ , начало которого совпадает с началом координат, а конец - с точкой М.





Координатная плоскость называется комплексной плоскостью, ось абсцисс (Ох) - действительной осью, ось ординат (Оу) -
B b 0
y
мнимой осью.

Модулем комплексного числа называется абсолютная величина вектора, соответствующего этому числу.
a A x
М(a;b)
Для модуля числа z = a + bi используются обозначения r, |z| или |a + bi| . На основании теоремы Пифагора
|z| = r = 

Аргументом комплексного числа называется величина угла между положительным направлением действительной оси и вектором, соответствующим этому числу
= arctg 
( arctg читается: угол, тангенс которого равен
читается: угол, тангенс которого равен  ).
).
Обозначения для аргумента числа z = a + bi : , arg z или
arg (a + bi).
Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.
Для этого рассмотрим формулы для нахождения  в зависимости от а и b.
в зависимости от а и b.
1.
2.
3.
4.
5. 
6. 
7. 
8. 
Пример Представим в тригонометрической форме число  . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.

Поскольку  (случай 2), то
(случай 2), то  – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение
– вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение  , поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
 – число
– число  в тригонометрической форме.
в тригонометрической форме.
Список использованной литературы
Основные источники
для обучающихся
Омельченко В.П., Курбатова Э.В. Математика 2-е издание, среднее профессиональное образование. Ростов – на – Дону: «Феникс», 2014г.
Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике: учеб. пособие: Рекомендовано ФГУ «ФИРО». – 160с., 2014г.
Основные источники
для преподавателей
Григорьев В.П., Дубинский Ю.А. Элементы высшей математики: учебник: Допущено Минобразованием России. – 5-е изд., стер. – 320с., 2014г.
Григорьев С.Г., Задулина С.В. Математика: Учебник: Допущено
Минобразованием России / Под ред. Гусева В.А. 4-е изд., стер. 384с., 2014г.
Дополнительные источники
для преподавателей
Спирина М.С., Спирин П.А. Дискретная математика: учебник: Допущено Минобразованием России - 5-е изд., стер. - 386., 2014г.
Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика:: учебник: Допущено Минобразованием России 352с., 2014г.
Пехлецкий И.Д. Математика: учебник. – М., 2014г.
Дополнительные источники
Для обучающихся
Пехлецкий И.Д. Математика: учебник. – М., 2014г.







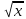 , y = x2 , y = x3, y = sinx, y =cosx, y = tgx, y = ctgx и т.п.
, y = x2 , y = x3, y = sinx, y =cosx, y = tgx, y = ctgx и т.п.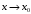 (и пишут
(и пишут 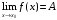 ), если для любого
), если для любого  найдется число
найдется число 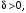 зависящее от , такое, что для всех
зависящее от , такое, что для всех 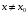 , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 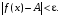
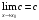 (c=const).
(c=const).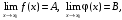 то:
то: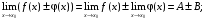
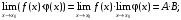
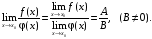
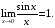
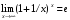 или
или