Тема: Цикл с условием. Алгоритм Евклида для нахождения наибольшего общего делителя двух натуральных чисел. Разбиение записи натурального числа в позиционной системе с основанием, меньшим или равным 10, на отдельные цифры

Информатика 8 класс 11.04.2023

Тема: Цикл с условием. Алгоритм Евклида для нахождения наибольшего общего делителя двух натуральных чисел. Разбиение записи натурального числа в позиционной системе с основанием, меньшим или равным 10, на отдельные цифры.

Как мы уже с Вами разобрались, в программировании оперируют переменными, а одними из самых частоиспользуемых переменных являются переменные числового типа.

Среди переменных числового типа особое внимание уделяется целым неотрицательным числам, потому что с их помощью в компьютере представлено большое количество информации (например, адреса переменных в памяти). Сегодня мы с Вами разберемся с тем, как можно обрабатывать целые неотрицательные числа.

Выделение разрядов числа

Для начала стоит разобраться, для чего вообще может понадобиться обработка чисел? Приведем простой пример: Вам в автобусе попался билет и Вы хотите проверить, является ли он счастливым (сумма первых трёх цифр равна сумме последних трёх)? Да, можно посчитать самому, но мы же начали разбираться с программированием, так почему же не попробовать решить задачку с помощью мощностей компьютера? :)

Чтобы решить задачку, необходимо выделить первые три цифры и последние три цифры, но как это сделать? Для того, чтобы ответить на этот вопрос, обратимся к школьной математике: каждое число состоит из суммы разрядных слагаемых - единиц, десятков, сотен и т.д. Например, число 2019 состоит из 9 единиц, 1 десятка, 0 сотен и 2 тысяч. Уже понимаете, к чему идёт дело? :)

Вернёмся к нашим билетам. Имеем на руках билет, номер которого состоит из 6 цифр, то есть имеем 6 разрядов. Представим номер билета в виде ABCDEF, где каждая буква отвечает за соответствующий разряд. Тогда для решения задачи нужно выделить разряды A, B, C и D, E, F, найти сумму двух серий и сравнить. Данную задачу можно решить разными способами: разделить число на два трёхначных, преобразовать число в строку, обработать все разряды числа. Так как мы с Вами разбираемся с операциями над целыми числами, мы прибегнем к последнему способу из предложенных и обработаем число целиком.

Давайте теперь разберемся, как выделить определенный разряд из десятичного числа. Пойдём справа налево - от меньшего разряда к большему. Итак, имеем шестизначный номер нашего билета:

Объявление переменной в Python

Чтобы взять наименьший разряд числа десятичного, то есть разряд единиц, необходимо взять остаток от деления исходного числа на основание системы счисления, то есть 10. Действительно, таким образом мы делим число на какое-то количество частей, каждая из которых равна 10, и получаем еще одну часть, которой не хватило до 10. Чтобы взять остаток от деления числа a на число b в Python применяется оператор %.

Применение оператора %

Для десятков операция практически аналогичная. Теперь мы берем остаток от деления на 100, но в таком случае мы можем получить число в диапазоне от 0 до 99. Как быть в таком случае? Ответ прост: выполнить целочисленное деление полученного числа на 10! Если в случае с единицами мы делили число на какое-то количество частей, равное 10, то операция целочисленного деления позволяет узнать точное количество этих частей, что нам с Вами и нужно! Чтобы взять результат целочисленного деления числа a на b в Python применяется оператор //.

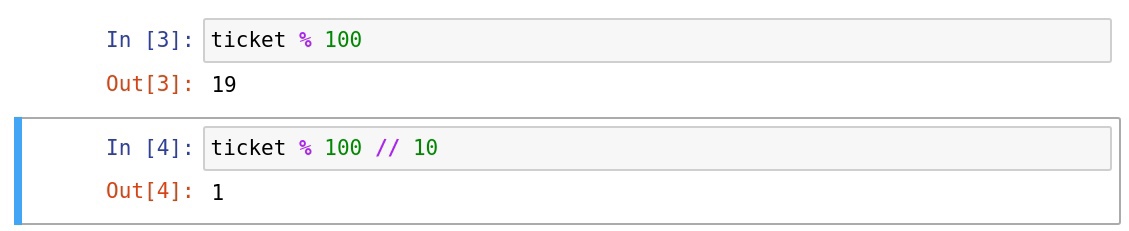
Выделение десятков

Аналогичные операции производятся и для выделения последующих разрядов со смещением разряда влево.

Выделение сотен

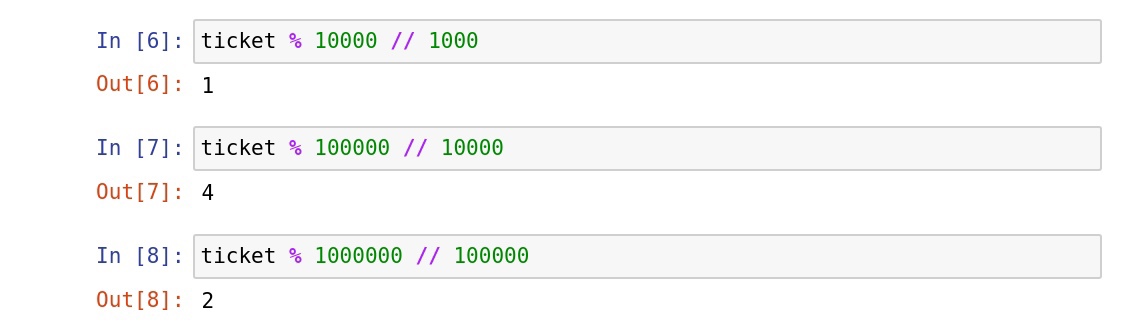
Выделение тысяч, десятков тысяч и сотен тысяч (сверху-вниз)

Теперь давайте решим нашу задачу: выделим первые три цифры и последние три цифры числа, найдем их сумму и сравним. Для начала используем отдельную переменную для хранения каждого разряда, затем оптимизируем задачу.

Исходный код задачи

Как видите, с билетом нам не повезло! Теперь рассмотрим оптимизированную реализацию.

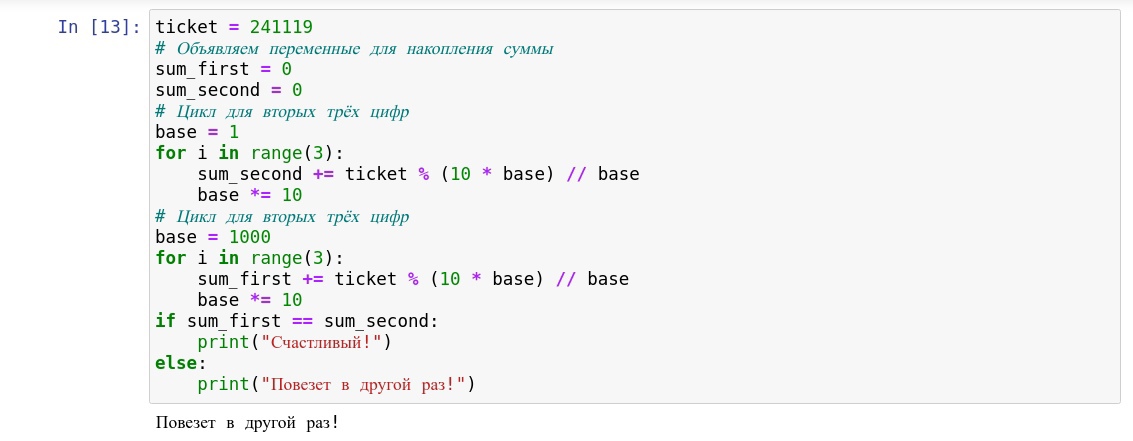
Обратите внимание на расстановку скобок в примерах sum_second и sum_first

В данной реализации мы никак не изменяем исходное число и не обрабатываем его как строку.

Теперь рассмотрим реализацию, которая встречается в Задании №22 ЕГЭ по Информатике — реализация с изменением исходного числа. Если Вы уже решали 22-ый номер, то Вам наверняка знакома подобная конструкция:

Если Вы в первый раз видите данный код, то давайте разберем, что означает каждая его строчка.

x = int(input()) — помещение в переменную x целого числа, введенного с клавиатуры;

while x 0: — условие цикла «Пока введенный нами x больше нуля»;

d = x % 10 — помещение в переменную d остатка от деления x на число 10;

x = x // 10 — перезапись переменной x на результат выполнения целочисленного деления x на 10.

Ничего не напоминает? Да это же выделение разряда единиц в десятичном числе в первой строчке! Но что означает вторая строчка? В ней мы находим сколько раз число 10 вместится в наше число, то есть по факту, если мы вспомним наш пример с билетом, это обрасывание самого правого разряда числа, тобишь разряда единиц!

Соединяя картину воедино, мы получаем, что наш алгоритм:

1. Находит значение разряда единиц;

2. Отбрасывает разряд единиц;

3. Повторяет пункты 1 и 2 до тех пор, пока число существует (не равно нулю).

Пример выполнения программы

Обычно, третьей инструкцией в цикле является какое-либо арифметическое действие с цифрами числа, например, нахождение суммы или произведения. Давайте немного модифицируем нашу с Вами программу, чтобы она находила и то, и другое!

Переменная x_copy нужна для того, чтобы сохранить изначальный x для печати

Алгоритм справедлив не только для десятичной системы счисления. В следующем примере Вы увидите, как можно получить двоичную запись числа из десятичной:

Запись x_binary[::-1] означает, что проход по строке x_binary происходит справа налево

Выделение цифры из числа может понадобиться при переводе числа из одной СС в другую, сборе различных метрик о числе и т.п.

Алгоритм Евклида

Теперь перейдем к еще одному не менее важному алгоритму обработки чисел, а именно алгоритму Евклида — алгоритму нахождения НОД (наибольшего общего делителя) двух чисел.

Алгори́тм Евкли́да — эффективный алгоритм для нахождения наибольшего общего делителя двух целых чисел (или общей меры двух отрезков). Алгоритм назван в честь греческого математика Евклида (III век до н. э.), который впервые описал его в VII и X книгах «Начал». Это один из старейших численных алгоритмов, используемых в наше время.

А теперь о сути работы алгоритма: в самом простом случае алгоритм Евклида применяется к паре положительных целых чисел и формирует новую пару, которая состоит из меньшего числа и разницы между большим и меньшим числом. Процесс повторяется, пока числа не станут равными. Найденное число и есть наибольший общий делитель исходной пары. Евклид предложил алгоритм только для натуральных чисел и геометрических величин (длин, площадей, объёмов). Однако в XIX веке он был обобщён на другие типы математических объектов, включая целые числа Гаусса и полиномы от одной переменной. Позже алгоритм Евклида был обобщён на другие математические структуры, такие как узлы и многомерные полиномы.

Для данного алгоритма существует множество теоретических и практических применений. В частности, он является основой для криптографического алгоритма с открытым ключом RSA (алгоритм шифрования), широко распространённого в электронной коммерции. Также алгоритм используется при решении линейных диофантовых уравнений, при построении непрерывных дробей, в методе Штурма. Алгоритм Евклида является основным инструментом для доказательства теорем в современной теории чисел, например таких как теорема Лагранжа о сумме четырёх квадратов и основная теорема арифметики (все эти интересные вещи Вас ждут в университете совсем скоро :) ).

Реализация алгоритма Евклида, как уже было сказано, довольно проста: вычитанием из большего числа меньшее и выполняя вычитание до того момента, пока числа не сравняются, находится НОД данных чисел.

Разницы, какое число выводить в конце, нет, так как оба числа равны друг другу

Алгоритм Евклида является одним из «жадных» алгоритмов (greedy algorithm — алгоритм, который на каждом шагу делает локально наилучший выбор в надежде, что итоговое решение будет оптимальным), которые широко применяются при решении различных олимпиадных задач и задач повышенной сложности.

Задание: составить конспект по теме.

Готовое ДЗ прислать учителю в ЛС