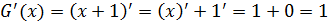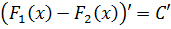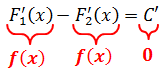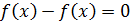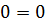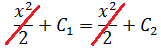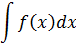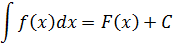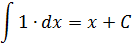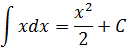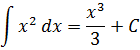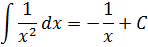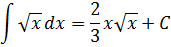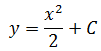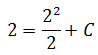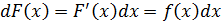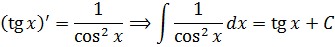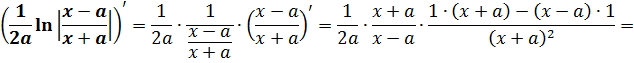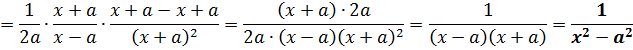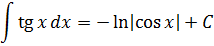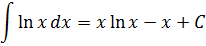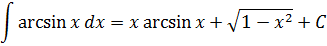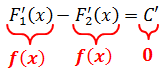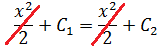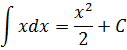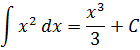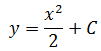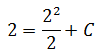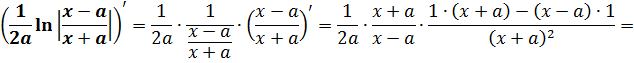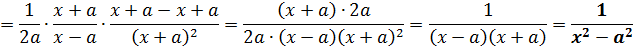Дата проведения: 27.01.2022г.
Группа 1-3
Предмет: Математика
Преподаватель: Амирханова А. К.
Тема урока: Неопределенный интеграл. Таблица интегралов.
Идём дальше. Те студенты, которые хотя бы мало-мальски "шарят" в производных, — люди грамотные. И, возможно, уже приготовили мне убойный вопрос. :)
Скажем, чему равна производная для функции F(x) = x? Ну, единица, единица — слышу недовольные ответы… Всё верно. Единица. Но… Для функции G(x) = x+1 производная тоже будет равна единице:
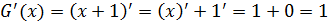
Также производная будет равна единице и для функции x+1234, и для функции x-10, и для любой другой функции вида x+C, где С — любая константа. Ибо производная любой константы равна нулю, а от прибавления/вычитания нуля никому ни холодно ни жарко.)
Получается неоднозначность. Выходит, что для функции f(x) = 1 первообразной служит не только функция F(x) = x, но и функция F1(x) = x+1234 и функция F2(x) = x-10 и так далее!
Да. Именно так.) У всякой (непрерывной на промежутке) функции существует не какая-то одна первообразная, а бесконечно много - целое семейство! Не одна мама или папа, а целая родословная, ага.)
Но! Всех наших родственников-первообразных объединяет одно важное свойство. На то они и родственники.) Свойство настолько важное, что в процессе разбора приёмов интегрирования мы про него ещё не раз вспомним. И будем вспоминать ещё долго.)
Вот оно, это свойство:
Любые две первообразные F1(x) и F2(x) от одной и той же функции f(x) отличаются на константу:
F1(x) - F2(x) = С.
Кому интересно доказательство — штудируйте литературу или конспекты лекций.) Ладно, так уж и быть, докажу. Благо доказательство тут элементарное, в одно действие. Берём равенство
F1(x) - F2(x) = С
и дифференцируем обе его части. То есть, просто тупо ставим штрихи:
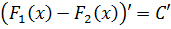
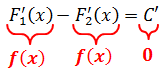
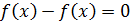
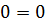
Вот и всё. Как говорится, ЧТД. :)
О чём говорит это свойство? А о том, что две различные первообразные от одной и той же функции f(x) не могут отличаться на какое-то выражение с иксом . Только строго на константу! Иными словами, если у нас есть график какой-то одной из первообразных (пусть это будет F(x)), то графики всех остальных наших первообразных строятся параллельным переносом графика F(x) вдоль оси игреков.
Посмотрим, как это выглядит на примере функции f(x) = x. Все её первообразные, как нам уже известно, имеют общий вид F(x) = x2/2+C. На картинке это выглядит как бесконечное множество парабол, получаемых из "основной" параболы y = x2/2 сдвигом вдоль оси OY вверх или вниз в зависимости от значения константы С.
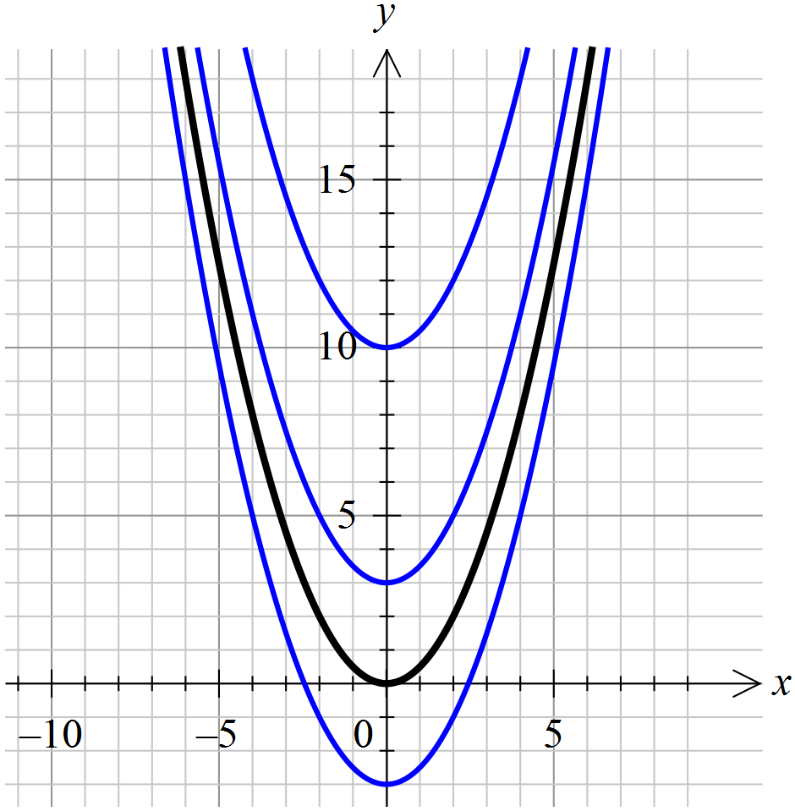
Помните школьное построение графика функции y=f(x)+a сдвигом графика y=f(x) на "а" единиц вдоль оси игреков?) Вот и тут то же самое.)
Причём, обратите внимание: наши параболы нигде не пересекаются! Оно и естественно. Ведь две различные функции y1(x) и y2(x) неизбежно будут соответствовать двум различным значениям константы — С1 и С2.
Поэтому уравнение y1(x) = y2(x) никогда не имеет решений:
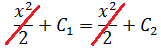
С1 = С2
x ∊ ∅, так как С1 ≠ С2
А теперь мы плавненько подходим ко второму краеугольному понятию интегрального исчисления. Как мы только что установили, у всякой функции f(x) существует бесконечное множество первообразных F(x) + C, отличающихся друг от друга на константу. Это самое бесконечное множество тоже имеет своё специальное название.) Что ж, прошу любить и жаловать!
Что такое неопределённый интеграл?
Множество всех первообразных для функции f(x) называется неопределённым интегралом от функции f(x).
Вот и всё определение.)
"Неопределённый" - потому, что множество всех первообразных для одной и той же функции бесконечно. Слишком много различных вариантов.)
"Интеграл" — с подробной расшифровкой этого зверского слова мы познакомимся в следующем большом разделе, посвящённом определённым интегралам. А пока, в грубой форме, будем считать интегралом нечто общее, единое, целое. А интегрированием — объединение, обобщение, в данном случае переход от частного (производной) к общему (первообразным). Вот, как-то так.
Обозначается неопределённый интеграл вот так:
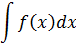
Читается так же, как и пишется: интеграл эф от икс дэ икс. Или интеграл от эф от икс дэ икс. Ну, вы поняли.)
Теперь разберёмся с обозначениями.
∫ — значок интеграла. Смысл тот же, что и штрих для производной.)
d — значок дифференциала. Не пугаемся! Зачем он там нужен — чуть ниже.
f(x) — подынтегральная функция (через "ы").
f(x)dx — подынтегральное выражение. Или, грубо говоря, "начинка" интеграла.
Согласно смыслу неопределённого интеграла,
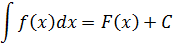
Здесь F(x) — та самая первообразная для функции f(x), которую мы так или иначе нашли сами. Как именно нашли — не суть. Например, мы установили, что F(x) = x2/2 для f(x)=x.
"С" - произвольная постоянная. Или, более научно, интегральная константа. Или константа интегрирования. Всё едино.)
А теперь вернёмся к нашим самым первым примерам на поиск первообразной. В терминах неопределённого интеграла можно теперь смело записать:
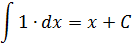
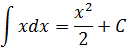
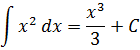
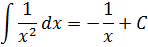
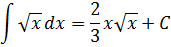
И так далее.) Идея понятна, думаю. Ни в коем случае не забываем приплюсовывать константу С!
Что такое интегральная константа и зачем она нужна?
Вопрос очень интересный. И очень (ОЧЕНЬ!) важный. Интегральная константа из всего бесконечного множества первообразных выделяет ту линию, которая проходит через заданную точку.
В чём суть. Из исходного бесконечного множества первообразных (т.е. неопределённого интеграла) надо выделить ту кривую, которая будет проходить через заданную точку. С какими-то конкретными координатами. Такое задание всегда и везде встречается при начальном знакомстве с интегралами. Как в школе, так и в ВУЗЕ.
Типичная задачка:
Среди множества всех первообразных функции f=x выделить ту, которая проходит через точку (2;2).
Начинаем думать головой… Множество всех первоообразных — это значит, сначала надо проинтегрировать нашу исходную функцию. То есть, икс (х). Этим мы занимались чуть выше и получили такой ответ:
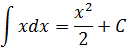
А теперь разбираемся, что именно мы получили. Мы получили не одну функцию, а целое семейство функций. Каких именно? Вида y=x2/2+C. Зависящее от значения константы С. И вот это значение константы нам и предстоит теперь "отловить".) Ну что, займёмся ловлей?)
Удочка наша — семейство кривых (парабол) y=x2/2+C.
Константы — это рыбины. Много-много. Но на каждую найдётся свой крючок и приманка.)
А что же служит приманкой? Правильно! Наша точка (-2;2).
Вот и подставляем координаты нашей точки в общий вид первообразных! Получим:
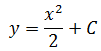
y(2) = 2
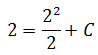
Отсюда уже легко ищется C = 0.
Что сиё означает? Это значит, что из всего бесконечного множества парабол вида y=x2/2+C только парабола с константой С=0 нам подходит! А именно: y=x2/2. И только она. Только эта парабола будет проходить через нужную нам точку (-2; 2). А все остальные параболы из нашего семейства проходить через эту точку уже не будут. Через какие-то другие точки плоскости — да, а вот через точку (2; 2) — уже нет. Уловили?
Для наглядности вот вам две картинки — всё семейство парабол (т.е. неопределённый интеграл) и какая-то конкретная парабола, соответствующая конкретному значению константы и проходящая через конкретную точку:
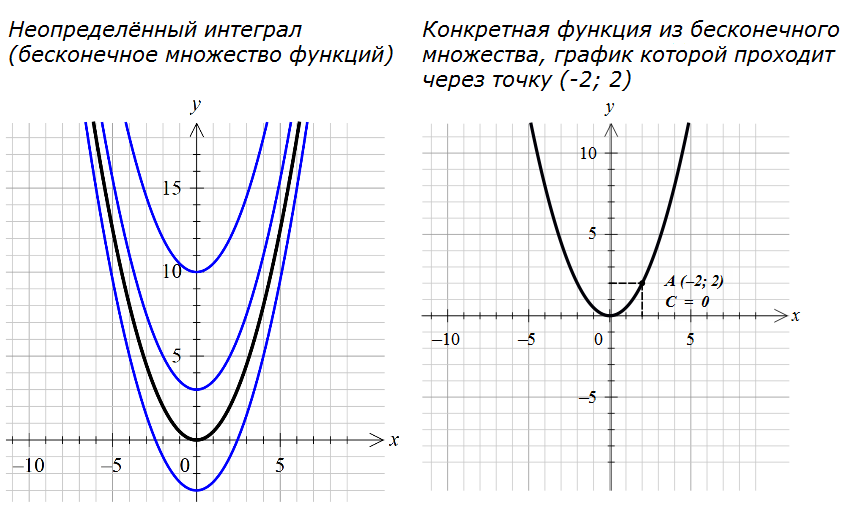
Видите, насколько важно учитывать константу С при интегрировании! Так что не пренебрегаем этой буковкой "С" и не забываем приписывать к окончательному ответу.
А теперь разберёмся, зачем же внутри интегралов везде тусуется символ dx. Забывают про него студенты частенько… А это, между прочим, тоже ошибка! И довольно грубая. Всё дело в том, что интегрирование — операция, обратная дифференцированию. А что именно является результатом дифференцирования? Производная? Верно, но не совсем. Дифференциал!
В нашем случае, для функции f(x) дифференциал её первообразной F(x), будет:
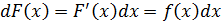
Кому непонятна данная цепочка — срочно повторить определение и смысл дифференциала и то, как именно он раскрывается! Иначе в интегралах будете тормозить нещадно….
Напомню, в самой грубой обывательской форме, что дифференциал любой функции f(x) - это просто произведение f’(x)dx. И всё! Взять производную и помножить её на дифференциал аргумента (т.е. dx). То есть, любой дифференциал, по сути, сводится к вычислению обычной производной.
Поэтому, строго говоря, интеграл "берётся" не от функции f(x), как принято считать, а от дифференциала f(x)dx! Но, в упрощённом варианте, принято говорить, что "интеграл берётся от функции". Или: "Интегрируется функция f(x)". Это одно и то же. И мы будем говорить точно так же. Но про значок dx при этом забывать не будем! :)
И сейчас я подскажу, как его не забыть при записи. Представьте себе сначала, что вы вычисляете обычную производную по переменной икс. Как вы обычно её пишете?
Вот так: f’(x), y’(x), у’x. Или более солидно, через отношение дифференциалов: dy/dx. Все эти записи нам показывают, что производная берётся именно по иксу. А не по "игреку", "тэ" или какой-то там другой переменной.)
Так же и в интегралах. Запись ∫f(x)dx нам тоже как бы показывает, что интегрирование проводится именно по переменной икс. Конечно, это всё очень упрощённо и грубо, но зато понятно, я надеюсь. И шансы забыть приписать вездесущее dx резко снижаются.)
Итак, что такое же неопределённый интеграл — разобрались. Прекрасно.) Теперь хорошо бы научиться эти самые неопределённые интегралы вычислять. Или, попросту говоря, "брать". :) И вот тут студентов поджидает две новости — хорошая и не очень. Пока начнём с хорошей.)
Новость хорошая. Для интегралов, так же как и для производных, существует своя табличка. И все интегралы, которые нам будут встречаться по пути, даже самые страшные и навороченные, мы по определённым правилам будем так или иначе сводить к этим самым табличным.)
Итак, вот она, таблица интегралов!

Вот такая вот красивая табличка интегралов от самых-самых популярных функций. Рекомендую обратить отдельное внимание на группу формул 1-2 (константа и степенная функция). Это — самые употребительные формулы в интегралах!
Третья группа формул (тригонометрия), как можно догадаться, получена простым обращением соответствующих формул для производных.
Например:
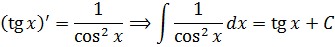
C четвёртой группой формул (показательная функция) — всё аналогично.
А вот четыре последние группы формул (5-8) для нас новые. Откуда же они взялись и за какие такие заслуги именно эти экзотические функции, вдруг, вошли в таблицу основных интегралов? Чем же эти группы функций так выделяются на фоне остальных функций?
Так уж сложилось исторически в процессе развития методов интегрирования. Когда мы будем тренироваться брать самые-самые разнообразные интегралы, то вы поймёте, что интегралы от перечисленных в таблице функций встречаются очень и очень часто. Настолько часто, что математики отнесли их к табличным.) Через них выражаются очень многие другие интегралы, от более сложных конструкций.
Ради интереса можно взять какую-нибудь из этих жутких формул и продифференцировать. :) Например, самую зверскую 7-ю формулу.
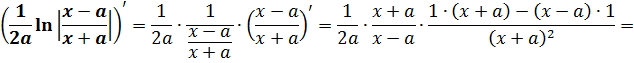
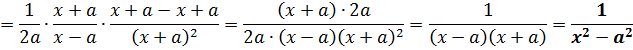
Всё нормально. Не обманули математики. :)
Таблицу интегралов, как и таблицу производных, желательно знать наизусть. Во всяком случае, первые четыре группы формул. Это не так трудно, как кажется на первый взгляд. Заучивать наизусть последние четыре группы (с дробями и корнями) пока не стоит. Всё равно поначалу будете путаться, где логарифм писать, где арктангенс, где арксинус, где 1/а, где 1/2а … Выход тут один - решать побольше примеров. Тогда таблица сама собой постепенно и запомнится, а сомнения грызть перестанут.)
Особо любознательные лица, присмотревшись к таблице, могут спросить: а где же в таблице интегралы от других элементарных "школьных" функций — тангенса, логарифма, "арков"? Скажем, почему в таблице ЕСТЬ интеграл от синуса, но при этом НЕТУ, скажем, интеграла от тангенса tg x? Или нету интеграла от логарифма ln x? От арксинуса arcsin x? Чем они хуже? Но зато полно каких-то "левых" функций - с корнями, дробями, квадратами…
Ответ. Ничем не хуже.) Просто вышеназванные интегралы (от тангенса, логарифма, арксинуса и т.д.) не являются табличными. И встречаются на практике значительно реже, нежели те, что представлены в таблице. Поэтому знать наизусть, чему они равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются.)
Что, кому-то всё-таки невтерпёж? Так уж и быть, специально для вас!
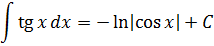
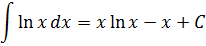
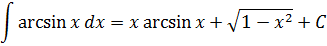
Ну как, будете заучивать? :) Не будете? И не надо.) Но не волнуйтесь, все подобные интегралы мы обязательно найдём. В соответствующих уроках. :)
Что ж, теперь переходим к свойствам неопределённого интеграла. Да-да, ничего не поделать! Вводится новое понятие — тут же и какие-то его свойства рассматриваются.
Просмотр содержимого документа
«Тема урока: Неопределенный интеграл. Таблица интегралов.»
Дата проведения: 27.01.2022г.
Группа 1-3
Предмет: Математика
Преподаватель: Амирханова А. К.
Тема урока: Неопределенный интеграл. Таблица интегралов.
Идём дальше. Те студенты, которые хотя бы мало-мальски "шарят" в производных, — люди грамотные. И, возможно, уже приготовили мне убойный вопрос. :)
Скажем, чему равна производная для функции F(x) = x? Ну, единица, единица — слышу недовольные ответы… Всё верно. Единица. Но… Для функции G(x) = x+1 производная тоже будет равна единице:
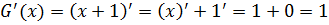
Также производная будет равна единице и для функции x+1234, и для функции x-10, и для любой другой функции вида x+C, где С — любая константа. Ибо производная любой константы равна нулю, а от прибавления/вычитания нуля никому ни холодно ни жарко.)
Получается неоднозначность. Выходит, что для функции f(x) = 1 первообразной служит не только функция F(x) = x, но и функция F1(x) = x+1234 и функция F2(x) = x-10 и так далее!
Да. Именно так.) У всякой (непрерывной на промежутке) функции существует не какая-то одна первообразная, а бесконечно много - целое семейство! Не одна мама или папа, а целая родословная, ага.)
Но! Всех наших родственников-первообразных объединяет одно важное свойство. На то они и родственники.) Свойство настолько важное, что в процессе разбора приёмов интегрирования мы про него ещё не раз вспомним. И будем вспоминать ещё долго.)
Вот оно, это свойство:
Любые две первообразные F1(x) и F2(x) от одной и той же функции f(x) отличаются на константу:
F1(x) - F2(x) = С.
Кому интересно доказательство — штудируйте литературу или конспекты лекций.) Ладно, так уж и быть, докажу. Благо доказательство тут элементарное, в одно действие. Берём равенство
F1(x) - F2(x) = С
и дифференцируем обе его части. То есть, просто тупо ставим штрихи:
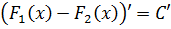
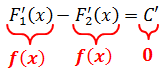
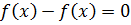
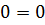
Вот и всё. Как говорится, ЧТД. :)
О чём говорит это свойство? А о том, что две различные первообразные от одной и той же функции f(x) не могут отличаться на какое-то выражение с иксом . Только строго на константу! Иными словами, если у нас есть график какой-то одной из первообразных (пусть это будет F(x)), то графики всех остальных наших первообразных строятся параллельным переносом графика F(x) вдоль оси игреков.
Посмотрим, как это выглядит на примере функции f(x) = x. Все её первообразные, как нам уже известно, имеют общий вид F(x) = x2/2+C. На картинке это выглядит как бесконечное множество парабол, получаемых из "основной" параболы y = x2/2 сдвигом вдоль оси OY вверх или вниз в зависимости от значения константы С.
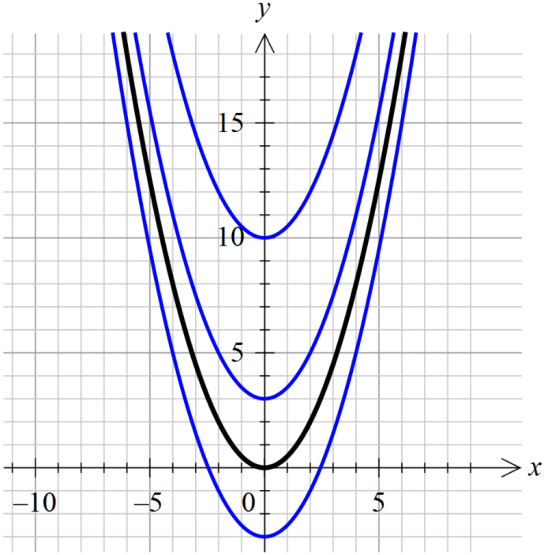
Помните школьное построение графика функции y=f(x)+a сдвигом графика y=f(x) на "а" единиц вдоль оси игреков?) Вот и тут то же самое.)
Причём, обратите внимание: наши параболы нигде не пересекаются! Оно и естественно. Ведь две различные функции y1(x) и y2(x) неизбежно будут соответствовать двум различным значениям константы — С1 и С2.
Поэтому уравнение y1(x) = y2(x) никогда не имеет решений:
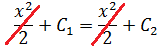
С1 = С2
x ∊ ∅, так как С1 ≠ С2
А теперь мы плавненько подходим ко второму краеугольному понятию интегрального исчисления. Как мы только что установили, у всякой функции f(x) существует бесконечное множество первообразных F(x) + C, отличающихся друг от друга на константу. Это самое бесконечное множество тоже имеет своё специальное название.) Что ж, прошу любить и жаловать!
Что такое неопределённый интеграл?
Множество всех первообразных для функции f(x) называется неопределённым интегралом от функции f(x).
Вот и всё определение.)
"Неопределённый" - потому, что множество всех первообразных для одной и той же функции бесконечно. Слишком много различных вариантов.)
"Интеграл" — с подробной расшифровкой этого зверского слова мы познакомимся в следующем большом разделе, посвящённом определённым интегралам. А пока, в грубой форме, будем считать интегралом нечто общее, единое, целое. А интегрированием — объединение, обобщение, в данном случае переход от частного (производной) к общему (первообразным). Вот, как-то так.
Обозначается неопределённый интеграл вот так:
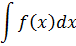
Читается так же, как и пишется: интеграл эф от икс дэ икс. Или интеграл от эф от икс дэ икс. Ну, вы поняли.)
Теперь разберёмся с обозначениями.
∫ — значок интеграла. Смысл тот же, что и штрих для производной.)
d — значок дифференциала. Не пугаемся! Зачем он там нужен — чуть ниже.
f(x) — подынтегральная функция (через "ы").
f(x)dx — подынтегральное выражение. Или, грубо говоря, "начинка" интеграла.
Согласно смыслу неопределённого интеграла,
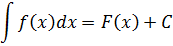
Здесь F(x) — та самая первообразная для функции f(x), которую мы так или иначе нашли сами. Как именно нашли — не суть. Например, мы установили, что F(x) = x2/2 для f(x)=x.
"С" - произвольная постоянная. Или, более научно, интегральная константа. Или константа интегрирования. Всё едино.)
А теперь вернёмся к нашим самым первым примерам на поиск первообразной. В терминах неопределённого интеграла можно теперь смело записать:
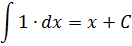
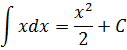
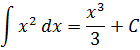
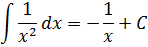
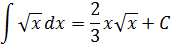
И так далее.) Идея понятна, думаю. Ни в коем случае не забываем приплюсовывать константу С!
Что такое интегральная константа и зачем она нужна?
Вопрос очень интересный. И очень (ОЧЕНЬ!) важный. Интегральная константа из всего бесконечного множества первообразных выделяет ту линию, которая проходит через заданную точку.
В чём суть. Из исходного бесконечного множества первообразных (т.е. неопределённого интеграла) надо выделить ту кривую, которая будет проходить через заданную точку. С какими-то конкретными координатами. Такое задание всегда и везде встречается при начальном знакомстве с интегралами. Как в школе, так и в ВУЗЕ.
Типичная задачка:
Среди множества всех первообразных функции f=x выделить ту, которая проходит через точку (2;2).
Начинаем думать головой… Множество всех первоообразных — это значит, сначала надо проинтегрировать нашу исходную функцию. То есть, икс (х). Этим мы занимались чуть выше и получили такой ответ:
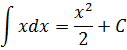
А теперь разбираемся, что именно мы получили. Мы получили не одну функцию, а целое семейство функций. Каких именно? Вида y=x2/2+C. Зависящее от значения константы С. И вот это значение константы нам и предстоит теперь "отловить".) Ну что, займёмся ловлей?)
Удочка наша — семейство кривых (парабол) y=x2/2+C.
Константы — это рыбины. Много-много. Но на каждую найдётся свой крючок и приманка.)
А что же служит приманкой? Правильно! Наша точка (-2;2).
Вот и подставляем координаты нашей точки в общий вид первообразных! Получим:
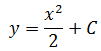
y(2) = 2
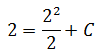
Отсюда уже легко ищется C = 0.
Что сиё означает? Это значит, что из всего бесконечного множества парабол вида y=x2/2+C только парабола с константой С=0 нам подходит! А именно: y=x2/2. И только она. Только эта парабола будет проходить через нужную нам точку (-2; 2). А все остальные параболы из нашего семейства проходить через эту точку уже не будут. Через какие-то другие точки плоскости — да, а вот через точку (2; 2) — уже нет. Уловили?
Для наглядности вот вам две картинки — всё семейство парабол (т.е. неопределённый интеграл) и какая-то конкретная парабола, соответствующая конкретному значению константы и проходящая через конкретную точку:
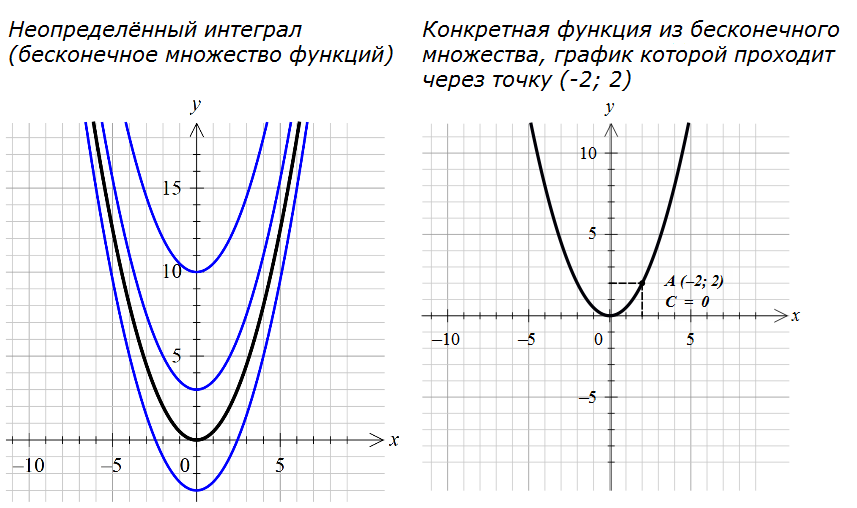
Видите, насколько важно учитывать константу С при интегрировании! Так что не пренебрегаем этой буковкой "С" и не забываем приписывать к окончательному ответу.
А теперь разберёмся, зачем же внутри интегралов везде тусуется символ dx. Забывают про него студенты частенько… А это, между прочим, тоже ошибка! И довольно грубая. Всё дело в том, что интегрирование — операция, обратная дифференцированию. А что именно является результатом дифференцирования? Производная? Верно, но не совсем. Дифференциал!
В нашем случае, для функции f(x) дифференциал её первообразной F(x), будет:
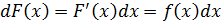
Кому непонятна данная цепочка — срочно повторить определение и смысл дифференциала и то, как именно он раскрывается! Иначе в интегралах будете тормозить нещадно….
Напомню, в самой грубой обывательской форме, что дифференциал любой функции f(x) - это просто произведение f’(x)dx. И всё! Взять производную и помножить её на дифференциал аргумента (т.е. dx). То есть, любой дифференциал, по сути, сводится к вычислению обычной производной.
Поэтому, строго говоря, интеграл "берётся" не от функции f(x), как принято считать, а от дифференциала f(x)dx! Но, в упрощённом варианте, принято говорить, что "интеграл берётся от функции". Или: "Интегрируется функция f(x)". Это одно и то же. И мы будем говорить точно так же. Но про значок dx при этом забывать не будем! :)
И сейчас я подскажу, как его не забыть при записи. Представьте себе сначала, что вы вычисляете обычную производную по переменной икс. Как вы обычно её пишете?
Вот так: f’(x), y’(x), у’x. Или более солидно, через отношение дифференциалов: dy/dx. Все эти записи нам показывают, что производная берётся именно по иксу. А не по "игреку", "тэ" или какой-то там другой переменной.)
Так же и в интегралах. Запись ∫f(x)dx нам тоже как бы показывает, что интегрирование проводится именно по переменной икс. Конечно, это всё очень упрощённо и грубо, но зато понятно, я надеюсь. И шансы забыть приписать вездесущее dx резко снижаются.)
Итак, что такое же неопределённый интеграл — разобрались. Прекрасно.) Теперь хорошо бы научиться эти самые неопределённые интегралы вычислять. Или, попросту говоря, "брать". :) И вот тут студентов поджидает две новости — хорошая и не очень. Пока начнём с хорошей.)
Новость хорошая. Для интегралов, так же как и для производных, существует своя табличка. И все интегралы, которые нам будут встречаться по пути, даже самые страшные и навороченные, мы по определённым правилам будем так или иначе сводить к этим самым табличным.)
Итак, вот она, таблица интегралов!

Вот такая вот красивая табличка интегралов от самых-самых популярных функций. Рекомендую обратить отдельное внимание на группу формул 1-2 (константа и степенная функция). Это — самые употребительные формулы в интегралах!
Третья группа формул (тригонометрия), как можно догадаться, получена простым обращением соответствующих формул для производных.
Например:
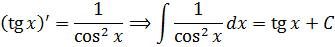
C четвёртой группой формул (показательная функция) — всё аналогично.
А вот четыре последние группы формул (5-8) для нас новые. Откуда же они взялись и за какие такие заслуги именно эти экзотические функции, вдруг, вошли в таблицу основных интегралов? Чем же эти группы функций так выделяются на фоне остальных функций?
Так уж сложилось исторически в процессе развития методов интегрирования. Когда мы будем тренироваться брать самые-самые разнообразные интегралы, то вы поймёте, что интегралы от перечисленных в таблице функций встречаются очень и очень часто. Настолько часто, что математики отнесли их к табличным.) Через них выражаются очень многие другие интегралы, от более сложных конструкций.
Ради интереса можно взять какую-нибудь из этих жутких формул и продифференцировать. :) Например, самую зверскую 7-ю формулу.
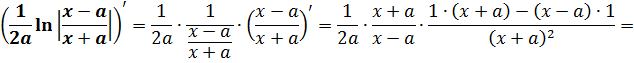
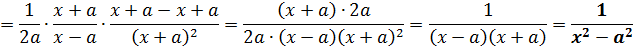
Всё нормально. Не обманули математики. :)
Таблицу интегралов, как и таблицу производных, желательно знать наизусть. Во всяком случае, первые четыре группы формул. Это не так трудно, как кажется на первый взгляд. Заучивать наизусть последние четыре группы (с дробями и корнями) пока не стоит. Всё равно поначалу будете путаться, где логарифм писать, где арктангенс, где арксинус, где 1/а, где 1/2а … Выход тут один - решать побольше примеров. Тогда таблица сама собой постепенно и запомнится, а сомнения грызть перестанут.)
Особо любознательные лица, присмотревшись к таблице, могут спросить: а где же в таблице интегралы от других элементарных "школьных" функций — тангенса, логарифма, "арков"? Скажем, почему в таблице ЕСТЬ интеграл от синуса, но при этом НЕТУ, скажем, интеграла от тангенса tg x? Или нету интеграла от логарифма ln x? От арксинуса arcsin x? Чем они хуже? Но зато полно каких-то "левых" функций - с корнями, дробями, квадратами…
Ответ. Ничем не хуже.) Просто вышеназванные интегралы (от тангенса, логарифма, арксинуса и т.д.) не являются табличными. И встречаются на практике значительно реже, нежели те, что представлены в таблице. Поэтому знать наизусть, чему они равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются.)
Что, кому-то всё-таки невтерпёж? Так уж и быть, специально для вас!
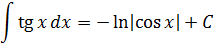
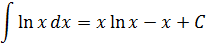
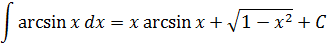
Ну как, будете заучивать? :) Не будете? И не надо.) Но не волнуйтесь, все подобные интегралы мы обязательно найдём. В соответствующих уроках. :)
Что ж, теперь переходим к свойствам неопределённого интеграла. Да-да, ничего не поделать! Вводится новое понятие — тут же и какие-то его свойства рассматриваются.