Электронный учебник по теме "Тела вращения"

Тела вращения

Содержание

• Из истории геометрии и тел вращения:

• измерение размеров земного шара Эратосфеном; история происхождения названий;
• измерение размеров земного шара Эратосфеном;
• история происхождения названий;
• Тела вращения: конус; сфера и шар; цилиндр.
• конус;
• сфера и шар;
• цилиндр.

Содержание

• Объемы тел вращения:

– объем цилиндра;

– объем конуса;

– объем шара;

– общая формула вычисления объемов;

– вычисление объемов частей шара с использованием общей формулы.

• Площади поверхностей тел вращения:

– площадь поверхности цилиндра;

– площадь поверхности конуса;

– площадь поверхности шара и его частей.

Содержание

• Вписанные и описанные многогранники:

– теорема об описанной сфере треугольной пирамиды;

– теорема о вписанной сфере треугольной пирамиды.

• Плоскости и прямые, касательные к сфере, и плоскости, секущие сферу:

– плоскость, касательная к сфере;

– сечение сферы плоскостью;

– плоскости, равноудаленные от центра сферы.

• Примеры комбинаций тел вращения.
• Конические сечения.

Содержание

• Задачи с решениями:

• высота конуса; объем конуса; площадь сечения шара; отношение объемов Луны и Земли; диагональ осевого сечения цилиндра; объем, радиус и высота цилиндра; площадь части поверхности; ребро куба, вписанного в конус; объем составного тела вращения.
• высота конуса;
• объем конуса;
• площадь сечения шара;
• отношение объемов Луны и Земли;
• диагональ осевого сечения цилиндра;
• объем, радиус и высота цилиндра;
• площадь части поверхности;
• ребро куба, вписанного в конус;
• объем составного тела вращения.
• Викторина.

Измерение размеров земного шара Эратосфеном

Очень интересную задачу решил Эратосфен — он впервые определил размеры земного шара.

Эратосфен жил около двух тысяч лет назад в Египте, в горо­де Александрии. Южнее Александрии на берегу Нила лежал город Сиена. Эрастофен знал, что в день летнего солнцестояния — самый длинный день года — в Сиене солнце заглядывает на дно самых глубоких колодцев. А в Александрии в этот день дно колодцев остается в тени. Там солнечные лучи падают на землю не отвесно, как в Сиене, а под углом и освещают только стенку колодца.

Эратосфен измерил угол между направлением солнечного луча и стенкой колодца. Оказалось, что этот угол равен развернутого угла.

Наверное, Эратосфен рассуждал так:

Солнечные лучи всюду параллельны, а колодцы всегда копают по отвесу. Солнце может по-разному освещать колодцы в Сиене и Александрии только потому, что Земля не плос­кая. Скорее всего, она круглая, как шар. Но раз угол между солнечным лучом и отвесом в Александрии равен развернутого угла, то расстояние между Александрией и Сиеной в 25 раз меньше длины меридиана, соединяющего полюса земного шара.

Расстояние от Александрии до Сиены было приблизи­тельно известно. Умножив его на 25, Эратосфен определил длину меридиана. Если эту длину разделить на 3,14, то и полу­чится радиус земного шара. Ошибка, сделанная Эратосфеном, была совсем невелика, особенно если учитывать, как неточны были в то время измерения расстояний и углов.

История происхождения названий тел вращения

Последователи Фалеса, занявшиеся геометрией, оказались в том же затруднении, что и все первоначинатели. Так как до Фалеса никто в Греции геометрией не занимался, у геомет­рических фигур еще не было названий. Греки стали называть фигуры словами, обозначавшими окружающие их предметы похожей формы. Например, для прокатки белья женщины при­меняли скалку, которую по-гречески называли «каландер». Поэтому все вытянутые тела с округлым сечением получили название цилиндра . А тело, изображенное на рисунке слева , похоже на еловую шишку. Эту шишку по-гречески называли «конос». Поэтому и тела такой формы получили название конуса .

Сферой по-гречески назывался мяч, с ко­торым играли дети.

Таким образом, сами названия геометрических фигур по­казывали, что геометрия возникла для решения практических задач и с самого начала была тесно связана с практикой, с человеческим трудом.

Конус

Конус — это тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

Конус

Коническая поверхность — поверхность, которая образуется движением отрезка, один из концов которого неподвижен. А другой перемещается на плоскости вдоль некоторой кривой. Отрезки называют образующими конической поверхности, а кривую — направляющей. Неподвижная точка — вершина конической поверхности.

Конус — тело, которое ограничено конической поверхностью и плоскостью, на которой лежат концы образующих конической поверхности.

Боковая поверхность конуса — часть конической поверхности, ограниченная плоскостью.

Основание конуса — часть плоскости, отсекаемая боковой поверхностью конуса. Круговой конус — конус, у которого в основании круг.

Прямой круговой конус (просто конус) — круговой конус, у которого прямая, соединяющая вершину конуса с центром круга, лежащего в основании, перпендикулярна плоскости основания.

Ось конуса — прямая, проходящая через вершину конуса и центр основания.

Высота конуса — отрезок оси конуса, соединяющий вершину конуса с центром основания.

Образующие конуса совпадают с образующими конической поверхности. Развертка боковой поверхности конуса — круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

Сфера и шар

Сфера — это тело вращения, получаемое вращением окружности вокруг своего диаметра.

Шар — это тело вращения, получаемое вращением круга вокруг своего диаметра.

Сфера и шар

Сферу обозначают так: ω (O, R). Можно определить сферу и как тело, образованное при вращении окружности вокруг своего диаметра.

Множество всех точек пространства, удаленных от данной точки O на расстояние, не большее R, называется шаром.

Иными словами шар – это объединение сферы и всех ее внутренних точек.

Можно также определить шар и как тело, образованное при вращении круга вокруг своего диаметра.

Шар обозначают так же, как сферу: ω (O, R). Точка O называется центром сферы (шара). Отрезок, соединяющий центр сферы с любой ее точкой, называется радиусом сферы (шара). Отрезок, соединяющий любые две точки сферы, называется хордой сферы (шара). Иногда под радиусом или хордой подразумевают их длину. Хорда, проходящая через центр сферы, называется ее диаметром.

Цилиндр

Цилиндр — это тело вращения, получаемое вращением прямоугольника вокруг одной из своих сторон

Цилиндр

Цилиндрическая поверхность – поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию – направляющей цилиндрической поверхности.

Цилиндр – тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующими данной поверхности.

Боковая поверхность цилиндра – часть цилиндрической поверхности, которая ограничена параллельными плоскостями.

Основания цилиндра – части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.

Прямой цилиндр – цилиндр, у которого образующие перпендикулярны основаниям.

Круговой цилиндр – цилиндр, основания которого являются кругами.

Прямой круговой цилиндр (просто цилиндр) – цилиндр вращения, его можно получить, вращая прямоугольник вокруг одной из его сторон.

Радиус цилиндра – радиус его основания.

Ось цилиндра – прямая, которая проходит через центры оснований цилиндра.

Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.

Высота цилиндра – отрезок оси цилиндра, который соединяет центры оснований. Также высотой называют длину этого отрезка.

Развертка боковой поверхности цилиндра – прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.

Объем цилиндра

Теорема. Объем цилиндра равен произведению площади основания на высоту.

Доказательство.

Пусть P — цилиндр с радиусом основания r и высотой h.

1. Вписываем в цилиндр правильную n-угольную призму Fn.

2. В полученную призму впишем цилиндр Pn.

3. Пусть V — объем цилиндра P, Vn — объем цилиндра Pn, rn — радиус цилиндра Pn, Sn — площадь основания призмы Fn

4. Так как объем призмы Fn равен произведению площади основания призмы на ее высоту (которая равна высоте каждого из цилиндров), а призма Fn располагается между цилиндрами, получаем неравенство: Vn

5. Будем неограниченно увеличивать n. Тогда радиус внутреннего цилиндра rn стремится к радиусу внешнего цилиндра r. А значит (так как высоты цилиндров равны), объем внутреннего цилиндра Vn стремится к объему внешнего цилиндра V.

6. Имеем

V = Sосн h

Vn

Vn = V (из п. 5)

7. Sосн = πr2 (так как площадь основания внутреннего цилиндра стремится к площади основания призмы).

V = π r2 h = S h

8. V = Sосн h (из 6)

Sосн = π r2 (из 7)

Теорема доказана.

V = S осн h

V = π r 2 h = S h

Объем конуса

Теорема. Объем конуса равен произведению трети площади основания на высоту.

Доказательство.

Аналогично доказательству, представленному в предыдущей теореме, будем вписывать в конус правильную n-угольную пирамиду. В полученную пирамиду впишем конус. Тогда будем иметь неравенство Vn

Будем неограниченно увеличивать n. Тогда радиус основания внутреннего конуса rn стремится к радиусу основания внешнего конуса r. А значит (так как высоты конусов равны), объем внутреннего конуса Vn стремится к объему внешнего конуса V.

Имеем

V = 1/3 Sосн h

Vn

Vn = V

Sосн = πr2 (так как площадь основания внутреннего конуса стремится к площади основания пирамиды).

V = 1/3 π r2 h = 1/3 S h

V = 1/3 Sосн h

Sосн = π r2

Теорема доказана.

V = 1/3 S осн h

V = 1/3 π r 2 h = 1/3 S h

Объем шара

Теорема. Объем шара равен 4/3 π r3, где r — радиус шара.

Доказательство Архимеда.

Рассмотрим сложные тела, изображенные на рисунке: все они состоят из цилиндров с высотой δ, радиус большего цилиндра у каждого тела равен r. Высота каждого из тел также равна r.

Первое тело «напоминает» цилиндр, второе — конус, третье — полушар. Положим тела на чаши очень точных весов так, как это показано на рисунке:

В этом случае возникнет полное равновесие.

Будем стремить δ к нулю, тогда объем первой фигуры будет в пределе равен объему цилиндра, объем второй фигуры — объему конуса, а объем третей — объему полушара.

Получаем: Vполушара = Vцилиндра – Vконуса = π r3 – 1/3 π r3 = 2/3 π r3, а значит

Vшара = 4/3 π r3.

Теорема доказана.

Общая формула вычисления объемов

Пусть криволинейная трапеция, то есть фигура, ограниченная осью Ox, прямыми x = a, x = b и графиком непрерывной возрастающей неотрицательной функции y = f (x), вращается вокруг оси Ox, вследствие чего образуется тело вращения.

Сечение этого тела плоскостью, перпендикулярной оси Ox, есть круг или точка. На промежутке (a; b) выберем точку x. Сечение, проведенное через эту точку перпендикулярно оси Ox, есть круг площадью S (x) = πf 2 (x). Объем части тела вращения, ограниченной сечениями, проведенными через точки a и x, обозначим через V (x), а объем данного тела вращения – через V.

 0 (x + Δx Построим два цилиндра с общей высотой Δx. Меньший цилиндр имеет своим основанием круг площадью S (x), а больший – круг площадью S (x + Δx). Если ΔV – прирост объема тела вращения, то S (x)Δx Поскольку функция f (x) непрерывна, то непрерывна и функция следовательно, " width="640"

Общая формула вычисления объемов

Теорема.  Объем тела вращения равен

Доказательство.

Придадим x приращение Δx  0 (x + Δx 

Построим два цилиндра с общей высотой Δx. Меньший цилиндр имеет своим основанием круг площадью S (x), а больший – круг площадью S (x + Δx). Если ΔV – прирост объема тела вращения, то S (x)Δx 

Поскольку функция f (x) непрерывна, то непрерывна и функция

следовательно,

Общая формула вычисления объемов

Переходя к пределу в двойном неравенстве, имеем

то есть V' (x) = S (x).

Объем V (x) является первообразной для функции S (x) на промежутке [a; b]. Отсюда имеем

Вычисление объемов частей шара с использованием общей формулы

Шаровым сегментом называется часть шара, отсеченная от него плоскостью. Если OP – радиус шара, перпендикулярный отсекающей плоскости, то точку P назовем в этом случае полюсом шара. Высотой шарового сегмента называется отрезок PO1, соединяющий полюс шара с центром основания шарового сегмента.

Шаровой сегмент можно рассматривать как тело, образованное вращением кругового сегмента вокруг диаметра, перпендикулярного его хорде. Формулу объема шарового сегмента получают, например, из общей формулы: интегрируют на промежутке (0; H) (H – высота шарового сегмента):

Следовательно, объем шарового сегмента равен

Вычисление объемов частей шара с использованием общей формулы

Шаровым сектором называется тело, образованное вращением кругового сектора вокруг оси, содержащей один из его граничных радиусов.

Шаровой сектор состоит из шарового сегмента и конуса. Поэтому его объем является суммой объемов шарового сегмента V1 и конуса V2: V = V1 + V2. Высота P1O1 шарового сегмента является также высотой и шарового сектора. Имеем

где r – радиус конуса. Пусть P1, P2 – полюса шара, O1A = r.

Из прямоугольного треугольника P1AP2 находим r2 = H (2R–H), следовательно,

Объем шарового сектора

или

Площадь поверхности цилиндра

Для определения площади поверхности цилиндра рассмотрим его развертку.

Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C, где H – высота цилиндра, а C – длина окружности основания.

Тогда формулы для боковой Sб и полной Sп поверхностей соответственно имеют вид:

Sб = H · C = 2πRH Sп = Sб + 2S =  2πR(R + H).

Площадь поверхности конуса

С конусом поступим аналогично:

Разверткой боковой поверхности конуса является круговой сектор. Обозначим через Sб и Sп соответственно площади боковой и полной поверхности конуса:

где φ – угол при вершине развертки. Далее заметим, что PA · φ = 2πR. Следовательно,

где R – радиус, а l – образующая конуса. Получаем формулу для полной поверхности:

Sп = πRl + πR2 = πR(l + R).

Площадь поверхности шара и его частей

Площадь поверхности шарового сегмента можно определить как предел отношения приращения объема соответствующего шарового сектора к приращению радиуса, когда приращение радиуса стремится к нулю:

На рисунке изображен полукруг радиуса R = OB = OA и половина плоского сегмента ACB. При вращении этого полукруга вокруг оси AA1 получается шар радиуса R, шаровой сектор с углом γ между осью и образующей, и шаровой сегмент. Высота H шарового сегмента есть:

H = AC = OA – OC = R – R cos γ = R (1 – cos γ).

Объем шарового сектора

Дадим радиусу R приращение ΔR. Тогда объем шарового сегмента получит приращение ΔV, где ΔV – объем фигуры, полученной при вращении заштрихованной на рис. 7.4.1 части полукольца.

В процессе приращения объема изменяется только R, а угол γ остается постоянным, поэтому S = V' (R) = 2πR2 (1 – cos γ) = 2πRH, где S – площадь сферической части поверхности шарового сегмента (или сектора). Принимая H = 2R, получаем площадь поверхности сферы

S = 4πR2.

Вписанные и описанные многогранники

Выпуклый многогранник называется вписанным , если все его вершины лежат на некоторой сфере. Эта сфера называется описанной для данного многогранника.

Выпуклый многогранник называется описанным , если все его грани касаются некоторой сферы. Эта сфера называется вписанной для данного многогранника.

При рассмотрении понятий вписанной и описанной сферы обнаруживается аналогия с понятием вписанной и описанной окружности. Однако, если в любой треугольник можно вписать окружность и около любого треугольника можно описать окружность, то не всякий многогранник является вписанным или описанным. Несмотря на это, оказывается, что пространственный аналог треугольника – треугольная пирамида, тем не менее, всегда имеет единственную вписанную и описанную сферу.

Теорема об описанной сфере треугольной пирамиды

Треугольная пирамида имеет единственную описанную сферу.

Доказательство.

Поступим аналогично доказательству существования единственной

окружности, описанной около данного треугольника. В данной

пирамиде ABCD построим плоскости, перпендикулярные

соответственно ребрам AB, AC и AD и проходящие через их середины. Эти плоскости будут равноудалены от точек A и B, A и C, A и D соответственно, поскольку геометрическим местом точек, равноудаленных от концов данного отрезка, является плоскость, проходящая через его середину и перпендикулярная ему. Обозначим точку пересечения этих плоскостей через O. Докажем, что эта точка существует и единственна. Действительно, две из этих плоскостей пересекаются по прямой l, поскольку они перпендикулярны двум непараллельным прямым. Эта прямая перпендикулярна к плоскости ABC. Плоскость, перпендикулярная AD, не параллельна l и не содержит ее, поскольку в противном случае прямая AD перпендикулярна l, то есть лежит в плоскости ABC. Итак, точка O равноудалена от всех вершин треугольной пирамиды, значит эта точка является центром описанной сферы. Тем самым доказано существование такой сферы.

Докажем теперь ее единственность. Заметим, что центр любой другой сферы, проходящей через все вершины пирамиды, равноудален от всех этих вершин и, значит, принадлежит всем плоскостям, проходящим через середины ребер перпендикулярно последним. А это и означает, что центр такой сферы и точка O совпадают.

Теорема о вписанной сфере треугольной пирамиды

Треугольная пирамида имеет единственную вписанную сферу.

Доказательство.

В треугольной пирамиде ABCD проведем биссекторные плоскости ее двугранных углов с ребрами AB, AC и DC. Эти плоскости имеют единственную общую точку Q, что доказывается аналогично предыдущей теореме. Понятно, что точка Q равноудалена от всех граней пирамиды. Таким образом, установлено существование вписанной сферы, единственность которой доказывается опять-таки аналогично.

Плоскость, касательная к сфере

Касательной плоскостью к сфере называется плоскость, имеющая единственную общую точку со сферой.

Теорема.  

Через любую точку A сферы проходит единственная касательная плоскость. Эта плоскость перпендикулярна радиусу OA сферы, где O – центр сферы.

Доказательство.

Пусть α – некоторая плоскость, проходящая через A и перпендикулярная OA. Все точки плоскости α, кроме точки A, удалены от точки O на расстояние большее, чем OA, поскольку кратчайший путь от точки до плоскости – это путь по перпендикуляру к плоскости. Значит, α – касательная плоскость. Обратно, если некоторая плоскость касается сферы в точке A, то A – ближайшая к O точка плоскости. Значит, эта плоскость совпадает с α.

Сечение сферы плоскостью

Теорема.  

Если расстояние от центра сферы до плоскости меньше радиуса сферы, то линия сечения сферы этой плоскостью – окружность.

Доказательство.

Пусть задана сфера ω (O, R) и плоскость α, O1 = ПpαO, OO1 

Поскольку величины R и OO1 фиксированы, то и величина O1A фиксирована. Это означает, что точка пересечения плоскости α и сферы ω лежит на данном расстоянии от точки O1, следовательно, точка A лежит на окружности

Плоскости, равноудаленные от центра сферы

Теорема. 

Плоскости, равноудаленные от центра сферы, пересекают ее по равным окружностям.

Ясно, что наибольшая окружность образуется при пересечении плоскостью, проходящей через центр сферы. Линия пересечения называется большой окружностью сферы. Соответствующее сечение шара называется большим кругом шара.

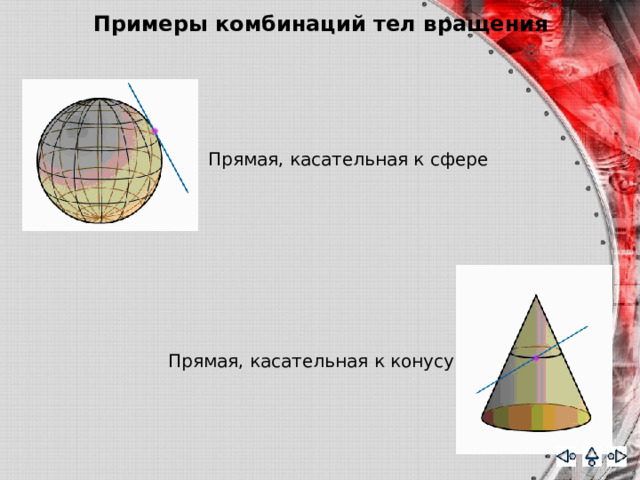
Примеры комбинаций тел вращения

Прямая, касательная к сфере

Прямая, касательная к конусу

Примеры комбинаций тел вращения

Варианты касания двух сфер и сфера, касающаяся конуса

Конические сечения

Конические сечения

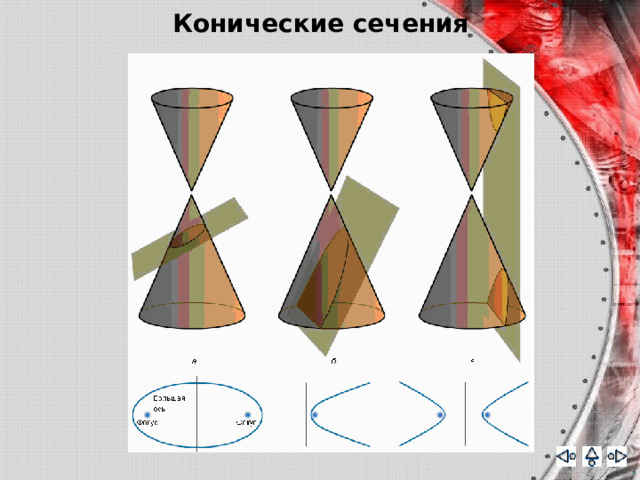
Конические сечения — это плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью. За исключением вырожденных случаев, коническими сечениями являются эллипсы, гиперболы или параболы.

Открывателем конических сечений предположительно считается Менехм (IV в. до н. э.). Менехм использовал параболу и равнобочную гиперболу для решения задачи об удвоении куба.

Трактаты о конических сечениях, написанные Аристеем и Евклидом в конце IV в. до н. э., были утеряны, но материалы из них вошли в знаменитые «Конические сечения» Аполлония Пергского, которые сохранились до нашего времени. Аполлоний, варьируя угол наклона секущей плоскости, получил все конические сечения из одного кругового конуса, прямого или наклонного. Аполлонию мы обязаны и современными названиями кривых — эллипс, парабола и гипербола.

В своих построениях Аполлоний использовал двуполостной круговой конус, поэтому впервые стало ясно, что гипербола – кривая с двумя ветвями. Со времен Аполлония конические сечения делятся на три типа в зависимости от наклона секущей плоскости к образующей конуса. Эллипс образуется, когда секущая плоскость пересекает все образующие конуса в точках одной его полости; парабола – когда секущая плоскость параллельна одной из касательных плоскостей конуса; гипербола – когда секущая плоскость пересекает обе полости конуса.

Итак, конические сечения сыграли очень важную роль, так как именно они позволили научиться строить эллипс, гиперболу и параболу с помощью нити, карандаша и линейки.

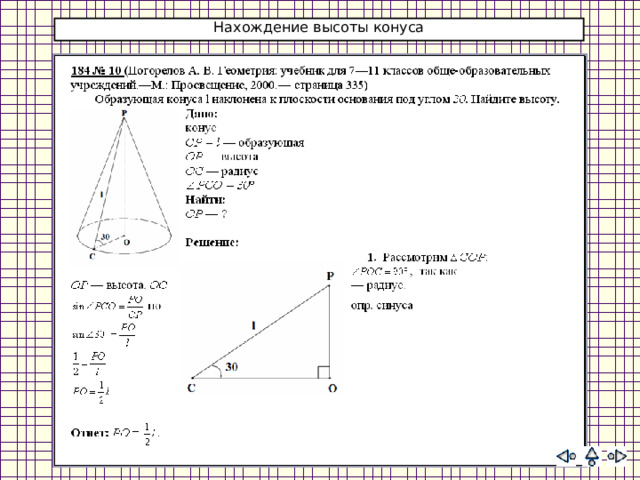
Нахождение высоты конуса

Нахождение объема конуса

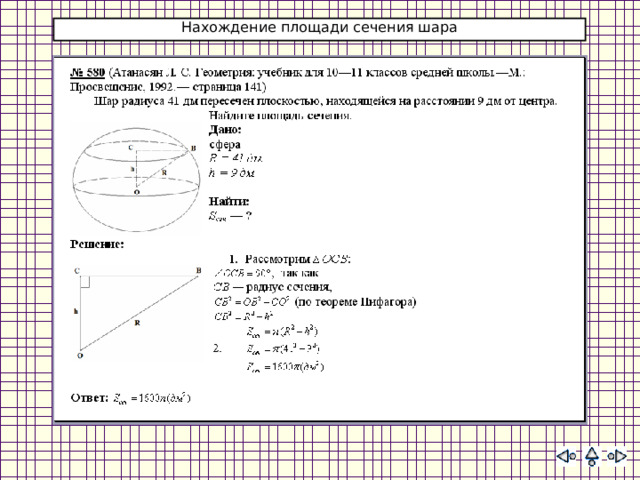
Нахождение площади сечения шара

Нахождение отношений объемов Луны и Земли

Нахождение отношений объемов Луны и Земли

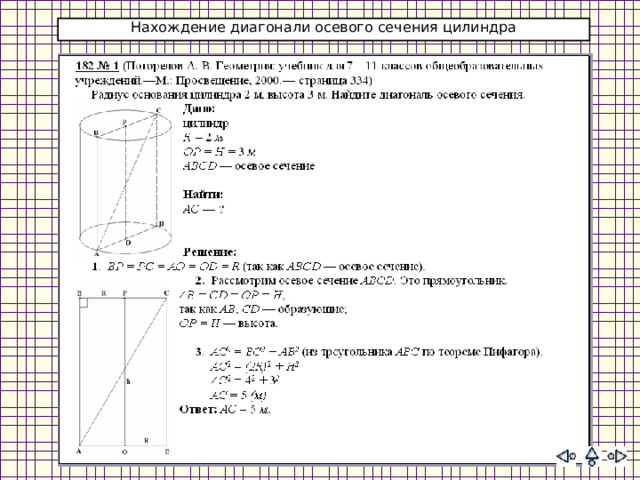
Нахождение диагонали осевого сечения цилиндра

Нахождение объема, радиуса и высоты цилиндра

Нахождение площади части поверхности

Нахождение ребра куба, вписанного в конус

Нахождение объема составного тела вращения

(начало)

Нахождение объема составного тела вращения

(продолжение)

Нахождение объема составного тела вращения

(окончание)

" width="640"

Викторина

Перейти к тесту