“ Matematik induksiya usulini o`rganish”

O`ZBEKISTON RESPUBLIKASI OLIY VA O`RTA MAXSUS TA`LIM VAZIRLIGI

FARG`ONA DAVLAT UNIVERSITETI

FIZIKA- MATEMATIKA FAKULTETI

AMALIY MATEMATIKA VA INFO RMATIKA KAFEDRASI

KURS ISHI

Mavzu: “ Matematik induksiya usulini o`rganish”

Bajardi: Amaliy matematika va informatika yo`nalishi 19.08 A guruh talabasi : Rahmonov Xurshidbek

Rahbar: ___________________

Farg`ona - 2021

Mundarija

Kirish………………………………………………………………………………………3

1-BOB. TAYANCH MA’LUMOTLAR…………………………….…………………….7

1.1.Sonlar nazariyasining ba’zi masalalari va mashxur olimlarning ayrim tadqiqotlari..7

1.2. Matematik induksiya metodi haqida umumiy ma’lumotlar………………………..13

1.3. Matematik induksiya metodi haqida……………………………………………….18

2-BOB. MATEMATIK INDUKSIYA METODI TADBIQLARI…...…………………..21

2.1. Ayrim matematik ayniyat va tengliklarni isbotlashda

Matematik induksiyadan foydalanish………………………….………………………..21

2.2. Formula va teng kuchlilik tushunchalarini matematik induksiya usulida ishlatish.24

2.3. Xaritani bo`yashda matematik induksiya usuli tadbiqlari………………………...33

2.4. Paskal uchburchagini matematik induksiya usulidagi tadbiqi…………………...35

2.5. Matematik induktsiya usuli yordamida tengsizlikni va bo’linishni isbotlash……37

2.6. Muavr formulasini matematik induksiya usulida isbotlanishi. …………………….40

Xulosa……………………………………………………………….…………………...42

Foydalanilgan adabiyotlar……………………………………….………………………43

Kirish

hech qaysi sohada bo`sh kelmaydigan insonlar bo`lib kamol topishi , mustaqil fikrlaydigan, yuksak intellektual va baxtli bo`lishi uchun davlatimizning va jamiyatimizning bor kuch va imkoniyatlarini safarbar etamiz

Sh.M.Mirziyoyev

O`zbekiston Respublikasi Prezidenti.

Mamlakatimizda zamonaviy axborot texnologiyalari va kommunikatsiyalarini rivojlantirish, elektron davlat xizmatlarini ko’rsatishning yaxlit tizimini yaratish, davlat organlarining aholi bilan muloqot qilishining yangi mexanizmlarini joriy etish maqsadida 2018 yil 19 fevralida O’zbekiston Respublikasi Prezidentining ”Axborot texnologiyalari va kommunikatsiyalari sohasini yanada takomillashtirish chora- tadbirlari to’g’risida” gi PF-5349-sonli farmoni qabul qilindi. Ushbu farmonda, O’zbekiston Respublikasi Oliy va o’rta maxsus ta’lim vazirligi bilan kelishgan holda o’quv jarayonining axborot-kommunikatsiya texnologiyalarini rivojlantirish sur’atlari bilan uzluksiz aloqasini ta’minlashni hisobga olgan holda mustaqil ravishda o’quv rejalar va dasturlar, bitiruvchilar uchun malaka talablarini ishlab chiqish va tasdiqlash, hamda professor o’qituvchilar tarkibi mehnatini o’qitishning kredit tizimi shartlaridan kelib chiqib faqat ta’limga xos tadbirlar asosida ish vaqti hisobga olinishiga asoslangan holda mustaqil normalashni amalga oshirish, shuningdek, pedagog xodimlar tomonidan ilmiy-uslubiy, ilmiy- tadqiqot, tashkiliy-uslubiy, ma’naviy-ma’rifiy va tarbiyaviy ishlarning bajarilishini rag’batlantirish huquqi berish to’g’risida ta’kidlab o’tilgan. Ma’lumki, o’rta maxsus, kasb-hunar ta’limini asosiy bo’g’inini uzluksiz ta’lim tizimi tashkil etadi. Uzluksiz ta’limni davlat ta’lim standartlari va tegishli ta’lim dasturlari bilan ta’minlashda avvalo ularning jahon talablari darajasiga javob berishi yuksak ma’naviyat zamirida qurilganiga asosiy e’tibor berish kerak.

O’rta maxsus, kasb-hunar ta’limi bilimlarning zarur hajmini beradi,
mustaqil fikrlash, tashkilotchilik qobiliyati va amaliy tajriba ko’nikmalarini
rivojlantiradi, dastlabki tarzda kasbga yo’naltirishga va ta’limning navbatdagi
bosqichini tanlashga yordam beradi. Hozirgi zamon mutaxassislari, faoliyat
doiralari qanday bo’lishidan qat’iy nazar, fizika va informatika bo’yicha keng
ko’lamdagi bilimlarga, zamonaviy hisoblash texnikasi, informatsion aloqa va
kommunikatsiya tizimlari, orgtexnika vositalari va ulardan foydalanish borasida
yetarli malakalarga ega bo’lishi, hamda, yangi informatsion texnika va
texnologiya asoslarini uning ertangi kuni, rivoji to’g’risidagi bilimlarni o’zida
mujassamlashtirgan bo’lishi kerak.

Kadrlar tayyorlash milliy dasturida ma’lum sohani tubdan isloh qilishorqali rivojlangan demokratik davlatlar darajasida yuqori malakali kadrlartayyorlash milliy tizimni yaratish maqsad qilib qo’yilgan.

Ta'lim sohasidagi o`zgarishlarni hozirgi kunda tubdan isloh qilish, uni o'tmishdan qolgan mafkuraviy qarashlar va sarqitlardan to'la xalos etish,
rivoglangan demokratik davlatlar darajasida, yuksak ma'naviy va axloqiy
talablarga javob beruvchi malakali kadrlar tayorlashning milliy tizimini yaratish
Kadrlar tayorlash milliy dasturining asosiy maqsadi hisoblanadi. Bu maqsadga
erishish uchun ta'lim jarayoniga yangicha nazar bilan qarash talab etiladi: "... Oliy
ta'limni butun ta'lim tizimining katalizatori sifatida ko'rish va undan foydalanish ...
oliy ta'lim butun ta'lim tizimining rivojiga yanada faol, shu jumladan, pedagogik
ta'limni takomillashtirish yo'li bilan ulush qo'shishi ... o'z faoliyatiga tanqidiy
yondashuvchi yuqori malakali va o'qimishli insonlar ommasini yaratuvchi adekvat
oliy ta'limsiz va ilmiy tadqiqot muassasalarsiz birorta mamlakat real barqaror
rivojlanishni taminlay olmaydi, rivojlanayotgan mamlakatlar esa, o'zlari va
rivojlangan mamlakatlar o'rtasidagi farqni qisqartira olmaydilar. Bilimlardan
hamkorlikda foydalanish, xalqaro hamkorlik va yangi texnologiyalar bu uzilishni
kamaytirishga yangi imkonlar yaratadi... Oliy ta'lim o'quvchilarning shunday
ta'limini ta'minlashi kerakki, ular tanqidiy fikrlash, ijtimoiy muammolarni tahlil
qilish, jamiyat oldida turgan muamolar yechimini topish va ulardan foydalanish
hamda o'z zimmasiga ijtimoiy ma'suliyatni olishga qodir bo'lishi, yangi pedogogik
va didaktik yondashuvlarga, ularning rivojlanishiga yo'l ochish kerak. Ular
ko'nikmalarga ega bo'lishda ко'такberishi, bilimdonlik va komunnikatsiya, ijodiy -
tanqidiy tahlil, mustaqil fikrlash va ijod hamda an'anaviy yoki mahalliy ko'nikma
va bilimlar zamonaviy fan va texnika birikuviga asoslangan ko'pmadaniyatli
konteksda birgalikdagi mehnat bilan bog'liq qobiliyatlarni rivojlantirishi zarur"
["XXI asr uchun oliy ta'lim haqidagi jahon deklarasiyasi: yondashish va amaliy
choralar" (UNESKO, Parij, 1998)]. Respublikamiz ta’lim tizimida kechayotgan islohotlar ta’lim mazmunini tubdan o’zgartirishga qaratilgan. Xususan, ta’lim tizimida bosqichma – bosqich bo`ladigan ta`lim: ya`ni, maktab, kasb – hunar kollejlari, akademik litseylarda matematika fanini o’qitish mazmunini chuqurlashtirish, uning amaliy yo’nalishini kuchaytirishga alohida e’tibor berilmoqda. Tabiiyki, bunga talabalarning mantiqiy va matematik tafakkurlarini rivojlantirish, abstrakt tasavvurlarini kengaytirish orqali zamin yaratish mumkin.

Ma’lumki, tabiatdagi ko’plab jarayonlar va muammolar matematik modellashtirish orqali u yoki bu masala yechimini topishga, matematik mulohazalar ustida mushoxada yuritishga, ba’zi tasdiqlarni isbotlashga keltiriladi. Matematik mushohada yuritish orqali o’quvchining tafakkuri ortadi, ilmiy salohiyati yuksaladi. Ko’plab natural parametrli matematik ayniyatlar, tengliklar, tasdiqlar, tenlama va tengsizliklarni isbotlashda matematik induksiya metodidan foydalanish samarali hisoblanadi. Ushbu metod induktiv o’tish orqali natural sonlar to’plami yoki uning biror cheksiz qism to’plamida berilgan ayniyat, tenlik va tengsizliklarni isbotlash orqali umumiy tasdiqning to’g’riligini asoslashga asoslanganligi, isbotlash umumiy strukturaga egaligi bilan ham o’quvchiga tushunarli va qo’llash qulaydir. Uni puxta o’rganish orqali bitiruvchilar kelgusi pedagogik foaliyatida yoshlarga samarali saboq berishi bilan ham muhim ahamiyatlidir. Ma’lumki, maktab, akademik litsey bitiruvchilarini fundamental fanlar bo’yicha zamon talablari asosida faoliyat ko’rsatadigan universitetlarga talaba darajasida tayyorlash hamda iqtidorli yosh matematiklarini viloyat, jumhuriyat va xalqaro matematika olimpiadalariga tayyorlanish vazifasi yuklatilgan. Bitiruvchilarning tanlagan fanlari, sohalari bo’yicha chuqur va puxta bilimlarga ega bo’lishlari kerak. Shuning uchun ta`lim dargohlarida darsdan tashqari mashg’ulotlarda matematik induktsiya usuliga doir mavzularni o’rganish ko’zda tutilgan.. Akademik litsey matematika kursida matematik induktsiya usuliga doir mavzular bo’yicha darslar uslubiy jihatdan to’g’ri tashkil etilib o’tkazilsa, bu darsda o’quvchilar mazkur mavzularga doir bilimlarini tizimlashtirishga imkoniyat yaratiladi. Agar shunday darslarda matematik indutsiyani qullashga doir misol va masalalar talabalarga yechtirilsa, u holda bunday misol va masalalar talabalarning matematik tafakkurini rivojlantirishga va turli olimpiadalarga muay’an natijalarni ko’rsatishga yordam beradi.

Kurs ishining maqsadi: Ushbu ishni bajarishdan ko’zlangan asosiy maqsad pedagogik faoliyat boshlash oldida turgan bitiruvchida natural sonlar to’plamida berilgan ko’plab auniyat, tengliklar, tenglama va tengsizliklarni isbotlashda matematik induksiya metodining asosiy prinsiplarini o’rgatish, ulardan amalda foydalanish bilim, ko’nikma va malakalarini yuksaltirishdan iboratdir.

Kurs ishining ilmiy va amaliy ahamiyati: O`rganuvchi matematik induksiya metodini puxta o’zlashtirib olishi bilan undan kelgusida ilmiy izlanish davomida ayrim isbotlanishi zarur bo’lgan jarayonlarda foydalanishi, o’rta-maxsus va umumta’lim maktablarida yoshlarning matematikaga bo’lgan qiziqishlarini o’stirish, samarali pedagogik faoliyt olib borish uchun ahamiyatli hisoblanadi.

Kurs ishining ob’ekti: Kurs ishining asosiy tadqiqot ob’ekti matematik induksiya prinsipi tarixi, uning asosiy prinsiplari, ularni amaliy
masalalarda, ya’ni natural parametrli tenglik va tengsizliklarni isbotlash usullari hisoblanadi.

Kurs ishi shakli va hajmi: Ushbu kurs ishi kirish, 2 bob, 9 ta mavzu, xulosa va foydalanilgan adabiyotlardan iborat. 1- bobda matematik induksiya haqida boshlang`ich ma`lumotlar keltirilgan. 2- bobida esa deyarli asosiy qismida matematik induksiya usulida turli tenglama, tengsizliklar, olimlarning teorema va formulalarini isbotlashda qo`llaniladi.

1-BOB. TAYANCH MA’LUMOTLAR

1.1.Sonlar nazariyasining ba’zi masalalari va mashxur olimlarning ayrim tadqiqotlari

Son – matematikaning asosiy tushunchalaridan biri. Son tushunchasi eng
sodda ko’rinishda ibtidoiy jamoa davrida vujudga kelgan, insoniyat faoliyat
doirasining kengayishi va matematik bilimlarning rivojlanishi bilan
takomillashgan.
Al-Xorazmiyning «Kitob al-muxtasar fi hisob al-jabr va-muqobala»
(«Tiklash va qarama-qarshi qo’uish haqida qisqacha kitob») nomli algebraik
risolasida birinchi marta algebra matematikaning mustaqil bo’limi sifatida qaraladi. Unda algebraik miqdorlar ustida amallar bajarish qoidalari, 1-, 2-darajali algebraic tenglamalarni echish usullari va bundau tenglamalarga keladigan turli hayotiy masalalar, jumladan merosni bo’lish masalasi qaralgan. Risola latinchaga tarjima qilinganda «val-muqobala» so’zlari tushib qoldirilgan va «algebra» nomi bilan jahonga tarqalgan. (Shuning uchun bo’lsa kerak o’rta asrlarda Evropa davlatlarida singan qo’l-oyoqni tiklaydigan tabib (kostoprav) ni algebrist deb atashgan). 16-asrdayoq uzluksiz kasrlar matematikaga kira boshladi, u italiyalik matematik Bombelli (Rafaele, 1530-1572) ishlarida uchraudi. Boshqa bir italiyalik matematik Kataldi (Cataldi P.A. 1626 uilda o’lgan) 1613 uilda uzluksiz kasrlarni ma’lum ko’rinishda tasvirlagan, faqat «+» o’rniga «et» yozgan. Nemis matematigi, astronomi va fizigi Lambert (Johan Heinrich, 1728-1777) 1766 yilda uzluksiz kasrlar yordamida e va π sonlarning irrasionalligini isbotladi. Fransuz matematigi, mexanigi Lagranj (Lagrange Jozeph-Louis, 1736-1813) va L.Eylerlar chekli va cheksiz uzluksiz kasrlarning asosiu xossalarini o’rganishdi, har xil tadbiqlarini topishdi. Rus matematigi P.L.Chebishev (Pafnutiy Lvovich, 1821-1922) elementlari ko’phadlardan iborat bo’lgan uzluksiz kasrlarni orthogonal ko’phadlarni o’rganishga qo’lladi.

Sonlar nazariyasi tarixida uzoq muddat matematiklarning e’tiborini o’ziga tortgan ikkita masala to’g’risida to’xtalamiz.

Ta’rif. Agar m natural sonning o’zidan boshqa natural bo’luvchilari
y’g’indisi uning o’ziga teng bo’lsa, u holda m ga mukammal son deyiladi.
Masalan 6 ning o’zidan boshqa natural bo’luvchilari 1,2 va 3 bo’lib, ularning
yig’indisi 6 ga teng, ya’ni 6=1+2+3. Xuddi shu kabi 28 ning ham natural o’zidan boshqa bo’luvchilari yig’indisi o’ziga teng: 28=1+2+4+7+14. Demak 6 va 28 mukammal sonlardir. Mukammal sonlar Evklidning «Negizlar» asarida ham uchraydi.

Sharq va G’arb allomalari tub va murakkab sonlar, nukammal sonlar,
ularning soni haqida ko’plab izlanishlar olib borganlar. Jumlajdan Yevklid
o’zining «Negizlar» asarida ta’kidlanishicha, agar r va 2^r-1 sonlar tub bo’lsa, u holda n=2^p-1(2^p-1) mukammal son bo’ladi. 18-asrda L.Euler ko’rsatdiki, agar n son mukammal bo’lsa, u holda 2^r-1 tub bo’ladi. Hozirgi vaqtda 27 ta juft mukammal sonlar ma’lum, ularning eng kattasi 2⁴⁴⁴⁹⁶ (2⁴⁴⁴⁹⁷-1) bo’lib, 1962 uilda EHM yordamida topilgan.

Hozirgi vaqtda [1, 10⁵⁰] oraliqda toq mukammal sonning mavjud emasligi aniqlangan.

Ta’rif. Agar m va n natural sonlarning har biri ikkinchisining o’zidan
boshqa bo’luvchilari yig’indisiga teng bo’lsa, u holda bu sonlarga o’zaro do’st sonlar deyiladi.

Masalan, 220 va 284 sonlari o’zaro do’st sonlarga misol bo’ladi. Chunki,
220 ning o’zidan boshqa bo’luvchilari 1,2,4,5,10,11,20,22,44,55,110 bo’lib,
ularning yig’indisi 284 ga teng. Xudi shu kabi 284 ning o’zidan boshqa
bo’luvchilari 1,2,4,71,142 larning yigindisi 220 ga teng, ya’ni 220=1+2+4+71+142 va 284=1+2+4+5+10+11+20+22+44+55+110

Do’st sonlarni dastlab Pifagor (miloddan avvalgi taxminan 570-500 yillar)
kiritgan. Pifagorchilar do’st sonlar ilohiy qudratga ega deb, katta e’tibor berishar edi. Sharq matematiklari ham do’st sonlar bilan shug’ullanishgan. Bular quyidagilardir:

- 9 asrda Bog’dodda ishlagan Sobit ibn Qurra o’zining ―Do’st sonlarni oson
uo’l bilan topish haqidagi risola‖sida birinchilardan bo’lib natural sonlarning
o’zaro do’st son bo’lish mezonini keltiradi.

- 13-asrda yashagan tojik matematigi Mahmud bin-al-Vusudiu 1228 yilda
yozgan ―Lubob al-hisob‖ (―Hisob mag’izi‖) asarida Sobit ibn Qorra usulidan farqli ravishda do’st sonlarni aniqlash mezonini beradi.

- Ulug’bekning shogirdi, samarqandlik matematik G’iyosiddin Jamshid alKoshiu ―Arifmetika kaliti‖ nomli asarida do’st sonlar bilan shug’ullanib,
ularning do’st bo’lish mezonini keltiradi. - Sherozlik matematik va astronom Mahmud ibn Ma’sud Qutbiddin Sheroziy (1236-1311) o’zining ―Durra at-toj‖ (―Toj duri‖) nomli ensiklopedik asarida do’st sonlarni o’rgangan. Ma’lumki, 17-asrgacha matematik asarlar formulasiz, so’z bilan yozilar edi. Yuqorida nomlari keltirilgan olimlar ko’rsatgan mezonlarni hozirgi zamon simvolikasi bilan yozganda ular bir xil bo’ladi yoki ma’lum almashtirish bajarib, ularni bir xil ko’rinishga keltirish mumkin.

Masalan, Mahmud al-Vusudiy mezonini quyidagicha bayon qilish mumkin:
― Agar sonlarning har biri tub bo’lsa, u holda do’st sonlarning birinchisi m=2^kpq va ikkinchisi n=2^kr bo’ladi‖.

p 32^2k-1 1, q 32^2k-1 1 , r 9 2^2k-1 1

U shu mezon yordamida 17296 va 18416 sonlarning do’stligini ko’rsatgan (k=4 ga to’g’ri keladi). Bu do’st sonlarning fransuz matematiklari P.Ferma va R.Dekart 17-asrda qauta topishdi. L.Euler qariuib 60 juft do’st sonlarni topdi. Hozirgacha ularning soni cheklimi yoki cheksizmi noma’lum. P.Ferma (Pierre de Fermat, 1601-1665) fransuz matematigi, kasbi huquqshunos (yurist), 1631 uildan Tuluzada parlament maslahatchisi bo’lib ishlagan. Ferma matematikaning turli sohalarida ishlagan. U sonlar nazariyasining asoschilaridan biri hisoblanadi. Sonlar nazariyasida Fermaning nomini olgan ikkita teorema bor. Birinchisi Fermaning kichik teoremasi. Ikkinchisi (Fermaning buyuk teoremasi yoki Fermaning mashhur teoremasi) quyidagi tasdiqdan iborat:

Teorema. Agar n ikkidan katta natural son bo’lsa, u holda xn+yn=zn
(Diofant tenglamasi) noldan farqli butun x, y, z echimga ega emas.

Bu tasdiqni Ferma 1630 uilda Diofantning «Arifmetika» asarining
hoshiyasida quyidagicha yozgan edi: «Kubni ikkita kubga, bikvadratni ikkita
bikvadratga, umuman, kvadratdan katta hech qandau darajani shu ko’rsatgichga ega bo’lgan ikkita darajaga ajratish mumkin emas». Keyin u qo’shib qo’ygan edi: «Men buning haqiqatan ajoyib isbotini topdim, lekin buning uchun bu hoshiyalar juda kichik». Fermaning qog’ozlarida bu teoremani n=4 bo’lgan holining isbotini topishgan. n=3 bo’lganda bu teoremani L.Euler (1770 u.) isbotladi, n=5 bo’lganda L.Dirixle va A.Lejandr (1825 u.), n=7 bo’lganda G.Lame (1839 u.) isbotladi. Nemis matematigi E.Kummer (Ernst Eduard, 1810-1893) algebraik sonlar nazariyasida ideal tushunchasini kiritib, 100 dan ortmaydigan barcha n=p tub sonlar uchun Fermaning buyuk teoremasini isbot qildi.

Fermaning buyuk teoremasini sodda ta’riflanishiga qaramasdan, uning to’liq isboti Diofant tenglamalari nazariyasida yangi va chuqur metodlar yaratishni talab qilmoqda.

Matematika sohasida mutaxassis bo’lmagan kishilar orasida bu teoremani isbot qilishga bo’lgan o’rinsiz urinishlar o’z vaqtida bunday isbot uchun katta xalqaro mukofot ta’sis etilishi bilan bog’liq bo’lgan. Bu mukofot Birinchi jahon urushi oxiridayoq (1914-1918) bekor qilingan. Narsalarni sanashda ishlatiladigan sonlar natural sonlar deyiladi. Barcha natural sonlar hosil qilgan cheksiz to'plam N harfi bilan belgilanadi:N = {1, 2, ..., n, ...}. Natural sonlar to'plamida eng katta son (element) mavjud emas, lekin eng kichik son (element) mavjud, u 1 soni. 1 soni faqat 1 ta bo'luvchiga ega (1 ning o'zi). 1 dan boshqa barcha natural sonlar kamida ikkita bo'luvchiga ega (sonning o'zi va 1). 1 dan va o'zidan boshqa natural bo'luvchiga ega bo'lmagan 1 dan katta natural son tub son deyiladi. Masalan, 2, 3, 5, 7, 11, 13, 17, 19 sonlar 20 dan kichik bo'lgan barcha tub sonlardir. 1 dan va o'zidan boshqa natural bo'luvchiga ega bo'lgan 1 dan katta natural son murakkab son deyiladi. Masalan, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18 sonlar 20 dan kichik bo'lgan barcha murakkab sonlardir. Tub va murakkab sonlarga berilgan ta'riflardan 1 soni na tub, na murakkab son ekanligi ma'lum bo'ladi. Bunday xossaga ega natural son faqat 1 ning o'zidir.

1. misol. 827 sonining eng kichik tub bo'luvchisini toping.

Y e c h i s h. Bu 827 dan kichik bo'lgan tub sonlar 2, 3, 5, 7, 11, 13, 17, 19, 23 ekanligini aniqlab, 827 ni shu sonlarga bo'lib chiqamiz. 827 u sonlarning hech qaysisiga bo'linmaydi, bundan 827 ning tub son ekanligi kelib chiqadi.

2- misol. 15 va 50 sonlari orasida joylashgan tub sonlarni aniqlang.
Y e c his h . 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50 sonlarni olib, 2, 3, 5, 7 ga karrali sonlarning tagiga chizamiz. 17, 19, 23, 29, 31, 37, 41, 47 sonlari izlangan tub sonlardir.

Natural sonlar qatorida tub sonlar turlicha taqsimlangan. Ba'zan qo'shni tub sonlar bir-biridan 2 gagina farq qiladi, masalan, 11 va 13, 101 va 103 va hokazo. Bu sonlar egizak tub sonlar deyiladi. Egizak tub sonlar to'plamining chekli yoki cheksizligi hozirgacha noma'lum. Hisoblash mashinalari yordami bilan juda katta tub sonlar topilgan. Masalan, 25000 xonali 2⁸⁶²⁴³- 1 son tub sondir.

Tub sonlar haqidagi ko'p ma'lumotlar juda katta sonlar uchun
tekshirilgan, lekin isbotlangan emas. Masalan, istalgan juft sonni ikki tub sonning ayirmasi (masalan, 14 = 127 - 113, 20 = 907 - 887 va hokazo) ko'rinishida yozish mumkinmi yoki yo'qmi, buni biz bilmaymiz. Har qanday juft son uchun bunday tasBirlanishlar cheksiz ko'p bo'ladi, deyilgan taxminlar ham bor.

1-teorema (arifmetikaning asosiy teoremasi). Har qanday murakkab son
tub sonlar ko'paytmasiga yoyiladi va agar ko'paytuvchilarning yozilish
tartibi nazarga olinmasa, bu yoyilma yagonadir.

1. Sonlarning bo'linish belgilari. Matematikada sonlarning bo'linish
belgilari juda muhim ahamiyatga ega. Bu belgilar asosida sonlarning
bo'luvchilarini, bo'linuvchilarini topish, ularninig xossalarini o'rganish mumkin. Bu xulosadan sonlarning bo'linish belgilarini topishda foy- dalaniladi.

2. 2 ga bo'linish belgisi. 10k (k= 1, 2, ..., n) ni b= 2 ga bo'lishdan
chiqadigan qoldiqlar nolga teng. Shuning uchun B=a0 bo'ladi. Bundan a sonning oxirgi raqami2ga qoldiqsiz bo'linsa, bu son2ga qoldiqsiz bo'linadi, degan xulosaga kelamiz.

3. 3 va 9 ga bo'linish belgisi.10 ning darajalarini 10n= =(9 +1)n=9An+
1 ko'rinishda ifodalasak (bu yerda An N), 10n darajalarni b= 9 (yoki b= 3) ga
bo'lishdan chiqadigan qoldiqlar 1 ga tengligi kelib chiqadi. Shuning uchun
B=a0+a1+ ... +a n hosil bo'ladi. Bu yerdan ushbu qoida kelib chiqadi: agar
berilgan a sonning raqamlari yig'indisi9ga(3ga) qoldiqsiz bo'linsa, u holda
bu son9ga(3ga) qoldiqsiz bo'linadi.

4. 5 ga bo'linish belgisi. 10^k (k= 1, 2, ..., n) darajalar b= 5 ga qoldiqsiz
bo'linadi: r1=r2= ... =rn= 0.B=a0 bo'lgani uchun ushbu qoida kelib chiqadi: oxirgi raqami 5ga qoldiqsiz bo 'linadigan sonlar Ba faqat shunday sonlar 5 ga qoldiqsiz bo'linadi.

5. 4 va 25 ga bo'linish belgilari. b = 4 bo'lganda 10 = 2b + 2,
102=25b+ 0, 103=250b+ 0, ..., r,= 2, r2=r3= • • • =rn= 0bo'lib, B=a0+2a1 bo'ladi, ya'ni sonning 4 ga bo'linishi uchun, uning birlik raqami bilan o'nlik raqami ikkilanganining yig'indisi 4 ga bo'linishi zarur Ba yetarlidir. B=a0+2a1 ifodani bunday yozamiz:

B1=a0+2a1+8a1=B+8a1=10a1+a0= . B=a0+2a1= (a0+10a1)-8a1= -8a1 yoki B+8a1= bo'lgani uchun B son soni 4 ga bo'linganda Ba faqat shu holdagina 4 ga qoldiqsiz bo'linadi. Bundan, oxirgi ikkita raqamidan tuzilgan son 4ga bo 'linadigan sonlar Ba faqat shunday sonlar 4 ga bo 'linishi kelib chiqadi. Masalan, 14 024 sonining oxirgi 2 va 4 raqamlaridan tuzilgan 24 soni 4 ga bo'linadi, demak, 14 024 soni ham 4 ga bo'linadi.
Xuddi shunday oxirgi ikki raqamidan tuzilgan son 25 ga bo 'linadigan sonlar Ba faqat shunday sonlar 25 ga bo'linadi. Masalan, 1 350 sonida oxirgi ikki raqamidan iborat son 50, bu 25 ga qoldiqsiz bo'linadi. Demak, 1 350 ham 25 ga qoldiqsiz bo'linadi. 22 Ba 52 uchun olingan xulosani 2^m, 5^m(m N) sonlari uchun ham umumlashtirish mumkin. Agar berilgan sonning oxirgi m ta raqamidan tuzilgan son 2^m ga (5^mga) qoldiqsiz bo'linsa, berilgan son ham 2^m ga (5^m ga) qoldiqsiz bo'linadi.

6. 7 ga bo'linish belgisi. Bizda b = 7 va 10 = 7 + 3, r1 = 3;

10²= 7 • 14 + 2, r2= 2;

10³= 7 • 142 + 6, r3= 6;

10⁴= 7 • 1 428 + 4, r4= 4;

10⁵= 7 • 14 285 + 5, r5= 5;

10⁶= 7 • 142 857 + 1, r6= 1.

10⁷ da r7= 3 =r1 qoldiqlar qaytadan takrorlanyapti. Topilgan natijalarni
(1) ga qo'ysak, u holda a=A• 7 +B da

qoldiqsiz bo'linsa, berilgan a son ham 7 ga qoldiqsiz bo'linishi kelib chiqadi.

14 +12 + 2 = 28 0 +15 + 6 = 21 12 + 21 + 5 = 38, 38 + 28 - 21 = 66 - 21 = 45 soni 7 ga bo'linmaydi. Demak, berilgan son 7 ga bo'linmaydi.

7. 11 ga bo'linish belgisi. Berilgan a sonda qatnashayotgan 10 ning
darajalarini 11 ga bo'lishdagi qoldiq har doim 10 yoki 1 bo'ladi. Demak, berilgan sonning juft o'rinda turgan raqamlari yig'indisidan toq o'rinda turgan
raqamlari yig'indisi ayirilganda hosil bo'ladigan ayirma 11 ga bo'linsa, son
11 ga qoldiqsiz bo 'linadi. (7 + 8) - (4 + 8) = 15 - 12 = 3 soni 11 ga bo'linmaydi, demak, berilgan son 11 ga bo`linmaydi.

2- misol. 4 788 sonining 11 ga bo'linishini aniqlang.

(7 + 8) - (4 + 8) = 15 - 12 = 3 soni 11 ga bo'linmaydi, demak, berilgan son
ham 11 ga bo'linmaydi.

1.2. Matematik induksiya metodi haqida umumiy ma’lumotlar

Mantiqiy ifoda tushunchasiga ham formula tushunchasiga matematik induksiya
usuliga tayangan holda berilgan ta’rifga o‘xshash qat’iy ta’rif berilishi mumkin. Mantiqiy
ifodalarning teng kuchliligi tushunchasini ham formulalar teng kuchliligi tushunchasiga o‘xshash aniqlash mumkin. Oddiy algebrada aynan teng qiymatga ega ifodalarni bir-biri bilan almashtirish mumkin bo‘lganidek, mulohazalar algebrasida ham mantiqiy ifoda tarkibidagi qismiy mantiqiy ifodalarni (formulalarni, mulohazalarni) ularga teng kuchli bo‘lgan ifodalar (formulalar, mulohazalar) bilan almashtirish, ya’ni o‘rniga qo‘yish usulidan foydalanish mumkin. Bu esa murakkab ifodalarni (formulalarni, mulohazalarni) soddalashtirish imkonini beradi. Faraz qilaylik P(n) – bu n butun son to’g’risidagi biror bir tasdiq bo’lsin. «n(n+3) – juft son» n  10 bo’lsa, u holda 2n  23n . Bizdan P(n) ning barcha butun musbat n sonlar uchun o’rinli ekanligini isbotlash talab qilinsin. Isbotning asosiy usuli quyidagilardan iborat: `
1. P(1) o’rinli ekanligini isbotlash.

2. P(1), P(2), …, P(n) lar o’rinli bo’lsa, u holda P(n+1) ham o’rinli ekanligini isbotlash.
bu isbot barcha butun musbat n lar uchun o’rinli bo’lishi kerak.

Misolni keltiramiz.

1  12 1 3  2 2 1 3  5  32 1 3  5  7  4 2 (1)

Ularning umumiy ko’rinishda quyidagicha yozish mumkin:
P(n)  1 3  ... (2n 1)  n² (2).

Biz P(n) ning barcha musbat n lar uchun o’rinli ekanini isbotlashimiz kerak.Yuqoridagi proseduraga muvofiq: ` a). P(1) o’rinli, chunki 1  1²

b). agar barcha P(1), P(2), …,P(n) tasdiqlar o’rinli bo’lsa, P(n) uchun ham o’rinli, ya’ni(2) munosabat bajariladi. (2) ning har ikkala tomoniga 2n+1 ni qo’shsak, quyidagiga ega bo’lamiz: 1 3  5  ... (2n 1)  2n 1  n²  2n 1  (n 1)²

Bu esa P(n+1) ning ham to’g’riligini ko’rsatadi. Bu metodni isbotlashning algoritmik prosedurasi deb qarash mumkin. Haqiqatan ham, agar a) va b) bosqichlar amalga oshgan deb hisoblasak, quyidagi algoritmP(n) tasdiqning ixtiyoriy butun musbat n uchun isbotini beradi. Berilgan butun musbat n uchun P(n) ning o’rinli ekanini isbotlash algoritmi.

A1 algoritm.

1. boshlash.

2. k  1 {((a)ga asosan P(1) tasdiqni isbotlang}

3. agar k=n bo’lsa, u holda 6 ga o’ting `
4. p(k+1) uchun isbotlang ((b) ga asosan p(2), p(3), p(k) to’g’riligini isbotlang va
p(k+1) uchun to’g’ri degan xulosaga keling)

5. k  k 1 3 ga o’ting `
6. tugash (so’ralayotgan isbot bajarildi) `
(a) va (b) bosqichlar (a1 algoritm) shaklidagi isbotlash matematik induksiya yordamida isbotlashdir Dastlab o’xshatish tushunchasini tahlil etamiz. O’xshatish belgisi qadimgi yunonlarda boshlanishida sonlar proportsiyasi shaklida ifodalangan. Masalan, 10 : 5 =14 : 7.

Keyinchalik o’xshatish so’zi shakllarga va boshqa narsalarga ham tatbiq etila boshlandi. Misollar ko’rib chiqamiz. Quidagi shakllar berilgan:

a) b) c) d)

O’xshash shakllar juftini topish talab etiladi. Qaysi xossasiga ko’ra, ushbu juftlarni tanlash masalasi qo’yiladi. Bu masalani yechish kompyuterga yuklatildi. Kompyuter shakllarni taqqoslab, quyidagi natijalarni qog’oz varag’iga chizib berdi va A : B = a : b tenglikni yozdi.

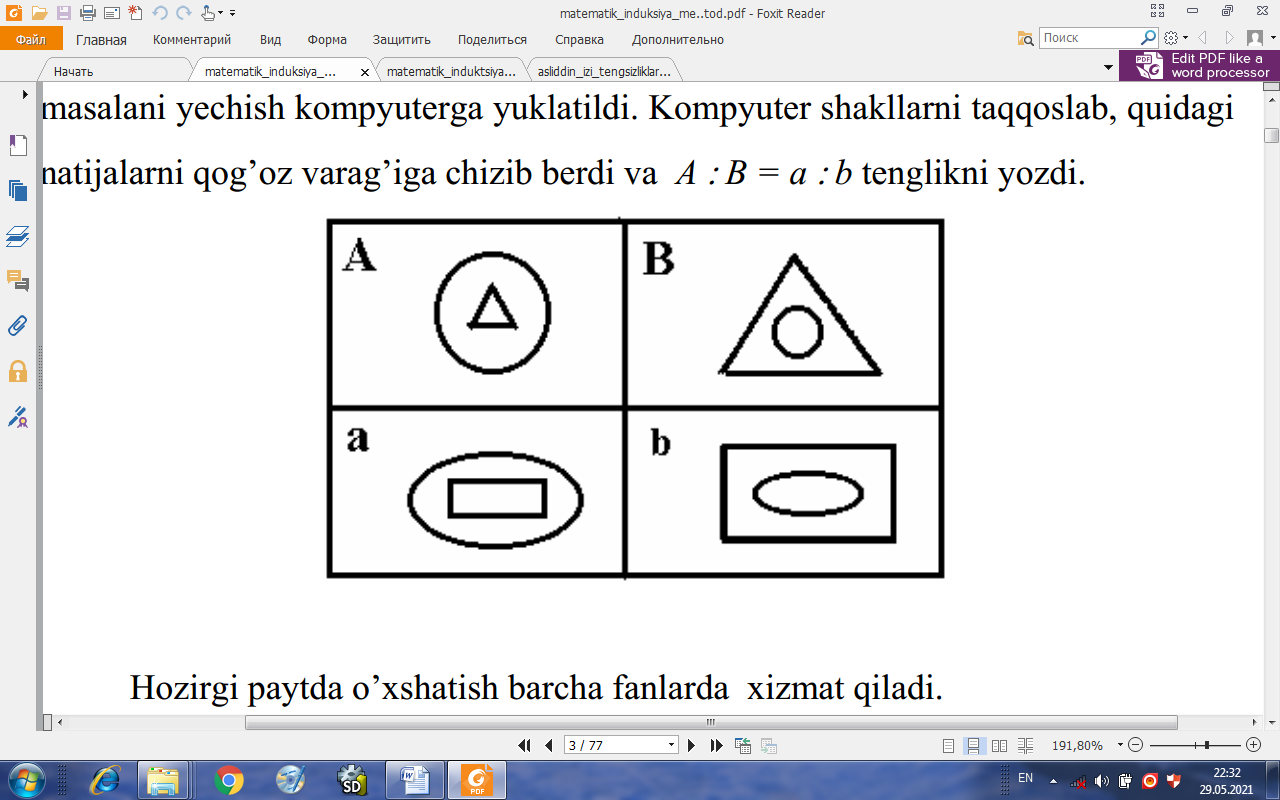
Hozirgi paytda o’xshatish barcha fanlarda xizmat qiladi.
Kimyo. D.I.Mendeleyev kimyoviy elementlarning davriy sistemasini yaratdi
va yangi elementlarning xossflarini o’xshatish bo’yicha ayta oldi.

Biologiya. Charl’z Darvin su’niy tanlash hodisasiga o’xshash “tabiiy

tanlash” tushunchasini kiritdi.

Fizika. Tovushning havoda tarqalish qonuniyati ushbu hodisaning suv
sirtida to’lqinini tarqalish hodisasiga asoslangan holda o’rnatildi.
Geologiya. Yoqutistonda olmos qazilma boyliklari topilgunga qadar Janubiy
Afrika yassi tog’liklari geologik tuzilishi G’arbiy-Sibir platformasi geologik
strukturasi bilan umumiy o’xshashliklari ma’lum bo’lgan. Tasodifiy holda
Yoqutiston daryolaridan birida Janubiy Afrikaning olmosli yo’nalishida mavjud
bo’lgan havorangli mineralga o’xshash mineral topilgan. Shundan so’ng
Yoqutistonda olmos izlana boshlandi. Haqiqatdan ham u yerdan olmos topildi,
keyinroq olmos boyliklari qazib olina boshlandi. Matematikada shunday masalalar mavjudki, ba’zi farazlar yakuniy natijalarga ko’ra, noto’g’ri bo’lib chiqadi. Shunday masalalardan biri 1640 yilida tug’ilgan P.Fermaning o’ziga tegishli hisoblanadi:

U f_n = 2^{2^n} + 1 ko’rinishidagi natural sonlarning barchasi tub son deb faraz qilingan va faqat n = 0, 1, 2, 3, 4 lar uchun tekshirilgan. Lekin 1732 yili Leonard Eyler Pyer Fermaning farazini inkor etdi. Buning uchun u f5 =2^{2^5} +1 soni 641 ga bo`linishini isbotladi.

Matematikada shunday masalalar uchraydiki, unda keltirilgan ba’zi xusuiy xulosalarga tayanib chiqarilgan farazlar yakuniy natijalarga ko’ra xato bo’lib chiqishi mumkin. Ana shunday masalalardan biri 1640 yilida tug’ilgan mashxur matematik P.Fermaga tegishlidir. Ushbu faraz quyidagicha bayon etilgan:

―Istalgan nN natural son uchun c(n) 2^{2^n}+1 tenglik bilan aniqlangan
natural sonlarning barchasi tub sonlar bo’ladi”.
Ushbu tasdiq olim tomonidan n 1,2,3,4 kabi hollardagi natural
sonlargachagina tekshirib ko’rgan va yuqoridagi xulosaga kelgan. Ammo Pyer Ferma tomonidan bildirilgan ushbu tasdiq 1732 yilga kelib Leonard Eyler tomonidan xato ekanligi isbotlandi. Buning uchun Leonard Eyler c(n) 2^{2^n} sonnig n=5 bo’lganda, ya’ni c(5) 2^{2^5} 1 sonning 641 ga karrali ekanligini ko’rsatdi. P.Fermaning yo’l qo’ygan asosiy xatosi – bu

c(n) 2^{2^n} 1 sonlarning tub yoki tub emasligini faqatgina chekli n1,2,3,4 qiymatlardagina tekshirib ko’rish (xususiy tasdiq) natijasida c(n)= 2^{2^n}+1 sonning 641 ga karrali ekanligini ko`rsatadi. P.Fermaning yo’l qo’ygan asosiy xatosi – bu c(n) 2²^ⁿ+1 sonlarning tub yoki tub emasligini faqatgina cheklita n 1,2,3,4 qiymatlardagina tekshirib ko’rish (xususiy tasdiq) natijasida c(n) 2^{2^n}+1 sonning barcha natural n larda tub ekanligi (umumiy tasdiq) haqidagi farazga kelganligidir. Lekin mashxur olim Leonard Eylerning o’zi ham tub va murakkab sonlar ustida to’xtalar ekan, dastlab quyidagi farazlarni kiritadi:

1) “ k(n) n² n 41

kvadrat uchhadning qiymatlari natural n larda tub son bo’ladi”. Ammo
keyinchalik uning o’zi ushbu k(n) n(n 1) 41 ko’phad n=40 bo’lgandagi qiymati k(40) 41² bo’lib, u 41 ga karrali ekanligini, ya’ni uning barcha natural n lardagi qiymatlari tub bo’lavermasligini isbotladi.

2) Xuddi shu kabi olimning yana birnechta xususiy xulosalarga asoslangan
farazi quyidagicha keltiladi: “ f (n) 991n² 1 ifoda n ning har qanday natural qiymatida biror natural sonning to’la kvadratiga teng bo’lmaydi”. Ammo keyinchalik ucshbu tasdiqning ham xato ekanligi isbotlanadi.

Chunki, keltirilgam ifoda faqatgina to n 12 055735790331359 447 442538767n bo’lgan holdagina f (n) 991n² 1 son natural sonning to’liq kvadrat bo’lishi hisoblab topilgan. Ushbu xulosalarga tayangan holda L.Eyler soda yoki to’liqsiz amalga oshirilgan matematik induksiya xatolikka olib kelishi mumkinligi haqida fikrlar bildirgan.

Matematik induksiya metodi bilan ishlaganda quyidagi ikkita asosiy
tushunchalarni ajrata bilish lozim bo’ladi:

1. Xususiy tasdiq

2. Umumiy tasdiq.

Masalan, a) Raqamlar yigindisi 3 ga bo’linadigan ko’p xonali natural sonning o’zi ham 3 ga qoldiqsiz bo’linadi; b) 3429 va 702 sonlari 3 ga karralidir. Ushbu keltirilgan tasdiqlardan birinchisi umumiy tasdiqdir, chunki u barcha narural sonlar uchun bir vaqtda tegishli bo’lib, umumiy holda isbotlanadi. Ikkinchisi esa birinchi tasdiqning ayrim natural sonlarga tatbiqi sifatida xususiy tasdiq hisoblanadi. Odatda xususiy tasdiqlardan umumiy tasdiqqa o’tish induksiya deyiladi. Xususiy tasdiqlarning qo’llanilishi va qo’llanilish mezoniga asoslangan holda induktiv xulosa to’g’ri yoki xato ham bo’lishi mumkin. Masalan, ―4239, 1839, 3039 sonlari 3 ga qoldiqsiz bo’linadi, tasdig’i natijasida quyidagi induktiv xulosalarga kelinishi mumkin: 1) Raqamlar yig’indisi 3 ga karrali bo’lgan natural sonlar 3 ga karralidir. 2) Oxirgi raqami 9 bo’lgan to’rt xonali natural sonlar 3 ga karrali bo’ladi. 3) Oxirgi ikki raqamidan iborat son 3 ga karrali bo’lgan ko’p xonali natural sonlar 3 ga qoldiqsiz bo’linadi. Ushbu keltirilgan uchta induktiv xulosalardan birinchisi to’g’ri, ikkinchi va uchinchisi xatodir. Chunki ularning bajarilmasligini 4169 va 7609 sonlarining 3 ga karrali emasligi asosida tushuntiriladi.

Keltirilgan uchbu mulohazalardan keyin o’z-o’zidan quyidagi savol
tug’iladi: Induksiya metodidan qay tarzda foydalanilganda va qanday mulohazalar uchun qo’llanilganda to’g’ri matematik xulosa chiqarish mumkin bo’ladi? Cheksiz sonlar ustida kiritilgan matematik mulohazani tekshirishda qaysi usullar amalga oshiriladi? Bunday usulni B.Pascal va Ya.Bernullilar taklif qilishdi. Bu usul hozirgi kunda matematik induksiya metodi deyiladi. Ushbu metodni ba’zi qadimgi grek olimlari ham foydalanishgan. Dastalab bu metod 1321 yillarda Gersonid tomonidan foydalanilgan. XIX asrning ikkinchi yarmigacha bu metod matematikada asosiy isbotlash metodi hisoblangan. Shu davrdan boshlab, O.Boltsano, O.L.Koshi, K.F.Gauss, N.X.Abelning ilmiy ishlaridan so’ng, induktiv isbotlashlar o’z ahamiyatini matematikada qisman yo’qotganday bo’ldi.

1.3. Matematik induksiya metodi haqida.

Matematik induksiya metodini misollarda tushuntiramiz.

Berilgan. Kitob javonida kitoblar quidagicha joylashtirilgan: 1) eng chekka qismida joylashgan kitob qizil muqovada. 2) Qizil muqovali kitobning o’ng tomonida qizil muqovali kitob joylashgan.

Xulosa. Kitob javonida joylashgan barcha kitoblar qizil muqovada. “Javonda barcha kitoblar qizil muqovada” xulosasi haqiqatdan ham to’g’ri

hosoblanadi. Lekin, agar eng chekkadagi kitob qizil muqovaliligi ma’lum bo’lsa, “javondagi barcha kitoblar qizil muqovali “ degan xulosa chiqarish uchun etarli darajada emas.

Qizil muqovali kitobning o’ng tomonida joylashgan kitob qizil muqovali degan xulosa chiqarishga etarli emas (Chap ttomondagi birinchi kitob yashil muqovada ham bo’lishi mumkin). Shuning uchun ,xulosa to’g’ri bo’lishi uchun ikkala shrt ham bajarilishi lozim. Matematika ensiklopediyasida quyidagi tushunchalar berilgan.

` Matematik induksiya – matematik induksiya prinsipiga asoslanib,
natural qiymat qabul qiluvchi parametrlarga bog’liq matematik tasdiqlarni
isbotlash metodidir.

Ma’lumki, tabiatdagi ko’plab jarayonlar va muammolar matematik modellashtirish orqali u yoki bu masala yechimini topishga, matematik mulohazalar ustida mushoxada yuritishga, ba’zi tasdiqlarni isbotlashga keltiriladi. Matematik mushohada yuritish orqali o’quvchining tafakkuri ortadi, ilmiy salohiyati yuksaladi. Ko’plab natural parametrli matematik ayniyatlar, tengliklar, tasdiqlar, tenlama va tengsizliklarni isbotlashda matematik induksiya metodidan foydalanish samarali hisoblanadi. Ushbu metod induktiv o’tish orqali natural sonlar to’plami yoki uning biror cheksiz qism to’plamida berilgan ayniyat, tenlik va tengsizliklarni isbotlash orqali umumiy tasdiqning to’g’riligini asoslashga asoslanganligi, isbotlash umumiy strukturaga egaligi bilan ham o’quvchiga tushunarli va qo’llash qulaydir. Uni puxta o’rganish orqali bitiruvchilar kelgusi pedagogik foaliyatida yoshlarga samarali saboq berishi bilan ham muhim ahamiyatlidir. Ushbu metodni tatbiq etish odatda quyidagi tartibda amalga oshiriladi:

1) Biror n natural parametrga bo’g’liq A(n),n n₀ matematik tasdiqning n n₀ boshlang’ich qiymatdagi A(n0) xususiy tasdig’i o’rinli ekanligi isbotlanadi (bunda odatda o’rniga qo’yib tekshirib ko’riladi);

2) Tayinlangan nk (k n₀) natural son uchun A(k) to’g’ri deb
faraz qilinadi va n=k+1 uchun A(k 1) to’g’riligi isbotlanadi. Shu asosda
barcha natural n n₀ lar uchun A(n) tasdiq to’g’ri deb qabul qilinadi.
A(n0) tasdiqning isbotlanishi induksiyaning birinchi qadami hisoblanadi,
A(n) uchun to’g’ri deb qabul qilingan farazdan A(n 1) tasdiqning o’rinliligini isbotlanish induksiyali o’tish deyiladi. Bunda n induksiya parametri deyiladi,

A(n 1) tasdiqni isbotlashda A(n)ni to’g’ri deb faraz qilish induktivli faraz deyiladi. Matematik induksiya metodining asosiy mohiyati quyidagida iborat:
Agar tasdiqlash ketma-ketligi mavjud bo’lsa, birinchi tasdiq to’g’ri va
har bir to’g’ri tasdidan so’ng to’g’ri tasdiq mavjud bo’lsa, ketma-ketlikdagi
barcha tasdiqlar to’g’ri hisoblanadi.

Shunday qilib, matematik induksiya metodi yordamida isbotlash ikkita
teoremani ketma-ket tatbiq etishdan iborat ekan:

1-Teorema. Isbotlanishi lozim bo’lgan natural parametrli biror A(n)
matematik tasdiq parametrning boshlang’ich n n₀ qiymatida o’rinli.
Ushbu teorema berilgan A(n) matematik tasdiqda n parametrning dastlabki
n₀ qiymatini qo’yib, tekshirib ko’rish orqali isbotlanadi.

2-Teorema. n=k da berilgan A(k) tasdiq to’g’ri deb faraz qilsak, u holda
bu tasdiq n = k +1 da ham o’rinli bo’ladi.

1 – MISOL.

(n⁴+6n³+11n²+6n):24 ifodaning ixtiyoriy n natural son bo’lganda 24 ga bo’linishini isbotlang.

n=1 da 24:24=2

n=2 da 16+48+44+12=120:24, 120:24=5

n=k uchun o’rinli deb n=k+1 uchun isbotlaymiz.

(k+1)⁴+6(k+1)³+11(k+1)²+6(k+1)=qavslarni ochib, guruhlab, soddalashtirsak=(k⁴+6 k³+11 k²+6k)+24(k²+1)+4(k³+11k) hosil bo’ladi. Bunda birinchi va ikkinchi qo’shiluvchi ikkiga bo’linadi. 3 chi qo’shiluvchida k³+11k ning 6 ga bo’linishini isbotlash kerak. Yana induksiya metodini qo’llaymiz.

k=1 da 12:6=6

k=2 da 8+22=30:6=5

k=m da o’rinli deb k=m+1 uchunko’ramiz. (m+1)³+11(m+1)+(m³+11m)+3m(m+1)+12

Birinchi va ikkinchi qo’shiluvchi 6ga bo’linadi. Ikkinchi qo’shiluvchidan 3m(m+1),m yoki m+1 sonlardan biri albatta juft, shuning uchun u ham 6 ga bo’linadi.

Demak, k³+11k ifoda ixtiyoriy n natural son bo’lganda 6 ga bo’linar ekan.

2-BOB. MATEMATIK INDUKSIYA METODINING TATBIQLARI
2.1. Ayrim matematik ayniyat va tengliklarni isbotlashda matematik
induksiyadan foydalanish.

1-Misol. 1 dan 2n gacha bo’lgan juft natural sonlar yig’indisining n(n+1) ga
tengligini isbotlang.

Yechish. Ushbu masalani yechish uchun quyidagi tenglikni isbotlash
yetarli:
2462n n(n1)

Bu tenglik esa umumiy ko’paytuvchi 2 ni chap tomonda qavsdan tashqariga
chiqarish va tenglikning ikki tomonini 2 ga bo’lish bilan quyidagi tenglikni
isbotlashga teng kuchlidir:

12 3n n( n .

Ushbu ifodaning chap qismini S(n) orqali belgilab, ya’ni

S n n n*(n , n

tasdiqni isbotlash uchun matematik induksiya prinsipini tatbiq etamiz.

1) Dastlab (2.1) tenglikni n=1 uchun to’g’ri ekanligini tekshirib
ko’ramiz. Haqiqatan ham bu holda S(1) 1bo’lib, tasdiq o’rinli

2) Endi (2.1) tenglik 1 dan katta ixtiyoriy natural k uchun bajarilgan deb faraz qilamiz, ya’ni

S(k) 12 3k k*(k

tenglik o’rinli bo’lsin. Induktiv o’tish orqali bu tenglikninig n=k+1 uchun ham o’rinli ekanligini, ya’ni `
S(k 1) 12 3k (k 1) k k+2)/2

tenglikning bajarilishini isbotlaymiz. Haqiqatan ham berilishiga ko’ra S(k 1)
ifodaning dastlabki k ta yig’indisi 123k belgilashga ko’ra S(k) bo’lganligi uchun hamda yuqoridagi farazga ko’ra quyidagilarni olamiz:

Bunda kasrlarni qo’shish va qo’shishning ko’paytirishga nisbatan taqsimot qonunidan faoydalanildi.

Eslatma. (2.1) tenglikni arifmetik progressiya formulasi asosida va
qo’shiluvchilarni guruhlash usulida yig’ish yoki S(n) dagi qo’shiluvchilarni teskari tartibda yozish vaavvalgi ko’rinishi bilan qo’shish orqali ham osongina isbotlash mumkin.

2-Misol. Boyi va eni n ta katakdan iborat matematika daftari sahifasida
n(n 1)(2n 1)/6 ta kvadrat borligini isbotlang.

Yechish. Ushbu matematika daftaridagi tomoni n birlik (1 birlik 1 ta katak
tomoni uzunligi) katta kvadratda avval tomoni 1 birlik uzunlikli kvadratlar sonini
(ularning soni n² ta), keyin tomoni 2 birlik uzunlikli kvadratlar sonini

( (n 1)²) va hakazo tomoni n birlik uzunlikli kvadratlar sonini (ular 1 ta) qo’shib chiqsak aytilgan masalaning matematik ifodasiga kelamiz.

Demak biz 1 dan n gacha natural sonlar kvadratlari yig’indisi

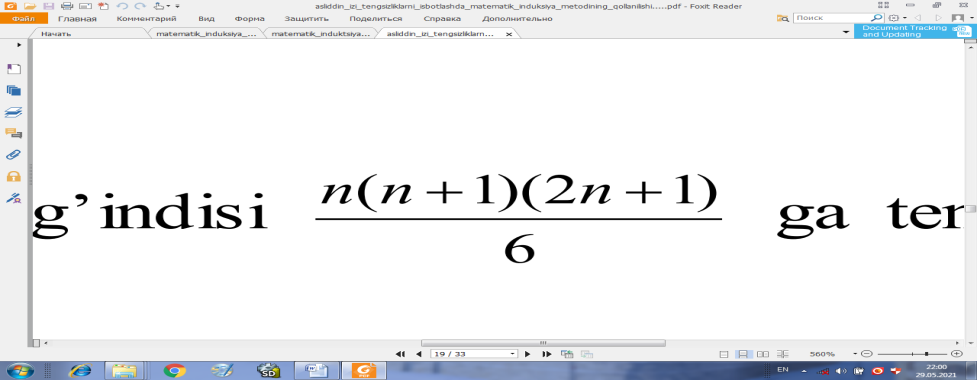
ga teng ekanligini isbotlashimiz lozim:

Yuqoridagi misoldagi kabi tenglikning chap qismini A(n) orqali belgilaymiz.
Natijada quyidagi ayniyatni isbotlashimiz kerak:

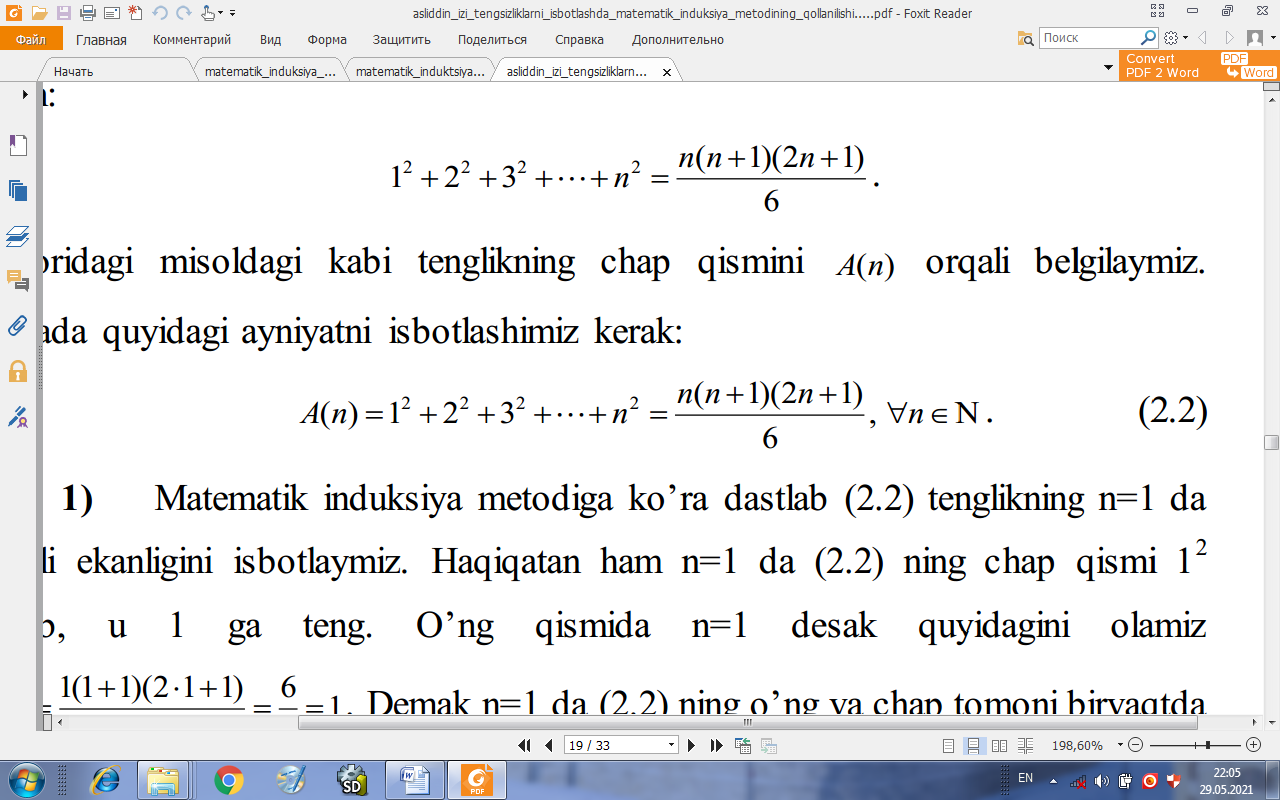(2.2)

1) Matematik induksiya metodiga ko’ra dastlab (2.2) tenglikning n=1 da
o’rinli ekanligini isbotlaymiz. Haqiqatan ham n=1 da (2.2) ning chap qismi 12
bo’lib, u 1 ga teng. O’ng qismida n=1 desak quyidagini olamiz

Demak n=1 da (2.2) ning o’ng va chap tomoni birvaqtda
1 ga teng ekan.

2) Endi (2.2) tenglik 1 dan katta ixtiyoriy natural k son uchun bajarilsin
deb faraz qilamiz, ya’ni

O’rinli bo’lsin. Bu tasdiqdan foydalanib (2.2) tenglikning k=n+1 da ham
bajarilishini isbotlaymiz. Belgilanishiga va qilingan farazga ko’ra quyidagiga
egamiz:

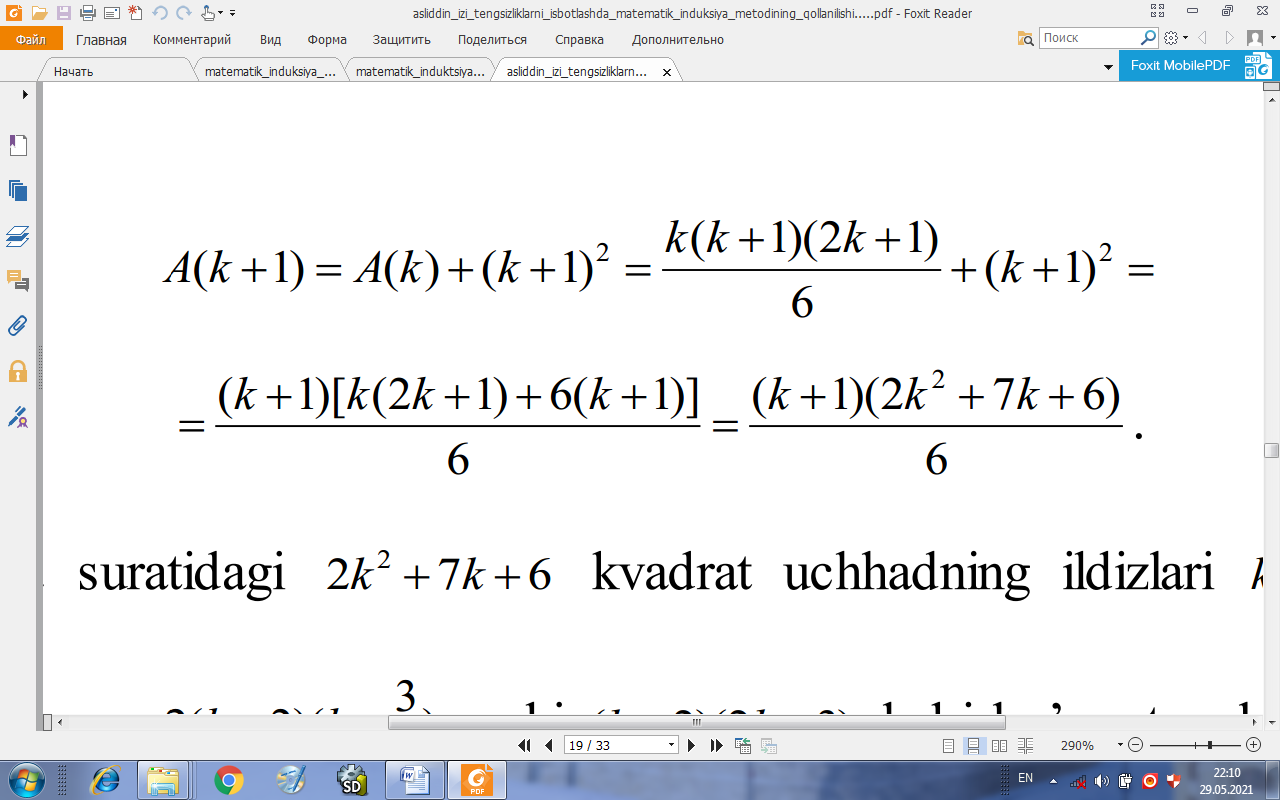
So’ngi ifoda suratidagi 2k² 7k 6 kvadrat uchhadning ildizlari k1 2, k2 bo’lgani uchun u 2(k 2)(k yoki (k 2)(2k 3) kabi ko’paytuvchilarga ajraladi. Bu ifodani o’z o’rniga qo’yib, quyidagi tenglikka kelamiz:

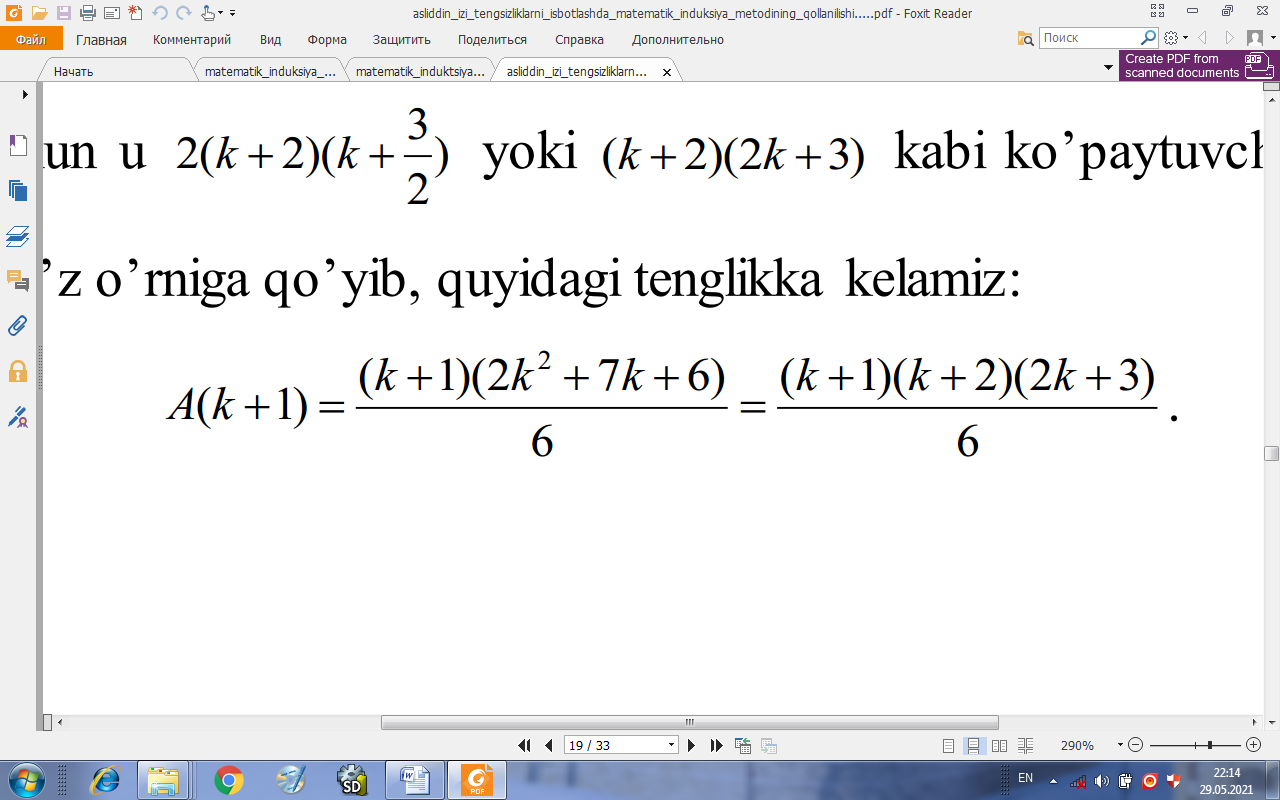
Bu esa biz isbotlashimiz kerak bo’lgan tenglikdir. Matematik induksiay metodiga
asosan (2.2) tenglik barcha natural sonlar uchun o’rinli.

2.2. Formula va teng kuchlilik tushunchalarini matematik induksiya usulida ishlatish

Mantiqiy amallar orasidagi bog‘lanishlar bilan bilan tanishmiz: ekvivalensiya ikki tomonli implikatsiyadir, aniqrog‘i, berilgan x va y mulohazalarning x  y ekvivalensiyasi ikkita x  y va y  x implikatsiyalarning (x  y)  (y  x) kon’yunksiyasi shaklida ifodalanadi. Dastlab mulohazalar algebrasining formula tushunchasiga murojaat qilib, intiutiv ravishda, uni berilgan elementar mulohazalardan inkor, diz’yunksiya, kon’yunksiya, implikasiya, ekvivalensiya mantiqiy amallarining chekli kombinatsiyasi va, zarur bo‘lganda, mulohazalar ustida mantiqiy amallarning bajarilish tartibini ko‘rsatuvchi qavslar vositasida hosil qilingan murakkab mulohaza deb tushunamiz. Bu yerda qavslarni ishlatish qoidalari sonlar bilan ish ko‘ruvchi (oddiy) algebradagidek saqlanadi.

1- m i s o l . Ushbu x , ch , yo  (yo  y) , x  y  x , [x1(x2  x3)x1]x4, y  x , (x  y)  (y  z)  (z  x) , [x1(x3 x3)](x4 x2)yo va (x  y)  (x y) ko‘rinishda yozilgan murakkab mulohazalarning har biri formuladir, lekin [x1(x2  x3)]x1 va (x  y)  (z  (z  y) yozuvlarni formula sifatida qabul qilish mumkin emas, chunki ularning birinchisida kon’yunksiya belgisidan keyin yopuvchi “]” qavs yozilgan, ikkinchisida esa ikkinchi ochuvchi “(“ qavsga mos yopuvchi “)” qavs yozilmagan.

Formula tushunchasiga matematik induksiya usuliga tayangan holda quyidagicha qat’iy ta’rif beriladi.

1-t a ’ ri f . 1) Agar x elementar mulohaza bo‘lsa, u holda x formuladir;
2) agar A formula bo‘lsa, u holda A formuladir;

3) agar A va B formulalar bo‘lsa, u holda (A B) , (A B) , (A  B) va (A  B)
formulalardir;
4) 1-, 2- va 3- bandlardagidan tashqari boshqa formula yo‘q.

1- ta’rifga ko‘ra ixtiyoriy formulaga, uning qiymati sifatida, vaziyatga qarab, {ch, yo} to‘plamning biror elementi mos qo‘yiladi. Formula tarkibidagi o‘zgarmas va o‘zgaruvchi (elementar) mulohazalarning har biri elementar formulalar deb hisoblanadi. Formula qiymatining x1, x2,..., xn o‘zgaruvchilarga (elementar mulohazalarga) bog‘liqligini ta’kilash kerak bo‘lgan holda f (x1, x2 ,..., xn ) ko‘rinishdagi yozuvdan foydalaniladi. Tabiiyki, formula tushunchasiga berilgan 1- ta’rif asosida ish yuritilsa, tuzilgan formula tarkibida qavslar ko’p bo‘ladi.

Matematik mantiqda formula tarkibidagi qavslar sonini kamaytirish maqsadida, odatda, quyidagi kelishuvlardan foydalaniladi.

1) biror formula inkor ishorasi ostida bo‘lsa, u qavssiz yoziladi (masalan, (x  y)  z formulani x  y  z ko‘rinishda yozish mumkin).

2) kon’yunksiya amali diz’yunksiya, implikatsiya va ekvivalensiya amallariga nisbatan formulalarni mustahkamroq bog‘laydi deb hisoblanadi (masalan, x  (yz) formulani x  yz , xy  (yz) formulani xy  yz , (xy)  (zu) formulani esa xy  zu ko‘rinishda yozish mumkin).

3) diz’yunksiya amali implikatsiya va ekvivalensiya amallariga nisbatan formulalarni mustahkamroq bog‘laydi deb hisoblanadi (masalan, x  (y  z) formulani x  y  z , x y  (z  y) formulani esa x y  z  y ko‘rinishda yozish mumkin).
4) implikatsiya amali ekvivalensiya amaliga nisbatan formulalarni mustahkamroq bog‘laydi deb hisoblanadi (masalan, x  (y  z) formulani x  y  z ko‘rinishda yozish mumkin). Bu kelishuvlar, yuqorida ta’kidlanganidek, formulalar tarkibidagi qavslar sonini kamaytirish imkonini beradi. Masalan, (((x  y)  (x  z))  (((x  y) (x  y)) (x  z))) formulani (x  y)  xz  xy  xy  (x  z) ko‘rinishda yozish mumkin.

Matematik induksiya usulini yig‘indilarni hisoblashga, ayniyatlami, tenglik va tengsizliklami isbotlashga, holinish belgilarini isbotlashga, sonli ^ketma-ketliklarning xossalarini o‘rganishga, shuningdek, boshqa har xil masalalarni yechishga qo‘llash mumkin.
10-misol. Istalgan n natural son uchun yig`indini hisoblang.

Y e c h i s h : Bu yig‘indini S_n orqali belgilaylik. Sn yig'indini hisoblash uchun formula topamiz. Buning uchun S_n yig‘indining dastlabki S1 S2, S3, yig'indilarini hisoblaymiz:

;

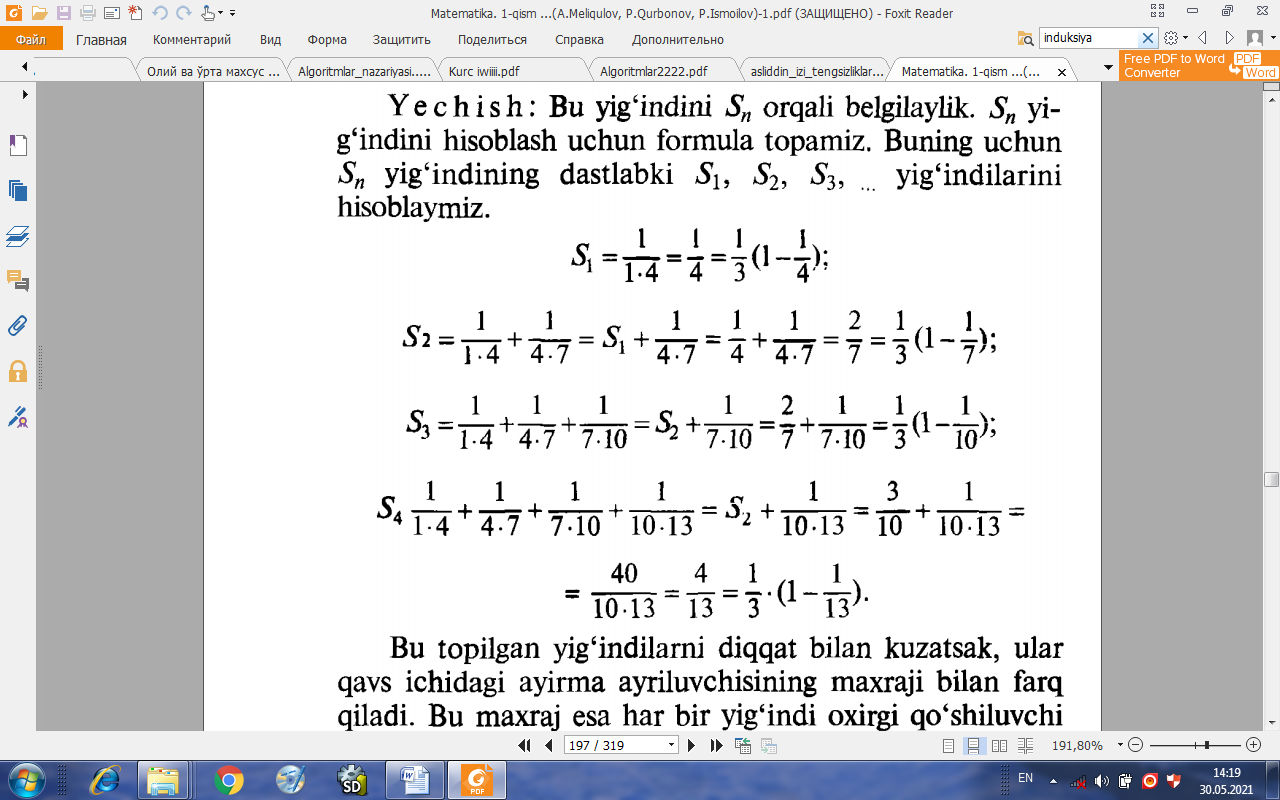Bu maxraj esa har bir yig‘indi oxirgi qo‘shiluvchi maxrajidagi ikkinchi ko‘paytuvchisiga teng. Bu esa bizni

(2.1)

induktiv faraz qilishga olib keladi.

Bu tenglikni matematik induksiya usuli bilan isbotlaymiz:

1) n= 1, 2, 3, 4 uchun mulohazamizning to‘g‘riligi isbotlandi;

2) faraz qiliyhk, mulohazamiz n = k uchun to‘g‘ri bo‘lsin:

Bo`lishini isbotlaymiz.

S_k+1 =1/3(1-1/3*k+4) tenglik (1) dan n = k + 1 bo‘lganda hosil bo‘ladi.

. Agar n€ N bo‘lsa, (3²ⁿ⁺¹+40n-67):64 bo‘Iishini isbotlang

Y e c h i s h : Agar n =1 bo‘lsa, u holda 3³ + 40 — 67 = 0
bo‘lib, 0:64 bo‘ladi.

Faraz qilaylik, n=k bo‘lganda (3^2k+1+40k + 67):.64 bo`lsin.

n = k + 1 bo‘lganda [ 3^2k+3 + 40 (k+1) — 67]: 64 bo`lishini isbotlaylik.

Bunda \9(3^2k+1 +40k - 67)]: 64 va [64(5* - 9)] = 64.

Demak, berilgan tasdiq istalgan n natural son uchun o'rinli.

Misol. Agar a€N bo`lsa (a<sup>5</sup>-5a<sup>3</sup>+4a):120 bo`lishini isbotlang.

Yechish: a= 1 boisa, tasdiq to‘g‘ri, ya’ni (l⁵- 5 1³+ 4*1): 120 • a + 2 bo`lsa ham (2⁵-5*2³ +4*2]':120.

Faraz qilaylik, a =/cbo‘lganda (*5 - 5*3 + 4*) • 120bo‘lsin. a = k + 1 bo‘lganda [(k + 1)⁵ - 5(k+1)³ + 4(k+1)] : 120 bo‘lishini isbotlaymiz:

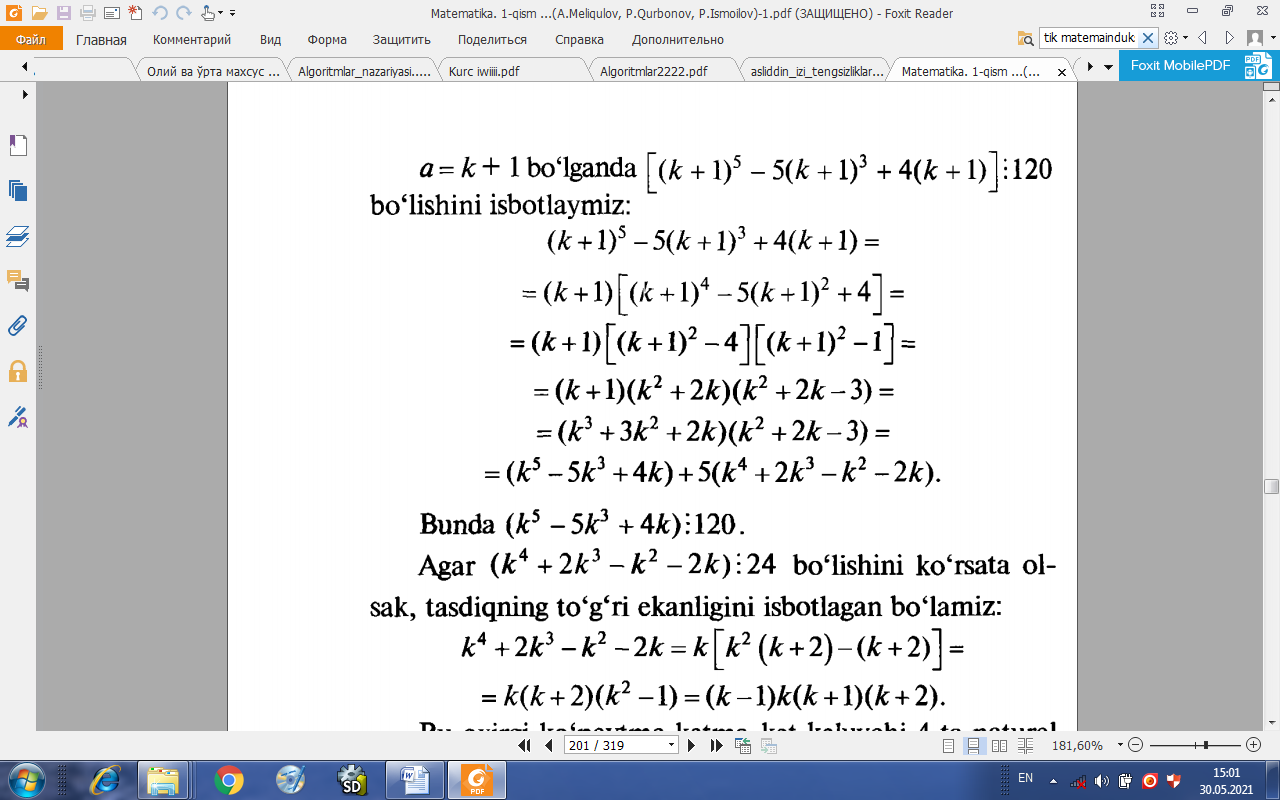
Agar (k⁴ + 2k³ – k² – 2k) : 24 bo‘lishini ko‘rsata olsak, tasdiqning to‘g‘ri ekanligini isbotlagan bo‘lamiz:

k⁴ + 2k^3 – k² – 2k = k [k^2 (k + 2) - (k + 2)] = k(k + 2)(k^2-1) = (k - 1)k(k + 1)(k +2).

Bu oxirgi ko'paytma ketma-ket keluvchi 4 ta natural sonning ko‘paytmasini ifodalaydi. Bunday ko‘paytma tarkibida hamma vaqt 24 ko‘paytuvchi bo‘ladi. Demak,
k € N bo‘lganda (k^4 +2k^3 –k^ 2-2k):24 bo‘ladi.

2 dan kam bo’lmagan ixtiyoriy natural n uchun

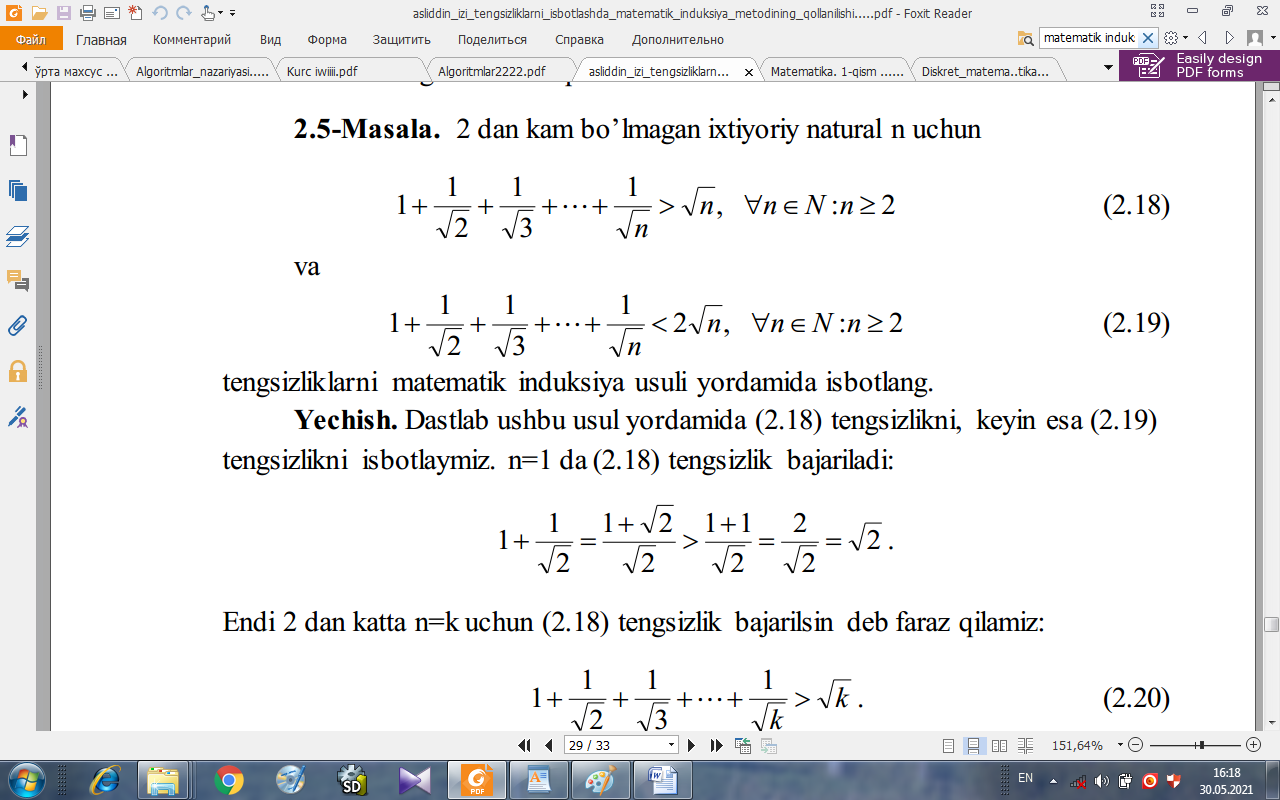(2.2)

va

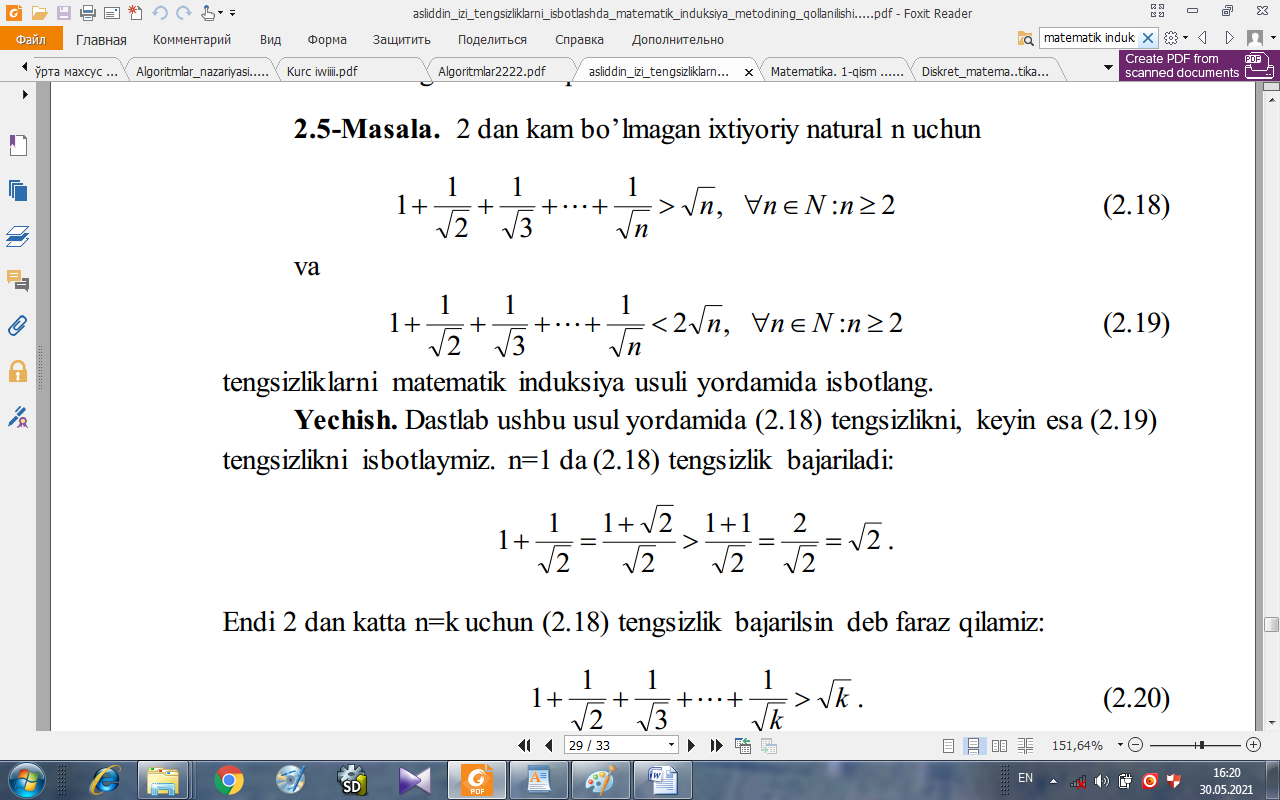(2.3)

tengsizliklarni matematik induksiya usuli yordamida isbotlang.

Yechish. Dastlab ushbu usul yordamida (2.1) tengsizlikni, keyin esa (2.3)
tengsizlikni isbotlaymiz. n=1 da (2.1) tengsizlik bajariladi:

Endi 2 dan katta n=k uchun (2.1) tengsizlik bajarilsin deb faraz qilamiz:

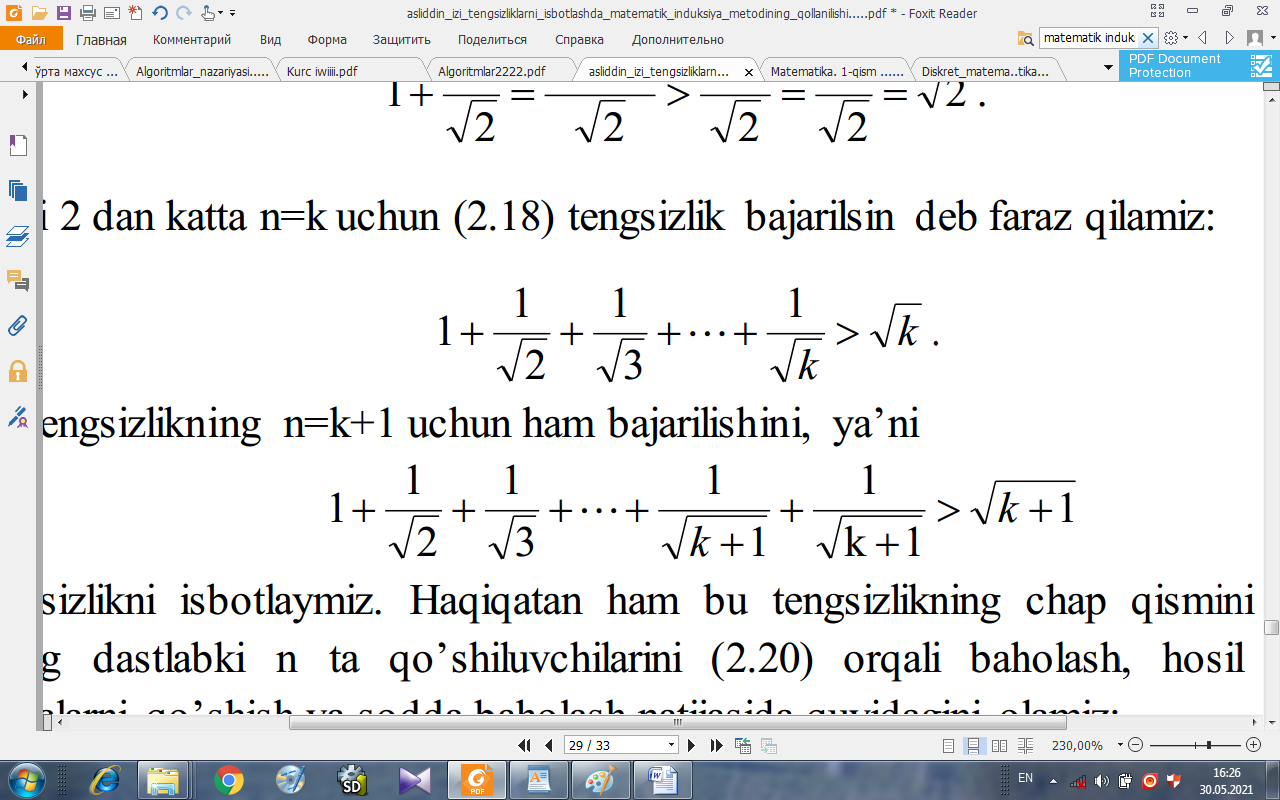(2.4)

Bu tengsizlikning n=k+1 uchun ham bajarilishini, ya’ni

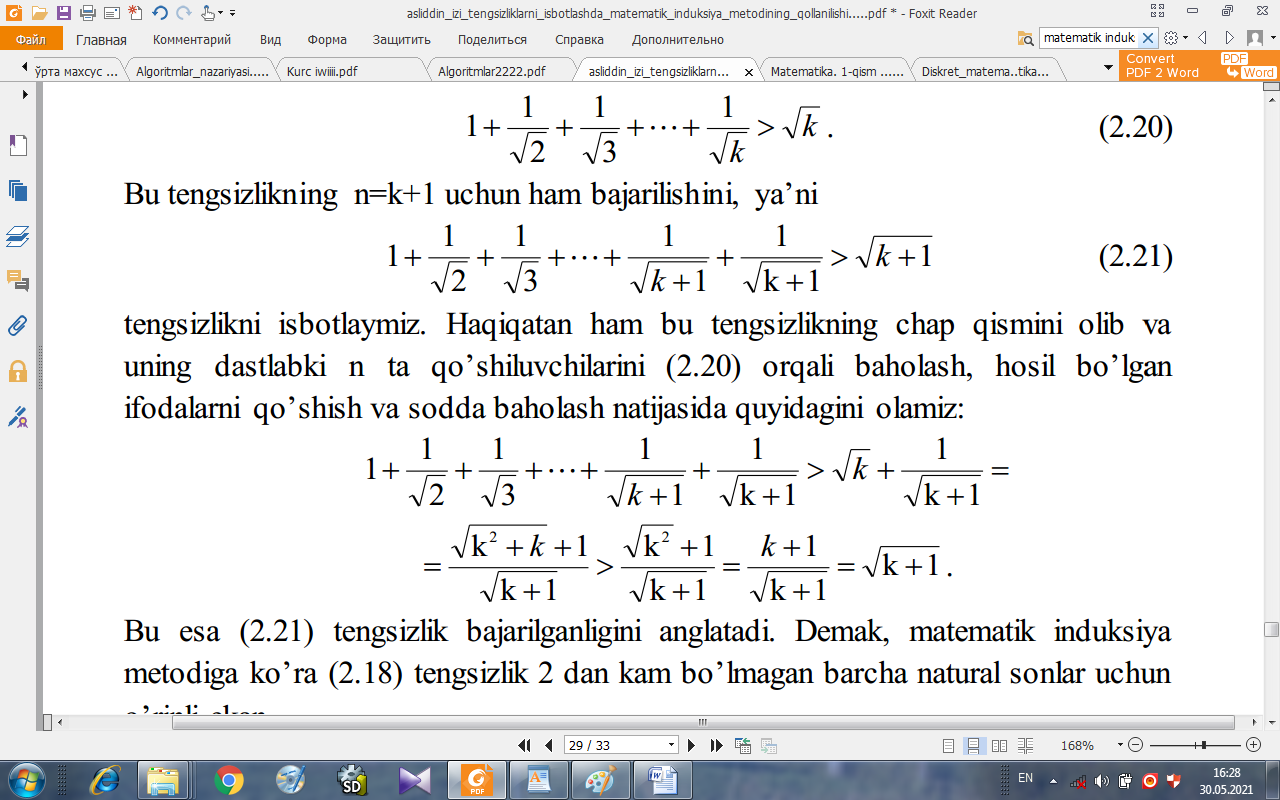(2.5)

tengsizlikni isbotlaymiz. Haqiqatan ham bu tengsizlikning chap qismini olib va uning dastlabki n ta qo’shiluvchilarini (2.4) orqali baholash, hosil bo’lgan ifodalarni qo’shish va sodda baholash natijasida quyidagini olamiz:

Bu esa (2.3) tengsizlik bajarilganligini anglatadi. Demak, matematik induksiya metodiga ko’ra (2.1) tengsizlik 2 dan kam bo’lmagan barcha natural sonlar uchun o’rinli ekan. Endi shunga o’xshash tarzda (2.2) tengsizlikni shu usul yordamida isbotlaymiz. Bunda ham n=2 uchun dastlabki tasdiqning o’rinli ekanligini tekshiramiz:

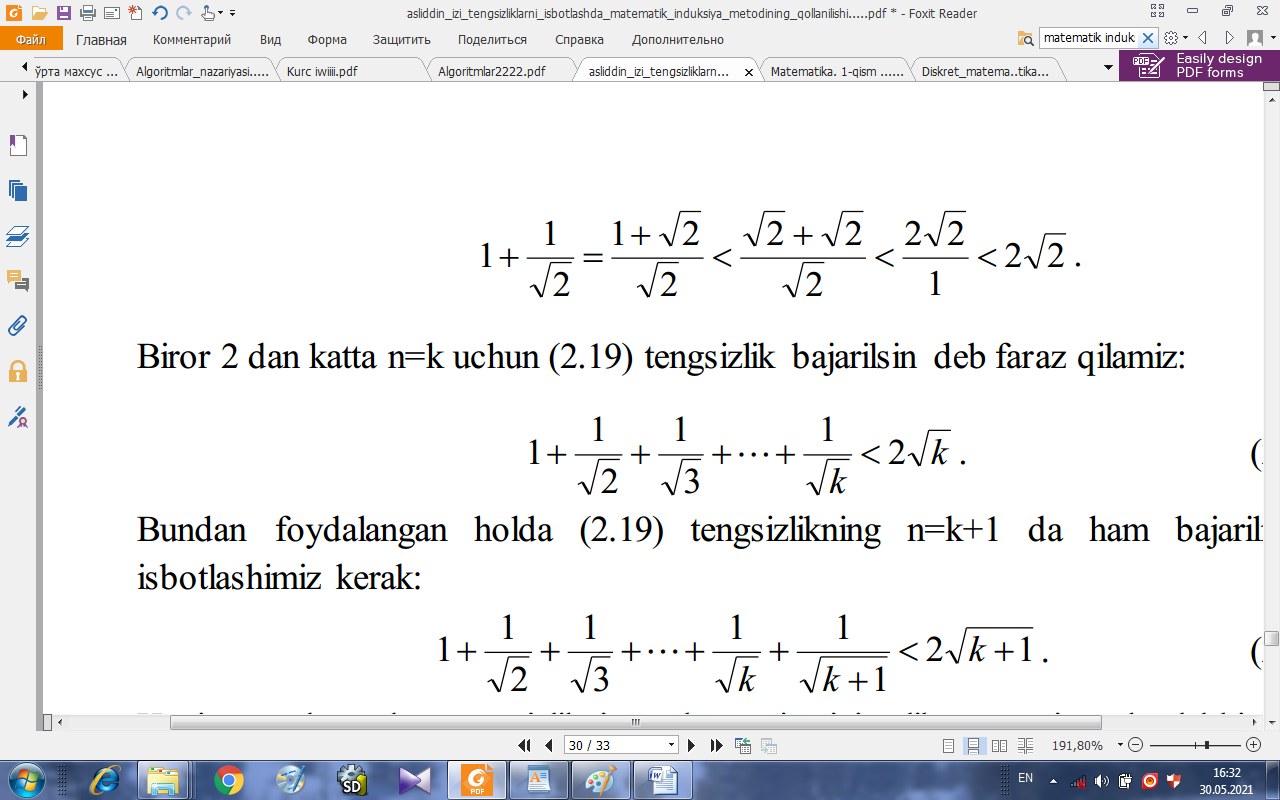
Biror 2 dan katta n=k uchun (2.2) tengsizlik bajarilsin deb faraz qilamiz:

(2.6)

Bundan foydalangan holda (2.2) tengsizlikning n=k+1 da ham bajarilishini
isbotlashimiz kerak:

(2.7)

Haqiqatan ham bu tengsizlikning chap qismini olib va uning dastlabki n ta
qo’shiluvchilarini (2.7) orqali baholash, hosil bo’lgan ifodalarni qo’shish va
sodda baholash natijasida quyidagini olamiz

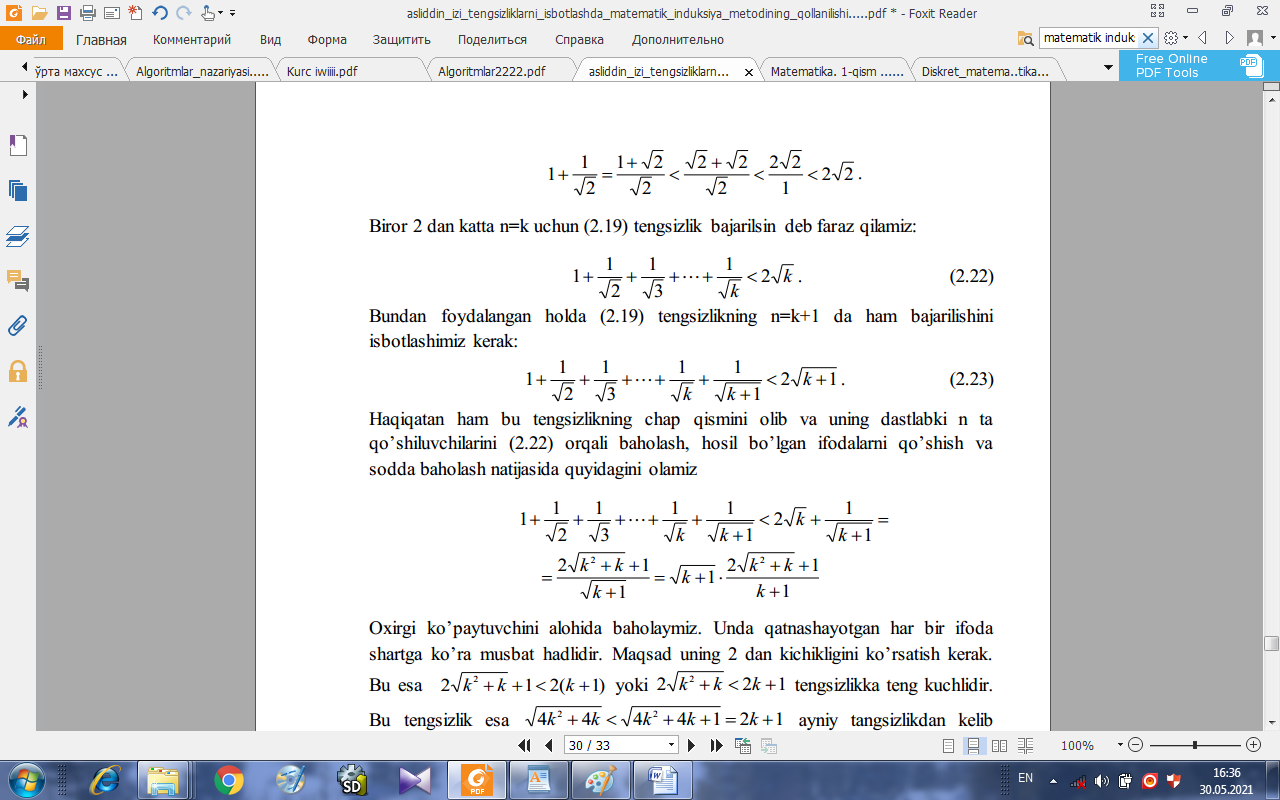
Oxirgi ko’paytuvchini alohida baholaymiz. Unda qatnashayotgan har bir ifoda shartga ko’ra musbat hadlidir. Maqsad uning 2 dan kichikligini ko’rsatish kerak . Bu esa 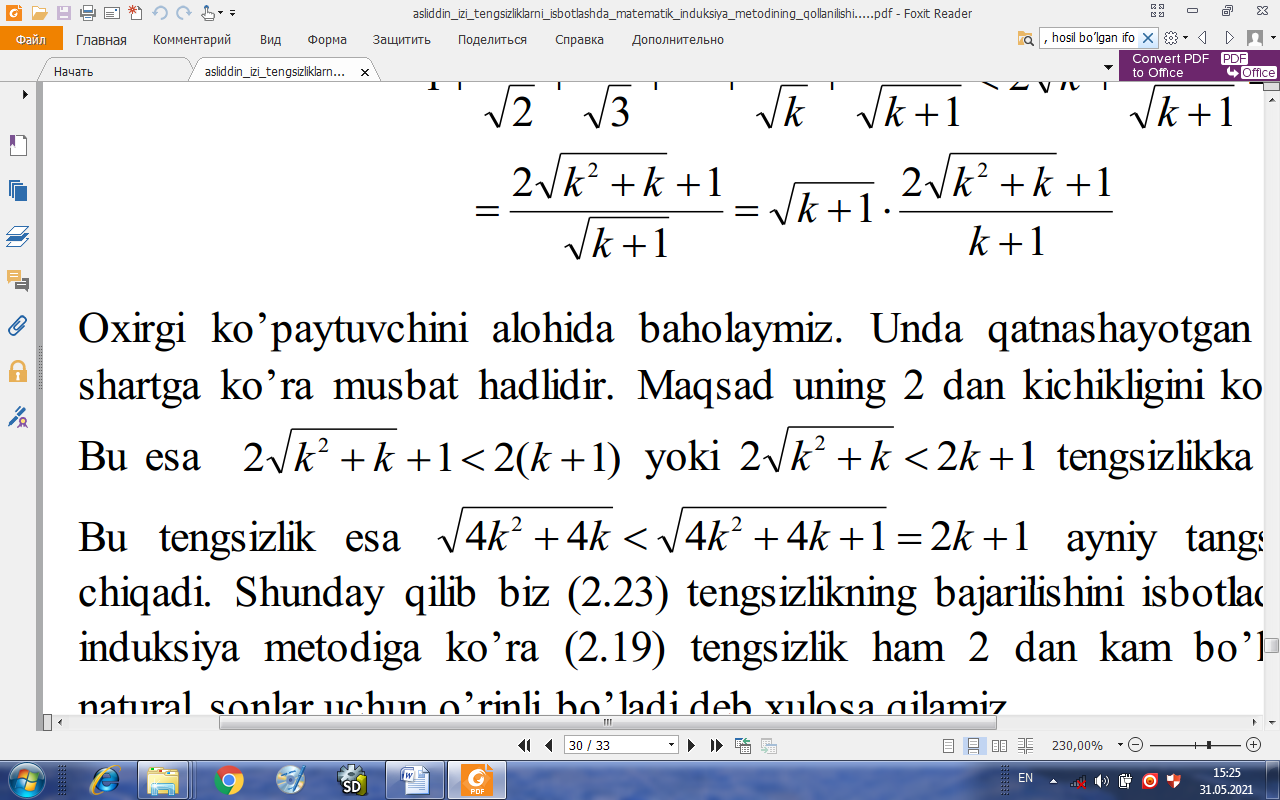yoki

tengsizlikka teng kuchlidir. Bu tengsizlik esa

ayniyatdagi tangsizlikdan kelib chiqadi. Shunday qilib biz (2.7) tengsizlikning bajarilishini isbotladik. Matematik induksiya metodiga ko’ra (2.2) tengsizlik ham 2 dan kam bo’lmagan barcha natural sonlar uchun o’rinli bo’ladi deb xulosa qilamiz.

2.6-Masala. 3 dan kam bo’lmagan ixtiyoriy n natural son uchun
nⁿ⁺¹ (n 1)ⁿ, n 3, nN . (2.8)

tengsizlikni isbotlang.

Yechish. Isbotni matematik induksiya usulida bajaramiz. Dastlab qaralayotgan (2.8) tengsizlikning n=3 da to’gri ekanligiga ishonch hosil qilamiz:

^{34  81  64  43} .

Berilgan (2.8) tengsizlik 3 dan katta biror n=k natural sonda bajarilsin deb faraz qilamiz

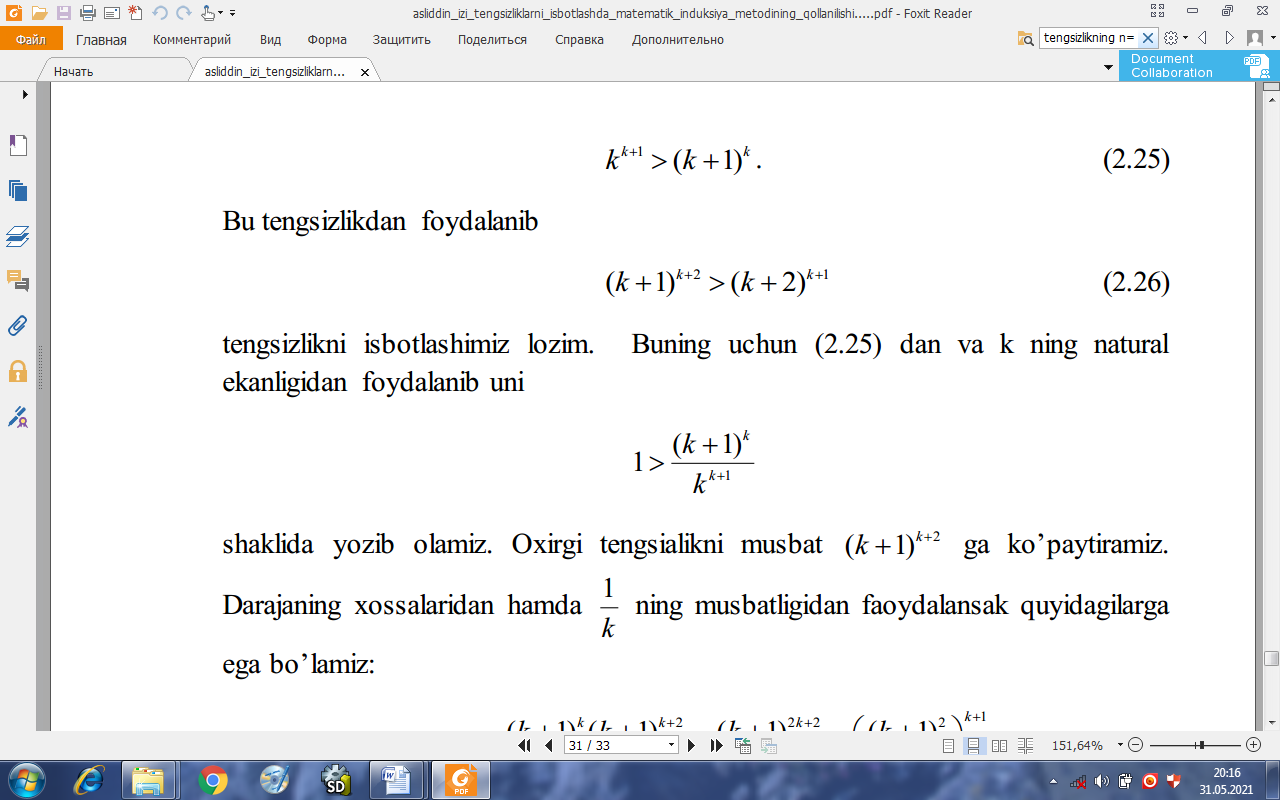(2.9)

Bu tengsizlikdan foydalanib

(k+1)^k+2(k+2)^k+1 (2.10)

tengsizlikni isbotlashimiz lozim. Buning uchun (2.10) dan va k ning natural
ekanligidan foydalanib uni

shaklida yozib olamiz. Oxirgi tengsialikni musbat (k 1)^k+2 ga ko’paytiramiz. Darajaning xossalaridan hamda 1 /k ning musbatligidan faoydalansak quyidagilarga ega bo’lamiz:

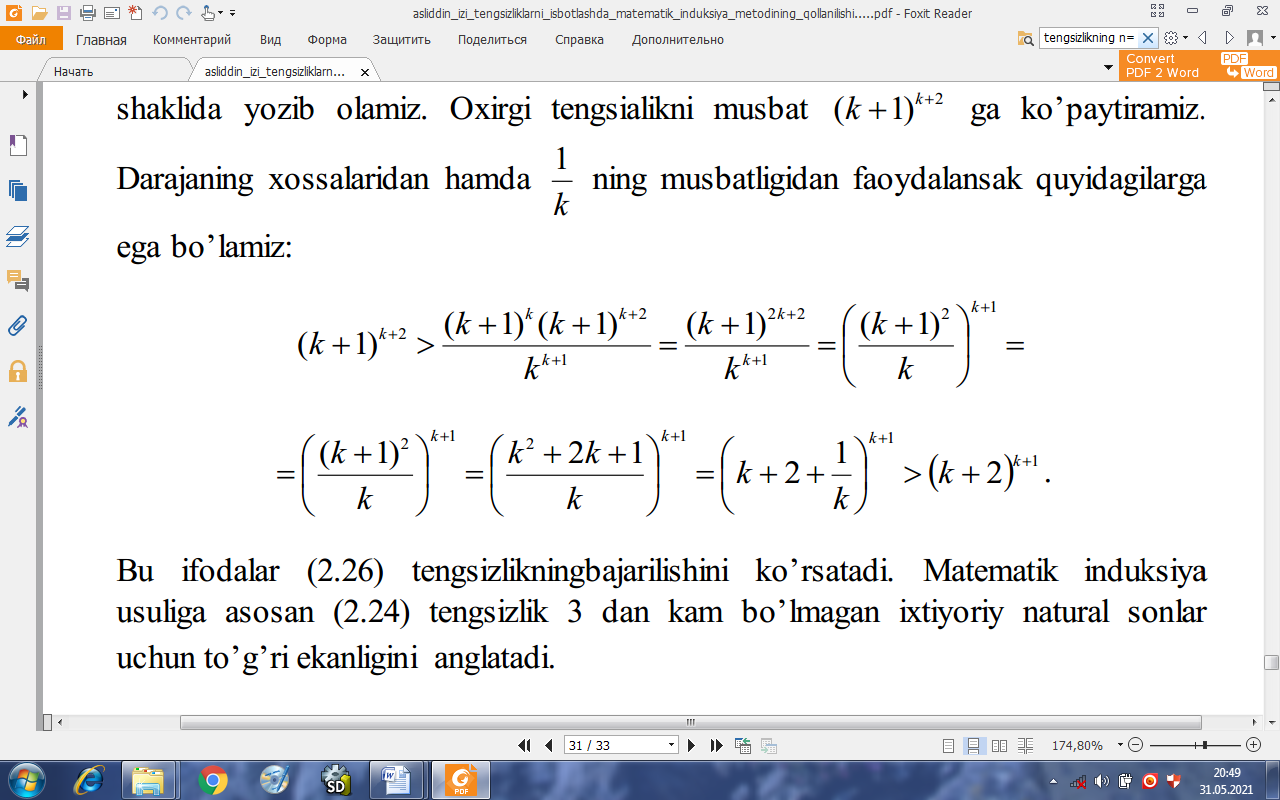
Bu ifodalar (2.10) tengsizlikningbajarilishini ko’rsatadi. Matematik induksiya usuliga asosan (2.8) tengsizlik 3 dan kam bo’lmagan ixtiyoriy natural sonlar uchun to’g’ri ekanligini anglatadi.

Masala. n natural sonning qaysi qiymatlarida quyidagi tengsizliklar bajariladi:

2ⁿ  n² ; (2.11)

3ⁿ  n³ ; (2.12)

2ⁿ  5n  3? (2.13)

(2.11) tengsizlikni n ning quyidagi qiymatlarida bajarilishini tekshiramiz:

n = 1 da:

2¹  1² ; n =2 da:

2²  2² ; n = 3 da:

2³  8  9  3² ;

n =4 da:

2⁴  16  4² ; n = 5 da:

2⁵  32  25  5² .

Hosil qilingan yuqoridagi tengsizlikdan (2.11) tengsizlik n = 1 da

bajarilishi kelib chiqadi. Lekin bu tengsizlik n = 2, 3, 4 bajarilmaydi. n = 5 dan boshlab yana bajariladi.

(2.11) tengsizlik ixtiyoriy

n  5

da bajariladi deb faraz qilamiz. Ushbu

farazni matematik induksiya metodi bilan isbotlaymiz.

1. teorema. n = 5 da isbotlandi.

2⁵  32 

25  5²

ega bo’lamiz. 1-teorema

1. teorema. n = k da

2^k  k ² ,

k  5

tengsizlikning o’rinli ekanligi

berilgan bo’lsin. n = k+1 da ekanligini isbotlaymiz.

2^k1  (k 1)² ,

k  5

tengsizlikning o’rinli

Isbotlash.

2^k1  2^k  2  k ²  2  k ²  k ² 

k  5  k 1  4  (k 1)²  16  k ²  2k 1  16  k ²  15  2k

 k ²  2k 15  k ²  2k 1  (k 1)² .

1. teorema isbotlandi. Matematik induksiya prinsipiga ko’ra (2.11) tenglikning

ixtiyoriy n  5

natural sonda bajarilishi kelib chiqadi.

(5.6.2) tengsizlikning n ning quyidagi qiymatlarida bajarilishini tekshiramiz:

n = 1 da

3¹  1³ ; n = 2 da:

3²  9  8  2³ ;

n = 3 da 3³  27  3³ ; n = 4 da: 3⁴  81  64  4³ .

n = 5 da

3⁵  243  125  5³ .

Hosil qilingan tengsizlikdan (2.11) tengsizlik n=1 va n=2 da bajariladi. Bu tengsizlik n=3 uchun bajarilmaydi. Lekin n = 4, 5 uchun yana bajariladi. Ixtiyoriy

n  4

da (2.11) tengsizlik bajariladi deb faraz qilinadi. Ushbu farazni matematik

induksiya metodi bilan isbotlaymiz.

1. teorema. n = 4 da isbotlandi.

3⁴  81  64  4³

ga ega bo’lamiz. 1-teorema

1. teorema. n = k da 3^k

• k ³,

k  4 tengsizlikning bajarilishi berilgan.

n = k+1 da lozim.

3^k1  (k 1)³,

k  4

tengsizlikning to’gri ekanligini isbotlash

Isbotlash.

3^k1  3^k  3  k ³  3  k ³  2k ³ 

k  4  k 1  3  (k 1)³  27  k ³  3k ²  3k 1  27  k ³  3k ²  3k  28

––_––,

 k ³  2  (3k ²  3k  28)  k ³  3k ²  3k 1 3k ²  9k  55  (k  1)³ .

• 0

k  4 da

3k ²  9k  3k (k  3)  0

ning o’rinli ekanligi kelib chiqadi.

2-teorema isbotlandi.

1. Xaritani bo’yashda matematik induksiya usulining tadbiqlari

Tekislikda biror geografik xarita berilgan deb faraz qilaylik.

Ta’rif. Agar ixtiyoriy davlat ma’lum bo’yoq bilan bo’yalgan, umumiy chegaraga ega bo’lgan ikkita davlat turli ranglar bilan bo’yalsa xarita to’g’ri bo’yalgan deyiladi.

To’g’ri bo’yalgan xaritaga ixtiyoriy geografik xarita misol bo’la oladi. Ixtiyoriy xaritani ma’lum bo’yoq bilan bo’yash mumkin, lekin bunday bo’yash tejamli bo’lmaydi. Shuning uchun quyidagi masalani qo’yish lozim bo’ladi: xaritani bo’yash uchun bo’yoqlar turlari iloji boricha kam bo’lsin.

3.1-masala.

2 ta rang 3 ta rang 4 ta rang

Har qanday xaritani bo’yash uchun 5 ta turdagi bo’yoqlarni yetarli ekanligi isbotlangan. Hozirgi kungacha to’rta bo’yoq bilan to’g’ri bo’yash mumkin bo’lgan xarita topilmagan. Birinchi marotaba ushbu holatga nemis matematigi Myobius e’tibor berdi. Shu paytgacha yirik olimlar “To’rtta bo’yoq muommosi”ni yechish uchun harakat qilishgan. Ma’lumki, tabiatdagi ko’plab jarayonlar va muammolar matematik modellashtirish orqali u yoki bu masala yechimini topishga, matematik mulohazalar ustida mushoxada yuritishga, ba’zi tasdiqlarni isbotlashga keltiriladi. Matematik mushohada yuritish orqali o’quvchining tafakkuri ortadi, ilmiy salohiyati yuksaladi. Ko’plab natural parametrli matematik ayniyatlar, tengliklar, tasdiqlar, tenlama va tengsizliklarni isbotlashda matematik induksiya metodidan foydalanish samarali hisoblanadi. Ushbu metod induktiv o’tish orqali natural sonlar to’plami yoki uning biror cheksiz qism to’plamida berilgan ayniyat, tenlik va tengsizliklarni isbotlash orqali umumiy tasdiqning to’g’riligini asoslashga asoslanganligi, isbotlash umumiy strukturaga egaligi bilan ham o’quvchiga tushunarli va qo’llash qulaydir. To’rtta bo’yoq ixtiyoriy xaritani bo’yash yoki bo’yash mumkin emasligini isbotlashga harakat qilishgan. Lekin shu kunga qadar hech kim bajara olmagan. Qiziqarlisi shundaki, ba’zi sirtlar uchun xaritani bo’yash muommasi hal etilgan. Ixtiyoriy xaritani bo’yashda shunday sirtlar mavjudki, uni bo’yash uchun 7 ta bo’yoq etarli hisoblanadi. Shunday sirtlar ham mavjudki, 6 ta bo’yoq bilan ham xaritani bo’yash qiyin.

3.2-masala. To’g’ri tortburchak to’g’ri chiziq bilan n ta qismga bo’lingan deb faraz qilaylik. Bunday holda umumiy tomonga ega bo’lgan ikkita qismni turli rangdagi qora va oq bo’yoqga bo’yash mumkin.

Isbotlash. n = 1da quidagiga egamiz:

n=k uchun tasdig to’g’ri deb faraz qilaylik. U holda da ham to’g’ri hisoblanadi.

n = k + 1 da k to’g’ri chiziqdan iborat k+1 to’g’ri chiziqli ma’lumotlardan tashkil etgan to’g’ri to’rtburchakni bo’yash lozim:

(k+1) to’g’ri chiziqdan qolgan qismlarni qarama-qarshi bo’yoqga bo’yash lozim bo’ladi:

(k+1) to’g’ri chiziq

3.3-masala. Tekislikda n ta aylana berilgan (n  2). Ushbu aylanalardan tashkil topgan xaritada ularni ixtiyoriy joylashtirilganda ikkita bo’yoq bilan to’g’ri bo’yash mukinligini isbotlang.

Isbotlash. n = 2 da aylanalarning quyidagi imkoniyatlarini ko’rish mumkin:

n = k  2 uchun tasdiq to’g’ri deb faraz qilaylik. Bunday holda tasdiq n = k +1 da ham to’g’ri bo’ladi. Tekislikda k+1 aylanalar berilgan deb faraz qilaylik.

2.4. Paskal uchburchagini matematik induksiya usulidagi tadbiqi

Faraz qilaylik, a va b – haqiqiy sonlar. Turli n natural sonda (a  b)ⁿ ko’rib chiqamiz:

n = 0 da: (a  b)⁰=1

n= 1 da:(a  b)¹ = (1 a + 1 b).

n = 2 da: (a  b)²=1 a²+2 a b 1 b²

n = 3 da: (a  b)³=1 a³+3 a² b+3 a b² 1 b³

n = 4 da: (a  b)⁴= 1 a⁴+4 a³ b 6 a² b² 4 a b³ 1 b⁴

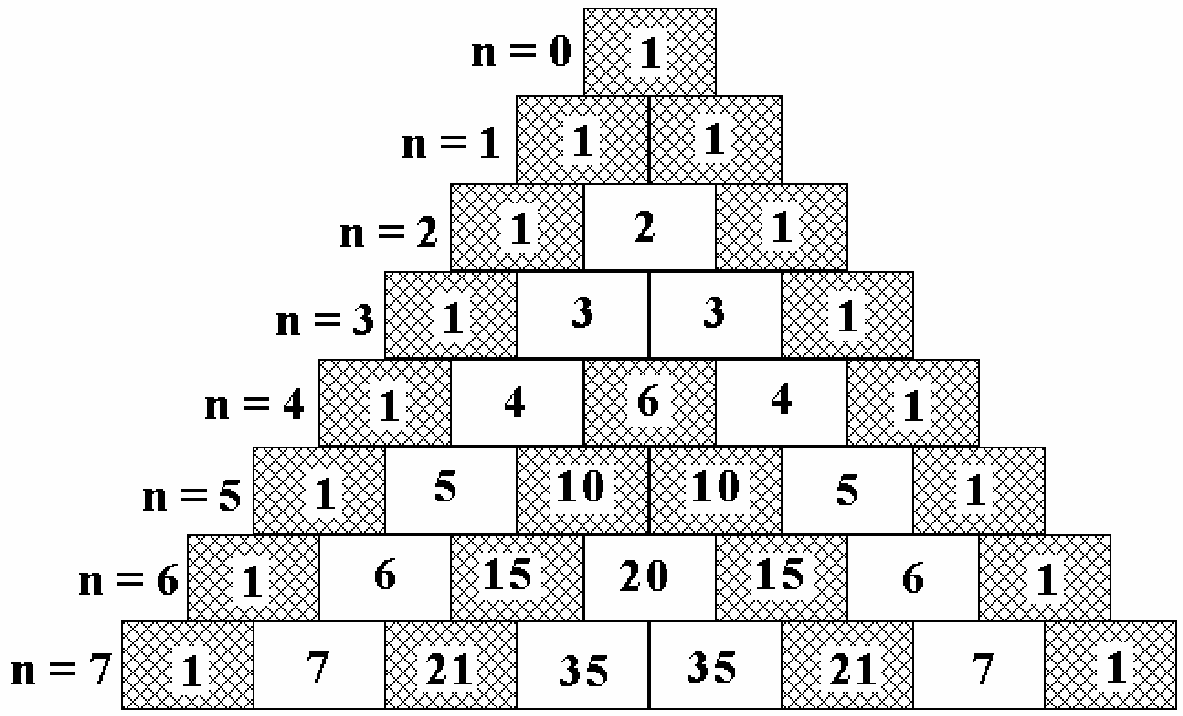Agar koeffitsentlarni a^n+kb^k , k = 0,1, 2,..., n darajada yozsak va ularni n= 1, 2, 3, 4 da quyidagi uchburchakdagi sonlar bilan taqqoslaymiz:

U holda ushbu sonlarning mos ekanligini hosil qilamiz. Yuqoridagi rasmda uchburchak quyidagi qoida bo’yicha tashkil etiladi. Ya`ni, har bir qatorning eng chekkalari 1 bilan boshlanib, 1 bilan tugaydi, shunday ekan, Har bir qatorning chekka qismida 1 raqami joylashgan, har bir navbatdagi son oldingi qatorda joylashgan ikkita sonning yig’indisiga teng. Ushbu qoyida asosida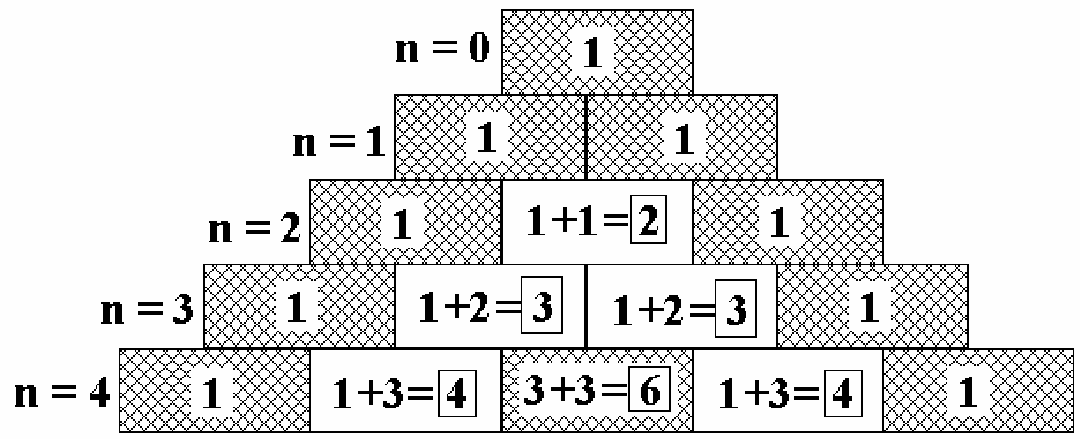 ushbu uchburchakning yangi qatorini ketma-ket yozish mumkin. Bunday ta’rif 1665 yil fransuz matematigi B.Paskalning “Arifmetik uchburchak haqida traktat” olimdan so’ng chop etildi. Uchburchakning shunga o’xshash variyantlari italiyan matematigi N.Tartalya, shu davrga qadar bir necha asr oldin o’rta osiyolik olim va shoir Umar Xayyom asarlarida bayon etilgan.

Fanning bir yo’nalishlaridan biri kombinatorika bo’lib, uning asosiy mohiyati quyidagicha: m elementlardan iborat nechta to’plam qismi mavjud va hech bo’lmaganda bittasi farqli bolgan, n elementlardan iborat A to’plamdan bitta elementni olib tashlash mumkin. Bunday to’plam qismi n ta elementlardan iborat m ta elementlar guruh deyiladi, ularning soni С^m_n bilan belgilanadi va

С^m_n  n! /m!(n  m)!, m!=1*2*3…..*m, n!=1*2*3…..*n , 0!=1 n

formula bo’yicha hisoblanadi.

Bu son Pascal uchburchagidagi sonlar bilan uzviy bog`liq. Haqiqatdan ham

n=0 da C⁰₀=1 ga ega bo`lamiz. Uchburchakning yuqoridagi qatori (nolinchi) bitta sondan iborat. Navbatdagi qator – ikkita sondan iborat.

Hisoblashda С^m_n  n! /m!(n  m)! shu formula asosida hisoblanadi, bunda ayni bir sonning qiymati boshqa bir son hosil qilgan natija bilan bir xil bo`lishi mumkin, masalan, 1 bilan 4 dagi natija 3 bilan 4 dagi natija bilan bir xil, quyida uning matematik formulasi orqali yaxshi tushuntirilgan.

С⁰₁ = С¹₁ =1. To’rtinchi qator 5 ta sondan iborat:

C⁰₄ =C⁴₄=1 , C¹₄=C³₄=4, C²₄=6.

2.5. Matematik induktsiya usuli yordamida tengsizlikni va bo’linishni isbotlash

Misol 5. Tenglik barcha natural n lar uchun bajarilishini isbotlang.

1 2  3  2  3  4  ...  n  (n  1)  (n  2)  ¹ n (n  1)(n  2)(n  3) ^{. (1)}

4

Yechim. Belgilash:

S_n  1 2  3  2  3 4  ...  n  (n 1)  (n  2) ^.

Induktsiya bazisi. n = 1 da

S₁  1 2  3^{. (5) ning o’ng tarafi:}

¹_{1 (1  1)  (1  2)  (1  3)  1 2  3}. Induktsiya bazisi isbotlandi.

4

Induktiv qadam. n = k da:

S_k  1 2  3  2  3  4  ...  k  (k  1)  (k  2)  ¹ k  (k  1)  (k  2)  (k  3)

4

bo’lsin.

S_{k 1}  1 2  3  2  3  4  ...  (k  1)(k  2)(k  3)  ¹ (k  1)(k  2)(k  3)(k  4) ^.

ni isbotlaymiz.

1-MISOL. N{1;2;3;4;…,}natural sonlar to’plamida aniqlangan.A(n)=n² +n=17 ifodasiga qaraymiz.

A(1)=+1+17=19 A(2)=+2+17=23 A(3)=+3+17=29

A(4)= +4+17=37 sonlari tub sonlardir. Shuning uchun, barcha n A(n)=n+n+17 ifodaning qiymati tub son bo’ladi.

Bu yerda to’liqmas induksiya yordamida hulosa chiqildi. CHiqarilgan bu hulosa noto’g’ridir, chunki A(16)=289=soni tub son emas.

2-MISOL. X={10;20;30;40;50;..,} to;plam yozuvi 0 raqami bilan tugaydigan barcha natural sonlar to’plami bo’lsin 10;20;30;40;50 sonlarning har biri ikkiga qoldiqsiz bo’linadi. Shuning uchun X to’plamining har qanday x elementi 2 ga bo’linadi.

To’liqmas induksiya yordamida chiqarilgan bu hulosa to’g’ri hulosadir, chunki X to’plamning har qanday elementi juft sondir.

3 -masala. Agar a  1 bo’lsa,

(1 a)ⁿ 1 na, n  N , (2)

bajarilishini isbotlang.

Induktsiya bazisi. n = 1 bo’lganda

(1 a)¹  (1 a)

va (11 a)  1 a bo’ladi

Induktiv qadam. (1) tengsizlik n = k bo’lganda bajarilsin: (1 a)^k  1 ka .

U holda (1) tengsizlik n = k +1 uchun ham o’rinli: (1 a)^k1  1 (k 1)a .

Haqiqatdan ham, (1 a)  0 bo’lgani uchun,

^{(1 a)k1  (1 a)k (1 a)  (1 ka)(1 a)}  1 (k 1)a  ka²  1 (k 1)a ^.

Demak, matematik induktsiya printsipiga asosan (1) tengsizlik barcha natural n lar uchun o’rinlidir.

4- Misol. A) 3^2n+1+2^n+2 son 7ga; n^3+5n son 6 ga bo`linishini ko`rsating.

Induktsiya bazisi. n = 1 da: 3³  2³  27  8  35, son 7 ga bo’linadi.

Induktiv qadam.

3^{2 k 1}  2^{k 2} son 7 ga bo’linsin. 3^{2 k 3}  2^{k 3} sonini 7 ga

bo’lininishini ko’rsatamiz.

₃2 (k 1)1 _{ 2}k+1)+2

 3^{2 k 1}  9  2^{k 2}  2  9  2^{k 2}  9  2^{k 2} 

 9  3^2k1  2^k2  2^k2 (2  9) ^.

Induktiv qadam isbotlandi.

1. Induktsiya bazisi. n = 1 da

1³  5 1  6.

Induktiv qadam.

k ³  5k

son 6 ga bo’linsin.

(k 1)³  5(k  1)

son 6 ga bo’linishini ko’rsatamiz.

(k 1)³  5(k 1)  k ³  5k  3k (k 1)  6 .

k ³  5k

soni 6 ga o’blinishini faraz qilganmiz. k (k+1) son 2 bo’linganligi uchun

3k(k+1) soni ham 6 ga bo`linadi.

5-misol. To’liq induktiv metodga misol.

Bu metodda berilgan masalada n ning n=1, n=2 uchun o’rinli ekanligini bilgan holda n=k uchun ham o’rinli deb bilib n=k+1 uchun ham o’rinli ekanini isbotlash kifoya. Berilgan ifodaning n –natural son bo’lganda 9 ga qoldiqsiz bo’lininshini isbotlang

uchun ham o’rinli deb, faraz qilamizda n=k+1 uchun hisoblaymiz

n=k+1, (k+1)³+(k+2)³+(k+3)³=(k+1)³+(k+1)³+(k+2)³+k³+9k²+27k=( k³+ (k+1)³+ (k+2)³)+9(k²+3k+3):

n=k da o’rinli bo’lgani uchun birinchi qo’shiluvchi 9 ga bo’linadi, ikinchisi ham 9 ga bo’linishini ko’rib turibmiz. Demak, ifoda n ning ixtiyoriy natural qiymatida 9 ga bo’linar ekan.

7-misol.

1²+2²+3²+…+n²= ayniyatni isbotlang. n=1 1= to’g’ri

n=2 1+4==5 to’g’ri

n=k da to’g’ri deb faraz qilamizda n=k+1 uchun isbotlaymiz.

1²+2²+3²+…+k²+(k+1)²=demak n=k+1 da ham to’g’ri ekan.

8-misol.

13+23+33+…+n3=ayniyatni isbotlang, n natural son bo’lganda n=1 da 1³=

n=2 da 1+8=,to’g’ri

n=k da ham to’g’ri deb faraz qilib n=k+1 uchun isbotlaymiz. 1³+2³+3³+…+k³+(k+1)³=

Demak, n=k+1 da ham to’g’ri ekan.

2.6. Muavr formulasini matematik induksiya usulida isbotlanishi

Muavr formulasini isbotlang.

r (cos  i sin )ⁿ

 rⁿ (cos n  i sin n), n  N . (1)

Induktsiya bazisi. n = 1 da : r (cos  i sin )¹

 r¹ (cos   i sin ) .

Induktsiya bazisi isbotlandi.

Induktiv qadam. r (cos  i sin )^k

 r^k

(cos k  i sin k)

bajarilsin.

r (cos  i sin )^k1  r^k1 (cos (k 1)  i sin

(k 1)) ni isbotlaymiz:

r (cos  i sin )^k1  r (cos  i sin )^k  r (cos  i sin ) 

 r^k

(cos k  i sin k)r (cos  i sin ) = r^k+1cos k  cos  sin k  sin   i(cos k  sin   sin k  cos) 

 r^k1 (cos(k 1)  i sin( k 1)) . Induktiv qadam isbotlandi.

Demak, matematik induktsiya printsipiga asosan (13) tenglik barcha natural n lar uchun bajariladi.

Xulosa

Ushbu kurs ishida sonlar nazariyasida turli muammoli masala, tenglama, teorema va tengsizliklarni, balki, boshqa sohalarda muammoli isbotlashlarni matematik induksiya usulida hisoblash bir qator tadbiqlari bilan keltirilgan. Natural sonlar to’plami yoki uning biror cheksiz qism to’plamida berilgan ayniyat, tenlik va tengsizliklarni matematik induksiya usulida isbotlash orqali umumiy tasdiqning to’g’riligini asoslashga asoslanganligi, isbotlash umumiy strukturaga egaligi bilan ham o’quvchiga tushunarli va qo’llash qulaydir. Matematik mushohada yuritish orqali o’quvchining tafakkuri ortadi, ilmiy salohiyati yuksaladi. Uni puxta o’rganish orqali o`rganuvchilar kelgusi pedagogik foaliyatida yoshlarga samarali saboq berishi bilan ham muhim ahamiyatlidir. O`rganuvchi matematik induksiya metodini puxta o’zlashtirib olishi bilan undan kelgusida ilmiy izlanish davomida ayrim isbotlanishi zarur bo’lgan jarayonlarda foydalanishi, o’rta-maxsus va umumta’lim maktablarida yoshlarning matematikaga bo’lgan qiziqishlarini o’stirish, samarali pedagogik faoliyt olib borish uchun ahamiyatli hisoblanadi.

Agar shunday darslarda matematik indutsiyani qullashga doir misol va masalalar o`quvchilarga yechtirilsa, u holda bunday misol va masalalar o`quvchilarning matematik tafakkurini rivojlantirishga va turli olimpiadalarga muay’an natijalarni ko’rsatishga yordam beradi. Ushbu matematik induksiya usuli orqali o`rganuvchi mantiqiy fikrlashni, biror muammoli masalani turli usullar, yo`llar bilan tadbiq etishga imkon beradi va chorlaydi. Ko’plab natural parametrli matematik ayniyatlar, tengliklar, tasdiqlar, tenlama va tengsizliklarni isbotlashda matematik induksiya metodidan foydalanish samarali hisoblanadi. Maktablarda, undan keyingi o`quv dargohlarida matematik induktsiya usuliga doir mavzular bo’yicha darslar uslubiy jihatdan to’g’ri tashkil etilib o’tkazilsa, bu darsda o’quvchilar mazkur mavzularga doir bilimlarini tizimlashtirishga imkoniyat yaratiladi. Agar shunday darslarda matematik indutsiyani qullashga doir misol va o`quvchilarga yechtirilsa, u holda bunday misol va masalalar talabalarning matematik tafakkurini rivojlantirishga va turli olimpiadalarga muay’an natijalarni ko’rsatishga yordam beradi.

Foydalanilgan adabiyotlar

1.Oʻzbekiston Respublikasi Prezidentining 2017 yildagi ―Zamonaviy axborot- kommunikatsiya texnologiyalarini yanada joriy etish va rivojlantirish chora- tadbirlari toʻgʻrisida‖gi PQ-1730 sonli qarori.

2. Erkin va farovon, demokratik O`zbekiston davlatini birgalikda barpo etamiz. O`zbekiston Respublikasi Prezidenti lavozimiga kirishish tantanali marosimiga bag`ishlangan Oliy Majlis palatalarining qo`shma majlisidagi nutq / SH.M. Mirziyoev. – Toshkent : O`zbekiston, 2016. - 56 b.

3. B. Abdurahmonov. Matematik induksiya metodi/ Toshkent, 2008 y.

1. Головина Л. И., Яглом И. М. Индукция в геометрии. Серия «популярные лекции по математике» — Вып. 21.— М.: Наука, 1961.

2. Соминский И. С. Метод математической индукции. Серия «популярные лекции по математике» — Вып. 3. — М.: Наука, 1974.

3. Meliqulov, Matematika, I-qism. Toshkent, 2004, 192-197 betlar.

4. A. Nasimov va boshqalar. Algebra va analiz asoslari. Akademik letsiy va
   kasb-hunar kollejlari uchun darslik. Toshkent, ―O’qituvchi‖ nashriyoti,
   2003y

5. Sh.N.Ismailov. Sonlar nazariyasi. O’quv qo’’anma, Toshkent, 2008

6. Sh.Ismailov, A.Qo’chqorov, B.Abduraxmonov. Tengsizliklarni
   issbotlashning klassik usullari. Toshkent, 2008y.

7. Sh.Ismailov, O.Ibragimov. Tengsizliklarni issbotlashning zamonaviy
   usullari. Toshkent, 2008y

8. M.O‘.Ashurov, Sh.A.Sattarova, Sh.U.Usmonqulov. Algoritmlar. -Т.: «Fan va texnologiya», 2018,

9. To’rayev Hotam To’rayevich, O’rinboyev Erkin «Diskret matematika va matematik mantiq» fanidan o’quv – uslubiy majmua («5480100 - Amaliy matematika va informatika» ta’lim yo’nalishi bakalavr talabalari uchun). O’quv-uslubiy majmua. – Samarqand: SamDU nashri, 2010.

9