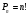ОБ ОБУЧЕНИИ УЧАЩИХСЯ МЕТОДАМ РЕШЕНИЯ ЗАДАЧ
ПО КОМБИНАТОРИКЕ
Останов К.
При изучении комбинаторики надо сначала дать учащимся исторические аспекты возникновения этого раздела математики. Поэтому учащимся можно рассказать о том, что первоначальные понятия развивалась в Древнем Китае, а потом в Европе, в период Римской империи. Окончательно как один из раздел математической науки возникло в XVIII в. Этому также содействовало исследования ученых методов решения задач, связанные с нахождением вероятности событий. В то время математиков заинтересовало проблемы поиска формул для вычисления так называемых фигурных чисел, т.е. чисел которые представляли какую-то определенную геометрическую фигуру. Например, квадратных чисел (1, 4, 16, 25, …), можно было изобразить с помощью точек в виде квадрата. Так математики нашли формулу для вычисления таких чисел  . Таким же образом были найдены формулы треугольных (1, 3, 6, 10,15, . . .)
. Таким же образом были найдены формулы треугольных (1, 3, 6, 10,15, . . .) 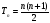 а также пятиугольных (1, 5, 12, 22, . . .)
а также пятиугольных (1, 5, 12, 22, . . .) 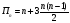 чисел.
чисел.
При обсуждении формул этих чисел целесообразно самим найти закономерность это числовой последовательности и убедиться их правильности при конкретных значениях натуральной переменной и затем предлагать учащимся решать следующих типов:
1.Нахождение по формуле какое-то определенное число по расположению и вида числа, здесь два параметра: место и вид числа.
2.Решить обратную задачу по числу найти к какому виду относится данное число
Затем учащимся рассказывать о том, что в практической деятельности иногда встречаются таки моменты или ситуации, в которых человеку приходится найти правильный выбор из возможных вариантов . При этом ему нужно сделать такой выбор, чтобы это способствовало решению предложенной задачи. В этом случае проверяется все возможные решения поставленной задачи.
Решая например задачу с учащимися можно сосчитать сколько двузначных чисел используя 2, 3 и 5, они с помощью подбора найдут
что таких чисел имеется ровно 9 : 22, 23, 32, 33, 25, 35, 52, 53, 55. Поэтому учащимся важно понять, что для того чтобы найти число всех возможных вариантов в процессе осуществления двух независимых опытов необходимо найти произведения количества этих двух опытов.
Например, чтобы составить из нескольких различных цифр, четырехзначных нечетных чисел чисел, в которых цифры может повторяться сначала подсчитывается все возможные варианты для цифры стоящее на первом месте, а потом для цифры стоящего на втором месте и т.д. В конце все эти возможные варианты умножаются и получается решение задачи. Например, при нахождении количества двухзначных чисел, составленных из цифр 1,3,5,7,9, найдем: для цифры 1: 11, 13,15, 17,19, для цифры 3: 31,33,35, 37,39 , для цифры 5: 51,53,55,57,59, и т.д. т.е. для каждой цифры по 5 двухзначных чисел и всего таких чисел будет 25 штук. Такую закономерность можно увидеть 52=25. Поэтому для продолжения этой закономерности проверить, сколь трехзначных чисел можно составить из этих пяти цифр, цифры которых могут повторяться. Гипотеза 53=125. Будет ли верна?
Теперь уже учащимся будет понятным, что проверка этой гипотезы вовлечет их к способу проверки правила умножения для любого числа опытов, которые находятся поиском различных вариантов решения задачи. При обсуждении решении известной задачи, в котором требуется найти число возможных посадок мест людьми, количество которых равен числу мест сначала нумеруются места, затем найдется количество перестановок посадки этих мест людьми. Такое количество будет уменьшаться и с помощью вышеуказанного правила поиска различных вариантов найдем общее количество посадок в зависимости от числа посадки мест и людей, т.е. получается такая гипотеза: общее число перестановок равно произведению всех чисел от одного до общего количества посадки мест.
Для проверки этой гипотезы учащимся предлагается решать задачи с конкретным содержанием. Например, раскладка некоторого количества различных писем по одному в конверты или число рукопожатий некоторого количества друзей и т.д.
Процесс изучения методов решения задач показывает, что фабула и сюжет задач различны, но полученные решения представляются по одинаковой закономерности. Так учащиеся приводятся к понятию факториал, т.е произведению первых чисел натурального ряда n!=1·2·3·. . .(n-2) · (n-1) ·n. и обозначению n!. При этом важно подчеркнуть, что в математике принято, что 0!=1. Затем предлагается вычислить несколько первых значений 1!=1, 2!=1·2=2, 3!=1·2·3=6, 4!=1·2·3·4=24 и т. д.
Отсюда с учащимися можно обсудить следующий вопрос: если множество состоит из n различных элементов, то сколькими способами их можно нумеровать с помощью чисел от 1 до n. [2]
При этом любой такой способ обозначения элементов с номерами нумерации от 1 до n является перестановками элементов данного множества, в котором имеется п элементов. Здесь основное внимание обратить на тот факт, что при выполнении каждого такого способа элементы данного множества будут находится в определенном порядке и таким образом в общем случае количество перестановок Pn выражается формулой, т.е. о равен факториалу от числа элементов данного множества. 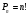
Для отработки умений воспользоваться формулой факториала можно дать задачи на вычисления конкретного значения факториала, задачи деления факториала на данное число, задачи на определение количества нулей в конце факториала. При этом в процессе решения этих задач целесообразно формирование умений у учащихся не только использовать формулу, но и умений применять их для решения других математических задач комбинаторного характера.
При формулировке общего определения перестановок надо обращать внимание учащихся на две признака этих перестановок: во первых, они составляется из всех элементов по одному разу, и во- вторых, эти соединения отличаются порядком, с которыми размещаются элементы. Иногда их называют комбинациями, иногда соединениями, но смысл их одинаково выражает сущности данного понятия. Кроме того, с учащимися надо выяснить, что число перестановок обосновывается на основе правила умножения. При закреплении этого понятия с учащимися можно решать задачи жизненного характера, т.е. задачи которые встречаются в быту, при решении задач других предметов, например, задачи по определению количества очередей в ту или иную кассу для получения товара, билета или приему врачу, на определения и составления различных чисел с заданным количеством знаков из некоторого количества цифр или задачи на определения количества способов разложения чисел на простые множители, количество членов произведения многочлена на многочлен, задачи геометрии, требующие определение способов размещения заданного количества точек на плоскости.
Список литературы/ References
1. Виленкин, Н.Я. Индукция. Комбинаторика / Н.Я. Виленкин. - М.: Просвещение, 1976. - 46 c.
2. Ежов И. И., Скороход А. В., Ядренко М. К. Элементы комбинаторики, перев. с укр. – М.:Наука, 1977,80 стр.
1






 . Таким же образом были найдены формулы треугольных (1, 3, 6, 10,15, . . .)
. Таким же образом были найдены формулы треугольных (1, 3, 6, 10,15, . . .) 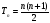 а также пятиугольных (1, 5, 12, 22, . . .)
а также пятиугольных (1, 5, 12, 22, . . .) 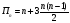 чисел.
чисел.