Просмотр содержимого документа
«Практическое занятие»
Практическая работа №7
Определенный интеграл и его свойства
Цель: научиться вычислять определенные интегралы, используя непосредственное интегрирование, метод подстановки, интегрирование по частям.
1. Определенный интеграл
Пусть функция f(x) определена на отрезке [a; b]. Разобьем этот отрезок на n частей точками a012 n=b, выберем на каждом элементарном отрезке xk – 1 x xkпроизвольную точку k и обозначим через xk длину каждого такого отрезка.
Интегральной суммой для функции f(x) на отрезке [a; b] называется сумма вида:
n
f(k) xk = f(1) x1 + f(2) x2 +...+ f(n) xn
k=1
Определение. Определенным интегралом от функции f(x) на отрезке [a; b] называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

Для вычисления определенного интеграла от функции f(x) служит формулаНьютона-Лейбница:
т. е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
2. Основные свойства определенного интеграла
10. Постоянный множитель можно выносить за знак интеграла, т. е. если а = const, то
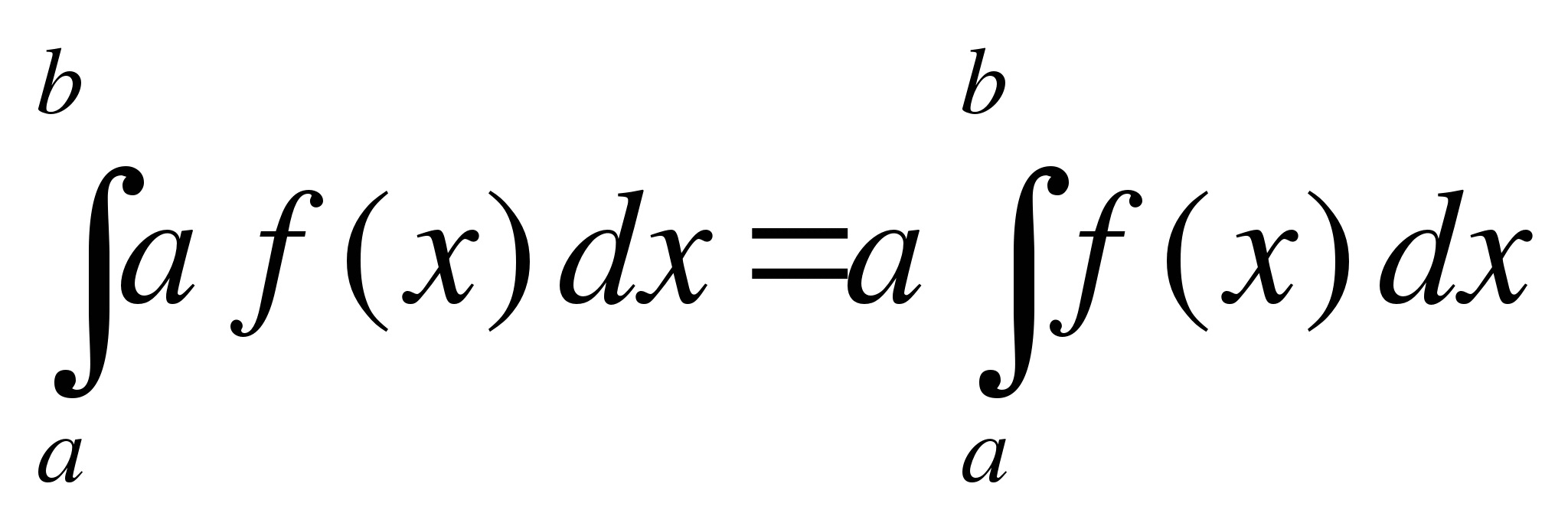
20. Определенный интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме их интегралов, т. е.

30. Если a

40. Если функция f(x) неотрицательна на отрезке [a; b], где a

50. Если f(x) g(x) для всех x [a; b], где a

3. Методы вычисления определенного интеграла
Непосредственное интегрирование
Чтобы вычислить определенный интеграл  , нужно:
, нужно:
1) найти какую-нибудь первообразную F(x) для функции f(x) (найти неопределенный интеграл от функции f(x), в котором можно принять С = 0);
2) в полученном выражении подставить вместо x сначала верхний предел a, а затем нижний предел b, и из результата первой подстановки вычесть результат второй.
Пример 1. Вычислить 
Решение. По формуле Ньютона-Лейбница получаем:  =
=
 =
= 19, 5
19, 5
Пример 2. Вычислить 
Решение. По формуле Ньютона-Лейбница: =
= 
Пример 3. Найти 
Решение.  =
= 
Метод замены переменной (метод подстановки)
При вычислении определенного интеграла методом подстановки новая переменная вводится подобно случаю неопределенного интеграла. Однако в отличие от неопределенного интеграл а, где в полученном результате мы снова возвращались к прежнему переменному, здесь этого делать не надо.
Пример. Вычислить 
Решение. Введем новую переменную интегрирования с помощью подстановки  . Дифференцируя, имеем:
. Дифференцируя, имеем:

Находим новые пределы интегрирования. Для этого подставим в соотношение  значения x = 1 и x = 2, соответственно получим:
значения x = 1 и x = 2, соответственно получим: 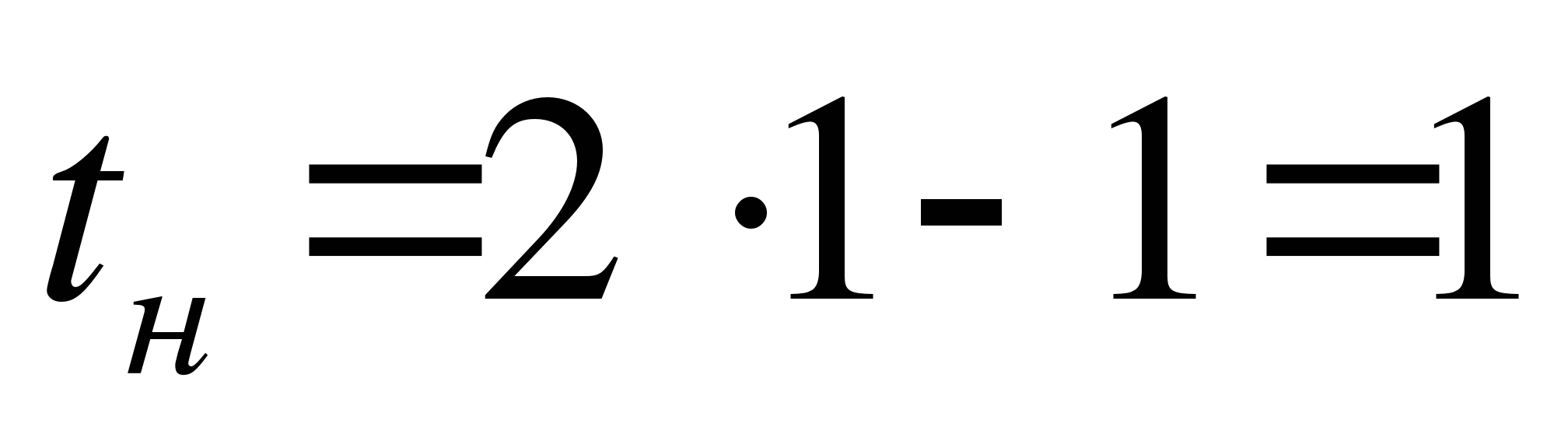


Следовательно,
 =
=
Интегрирование по частям
Если функции u(x) и v(x) и их производные u(x) и v(x) непрерывны в промежутке , то формула интегрирования по частям для определенного интеграла имеет вид:
Пример. Вычислить
Решение. Положим ,
Тогда ,
Следовательно, =
Упражнения
Вычислить определенные интегралы:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.







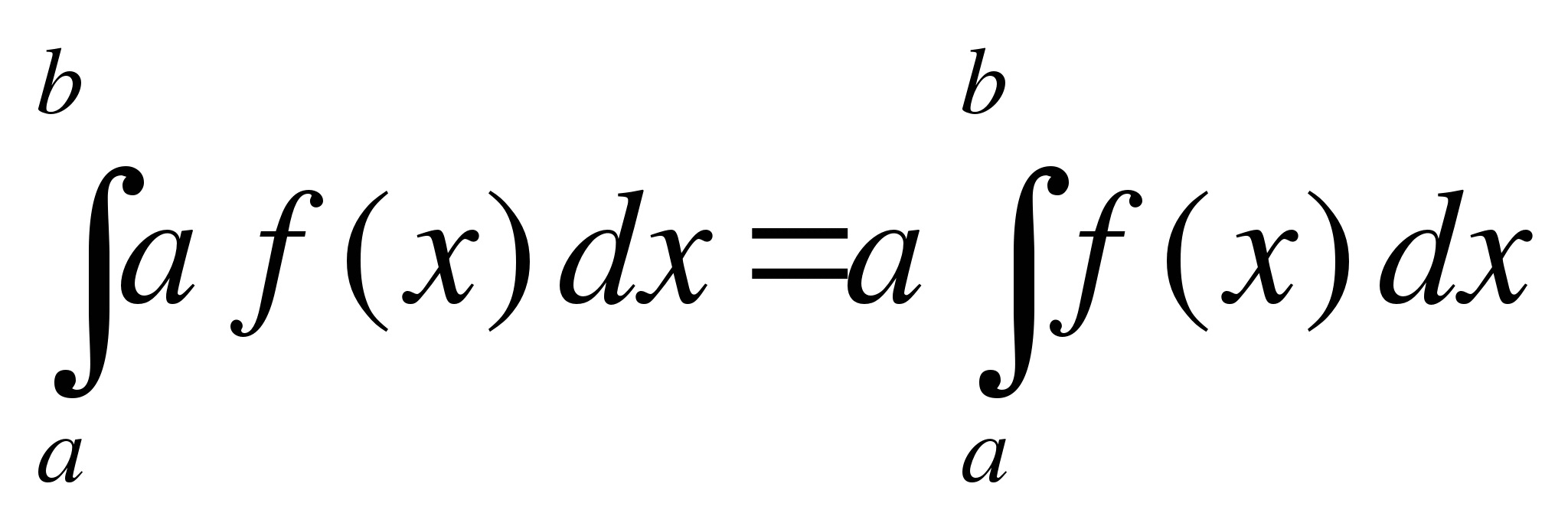




 , нужно:
, нужно: =
=
















