Презентация № 13 Логические функции. Логические элементы компьютера. Законы алгебры логики

Логические функции. Логические элементы компьютера.

Практическая работа № 13

Преподаватель кафедры

ООД Ленинградского машиностроительного факультета

Михальченко Ольга Сергеевна

Цель занятия:

• Сформировать представление о логических схемах и логических элементах.
• Формировать умения построения логического выражения по схеме и логической схемы по данному логическому выражению.
• Рассмотреть процесс составления таблицы истинности для выяснения значения логического выражения представленного в виде логической схемы

• Формирование навыков применения технологии построения таблиц истинности для составных логических выражений.

ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА.

ФОРМЫ МЫШЛЕНИЯ

АЛГЕБРА ЛОГИКИ

ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ. ЗАКОНЫ ЛОГИКИ

Формы мышления

Мышление всегда осуществляется через понятия, высказывания и умозаключения

Понятие - это форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличать их от других.

Высказывание - это формулировка своего понимания окружающего мира. Высказывание является повествовательным предложением, в котором что-либо утверждается или отрицается. По поводу высказывания можно сказать, истинно оно или ложно .

Умозаключение - это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение.

Выражения.

Выражение — это конструкция, которая возвращает величину.

Операция — это определенное действие над элементами данных.

Сами элементы данных, над которыми выполняется операция, называются операндами .

Основные определения

Сигнал, который может принимать только одно из двух установленных значений, называется цифровым

Устройства, которые обрабатывают такие сигналы, называются дискретными преобразователями

Преобразователь, который получает сигналы об истинности отдельных высказываний, обрабатывает их и в результате выдает значение логического отрицания, логического произведения или логической суммы этих высказываний, называется логическим элементом

Понятие

Существенными называются такие признаки, каждый из которых, взятый отдельно, необходим, а все вместе достаточны, чтобы с их помощью отличить данный предмет от всех остальных и сделать обобщение, объединив однородные предметы в множество.

• Единичные понятия: самая высокая гора в Европе, этот стол, Москва и т.д.
• Общие понятия: красота, металл, доброта, глупость, лес, коллектив и т.д.
• Абстрактные понятия: вес, жесткость, цвет, вселенная, человечество и т.д.
• Конкретные понятия: круг, дом, пламя, битва и т.д.

Примеры понятий:

Рядом с названием предмета перечислены его признаки. Какие из них являются существенными для данного предмета?

А) Ученик - высокий; умный; одет в форму; на спине - ранец; посещает школу; любит книги; много знает; овладевает знаниями; учится; веселый.

Б) Ромашка - полевой цветок; имеет белые лепестки и желтую середину; лекарственное растение; неприхотливый цветок; цветок, растущий у дороги.

Любое понятие характеризуется содержанием и объемом .

Содержание понятия - совокупность (множество) его признаков. Среди признаков предмета есть существенные и второстепенные. Содержание понятия может меняться в зависимости от знаний, от точки зрения и т.д. Например, для обычного человека содержанием понятия "вода" являются следующие ее признаки: прозрачная, жидкая, безвкусная, ее пьют, утоляя жажду. Для химика вода - вещество, содержащее водород и кислород, компонент многих реакций.

Объем понятия - множество предметов, к которым прилагается понятие.

Например, объем понятия "четырехугольник": параллелограмм, ромб, прямоугольник, квадрат, трапеция. Между объемом и содержанием понятия существует важное соотношение: при увеличении содержания понятия уменьшается его объем и наоборот.

Расположите и запишите понятия в порядке расширения их объемов: насекомое, живое существо, комар.

Понятие

Комар, насекомое, живое существо.

Высказывание

Высказывание (суждение) - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.

В русском языке высказывания выражаются повествовательными предложениями:

Алупкинский дворец находится в Крыму.

Кащей Бессмертный – скупой и жадный .

Но не всякое повествовательное предложение является высказыванием:

Это высказывание ложное .

Побудительные и вопросительные предложения высказываниями не являются.

Без стука не входить!

Откройте учебники.

Ты выучил стихотворение?

Высказывание или нет?

Зимой идет дождь.

Снегири живут в Крыму.

Кто к нам пришел?

У треугольника 5 сторон.

Как пройти в библиотеку?

Переведите число в десятичную систему.

Запишите домашнее задание

5) Частные (35) Ложные (-5Истинные (1=1) Тождественно ложные ( (x 2 +y 2 )Тождественно истинные (x 2 +1)0 Зависящие от условий (x+y11 " width="640"

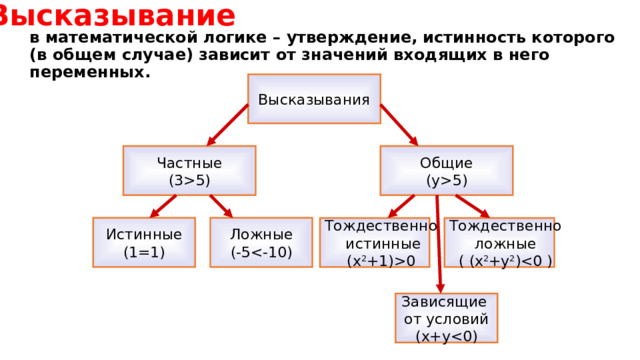
Высказывание

в математической логике – утверждение, истинность которого (в общем случае) зависит от значений входящих в него переменных.

Высказывания

Общие (y5)

Частные (35)

Ложные (-5

Истинные (1=1)

Тождественно ложные ( (x 2 +y 2 )

Тождественно истинные (x 2 +1)0

Зависящие от условий (x+y

11

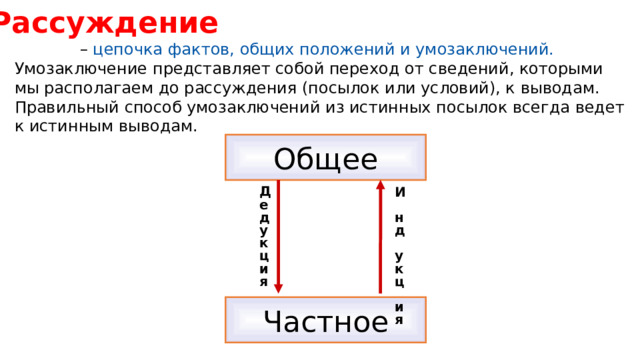
Рассуждение

– цепочка фактов, общих положений и умозаключений.

Умозаключение представляет собой переход от сведений, которыми мы располагаем до рассуждения (посылок или условий), к выводам.

Правильный способ умозаключений из истинных посылок всегда ведет к истинным выводам.

Общее

Д е д у к ц и я

И н д у к ц и я

Частное

12

Сегодня вы узнаете

• Что такое алгебра логики?

• Как вычислить истинность логического выражения?

• Для чего нужны законы логики?

12

История

Логикой называется наука о законах и формах мышления. Основоположником ее является древнегреческий ученый Аристотель (IV век до н. э.).

М а те м а тичес к ая лог и к а , называ е м а я так ж е символической , есть часть общей т еорет и ч ес к ой или логики, в которой законы мышления выражаются формулами аналогично тому, как в алгебре выражаются правила действий с числами. Идея математической логики впервые была высказана немецким математиком и философом Лейбницем в XVII веке. Но систематическое её развитие началось только с середины ХIХ века с опубликования английским математиком Дж. Булем работы «Математический анализ логики» (1847 г.).

Новый этап в развитии математической логики начался в 20-х годах XX века, когда немецкий математик Д. Гильберт разработал теорию математического доказательства, теорию формального построения математических наук.

В настоящее время математическая логика имеет большое практическое значение, она широко применяется в вычислительной математике и в теории конечных автоматов.

2

12

Логика

Логика – это наука о формах и способах мышления .

Первые учения о формах и способах мышления возникли в Древнем Китае и Индии. Основоположником формальной логики является Аристотель.

Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение, умозаключение).

Джордж Буль (1815-1864). Создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний).

Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике

12

Впервые основы теории графов появились в работах Леонарда Эйлера ( 1707-1783 ; швейцарский, немецкий и российский математик ) , в которых он описывал решение головоломок и математических развлекательных задач.

Теория графов началась с решения Эйлером задачи о семи мостах Кёнигсберга.

12

Логика  (от греч. logos — слово, понятие, рассужде­ние, разум) — наука о законах и операциях правильного мышления.

    Логика  – это наука о формах и способах мышления. Это учение о способах рассуждений и доказательств.

    Логика  – это наука об общих операциях, аналогичных сложению и умножению, которые выполняются не только над числами, но и над другими математическими объектами, в том числе и над высказываниями. 

   Алгебра логики отвлекается от смысловой содержательности высказываний и принимает во внимание только истинность или ложность высказывания.

       Формальная логика содержит в себе некоторые основ­ные  понятия , такие как:

•      высказывание,
•      истинность вы­сказывания и
•      вывод.

12

Алгебра логики

Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями .

Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний.

В алгебре логики высказывания обозначают буквами и называют логическими переменными.

Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей ( А = 1 ), а если ложно - нулём ( В = 0 ).

0 и 1 называются логическими значениями .

12

Простые и сложные высказывания

Высказывания бывают простые и сложные.

Высказывание называется простым , если никакая его часть сама не является высказыванием.

Сложные (составные) высказывания строятся из простых с помощью логических операций.

Название логической операции

Логическая связка

Инверсия (логическое отрицание)

«не»; «неверно, что»

Дизъюнкция (логическое сложение)

«или»

Конъюнкция (логическое умножение)

«и»; «а»; «но»; «хотя»

Импликация (логическое следование)

если – то;

Эквивалентность (логическая равнозначность)

тогда, и только тогда

Логические операции имеют следующий приоритет:

инверсия, конъюнкция, дизъюнкция , импликация, эквивалентность

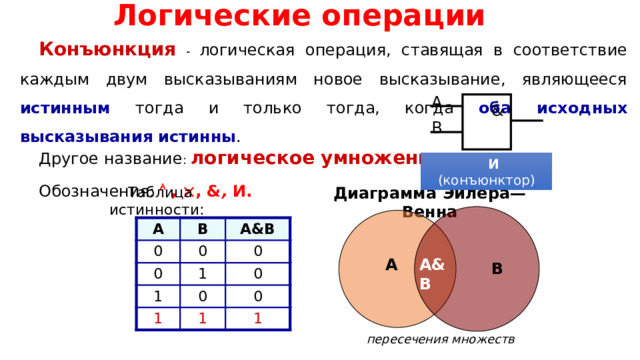
Логические операции

Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны .

Другое название : логическое умножение .

Обозначения:  ,  , & , И.

А

&

В

И (конъюнктор)

Таблица истинности:

Диаграмма Эйлера—Венна

А

0

В

А&В

0

0

0

1

1

1

0

0

0

1

1

А&В

A

B

пересечения множеств

20

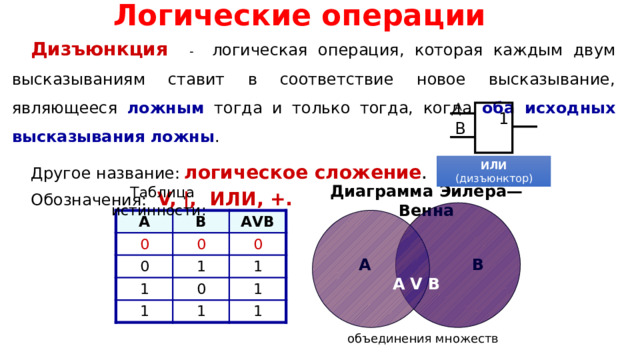
Логические операции

Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны .

Другое название: логическое сложение .

Обозначения: V, |, ИЛИ, +.

А

1

В

ИЛИ (дизъюнктор)

Диаграмма Эйлера—Венна

Таблица истинности:

А

0

В

0

АVВ

0

1

0

1

1

1

0

1

1

1

B

A

А V В

  объединения множеств

21

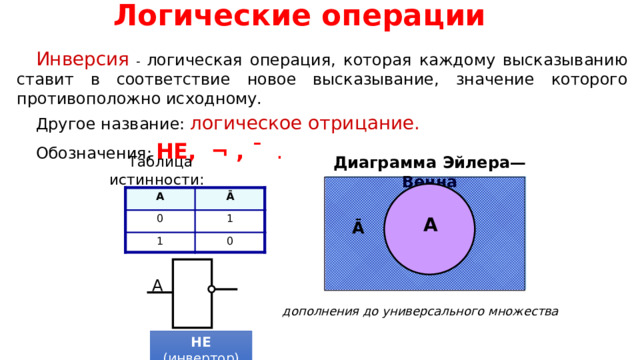
Логические операции

Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.

Другое название: логическое отрицание.

Обозначения: НЕ, ¬ , ¯ .

Диаграмма Эйлера—Венна

Таблица истинности:

А

0

Ā

1

1

0

A

Ā

А

дополнения до универсального множества

НЕ (инвертор)

22

Логические операции

Импликация – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно , а следствие (второе высказывание) ложно .

В естественном языке – «Если A, то B»;

Обозначение – →

Графическое представление

Таблица истинности:

А

0

В

0

0

А  В

1

1

1

1

0

1

0

1

1

A  B

А

B

23

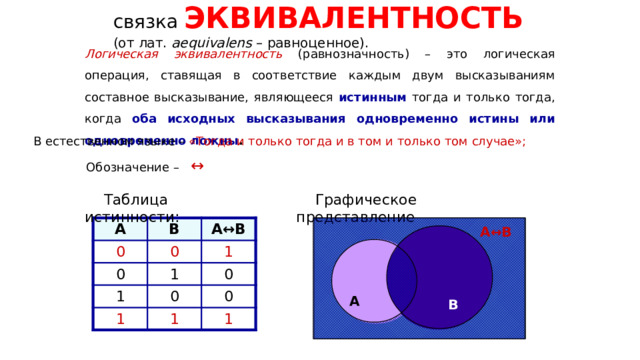
Логическая связка  ЭКВИВАЛЕНТНОСТЬ  (от лат.  aequivalens  – равноценное).

Логическая эквивалентность (равнозначность) – это логическая операция, ставящая в соответствие каждым двум высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истины или одновременно ложны .

В естественном языке – «Тогда и только тогда и в том и только том случае»;

Обозначение – ↔

Таблица истинности:

Графическое представление

А

0

В

А↔В

0

0

1

1

1

1

0

0

1

0

1

A ↔B

B

A

A

B

24

16) И НЕ ( x нечётное). 1 1 В условии фигурируют высказывания «И» «НЕ».   « НЕ » —  инверсия   « И » — Конъюнкция. Давайте попробуем рассуждать логически: число x должно быть больше 16. по правилам алгебры логики «НЕ» « НЕ (x нечётное)» отрицание, значит число будет чётное. по правилам алгебры логики «И» конъюнкция истинна только если истинно оба условия. Проверим наши условия в таблице 24 " width="640"

Задание 3 (ОГЭ)

Напишите наименьшее число x , для которого истинно высказывание:

( x 16) И НЕ ( x нечётное).

1

1

В условии фигурируют высказывания «И» «НЕ».

  « НЕ » —  инверсия

  « И » — Конъюнкция.

Давайте попробуем рассуждать логически: число x должно быть больше 16.

по правилам алгебры логики «НЕ»

« НЕ (x нечётное)» отрицание, значит число будет чётное.

по правилам алгебры логики «И» конъюнкция истинна только если истинно оба условия. Проверим наши условия в таблице

24

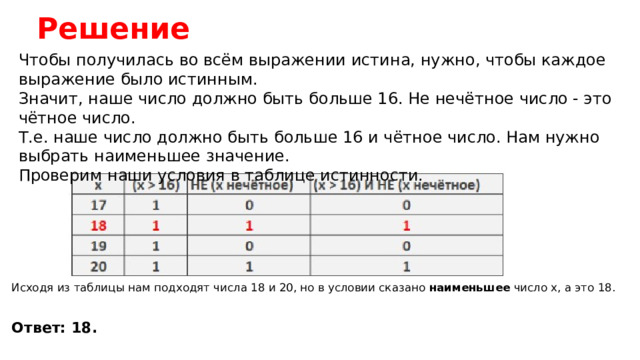
Решение

Чтобы получилась во всём выражении истина, нужно, чтобы каждое выражение было истинным. Значит, наше число должно быть больше 16. Не нечётное число - это чётное число.

Т.е. наше число должно быть больше 16 и чётное число. Нам нужно выбрать наименьшее значение. 

Проверим наши условия в таблице истинности.

Исходя из таблицы нам подходят числа 18 и 20, но в условии сказано наименьшее число х, а это 18.

Ответ: 18.

24

Напишите число X , для которого истинно высказывание:

( X И НЕ ( X

Решение.

Логическое «И» истинно тогда, когда истинны оба высказывания. Запишем выражение в виде

( X И ( X ≥ 7).

Значит, число, для которого высказывание будет истинным  — 7. 

Ответ: 7.

Напишите наибольшее двузначное число, для которого истинно высказывание:

(первая цифра нечетная) И НЕ (число делится на 3).

Решение.

Логическое «И» истинно тогда, когда истинны оба высказывания. Запишем выражение в виде

(первая цифра нечетная) И (число не делится на 3).

Значит, наибольшее число, для которого высказывание будет истинным  — 98.

24

= 20 Ответ : плодов не менее, чем 35 (15 груш и не менее 20 яблок) Ответ : условие задачи некорректно, так как 2 условия противоречат друг другу, то есть не может быть одновременно яблок не больше 15 и не меньше 20. ? 24 " width="640"

Решите самостоятельно:

Реши сам

2. В корзине лежат 15 груш и несколько яблок. Сколько в корзине может лежать плодов (яблок и груш), если известно, что

(яблок не больше, чем груш) или (яблок не меньше, чем 20)?

1) 33 2) 20

3) 14 4) 31

Видимо у вас 2 условия :

1 - я задача : ЯБЛОК НЕ БОЛЬШЕ, ЧЕМ ГРУШ

1 - я задача : Я

Ответ : плодов не более 30

(15 груш и не более 15 яблок)

2 - я задача : ЯБЛОК НЕ МЕНЬШЕ, ЧЕМ 20

Г = 15 и Я = 20

Ответ : плодов не менее, чем 35

(15 груш и не менее 20 яблок)

Ответ : условие задачи некорректно, так как 2 условия противоречат друг другу, то есть не может быть одновременно яблок не больше 15 и не меньше 20.

?

24

Таблица истинности

Таблица истинности - таблица, с помощью которой устанавливается истинностное значение сложного высказывания при данных значениях входящих в него простых высказываний .

В к л а с сичес к о й м а т е м а т и чес к о й л о г и к е пр е д п о ла г а е т ся, ч т о каждое простое (не содержащее логических операций) высказывание я в ля е т ся л и бо и с тин н ым , л и бо л о жн ы м , н о н е т е м и д р у г и м одновременно.

Когда с помощью логических операций мы соединяем простые высказывания в сложное, встает вопрос: при каких условиях сложное высказывание считается истинным, а при каких — ложным?

Для ответа на этот вопрос и служат таблицы истинности. Каждая логическая операция имеет свою таблицу, которая показывает, при каких наборах значений простых высказываний сложное высказы- вание с этой операцией будет истинным, а при каких — ложным.

24

24

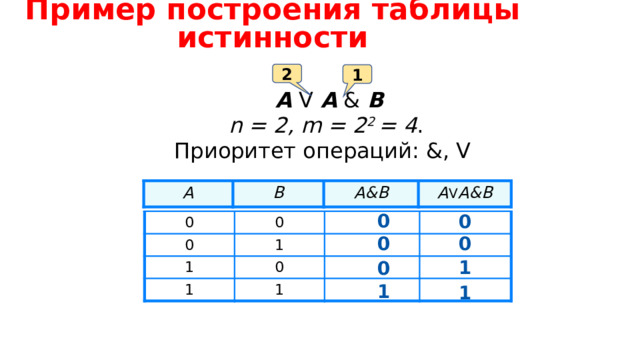
Пример построения таблицы истинности

2

1

А V A & B

n = 2, m = 2 2 = 4 .

Приоритет операций: &, V

A

B

A&B

A V A&B

0

0

0

0

0

1

1

1

0

1

0

0

1

0

1

1

Построение таблиц истинности для логических выражений

подсчитать n - число переменных в выражении

подсчитать общее число логических операций в выражении

установить последовательность выполнения логических операций

определить число столбцов в таблице

вычисляется как количество переменных + количество логических операций

заполнить шапку таблицы, включив в неё переменные и операции

определить число строк в таблице без шапки: m =2 n

выписать наборы входных переменных

провести заполнение таблицы по столбцам, выполняя логические

операции в соответствии с установленной последовательностью

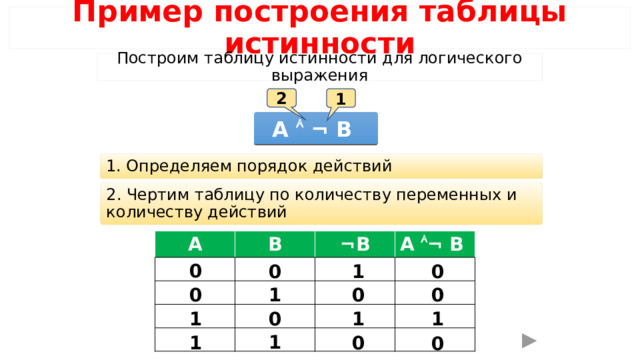
Пример построения таблицы истинности

Построим таблицу истинности для логического выражения

1

2

A  ¬ B

1. Определяем порядок действий

2. Чертим таблицу по количеству переменных и количеству действий

A

B

¬B

A  ¬ B

0

0

1

0

0

0

1

0

1

0

1

1

1

1

0

0

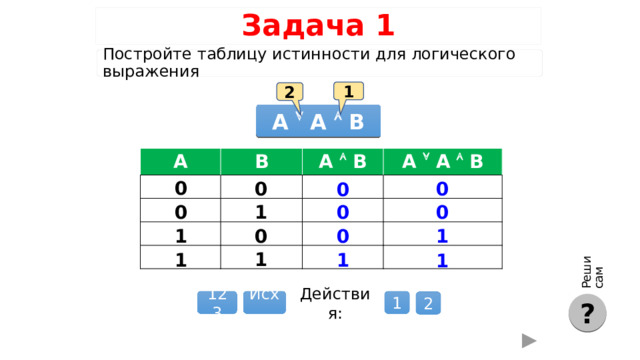
Реши сам

Задача 1

Постройте таблицу истинности для логического выражения

1

2

А  A  B

A

B

A  B

А  A  B

0

0

0

0

0

0

1

0

1

0

1

0

1

1

1

1

Исх.

Действия:

1

123

2

?

33

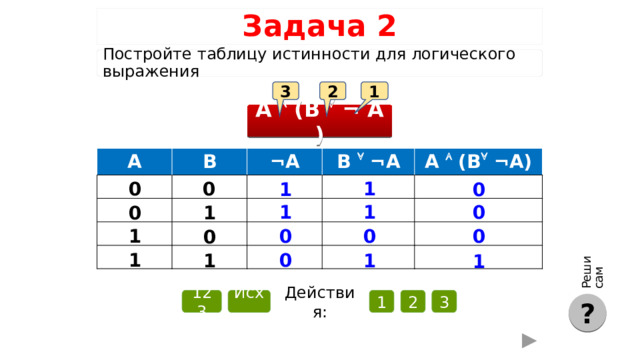
Реши сам

Задача 2

Постройте таблицу истинности для логического выражения

3

2

1

А  (B  ¬ A )

A

B

¬ A

B  ¬ A

A  ( B  ¬ A)

0

0

1

0

1

1

0

1

0

1

0

0

0

1

0

0

1

1

1

1

123

Исх.

Действия:

1

2

3

?

34

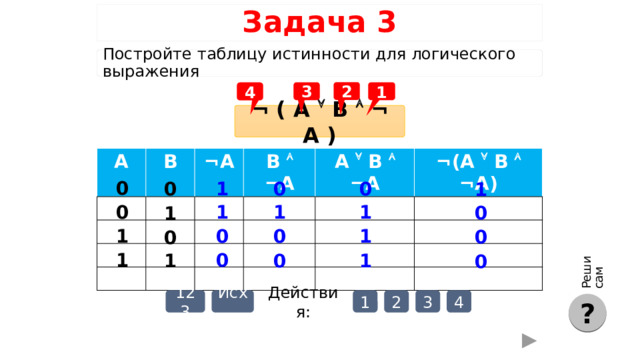
Реши сам

Задача 3

Постройте таблицу истинности для логического выражения

2

3

1

4

¬ ( A  B  ¬ A )

A

B

¬ A

B  ¬ A

A  B  ¬ A

¬( A  B  ¬ A)

0

0

0

1

0

1

1

1

1

0

0

1

0

1

1

0

0

0

1

0

1

1

0

0

2

3

1

4

Действия:

Исх.

123

?

35

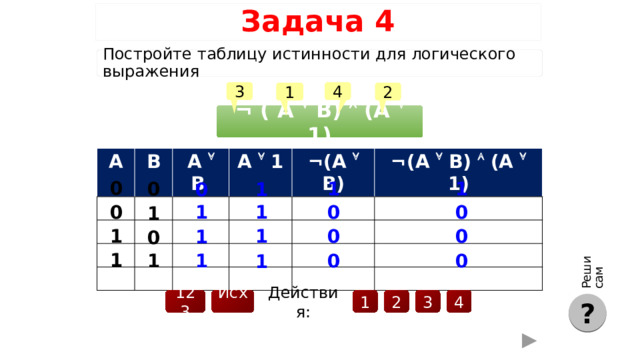
Реши сам

Задача 4

Постройте таблицу истинности для логического выражения

3

4

1

2

¬ ( A  B)  (A  1)

A

B

A  B

A  1

¬( A  B)

¬( A  B)  ( A  1)

0

1

1

0

1

0

0

0

1

1

0

1

0

0

1

1

1

0

1

1

1

0

0

1

2

3

1

4

Действия:

Исх.

123

?

36

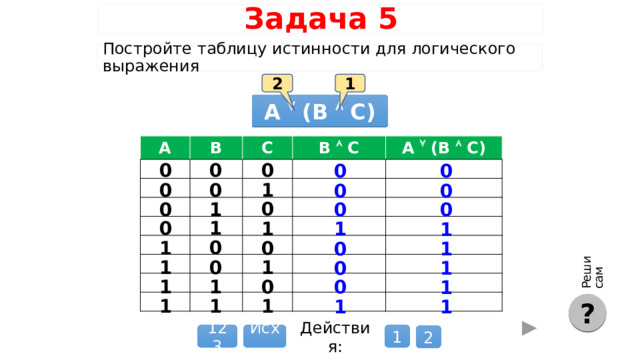
Реши сам

Задача 5

Постройте таблицу истинности для логического выражения

1

2

А  (B  C)

A

B

C

B  C

А  (B  C)

0

0

0

0

0

0

1

0

0

0

0

0

1

0

0

1

0

1

1

1

0

1

0

0

1

1

0

1

0

1

0

1

1

0

1

1

1

1

1

1

?

123

1

Исх.

Действия:

2

37

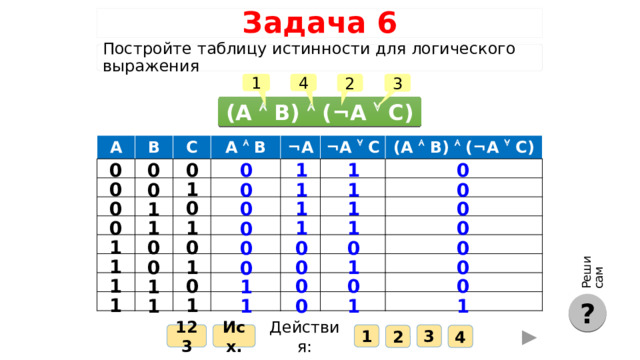
Реши сам

Задача 6

Постройте таблицу истинности для логического выражения

4

1

2

3

(А  B)  (¬A  C)

A

B

C

A  B

¬ А

¬ А  C

(A  B)  (¬ А  C)

0

0

0

1

1

0

0

0

1

1

1

0

0

0

0

0

0

1

1

0

1

0

1

1

1

0

1

0

0

1

0

0

0

0

0

1

1

0

1

0

0

0

0

1

0

0

0

1

1

1

1

1

0

1

1

1

?

123

1

Действия:

Исх.

3

2

4

38

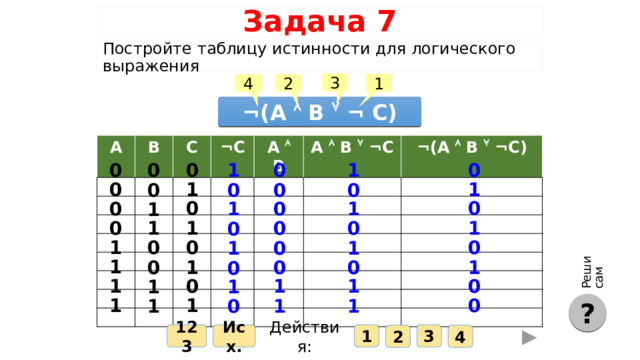
Реши сам

Задача 7

Постройте таблицу истинности для логического выражения

3

1

2

4

¬(А  B  ¬ C)

A

B

C

¬ C

A  B

A  B  ¬ C

¬ (A  B  ¬ C)

0

0

0

0

1

0

1

1

0

1

0

0

0

0

0

0

1

0

0

1

1

0

1

1

0

1

0

0

1

0

0

0

0

1

1

1

1

1

0

0

0

0

0

0

1

1

1

1

1

1

0

1

1

1

1

0

?

123

1

Действия:

Исх.

3

2

4

39

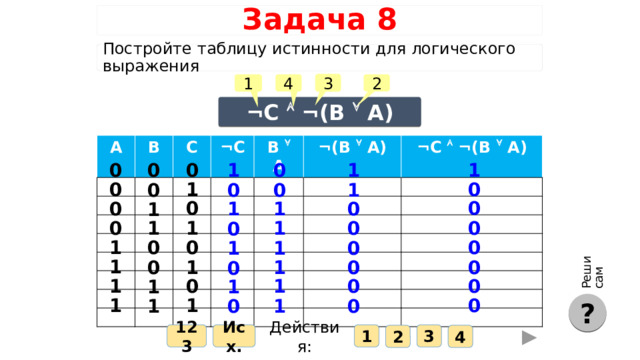
Реши сам

Задача 8

Постройте таблицу истинности для логического выражения

3

2

4

1

¬C  ¬(B  A)

A

B

C

¬ C

B  A

¬( B  A)

¬ C  ¬( B  A)

0

1

0

0

1

0

1

0

0

1

0

1

0

0

0

0

0

1

0

1

1

0

0

1

0

1

1

0

1

0

0

0

1

0

1

1

1

0

0

1

0

0

0

0

1

1

0

1

1

1

0

1

1

0

1

0

?

123

1

Действия:

Исх.

3

2

4

40

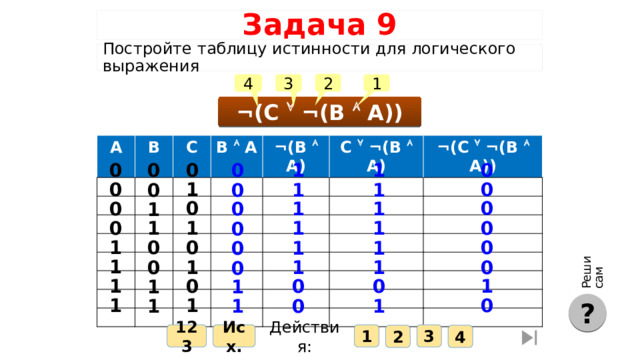
Реши сам

Задача 9

Постройте таблицу истинности для логического выражения

2

1

3

4

¬(C  ¬(B  A))

A

B

C

B  A

¬( B  A)

C  ¬( B  A)

¬( C  ¬( B  A))

0

0

0

1

1

0

0

0

0

1

1

1

0

0

0

0

1

1

0

0

1

0

0

1

1

1

1

0

1

0

0

0

1

1

0

1

1

0

0

1

1

0

1

0

1

0

0

1

1

1

0

1

0

1

1

1

?

123

1

Действия:

Исх.

3

2

4

41

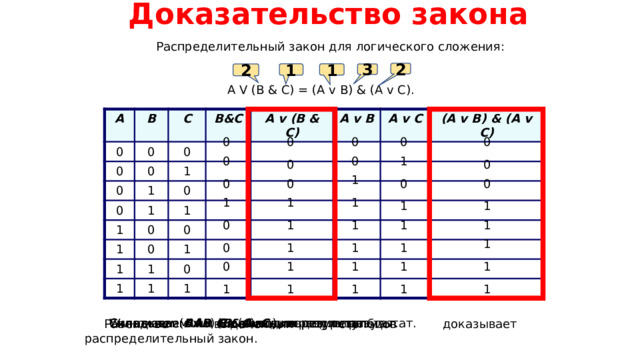
Доказательство закона

Распределительный закон для логического сложения:

A V (B & C) = (A v B) & (A v C).

2

1

2

1

3

A

B

0

0

0

C

0

0

B&C

0

1

0

1

A v (B & C)

0

1

A v B

1

0

1

1

A v C

(A v B) & (A v C)

1

0

0

1

1

1

0

1

1

0

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

1

1

1

1

1

1

0

1

1

1

1

1

1

0

1

0

1

1

1

1

1

1

1

1

Складываем А и В и выводим результат.

Умножаем ( А v B ) на ( A v C )и выводим результат.

Складываем А и C и выводим результат.

Складываем А и ( В & С ) и выводим результат.

Умножаем В на С и выводим результат.

Равенство выделенных столбцов доказывает распределительный закон.

Построить таблицы истинности для логических функций

Итог:

• Вы познакомились с основными понятиями алгебры логики.

• Рассмотрели элементарные логические операции.

• Разобрали для каждой логической операции таблицу истинности.

Домашнее задание

Построить таблицы истинности для данных ниже сложных высказываний. По таблице истинности определить тип формулы логики высказываний.

• F = (A ᴠ B) ʌ (¬ A ᴠ¬ B)
• F = X ᴠ Y ʌ ¬ Z
• F = X ʌ Y ᴠ ¬ (X ᴠ Y) ᴠ X
• F = А ʌ (В → С)
• F = (В ʌ ¬ В)↔(A ᴠ D)
• F = (В ʌ ¬ В)↔(A ᴠ D)

Спасибо за внимание!