Урок №59
Класс 9
Тема урока: Промежутки знакопостоянства. Возрастающая и убывающая функции
Цели урока:
Обучающие: систематизировать знания по теме «функция,нули функции»; добиться усвоение учащимися понятия: промежутки, на которых функция сохраняет свой знак (промежутки знакопостоянства функции, возрастающая и убывающая функция); сформировать умения формулировать определения изученного понятия, а также решать задачи с использованием изученного на уроке определения;
Развивающие: развитие умения определять промежутки знакопостоянства функции, определять возрастание и убывание функции, заданной графически; способствовать развитию математической речи; развитию умения читать и анализировать графики;
Воспитательные: учить правильно использовать терминологию; прививать интерес к предмету через компьютер.
Материально-техническое обеспечение: компьютер, интерактивная доска
Компетентности: математическая грамотность, информационно-цифровая компетентность
Сквозные умения: решение проблемы, сотрудничаю, эффективно общаюсь, исследую, рефлексирую
Тип урока: усвоение знаний, формирование умений
Ход урока:
I. Организационный момент
Проверка готовности учащихся к уроку, настрой их на урок.
Проверка д/з
2. Определите нули функции ( слайд 2)
II. Формулирование цели и задач урока. Мотивация учебной деятельности учащихся ( слайд 3)
Как заметил Г.Галилей, книга природы написана на математическом языке и её буквы - математические знаки и геометрические фигуры - невозможно понять её слова. И именно функция является тем средством математического языка, которое позволяет описывать процессы движения, изменения, присущие природе.
Почти все, что происходит с нами или вокруг нас связано с понятием «функция», потому что все вокруг взаимосвязано, а «функция»- это зависимость между двумя величинами, которая обладает определённым свойством: каждому значению независимой переменной соответствует единственное значение зависимой переменной. Именно такие зависимости называются функциями. Таким образом, функция — одно из важнейших математических понятий.
Итак, цель нашего урока – повторить основные сведения о функции, с которыми вы познакомились на предыдущих уроках, а также познакомиться с новым свойством функции: промежутками знакопостоянства, возрастающей и убывающей функциями и научиться применять полученные знания на практике.
III. Актуализация опорных знаний и уменийй учашихся
Игра «Математический футбол»
Учащиеся задают друг другу вопросы по раннее изученному материалу. По заданным вопросам и ответам я определю, как вы готовы сегодня к уроку.
1. Что такое функция?
Это зависимость переменной у от переменной х, при которой каждому значению х соответствует единственное значение у.
2. Как обозначается функция? у = f(х)
3. Что называют аргументом функции? х- аргумент (независимая переменная)
4. Как по другому называют функцию у? зависимая переменная
5. Приведите примеры функций.
у=2х-8 ; у= х2; у=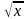 ; у= 5х; у=
; у= 5х; у= 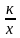 .
.
5. Что называют областью определения функции? Обозначение: D(f)
Это множество значений, которые принимает аргумент,т.е. х.
6. Что называют областью значений функции? Обозначение: Е(f)
Это множество всех значений переменной у, которые она может приобретать при всех значениях аргумента, взятых из D(f).
7. Какие способы задания функции вы знаете?
- С помощью формулы.Такой способ задания функции называют аналитическим.
- с помощью таблицы
- графический
- описательный (словесное описание)
Например: Сила равна скорости изменения импульса
8. Какое значение аргумента называют нулём функции?
Это значение аргумента, при котором значении функции равно 0.
IV. Усвоение знаний (слайд 4)
Итак, рассмотрим график изменения температуры воздуха с течением времени.
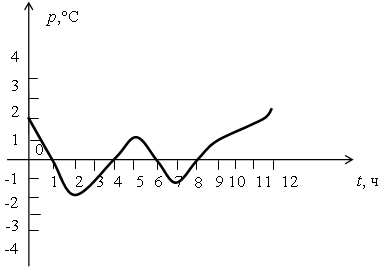
В о п р о с ы:
1) В течение какого промежутка времени шло наблюдение? (0-12 ч)
2) В каких пределах изменялась за это время температура?(-2 до 3°С)
3) В какое время температура воздуха была равна 0? (1ч, 4ч, 6ч, 8ч)
4) В какие промежутки времени температура была выше нуля? ниже нуля?
5) В какие промежутки температура повышалась? понижалась?
Отвечая на эти вопросы, мы, по сути, перечислили с вами основные свойства функции.
Продолжаем с вами знакомиться со свойствами функции.
( слайд 5)
1. Промежутки знакопостоянства
Промежутки, к которых функция сохраняет свой знак, называют промежутками знакопостоянства.
( слайды 6, 7) – найти промежутки знакопостоянства
( слайды 8 и 9)
2. Возрастающая и убывающая функция
Функцию у = f(х) называют возрастающей на некотором промежутке, если для любых двух значений аргумента х1 и х2 из области определения, таких, что х2 х1, выполняется неравенство f(х2) f(х1).
Функцию у = f(х) называют убывающей на некотором промежутке, если для любых двух значений аргумента х1 и х2 из области определения, таких, что х2 х1, выполняется неравенство f(х2) f(х1).
( слайды 10 и 11) – решение заданий
V. Историческая пауза
Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5тыс. лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r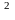 .
.
VI. Формирование умений
( слайд 12)
С х е м а для исследования любой функции: 1) Найти область определения функции, D (у). 2) Найти область значений функции, Е (у). 3) Найти нули функции. 4) Найти промежутки знакопостоянства функции. 5) Найти промежутки возрастания и убывания функции. 1. Решение упражнений ( слайды 13, 14)
( слайд 15)
Cамостоятельная работа
Учащиеся самостоятельно выполняют работу в тетрадях, после этого проводят взаимопроверку по готовым ответам и оценивают работу соседа.
( слайд 16)
| 1 вариант | 2 вариант |
| 1) D(f) = [– 3; 3] 2) E (f) = [– 2; 3] 3) f(x) = 0, х = – 2,5; х = 1 4) f(x) 0 при х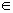 (– 3;- 2,5]; (1;3) (– 3;- 2,5]; (1;3) f(х) [– 2,5; 1) 5) f(x) ↑ при х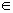 [–0,5; 2] [–0,5; 2] f(x) ↓ при х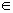 [– 3; –0,5]и [2; 3] [– 3; –0,5]и [2; 3] | 1) D(f) = [– 5; 4] 2) E (f) = [-1,5; 4] 3) f(x) = 0, х = – 3,5; х = 1; х = 3 4) f(x) 0при х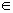 [– 3,5;1) и (3; 4] [– 3,5;1) и (3; 4] f(х) (– 5;- 3,5) и (1;3) 5) f(x) ↑ при х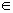 [-5; -1] и [2;4] [-5; -1] и [2;4] f(x) ↓ при х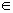 [– 1; 2] [– 1; 2] |
VII. Итоги урока
( слайд 17)
Сегодня на уроке мы познакомились со схемой исследования функции. Расскажите, как провести исследование функции. Скажите, пожалуйста, какие из выполненных заданий вызвали у вас наибольшее затруднение?
| Свойства функции |
| Если для функции y = f(x) выполняется условие f (х0) = 0 (х0 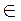 D( f )), то х0 — ноль функции. D( f )), то х0 — ноль функции. |
| 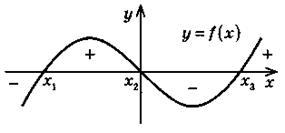 | На рисунке х1, х2, х3 — нули функции ( f (x1) = f (x2) = f (x3) = 0). Промежутки (-∞; x1), (x1; x2), (х2; х3), (х3; +∞) — интервалы постоянства знака функции y = f(x). Если х1 х2 и у 1 у2, то функция –возрастающая. Если х1 х2 и у1 у2, то функция – убывающая. |
VIII. Рефлексия
1. На уроке я работал активно/ пассивно
2. Своей работой я доволен/ не доволен
3. За урок я устал/ не устал
4. Моё настроение стало лучше/ хуже
5. Материал урока для меня был понятным/ непонятным
полезным/ бесполезным
лёгким/ тяжёлым
интересным/ неинтересным
IX. Домашнее задание: § 8, № 8 (2, 5, 8), на повторение: № 28(1, 2), 29(1,2)
Комментирование д/з.
6







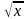 ; у= 5х; у=
; у= 5х; у= 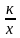 .
.
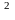 .
.

















