Уравнение плоскости

Уравнение плоскости

Уравнение плоскости

• Всякое уравнение первой степени относительно координат x, y, z

• Ax + By + Cz +D=0  

• задает плоскость, и наоборот:

всякая плоскость может быть представлена уравнением, которое называется уравнением плоскости.

Уравнение плоскости

• Ax + By + Cz +D=0  

Составить уравнение какой-нибудь плоскости, в которой лежит точка (2; -1; 3)

• Ax + By + Cz +D=0
• 3x + 4y + 5z +D=0 (3,4,5-любые числа)
• 3·2 + 4·(-1) + 5·3 +D=0
• 6- 4+ 15+D=0
• 17+D=0
• D=-17
• Ответ: 3x + 4y + 5z -17=0-уравнение плоскости на которой лежит точка (2; -1; 3)

Особые случаи уравнения плоскости

• 1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.
• 2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.
• 3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.
• 4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей:

• x = 0, y = 0, z = 0.

Задания

• 1) Найдите аппликату точки А(1;-3; z) , если она принадлежит плоскости, заданной уравнением 5х-2у+3z-1=0.
• 2) Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0
• 3) Принадлежит, ли точка Е (0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0
• 4) При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0

• Сколько точек достаточно для построения плоскости?

Теорема стереометрии

• Через три точки не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Теорема Т3

В

A

С



Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Составьте уравнение плоскости, проходящей через точки

• А(1; 2;-3)
• В (0; 4; 2)
• С (2;-3;5)

Решение системы находим по формулам:

которые называют формулами Крамера

Составим определитель

из коэффициентов при неизвестных

Если Δ≠0, то система совместна

Далее составим три вспомогательных определителя:

, ,

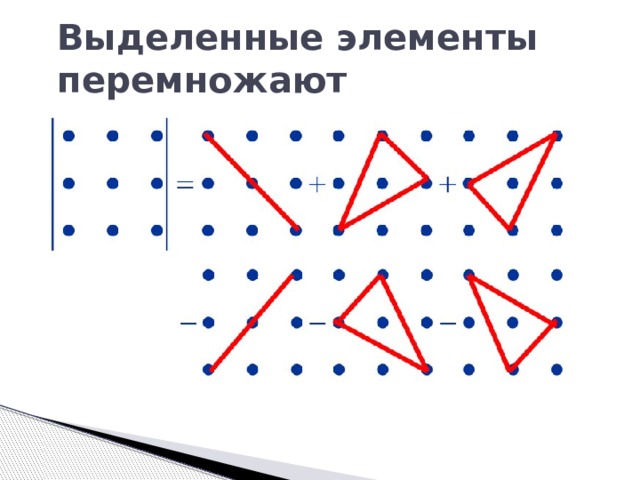
Выделенные элементы перемножают

Вектор нормали

• Если плоскость задана уравнением

Ax + By + Cz +D=0, то вектор n={А, В,С} перпендикулярен этой плоскости.

Этот вектор называется вектором нормали к плоскости или нормальным вектором к данной плоскости.

Дан вектор нормали некоторой плоскости n={2; -3;1}, проходящей через точку А(-1;0;2) Составьте общее уравнение этой плоскости.