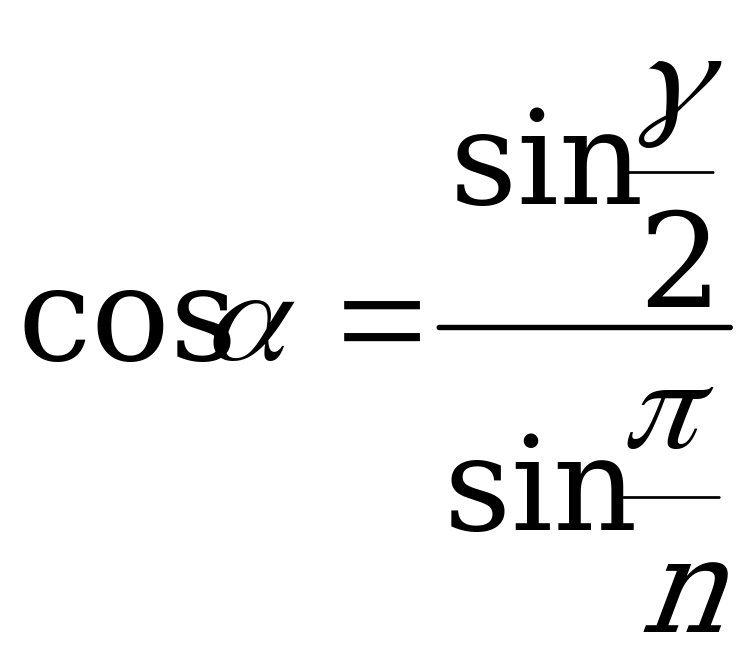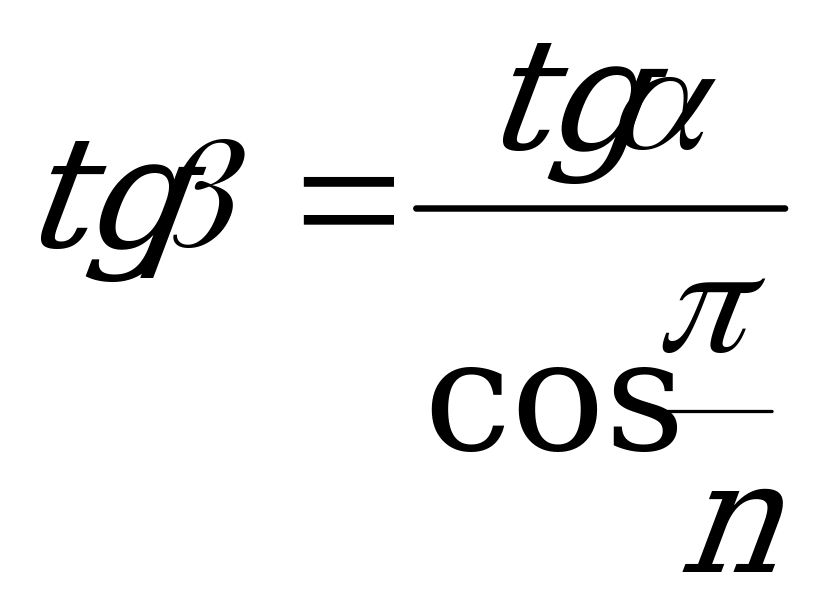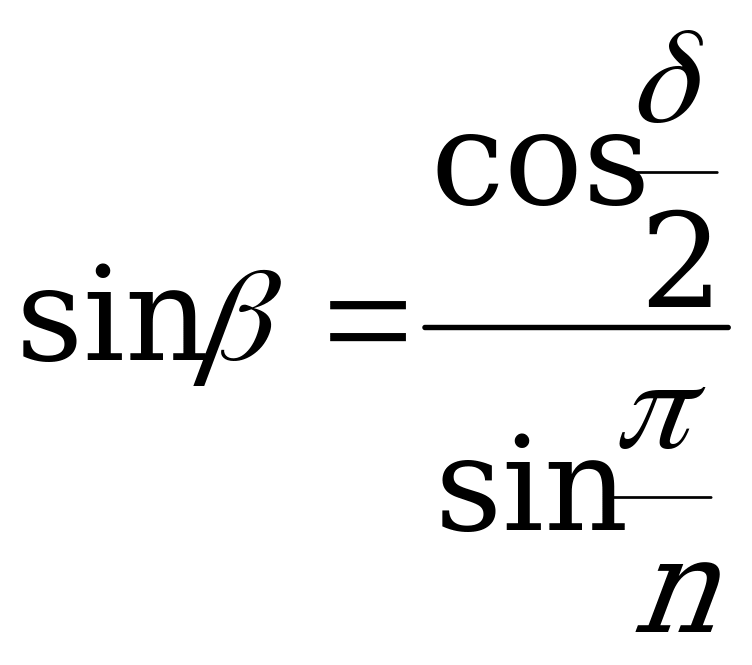ФОРМУЛЫ ПЕРЕХОДА
Рассмотрим углы в правильной пирамиде, наиболее часто встречаются в задачах:
а) угол наклона бокового ребра к плоскости основания пирамиды, его величину условимся обозначать буквой  ;
;
б) угол наклона боковой грани к плоскости основания  ;
;
в) плоский угол при вершине пирамиды 

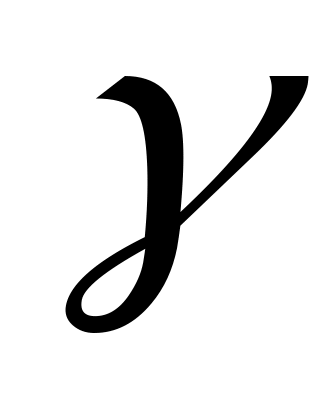 ;
;
г) двугранный угол при боковом ребре пирамиды 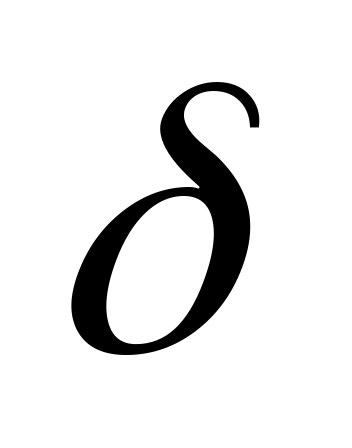 .
.
Все перечисленные выше углы, называемые иногда основными, лежат в разных плоскостях. Зная величину любого из них, можно определить величину всех остальных углов. Эти зависимости мы назовем формулами перехода.
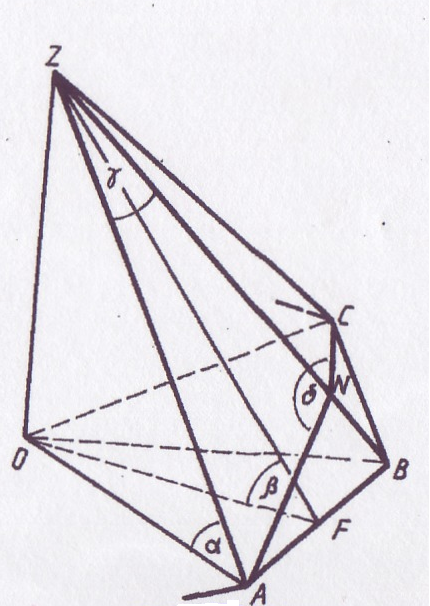
Дана правильная  n-угольная пирамида с обозначенными выше углами
n-угольная пирамида с обозначенными выше углами  ,
, ,
,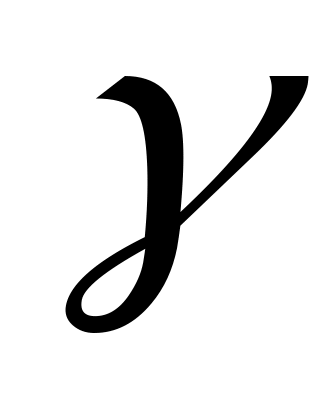 и
и 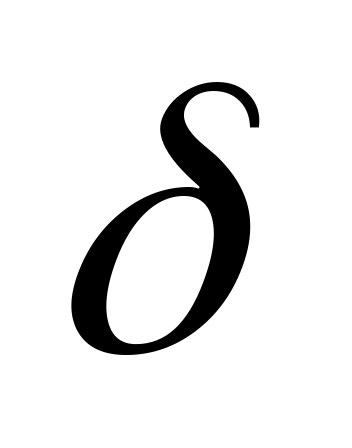 . Вывести формулы перехода, связывающие эти углы между собой.
. Вывести формулы перехода, связывающие эти углы между собой.
Примечание. Поскольку для решения многих задач желательно знать величину угла наклона бокового ребра к плоскости основания пирамиды либо угла наклона боковой грани к плоскости основания, то мы будем выводить формулы перехода только к этим углам.
 Решение. Обозначим через x длину отрезка в правильной пирамиде, входящего как в прямоугольный треугольник, содержащий данный угол, так и в треугольник, содержащий искомый угол. Выразим далее через x и функции данного угла одну из двух других сторон в том треугольнике, который содержит искомый угол. Затем найдём функцию искомого угла.
Решение. Обозначим через x длину отрезка в правильной пирамиде, входящего как в прямоугольный треугольник, содержащий данный угол, так и в треугольник, содержащий искомый угол. Выразим далее через x и функции данного угла одну из двух других сторон в том треугольнике, который содержит искомый угол. Затем найдём функцию искомого угла.
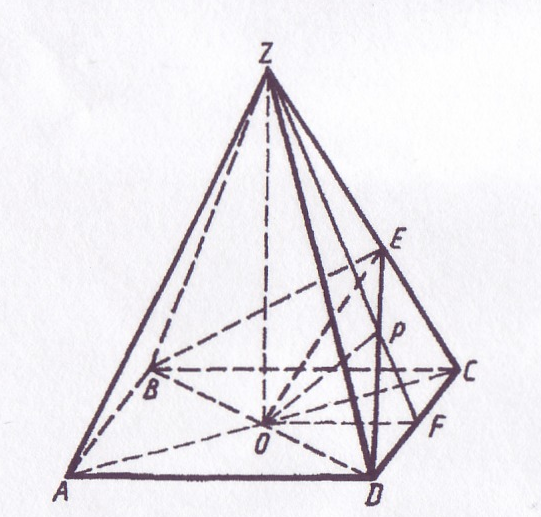
Вывод формул перехода для правильной четырёхугольной пирамиды.
В правильной четырёхугольной пирамиде ZABCD как было обусловлено выше, обозначим:
 ZAO =
ZAO =  ZBO =
ZBO =  ZCO =
ZCO =  ZDO =
ZDO = ,
,
 CZD =
CZD =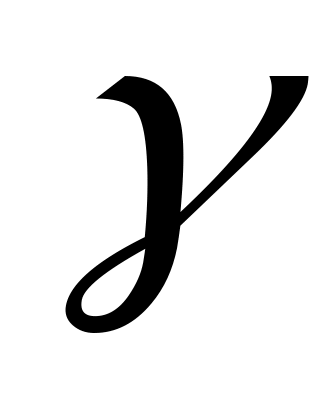 ,
,  ZFO =
ZFO =  и
и  BED =
BED =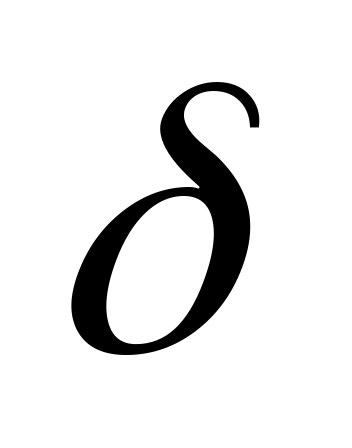 .
.
Опишем построение  BED – линейного угла двугранного угла при боковом ребре ZC.
BED – линейного угла двугранного угла при боковом ребре ZC.
В грани ZCD проводим DE 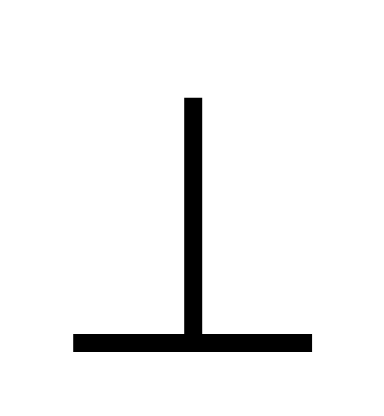 ZC и соединяем точку Е с вершиной основания В. Треугольники ВЕС и DEC равны. Из этого следует, что ВЕ = ED и
ZC и соединяем точку Е с вершиной основания В. Треугольники ВЕС и DEC равны. Из этого следует, что ВЕ = ED и  BEC =
BEC =  DEC =
DEC = /2. Таким образом,
/2. Таким образом,  BED – линейный угол двугранного угла при ребре ZC. Отрезок ОЕ – медиана равнобедренного треугольника BED, следовательно, и биссектриса и высота этого треугольника. Поэтому
BED – линейный угол двугранного угла при ребре ZC. Отрезок ОЕ – медиана равнобедренного треугольника BED, следовательно, и биссектриса и высота этого треугольника. Поэтому  OED =
OED = 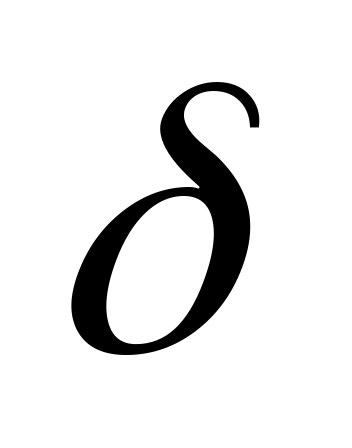 /2.
/2.
Отрезок ОР принадлежит линии пересечения плоскостей линейных углов BED и ZFO. Так как плоскость линейного угла перпендикулярна граням двугранного угла, то каждая из плоскостей – BED и ZOF - перпендикулярна плоскости ZCD. Можно показать, что линия пересечения двух плоскостей, каждая из которых перпендикулярна третьей плоскости, перпендикулярна к этой третьей плоскости. Поэтому OP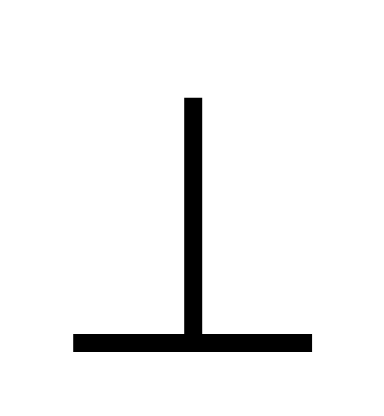 ZCD. Из этого, в частности, следует, что треугольники OPF и OPD прямоугольные и
ZCD. Из этого, в частности, следует, что треугольники OPF и OPD прямоугольные и  DOP =
DOP = 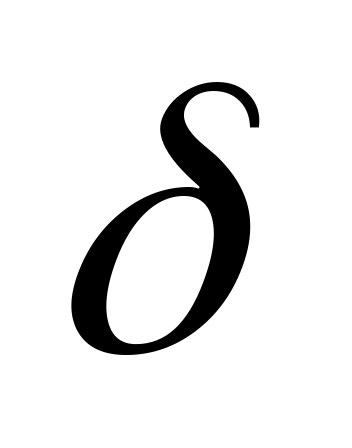 /2.
/2.
Перейдём теперь к выводу формул перехода:
а) от  к
к  .
.
Положим ZO = x.
Из  ZOF
ZOF
OF = x ctg .
.
Из  OFD
OFD
OD = x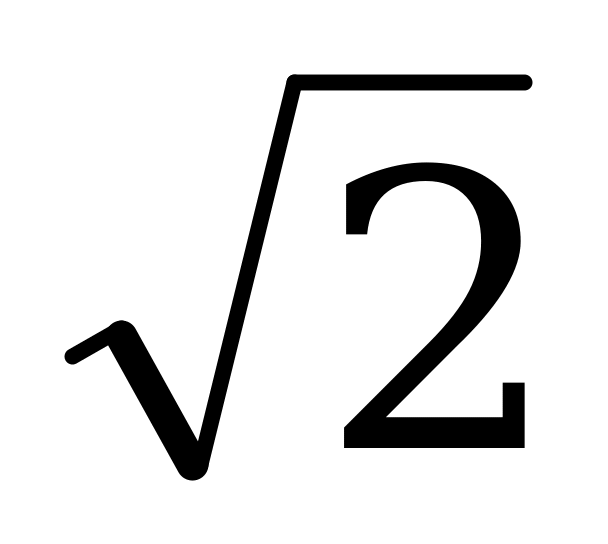 ctg
ctg .
.
Из  ZOD
ZOD
tg =
= 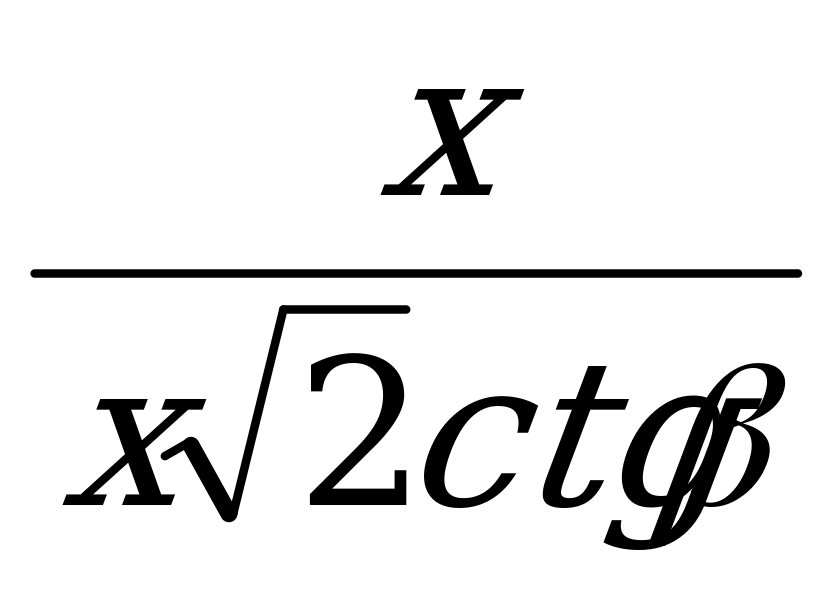 =
= 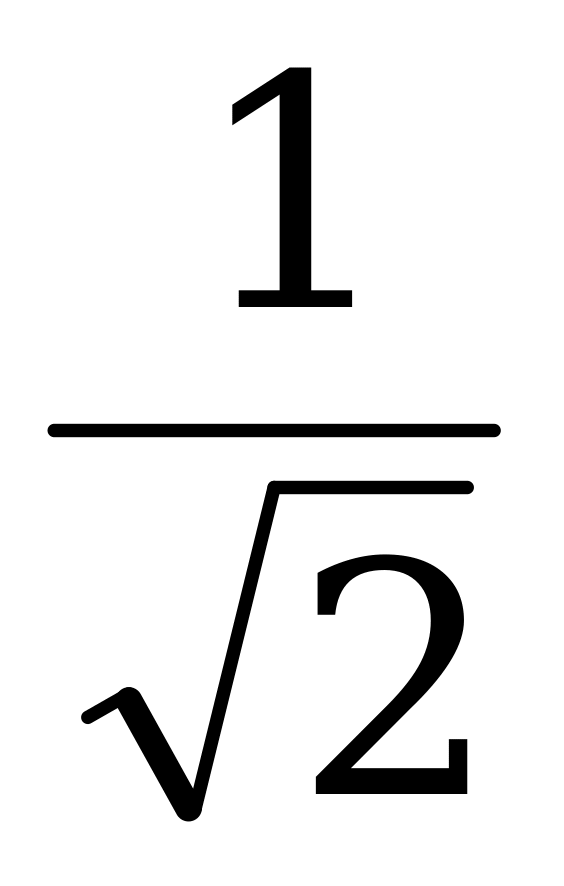 tg
tg .
.
tg =
= 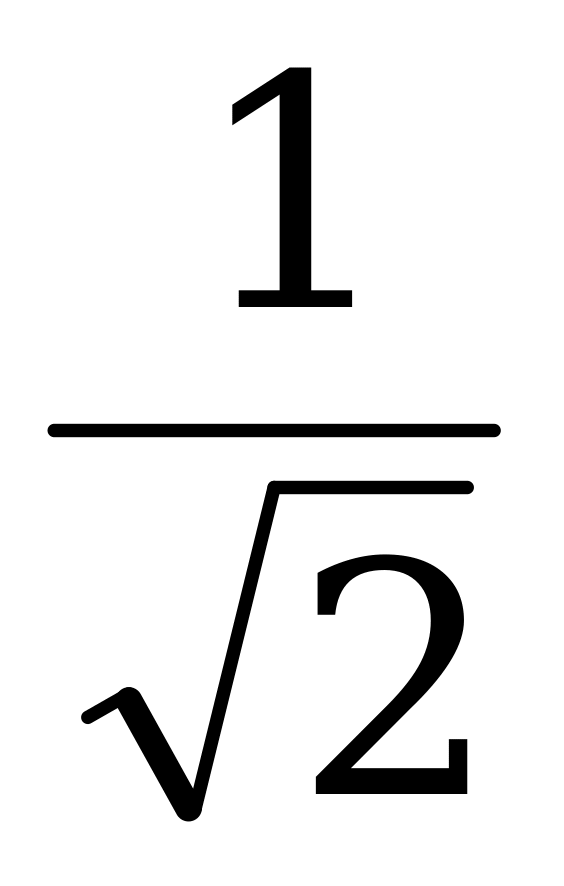 tg
tg ; (I)
; (I)
б) от 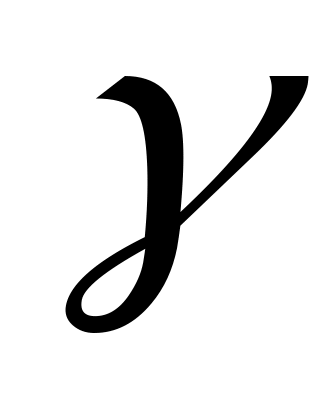 к
к  .
.
Положим ZD = x.
Из  ZDF
ZDF
DF = x sin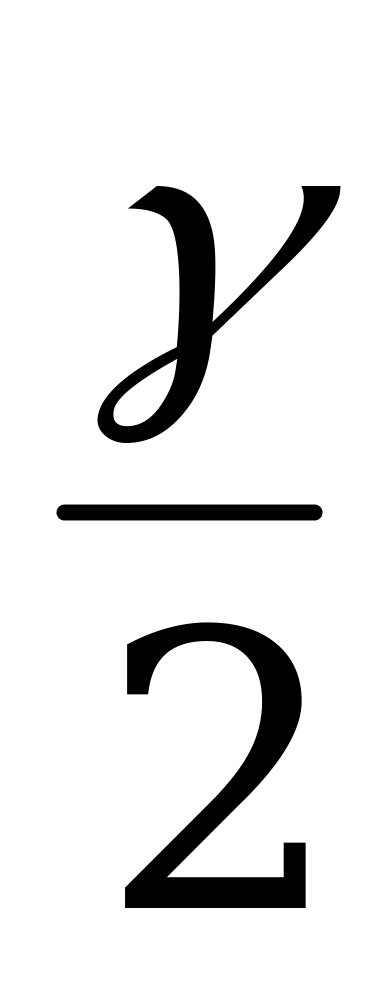 .
.
Из  OFD
OFD
OD = x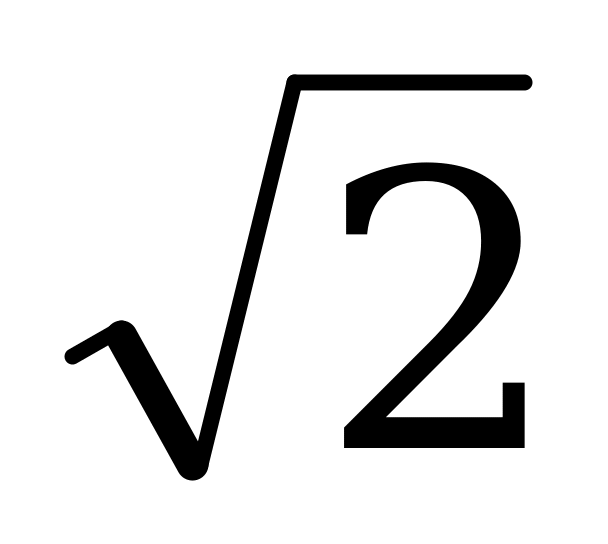 sin
sin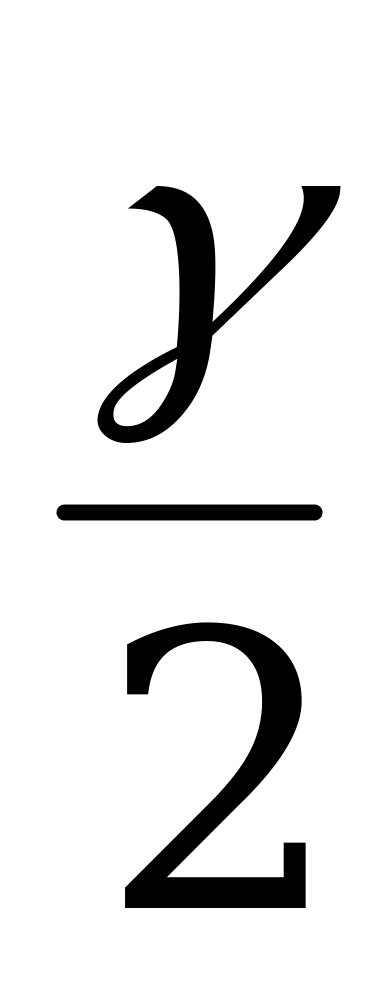 .
.
Из  ZOD
ZOD
cos  =
= 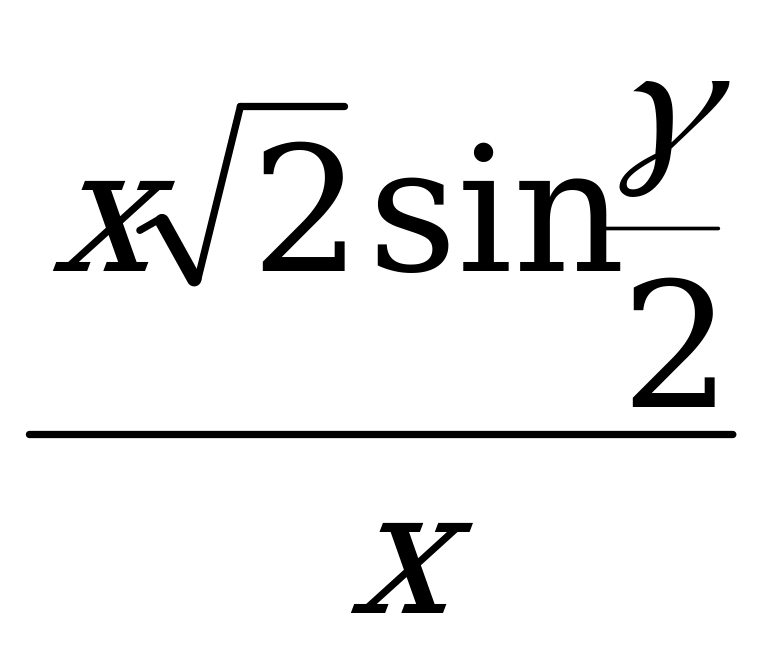 =
= 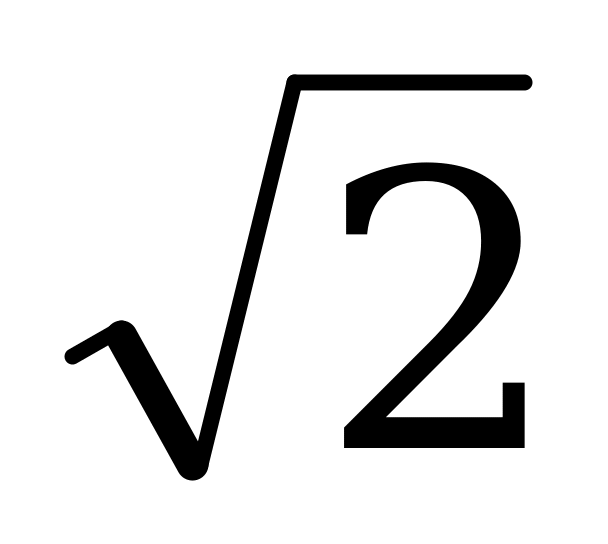 sin
sin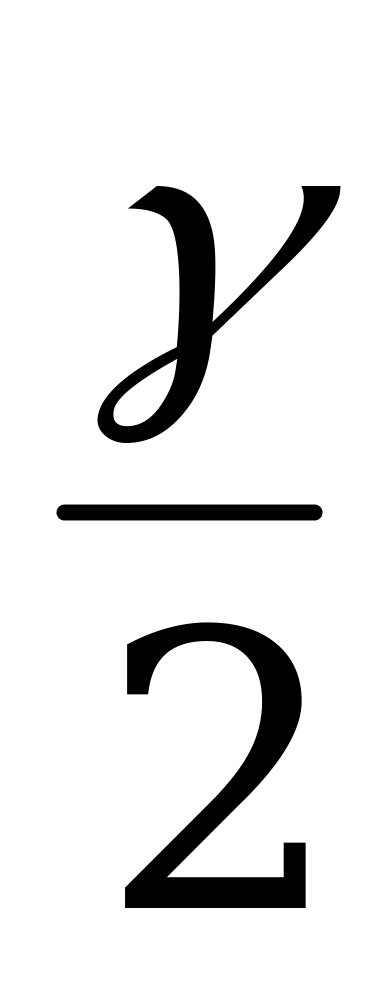 ;
;
cos  =
= 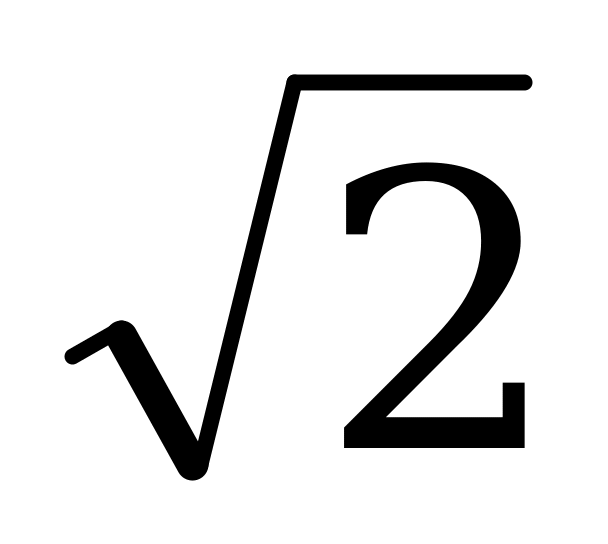 sin
sin 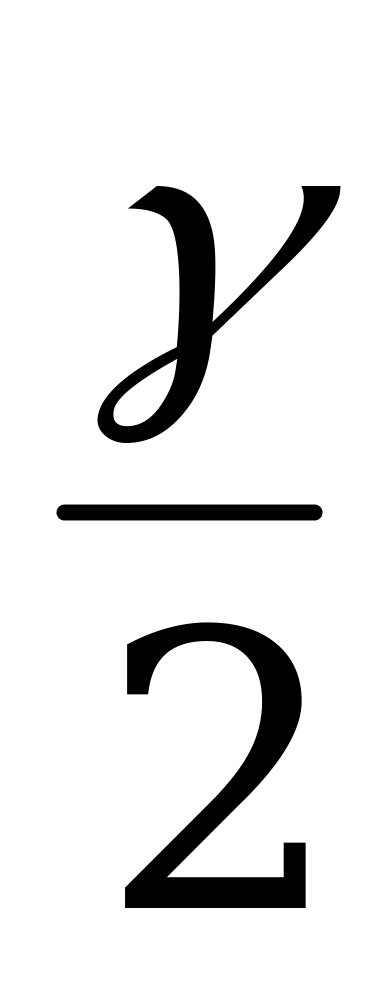 ; (II)
; (II)
в) от 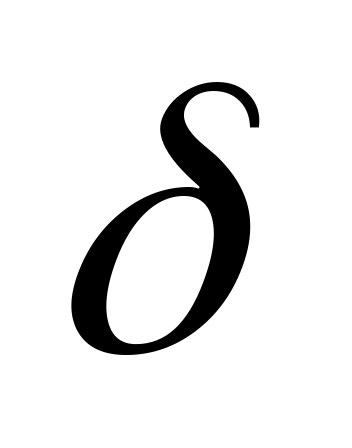 к
к  .
.
Положим EO = x.
Из  EOD
EOD
OD – x tg 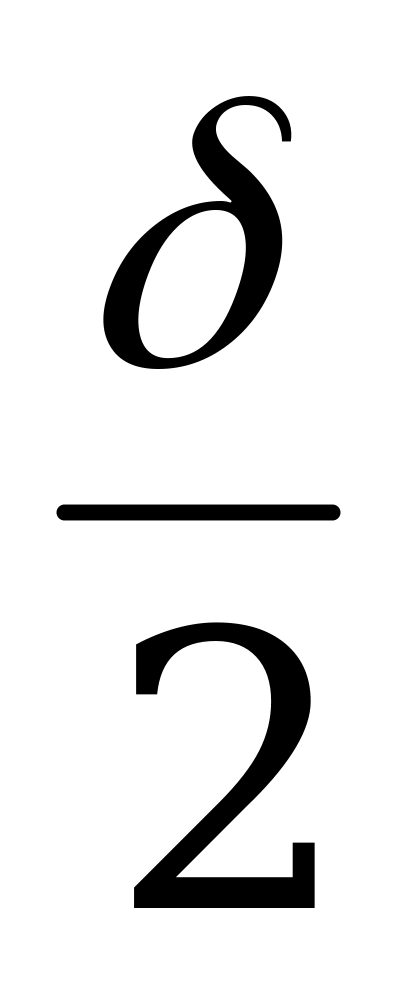 , OC = OD = x tg
, OC = OD = x tg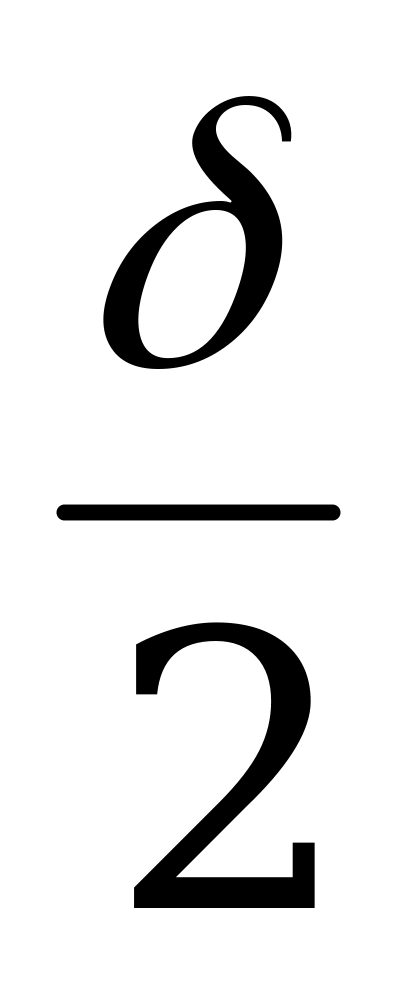 .
.
Из  EOC
EOC
sin  =
= 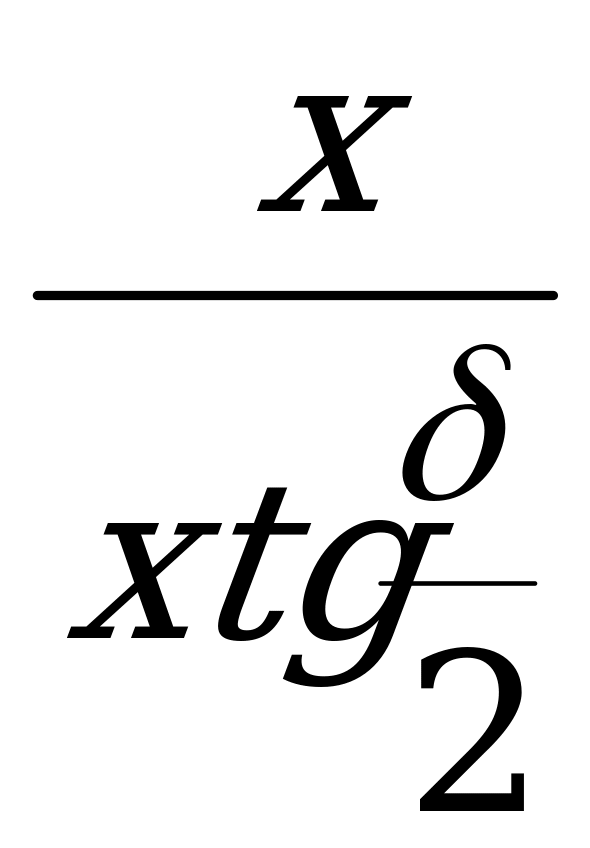 = ctg
= ctg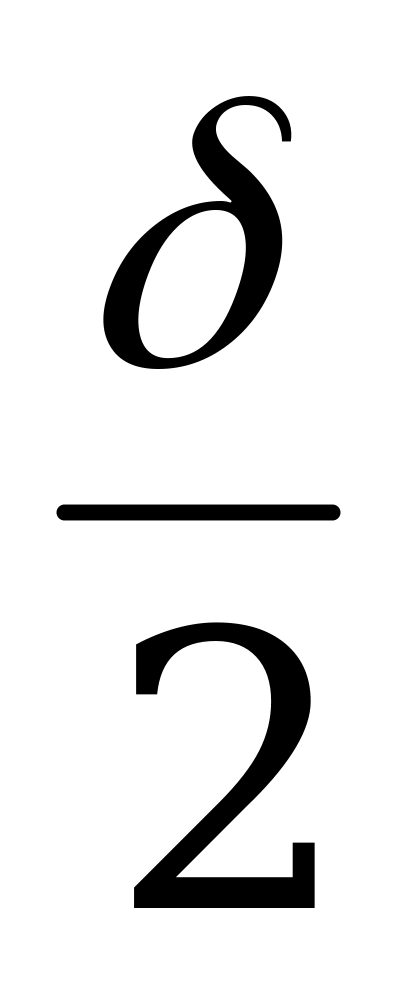 ,
,
sin = ctg
= ctg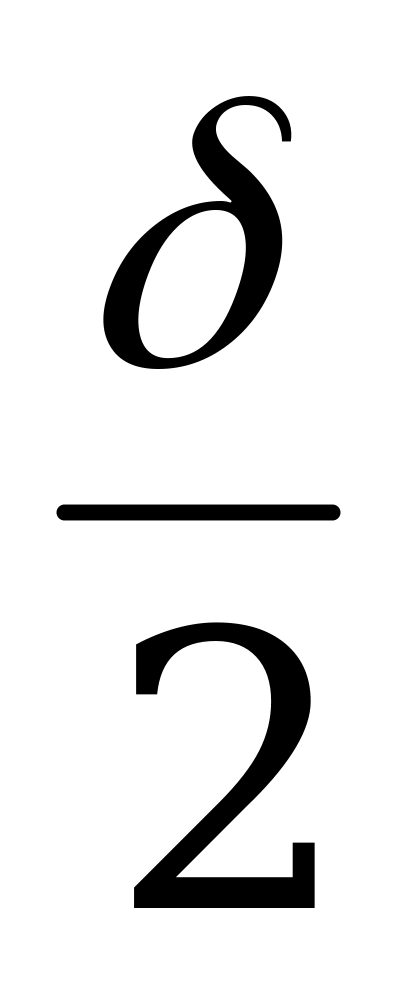 ; (III)
; (III)
г) от  к
к  .
.
Формулу перехода для этой задачи получаем из (I):
tg  =
= 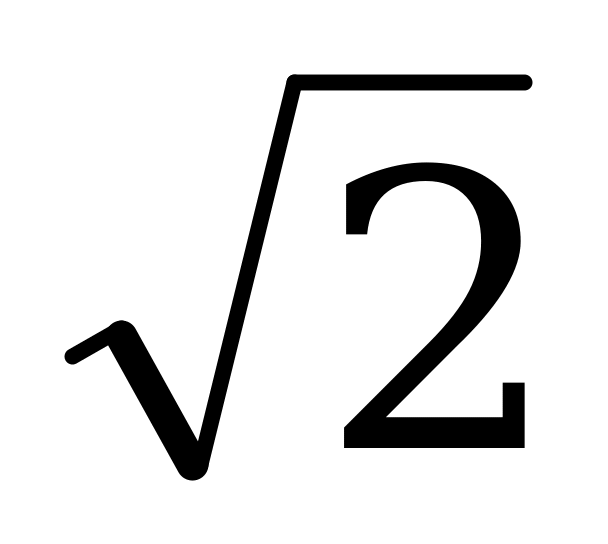 tg
tg ; (IV)
; (IV)
д) от 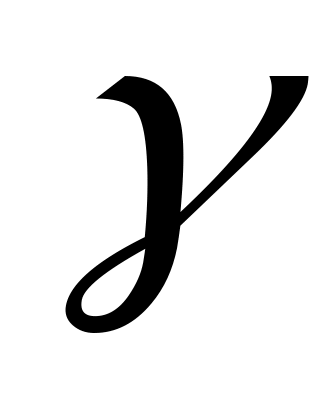 к
к  .
.
Эта задача решается аналогично задаче б). Запишем получающуюся при этом формулу перехода:
cos  = tg
= tg 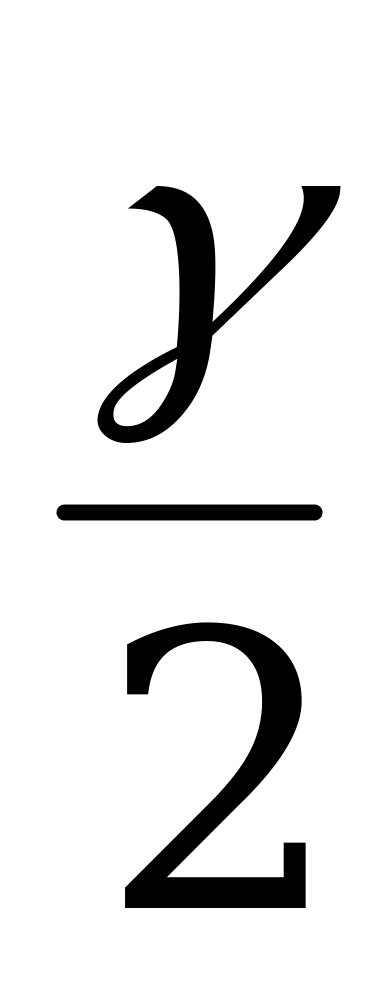 ; (V)
; (V)
е) от 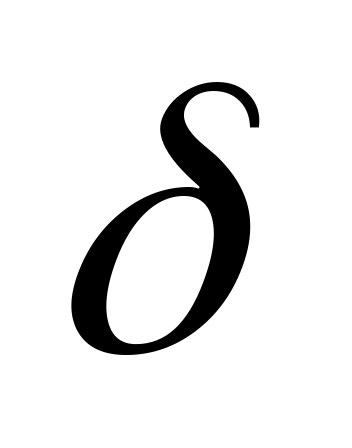 к
к  .
.
Выше было, в частности, показано, что треугольники OPD и OPF прямоугольные и что  DOP =
DOP = 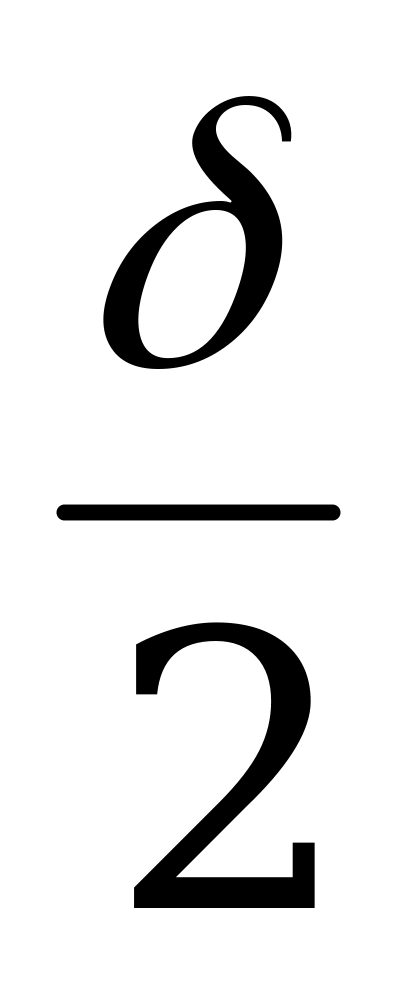 . Поэтому переходим непосредственно к выводу формулы.
. Поэтому переходим непосредственно к выводу формулы.
Положим OP = x.
Из  OPD OD =
OPD OD = 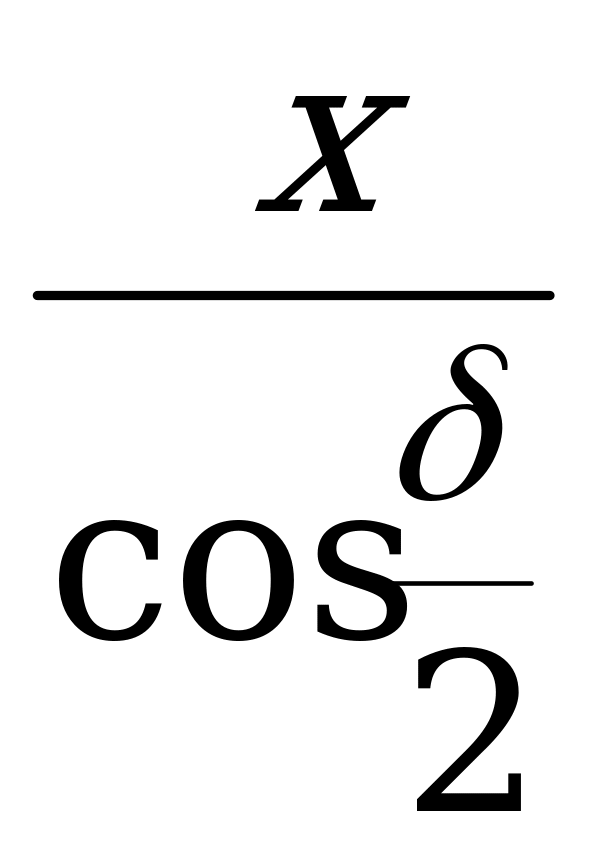 . Из
. Из  OFD OF =
OFD OF = 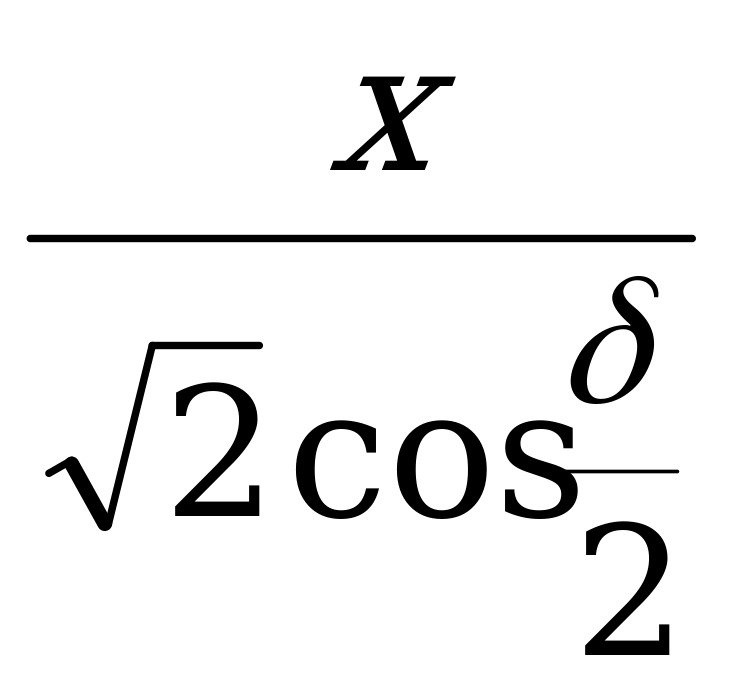 .
.
Из  OPF
OPF
sin  =
= 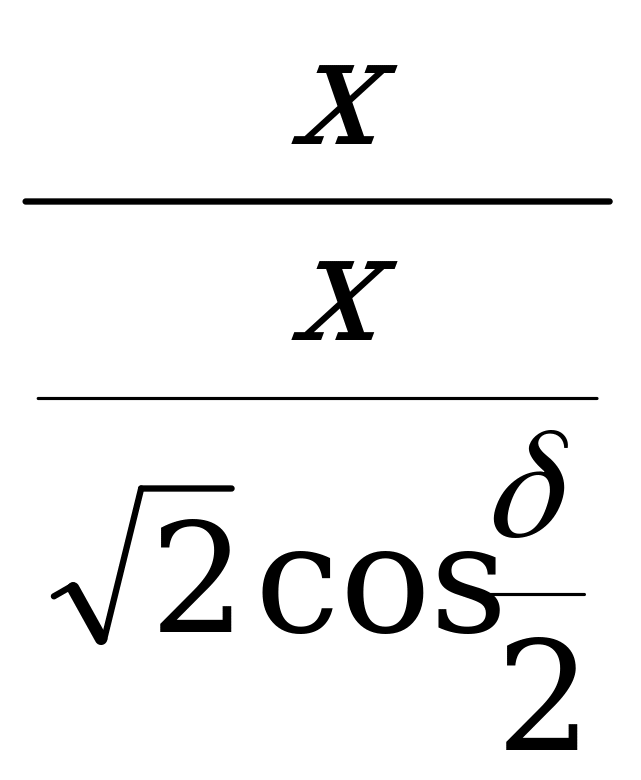 =
= 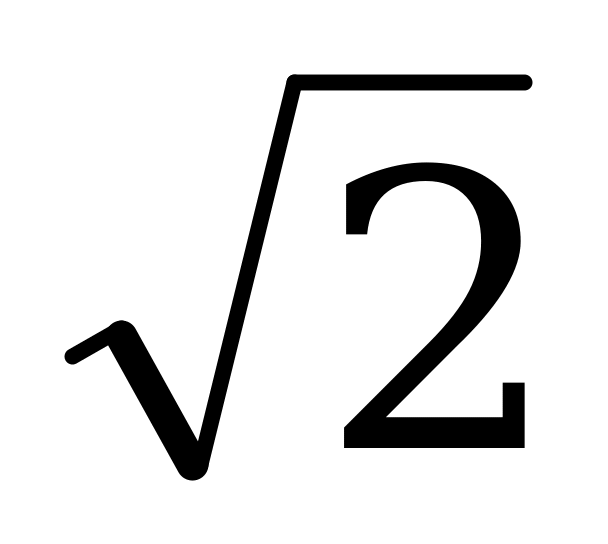 cos
cos 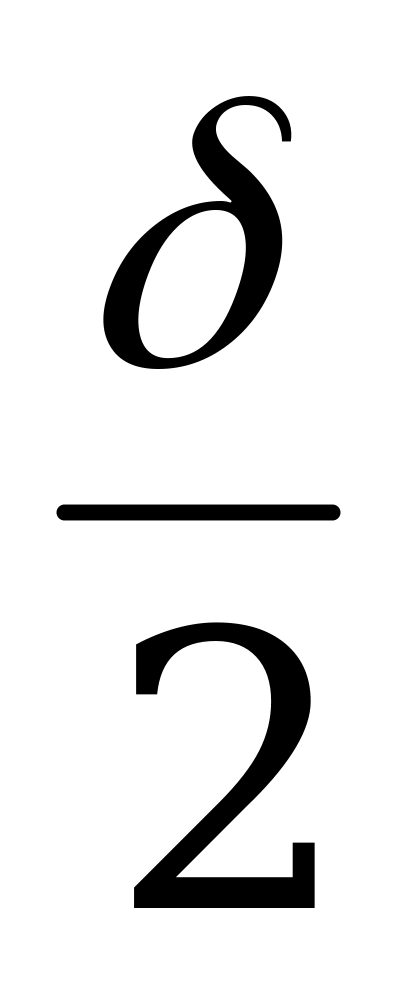 ,
,
sin  =
= 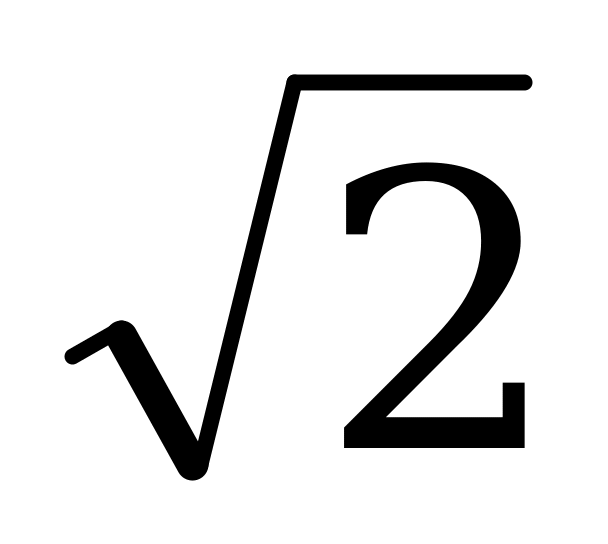 cos
cos 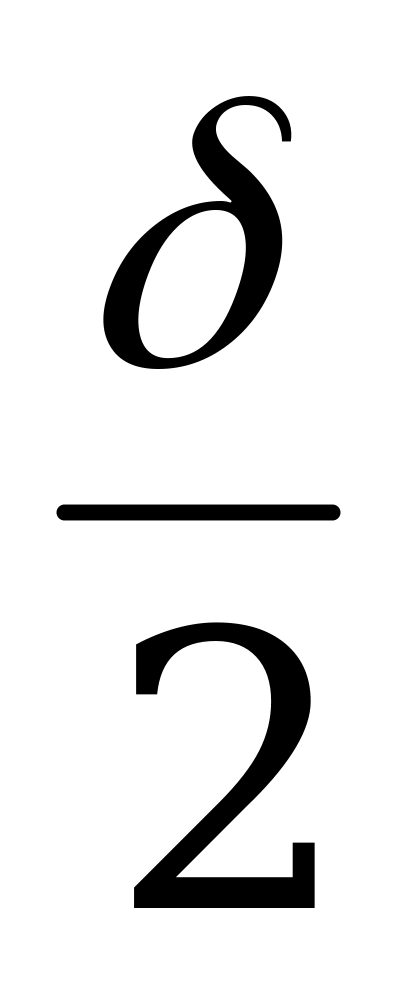 . (VI)
. (VI)
В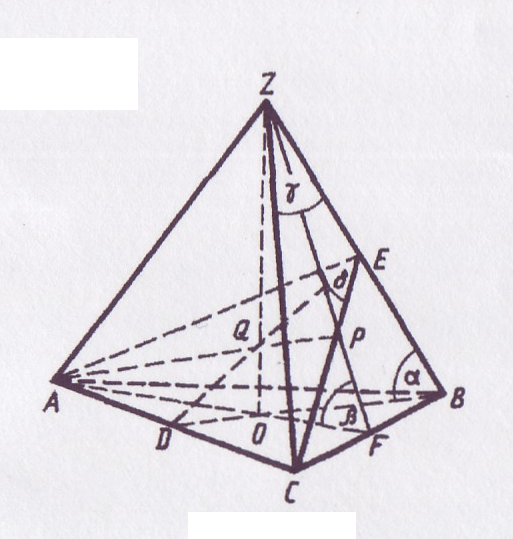 ывод формул перехода для правильной треугольной пирамиды.
ывод формул перехода для правильной треугольной пирамиды.
В правильной треугольной пирамиде  ZFO – линейный угол при основании пирамиды. Описание построения
ZFO – линейный угол при основании пирамиды. Описание построения  AEC – линейного угла двугранного угла при боковом ребре ZB – опускаем, поскольку оно аналогично описанию соответствующего угла в правильной четырёхугольной пирамиде, приведённому выше. Из рисунка видно, что АР – линия пересечения плоскостей AZF и AEC. Аналогично тому, как было сделано для правильной четырёхугольной пирамиды, доказывается, что АР
AEC – линейного угла двугранного угла при боковом ребре ZB – опускаем, поскольку оно аналогично описанию соответствующего угла в правильной четырёхугольной пирамиде, приведённому выше. Из рисунка видно, что АР – линия пересечения плоскостей AZF и AEC. Аналогично тому, как было сделано для правильной четырёхугольной пирамиды, доказывается, что АР 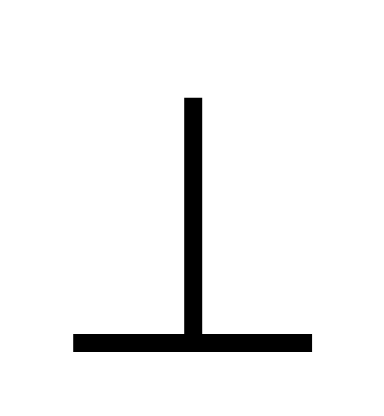 пл.ZBC. Следовательно, треугольники АРС и APF – прямоугольные и
пл.ZBC. Следовательно, треугольники АРС и APF – прямоугольные и  САР =
САР = 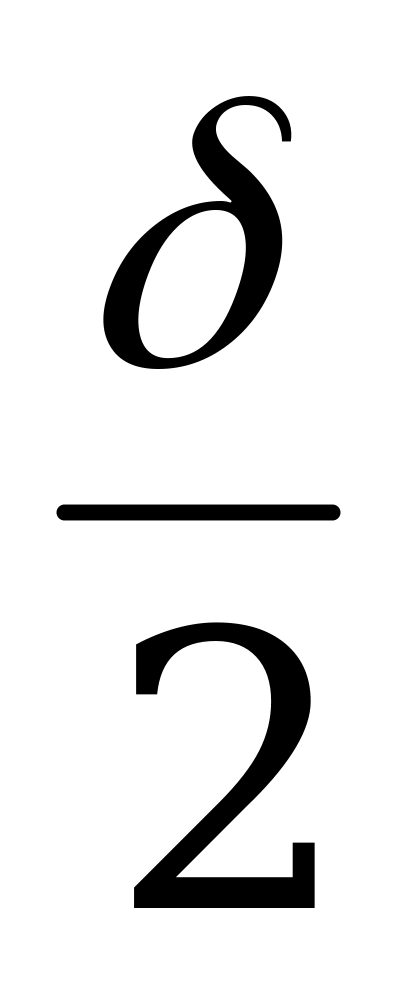 .
.
Для обозначения величин основных углов в правильной треугольной пирамиде употребим те же буквы, которыми обозначались величины этих углов в правильной четырёхугольной пирамиде:  ,
,  ,
, 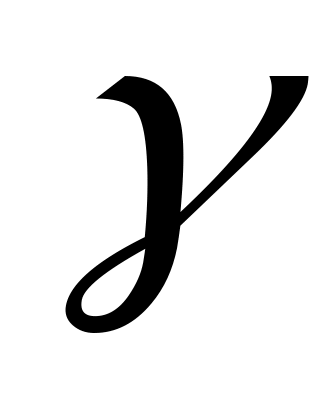 и
и 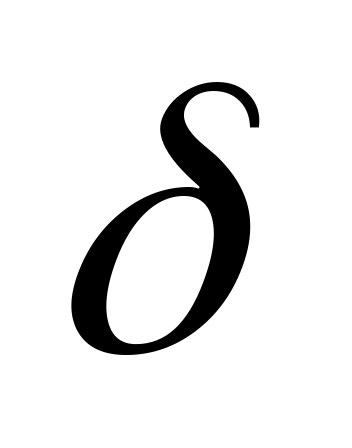 .
.
Перейдём к выводу формулы перехода:
а) от к
к  .
.
Положим ZO = x.
Из  ZOF
ZOF
OF = x ctg  .
.
Из  OFB
OFB
OB = 2x ctg  .
.
Из  ZOB
ZOB
tg  =
= 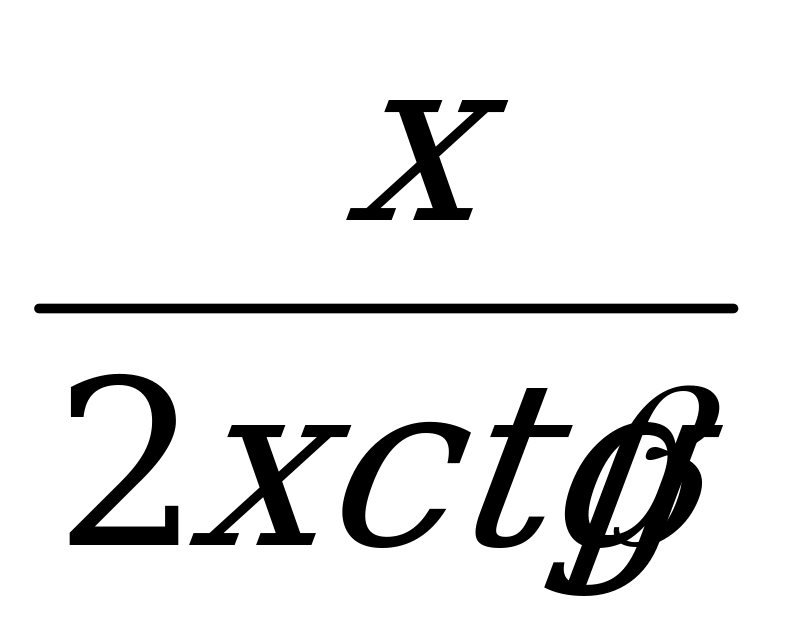 =
= 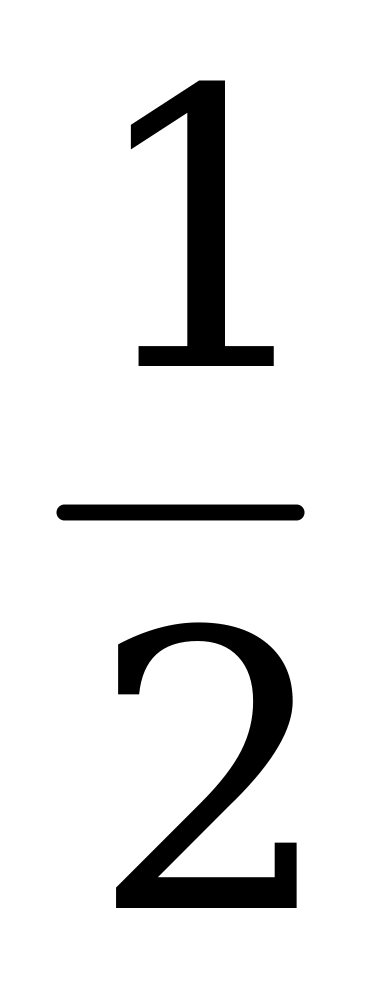 tg
tg  ,
,
tg  =
= 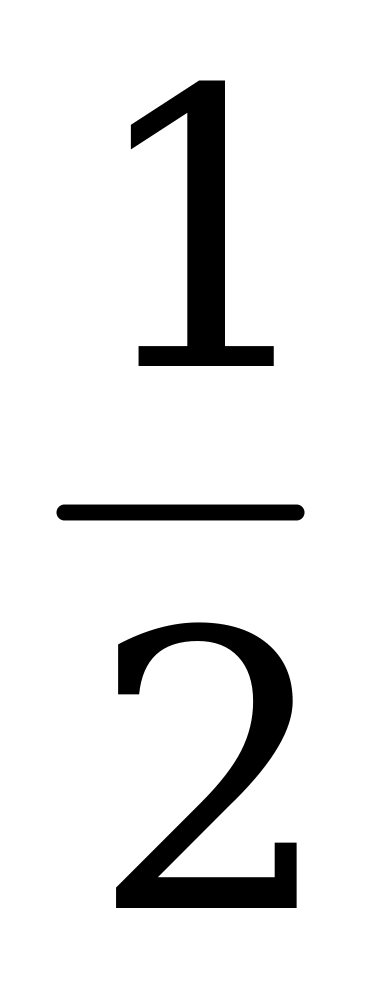 tg
tg  . (VII)
. (VII)
Решение задачи аналогично решению задачи для правильной четырёхугольной пирамиды.
б) cos =
= 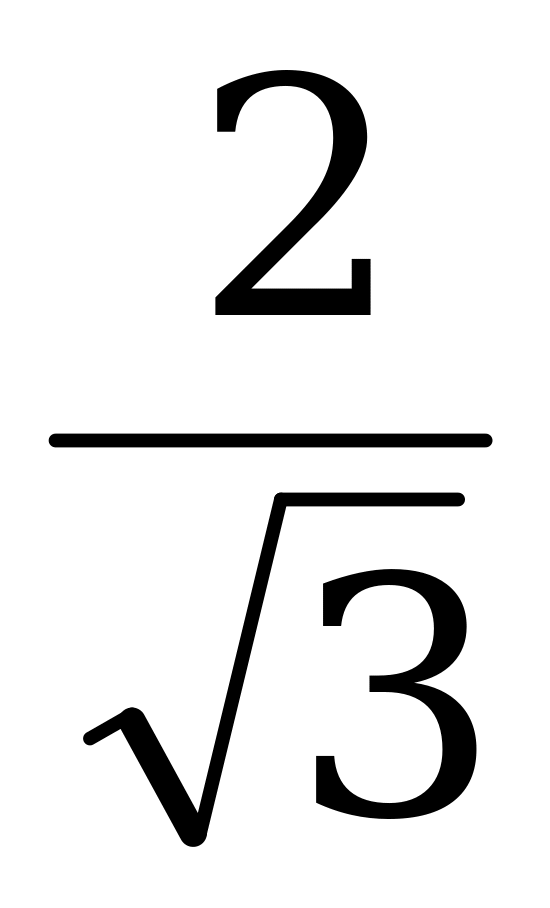 sin
sin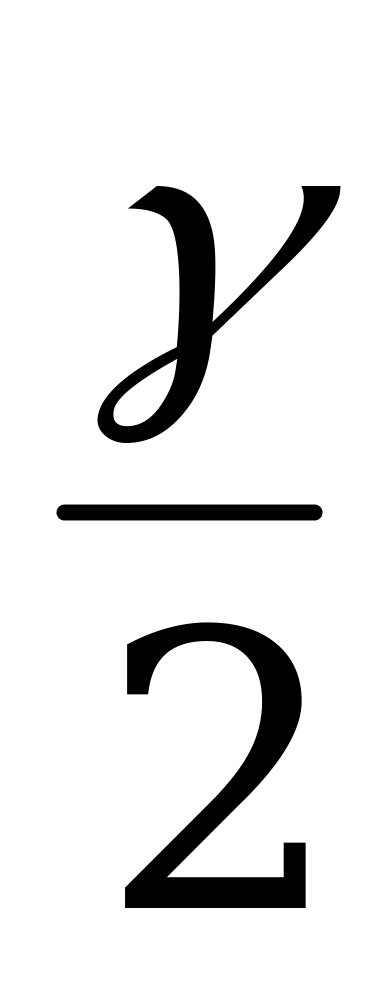 ; (VIII)
; (VIII)
в) sin =
= 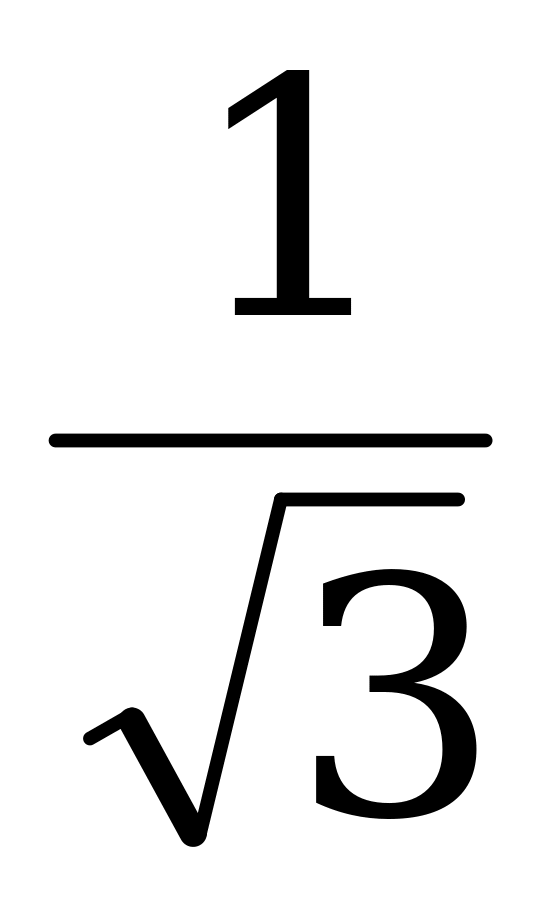 ctg
ctg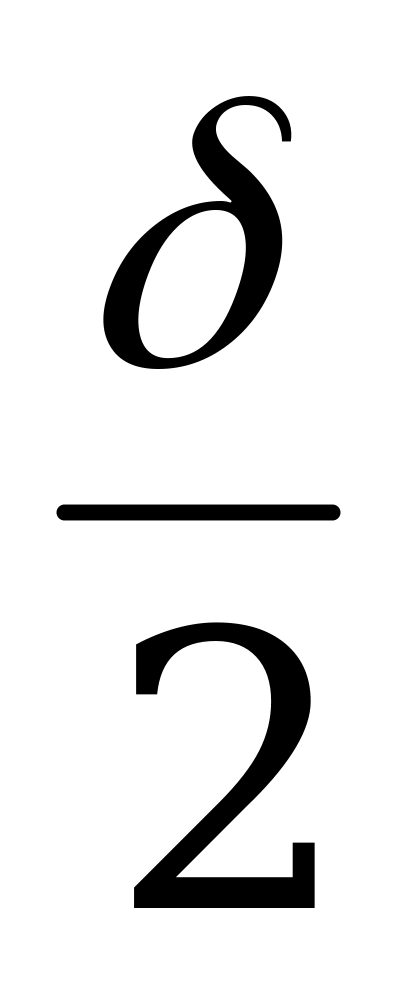 ; (IX)
; (IX)
г) tg = 2tg
= 2tg ; (X)
; (X)
д) cos =
= 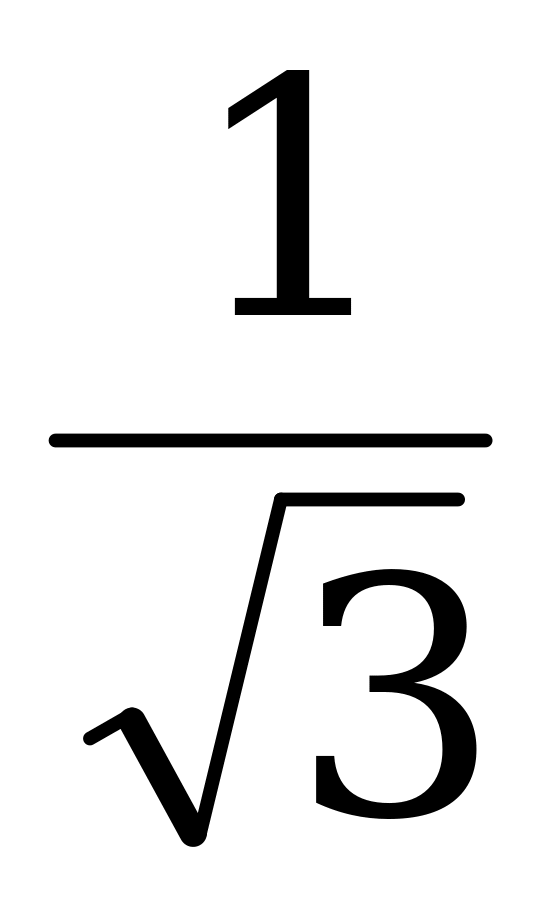 tg
tg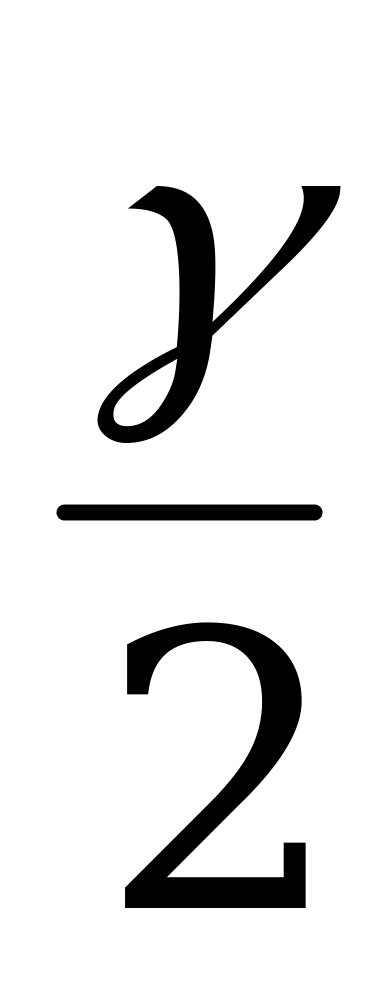 ; (XI)
; (XI)
е) sin =
= 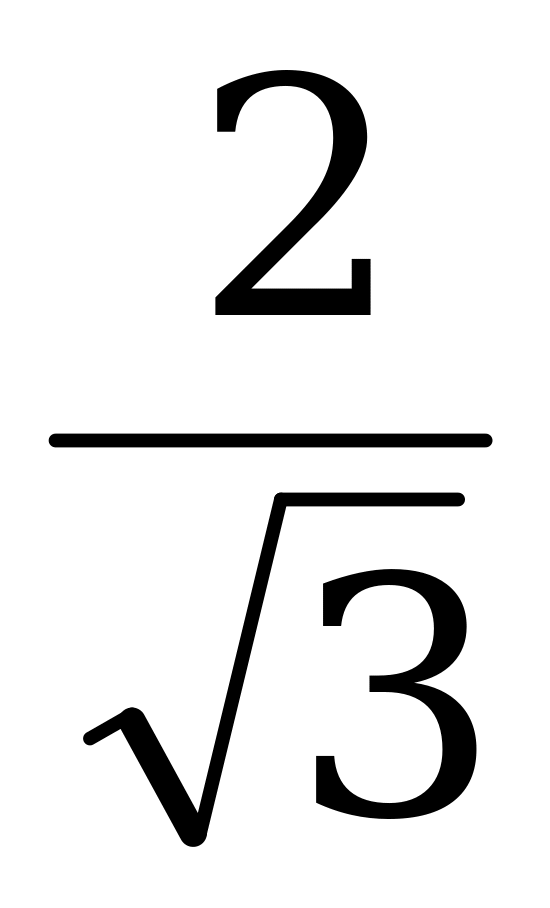 cos
cos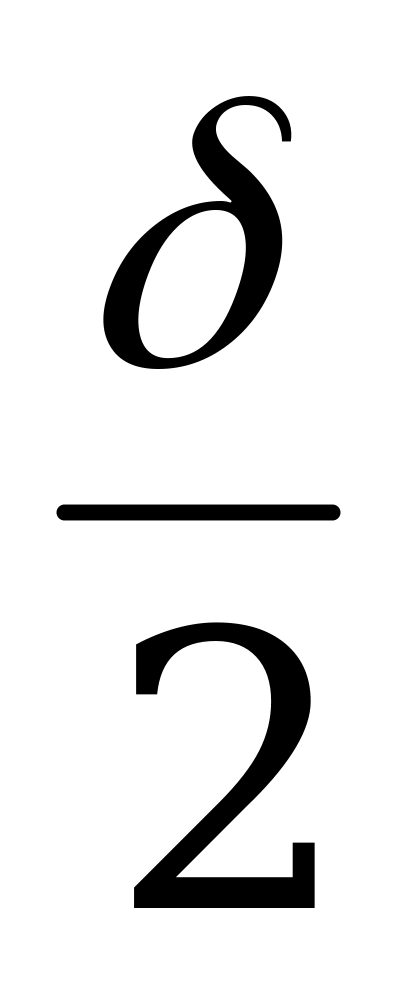 . (XII)
. (XII)
 Формулы перехода для правильной n-угольной пирамиды.
Формулы перехода для правильной n-угольной пирамиды.
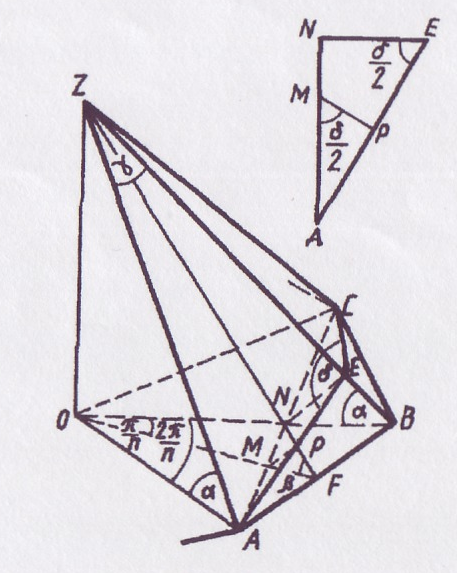
На рисунке изображена часть правильной n-угольной пирамиды ZFDC… . Величины основных углов обозначены, как и ранее, буквами  ,
,  ,
, 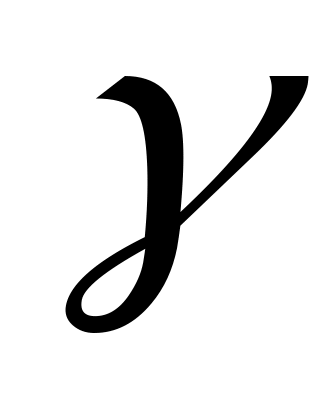 и
и 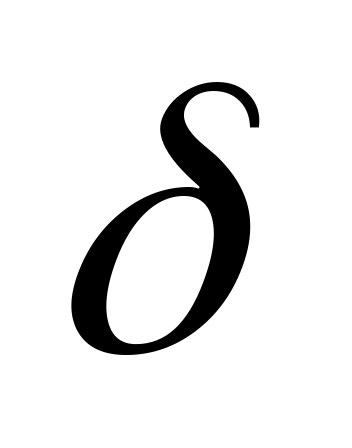 .
.  ZFO – линейный угол двугранного угла при ребре основания АВ:
ZFO – линейный угол двугранного угла при ребре основания АВ:  ZFO =
ZFO = . Построение
. Построение  АЕС – линейного угла двугранного угла при боковом ребре ZB, как и в случае правильной треугольной пирамиды, опускаем.
АЕС – линейного угла двугранного угла при боковом ребре ZB, как и в случае правильной треугольной пирамиды, опускаем.
ВО – биссектриса  АВС и поэтому в равнобедренном треугольнике АВС отрезок BN – биссектриса, медиана и высота. Следовательно, N – середина АС. Очевидно, что АЕ = ЕС и поэтому треугольник АЕС равнобедренный и EN – его медиана, биссектриса и высота. Поэтому
АВС и поэтому в равнобедренном треугольнике АВС отрезок BN – биссектриса, медиана и высота. Следовательно, N – середина АС. Очевидно, что АЕ = ЕС и поэтому треугольник АЕС равнобедренный и EN – его медиана, биссектриса и высота. Поэтому  AEN =
AEN = 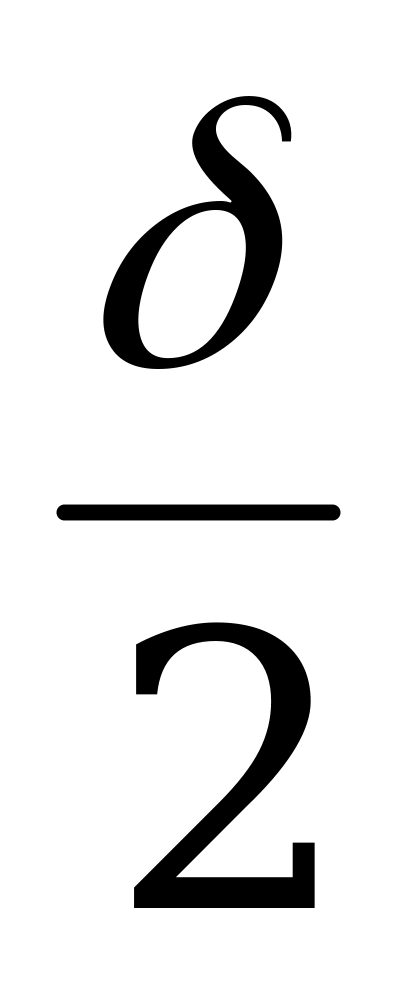 .
.
Отрезок МР принадлежит линии пересечения плоскостей линейных углов ZFO b AEC, и поэтому, как уже упоминалось выше при рассмотрении правильной четырёхугольной пирамиды, МР 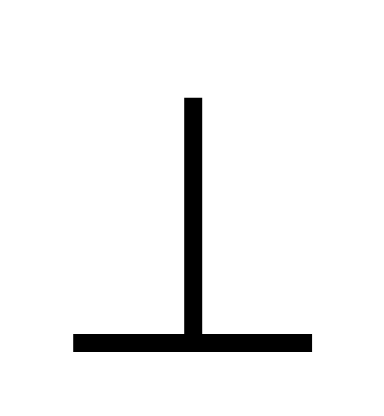 пл.ZAB. Из этого непосредственно следует, что треугольники АМР и МPF прямоугольные и
пл.ZAB. Из этого непосредственно следует, что треугольники АМР и МPF прямоугольные и  АМР =
АМР = АЕN =
АЕN =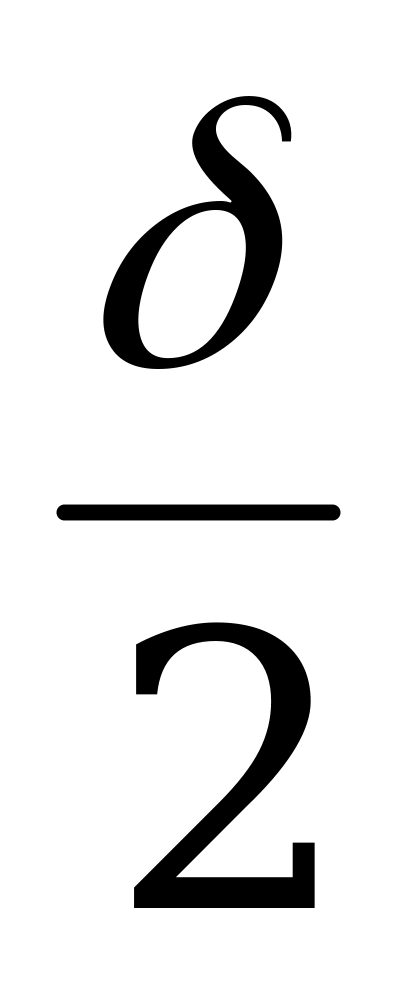 .
.
Поскольку ВN – высота треугольника АВС, то  ВАN =
ВАN = BOF =
BOF =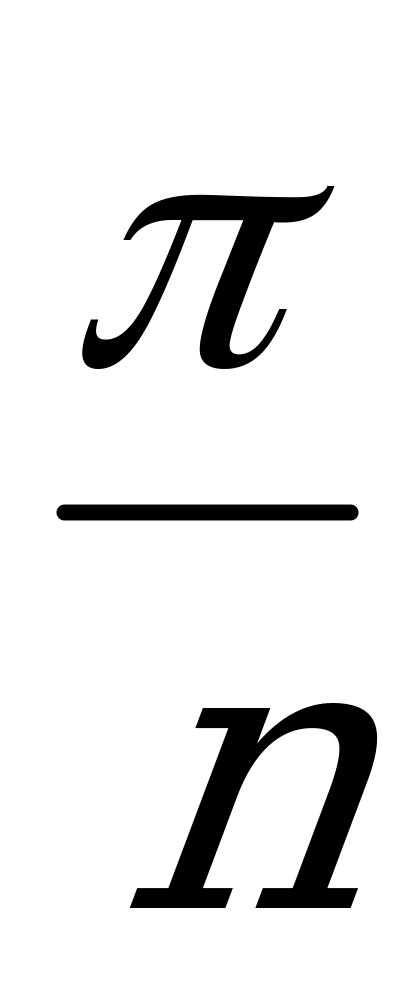 как острые углы с соответственно перпендикулярными сторонами.
как острые углы с соответственно перпендикулярными сторонами.
Из шести формул перехода для правильной n-угольной пирамиды первые пять мы приведём без доказательств, поскольку их вывод аналогичен выводу соответствующих формул перехода правильных четырёхугольной и треугольной пирамид, и докажем лишь одну: от 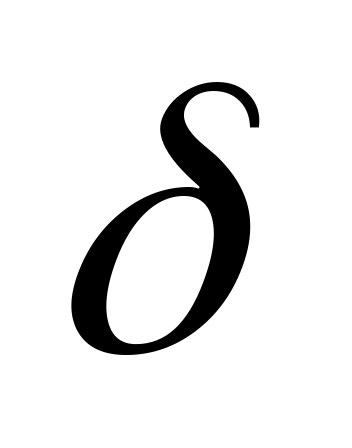 к
к  .
.
а) tg = tg
= tg cos
cos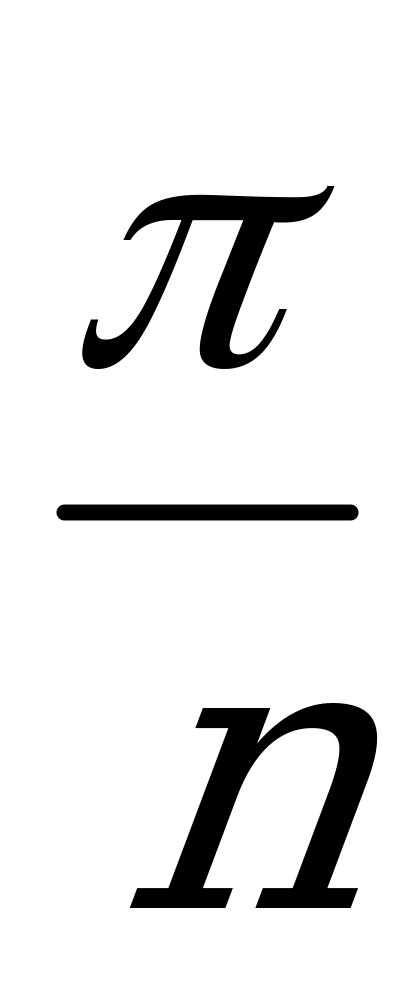 ; (XIII)
; (XIII)
б) cos =
=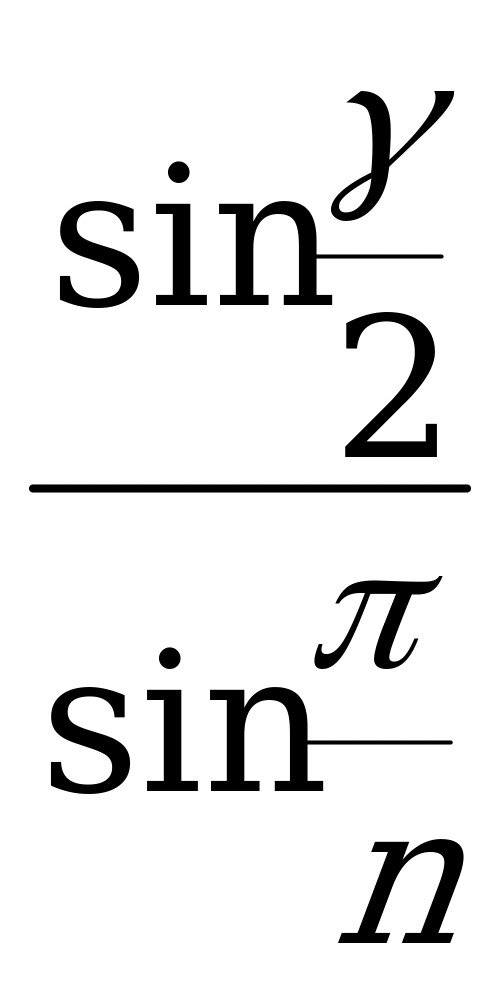 ; (XIV)
; (XIV)
в) sin = ctg
= ctg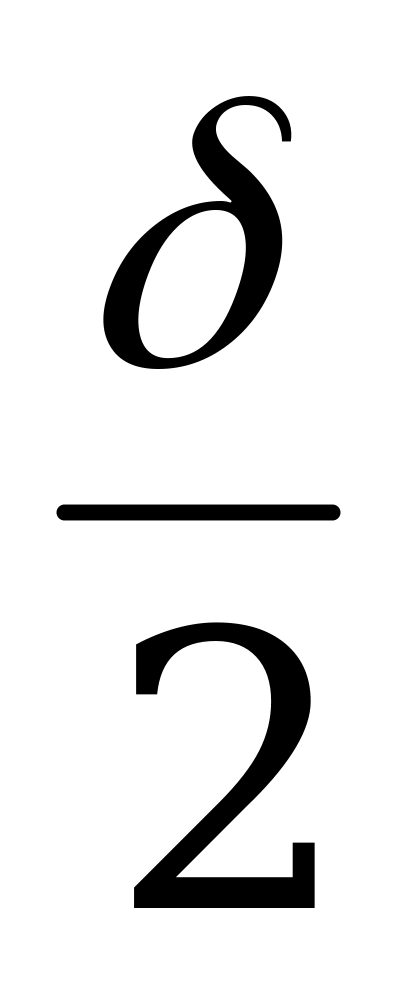 ctg
ctg
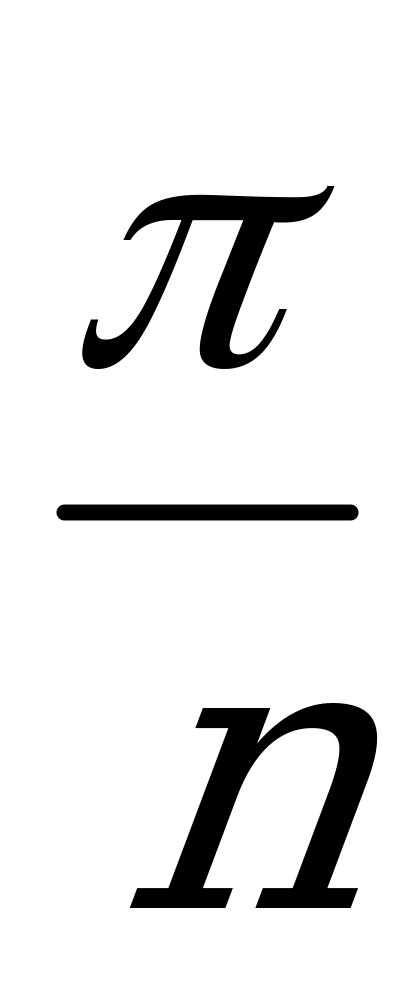 ; (XV)
; (XV)
г) tg =
= 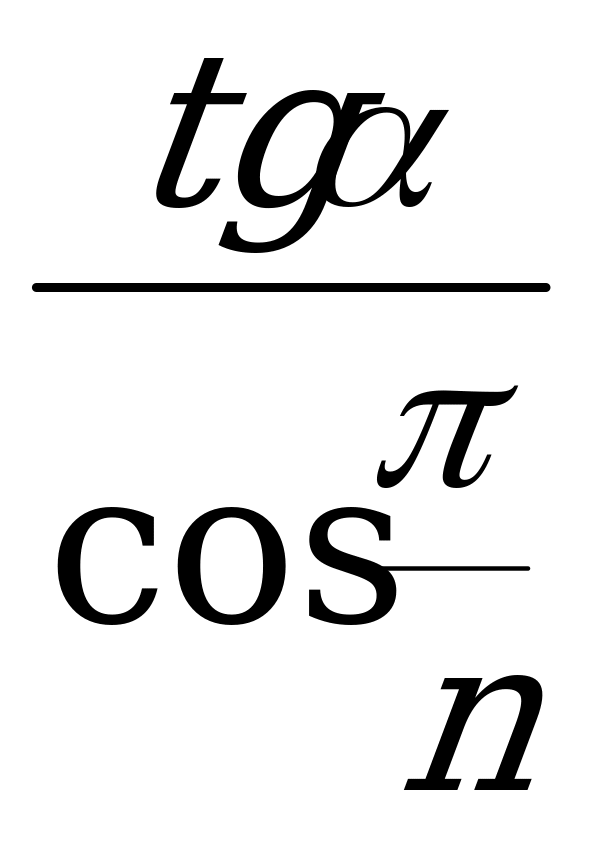 ; (XVI)
; (XVI)
д) cos = tg
= tg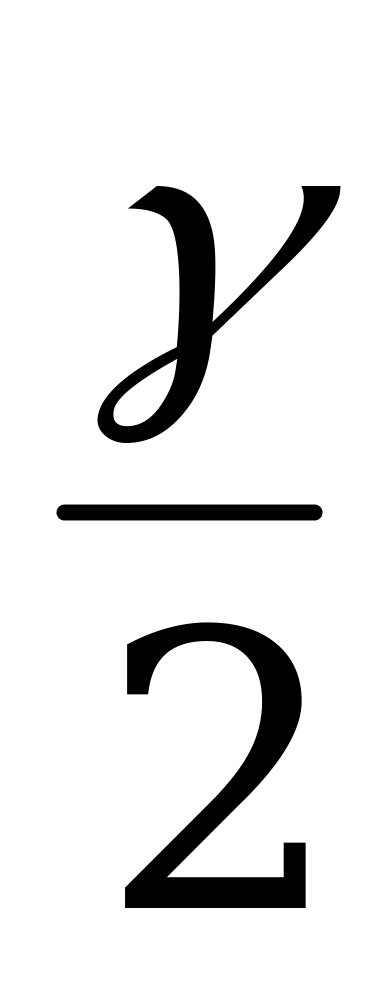 ctg
ctg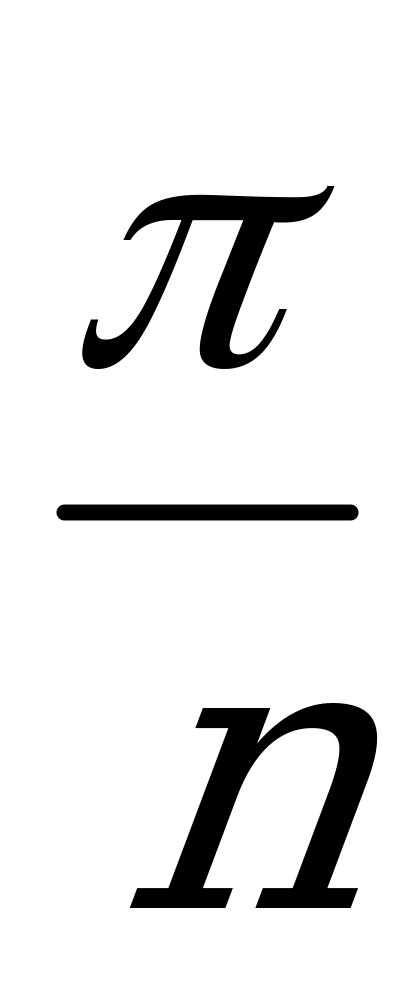 ; (XVII)
; (XVII)
е) от 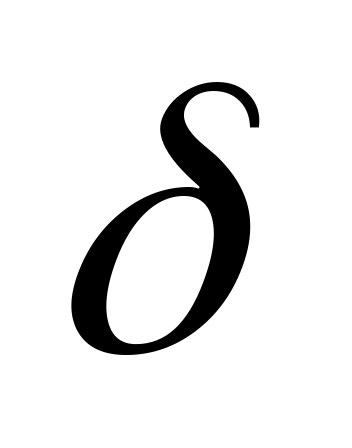 к
к  .
.
Положим MP = x.
Из  АМР
АМР
АМ = 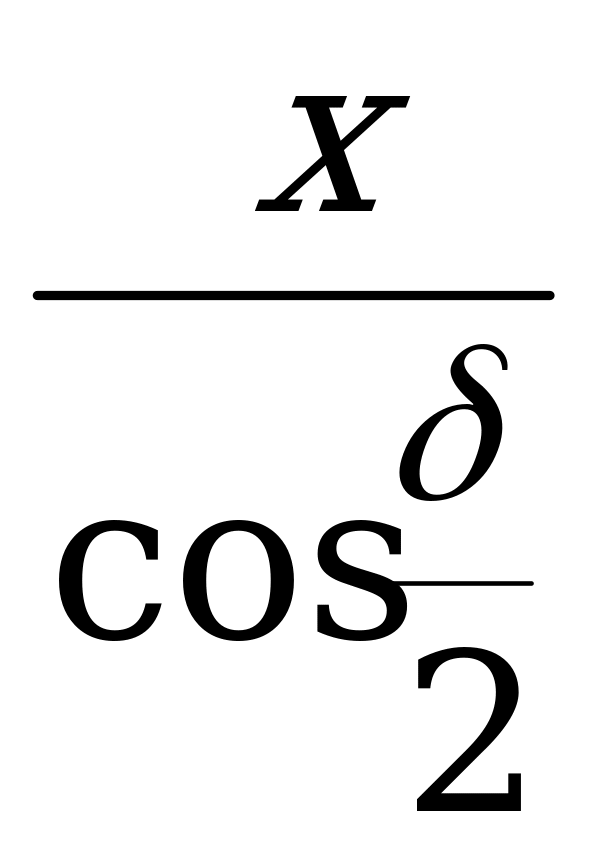 .
.
Из  AMF
AMF
MF = 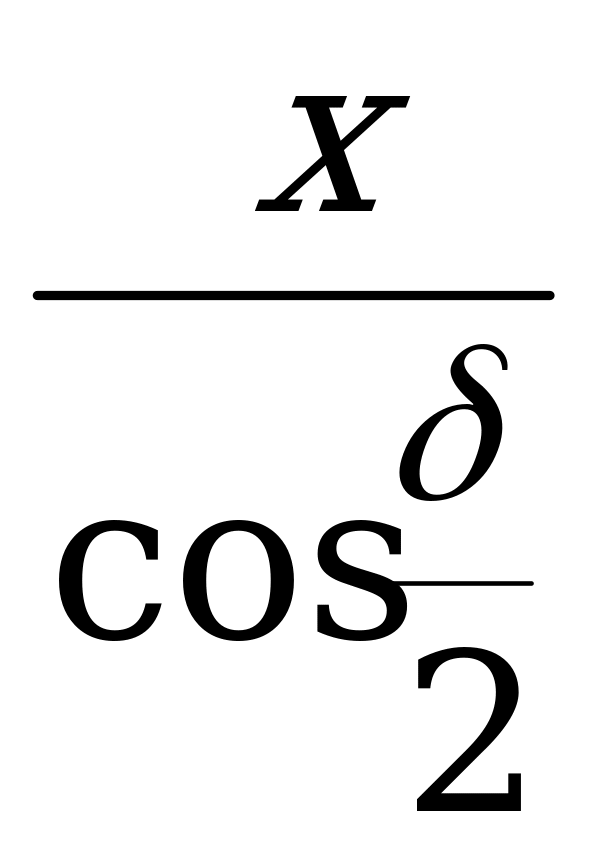 sin
sin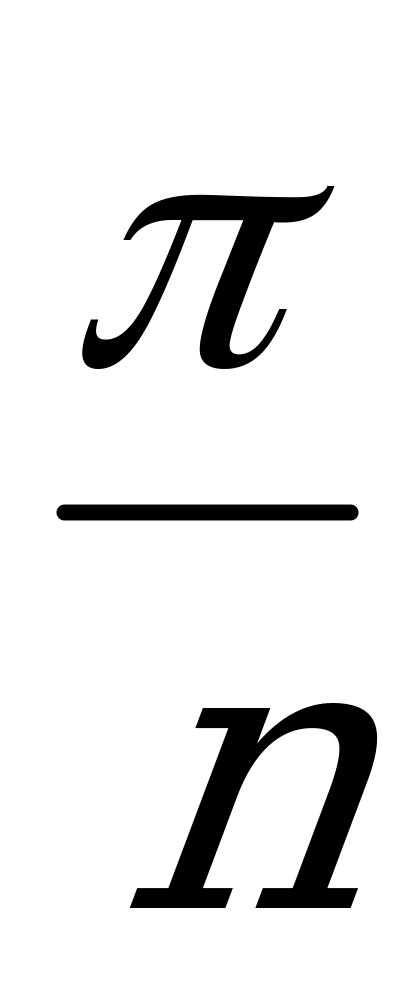 .
.
Из  MPF
MPF
sin =
= 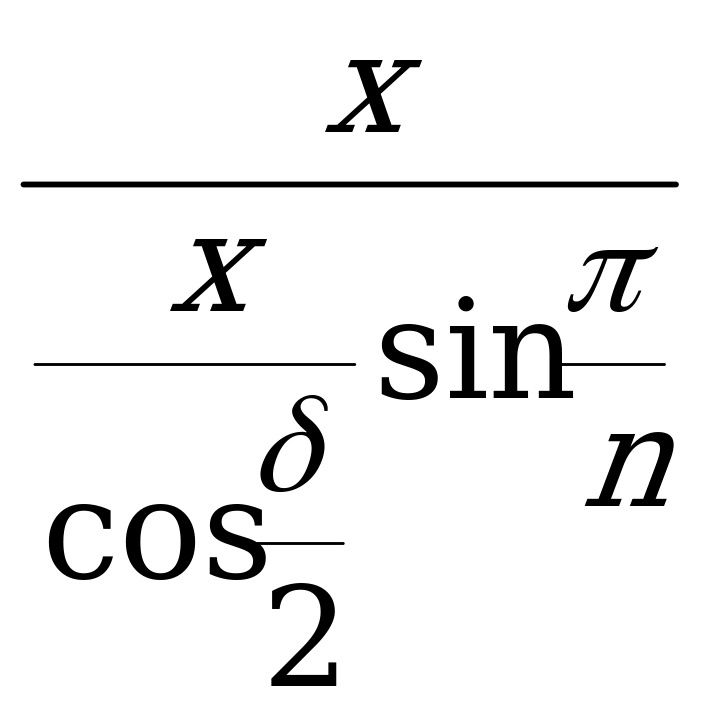 =
= 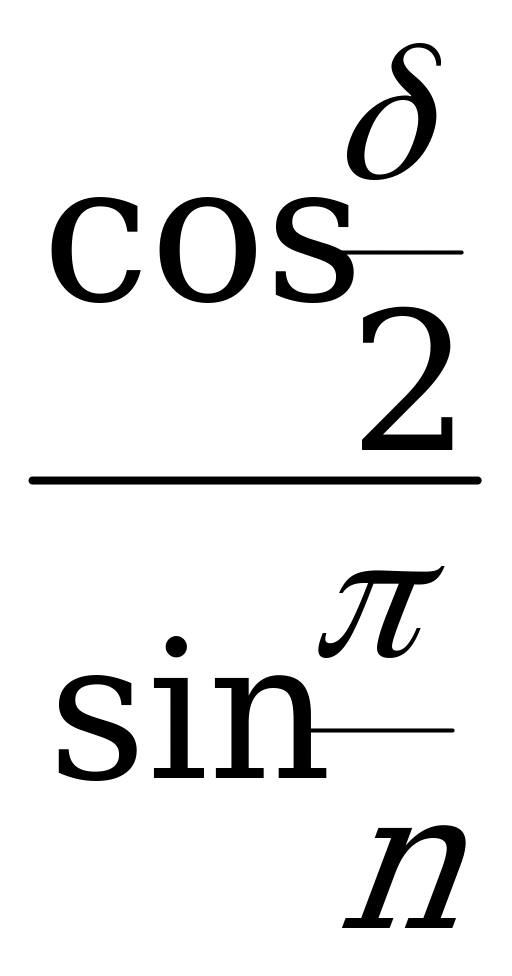 ,
,
sin =
= 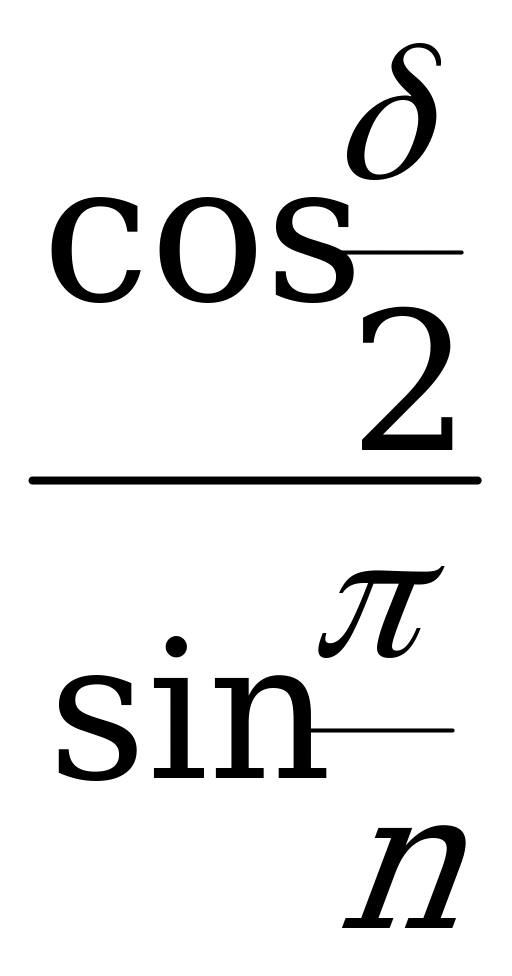 . (XVIII)
. (XVIII)
Формулы перехода включены в таблицу. Они эффективно используются при решении многих геометрических задач, но запоминать их, разумеется, не нужно. Достаточно знать идею их вывода.
| Переход/n | 3 | 4 | n |
| От  к к  | 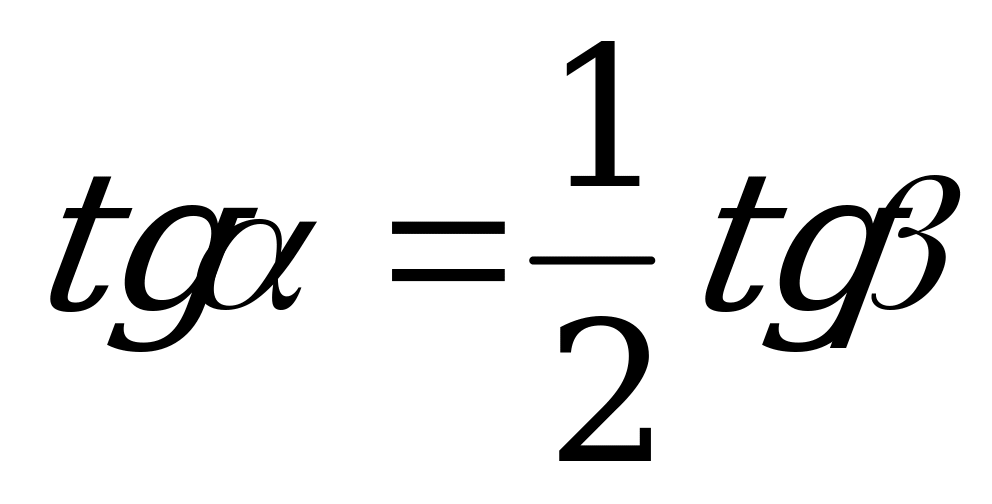
| 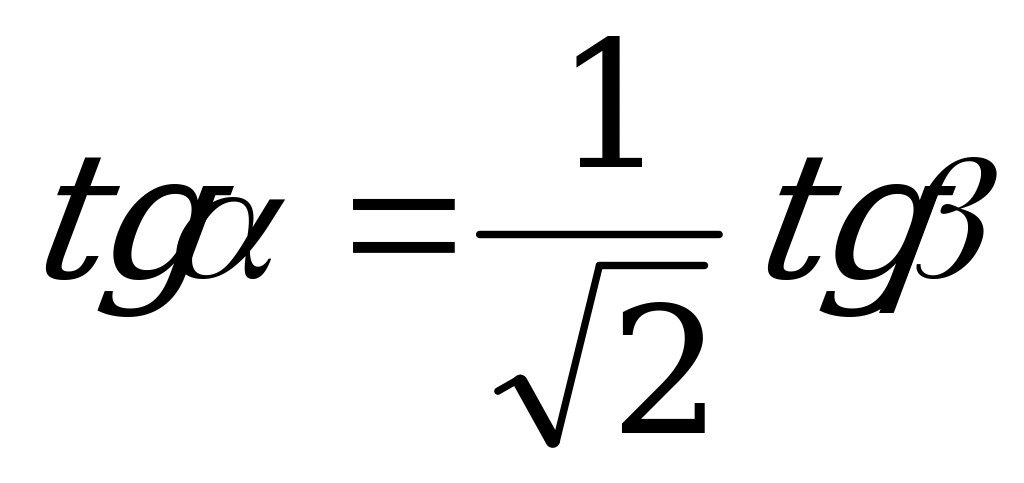
| 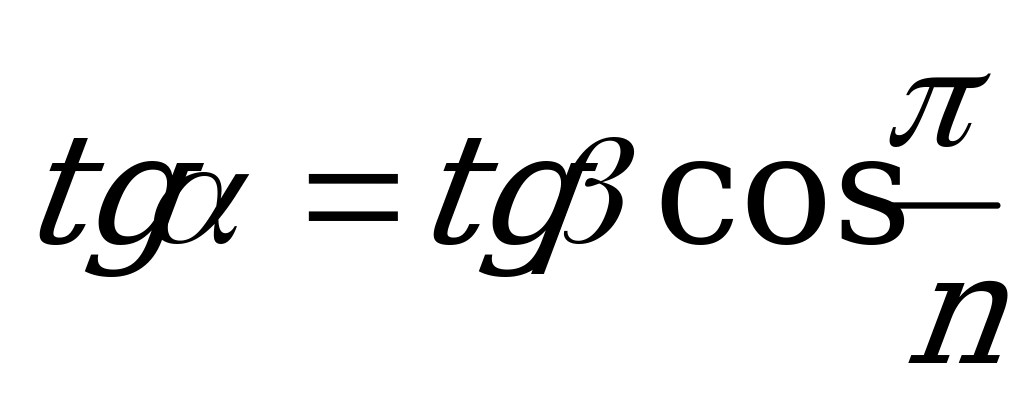
|
| От 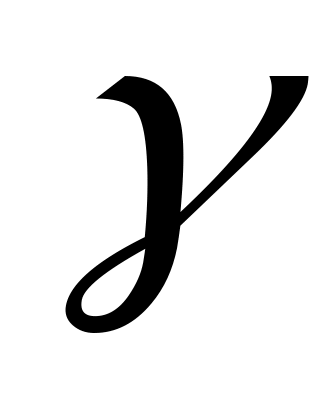 к к  | 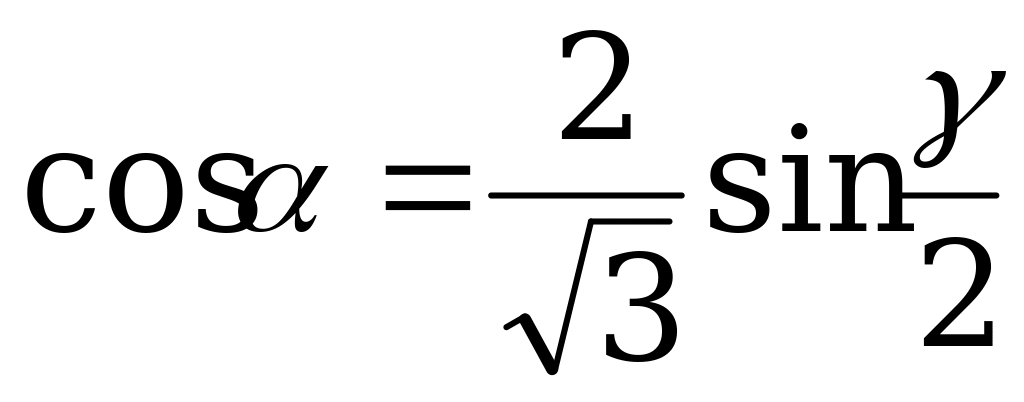
| 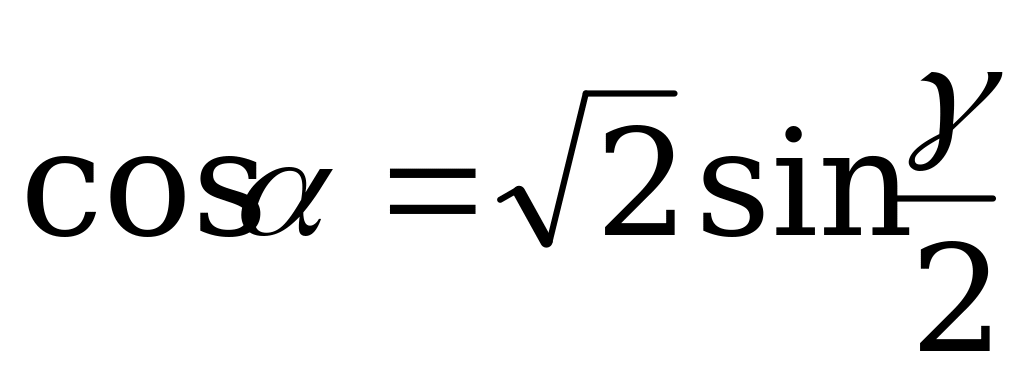
| 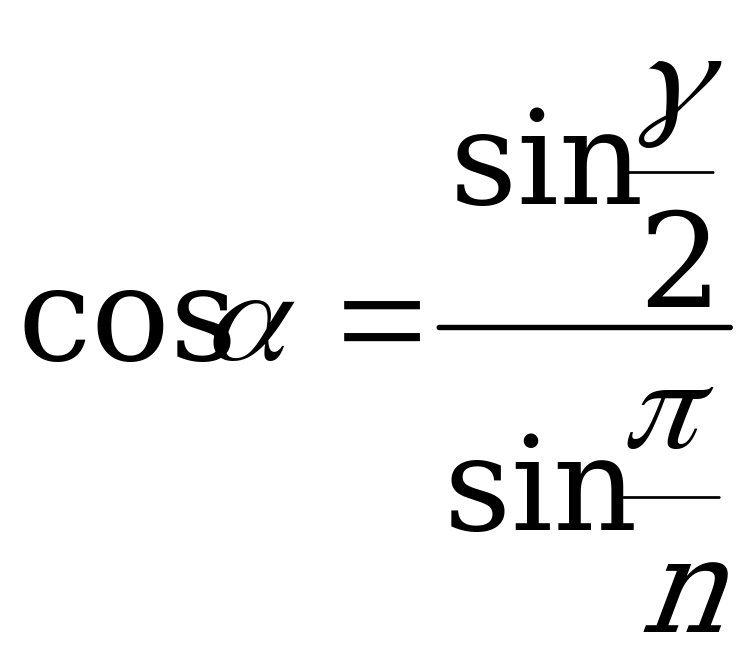
|
| От 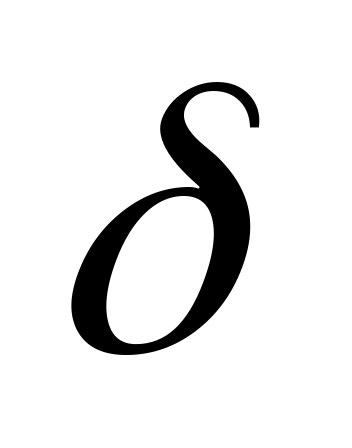 к к  | 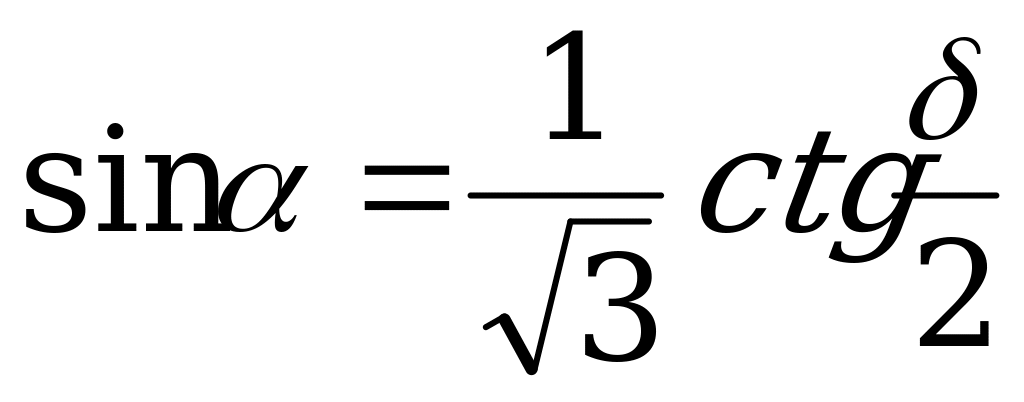
| 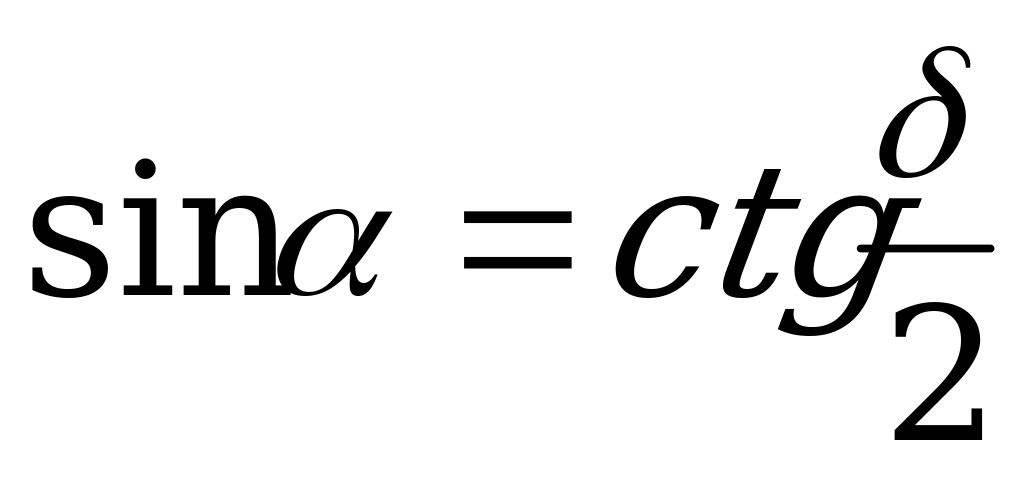
| 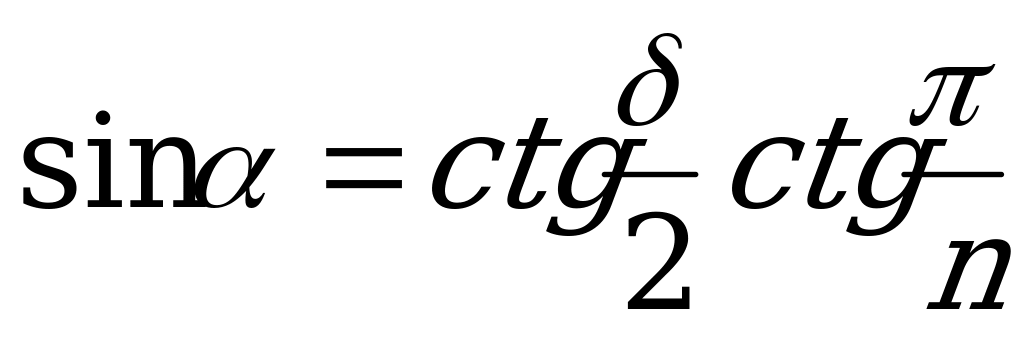
|
| От  к к  | 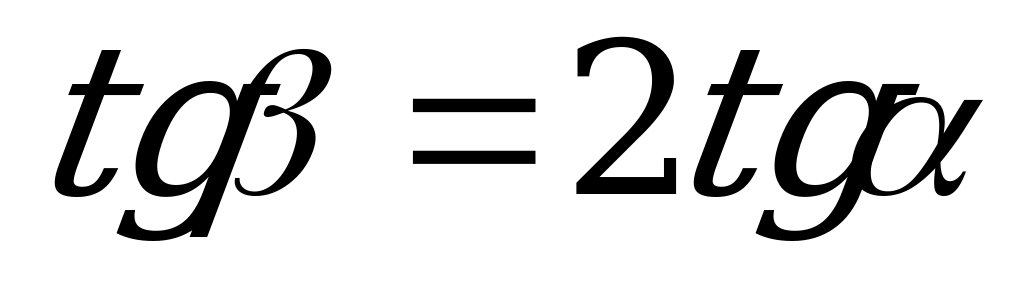
| 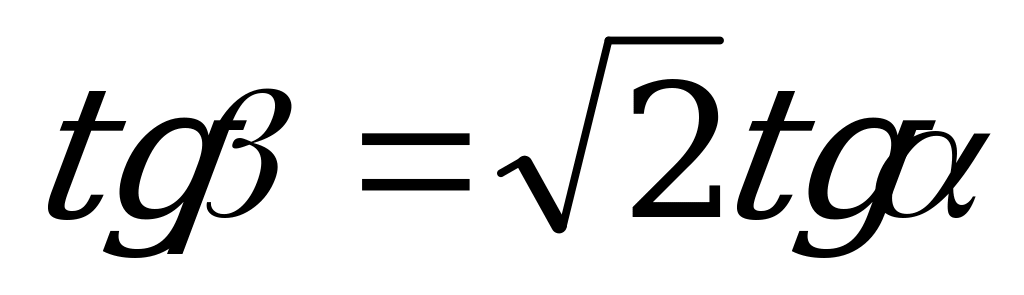
| 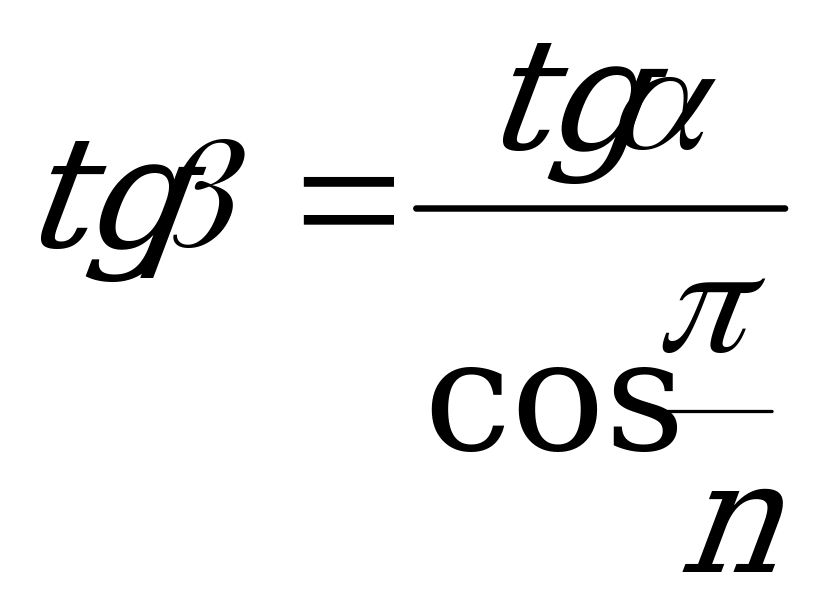
|
| От 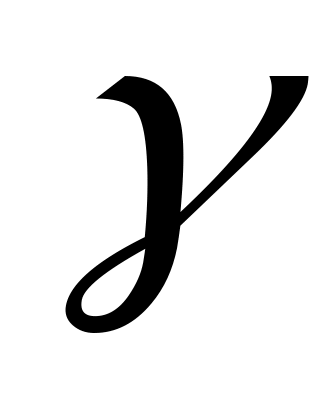 к к  | 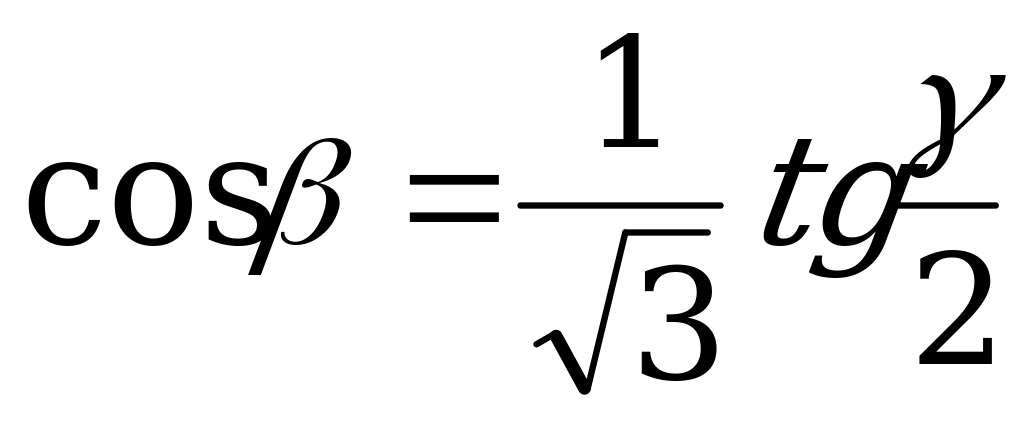
| 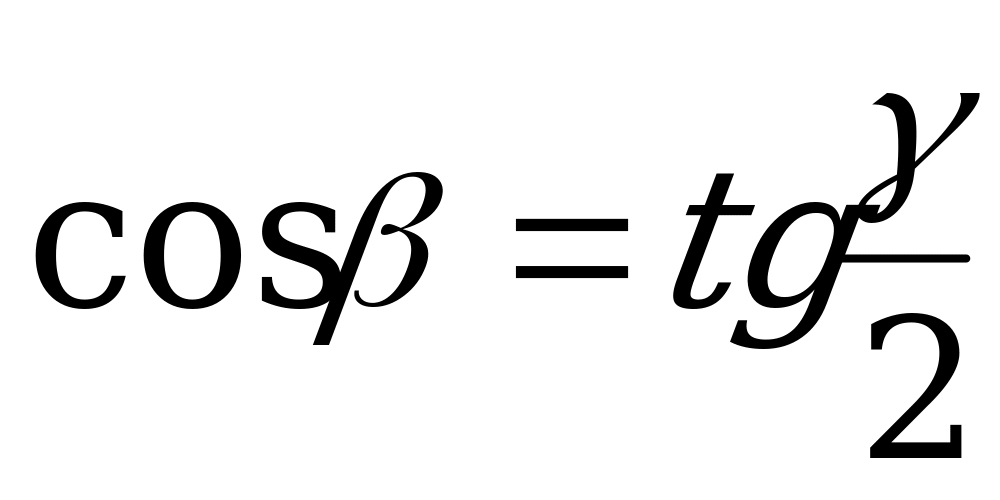
| 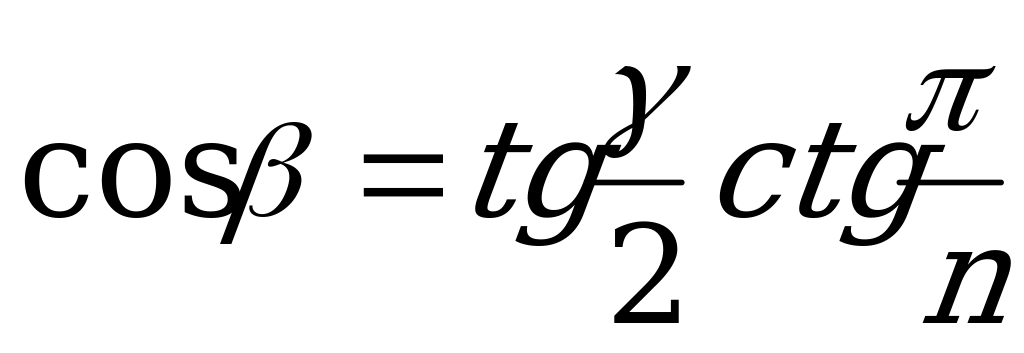
|
| От 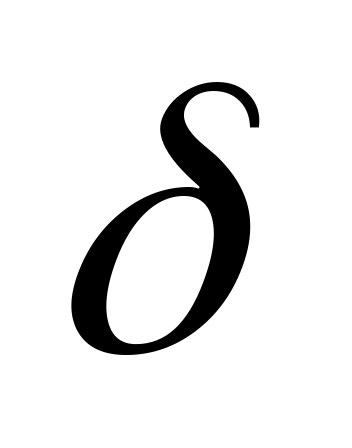 к к  | 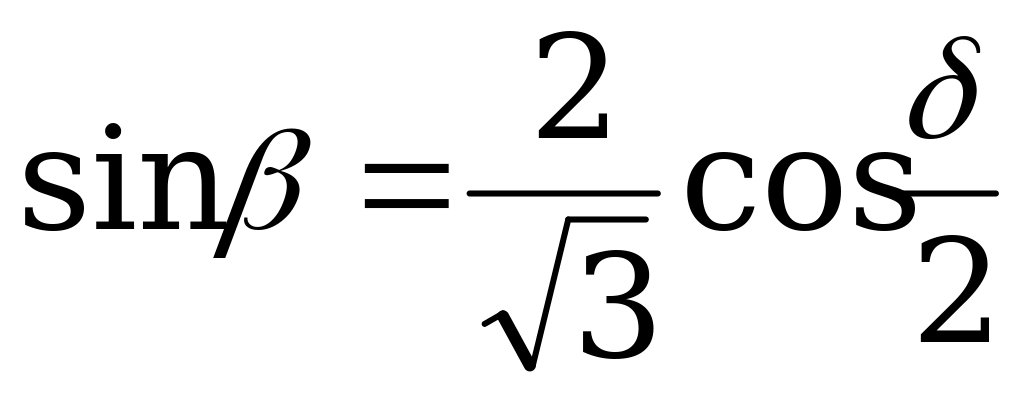
| 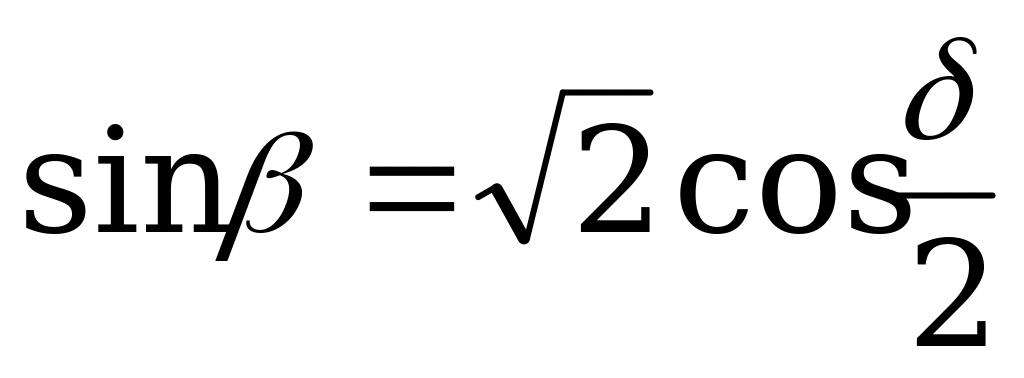
| 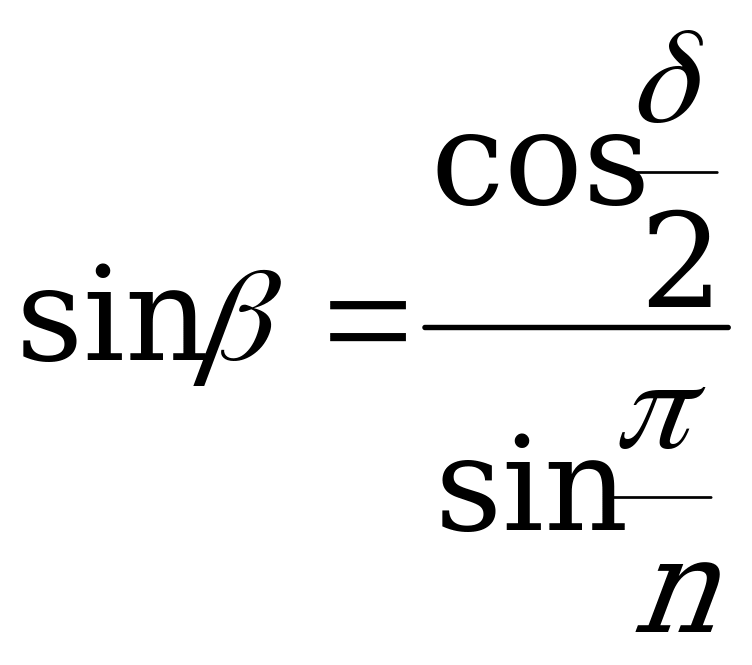
|
7








 Решение. Обозначим через x длину отрезка в правильной пирамиде, входящего как в прямоугольный треугольник, содержащий данный угол, так и в треугольник, содержащий искомый угол. Выразим далее через x и функции данного угла одну из двух других сторон в том треугольнике, который содержит искомый угол. Затем найдём функцию искомого угла.
Решение. Обозначим через x длину отрезка в правильной пирамиде, входящего как в прямоугольный треугольник, содержащий данный угол, так и в треугольник, содержащий искомый угол. Выразим далее через x и функции данного угла одну из двух других сторон в том треугольнике, который содержит искомый угол. Затем найдём функцию искомого угла.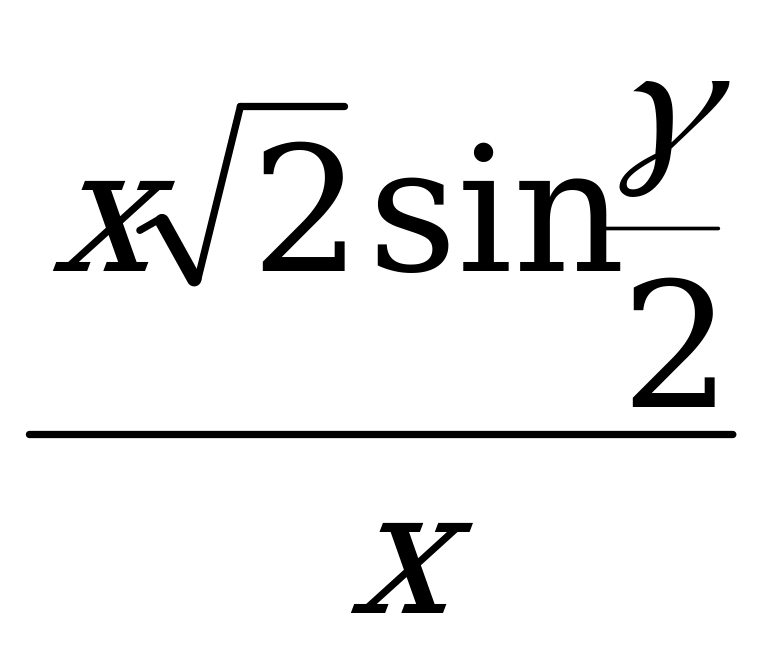 =
= 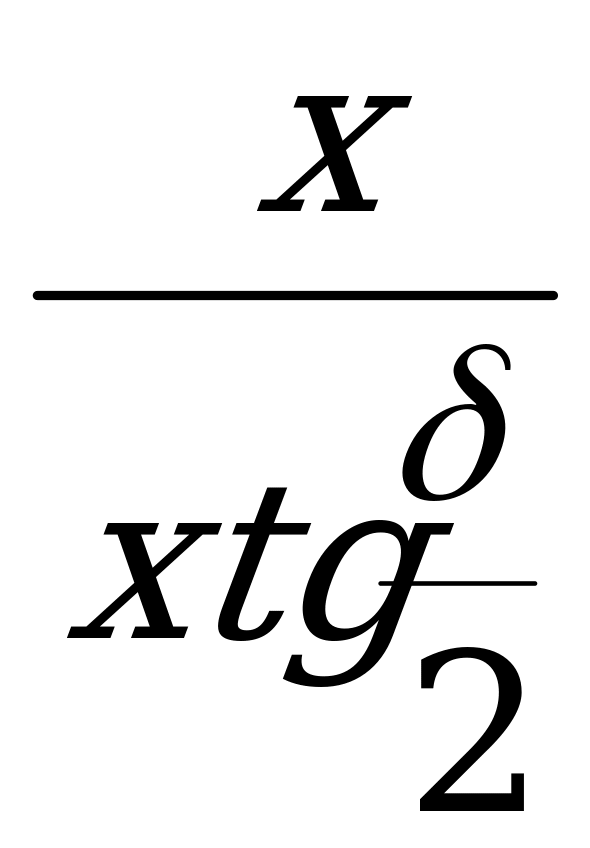 = ctg
= ctg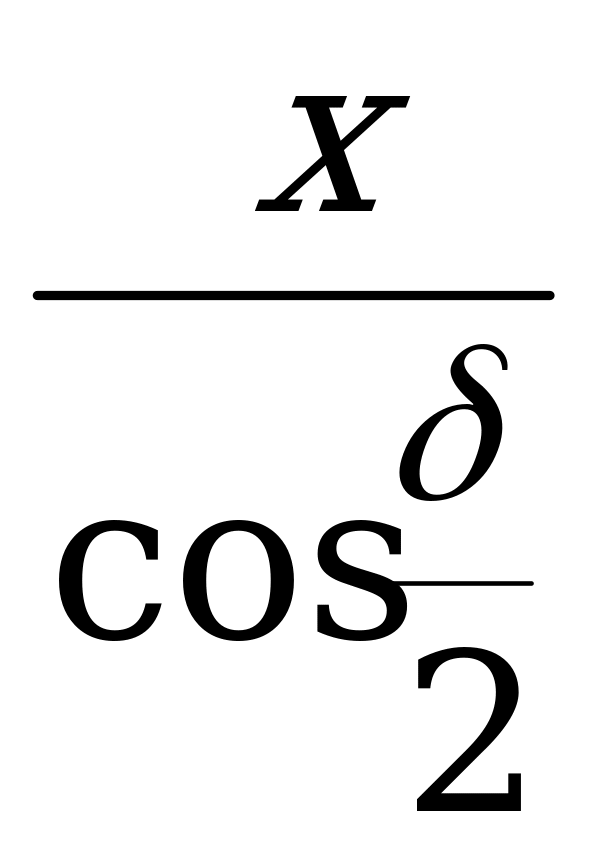 . Из
. Из 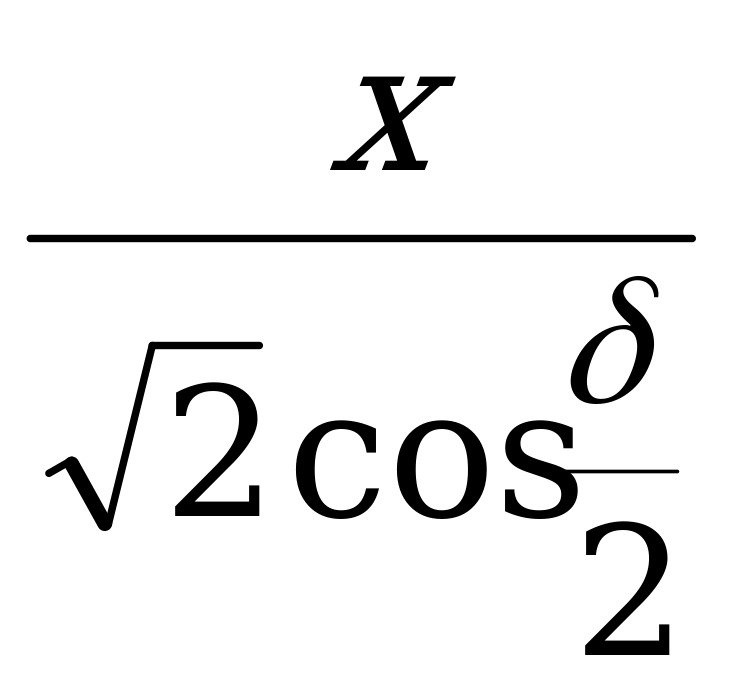 .
.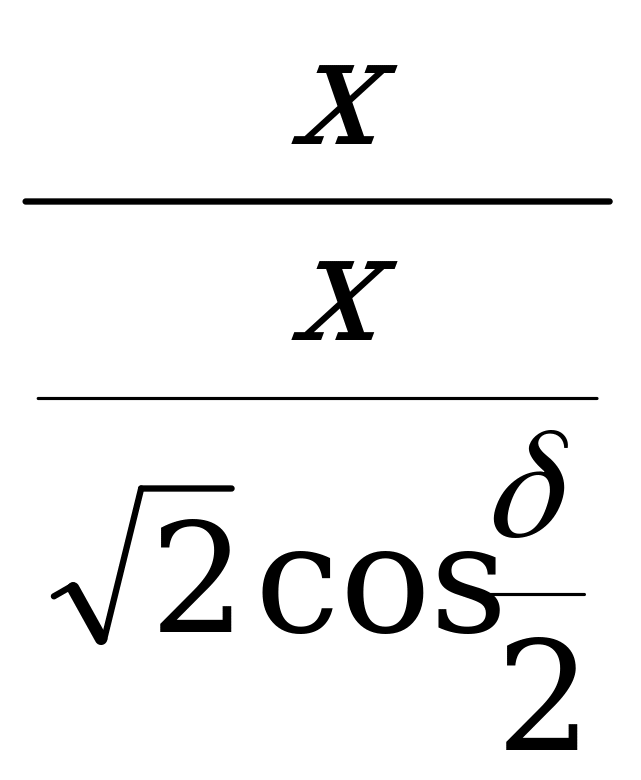 =
=  ывод формул перехода для правильной треугольной пирамиды.
ывод формул перехода для правильной треугольной пирамиды. Формулы перехода для правильной n-угольной пирамиды.
Формулы перехода для правильной n-угольной пирамиды.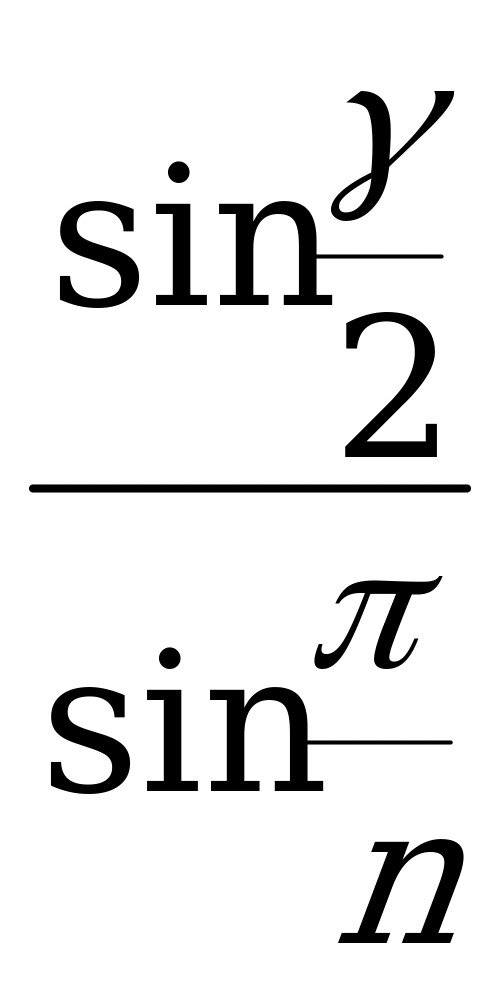 ; (XIV)
; (XIV)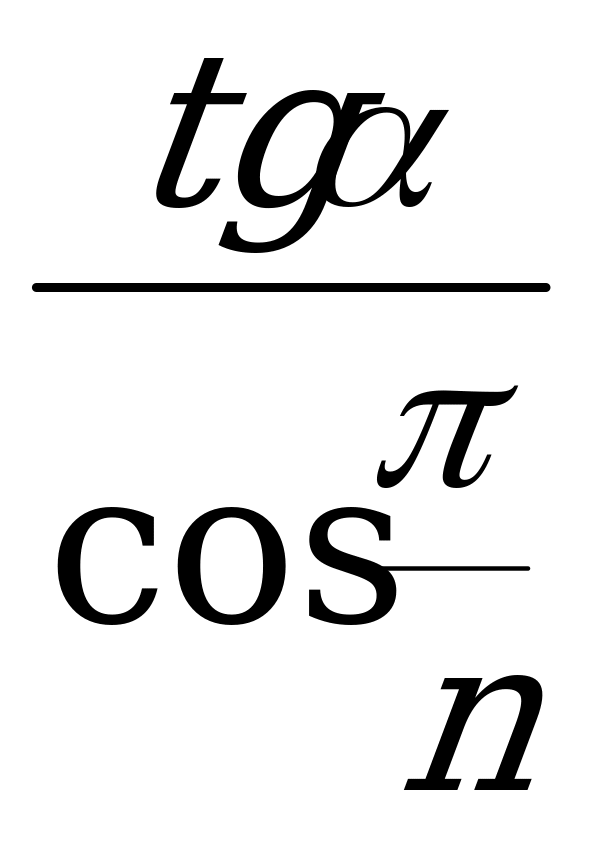 ; (XVI)
; (XVI)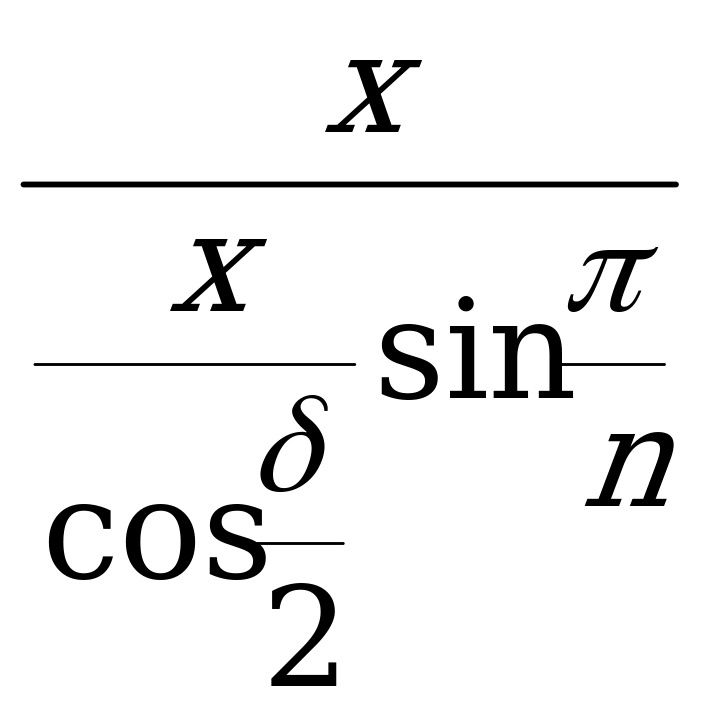 =
= 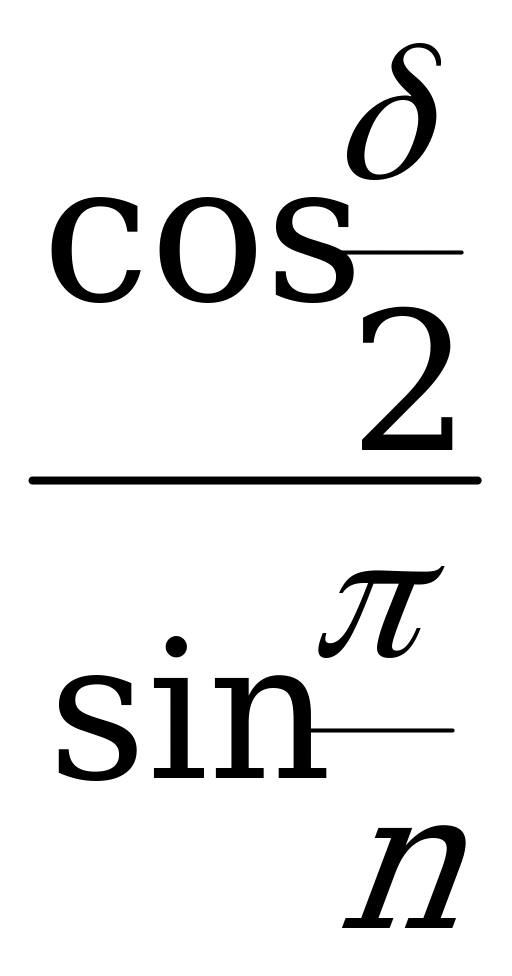 ,
,