"... и кругом только умные лица, потому что считаем в уме!"

Гомельская научно-практическая конференция учащихся по естественно-научным направлениям «Поиск»

ГУО «Движковская базовая школа Ельского района»

Учебно-исследовательская работа

«… и кругом только умные лица,

потому что считаем в уме!»

Учащейся 9 класса ГУО «Движковская базовая школа Ельского района»

Тимощенко Виктории

Научный руководитель – учитель математики ГУО «Движковская базовая школа Ельского района»

Черепанова Татьяна Михайловна

… и кругом только умные лица,

потому что считаем в уме!

Сейчас, на этапе стремительного развития информатики и вычислительной техники, современные школьники не хотят утруждать себя счетом в уме.

Очень полезный навык

логическое мышление

память

внимательность

сообразительность

точность

наблюдательность

интеллект

абстрактное мышление

гибкость ума

умение видеть главное

Уметь быстро считать полезно взрослым и детям

Описание проблемы

Цель моей работы: на основе собранной по заданной теме информации показать, что устный счет - это просто, и познакомить с наиболее простыми и наиболее эффективными приемами устного счета, которые подойдут каждому.

В соответствии с поставленной целью были определены задачи:

• Исследовать, применяют ли школьники приемы быстрого счета.
• Изучить приемы быстрого счета, которые можно использовать, упрощая вычисления.
• Познакомиться с заданиями из экзаменационного сборника по математике за курс базовой школы, выяснить есть ли среди них примеры, при решении которых можно будет применить выявленные способы устного счёта.
• Составить памятку для учащихся для применения приемов быстрого счета.

Гипотеза исследования: если показать, что применение приемов быстрого счета, облегчает вычисления, то можно добиться того, что повысится вычислительная культура учащихся, и нам будет легче решать практические задачи. Объектом исследования являются рациональные приёмы умножения и деления. Предмет исследования – использование рациональных приёмов для повышения скорости устных вычислений при решении примеров на умножение и деление.

Этапы решения проблемы

• Познакомиться с материалом, который предоставил мне учитель.
• Систематизировать закономерности натуральных чисел и свойства математических действий над ними.
• Применить их для упрощенных приемов вычислений.
• Изучить и применить найденные рациональные приемы на практике, на уроках математики.
• Выяснить, есть ли среди заданий из экзаменационного сборника по математике за курс базовой школы, примеры при решении которых можно будет использовать эти «хитрые» приёмы.
• Составить памятку для учащихся для применения приемов быстрого счета.

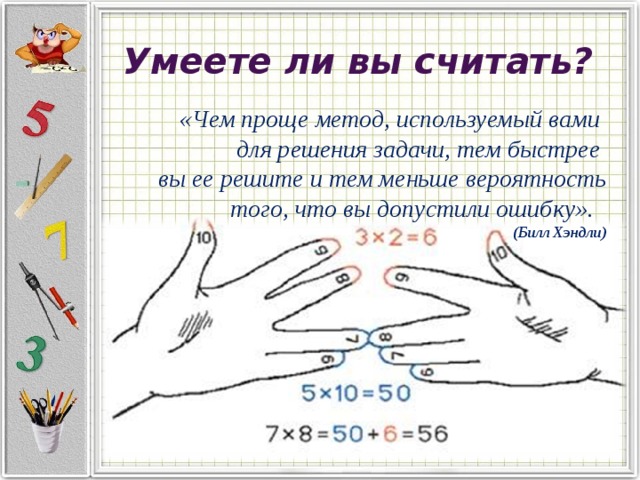
Умеете ли вы считать?

«Чем проще метод, используемый вами

для решения задачи, тем быстрее

вы ее решите и тем меньше вероятность того, что вы допустили ошибку».

(Билл Хэндли)

Анкетирование

• Зачем вообще нужно уметь считать?
• При изучении, каких школьных предметов требуется правильный счет?
• Знают ли они приемы быстрого счета?
• Хотели бы научиться быстро считать устно?

№

Вопрос

1

Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?

Да

2

3

Умеете ли вы умножать, складывать, вычитать числа столбиком, делить «уголком»?

23

Нет

Знаете ли Вы приемы быстрого счета?

3 

Не

знаю

  21

4

3 

5 

1 

Всего

А хотели бы узнать?

9 

31

  22

20

6 

  3

8 

Общие приемы устного счета

Общий прием заключается в следующем:

• пользуясь десятичным составом числа, разложить каждое слагаемое на разряды;
• использование переместительного свойства умножения;
• использование распределительного свойства при умножении и делении.

Вычитание числа меньше 100 из числа больше 100, но меньше 200

Например:

134-76=58

76 на 24меньше 100. 134 на 34 больше 100. Прибавим 24 к 34 и получим ответ: 58.

152-88=64

88 на 12 меньше 100,а 152 больше 100 на 52, значит

152-88=12+52=64

127-54=27+46=73

А также верно:

46-37=6+3=9

87-74=7+6=13

157-99=57+1=58 246-179=46+21=67 567-456=67+44=111 357-246=57+54=111 678-589=78+11=89 986-876=86+24=110 794-638=94+62=152 847-736=47+64=111

Специальные приемы устного счета

Приёмы умножения на 9, 99, 999

Приёмы умножения на 11, 101, 1001

Ещё один приём умножения на 11

Ещё один приём умножения на 101

Умножение двузначного числа на 111

Умножение на 5, 15, 25, 50, 125

Умножение на 37

Умножение на 22, 33, …, 99

Приём деления на 5, 50, 500

Приём деления на 25, 125

Возведение в квадрат чисел, оканчивающихся на 5

Возведение в квадрат двузначного числа, начинающегося на 5

Возведение в квадрат чисел, оканчивающихся на 1

Приёмы умножения на 11, 101, 1001

а*11=а*10+а

а*101=а*100+а

а*1001=а*1000+а

45*11=45*10+45=450+45=495

891*11=891*10+891=8910+891=9801

86*101=86*100+86=8600+86=8686

942*101=942*100+942=94200+942=95142

93*1001=93*1000+93=93000+93=93093

123*1001=123*1000+123=123000+123=123123

Ещё один приём умножения на 11

36*11=396

86*11=946

123*11=1353

489*11=5379

6521*11=71731

36789*11=404679

Ещё один прием умножения на 101

Например:

52*101=5252

74*101=7474

36*101=3636

Или применив прием описанный выше:

45*101=4500+45=4545

93*101=9300+93=9393

Это можно увидеть наглядно,

выполнив действия столбиком:

Ещё один прием умножения на 1001

Число Шахерезады

456*1001=456456

789*1001=789789

985*1001=985985

168*1001=168168

Умножение двузначного числа на 111

27*111=2997

31*111=3441

45*111=4995

54*111=5994

63*111=6993

71*111=7881

80*111=8880

93*111=10323

95*111=10545

39*111=4329

86*111=9546

57*111=6327

49*111=5439

86*111=9546

Умножение на 37

Зная это, можно решить многие примеры

Например:

37*5=37*(3+2)=37*3+37*2=111+74=185 37*5=37*(6–1)=37*6–37=222–37=185 37*300=37*3*100=11100 37*60=37*6*10=2220

Умножение на 22, 33, …, 99

Чтобы двузначное число умножить на 22, 33, …, 99, надо этот множитель представить в виде произведения однозначного числа на 11, то есть 44 = 4*11; 55 = 5*11. Затем произведение первых чисел умножить на 11:

24 * 22 = 24* 2*11 = 48*11 = 528

68*33=68*3*11=204*11=2244

123*55=123*5*11=615*11=6765

Возведение в квадрат чисел, оканчивающихся на 5

Например: 35²=?

Отделим 5 от цифр впереди нее. В данном случае речь идет всего лишь о цифре 3, стоящей перед 5. Прибавим 1 к 3 и получим в результате 4.

Перемножим числа: 3*4 = 12

Припишем 25 (5 в квадрате) справа к 12. Полученное число и есть искомый ответ: 1225.

35² = 1225

75²=5625 95²=9025

(8*7=56) 105²=11025

Возведение в квадрат двузначного числа, начинающегося на 5

Например:

52 2 = 2704, т.к. 25+2=27 и 2 2 =04;

57 2 = 3249

53 2 = 2809

58 2 = 3364, т.к. 25+8=33 и 8 2 =64.

31²=961

41²= 1681

221²=48400+220+221=48841

Возведение в квадрат чисел, оканчивающихся на 1

Пример:

121²= 14641

121-1 =120

120²= 14400

120 + 121 = 241

14400 + 241 = 14641

ОТВЕТ: 14641

Выводы:

Знание приемов быстрого счета позволяет упрощать вычисления, экономить время, развивает логическое мышление и гибкость ума.

Возможно, что с первого раза у многих не получится быстро, с ходу выполнять те или другие подсчеты. Пусть сначала не получится использовать прием, показанный в работе. Зато после тренировки он поможет приобрести полезные навыки устного и быстрого счета.

Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает на­стойчивость и упорство в достижении цели.

Довольно быстро получается умножать числа, если немного потренироваться!!!

Спасибо за внимание