ГОБПОУ «Конь-Колодезский техникум»
Практическое занятие №1
Тема: «Вычисление пределов функции с использованием первого и второго замечательных пределов. Исследование функций на непрерывность. Нахождение производных сложных функций. Нахождение производных»
Группа 25-Б
Специальность: 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство»)
Цель работы: научиться применять изученные формулы при выполнении практических заданий; закрепить алгоритм исследования функции на непрерывность.
Приобретаемые умения и знания:
уметь:
- вычислять пределы функции с использованием первого и второго замечательных пределов;
- исследовать функцию на непрерывность с помощью производной;
- вычислять производные функций с помощью таблицы производных и формул производных: суммы, произведения и частного.
знать:
- основные способы вычисления пределов функций;
- формулы первого и второго замечательных пределов;
- алгоритм исследования функции на непрерывность с помощью производной;
- таблицы производных и формул производных: суммы, произведения и частного.
Порядок выполнения работы:
Перед выполнением практического занятия повторите конспект лекций.
Изучите теоретическую часть работы.
Выполнить предложенные задания.
Составьте отчет по работе и сделайте выводы по результатам работы.
Теоретическая часть
Число А называют пределом функции f(x) при 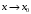 (и пишут
(и пишут 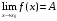 ), если для любого
), если для любого 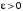 найдется число
найдется число 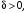 зависящее от , такое, что для всех
зависящее от , такое, что для всех 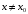 , удовлетворяющих условию
, удовлетворяющих условию 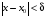 , выполняется неравенство
, выполняется неравенство 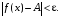
Теоремы о пределах:
1. 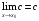 (c=const).
(c=const).
2. Если 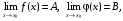 то:
то:
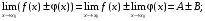
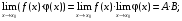
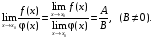
Первый замечательный предел: 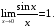
Второй замечательный предел (число е = 2,718…):
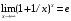 или
или 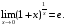
Пример 1. Вычислить предел 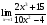
Решение:
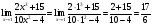
Пример 2. Вычислить предел 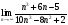
Решение:
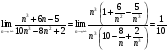
Пример 3. Вычислить предел 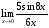
Решение:
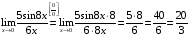
Пример 4. Вычислить предел 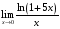
Решение:
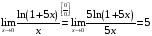
Формулы дифференцирования
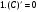
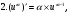 в частности,
в частности, 
 в частности,
в частности, 
 в частности,
в частности, 
Правила дифференцирования
1)  ;
;
2)  , в частности
, в частности  ;
;
3)  ;
;
4)  , если
, если ;
;
5)  , если
, если  и
и  .
.
Возрастание и убывание функций
Теорема 1. (необходимые условия). Если дифференцируемая на интервале (а;b) функция  возрастает (убывает), то
возрастает (убывает), то 
 для любого
для любого  .
.
Теорема 2. (достаточные условия). Если функция  дифференцируема на интервале (a;b) и
дифференцируема на интервале (a;b) и 
 для любого
для любого  , то эта функция возрастает (убывает) на интервале (a;b).
, то эта функция возрастает (убывает) на интервале (a;b).
Теоремы 1 и 2 позволяют довольно просто исследовать функцию на монотонность (функция, убывающая или возрастающая, называется монотонной).
Пример 5. Исследовать функцию  =x3-3x-4 на монотонность.
=x3-3x-4 на монотонность.
Решение:



 + - +
+ - +

-1 1
 при
при 
 при
при 
Ответ: данная функция возрастает при  и убывает
и убывает 
Пример 6. Исследовать функцию  на монотонность.
на монотонность.
Решение:

Так как у’0 в области определения, то функции является возрастающей на каждом интервале области определения.
Задания для закрепления полученных умений и знаний.
Вариант №1
Задание 1. Вычислить предел функции:




Задание 2. Вычислить пределы, используя 1-й и 2-й замечательные пределы:
а) 
б) 
Задание 3. Найдите производную функции:




Задание 4. Исследовать функцию на монотонность:
Вариант №2
Задание 1. Вычислить предел функции:
 ;
;
 ;
;


Задание 2. Вычислить пределы, используя 1-й и 2-й замечательные пределы:
а) 
б) 
Задание 3. Найдите производную функции:




Задание 4. Исследовать функцию на монотонность:
Контрольные вопросы
1. Основные способы вычисления пределов функций.
2. Алгоритм исследования функции на непрерывность с помощью производной.
3. Понятие производной функции.
ГОБПОУ «Конь-Колодезский техникум»
Практическое занятие №2
Тема: «Интегрирование простейших функций. Вычисление простейших определённых интегралов. Решение прикладных задач»
Группа 25-Б
Специальность: 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство»)
Цель работы: научиться применять изученные формулы интегрирования при выполнении практических заданий.
Приобретаемые умения и знания:
уметь:
- интегрировать простейшие определённые интегралы, используя таблицу простейших интегралов и формулу Ньютона – Лейбница;
- вычислять площади плоских фигур;
знать:
- формулы таблицы простейших неопределённых интегралов;
- формулу Ньютона – Лейбница.
Порядок выполнения работы:
Перед выполнением практического занятия повторите конспект лекций.
Изучите теоретическую часть работы.
Выполнить предложенные задания.
Составьте отчет по работе и сделайте выводы по результатам работы.
Теоретическая часть
Функция  , определенная на интервале
, определенная на интервале  , называется первообразной для функции
, называется первообразной для функции  , определенной на том же интервале
, определенной на том же интервале  , если
, если 
Если  — первообразная для функции
— первообразная для функции  , то любая другая первообразная
, то любая другая первообразная  для функции
для функции  отличается от
отличается от  на некоторое постоянное слагаемое, т. е.
на некоторое постоянное слагаемое, т. е.  где
где  .
.
Неопределенным интегралом от функции  называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:
называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:  где
где 
Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:

Свойства неопределенного интеграла:
1. 
2. 
3. 
4. 
Таблица основных неопределённых интегралов
Вычисление площади плоской фигуры
Найдем площадь S криволинейной трапеции, ограниченной кривой  осью
осью  и двумя прямыми
и двумя прямыми  и
и  , где
, где  ,
,  (рис. 1)
(рис. 1)
Так дифференциал переменной площади S есть площадь прямоугольника с основанием dx и высотой  , т. е.
, т. е.  , то, интегрируя это равенство в пределах от a до b, получим
, то, интегрируя это равенство в пределах от a до b, получим


Пример1. Вычислить площадь фигуры, ограниченной указанными линиями 

 и
и 
Решение:
Выполним построение фигуры. Строим прямую  по двум точкам А(4;0) и В(0;2) (рис.6). Выразив у через х, получим
по двум точкам А(4;0) и В(0;2) (рис.6). Выразив у через х, получим  По формуле (1), где
По формуле (1), где  ,
,  и
и  , находим
, находим
(кв. ед.)
Пример2. Скорость движения точки изменяется по закону  м/с. Найти путь, пройденный точкой за 10 с от начала движения.
м/с. Найти путь, пройденный точкой за 10 с от начала движения.
Решение:
Согласно условию,  ,
,  ,
,  . По формуле (6) находим
. По формуле (6) находим
(м).
Задания для закрепления полученных умений и знаний.
Задание 1. Вычислить неопределённый интеграл:
Вариант №1


Вариант №2


Задание 2. Вычислить определённый интеграл:
Вариант №1



Вариант №2



Задание 3. Найти площадь фигуры, ограниченной линиями
Вариант №1
 ,
,  ,
,  ,
, 
Вариант №2
 ,
,  ,
,  ,
, 
*Вычислить площадь плоской фигуры, ограниченной функциями:
2x-3y+6=0, y=0, x=3.
(*) – задание более высокого уровня сложности.
Контрольные вопросы
Понятие неопределённого интеграла.
Понятие определённого интеграла.
В чём заключается геометрический смысл определённого интеграла?
Площадь каких фигур можно вычислить с помощью формулы Ньютона-Лейбница?
ГОБПОУ «Конь-Колодезский техникум»
Практическое занятие №3
Тема: «Решение дифференциальных уравнений с разделяющимися переменными; однородных дифференциальных уравнений первого порядка; линейных дифференциальных уравнений первого порядка с постоянными коэффициентами. Решение прикладных задач»
Группа 25-Б
Специальность: 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство»)
Цель работы: научиться решать дифференциальные уравнения с разделяющимися переменными; однородные дифференциальные уравнения первого порядка; линейные дифференциальные уравнения первого порядка с постоянными коэффициентами.
Приобретаемые умения и знания:
уметь:
-решать дифференциальные уравнения с разделяющимися переменными; однородные дифференциальные уравнения первого порядка;
-линейные дифференциальные уравнения первого порядка с постоянными коэффициентами;
знать:
- основные понятия дифференциального исчисления;
- алгоритм решения дифференциальных уравнений с разделяющимися переменными.
Порядок выполнения работы:
Перед выполнением практического занятия повторите конспект лекций.
Изучите теоретическую часть работы.
Выполнить предложенные задания.
Составьте отчет по работе и сделайте выводы по результатам работы.
Теоретическая часть
Дифференциальное уравнение первого порядка содержит:
независимую переменную х;
зависимую переменную у;
первую производную у′ функции.
Решить дифференциальное уравнение – это значит, найти множество функций
у = f(x) + C, которые удовлетворяют данному уравнению.
Пример 1. Решить дифференциальное уравнение ху′ = у.
В первую очередь нужно переписать производную с помощью дифференциалов:
y′ =  . Теперь подставляем в уравнение, получаем
. Теперь подставляем в уравнение, получаем
х· = y.
= y.
Пробуем разделить переменные, то есть в левой части уравнения оставить только «угреки», а в правой «иксы» или наоборот.
 =
=
Переменные разделены.
Затем интегрируем полученное дифференциальное уравнение:
 =
=
ln =ln
=ln +C, где С=const.
+C, где С=const.
ln - ln
- ln =C
=C
ln =С
=С
 =еС
=еС
у=х· еС – общее решение дифференциального уравнения.
Пример 2. Найти частное решение дифференциального уравнения ху′ = у, удовлетворяющего начальному условию у(1) = 2.
По условию требуется найти частное решение дифференциального уравнения, удовлетворяющего начальному условию. Такая постановка вопроса называется задачей Коши.
Общее решение данного уравнения у нас уже имеется у=х· еС (пример 1).
Найдем частное решение. По условию у(1) = 2, получим
2 = 1· еС
еС=2
еС - тоже некоторая константа, которую обозначим через С.
С=2
Итак, в общее решение подставляем С=2, получим
у=х· е2 – частное решение дифференциального уравнения ху′ = у.
Задания для закрепления полученных умений и знаний.
Вариант №1
Решить дифференциальное уравнение с разделяющимися переменными:
xdx - 2ydy = 0;
3xdy= 3ydx
Найти частное решение дифференциального уравнения (задача Коши):
dy = xydx, если у(0) = 4
(1+х)dy = (y-1)dx, если у(1) = 2
Вариант №2
Решить дифференциальное уравнение с разделяющимися переменными:
2xdx - ydy = 0;
4xdy= ydx
Найти частное решение дифференциального уравнения (задача Коши):
dy = xydx, если у(1) = 2,5
(2+х)dy = (y+1)dx, если у(1) = 2
Контрольные вопросы
Понятие дифференциального уравнения. Привести пример.
Алгоритм решения дифференциального уравнения.
Понятие задачи Коши.
ГОБПОУ «Конь-Колодезский техникум»
Практическое занятие №4
Тема: «Решение простейших линейных дифференциальных уравнений относительно частных производных»
Группа 25-Б
Специальность: 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство»)
Цель работы: научиться решать простейшие дифференциальные уравнения в частных производных;
Приобретаемые умения и знания:
уметь:
знать:
- понятие дифференциальных уравнений в частных производных;
- методы решения простейших дифференциальных уравнений в частных производных.
Порядок выполнения работы:
Перед выполнением практического занятия повторите конспект лекций.
Изучите теоретическую часть работы.
Выполнить предложенные задания.
Составьте отчет по работе и сделайте выводы по результатам работы.
Теоретическая часть
Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.
Дифференциальное уравнение первого порядка в частных производных — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных U = U(x, y) и их частные производные,  .
.
Дифференциальные уравнения в частных производных можно решить по принципу разделения переменных для нахождения общего решения. Затем, для нахождения частного решения уравнение можно решить по принципу задачи Коши, рассмотренной в предыдущем практическом занятии (ПЗ №3), то есть сначала нужно найти общее решение дифференциального уравнения, затем подставив начальные условия (х0,у0), найти значение константы С. Записав общее решение с полученной константой, получим искомое частное решение дифференциального уравнения.
Уравнение с частными производными имеет бесчисленное множество решений. Кроме произвольных постоянных, в решение уравнений с частными производными могут входить произвольные функции тех же аргументов, от которых зависит искомая функция. Пример описан в конспекте.
Задания для закрепления полученных умений и знаний.
Вариант №1
Решить дифференциальное уравнение:
2ydy - xdx = 0;
уdy= хdx
Найти частное решение дифференциального уравнения:
dх = xydу, если у(0) = 4
(1-х)dy - (y+1)dx = 0, если у(1) = 2
Вариант №2
Решить дифференциальное уравнение:
2xdу- ydх = 0;
xdy= 2ydx
Найти частное решение дифференциального уравнения:
2dy = xydx, если у(1) = 2
(2-х)dy - (y+1)dx =0, если у(1) = 2
Контрольные вопросы
Понятие дифференциального уравнения. Привести пример.
Понятие дифференциального уравнения в частных производных. Привести пример.
Понятие задачи Коши.
ГОБПОУ «Конь-Колодезский техникум»
Практическое занятие №5
Тема: «Определение сходимости рядов по признаку Даламбера. Определение сходимости знакопеременных рядов. Разложение функций в ряд Маклорена»
Группа 25-Б
Специальность: 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство»)
Цель работы: научиться определять сходимость (расходимость) ряда по признаку Даламбера, сходимости знакопеременных рядов; раскладывать элементарные функции в ряд Маклорена».
Приобретаемые умения и знания:
уметь:
определять сходимость числовых и функциональных рядов по признаку Даламбера;
применять признак Лейбница для знакопеременных рядов;
разлагать элементарные функции в ряд Маклорена.
знать: основные понятия по теме «Ряды», признаки сходимости числовых и функциональных рядов, признак Даламбера.
Порядок выполнения работы:
Перед выполнением практического занятия повторите конспект лекций.
Изучите теоретическую часть работы.
Выполнить предложенные задания.
Составьте отчет по работе и сделайте выводы по результатам работы.
Теоретическая часть
Признак Даламбера заключается в следующем:
Если для числового ряда
 существует такое число q{\displaystyle q}, {\displaystyle 00˂q˂1, что, начиная с некоторого номера, выполняется неравенство
существует такое число q{\displaystyle q}, {\displaystyle 00˂q˂1, что, начиная с некоторого номера, выполняется неравенство
 ,{\displaystyle \left|{\frac {a_{n+1}}{a_{n}}}\right|\leqslant q,}то данный ряд абсолютно сходится; если же, начиная с некоторого номера
,{\displaystyle \left|{\frac {a_{n+1}}{a_{n}}}\right|\leqslant q,}то данный ряд абсолютно сходится; если же, начиная с некоторого номера ˃1, {\displaystyle \left|{\frac {a_{n+1}}{a_{n}}}\right|\geq 1}то ряд расходится.
˃1, {\displaystyle \left|{\frac {a_{n+1}}{a_{n}}}\right|\geq 1}то ряд расходится.
Пример 1. Исследовать на сходимость ряд  .
.
Решение:
Применим признак Даламбера; имеем 
 ,
,
Так как D
Задания для закрепления полученных умений и знаний.
Вариант 1
Написать первые пять членов ряда по заданному общему члену, и проверить, выполняется ли необходимый признак сходимости ряда.


Используя признак Даламбера, исследовать на сходимость ряд:


Вариант 2
Написать первые пять членов ряда по заданному общему члену, и проверить, выполняется ли необходимый признак сходимости ряда.


Используя признак Даламбера, исследовать на сходимость ряд:


Контрольные вопросы
Что такое ряд?
Понятие сходящегося ряда.
Понятие расходящегося ряда.
Необходимый признак сходимости.
Признак Даламбера.
ГОБПОУ «Конь-Колодезский техникум»
Практическое занятие №6
Тема: «Решение простейших задач на определение вероятности с использованием теоремы сложения и умножения вероятностей»
Группа 25-Б
Специальность: 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство»)
Цель работы: научиться решать простейшие задачи на определение вероятности, а также
простейшие задачи на определение вероятности с использованием теоремы сложения и
умножения вероятностей.
Приобретаемые умения и знания:
уметь:
- находить вероятность, в простейших задачах используя классическое определение вероятности;
- решать задачи с применением теоремы сложения вероятностей для несовместных событий.
знать:
- основные понятия теории вероятностей и математической статистики.
Порядок выполнения работы:
Перед выполнением практического занятия повторите конспект лекций.
Изучите теоретическую часть работы.
Выполнить предложенные задания.
Составьте отчет по работе и сделайте выводы по результатам работы.
Теоретическая часть
Опр. Событие – это любое явление, которое происходит или не происходит или результат испытаний, наблюдений и явлений. События обозначают заглавными латинскими буквами А, В, С, …
Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи.
Долю успеха того или иного события называют вероятностью этого события и обозначают Р(А)
Опр . Если в некотором испытании существует п равновозможных попарно несовместных исходов и т из них благоприятствуют событию А, то вероятностью наступления события А называют отношение  и записывают Р(А) =
и записывают Р(А) = 
Опр. Суммой (объединением) двух событий A и B (обозначается A+B, A B) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.
B) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.
Опр. Произведением (пересечением) двух событий A и B (обозначается A×B, A и B) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.
Типовые задачи:
Задача1. Найти вероятность появления при одном бросании игральной кости числа очков, большего 4.
Решение : А – « появление числа очков, большего 4» п = 6 - число всех исходов, т = 2 – благоприятствующих событию А ( 5, 6 ) Р(А) =  =
=  Ответ: Р(А) =
Ответ: Р(А) =  =
= 
Задача2. В коробке лежат 8 зелёных, 7 синих и 15 красных карандашей. Вычислить вероятность того, что взятый наугад карандаш будет синим или зелёным.
Решение:
А: взяли синий карандаш
В: взяли зелёный карандаш
С: взяли синий и зелёный карандаш
Событие С равно сумме событий А и В: С = А + В
Вероятность события А равна 
Вероятность события В равна 
Вероятность события С равна
Задача 3. В одной коробке находится 4 белых и 8 черных шаров, а в другой – 3 белых и 9 черных. Из каждой коробки вынули по шару. Вычислить вероятность того, что оба шара окажутся белыми.
Решение:
А: из первой коробки вынули белый шар
В: из второй коробки вынули белый шар
С: из коробок вынули белые шары
Вероятность события А равна 
Вероятность события В равна 
Вероятность события С равна
Ответ: Р ( С )  0,083
0,083
Задания для закрепления полученных умений и знаний.
Вариант №1
1. Среди 100 деталей, изготовленных на станке, оказалось 8 деталей, не отвечающих стандарту. Найдите вероятность выбора детали, не отвечающей стандарту.
2. Контролёр, проверяя качество 500 изделий, установил, что 10 из них относится ко 2-му сорту, а остальные к 1-му. Найдите вероятность: а) выбора изделия 1-го сорта; б) выбора изделия 2-го сорта.
3. Какова вероятность того, что сумма очков, выпавших на 2-х брошенных костях, равна 6 ?
4. На складе имеется 50 деталей, изготовленных тремя бригадами. Из них 25 изготовлено первой бригадой, 15- второй и 10 – третьей. Найти вероятность того, что на сборку поступила деталь, изготовленная второй или третьей бригадой.
5. Из колоды карт (36 листов ) наугад вынимается одна карта. Какова вероятность того, что эта карта: 1) валет; 2) король чёрной масти.
Вариант №2
1. Пусть имеется 80 деталей, среди которых 60 исправных, а 20 бракованных. Найти вероятность того, что взятая наугад деталь окажется исправной.
2. В партии из 100 деталей имеется 5 бракованных. Определить вероятность того, что взятая на удачу деталь окажется стандартной.
3. Какова вероятность того, что сумма очков, выпавших на 2-х брошенных костях, равна 5 ?
4. В коробке находятся 250 лампочек, из них 100 по 100 Вт, 50 - по 60 Вт, 50 – по 25 Вт и 50 – по 15 Вт. Вычислить вероятность того, что мощность любой взятой наугад лампочки не превысит 60 Вт.
5. Из колоды карт (36 листов ) наугад вынимается одна карта. Какова вероятность того, что эта карта: 1) дама; 2) туз чёрной масти.
Контрольные вопросы
С помощью какой формулы можно вычислить вероятность появления случайного события?
Приведите пример достоверного события.
Чему равна вероятность невозможного события?
ГОБПОУ «Конь-Колодезский техникум»
Практическое занятие №7
Тема: «По заданному условию построить закон распределения дискретной случайной величины»
Группа 25-Б
Специальность: 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство»)
Цель работы: по заданному условию научиться строить закон распределения дискретной случайной величины.
Приобретаемые умения и знания:
уметь:
знать:
- основные понятия по теме «Случайная величина, её функция распределения».
Порядок выполнения работы:
Перед выполнением практического занятия повторите конспект лекций.
Изучите теоретическую часть работы.
Выполнить предложенные задания.
Составьте отчет по работе и сделайте выводы по результатам работы.
Теоретическая часть
Случайной называется величина, которая принимает в результате испытаний то или иное (но при этом только одно) возможное значение, заранее известное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств.
Примерами случайной величины могут служить размер обрабатываемой детали, погрешность результата измерения какого-либо параметра изделия или среды. Среди случайных величин, с которыми приходится встречаться на практике, можно выделить два основных типа: дискретные величины и непрерывные.
Дискретной называется такая случайная величина, которая принимает конечное или бесконечное счетное множество значений.
Например,
частота попаданий при трех выстрелах;
число дефектных изделий в партии из n штук;
число вызовов, поступающих на телефонную станцию в течение суток;
число выстрелов до первого попадания в цель и т. д.
Непрерывной называется такая случайная величина, которая может принимать любые значения из некоторого бесконечного интервала. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Например,
безотказной работы микросхемы;
погрешность изготовления деталей;
концентрация соли в морской воде и т. д.
Случайные величины обычно обозначают буквами X,Y и т. д., а их возможные значения –x, y и т. д.
Для задания случайной величины недостаточно перечислить все ее возможные значения. Необходимо также знать, как часто могут появиться те или иные ее значения в результате испытаний при одних и тех же условиях, т. е. нужно задать вероятности их появления. Совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет распределение случайной величины.
Законом распределения случайной величины называется всякое соответствие между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения случайной величины может быть задан в виде таблицы, в виде функции распределения, в виде плотности распределения. Таблица, содержащая возможные значения случайной величины и соответствующие вероятности, является простейшей формой задания закона распределения случайной величины:
| X | x1 | x2 | x3 | ... | xn-1 | xn |
| P | p1 | p2 | p3 | ... | pn-1 | pn |
Табличное задание закона распределения может быть использовано только для дискретной случайной величины с конечным числом возможных значений.
Закон распределения задан, если сумма их вероятностей равна единице:
 = p1+p2+p3+…+pn = 1
= p1+p2+p3+…+pn = 1
Пример 1.
Доказать, что закон распределения случайной величины задан.
| хi | 1 | 2 | 3 | 4 |
| рi | 0,1 | 0,2 | 0,3 | 0,3 |
Решение:
 = p1+p2+p3+…+pn = 0,1 + 0,2 + 0,3 + 0,3 = 1 – закон задан
= p1+p2+p3+…+pn = 0,1 + 0,2 + 0,3 + 0,3 = 1 – закон задан
Пример 2.
Достроить закон распределения случайной величины:
| хi | 1 | 2 | 3 | 4 |
| рi | 0,1 | 0,24 | ? | 0,2 |
Решение:
0,1 + 0,24 + х + 0,2 = 1
0,54 + х =1
х = 0,46
Задания для закрепления полученных умений и знаний.
Доказать, что закон распределения случайной величины задан.
| хi | 2 | 5 | 8 | 9 |
| рi | 0,1 | 0,4 | 0,3 | 0,2 |
а)
| хi | 1 | 2 | 3 | 4 |
| рi | 0,3 | 0,2 | 0,2 | 0,3 |
б)
| хi | 1 | 2 | 3 | 4 |
| рi | 0,18 | 0,12 | 0,29 | 0,41 |
в)
| хi | 0 | 1 | 2 | 3 | 4 |
| рi | 1/6 | 1/6 | 1/12 | 1/4 | 1/3 |
г)
Достроить закон распределения случайной величины:
| хi | 1 | 2 | 3 | 4 |
| рi | 0,1 | 0,28 | ? | 0,2 |
а)
| хi | -1 | 2 | -3 | 0 |
| рi | 0,32 | 0,16 | 0,14 | ? |
б)
| хi | 1 | 2 | 3 | 4 |
| рi | 0,3 | 0,2 | 0,2 | 0,3 |
в)
Контрольные вопросы
Понятие случайной величины.
Понятие дискретной случайной величины.
Понятие непрерывной случайной величины.
Понятие закона распределения случайной величины.
Как проверить, задан ли закон распределения случайной величины.
ГОБПОУ «Конь-Колодезский техникум»
Практическое занятие №8
Тема: «Нахождение математического ожидания, дисперсии и среднего квадратичного отклонения дискретной случайной величины заданной законом распределения»
Группа 25-Б
Специальность: 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство»)
Цель работы: закрепить умение решать задачи на определение непрерывной дискретной величины, используя закон распределения случайной величины.
Приобретаемые умения и знания:
уметь:
знать:
понятие математического ожидания, дисперсии случайной величины и
среднего квадратичного отклонения случайной величины.
Порядок выполнения работы:
Перед выполнением практического занятия повторите конспект лекций.
Изучите теоретическую часть работы.
Выполнить предложенные задания.
Составьте отчет по работе и сделайте выводы по результатам работы.
Теоретическая часть
Случайная величина Х – это числовая функция  , определенная на пространстве элементарных событий. Случайные величины, имеющие счетные множества возможных значений, называются дискретными. Дискретная случайная величина определена, если известны все ее значения и соответствующие им вероятности. Соотношение между возможными значениями случайной величины и соответствующими им вероятностями называют распределением вероятностей случайной величины. Для дискретной случайной величины это соответствие может быть записано в виде таблицы:
, определенная на пространстве элементарных событий. Случайные величины, имеющие счетные множества возможных значений, называются дискретными. Дискретная случайная величина определена, если известны все ее значения и соответствующие им вероятности. Соотношение между возможными значениями случайной величины и соответствующими им вероятностями называют распределением вероятностей случайной величины. Для дискретной случайной величины это соответствие может быть записано в виде таблицы: 
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
Числовые характеристики дискретной случайной величины.
Математическим ожиданием (средним значением) дискретной случайной величины Х называют сумму произведений всех ее возможных значений на соответствующие им вероятности 
Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания  . Дисперсия дискретной случайной величины вычисляется по формулам:
. Дисперсия дискретной случайной величины вычисляется по формулам:


Средним квадратичным отклонением дискретной случайной величины называют корень квадратный из дисперсии  .
.
Пример 1: Случайная величина Х задана таблицей распределения вероятностей. Найти М(Х), D(Х), σ(Х).
| хi | 2 | 5 | 8 | 9 |
| рi | 0,1 | 0,4 | 0,3 | 0,2 |
Решение:
Задания для закрепления полученных умений и знаний.
Задание 1. Найти числовые характеристики дискретных случайных величин:
Найти математическое ожидание случайной величины Х, зная закон ее распределения:
Найти дисперсию случайной величины Х, которая задана следующим законом распределения:
Найти дисперсию случайной величины Х, которая задана следующим законом распределения:
Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.
| Значения xi | 1 | 2 | 3 | 4 | 5 | 6 |
| Вероятности pi | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Контрольные вопросы
Что такое математическая статистика?
Понятие случайной величины (дискретной случайной величины).
В чем заключается закон распределения случайной величины?
Назовите основные числовые характеристики дискретной случайной величины.
ГОБПОУ «Конь-Колодезский техникум»
Практическое занятие №9
Тема: «Вычисление определителей 2-го и 3-го порядка. Выполнение операций над матрицами»
Группа 25-Б
Специальность: 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство»)
Цель работы: сформировать умение вычислять определители 2-го и 3-го порядка; выполнять операций над матрицами.
Приобретаемые умения и знания:
уметь:
- вычислять определители 2-го и 3-го порядка;
- выполнять операции над матрицами;
знать:
- понятие определителей 2-го и 3-го порядка;
- понятие матрицы, квадратной матрицы;
- правила вычисления определителей 2-го и 3-го порядка.
Порядок выполнения работы:
Перед выполнением практического занятия повторите конспект лекций.
Изучите теоретическую часть работы.
Выполнить предложенные задания.
Составьте отчет по работе и сделайте выводы по результатам работы.
Теоретическая часть
Определение 1. Определителем второго порядка  называется выражение
называется выражение 
Определение 2. Определителем третьего порядка  называется выражение
называется выражение 
Есть другие способы для нахождения определителя третьего порядка.
1. 
 =
=
где  - элементы определителя,
- элементы определителя,
 - миноры элементов а1, b1, c1
- миноры элементов а1, b1, c1

Минором Мij какого – либо элемента аij определителя  порядка n называется определитель порядка n – 1, полученный из
порядка n называется определитель порядка n – 1, полученный из  вычерчиванием i– й строки и j – го столбца.
вычерчиванием i– й строки и j – го столбца.
2. 
Определитель III порядка можно найти по схеме:
+ -
















+ + +





 3.
3.  =
= 

- - -
Пример 1.
1. Найти определитель

Решение: Воспользуемся формулой (2) теоремы 1.
Проверим, найдём этот же определитель способом 3.

Задания для закрепления полученных умений и знаний.
1. 2.
2. 
3. 4.
4. 
Контрольные вопросы
Определение матрицы.
Какую матрицу называют квадратной порядка n?
Определение определителя 2-го порядка.
Определение определителя 3-го порядка.
Сформулируйте правило вычисления определителя 2-го порядка.
Сформулируйте правило вычисления определителя 3-го порядка.
ГОБПОУ «Конь-Колодезский техникум»
Практическое занятие №10
Тема: «Решение систем линейных уравнений. Решение экономических задач методом Крамера, методом Гаусса. Вычисление себестоимости продукции с помощью обратной матрицы»
Группа 25-Б
Специальность: 38.02.01 Экономика и бухгалтерский учёт (отрасль – «Сельское хозяйство»)
Цель работы: научиться решать экономические задачи методом Крамера, методом Гаусса, вычислять себестоимость продукции с помощью обратной матрицы.
Приобретаемые умения и знания:
уметь:
- решать системы линейных уравнений;
- решать экономические задачи методом Крамера, методом Гаусса;
- вычислять себестоимость продукции с помощью обратной матрицы.
знать:
- основные методы решения систем линейных уравнений, в частности метод Крамера, метод Гаусса;
- понятие обратной матрицы.
Порядок выполнения работы:
Перед выполнением практического занятия повторите конспект лекций.
Изучите теоретическую часть работы.
Выполнить предложенные задания.
Составьте отчет по работе и сделайте выводы по результатам работы.
Теоретическая часть
Метод Крамера.
Пример 1. Решить систему линейных уравнений методом Крамера:
.
Найдем определитель системы
 =
=  = 4 – 3 + 15 – 10 + 2 - 9 = -1
= 4 – 3 + 15 – 10 + 2 - 9 = -1
Так как  , система имеет единственное решение, которое определяется по
, система имеет единственное решение, которое определяется по
формулам Крамера:
х =  , у =
, у =  , z =
, z = 
Найдем определители  и подставим полученные значения в формулы Крамера:
и подставим полученные значения в формулы Крамера:
Ответ: x = 2, у = -1, z = 1.
Метод Гаусса.
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) или близкой к трапециевидной (прямой ход метода Гаусса)
Пример 2. Решить систему линейных уравнений, применяя обратный ход метода Гаусса:

Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y:

Теперь нам известны значения уже двух переменных - z и y. Подставляем их в первое уравнение и получаем значение переменной x:

Таким образом, получили решение системы уравнений:

Пример 3. Предприятие выпускает продукцию трех видов: Р1,Р2,Р3 и использует сырье двух типов: S1 и S2. Нормы расхода сырья характеризуются матрицей
, где каждый элемент aij (i=1,2,3; j=1,2) показывает, сколько единиц продукции j- типа расходуется на производства единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой С=(100 80 130), стоимость единицы каждого типа сырья (ден. ед.) – матрицей-столбцом
В =  .
.
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Решение. Затраты 1 –го сырья составляют S1=2∙100+5∙80+1∙130=730 ед., поэтому матрица-строка затрат сырья S может быть записана как произведение
S=C·A=(100 80 130)· = (730 980)
= (730 980)
Тогда общая стоимость сырья Q=730∙30+980∙50=70900 ден. ед. может быть записана в матричном виде Q=S∙B=(CA)B=(70900).Общую стоимость сырья можно вычислить и в другом порядке: вначале вычислим матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу
R=A·B = , а затем общую стоимость сырья
Q = C·R = (100 80 130)· = (70900)
Задания для закрепления полученных умений и знаний.
Решить систему линейных уравнений методом Крамера:
| вар | Задания 1. | Задания 2. | вар | Задания 1. | Задания 2. |
| 1. | | | 1. | | |
| 2. | | | 2. | | |
Решить систему линейных уравнений методом Гаусса:
Вариант №1
Вариант №2
Задача.
Вариант №1.
Предприятие выпускает продукцию трех видов: Р1,Р2,Р3 и использует сырье двух типов: S1 и S2. Нормы расхода сырья характеризуются матрицей
, где каждый элемент aij (i=1,2,3; j=1,2) показывает, сколько единиц продукции j- типа расходуется на производства единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой С=(50 50 100), стоимость единицы каждого типа сырья (ден. ед.) – матрицей-столбцом В =  .
.
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Вариант №2
Предприятие выпускает продукцию трех видов: Р1,Р2,Р3 и использует сырье двух типов: S1 и S2. Нормы расхода сырья характеризуются матрицей
, где каждый элемент aij (i=1,2,3; j=1,2) показывает, сколько единиц продукции j- типа расходуется на производства единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой С=(30 50 50), стоимость единицы каждого типа сырья (ден. ед.) – матрицей-столбцом В =  .
.
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Контрольные вопросы
В чем заключается метод Крамера?
В чем заключается метод Гаусса?
Понятие обратной матрицы.
Как вычислить себестоимость продукции с помощью обратной матрицы?
Список использованной литературы
Основные источники
для обучающихся
Омельченко В.П., Курбатова Э.В. Математика 2-е издание, среднее профессиональное образование. Ростов – на – Дону: «Феникс», 2014г.
Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике: учеб. пособие: Рекомендовано ФГУ «ФИРО». – 160с., 2014г.
Основные источники
для преподавателей
Григорьев В.П., Дубинский Ю.А. Элементы высшей математики: учебник: Допущено Минобразованием России. – 5-е изд., стер. – 320с., 2014г.
Григорьев С.Г., Задулина С.В. Математика: Учебник: Допущено
Минобразованием России / Под ред. Гусева В.А. 4-е изд., стер. 384с., 2014г.
Дополнительные источники
для преподавателей
Спирина М.С., Спирин П.А. Дискретная математика: учебник: Допущено Минобразованием России - 5-е изд., стер. - 386., 2014г.
Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика:: учебник: Допущено Минобразованием России 352с., 2014г.
Пехлецкий И.Д. Математика: учебник. – М., 2014г.
Дополнительные источники
Для обучающихся
Пехлецкий И.Д. Математика: учебник. – М., 2014г.







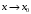 (и пишут
(и пишут 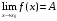 ), если для любого
), если для любого 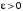 найдется число
найдется число 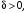 зависящее от , такое, что для всех
зависящее от , такое, что для всех 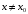 , удовлетворяющих условию
, удовлетворяющих условию 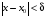 , выполняется неравенство
, выполняется неравенство 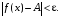
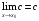 (c=const).
(c=const).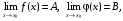 то:
то: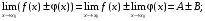
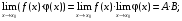
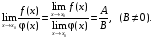
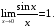
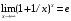 или
или 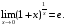
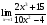
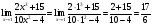
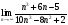
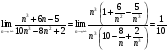
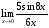
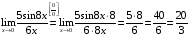
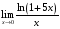
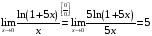
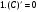
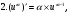 в частности,
в частности, 

















