Обобщающее повторение "Квадратное уравнение,квадратное неравенство, квадратичная функция"

Муниципальное бюджетное общеобразовательное учреждение «Подсосновская средняя общеобразовательная школа»

ОБОБЩАЮЩИЙ УРОК-ПРОЕКТ ПО ТЕМЕ

«КВАДРАТНОЕ УРАВНЕНИЕ. КВАДРАТНАЯ ФУНКЦИЯ. КВАДРАТНОЕ НЕРАВЕНСТВО».

УЧИТЕЛЬ МАТЕМАТИКИ: ПЕРКОВА ЕЛЕНА РОБЕРТОВНА.

Аннотация: Данный урок проводится в целях обобщения, систематизации знаний, подготовки к итоговой аттестации учащихся. Учащиеся были разбиты на группы. Каждая группа получила задание: изучить уровень знаний в различных возрастных группах ( 8, 9, 10, 11 классах) по темам «Квадратное уравнение», «Квадратное неравенство», «Квадратичная Функция». На уроке каждой группой был представлен анализ полученных данных. На урок был подобран материал сверх программы а также разобраны задания из материалов ОГЭ.

Обобщающий урок-проект по теме «Квадратное уравнение. Квадратичная функция. Квадратное уравнение.

Цель:

Образовательная

- создать условия для осознанного и успешного усвоения материала,

- систематизировать, обобщить расширить углубить теоретические знания,

- познакомить с нестандартными способами решения уравнений и неравенств,

- устранить пробелы в знаниях

Развивающая

- способствовать формированию умений применять приёмы: обобщения, выделения главного, переноса знаний в жизненную ситуацию;

-развитию математического кругозора в решении задач, мышления и речи, внимания, памяти.

Воспитательная

- содействовать воспитанию интереса к математике, активности, общей культуры.

Ход урока

1.ВСУПИТЕЛЬНОЕ СЛОВО УЧИТЕЛЯ (слайд 1-5)

Здравствуй ребята и гости.

Ребята, одной из основных задач, которая стоит перед нами это подготовка к основному госудаственному экзамену. Поэтому у нас сегодня на уроке обобщающее повторение по трем основным темам Модуля «Алгебра» это квадратное уравнении, квадратичная функция и квадратное неравенство. Научившись выполнять эти задания вы можете получить три заветных балла по модулю «Алгебра» а вы знаете что каждый балл на счету.

И пусть девизом нашего урока станут слова:

Три пути ведут к знанию:

путь размышления – это путь самый благородный,

путь подражания – это путь самый лёгкий

и путь опыта – это путь самый горький.
Конфуций

Цель нашего урока: Научиться размышлять, подражать т.е. работать по алгоритму. Решая одну задачу различными способами, путем сравнения выяснять, какой из них короче и эффективнее. Таким образом вырабатывать опыт.

Перед уроком вы были разбиты на 3 группы, и вам было дано задание.

Так как нам предстоит очень скоро сдавать экзамен и каждое задание считается решенным, если получен верный ответ, поэтому сегодня форма оценки знаю или не знаю. Результаты вы будете заносить в оценочный лист.

Тема «Квадратные уравнения» занимает в математике одно из центральных мест. Разнообразие задач относящихся к теме работы, очень велико. Они часто входят в состав решения более сложных задач математики и физики. Недаром среди математиков популярна такая фраза «Во многих задачах торчат уши квадратного уравнения». Вот эти «уши» и надо заметить, чтобы сообразить, как получить ответ.

Насколько разнообразны способы решения квадратных уравнений?

1.Выступление первой группы. (слайд 6-15) И так квадратное уравнение: Основные виды квадратных уравнений Неполные и Полные квадратные уравнения. Эта тема очень важна для изучения курса математики средней школы. Умение быстро, рационально и правильно решать квадратные уравнения облегчает прохождение многих тем курса математики. Например, решение задач на составление квадратных уравнений, разложение квадратного трехчлена на множители, квадратичная функция и ее график, неравенства второй степени .

Неполные квадратные уравнения

Анализ проведенного среза знаний

Неполные квадратные уравнения

ПЕРВЫЙ ТИП УРАВНЕНИЯ

Уравнение либо имеет два корня, либо не имеет ни одного. Если коэффициенты имеют одинаковые знаки, то уравнение корней не имеет. Если разные, то два противоположенных корня

Например,

ВТОРОЙ ТИП УРАВНЕНИЙ
уравнения один из корней которых всегда равен 0, другой вычисляется делением второго коэффициента на старший коэффициент взятый с противоположенным знаком.

Задание 1. Выберете из предложенных уравнений, те которые не имеют корней и запишите их попорядку в таблицу рядом с другими напишите ответы. Сделать это надо устно и как можно быстрее. (Проверяем и оцениваем)

Ответы:3,5,7,8.11,15

2.Выступление второй группы. Полные квадратные уравнения (слайд 16-31)

«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».

У. У. Сойер.

Решение квадратных уравнений по формулам

Повторяя материал по решению квадратных уравнений мы задались вопросом

Можно ли решать квадратные уравнения устно один из способов мы изучали в 8 классе это теорема Виета

Существуют ли ещё способы устного решения квадратных уравнений ,оказывается да

Вывод: Итак, решая квадратные уравнения, вы убедились в том, что зная различные способы решения, можно решать эти уравнения быстро, правильно и красиво.

Предлагаем решить квадратные уравнения используя предложенные способы решения

уравнений из материалов ОГЭ

3. Выступление третьей группы

« Квадратичная функция» Презентация (слайд 32-50) .

Учебные вопросы

1. Как зависит вид и расположение графика от коэффициентов a, b, c?

2. Как построить график квадратичной функции?

3.Как по графику квадратичной функции определить знаки коэффициентов a, b, c и найти значения х, у?

Предложить решить задания из ГИА

4.Выступление четвертой группы ( слайд 51-60)

EMBED PowerPoint.Slide.12

Предлагаем выполнить задание из ГИА

Рефлексия (слайд 61)

ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ ПО ТЕМЕ: «КВАДРАТНОЕ УРАВНЕНИЕ. КВАДРАТНОЕ НЕРАВЕНСТВО. КВАДРАТИЧНАЯ ФУНКЦИЯ» УЧИТЕЛЬ ПЕРКОВА Е.Р.

Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый лёгкий и путь опыта – это путь самый горький. Конфуций

• Результаты исследования
• Актуальность темы
• Постановка задач
• Повторение теоретического материала
• Разбор примеров
• Задания из материалов для подготовки ГИА

КВАДРАТНЫЕ УРАВНЕНИЯ

ТЕМА «КВАДРАТНЫЕ УРАВНЕНИЯ» ЗАНИМАЕТ В МАТЕМАТИКЕ ОДНО ИЗ ЦЕНТРАЛЬНЫХ МЕСТ. РАЗНООБРАЗИЕ ЗАДАЧ ОТНОСЯЩИХСЯ К ТЕМЕ РАБОТЫ, ОЧЕНЬ ВЕЛИКО. ОНИ ЧАСТО ВХОДЯТ В СОСТАВ РЕШЕНИЯ БОЛЕЕ СЛОЖНЫХ ЗАДАЧ МАТЕМАТИКИ И ФИЗИКИ. НЕДАРОМ СРЕДИ МАТЕМАТИКОВ ПОПУЛЯРНА ТАКАЯ ФРАЗА «ВО МНОГИХ ЗАДАЧАХ ТОРЧАТ УШИ КВАДРАТНОГО УРАВНЕНИЯ». ВОТ ЭТИ «УШИ» И НАДО ЗАМЕТИТЬ, ЧТОБЫ СООБРАЗИТЬ, КАК ПОЛУЧИТЬ ОТВЕТ.

НАСКОЛЬКО РАЗНООБРАЗНЫ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ?

НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ

РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ

НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ

ПЕРВЫЙ ТИП УРАВНЕНИЯ

Уравнение либо имеет два корня, либо не имеет ни одного. Если коэффициенты имеют одинаковые знаки, то уравнение корней не имеет. Если разные, то два противоположенных корня

Например,

ВТОРОЙ ТИП УРАВНЕНИЙ УРАВНЕНИЯ ОДИН ИЗ КОРНЕЙ КОТОРЫХ ВСЕГДА РАВЕН 0, ДРУГОЙ ВЫЧИСЛЯЕТСЯ ДЕЛЕНИЕМ ВТОРОГО КОЭФФИЦИЕНТА НА СТАРШИЙ КОЭФФИЦИЕНТ ВЗЯТЫЙ С ПРОТИВОПОЛОЖЕННЫМ ЗНАКОМ .

Например:

ВЫБЕРИТЕ ИЗ ПРЕДЛОЖЕННЫХ УРАВНЕНИЙ ТЕ, КОТОРЫЕ НЕ ИМЕЮТ КОРНЕЙ, И ЗАПИШИТЕ ИХ ПО ПОРЯДКУ В ТАБЛИЦУ, РЯДОМ С ДРУГИМИ НАПИШИТЕ ОТВЕТЫ.

САМОПРОВЕРКА. САМООЦЕНКА.

Не имеют корней

3

5

7

8

11

15

Имеют корни

1

0;5

2

4

6

-5;5

9

-4;4

10

12

0;

13

0;

14

0;

«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».

У. У. Сойер.

РЕШЕНИЕ ПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ

• 1 задание решали через D
• 2 задание решали через D- 50%

через

по теореме Виета - 20%

3 задание решали через D- 58%

через

Для достижения цели мы ставили перед собой следующие задачи

• 1.Изучить способы решения квадратных уравнений
• 2. Научиться решать квадратные уравнения устно

0" width="640"

1 СПОСОБ ( ТРАДИЦИОННЫЙ )

D 0

Корней нет

D = 0

D 0

2 СПОСОБ (ЧАСТНЫЙ СЛУЧАЙ )

b = 2k ( четное число)

Можно ли решать квадратные уравнения устно ?

3 СПОСОБ

2;5

-7;-3

-3;7

-6;3

4 СПОСОБ (И спользование свойств коэффициентов квадратного уравнения)

1) Если а+в+с=0,то

__________________________

Например,

а=1,в=4,с= -5

а+в=с=0

1+4+(-5)=0

2)Если а-в+с=0,то

_________________ ________

Например,

а=1,в=6,с=5

а-в+с=0 или в =а+с

1-6+5=0 или 6 =1+5

Приём «Переброски»

3) Если

Пример:

1. Умножим а на с :

2. Получим новое приведенное квадратное уравнение :

3. Используя теорему Виета, находим его корни 10 и 1, и делим на 2.

Ответ: 5; 1/2

4)

5)

6)

7)

К какому типу относится уравнение

1) Если а+в+с=0, то

Решите его

1)

2) Если в = а + с, то

2)

3)

3)

4)

4)

5)

5)

8 х 2 - 65 х + 8 = 0

Х 1 =8; Х 2 =1/8

5 х 2 + 26 х + 5 = 0

Х 1 = -5; Х 2 = -1/5

6)

6)

задание

1

ответы

-2;6

2

3

-3;6

-4;3

4

5

-1;8

-5;1

Итак, решая квадратные уравнения, вы убедились в том, что зная различные способы решения, можно решать эти уравнения быстро, правильно и красиво.

КВАДРАТИЧНАЯ ФУНКЦИЯ

Определить направление ветвей параболы.

1.

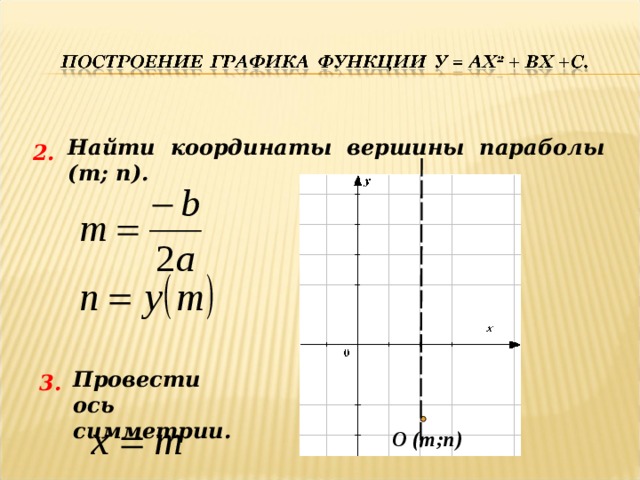
Найти координаты вершины параболы

(т; п).

2.

Провести ось

симметрии.

3.

О (т;п)

Определить точки пересечения графика

функции с осью О х , т.е. найти нули

функции.

4.

(х 1 ;0)

(х 2 ;0)

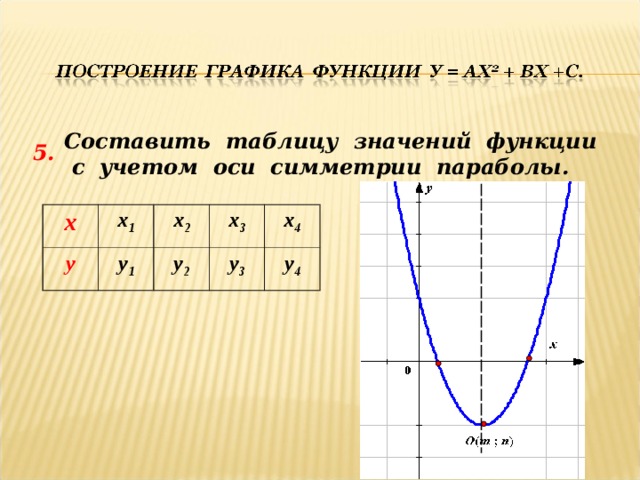
Составить таблицу значений функции

с учетом оси симметрии параболы.

5.

х

у

х 1

х 2

у 1

у 2

х 3

у 3

х 4

у 4

АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА ФУНКЦИИ У = АХ 2 + B Х +С.

1.

Определить направление ветвей параболы.

Найти координаты вершины параболы

(т; п).

2.

3.

Провести ось симметрии.

Определить точки пересечения графика

функции с осью О х , т.е. найти нули

функции.

4.

5.

Составить таблицу значений функции

с учетом оси симметрии параболы.

0 D=0 x x x ЗАВИСИМОСТЬ ДИСКРИМИНАНТА КВАДРАТНОГО ТРЕХЧЛЕНА ОТ ПАРАМЕТРОВ 2 D= b - 4ac" width="640"

D

y

y

y

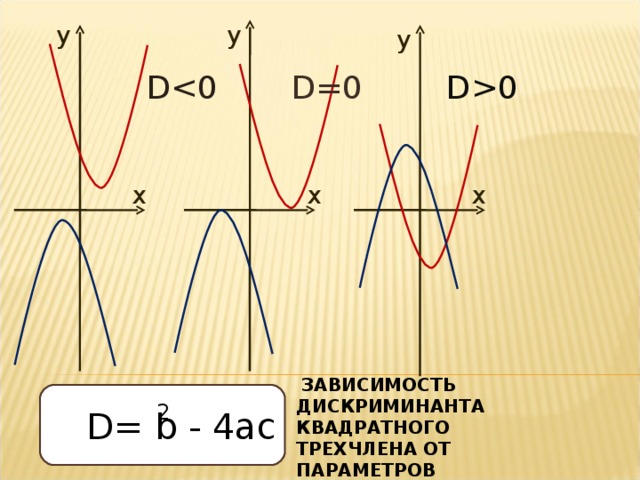
D0

D=0

x

x

x

ЗАВИСИМОСТЬ ДИСКРИМИНАНТА КВАДРАТНОГО ТРЕХЧЛЕНА ОТ ПАРАМЕТРОВ

2

D= b - 4ac

Какая группа параметров соответствует эскизу параболы?

y

x

c

0 b bc D c0 X 1 D0 X 2 X 1 0 X 2 0 y c x 2 x 1 x 0 x 0 y 0 СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ ВИЕТА b=-a(x 1 +x 2 )" width="640"

ОПРЕДЕЛЕНИЕ ЗНАКА ПАРАМЕТР A b ПАРАБОЛЫ

ПО ЕЕ ЭСКИЗУ

a

a0

b

b

c

D

c0

X 1

D0

X 2

X 1 0

X 2 0

y

c

x 2

x 1

x 0

x

0

y 0

СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ ВИЕТА

b=-a(x 1 +x 2 )

0 b b0 c D c0 X 1 D0 X 2 X 1 X 2 y c x 0 x 0 x 2 x 1 y 0 СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ ВИЕТА b=-a(x 1 +x 2 )" width="640"

ОПРЕДЕЛЕНИЕ ЗНАКА ПАРАМЕТР A b ПАРАБОЛЫ

ПО ЕЕ ЭСКИЗУ

a

a0

b

b0

c

D

c0

X 1

D0

X 2

X 1

X 2

y

c

x 0

x

0

x 2

x 1

y 0

СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ ВИЕТА

b=-a(x 1 +x 2 )

0 2) a0;c0; bx c 3) a0;c0 4) a0;c42" width="640"

Какая группа параметров соответствует эскизу параболы?

y

1) a0; b0

2) a0;c0; b

x

c

3) a0;c0

4) a0;c

42

Какая группа параметров соответствует эскизу параболы?

y

x

c

43

0 ( ветви параболы – вверх ), тогда рассматриваем 1) и 3) функции; 2. Найдем нули функций ( точки пересечения графика с осью Ох ): 1) х 2 – х = 0, 3) х 2 + х = 0 х (х – 1) =0 , х (х + 1) = 0 х = 0 х = 0 х = 1 х = -1 3) Ответ: 3. Сравниваем нули с графиком" width="640"

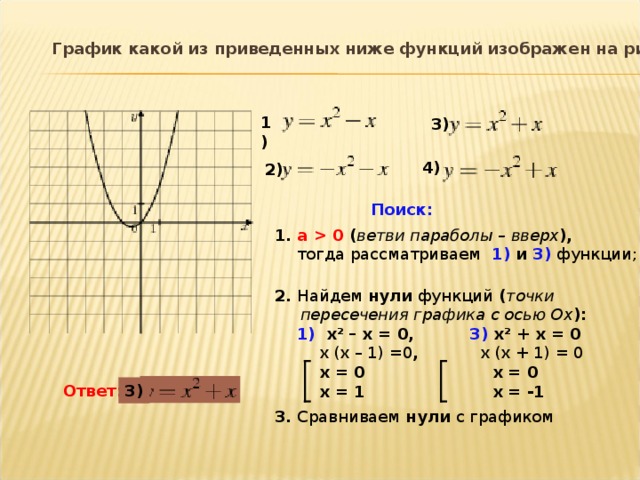
График какой из приведенных ниже функций изображен на рисунке?

1)

3)

4)

2)

Поиск:

1. a 0 ( ветви параболы – вверх ),

тогда рассматриваем 1) и 3) функции;

2. Найдем нули функций ( точки

пересечения графика с осью Ох ):

1) х 2 – х = 0, 3) х 2 + х = 0

х (х – 1) =0 , х (х + 1) = 0

х = 0 х = 0

х = 1 х = -1

3)

Ответ:

3. Сравниваем нули с графиком

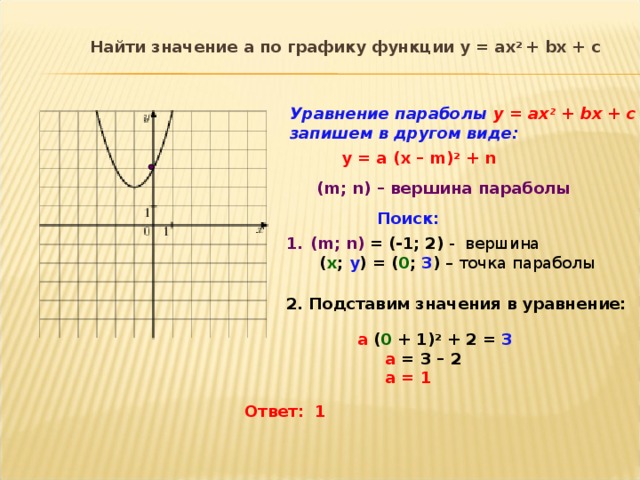
Найти значение a по графику функции у = ах 2 + bx + c

Уравнение параболы у = ax 2 + bx + c

запишем в другом виде:

y = a (x – m) 2 + n

( m; n) – вершина параболы

Поиск:

• ( m; n) = (-1; 2) - вершина

( х ; у ) = ( 0 ; 3 ) – точка параболы

2. Подставим значения в уравнение:

a ( 0 + 1 ) 2 + 2 = 3

а = 3 – 2

а = 1

Ответ: 1

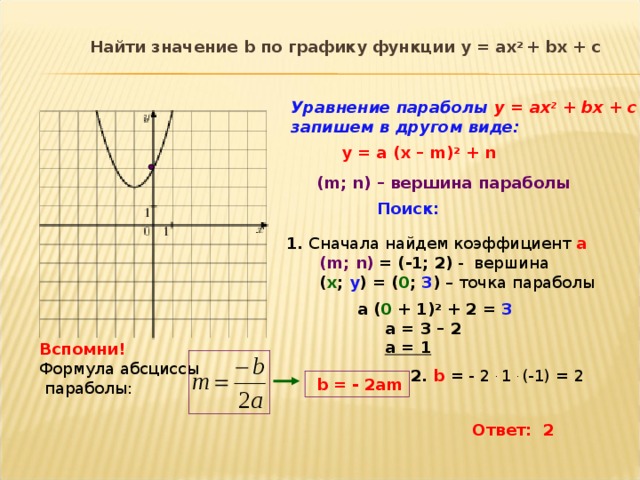
Найти значение b по графику функции у = ах 2 + bx + c

Уравнение параболы у = ax 2 + bx + c

запишем в другом виде:

y = a (x – m) 2 + n

( m; n) – вершина параболы

Поиск:

1. Сначала найдем коэффициент а

( m; n) = (-1; 2) - вершина

( х ; у ) = ( 0 ; 3 ) – точка параболы

a ( 0 + 1 ) 2 + 2 = 3

а = 3 – 2

а = 1

Вспомни!

Формула абсциссы

параболы:

2. b = - 2 . 1 . (-1) = 2

b = - 2am

Ответ: 2

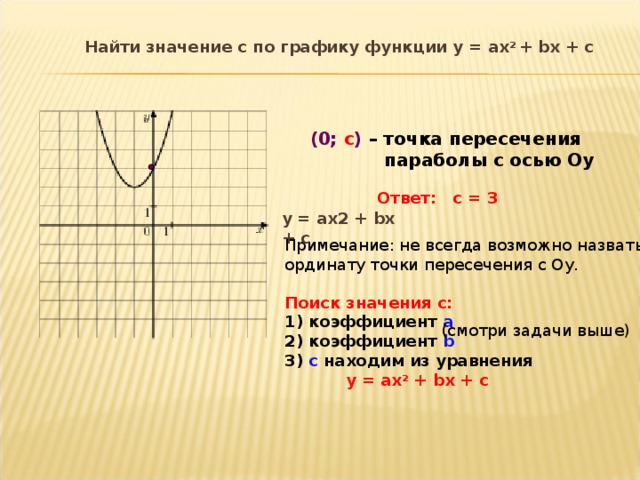
Найти значение c по графику функции у = ах 2 + bx + c

(0; c ) – точка пересечения

параболы с осью Оу

Ответ: с = 3

у = ах2 + bx + c

Примечание: не всегда возможно назвать

ординату точки пересечения с Оу.

Поиск значения с:

1) коэффициент а

2) коэффициент b

(смотри задачи выше)

3) с находим из уравнения

у = ах 2 + bx + c

На одном из рисунков изображен график

функции

Укажите номер этого рисунка.

Задание ГИА

(№ 193093)

1

3

2

4

задания

6

ответы

1

7

8

1

1

9

10

134

413

КВАДРАТНЫЕ НЕРАВЕНСТВА

КВАДРАТНЫЕ НЕРАВЕНСТВА ПРЕДЛОЖЕННЫЕ ДЛЯ РЕШЕНИЯ УЧАЩИМСЯ 9-11КЛАССОВ

РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ

0 Неравенство называется квадратным , если в левой его части стоит квадратный трехчлен, а в правой – нуль. Решением неравенства называется то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство . Решить неравенство – это значит найти все его решения или установить, что их нет." width="640"

Квадратное неравенство

ах 2 + bx + c ≤ 0

ах 2 + bx + c ≥ 0

ах 2 + bx + c 0

ах 2 + bx + c 0

Неравенство называется квадратным ,

если в левой его части стоит квадратный трехчлен,

а в правой – нуль.

Решением неравенства называется то значение неизвестного,

при котором это неравенство обращается

в верное числовое неравенство .

Решить неравенство – это значит найти все его решения

или установить, что их нет.

Графический способ решения

квадратного неравенства

1. Определить направление ветвей параболы

по знаку коэффициента а.

2.Найти корни соответствующего квадратного уравнения

или установить, что их нет.

3. Построить эскиз графика квадратичной функции.

4. По графику определить промежутки, на которых

функция принимает нужные значения.

0 9 8 7 6 5 4 3 2 1 х 2 – х – 6 0 № 2. о х -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 № 3. х 2 – х – 6 -1 -2 -3 -4 -5 -6 № 4. х 2 – х – 6 0" width="640"

Решите неравенство

у = х 2 – х – 6

у

№ 1.

х 2 – х – 6 0

9

8

7

6

5

4

3

2

1

х 2 – х – 6 0

№ 2.

о

х

-7 -6 -5 -4 -3 -2 -1

1 2 3 4 5 6 7

№ 3.

х 2 – х – 6

-1

-2

-3

-4

-5

-6

№ 4.

х 2 – х – 6 0

Метод интервалов для

квадратного неравенства

1. Найти корни соответствующего квадратного уравнения

или установить, что их нет.

2. Отметить корни на числовой прямой.

3. В крайнем правом интервале поставить знак, соответствующий

знаку коэффициента a квадратного трехчлена.

4. Расставить знаки на остальных интервалах в порядке чередования.

5. Определить промежутки, на которых функция принимает нужные

значения.

РЕШЕНИЕ НЕРАВЕНСТВА МЕТОДОМ ИНТЕРВАЛОВ

1

2

4

3

1

4

4

5

1

1

- СЕГОДНЯ Я УЗНАЛ… - ТЕПЕРЬ Я МОГУ… - МАТЕРИАЛ УРОКА МНЕ БЫЛ… - МНЕ ЗАХОТЕЛОСЬ… - УРОК МНЕ ДАЛ… - МОГУ ОЦЕНИТЬ СВОЮ РАБОТУ НА УРОКЕ…