Тема: Метрическая система. Запись больших и малых чисел.
Цели урока:
Образовательная
- Понимать суть физической теории и эксперимента, уметь их различать.
Развивающая
- Развивать речь, память, точность.
Воспитывающая
- Воспитывать внимательность, дисциплинированность.
Тип урока: комбинированный.
Орг. момент (2-3 мин)
Фронтальный опрос домашнего задания (8-10 мин)
Объяснение новой темы (20-22 мин)
Закрепление новой темы ( 3-5 мин)
Домашнее задание (2-3 мин)
Итоги урока (1-2 мин)
Ход урока.
Орг. момент.
II.
В чем смысл физических величин?
Что такое значение физической величины?
Как можно определить значение физической величины?
Что значит измерить физическую величину?
III. В жизни, в практических расчетах, особенно в научных исследованиях, точность измерения физических величин занимает особое место.
Точность измерения зависит от чувствительности прибора и опытности человека, выполняющего измерение. Например, попытаемся измерить длину тела с помощью двух линеек с различной ценой деления (рис. 1 а, б). Длина тела, измеренная с помощью линейки, изображенной на рисунке 1 а, равна 4 см, а с помощью второй линейки (рис. 1 б) - 4,1 см. Отсюда видим, что, несмотря на большой опыт, который имеет измеряющий, ошибки в измерении возникают, поэтому при записи значения измеренной величины нужно указывать и точность выполненного измерения. Например, точность измерения на рисунке 1 а – составляет 1 см, а точность измерения на рисунке 1б - 0,1 см. Результат второго измерения, по сравнению с первым, получен с большей точностью. Таким образом, мы часто сталкиваемся с так называемой инструментальной (приборной) погрешностью.
Кроме инструментальных погрешностей при измерениях возможны ошибки и в силу других различных причин. Некорректность выполнения измерения, неправильное использование прибора, изменчивость измеряемой величины - все это увеличивает погрешность измерения.
При выполнении исследовательских или лабораторных работ принята специальная форма записи значений измеряемых величин. При записи такой формы следует учитывать, что наибольшая погрешность правильно выполненных отсчетов с помощью большинства приборов составляет половину цены деления. Например, цена деления линейки на рисунке 1а - равна 0,5 см, поэтому погрешность измерения равна ее половине, т.е. 0,25 см. Тогда результат измерения величины записывают так:
 см
см
Отсюда вытекает вывод: при измерении первой линейкой длина тела находится в промежутке между 3,75см и 4,25см, т. е.

Цена деления линейки, представленной на рисунке 1б – 0,1см. длина тела – 4,1см. Погрешность измерения: 0,1/2=0,05см. значение измеренной величины:
 или
или 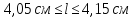
Из рассмотренных выше примеров вытекает такой вывод: чем меньше расстояние между делениями шкалы прибора, тем больше точность измерения, поэтому точность измерения, выполненного с помощью второй линейки, выше точности первого измерения.
Если обозначим значение величины буквой а, а погрешность измерения – h0, то результат измерения запишем в виде:
 , или
, или  .
.
В физике используются прямой и косвенный методы измерения. При прямом методе значение величины определяется непосредственным показанием прибора. Во многих случаях непосредственное измерение физической величины невозможно. Например, с помощью линейки невозможно непосредственно определить объем. Однако объем можно рассчитать измерением длины, ширины и высоты тела, поэтому этот способ называют косвенным. Точность расчетов косвенного метода такая же, как и точность измерений.
Современные единицы измерения Международной системы (СИ) были введены не сразу. Единицы, применяемые в настоящее время, - результат исторического развития.
В старину все страны пользовались своими единицами измерения. Например, казахи для измерения длины использовали такие единицы, как карыс (расстояние между раздвинутыми большим и средним пальцами, по-русски пядь), ель (ширина одного пальца), суйем (расстояние между вытянутыми большим и указательным пальцами), табан (длина ступни). Русская мера длины - 1 верста равна 500 саженям. В США и Англии до сих пор пользуются такими единицами длины, как миля, ярд, фут, дюйм. Такое разнообразие единиц измерения затрудняет переход от одних единиц к другим, затем к третьим, требует длительных вычислений.
Бессистемность единиц измерения затрудняла торговые отношения между народами, тормозила развитие промышленности. В связи с этим 1 августа 1793 г. важным актом Конвента (правительства Франции того времени) было принято историческое решение о введении Метрической системы мер. В качестве основной единицы длины был взят метр. На эталоне метра были высечены слова: «На все времена, для всех народов».
Впоследствии Метрическая система мер, предложенная Францией, была принята большинством стран мира. В настоящее время в научных исследованиях пользуются международной системой, в основе которой лежат единицы измерения, входящие в Метрическую систему мер.
Основу Метрической системы мер составляют: единица длины - метр (м)и единица массы - килограмм, которые входят и в Международную систему единиц (СИ). Другие единицы являются производными от них, например, единица площади - м2 (квадратный метр), единица объема - м3 (кубический метр), единица вместимости - литр (л), 1 л = 1 дм3 (кубический дециметр). На практике 1 литр определяют как объем, занимаемый одним килограммом воды.
Взятие десятичного принципа за основу Метрической системы мер, как общего способа исчисления для всех народов, является ее важнейшим достоинством.
Действительно, по десятичному принципу, умножив или разделив на 10 основные единицы, можно получить все остальные кратные и дольные единицы.
В связи с этим создана десятичная система приставок. Например, приставка «кило» означает тысяча, поэтому 1 километр (км) = 1000 метрам (м); 1 килограмм(кг) = 1000грамм (г); 1килоВольт = 1000 Вольт (В).
Приставка «милли» означает: одна тысячная доля; Миллиграмм - одна тысячная доля грамма; 1 миллиметр - одна тысячная метра; 1 миллилитр - одна тысячная литра.
Метрическая система мер облегчает переход от одних единиц к другим, особенно она незаменима при переходе к квадратным и кубическим единицам.. В таблице 1 приложения (с. 215) приведены некоторые приставки Метрической системы мер и их числовые значения относительно основных единиц.
В физике и астрономии часто приходится иметь дело с очень большими и очень маленькими числами. Например, расстояние от Земли до Солнца 150 000 000 км, скорость света 300 000 000 м/с (точнее, 299 792 458 м/с ), размер молекулы водорода равен 0,000 000 023 см. С такими числами крайне неудобно выполнять математические расчеты. Поэтому, чтобы записать очень большие и малые числа, используют запись в виде произведения двух множителей. Обычно первый множитель - однозначное или двузначное число с запятой, а второй множитель - число 10 с показателем степени. Например, расстояние между Землей и Солнцем можно записать в виде произведения двух чисел (множителей):
150 000 000км = 1,5*108км = 1,5*1011м.
Здесь 1,5 первый множитель, а 108 или 1011 – вторые множители, 8 и 11 – показатели степени.
Натуральные числа m и n, которые являются показателями степени числа 10, подсказывают, сколько надо число 10 умножить само на себя, чтобы получить искомое число. 100= 1.
То, что показатель степени числа 10 является натуральным числом, облегчает выполнение умножения и деления при расчетах.
10m*10n= 10m+n
10m:10n= 10m-n
При записи десятичных дробей 0,1; 0,001; и т. д. в виде10 со степенями перед показателем степени ставят знак минус (-). 0,1 = 10-1.
Запись чисел в таком виде очень удобна. Например, диаметр молекулы водорода: 0, 000 000 023см =2,3*10-8см.
Безусловно, запись числа 0, 000 000 023 в виде 2,3*10-8 намного проще.
Запись чисел с использованием степени 10 называют записью числа в стандартном виде.
IV. Ответить на вопросы со стр. 37, 39, 41. Упр. 3 № 1; упр. 4 №1, 2, 3.
V. Домашнее задание § 11-13, упр. 4 № 4-10.
VI. Итоги урока.







 см
см
 или
или 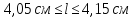
 , или
, или  .
.









