Методическая разработка по теме
«Квадратичная функция. Квадратные уравнения и неравенства с параметрами».
Решение квадратных уравнений с параметрами по определению.
Определение. Решить уравнение или неравенство с параметрами – это значит определить, при каких допустимых значениях параметров уравнение или неравенство
имеет решения
не имеет решений
установить количество решений
найти вид каждого решения при соответствующих ему значениях параметров
Задача 1. Решите уравнение 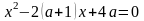
Решение. 1) Данное уравнение – квадратное относительно переменной 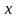 с параметром
с параметром 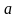 . Допустимыми являются любые действительные значения параметра. Для того, чтобы уравнение имело решения, необходимо и достаточно, чтобы дискриминант данного уравнения принимал неотрицательные значения.
. Допустимыми являются любые действительные значения параметра. Для того, чтобы уравнение имело решения, необходимо и достаточно, чтобы дискриминант данного уравнения принимал неотрицательные значения. 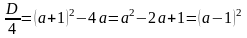 . Так как
. Так как 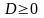 при всех значениях параметра, то уравнение имеет решение также при всех значениях параметра.
при всех значениях параметра, то уравнение имеет решение также при всех значениях параметра.
Если 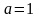 , то
, то  , следовательно, уравнению удовлетворяет единственное значение переменной
, следовательно, уравнению удовлетворяет единственное значение переменной 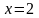 , т.е. уравнение имеет корень кратности два.
, т.е. уравнение имеет корень кратности два.
Если 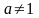 , то уравнение имеет два различных корня.
, то уравнение имеет два различных корня.
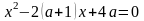
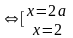 .
.
Ответ: При 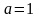 уравнению удовлетворяет единственное значение переменной
уравнению удовлетворяет единственное значение переменной 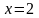 , при
, при 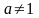 уравнение имеет два решения
уравнение имеет два решения 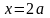 и
и 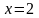 .
.
Задача 2. Решите уравнение 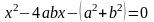
Решение. Допустимыми являются любые действительные значения параметров. Согласно схеме решения задач с параметрами, имеем:
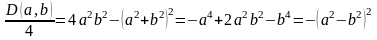 .
.
Если 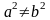 , то дискриминант уравнения отрицателен, и уравнение решений не имеет.
, то дискриминант уравнения отрицателен, и уравнение решений не имеет.
Если 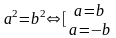 , то уравнение имеет решение, но при этом дискриминант равен нулю, и поэтому единственное значение переменной
, то уравнение имеет решение, но при этом дискриминант равен нулю, и поэтому единственное значение переменной 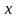 , удовлетворяющее уравнению, равно
, удовлетворяющее уравнению, равно 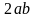 .
.
Ответ: При 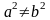 уравнение решений не имеет; при
уравнение решений не имеет; при 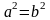 уравнению удовлетворяет единственное значение переменной
уравнению удовлетворяет единственное значение переменной 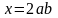 .
.
Упражнение 1. Решите уравнение при всех допустимых значениях параметра.
1) 2)
3) 4)
Ответ:
Упражнение 2. Решите уравнения
1) 2) 
3) Поезд был задержан на станции на  минут. Чтобы наверстать опоздание, машинист увеличил скорость на
минут. Чтобы наверстать опоздание, машинист увеличил скорость на 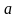 км/ч и на следующем перегоне длиной
км/ч и на следующем перегоне длиной  км наверстал потерянное время. С какой скоростью поезд шел после выхода со станции?
км наверстал потерянное время. С какой скоростью поезд шел после выхода со станции?
Решение. Пусть искомая скорость  км/ч, тогда скорость поезда до станции равна
км/ч, тогда скорость поезда до станции равна  км/ч. Перегон поезд прошел за
км/ч. Перегон поезд прошел за  часов, а с первоначальной скоростью он прошел бы его за
часов, а с первоначальной скоростью он прошел бы его за  часов.
часов.
Составим уравнение: ; ; ; ; .
Из условия задачи следует положительность всех входящих в ответ параметров.
Ответ: .
Дискриминант квадратного уравнения.
Задача 3. При каких значениях параметра 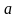 уравнению
уравнению  удовлетворяет единственное значение переменной
удовлетворяет единственное значение переменной 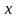 ?
?
Решение. В данной задаче не требуется решить это уравнение. Уравнению будет удовлетворять единственное значение переменной в том случае, если дискриминант этого уравнения будет равен нулю. Следовательно, искомые значения параметра 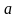 будут задаваться уравнением
будут задаваться уравнением  . Имеем
. Имеем 
 .
.
Ответ: -2; 2.
Замечание. В дальнейшем вместо формулировки «единственное значение переменной» будем придерживаться более простой и широко распространенной «единственный корень уравнения».
Задача 4. Найдите все значения параметра, при каждом из которых уравнение  имеет два различных корня.
имеет два различных корня.
Решение. Условие наличия различных корней равносильно условию положительности его дискриминанта. Поэтому, находя его дискриминант: , получим, что искомые значения параметра будут являться решениями неравенства  ,
,  .
.
Ответ:  .
.
Задача 4. Найдите все значения параметра 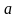 , при каждом из которых уравнение имеет единственный корень.
, при каждом из которых уравнение имеет единственный корень.
Решение. В данном случае реализуется один из основных принципов решения задач с параметрами: если старший коэффициент при выделенной переменной – параметрический, то должен быть рассмотрен случай, когда он равен нулю.
Таким образом, искомыми значениями параметра могут быть либо  , либо те его значения, отличные от 2, при которых дискриминант получающегося квадратного уравнения равен нулю.
, либо те его значения, отличные от 2, при которых дискриминант получающегося квадратного уравнения равен нулю.
При  имеем линейное уравнение
имеем линейное уравнение  . Оно имеет единственное решение
. Оно имеет единственное решение  .
.
Оставшиеся значения параметра будут решениями системы
; ;  .
.
Ответ: 1; 2; 6.
Упражнение 3. Найдите все значения параметра, при каждом из которых уравнение имеет два различных корня.
1) 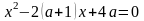 2)
2)
3)  4)
4)
Ответы: 1)  ; 2) ; 3)
; 2) ; 3)  ;
;
4) .
Упражнение 4. Найдите все значения параметра, при каждом из которых уравнение имеет один корень.
2)
3) 4)
Ответы: 1) -1,5 ; 3; 2) 1;  ; 2 ; 3) 0; 4; 4) -4; 3.
; 2 ; 3) 0; 4; 4) -4; 3.
Упражнение 5. Найдите все значения параметра, при каждом из которых уравнение не имеет решений.
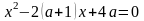 2)
2)
3)  4)
4)
Ответы: 1) пустое множество; 2) ; 3)  ;
;
4) .
Соотношение между корнями квадратного трехчлена. Теорема Виета.
Задача 5. Не решая уравнения  , найдите
, найдите  , где
, где и
и  - его корни.
- его корни.
Решение. Так как у данного квадратного трехчлена коэффициенты 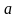 и
и  имеют разные знаки, то действительные корни уравнения существуют. Преобразуем искомое выражение следующим образом:
имеют разные знаки, то действительные корни уравнения существуют. Преобразуем искомое выражение следующим образом:
 =
= .
.
Согласно теореме Виета,  ;
;  .
.
Итак,  .
.
Ответ: 
Задача 6. Найдите 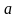 , если
, если  и
и  - корни трехчлена
- корни трехчлена  удовлетворяют соотношению
удовлетворяют соотношению  .
.
Решение. Согласно теореме Виета, значения  и
и  должны удовлетворять следующей системе уравнений .
должны удовлетворять следующей системе уравнений .
Решая линейную систему , получим .
Эти выражения подставим во второе уравнение. Имеем квадратное уравнение относительно параметра 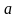 : . Его корни
: . Его корни  ;
;  .
.
Так как согласно условию, числа  и
и  действительные, проверять положительность дискриминанта при найденных значениях параметра не требуется.
действительные, проверять положительность дискриминанта при найденных значениях параметра не требуется.
Ответ:  ;
;  .
.
Задача 7. При каких значениях параметра 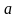 квадратный трехчлен
квадратный трехчлен  имеет два различных действительных корня, сумма кубов которых меньше 40?
имеет два различных действительных корня, сумма кубов которых меньше 40?
Решение. .
Решим систему неравенств ; ; ;  .
.
Ответ:  .
.
Задача 8. Действительные числа 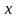 и
и  таковы, что . При каких значениях параметра a произведение
таковы, что . При каких значениях параметра a произведение  принимает наименьшее значение?
принимает наименьшее значение?
Решение.
;  .
.
Функция  принимает наименьшее значение при
принимает наименьшее значение при  .
.
Согласно теореме Виета, 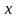 и
и  являются корнями квадратного уравнения , дискриминант которого
являются корнями квадратного уравнения , дискриминант которого  .
.
По условию, числа 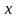 и
и  действительные, следовательно,
действительные, следовательно, 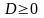 ;
;  ;
;  . Так как при
. Так как при  функция
функция  возрастает, то наименьшее значение
возрастает, то наименьшее значение  принимает при
принимает при  .
.
Ответ:  .
.
Упражнение 6. Найдите все значения параметра , при каждом из которых сумма квадратов различных корней уравнения  больше 10.
больше 10.
Ответ:  .
.
Упражнение 7. Найдите значения параметра  , при каждом из которых разность корней уравнения не зависит от значений параметра.
, при каждом из которых разность корней уравнения не зависит от значений параметра.
Pасположение корней квадратного трехчлена относительно выбранной точки числовой оси.
Пусть  и
и 
 - корни трехчлена
- корни трехчлена  ,
,  - некоторое заданное действительное число. Необходимые и достаточные условия различных вариантов расположения на числовой оси корней
- некоторое заданное действительное число. Необходимые и достаточные условия различных вариантов расположения на числовой оси корней  и
и  относительно числа
относительно числа  приведены в следующей таблице:
приведены в следующей таблице:
Задача 9. Найдите все значения параметра 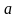 , при которых корни уравнения лежат по разные стороны от точки
, при которых корни уравнения лежат по разные стороны от точки  =1.
=1.
Решение. Так как в промежутке между корнями квадратный трехчлен имеет знак, противоположный коэффициенту при  , то имеем следующее неравенство: ; ; ;
, то имеем следующее неравенство: ; ; ;
;  .
.
Ответ:  .
.
Задача 10. Найдите все значения параметра 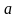 , при которых два корня уравнения различны и каждый из них больше 1.
, при которых два корня уравнения различны и каждый из них больше 1.
Решение. Составим следующую систему:
; ; ; ;  .
.
Ответ:  .
.
Задача 11. Найдите все значения параметра 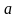 , при которых уравнение имеет два корня, причем один из них меньше
, при которых уравнение имеет два корня, причем один из них меньше 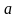 , а другой больше
, а другой больше 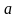 .
.
Решение. Искомые значения параметра задаются неравенством . Решим это неравенство.
;  ;
;  ;
;  .
.
Ответ:  .
.
Задача 12. Найдите все значения параметра 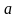 , при которых корни уравнения
, при которых корни уравнения  больше
больше 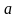 .
.
Решение. Искомые значения параметра задаются системой неравенств . Получим: ; ;  .
.
Ответ:  .
.
Решение квадратных неравенств
Задача 13. Найдите все значения параметра 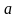 , при которых неравенство не выполняется ни при каких действительных значениях
, при которых неравенство не выполняется ни при каких действительных значениях 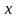 .
.
Решение. Из этого бесконечного множества неравенств выделим то, которое является линейным. При  неравенство имеет вид
неравенство имеет вид  . Его решение
. Его решение  не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
Квадратный трехчлен будет неположительным при всех действительных значениях 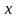 при выполнении следующих условий: .
при выполнении следующих условий: .
; ; ; ;
;  .
.
Ответ:  .
.
Задача 14. Для каждого значения параметра решить неравенство .
Решение.
Из этого бесконечного множества неравенств выделим то, которое является линейным. При  неравенство имеет вид
неравенство имеет вид  . Его решение:
. Его решение:  .
.
При всех значениях  неравенства этого семейства являются квадратными. При
неравенства этого семейства являются квадратными. При  ветви парабол направлены вниз, при
ветви парабол направлены вниз, при  - вверх. Следующее контрольное значение параметра найдем из условия равенства нулю дискриминанта квадратного трехчлена: ;
- вверх. Следующее контрольное значение параметра найдем из условия равенства нулю дискриминанта квадратного трехчлена: ;  ;
;  .
.
Если  , то
, то  ; если
; если  , то
, то  . Графически все эти случаи можно представить следующим образом:
. Графически все эти случаи можно представить следующим образом:




Ответ: при  при
при 

при  при
при 

при  решений нет.
решений нет.
Задача 15. Для каждого значения параметра 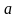 решить неравенство .
решить неравенство .
Решение. ;

 .
.
Так как неравенство строгое, то при  оно не имеет решений. При
оно не имеет решений. При  решением неравенства является промежуток между корнями трехчлена, равными
решением неравенства является промежуток между корнями трехчлена, равными  и
и  .
.
При 
 , следовательно,
, следовательно, 
 .
.
При 
 , значит,
, значит, 
 .
.
Ответ: При  неравенство не имеет решений; при
неравенство не имеет решений; при 
 ; при
; при 
 .
.
Задача 16. Найти все значения параметра 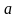 , при которых неравенство выполняется при всех действительных значениях
, при которых неравенство выполняется при всех действительных значениях 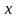 .
.
Решение. Представим неравенство как квадратное относительно  и сделаем замену
и сделаем замену  . Получим следующую систему неравенств:
. Получим следующую систему неравенств:
 .
.
А бсцисса вершины квадратного трехчлена зависит от параметра: .
.
Семейство парабол разделим на три группы. К первой отнесем те из них, вершины которых расположены левее промежутка  ; ко второй – вершины которых расположены внутри или на границе промежутка
; ко второй – вершины которых расположены внутри или на границе промежутка  ; к третьей - вершины которых расположены правее этого промежутка.
; к третьей - вершины которых расположены правее этого промежутка.
Необходимым и достаточным условием положительности функции в указанном промежутке является выполнение неравенства  при
при  . Для первой группы – это неравенство
. Для первой группы – это неравенство  , для второй -
, для второй -  , для третьей -
, для третьей -  . Таким образом, получим совокупность трех систем неравенств:
. Таким образом, получим совокупность трех систем неравенств:
(1) , (2) , (3) .
Решим последовательно каждую из них.
(1) ,  .
.
(2) . Система несовместна.
 (3) ,
(3) ,  .
.
Ответ:  ;
;  .
.
Задача 17. Для каждого значения параметра решить неравенство  .
.
 ,
,  ,
,  .
.
 ,
,  ,
,  ,
,  .
.
При 
 , при
, при 
 .
.
Следовательно,  .
.
Решение системы (1): при  решений нет; при
решений нет; при 
 .
.
Решение системы (2): при 
 ; при
; при 
 , но
, но  ; при
; при 
 ,
,  ; при
; при 
 .
.
Ответ: при 
 ;
;  ; при
; при  ; при
; при 
 ; при
; при  .
.
Задача 18. При каких значениях  вершины парабол
вершины парабол  и
и  расположены по разные стороны от оси абсцисс?
расположены по разные стороны от оси абсцисс?
Решение. Найдем ординаты вершин данных парабол.
 ;
;  ; .
; .
 ;
;  ;
;  .
.
Так как вершина первой параболы лежит ниже оси 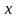 при всех значениях
при всех значениях  , то, следовательно, требуется найти, при каких значениях
, то, следовательно, требуется найти, при каких значениях вершина второй параболы расположена выше оси. Получаем
вершина второй параболы расположена выше оси. Получаем  .
.
Ответ:  .
.
12






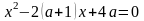
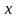 с параметром
с параметром 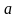 . Допустимыми являются любые действительные значения параметра. Для того, чтобы уравнение имело решения, необходимо и достаточно, чтобы дискриминант данного уравнения принимал неотрицательные значения.
. Допустимыми являются любые действительные значения параметра. Для того, чтобы уравнение имело решения, необходимо и достаточно, чтобы дискриминант данного уравнения принимал неотрицательные значения. 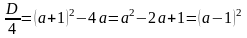 . Так как
. Так как 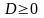 при всех значениях параметра, то уравнение имеет решение также при всех значениях параметра.
при всех значениях параметра, то уравнение имеет решение также при всех значениях параметра.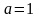 , то
, то  , следовательно, уравнению удовлетворяет единственное значение переменной
, следовательно, уравнению удовлетворяет единственное значение переменной 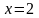 , т.е. уравнение имеет корень кратности два.
, т.е. уравнение имеет корень кратности два.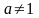 , то уравнение имеет два различных корня.
, то уравнение имеет два различных корня.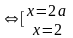 .
.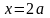 и
и 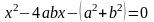
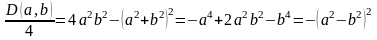 .
.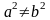 , то дискриминант уравнения отрицателен, и уравнение решений не имеет.
, то дискриминант уравнения отрицателен, и уравнение решений не имеет.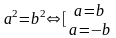 , то уравнение имеет решение, но при этом дискриминант равен нулю, и поэтому единственное значение переменной
, то уравнение имеет решение, но при этом дискриминант равен нулю, и поэтому единственное значение переменной 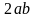 .
.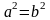 уравнению удовлетворяет единственное значение переменной
уравнению удовлетворяет единственное значение переменной 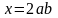 .
.
















