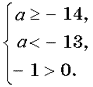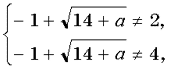Лекция: «Методы решения показательных уравнений».
1. Показательные уравнения.
Уравнения, содержащие неизвестные в показателе степени, называются показательными уравнениями. Простейшим из них является уравнение аx = b, где а 0, а ≠ 1.
1) При b b = 0 это уравнение, согласно свойству 1 показательной функции, не имеет решения.
2) При b 0 используя монотонность функции и теорему о корне, уравнение имеет единственный корень. Для того, чтобы его найти, надо b представить в виде b = aс, аx = bс x = c или x = logab.
Показательные уравнения путем алгебраических преобразований приводят к стандартным уравнения, которые решаются, используя следующие методы:
метод приведения к одному основанию 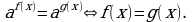 ;
;
метод оценки;
графический метод;
метод введения новых переменных;
метод разложения на множители;
показательно – степенные уравнения;
показательные с параметром.
2. Метод приведения к одному основанию.
Способ основан на следующем свойстве степеней: если равны две степени и равны их основания, то равны и их показатели, т.е. уравнение надо попытаться свести к виду
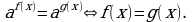
Примеры. Решить уравнение:
1. 3x = 81;
Представим правую часть уравнения в виде 81 = 34 и запишем уравнение, равносильное исходному 3 x = 34; x = 4. Ответ: 4.
 2.
2. 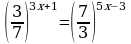
Представим правую часть уравнения в виде 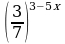 и перейдем к уравнению для показателей степеней 3x+1 = 3 – 5x; 8x = 4; x = 0,5. Ответ: 0,5.
и перейдем к уравнению для показателей степеней 3x+1 = 3 – 5x; 8x = 4; x = 0,5. Ответ: 0,5.
3. 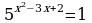
Представим правую часть данного уравнения в виде 1 = 50 и перейдем к уравнению для показателей степеней x2-3x+2 = 0, откуда легко получить решения x = 1 и x=2.
Ответ: 1 и 2.
4. 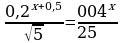
Заметим, что числа 0,2 , 0,04 , √5 и 25 представляют собой степени числа 5. Воспользуемся этим и преобразуем исходное уравнение следующим образом:
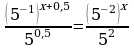 , откуда 5-x-1 = 5-2x-2 - x – 1 = - 2x – 2, из которого находим решение x = -1. Ответ: -1.
, откуда 5-x-1 = 5-2x-2 - x – 1 = - 2x – 2, из которого находим решение x = -1. Ответ: -1.
3x = 5. По определению логарифма x = log35. Ответ: log35.
62x+4 = 33x. 2x+8.
Перепишем уравнение в виде 32x+4.22x+4 = 32x.2x+8, т.е.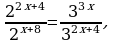 далее
далее
22x+4-x-8 = 33x-2x-4, т.е. 2x-4 = 3x-4. (Уже ясно, что x = 4). Перепишем уравнение, разделив на 3x-4 ≠ 0. 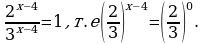 Отсюда x – 4 =0, x = 4. Ответ: 4.
Отсюда x – 4 =0, x = 4. Ответ: 4.
7. 2∙3x+1 - 6∙3x-2 - 3x = 9. Используя свойства степеней, запишем уравнение в виде 6∙3x - 2∙3x – 3x = 9 далее 3∙3x = 9, 3x+1 = 32 , т.е. x+1 = 2, x =1. Ответ: 1.
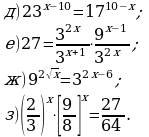
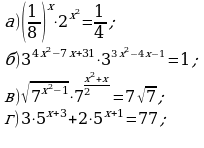
Банк задач №1.
Решить уравнение:

Тест №1. с выбором ответа. Минимальный уровень.
| А1 3-x+2 = 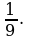
|
1) 0 2) 4 3) -2 4) -4 |
| А2 32x-8 = √3.
|
1)17/4 2) 17 3) 13/2 4) -17/4 |
|  А3 А3 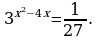
|
1) 3;1 2) -3;-1 3) 0;2 4) корней нет |
| А4 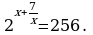
|
1) 7;1 2) корней нет 3) -7;1 4) -1;-7 |
| А5 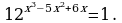 | 1) 0;2; 2) 0;2;3 3) 0 4) -2;-3;0 |
| А6 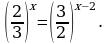 |
1) -1 2) 0 3) 2 4) 1 |
Тест №2 с выбором ответа. Общий уровень.
| А1 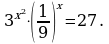 |
1) 3 2) -1;3 3) -1;-3 4) 3;-1 |
| А2 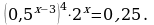 |
1) 14/3 2) -14/3 3) -17 4) 11 |
| А3 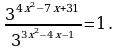
|
1) 2;-1 2) корней нет 3) 0 4) -2;1 |
| А4 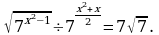
|
1) -4 2) 2 3) -2 4) -4;2 |
| А5 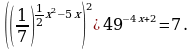
|
1) 3 2) -3;1 3) -1 4) -1;3 |
Теорема о корне: если функция f(x) возрастает (убывает) на промежутке I, число а –любое значение принимаемое f на этом промежутке, тогда уравнение f(x) = а имеет единственный корень на промежутке I.
При решении уравнений методом оценки используется эта теорема и свойства монотонности функции.
Примеры. Решить уравнения: 1. 4x = 5 – x.
Решение. Перепишем уравнение в виде 4x +x = 5.
1. если x = 1, то 41+1 = 5 , 5 = 5 верно, значит 1 – корень уравнения.
2. докажем, что он единственный.
Функция f(x) = 4x – возрастает на R, и g(x) = x –возрастает на R = h(x)= f(x)+g(x) возрастает на R, как сумма возрастающих функций, значит x = 1 – единственный корень уравнения 4x = 5 – x. Ответ: 1.
2. 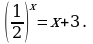
Решение. Перепишем уравнение в виде 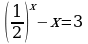 .
.
если x = -1, то 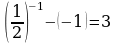 , 3 = 3-верно, значит x = -1 – корень уравнения.
, 3 = 3-верно, значит x = -1 – корень уравнения.
докажем, что он единственный.
Функция f(x) = 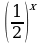 - убывает на R, и g(x) = -x – убывает на R= h(x) = f(x)+g(x) – убывает на R, как сумма убывающих функций. Значит по теореме о корне, x = -1 – единственный корень уравнения. Ответ: -1.
- убывает на R, и g(x) = -x – убывает на R= h(x) = f(x)+g(x) – убывает на R, как сумма убывающих функций. Значит по теореме о корне, x = -1 – единственный корень уравнения. Ответ: -1.
Банк задач №2. Решить уравнение
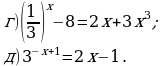
а) 4x + 1 =6 – x;
б) 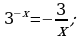
в) 2x – 2 =1 – x;
4. Метод введения новых переменных.
Метод описан в п. 2.1. Введение новой переменной (подстановка) обычно производится после преобразований (упрощения) членов уравнения. Рассмотрим примеры.
Примеры. Решить уравнение: 1. 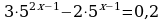 .
.
Перепишем уравнение иначе: 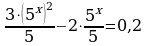
Обозначим 5x = t 0, тогда 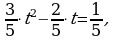 т.е. 3t2 – 2t – 1 =0, отсюда t1 = 1,
т.е. 3t2 – 2t – 1 =0, отсюда t1 = 1, 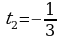 -не удовлетворяет условию t 0. Итак, 5x = 1 = 50 x = 0. Ответ: 0.
-не удовлетворяет условию t 0. Итак, 5x = 1 = 50 x = 0. Ответ: 0.
2. 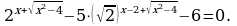
Решение. Перепишем уравнение иначе: 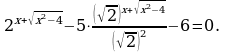
Обозначим 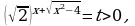 тогда
тогда 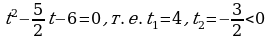 - не подходит.
- не подходит.
t = 4 = 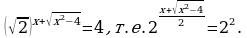 Отсюда
Отсюда 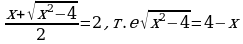 - иррациональное уравнение. Отмечаем, что
- иррациональное уравнение. Отмечаем, что 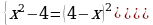
Решением уравнения является x = 2,5 ≤ 4, значит 2,5 – корень уравнения. Ответ: 2,5.
3. 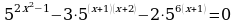 .
.
Решение. Перепишем уравнение в виде 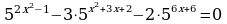 и разделим его обе части на 56x+6 ≠ 0. Получим уравнение
и разделим его обе части на 56x+6 ≠ 0. Получим уравнение
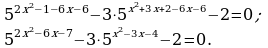
2x2-6x-7 = 2x2-6x-8 +1 = 2(x2-3x-4)+1, т.е 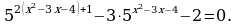
Заменим
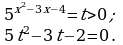
Корни квадратного уравнения – t1 = 1 и t2 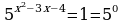 ,
,
x2-3x-4=0
x1 = -1, x2 = 4. Ответ: -1, 4.
4. 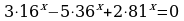 .
.
Решение. Перепишем уравнение в виде 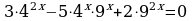
и заметим, что оно является однородным уравнением второй степени.
Разделим уравнение на 42x, получим 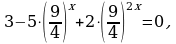
Заменим 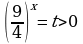 2t2 – 5t +3 = 0 , где t1 = 1, t2 =
2t2 – 5t +3 = 0 , где t1 = 1, t2 = 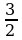 .
.
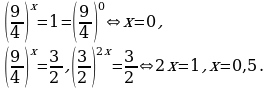
Ответ: 0; 0,5.
Банк задач № 3. Решить уравнение
а) 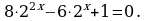
б) 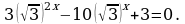
в) 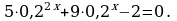
г) 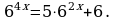
Тест № 3 с выбором ответа. Минимальный уровень.
| А1 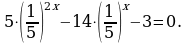
|
1) -0,2;2 2) log52 3) –log52 4) 2 |
| А2 0,52x – 3 0,5x +2 = 0.
|
1) 2;1 2) -1;0 3) корней нет 4) 0 |
| А3 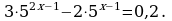
|
1) 0 2) 1; -1/3 3) 1 4) 5 |
| А4 52x-5x- 600 = 0. | 1) -24;25 2) -24,5; 25,5 3) 25 4) 2 |
| А5 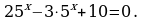 | 1) корней нет 2) 2;4 3) 3 4) -1;2 |
Тест № 4 с выбором ответа. Общий уровень.
| А1 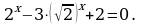 |
1) 2;1 2) ½;0 3)2;0 4) 0 |
| А2 2x – (0,5)2x – (0,5)x + 1 = 0
|
1) -1;1 2) 0 3) -1;0;1 4) 1 |
|
А3 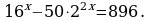 |
1) 64 2) -14 3) 3 4) 8 |
| А4 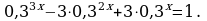 | 1)-1 2) 1 3) -1;1 4) 0 |
| А5 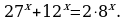
|
1) 0 2) 1 3) 0;1 4) корней нет |
5. Метод разложения на множители.
1. Решите уравнение: 5x+1 - 5x-1 = 24.
Решение. Перепишем уравнение в виде 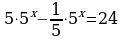
Теперь в левой части уравнения вынесем за скобки общий множитель 5x.
Получим 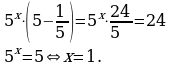 , откуда
, откуда
Ответ: 1.
2. 6x + 6x+1 = 2x + 2x+1 + 2x+2.
Решение. Вынесем за скобки в левой части уравнения 6x, а в правой части – 2x. Получим уравнение 6x(1+6) = 2x(1+2+4) 6x = 2x.
Так как 2x 0 при всех x, можно обе части этого уравнения разделить на 2x, не опасаясь при этом потери решений. Получим 3x = 1 x = 0.
Ответ: 0.
3. 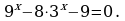
Решение. Решим уравнение методом разложения на множители.
Выделим квадрат двучлена 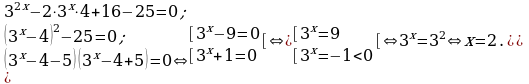

Ответ: 2.
4. 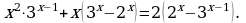
Решение. Преобразуем члены уравнения и перегруппируем слагаемые
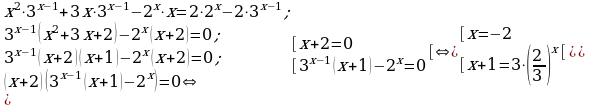
x = -2 – корень уравнения.
Уравнение x + 1 = 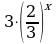 можно решить либо методом оценки, либо графически.
можно решить либо методом оценки, либо графически.
x = 1 – второй корень исходного уравнения.
Ответ: 1; -2.
Банк задач №4. Решить уравнение
а) 48x – 42x+1 – 3x+1 + 12 = 0.
б) 52x-1 + 22x – 52x +22x+2 = 0.
в) 3x – 2x+2 = 3x-1 – 2x-1 – 2x-3.
г) 4x – 5 2x+ 4 = 0.
Тест №5 Минимальный уровень.
| А1 5x-1 +5x -5x+1 =-19.
|
1) 1 2) 95/4 3) 0 4) -1 |
| А2 3x+1 +3x-1 =270.
|
1) 2 2) -4 3) 0 4) 4 |
| А3 32x + 32x+1 -108 = 0. x=1,5
|
1) 0,2 2) 1,5 3) -1,5 4) 3 |
| А4 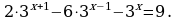 x=1 x=1
|
1) 1 2) -3 3) -1 4) 0 |
| А5 2x -2x-4 = 15. x=4
|
1) -4 2) 4 3) -4;4 4) 2 |
Тест № 6 Общий уровень.
| А1 (22x-1)(24x+22x+1)=7. |
1) ½ 2) 2 3) -1;3 4) 0,2 |
| А2 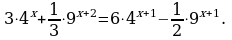 |
1) 2,5 2) 3;4 3) log43/2 4) 0 |
|
А3 2x-1-3x=3x-1-2x+2. |
1) 2 2) -1 3) 3 4) -3 |
| А4 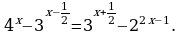 |
1) 1,5 2) 3 3) 1 4) -4 |
| А5 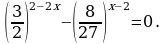 |
1) 2 2) -2 3) 5 4) 0 |
6. Показательно – степенные уравнения.
К показательным уравнениям примыкают так называемые показательно – степенные уравнения, т.е. уравнения вида (f(x))g(x) = (f(x))h(x).
Если известно, что f(x)0 и f(x) ≠ 1, то уравнение, как и показательное, решается приравниванием показателей g(x) = f(x).
Если условием не исключается возможность f(x)=0 и f(x)=1, то приходится рассматривать и эти случаи при решении показательно – степенного уравнения.
1. Решить уравнение 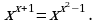
Решение. Для нахождения корней уравнения следует рассмотреть четыре случая:
x + 1=x2 – 1 ( показатели равны);
x = 1(основание равно единице);
x = 0 (основание равно нулю);
x = -1(основание равно -1).
Решим первое уравнение: x2 – x – 2 = 0, x = 2, x = -1.
Проверка:
x1 = 2 = 23 = 23 – верно;
x2 = -1 = (-1)0 =(-1)0 – верно;
x3 = 1 = 12 = 10 – верно;
x4 = 0 = 01 = 0(-1) – не имеет смысла.
Ответ: -1; 1; 2.
Уравнение вида f(x)g(x) = 1 равносильно совокупности двух систем
f(x)g(x) = 1 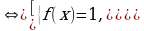
2. 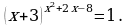
Решение. x2 +2x-8 – имеет смысл при любых x , т.к. многочлен, значит уравнение равносильно совокупности
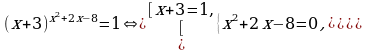
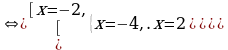
Ответ: -2; 2.
Банк задач №5. Решить уравнение
а) 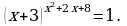
б) 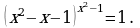
7. Показательные уравнения с параметрами. 1. При каких значениях параметра p уравнение 4 (5 – 3)2 +4p2–3p = 0 (1) имеет единственное решение?
Решение. Введем замену 2x = t, t 0, тогда уравнение (1) примет вид t2 – (5p – 3)t + 4p2 – 3p = 0. (2)
Дискриминант уравнения (2) D = (5p – 3)2 – 4(4p2 – 3p) = 9(p – 1)2.
Уравнение (1) имеет единственное решение, если уравнение (2) имеет один положительный корень. Это возможно в следующих случаях.
1. Если D = 0, то есть p = 1, тогда уравнение (2) примет вид t2 – 2t + 1 = 0, отсюда t = 1, следовательно, уравнение (1) имеет единственное решение x = 0.
2. Если p1, то 9(p – 1)2 0, тогда уравнение (2) имеет два различных корня t1 = p, t2 = 4p – 3. Условию задачи удовлетворяет совокупность систем
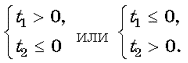
Подставляя t1 и t2 в системы, имеем
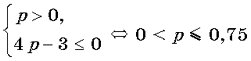
или
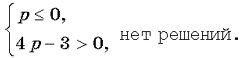
Ответ: p = 1, 0
Рассмотрим более общую задачу.
Задача 2. Сколько корней имеет уравнение 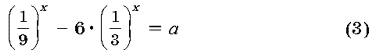 в зависимости от параметра a?
в зависимости от параметра a?
Решение. Пусть 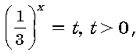 тогда уравнение (3) примет вид t2 – 6t – a = 0. (4)
тогда уравнение (3) примет вид t2 – 6t – a = 0. (4)
Найдем значения параметра a, при которых хотя бы один корень уравнения (4) удовлетворяет условию t 0.
Введем функцию f(t) = t2 – 6t – a. Возможны следующие случаи.
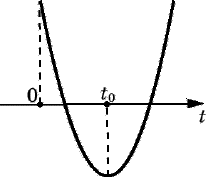
С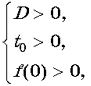 лучай 1. Уравнение (4) имеет два различных положительных корня, если выполнятся условия
лучай 1. Уравнение (4) имеет два различных положительных корня, если выполнятся условия
г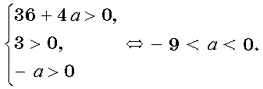 де t0 — абсцисса вершины параболы и D — дискриминант квадратного трехчлена f(t);
де t0 — абсцисса вершины параболы и D — дискриминант квадратного трехчлена f(t);
Т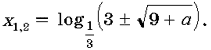 аким образом,
аким образом,
при – 9 a
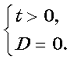
Случай 2. Уравнение (4) имеет единственное положительное решение, если
D = 0, если a = – 9, тогда уравнение (4) примет вид (t – 3)2 = 0, t = 3, x = – 1.
Случай 3. Уравнение (4) имеет два корня, но один из них не удовлетворяет неравенству t 0. Это возможно, если
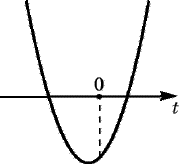
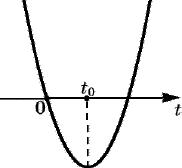
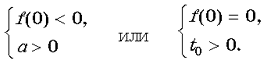
Таким образом, при a 0 уравнение (4) имеет единственный положительный корень 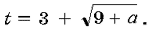 . Тогда уравнение (3) имеет единственное решение
. Тогда уравнение (3) имеет единственное решение 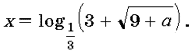
При a
Ответ:
е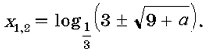 сли a a если a = – 9, то x = – 1;
сли a a если a = – 9, то x = – 1;
если a 0, то
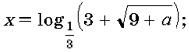
Сравним способы решения уравнений (1) и (3). Отметим, что при решении уравнение (1) было сведено к квадратному уравнению, дискриминант которого — полный квадрат; тем самым корни уравнения (2) сразу были вычислены по формуле корней квадратного уравнения, а далее относительно этих корней были сделаны выводы. Уравнение (3) было сведено к квадратному уравнению (4), дискриминант которого не является полным квадратом, поэтому при решении уравнения (3) целесообразно использовать теоремы о расположении корней квадратного трехчлена и графическую модель. Заметим, что уравнение (4) можно решить, используя теорему Виета.
Решим более сложные уравнения.
Задача 3. Решите уравнение 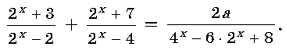
Решение. ОДЗ: x1, x2.
Введем замену. Пусть 2x = t, t 0, тогда в результате преобразований уравнение примет вид t2 + 2t – 13 – a = 0. (*)Найдем значения a, при которых хотя бы один корень уравнения (*) удовлетворяет условию t 0.
Р ассмотрим функцию f(t) = t2 + 2t – 13 – a. Возможны случаи.
ассмотрим функцию f(t) = t2 + 2t – 13 – a. Возможны случаи.
Случай 1. Для того чтобы оба корня уравнения (*) удовлетворяли неравенству t 0, должны выполняться условия
г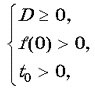 де t0 — абсцисса вершины f(t) = t2 + 2t – 13 – a, D — дискриминант квадратного трехчлена f(t).
де t0 — абсцисса вершины f(t) = t2 + 2t – 13 – a, D — дискриминант квадратного трехчлена f(t).
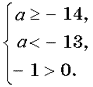
Система решений не имеет.
Случай 2. Для того чтобы только один корень уравнения (*) удовлетворял неравенству t 0, должно быть выполнено условие f(0) a – 13.
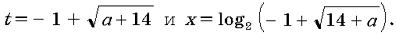
Тогда
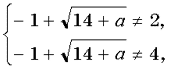
Случай 3. Найдем значения a, когда t 2, t 4.
откуда a 11, a – 5.
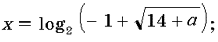
Ответ: если a – 13, a 11, a 5, то если a – 13,
a = 11, a = 5, то корней нет.
Список используемой литературы.
1. Гузеев В.В. Системные основания образовательной технологии.
М. 1995 г.
2. Гузеев В.В. Образовательная технология: от приема до философии.
М. «Директор школы»№4, 1996 г.
3. Гузеев В.В. Методы и организационные формы обучения.
М. «Народное образование», 2001 г.
4. Гузеев В.В. Теория и практика интегральной образовательной технологии.
М. «Народное образование», 2001 г.
5. Гузеев В.В. Одна из форм урока – семинара.
Математика в школе №2, 1987 г. с .9 – 11.
6. Селевко Г.К. Современные образовательные технологии.
М. «Народное образование», 1998 г.
7. Епишева О.Б. Крупич В.И. Учить школьников учиться математике.
М. «Просвещение», 1990 г.
8. Иванова Т.А. Как подготовить уроки – практикумы.
Математика в школе №6, 1990 г. с. 37 – 40.
9. Смирнова Н.М. Профильная модель обучения математике.
Математика в школе №1, 1997 г. с. 32 – 36.
10. Тарасенко Н.А. Некоторые способы организации практической работы.
Математика в школе №1, 1993 г. с. 27 – 28.
11. Утеева Р.А. Об одном из видов индивидуальной работы.
Математика в школе №2, 1994 г. с .63 – 64.
12. Хазанкин Р.Г. Развивать творческие способности школьников.
Математика в школе №2, 1989 г. с. 10.
13. Сканави М.И. Математика. Издатель В.М.Скакун, 1997 г.
14. Шабунин М.И. и др. Алгебра и начала анализа. Дидактические материалы для
10 – 11 классов. М. Мнемозина, 2000 г.
15. Кривоногов В.В. Нестандартные задания по математике.
М. «Первое сентября», 2002 г.
16. Черкасов О.Ю. Якушев А.Г. Математика. Справочник для старшеклассников и
поступающих в вузы. «А С Т -пресс школа», 2002 г.
17. Жевняк Р.М. Карпук А.А. Математика для поступающих в вузы.
Минск И РФ «Обозрение», 1996 г.
18. Письменный Д. Готовимся к экзамену по математике. М. Рольф, 1999 г.
19. Денищева Л.О. и др. Учимся решать уравнения и неравенства.
М. «Интеллект – Центр», 2003 г.
20. Денищева Л.О. и др. Учебно – тренировочные материалы для подготовки к Е Г Э.
М. «Интеллект – центр», 2003 г. и 2004 г.
21 Денищева Л.О. и др. Варианты КИМ. Центр тестирования МО РФ, 2002 г., 2003г.
22. Гольдберг В.В. Показательные уравнения. «Квант» №3, 1971 г.
23. Волович М. Как успешно обучать математике.
Математика, 1997 г. №3.
24 Окунев А.А. Спасибо за урок, дети! М. Просвещение, 1988 г.
25. Якиманская И.С. Личностно – ориентированное обучение в школе.
«Директор школы», 1996 г. сентябрь.
26. Лийметс Х. Й. Групповая работа на уроке. М. Знание, 1975 г.







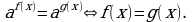 ;
;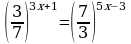
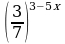 и перейдем к уравнению для показателей степеней 3x+1 = 3 – 5x; 8x = 4; x = 0,5. Ответ: 0,5.
и перейдем к уравнению для показателей степеней 3x+1 = 3 – 5x; 8x = 4; x = 0,5. Ответ: 0,5.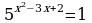
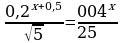
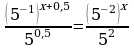 , откуда 5-x-1 = 5-2x-2 - x – 1 = - 2x – 2, из которого находим решение x = -1. Ответ: -1.
, откуда 5-x-1 = 5-2x-2 - x – 1 = - 2x – 2, из которого находим решение x = -1. Ответ: -1.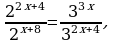 далее
далее 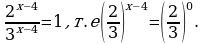 Отсюда x – 4 =0, x = 4. Ответ: 4.
Отсюда x – 4 =0, x = 4. Ответ: 4.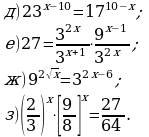
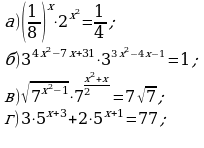
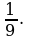
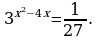
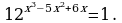
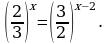
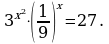
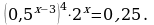
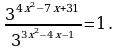
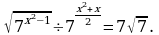
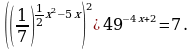
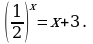
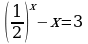 .
.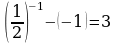 , 3 = 3-верно, значит x = -1 – корень уравнения.
, 3 = 3-верно, значит x = -1 – корень уравнения.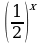 - убывает на R, и g(x) = -x – убывает на R= h(x) = f(x)+g(x) – убывает на R, как сумма убывающих функций. Значит по теореме о корне, x = -1 – единственный корень уравнения. Ответ: -1.
- убывает на R, и g(x) = -x – убывает на R= h(x) = f(x)+g(x) – убывает на R, как сумма убывающих функций. Значит по теореме о корне, x = -1 – единственный корень уравнения. Ответ: -1.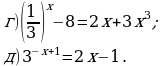
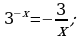
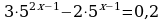 .
.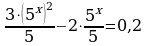
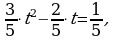 т.е. 3t2 – 2t – 1 =0, отсюда t1 = 1,
т.е. 3t2 – 2t – 1 =0, отсюда t1 = 1, 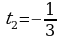 -не удовлетворяет условию t 0. Итак, 5x = 1 = 50 x = 0. Ответ: 0.
-не удовлетворяет условию t 0. Итак, 5x = 1 = 50 x = 0. Ответ: 0.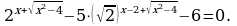
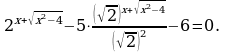
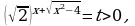 тогда
тогда 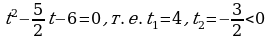 - не подходит.
- не подходит.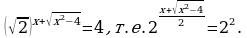 Отсюда
Отсюда 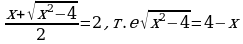 - иррациональное уравнение. Отмечаем, что
- иррациональное уравнение. Отмечаем, что 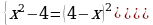
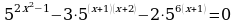 .
.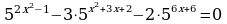 и разделим его обе части на 56x+6 ≠ 0. Получим уравнение
и разделим его обе части на 56x+6 ≠ 0. Получим уравнение 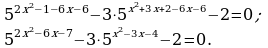
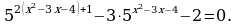
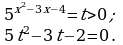
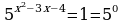 ,
,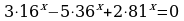 .
.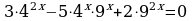
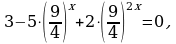
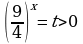 2t2 – 5t +3 = 0 , где t1 = 1, t2 =
2t2 – 5t +3 = 0 , где t1 = 1, t2 = 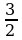 .
.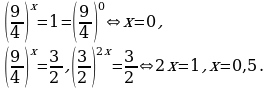
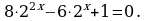
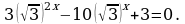
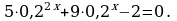
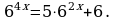
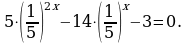
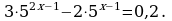
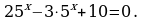
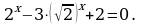
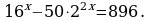
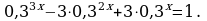
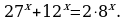
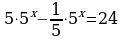
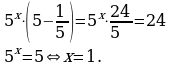 , откуда
, откуда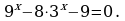
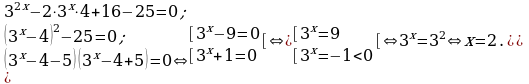
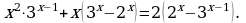
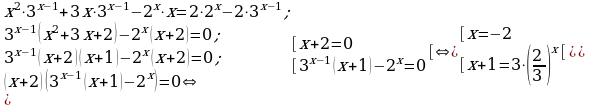
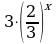 можно решить либо методом оценки, либо графически.
можно решить либо методом оценки, либо графически.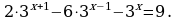 x=1
x=1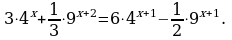
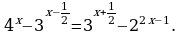
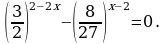
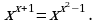
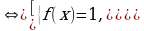
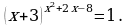
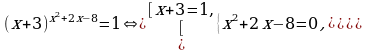
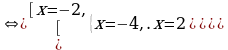
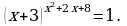
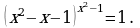
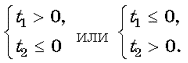
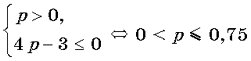

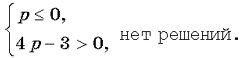
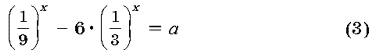 в зависимости от параметра a?
в зависимости от параметра a?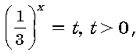 тогда уравнение (3) примет вид t2 – 6t – a = 0. (4)
тогда уравнение (3) примет вид t2 – 6t – a = 0. (4)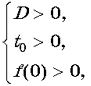 лучай 1. Уравнение (4) имеет два различных положительных корня, если выполнятся условия
лучай 1. Уравнение (4) имеет два различных положительных корня, если выполнятся условия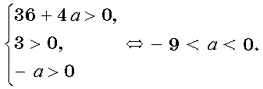 де t0 — абсцисса вершины параболы и D — дискриминант квадратного трехчлена f(t);
де t0 — абсцисса вершины параболы и D — дискриминант квадратного трехчлена f(t);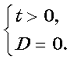


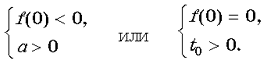
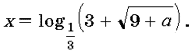
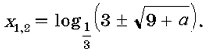 сли a a если a = – 9, то x = – 1;
сли a a если a = – 9, то x = – 1; 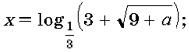
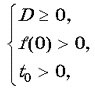 де t0 — абсцисса вершины f(t) = t2 + 2t – 13 – a, D — дискриминант квадратного трехчлена f(t).
де t0 — абсцисса вершины f(t) = t2 + 2t – 13 – a, D — дискриминант квадратного трехчлена f(t).