ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Содержание
| Теория | 1 |
| Упражнения | 8 |
| Решения | 11 |
| Ответы | 15 |
Одно из важнейших понятий современной науки - вероятность. Оно используется теперь и в математике, и в науках о природе, и непосредственно в практике - инженерном деле, организации производства, сельском хозяйстве.
С ситуациями, когда в результате некоторого испытания может произойти какой-то один из определённого числа n исходов, причём ни один из этих исходов не имеет преимущества перед другими, встречаются часто. Приведём пример, когда приходится иметь дело с таким положением. В тираже хорошо организованной лотереи или же государственного займа перед очередным извлечением может появиться любой номер, не имеющий каких-либо преимуществ перед другими. Такие исходы принято называть равновозможными или равновероятными. Само понятие равновероятности является первичным и не поддаётся строгому математическому определению. Его можно только прояснить и иллюстрировать различными примерами.
Предположим теперь, что при каждом из испытаний может появиться любой из n равновероятных и различных исходов, и притом только один. Обозначим их символами Е1, Е2, ..., Еn. При подбрасывании монеты могут появиться только два исхода - Е1 - герб и E2 - решка. При подбрасывании икосаэдра могут появиться 20 равновероятных исходов, которые мы обозначаем Е1, Е2, ..., Е20. Если в лотерее продан миллион билетов, то при приобретении одного билета имеется миллион равновероятных исходов.
Пусть A - некоторое случайное событие, которое наступает тогда и только тогда, когда наступает какой-то исход из определённых: Еi1, Еi2, ..., Еim. Для примера, при бросании трёх игральных костей возможны 216 исходов. Случайное событие А состоит в выпадении таких граней, для которых сумма проставленных на них чисел равна 12. Мы знаем, что наступление интересующего нас события происходит только в 25 определённых сочетаниях выпавших граней. Про каждый исход, при котором интересующее нас событие наступает, мы станем говорить, что он благоприятствует этому событию.
Классическое определение вероятности.
Если из всех n равновероятных исходов m благоприятствуют событию А, то вероятностью события А называется отношение 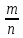 . Вероятность события А принято обозначать символом Р{A}.
. Вероятность события А принято обозначать символом Р{A}.
В частности, если m = 1, т. е. если событие А совпадает с одним из возможных исходов Еi то 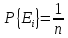
Если событие А таково, что каждый исход благоприятствует его появлению, то такое событие называют достоверным. Чтобы отличить достоверное событие от всех остальных, мы станем обозначать его (и только его) символом U. Достоверному событию благоприятствуют все исходы (т. е. m = n), поэтому
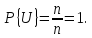
Пример 1. В лотерее выпущено 500 билетов, и среди них 40 выигрышных. Приобретён один билет. Чему равна вероятность того, что на него выпадает выигрыш?
В нашем примере исходов n = 500, и среди них благоприятствующих 40. Таким образом, вероятность того, что приобретённый билет окажется выигрышным равна
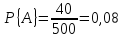 .
.
Пример 2. Известно, что в изготовленной партии сопротивлений, состоящей из 1200 изделий, имеется 900 сопротивлений первого сорта, 180 - высшего качества и 120 - второго сорта. Наудачу берётся из этой партии одно изделие. Спрашивается, чему равны вероятности того, что оно окажется высшего качества, 1-го сорта, 2-го сорта?
Пусть А, А1 и А2 обозначают последовательно события, состоящие в том, что выбранное событие окажется высшего сорта, 1-го сорта и 2-го сорта. Согласно определению находим, что
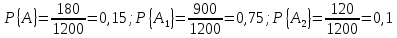 .
.
Пример 3. В школе 800 учащихся. Среди них имеются 72, которые по всем предметам систематически получают высшие оценки, и 320 учащихся, систематически получающих высшие оценки не по всем, но хотя бы по одному предмету. Спрашивается, чему равны вероятности того, что первый встреченный нами школьник окажется "отличником" (событие А); получающим систематически высшие оценки не по всем, но хотя бы по одному предмету (событие В)?
Согласно определению
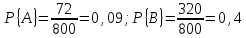 .
.
Для дальнейшего нам потребуются некоторые дополнительные сведения, относящиеся к случайным событиям и к действиям с вероятностями.
Суммой событий А и В называется событие, состоящее как из исходов, составляющих А, так и из исходов, составляющих В. Те исходы, которые благоприятствуют как А, так и В, считаются только один раз. Сумма событий А и В обозначается либо А + В, либо символом А∪В.
В только что рассмотренном примере 3 события А и В обозначали соответственно встречу с учеником, который либо систематически получает высшие оценки по всем предметам, либо получает высшие оценки не по всем предметам, но хотя бы по одному.
Очевидно, что событие С = А + В означает встречу с учащимся школы, который получает высшую оценку хотя бы по одному предмету.
Ещё один пример. Пусть события А и В означают соответственно следующие события - при бросании игральной кости выпадет чётное число очков; при бросании игральной кости выпадет число очков, кратное трём. Какие исходы благоприятствуют событию А + В?
Если через Еk мы обозначим исход, означающий выпадение грани, на которой обозначено k очков, то событию А благоприятствуют исходы Е2, E4, E6, а событию В благоприятствуют исходы Е3 и Е6.
Согласно определению событию А + В благоприятствуют исходы Е2, Е3, E4, Е6.
Заметим, что событие В может быть записано в виде суммы Е3 + Е6.
Понятие суммы, естественно, распространяется на любое число событий А, В,..., N. А именно событие А + В + ... + N состоит из тех и только тех исходов, которые входят в состав хотя бы одного из событий А, В, ..., N.
В последнем примере событие А, согласно сказанному, может быть записано в виде суммы Е2 + Е4 + Е6.
Если события А и В не имеют совпадающих исходов (иными словами, одни и те же исходы не благоприятствуют сразу и А, и В), то они называются несовместными.
События А и В, в только что рассмотренном примере с бросанием игральной кости, совместны, поскольку исход Е6 благоприятствует как А, так и В. В примере с учащимися школы события А и В несовместны. Заметим, что если каждые два события среди событий А, В, ..., несовместны, то они несовместны и все вместе (в совокупности).
Важность введённого понятия становится ясной из следующей теоремы, являющейся одним из основополагающих предложений теории вероятностей.
Теорема сложения вероятностей. Если события А и В несовместны, то
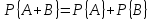 .
.
Действительно, пусть событию А благоприятствуют исходы Ei1, Еi2, ..., Eik, а событию В - исходы Еj1, Ej2, ..., Ejm.
Согласно предположению, среди этих двух групп исходов нет ни одного исхода, принадлежащего сразу первой и второй группе. Отсюда следует, что событию С = А + В благоприятствуют все исходы первой и второй группы, т. е. всего k + m исходов. Таким образом, вероятность события С равна
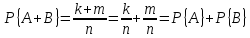 .
.
Теорема доказана.
В примере 3 вероятность встречи с учащимся, который систематически получает высшие оценки хотя бы по одному предмету, равна
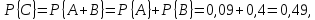
поскольку события А и В несовместны.
События А и В называются противоположными, если они несовместны и в сумме образуют достоверное событие.
Обычно событие, противоположное А, обозначается символом 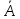 .
.
Событию 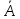 благоприятствуют все те исходы из n равновозможных и несовместимых исходов, которые не благоприятствуют А. Пусть
благоприятствуют все те исходы из n равновозможных и несовместимых исходов, которые не благоприятствуют А. Пусть
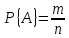 ;
;
тогда
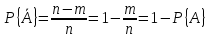 .
.
Полученное равенство очень полезно при вычислении вероятностей событий, поскольку нередко вероятность противоположного события вычисляется несравненно проще, чем вероятность прямого.
Пример 4. Бросаются три игральные кости. Чему равна вероятность того, что хотя бы на одной из них появится "шестёрка"?
Мы знаем, что общее число равновероятных исходов в нашей задаче равно 63 = 216. В данном примере проще сначала подсчитать вероятность не интересующего нас события А, а противоположного ему события 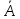 . Противоположное событие состоит в том, что ни на одной из трёх брошенных костей не появится "шестёрка". Пять исходов благоприятствуют тому, что на кости не появится "шестёрка". Чтобы ни на одной из трёх костей не появилась "шестёрка", необходимо, чтобы на каждой из них появилась грань из пяти отмеченных отличными от шести цифрами. Такое совпадение возможно 53 = 125 различными способами. Таким образом,
. Противоположное событие состоит в том, что ни на одной из трёх брошенных костей не появится "шестёрка". Пять исходов благоприятствуют тому, что на кости не появится "шестёрка". Чтобы ни на одной из трёх костей не появилась "шестёрка", необходимо, чтобы на каждой из них появилась грань из пяти отмеченных отличными от шести цифрами. Такое совпадение возможно 53 = 125 различными способами. Таким образом,
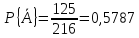 …
…
Согласно найденной формуле
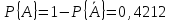 …
…
Пример 5. На электрической схеме, изображённой на рисунке 1, расположены выключатели, каждый из которых может быть включён и выключен, причём обе эти возможности одинаково вероятны. Чему равна вероятность, что схема не будет проводить ток?
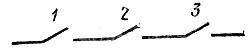
Рис. 1
Всего различных положений трёх выключателей может быть 23 = 8. Из них благоприятствующих пропусканию тока будет только одно, а именно то, когда все три выключателя будут включены. Вероятность того, что схема будет проводить ток, таким образом, равна
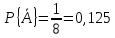 .
.
Согласно выведенной нами формуле, искомая вероятность равна
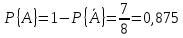 .
.
Произведением событий А и В называют событие, состоящее из тех и только тех исходов, которые входят как в А, так и в В.
Пусть бросаются две игральные кости - первая и вторая. Событие А состоит в том, что на первой кости выпадет чётное число очков, а событие В - в том, что на второй кости выпадет число очков, кратное трём. Всего равновероятных исходов в нашем примере 36, все их можно записать как пары чисел (k, l), где k и l могут принимать любые целые значения между 1 и 6. Событию А благоприятствуют 18 исходов - все пары (k, l), в которых на первом месте стоит чётное число (2, 4 или 6). Событию В благоприятствуют 12 исходов - все пары (k, l), в которых на втором месте стоит число, кратное трём (т. е. 3 или 6). Событию АВ благоприятствуют лишь шесть исходов - (2, 6), (4,6), (6,6), (2,3), (4,3), (6,3).
Произведение событий А и В обозначается одним из символов АВ или А∩В.
Обратим внимание на то, что в том множестве случайных событий, которое было введено в рассмотрение, операции умножения событий и разыскания противоположного события выполнимы не всегда. В самом деле, если А и В не содержат общих исходов, то событие, противоположное достоверному, не содержит ни одного благоприятствующего ему исхода. Чтобы исключить такую возможность выхода за пределы случайных событий при операциях над случайными событиями, расширяют само понятие случайного события. А именно, мы введём в рассмотрение невозможное событие, которому не благоприятствует ни один исход. Обозначим невозможное событие символом V. Теперь мы гарантированы, что операции над случайными событиями не выведут нас за пределы множества случайных событий. В частности, теперь мы можем написать равенство 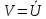 , а также противоположное ему равенство
, а также противоположное ему равенство 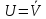 . Отсюда (так же как и из определения невозможного события) следует, что
. Отсюда (так же как и из определения невозможного события) следует, что 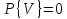 .
.
Мы можем теперь обобщить теорему сложения вероятностей и распространить её на тот случай, когда о событиях А и В уже не предполагается, что они несовместны. Мы докажем сейчас, что каковы бы ни были события А и В
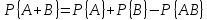 .
.
Действительно, пусть событиям А и В благоприятствуют соответственно k и m исходов. События А и В могут быть совместными. Это означает, что и тому и другому благоприятствуют в том числе и одни и те же l исходов. Таким образом, эти l исходов, и только они, благоприятствуют событию АВ, Теперь ясно, что событию А + В благоприятствуют k + m - l исходов. Отсюда и следует формула.
В качестве иллюстрации доказанной формулы рассмотрим такой пример: события А и В соответственно означают, что при бросании игральной кости выпадают грани с чётными очками, выпадают грани с очками, кратными трём. В данном примере k = 3, m = 2, l = 1, n = 6. Таким образом, вероятность того, что при бросании кости выпадет грань с чётным числом очков или числом очков, кратным трём, равна
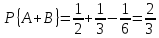 .
.
Статистическое определение вероятности.
Относительная частота события А (или просто частота) определяется формулой
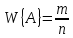 ,
,
где т – число опытов, в которых появилось событие А, а n – число всех проведённых опытов.
Упражнения
На экзамене по математике 35 билетов. Андрей выучил 14 из них. Найти вероятность того, что ему попадётся выученный билет.
На экзамене по философии 25 билетов. Наталья выучила 14 из них. Найти вероятность того, что ей попадётся выученный билет.
На экзамене по истории 30 билетов. Николай не выучил 12 из них. Найти вероятность того, что ему попадётся выученный билет.
На экзамене по литературе 25 билетов. Вероника не выучила 15 из них. Найти вероятность того, что ей попадётся выученный билет.
В фирме доставки в данный момент свободно 35 машин: 18 жёлтых, 10 зелёных и 7 красных. По вызову поехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет красная машина.
В фирме такси в данный момент свободно 18 машин: 9 чёрных, 5 жёлтых и 4 красных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет чёрная машина.
В магазин привезли 60 кувшинов: 48 с изображением белого цветка на зелёном фоне, остальные – с изображением белого цветка на голубом фоне. Продавец выставляет на витрину случайно выбранный кувшин. Найдите вероятность того, что это будет кувшин с изображением белого цветка на голубом фоне.
В магазин привезли 45 кружек: 27 с изображением белого голубя на голубом фоне, остальные – с изображением белого голубя на сером фоне. Продавец выставляет на витрину случайно выбранную кружку. Найдите вероятность того, что это будет кружка с изображением белого голубя на сером фоне.
В среднем на 200 холодильников, поступивших в продажу, приходится 30 со скрытыми дефектами. Найдите вероятность того, что случайно выбранный в магазине холодильник окажется со скрытыми дефектами.
В среднем на 200 пар обуви, поступивших в продажу, приходят 12 со скрытыми дефектами. Найдите вероятность того, что случайно выбранная в магазине пара обуви окажется со скрытыми дефектами.
В среднем на 300 пылесосов, поступивших в продажу, приходится 6 неисправных. Найдите вероятность того, что случайно выбранный в магазине пылесос окажется исправным.
В среднем на 120 аккумуляторов, поступивших в продажу, приходится 6 неисправных. Найдите вероятность того, что случайно выбранный в магазине аккумулятор окажется исправным.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно два раза.
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что первый раз выпадет решка, а второй и третий раз – орёл.
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что в первый раз выпадет орёл, а второй и третий раз – решка.
На экзамене по геометрии школьнику достаётся один вопрос из списка. Вероятность того, что это вопрос на тему «Описанная окружность», равна 0,1. Вероятность того, что это окажется вопрос на тему «Ромб», равна 0,15. В списке нет вопросов, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
На экзамене по биологии школьнику достаётся один вопрос из списка. Вероятность того, что это вопрос на тему «Млекопитающие», равна 0,15. Вероятность того, что это окажется вопрос на тему «Грибы», равна 0,23. В списке нет вопросов, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
На экзамене по истории школьнику достаётся один вопрос из списка. Вероятность того, что это будет вопрос на тему «Екатерина II», равна 0,11. Вероятность того, что это окажется вопрос на тему «Иван Грозный», равна 0,26. В списке нет вопросов, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
На экзамене по географии школьнику достаётся один вопрос из списка. Вероятность того, что это вопрос на тему «Полезные ископаемые», равна 0,15. Вероятность того, что это окажется вопрос на тему «Климат», равна 0,23. В списке нет вопросов, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Толя выбирает двузначное число. Найдите вероятность того, что оно делится на 2.
Ася выбирает двузначное число. Найдите вероятность того, что оно делится на 11.
На тарелке лежат пирожки: 18 с мясом, 4 с картошкой и 2 с повидлом. Оля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с мясом.
На тарелке лежат вареники: 12 с капустой, 2 с черешней и один с картошкой. Оля наугад берёт один вареник. Найдите вероятность того, что он окажется с капустой.
В соревнованиях по спортивному троеборью участвуют 8 спортсменов из России, 2 спортсмена из Дании, 4 спортсмена из Швеции и 6 спортсменов из Германии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что последним будет выступать спортсмен из России.
В чемпионате по лёгкой атлетике участвуют 16 спортсменов из России, 6 спортсменов из Дании, 18 спортсменов из Франции и 10 спортсменов из Германии. Порядок, в котором выступают спортсмены определяется жребием. Найдите вероятность того, что последним будет выступать спортсмен из Франции.
Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле, равна 0,8. Найдите вероятность того, что спортсмен первые два раза попал в мишени, а последние три раза промахнулся.
Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле, равна 0,9. Найдите вероятность того, что спортсмен первые три раза попал в мишень, а последние два раза промахнулся.
В магазине подарков продаётся 100 ёлочных шаров, из них – 39 красных, 14 – зелёных, 17 – жёлтых, есть ещё синие и оранжевые, их поровну. Покупатель случайно разбил один из шаров. Найдите вероятность того, что этот шар красный или оранжевый.
В магазине игрушек продаётся 400 мячей, из них 145 – красных, 57 – зелёных, 56 – фиолетовых, есть ещё синие и оранжевые, их поровну. Покупатель случайно уронил один из мячей. Найдите вероятность того, что этот мяч синий или зелёный.
Известно, что в некотором городе вероятность того, что родившийся младенец окажется мальчиком, равна 0,527. В 2005 году в этом городе из 1000 родившихся младенцев оказалась 491 девочка. На сколько относительная частота рождения девочки в 2005 году в этом городе отличается от вероятности этого события?
Известно, что в некотором городе вероятность того, что родившийся младенец окажется девочкой, равна 0,511. В 2001 году в этом городе из 1000 родившихся младенцев оказалось 498 мальчиков. На сколько относительная частота рождения мальчика в 2001 году в этом городе отличается от вероятности этого события?
Игральную кость бросают 3 раза. Найдите вероятность того, что все три раза выпало число очков, большее 3.
Игральную кость бросают 4 раза. Найдите вероятность того, что все четыре раза выпало число очков, меньшее 4.
В каждой двадцатой бутылке газированного напитка, согласно условиям акции, есть приз. Призы распределены по бутылкам случайно. Дима покупает бутылку газированного напитка в надежде выиграть приз. Найдите вероятность того, что Дима не найдёт приз в своей бутылке.
В каждой двадцать пятой банке с леденцами, согласно условиям акции, есть приз. Призы распределены по банкам случайно. Таня покупает банку с леденцами в надежде выиграть приз. Найдите вероятность того, что Таня не найдёт приз в своей банке.
В таблице представлены результаты четырёх стрелков, показанные ими на тренировке.
| Номер стрелка | Число выстрелов | Число попаданий |
| 1 | 100 | 28 |
| 2 | 80 | 22 |
| 3 | 75 | 27 |
| 4 | 60 | 18 |
Тренер решил послать на соревнования того стрелка, у которого относительная частота попаданий выше. Кого из стрелков выберет тренер? В ответе укажите его номер.
В таблице представлены результаты четырёх стрелков, показанные ими на тренировке.
| Номер стрелка | Число выстрелов | Число попаданий |
| 1 | 90 | 36 |
| 2 | 80 | 28 |
| 3 | 72 | 27 |
| 4 | 50 | 18 |
Тренер решил послать на соревнования того стрелка, у которого относительная частота попаданий выше. Кого из стрелков выберет тренер? В ответе укажите его номер.
На книжной полке 40 учебников: 6 – по математике, 7 – по химии, 12 – по физике, остальные по литературе. Коля случайным образом берёт учебник с полки. Найдите вероятность того, что это будет учебник по литературе.
В холодильнике 50 брикетов с мороженым: 16 – с клюквой, 15 – с брусникой, 17 – с черникой, остальные с шоколадной крошкой. Серёжа случайным образом берёт брикет из холодильника. Найдите вероятность того, что это будет мороженое с шоколадной крошкой.
РЕШЕНИЯ
Здесь возможных исходов n = 35, благоприятствующих событию А (попадётся выученный билет) т = 14, поэтому вероятность того, что ему попадётся выученный билет .
Здесь возможных исходов n = 25, благоприятствующих событию А (попадётся выученный билет) т = 14, поэтому вероятность того, что ей попадётся выученный билет .
Здесь возможных исходов n = 30, благоприятствующих событию А (попадётся выученный билет) т = 30 – 12 = 18, поэтому вероятность того, что ему попадётся выученный билет .
Здесь возможных исходов n = 25, благоприятствующих событию А (попадётся выученный билет) т = 25 – 15 = 10, поэтому вероятность того, что ей попадётся выученный билет .
Здесь возможных исходов n = 35, благоприятствующих событию А (приедет красная машина) т = 7, поэтому вероятность того, что к заказчику приедет красная машина
.
Здесь возможных исходов n = 18, благоприятствующих событию А (приедет чёрная машина) т = 9, поэтому вероятность того, что к заказчику приедет чёрная машина
.
Здесь возможных исходов n = 60, благоприятствующих событию А (кувшин с изображением белого цветка на голубом фоне) т = 60 – 48 = 12, поэтому вероятность того, что продавец выставит кувшин с изображением белого цветка на голубом фоне
.
Здесь возможных исходов n = 45, благоприятствующих событию А (кружка с изображением белого голубя на сером фоне) т = 45 – 27 = 18, поэтому вероятность того, что продавец выставит кружку с изображением белого голубя на сером фоне
.
Здесь возможных исходов n = 200, благоприятствующих событию А (холодильник со скрытыми дефектами) т = 30, поэтому вероятность того, что случайно выбранный в магазине холодильник окажется со скрытыми дефектами .
Здесь возможных исходов n = 200, благоприятствующих событию А (обувь со скрытыми дефектами) т = 12, поэтому вероятность того, что случайно выбранная в магазине пара обуви окажется со скрытыми дефектами.
Здесь возможных исходов n = 300, благоприятствующих событию А (пылесос будет исправен) т = 300 – 6 = 294, поэтому вероятность того, что случайно выбранный в магазине пылесос будет исправен .
Здесь возможных исходов n = 120, благоприятствующих событию А (аккумулятор будет исправен) т = 120 – 6 = 114, поэтому вероятность того, что случайно выбранный в магазине аккумулятор будет исправен .
Итак, монету бросают дважды. Если обозначить буквой Р выпадение решки (цифры), а буквой О - выпадение орла (герба), то все возможные выпадения можно записать так: РР, ОР, РО и ОО (соответственно, выпали две решки, орёл потом решка, решка потом орёл и два орла). Подсчитываем число этих комбинаций и получаем n = 4. Теперь из них надо отобрать только те, что удовлетворяют условию "решка выпадет ровно один раз", это комбинации ОР и РО и их ровно m = 2. Тогда искомая вероятность равна .
Итак, монету бросают дважды. Если обозначить буквой Р выпадение решки (цифры), а буквой О - выпадение орла (герба), то все возможные выпадения можно записать так: РР, ОР, РО и ОО (соответственно, выпали две решки, орёл потом решка, решка потом орёл и два орла). Подсчитываем число этих комбинаций и получаем n = 4. Теперь из них надо отобрать только те, что удовлетворяют условию "решка выпадет ровно два раза", это комбинации РР, значит, m = 1. Тогда искомая вероятность равна .
Итак, монету бросают трижды. Если обозначить буквой Р выпадение решки (цифры), а буквой О - выпадение орла (герба), то все возможные выпадения можно записать так: РРР, РРО, РОР, РОО, ООО, ООР, ОРО и ОРР (соответственно, выпали три решки; решка, решка, потом орёл; и т.д.). Подсчитываем число этих комбинаций и получаем n = 8. Теперь из них надо отобрать только те, что удовлетворяют условию "первый раз выпадет решка, а второй и третий раз – орёл", это комбинация РОО, значит, m = 1. Тогда искомая вероятность равна .
Итак, монету бросают трижды. Если обозначить буквой Р выпадение решки (цифры), а буквой О - выпадение орла (герба), то все возможные выпадения можно записать так: РРР, РРО, РОР, РОО, ООО, ООР, ОРО и ОРР (соответственно, выпали три решки; решка, решка, потом орёл; и т.д.). Подсчитываем число этих комбинаций и получаем n = 8. Теперь из них надо отобрать только те, что удовлетворяют условию "первый раз выпадет орёл, а второй и третий раз – решка", это комбинация ОРР, значит, m = 1. Тогда искомая вероятность равна .
Итак, вероятность того, что школьнику достанется один вопрос на тему «Описанная окружность»  , а вероятность того, что ему достанется вопрос на тему «Ромб»
, а вероятность того, что ему достанется вопрос на тему «Ромб»  . Так как в списке нет вопросов, которые одновременно относятся к этим двум темам, то события А и В несовместны, поэтому: .
. Так как в списке нет вопросов, которые одновременно относятся к этим двум темам, то события А и В несовместны, поэтому: .
Итак, вероятность того, что школьнику достанется один вопрос на тему «Млекопитающие»  , а вероятность того, что ему достанется вопрос на тему «Грибы»
, а вероятность того, что ему достанется вопрос на тему «Грибы»  . Так как в списке нет вопросов, которые одновременно относятся к этим двум темам, то события А и В несовместны, поэтому: .
. Так как в списке нет вопросов, которые одновременно относятся к этим двум темам, то события А и В несовместны, поэтому: .
Итак, вероятность того, что школьнику достанется один вопрос на тему «Екатерина II»  , а вероятность того, что ему достанется вопрос на тему «Иван Грозный»
, а вероятность того, что ему достанется вопрос на тему «Иван Грозный»  . Так как в списке нет вопросов, которые одновременно относятся к этим двум темам, то события А и В несовместны, поэтому: .
. Так как в списке нет вопросов, которые одновременно относятся к этим двум темам, то события А и В несовместны, поэтому: .
Итак, вероятность того, что школьнику достанется один вопрос на тему «Полезные ископаемые»  , а вероятность того, что ему достанется вопрос на тему «Климат»
, а вероятность того, что ему достанется вопрос на тему «Климат»  . Так как в списке нет вопросов, которые одновременно относятся к этим двум темам, то события А и В несовместны, поэтому: .
. Так как в списке нет вопросов, которые одновременно относятся к этим двум темам, то события А и В несовместны, поэтому: .
Всего двузначных чисел n = 90. На 2 делится каждое второе из них, то есть таких чисел т = 45. Значит, вероятность того, что Толя выбрал двузначное число, делящееся на 2: .
Всего двузначных чисел n = 90. На 11 делятся 9 из них, то есть таких чисел т = 9. Значит, вероятность того, что Ася выбрала двузначное число, делящееся на 11: .
Здесь возможных исходов n = 18 + 4 + 2 = 24, благоприятствующих событию А (попался пирожок с мясом) т = 18, поэтому вероятность того, что случайно выбранный Олей пирожок окажется с мясом: .
Здесь возможных исходов n = 12 + 2 + 1 = 15, благоприятствующих событию А (попался вареник с капустой) т = 12, поэтому вероятность того, что случайно выбранный Олей вареник окажется с капустой: .
Возможных исходов n = 8 + 2 + 4 + 6 = 20, благоприятствующих событию А (жребий выпал на спортсмена из России) т = 8, поэтому вероятность того, что последним будет выступать спортсмен из России: .
Возможных исходов n = 16 + 6 + 18 + 10 = 50, благоприятствующих событию А (жребий выпал на спортсмена из Франции) т = 18, поэтому вероятность того, что последним будет выступать спортсмен из России: .
Событие А состоит в том, что биатлонист попадёт в цель, а противоположное событие 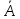 – что он промахнётся.
– что он промахнётся.  . Тогда . Вероятность того, что биатлонист первые два раза попал в мишень равна , а вероятность того, что последние три раза он промахнулся . Откуда, вероятность события, при котором биатлонист сначала два раза попадает в мишени, а последние три раза промахивается равна произведению этих вероятностей, т.к. необходимый нам исход состоит из первого и второго события
. Тогда . Вероятность того, что биатлонист первые два раза попал в мишень равна , а вероятность того, что последние три раза он промахнулся . Откуда, вероятность события, при котором биатлонист сначала два раза попадает в мишени, а последние три раза промахивается равна произведению этих вероятностей, т.к. необходимый нам исход состоит из первого и второго события  .
.
Событие А состоит в том, что биатлонист попадёт в цель, а противоположное событие 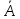 – что он промахнётся.
– что он промахнётся.  . Тогда . Вероятность того, что биатлонист первые три раза попал в мишень равна , а вероятность того, что последние два раза он промахнулся
. Тогда . Вероятность того, что биатлонист первые три раза попал в мишень равна , а вероятность того, что последние два раза он промахнулся  . Откуда, вероятность события, при котором биатлонист сначала три раза попадает в мишени, а последние два раза промахивается равна произведению этих вероятностей, т.к. необходимый нам исход состоит из первого и второго события
. Откуда, вероятность события, при котором биатлонист сначала три раза попадает в мишени, а последние два раза промахивается равна произведению этих вероятностей, т.к. необходимый нам исход состоит из первого и второго события  .
.
Итак, всевозможных исходов n = 100. Количество исходов, при которых был разбит красный шар  , а количество исходов, при которых был разбит оранжевый шар . Значит, благоприятствующих событий
, а количество исходов, при которых был разбит оранжевый шар . Значит, благоприятствующих событий  . Вероятность того, что разбитый шар окажется красный или оранжевый равна .
. Вероятность того, что разбитый шар окажется красный или оранжевый равна .
Итак, всевозможных исходов n = 400. Количество исходов, при которых уронили зелёный мяч  , а количество исходов, при которых уронили синий мяч . Значит, благоприятствующих событий
, а количество исходов, при которых уронили синий мяч . Значит, благоприятствующих событий  . Вероятность того, что покупатель уронил синий или зелёный мяч равна .
. Вероятность того, что покупатель уронил синий или зелёный мяч равна .
Вероятность рождения мальчика  . Так как рождение мальчика и рождение девочки противоположные события, то вероятность рождения девочки . Находим относительную частоту рождения девочки: . Итак, разница между относительной частотой рождения девочки и вероятностью этого события равна: .
. Так как рождение мальчика и рождение девочки противоположные события, то вероятность рождения девочки . Находим относительную частоту рождения девочки: . Итак, разница между относительной частотой рождения девочки и вероятностью этого события равна: .
Вероятность рождения девочки  . Так как рождение мальчика и рождение девочки противоположные события, то вероятность рождения мальчика . Находим относительную частоту рождения мальчика: . Итак, разница между относительной частотой рождения мальчика и вероятностью этого события равна: .
. Так как рождение мальчика и рождение девочки противоположные события, то вероятность рождения мальчика . Находим относительную частоту рождения мальчика: . Итак, разница между относительной частотой рождения мальчика и вероятностью этого события равна: .
При бросании одного кубика возможны 6 различных исходов. Событие А – «выпадет больше трёх очков», событие В – «выпадет меньше 3 очков». При бросании кубика трижды возможны исходы: ААА, ААВ, АВА, АВВ, ВАА, ВАВ, ВВА, ВВВ, т.е. п = 8. Благоприятствующих событию «все три раза выпало число очков, большее 3» т = 1 (ААА). Значит, вероятность того, что все три раза на кубике выпадет число, больше 3 равна .
При бросании одного кубика возможны 6 различных исходов. Событие А – «выпадет меньше 4 очков», событие В – «выпадет больше 4 очков». При бросании кубика четырежды возможны исходы: АААА, АААВ, ААВА, ААВВ, АВАА, АВАВ, АВВА, АВВВ, ВААА, ВААВ, ВАВА, ВАВВ, ВВАА, ВВАВ, ВВВА, ВВВВ, т.е. п = 16. Благоприятствующих событию «все четыре раза выпало число очков, меньше 4» т = 1 (АААА). Значит, вероятность того, что все четыре раза на кубике выпадет число, меньше 4 равна .
Количество возможных событий п = 20. Количество благоприятствующих событию «в бутылке есть приз» т = 1. Значит, вероятность наступления этого события . Так как события «есть приз» и «нет приза» противоположные, то вероятность события «нет приза» равна .
Количество возможных событий п = 25. Количество благоприятствующих событию «в банке есть приз» т = 1. Значит, вероятность наступления этого события . Так как события «есть приз» и «нет приза» противоположные, то вероятность события «нет приза» равна .
Находим относительную частоту попадания у каждого стрелка: . Относительная частота попадания выше у третьего стрелка, он и поедет на соревнование.
Находим относительную частоту попадания у каждого стрелка: . Относительная частота попадания выше у первого стрелка, он и поедет на соревнование.
Возможных исходов n = 40, благоприятствующих событию А (учебник по литературе) , поэтому вероятность того, что Коля возьмёт учебник по литературе равна .
Возможных исходов n = 50, благоприятствующих событию А (мороженое с шоколадной крошкой) , поэтому вероятность того, что Серёжа возьмёт мороженое с шоколадной крошкой равна

ОТВЕТЫ
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| ответ | 0,4 | 0,56 | 0,6 | 0,4 | 0,2 | 0,5 | 0,2 | 0,4 | 0,15 | 0,06 | 0,98 | 0,95 | 0,5 | 0,25 | 0,125 |
| № | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| ответ | 0,125 | 0,25 | 0,38 | 0,37 | 0,38 | 0,5 | 0,1 | 0,75 | 0,8 | 0,4 | 0,36 | 0,00512 | 0,00729 |
| № | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| ответ | 0,54 | 0,32 | 0,018 | 0,009 | 0,125 | 0,0625 | 0,95 | 0,96 | 3 | 1 | 0,375 | 0,04 |
4







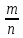 . Вероятность события А принято обозначать символом Р{A}.
. Вероятность события А принято обозначать символом Р{A}.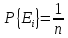
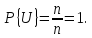
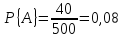 .
.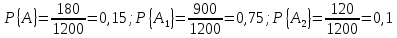 .
.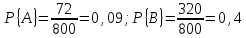 .
.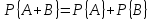 .
.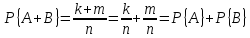 .
.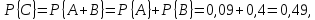
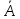 .
.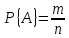 ;
;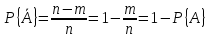 .
.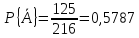 …
…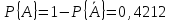 …
…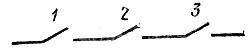
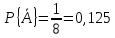 .
.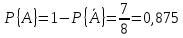 .
.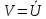 , а также противоположное ему равенство
, а также противоположное ему равенство 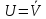 . Отсюда (так же как и из определения невозможного события) следует, что
. Отсюда (так же как и из определения невозможного события) следует, что 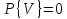 .
.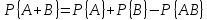 .
.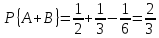 .
.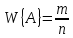 ,
,


















