Отношения. Бинарные отношения.

Отношения

Отношения

• Математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи.
• Примерами отношений в математике: являются равенство, делимость, подобие, параллельность…..

Примеры отношений в обществе

• - родственные связи
• -дружба, вражда
• -служебные отношения
• -экономические отношения
• -виды зависимостей

Примеры отношений в природе

• - магнетизм
• -растворимость, нерастворимость химических элементов
• -симбиоз живых организмов
• -паразитизм живых организмов
• -климатическая зависимость

Свойства отношений

• 1) симметричность
• 2) транзитивность
• 3) рефлексивность

 с   антирефлексивно, так как неравенство  а  а  невозможно. " width="640"

Рефлексивность

• Свойство отношения, когда каждый элемент множества находится в данном отношении к  самому себе.   
• Например, отношения равенства, параллельности, перпендикулярности между прямыми, равенство чисел. 
• Но отношение неравенства  а  с   антирефлексивно, так как неравенство  а  а  невозможно.

с антисимметрично, так как оно неэквивалентно отношению   са . " width="640"

Симметричность  

• Свойство отношения между объектами, предполагающее наличие этого отношения и в том случае, если объекты поменять местами.
• При симметричном отношении перестановка объектов не ведёт к изменению вида отношения. 
• Например, отношение равенства  а = с симметрично, так как оно эквивалентно (равносильно) отношению   с = а .
• Например, отношение равенства  ас антисимметрично, так как оно неэквивалентно отношению   са .

Транзитивность .

• Свойство отношения, предполагающее выполнение следующего требования, представляющее слова: «если ..., то ...»
• Если   у  принадлежит  х,    z  принадлежит  у,   то  z  принадлежит  х .
• Например, если прямая а параллельна с , и а параллельна b , то b параллельна с .

Определите свойства отношений

• - родственные связи
• -дружба, вражда
• -служебные отношения
• -экономические отношения
• -виды зависимостей

Определите свойства отношений

• - магнетизм
• -растворимость химических элементов
• -симбиоз живых организмов
• -паразитизм живых организмов
• -климатическая зависимость

Декартово произведение

• Декартовым произведением   множеств  X  и  Y  называется множество  X*Y  всех упорядоченных пар ( x ,  y ) таких, что  x ϵ  X ,  y ϵ Y .

Пример

• Пусть   X  = { a ,  b ,  c ,  d },  Y  = { 1 ,  2 ,  3 ,  4 ,  5 }. Тогда множество кортежей  a ={( a ,   1 ), ( b ,  2 ), ( c ,  3 ), ( d ,  4 )} являются соответствием из  X  в  Y .

Изобразим декартово произведение

Составим декартово произведения между множествами

• 1) Х={2, 4, 6} ; У={7, 3, 0}
• 2) Х={x|x-страна Европы} ; У={у|у-стоимость тура}
• 3)Х={х Iх- студентка колледжа} ; У={у|у- студент колледжа}
• 4) Х={х|х-новый компьютер} ; У={у|y-кабинет колледжа}

Бинарное отношения

• Если в декартовом произведении множества   X  и  Y  совпадают, то соответствие между множествами  X  и  Y  называют бинарным отношением  на множестве  X .

ИЛИ

• Бинарным отношением между элементами множества называется любое подмножество декартова произведения

Изобразим бинарное отношение

Изобразим декартово произведение

Примеры Бинарных отношений

• на множестве целых чисел Z отношения "делится", "делит", "равно", "больше", "меньше", "взаимно просты";
• на множестве прямых пространства отношения "параллельны", "взаимно перпендикулярны", "скрещиваются", "пересекаются", "совпадают";
• на множестве окружностей плоскости "пересекаются", "касаются", "концентричны".

Примеры Бинарных отношений

• Родственные и другие отношения между людьми   (быть отцом, дедушкой, матерью, ба­бушкой, братом, сестрой, другом, ровесником; старше, моложе)

Примеры Бинарных отношений

• между событиями во времени   (раньше, позже, одновременно),  
• между предметами по их расположению в пространстве   (выше, ниже, левее, правее, севернее, южнее   и др.)

Эквивалентность и порядок

• Если бинарное отношение рефлексивно, симметрично и транзитивно одновременно, то оно называется отношением эквивалентности .

Отношение порядка

• Бинарное отношение называется отношением порядка , если оно рефлексивно, антисимметрично и транзитивно.

Задание бинарных отношений

• 1) Список пар
• 2) График
• 3) Граф
• 4) Матрица

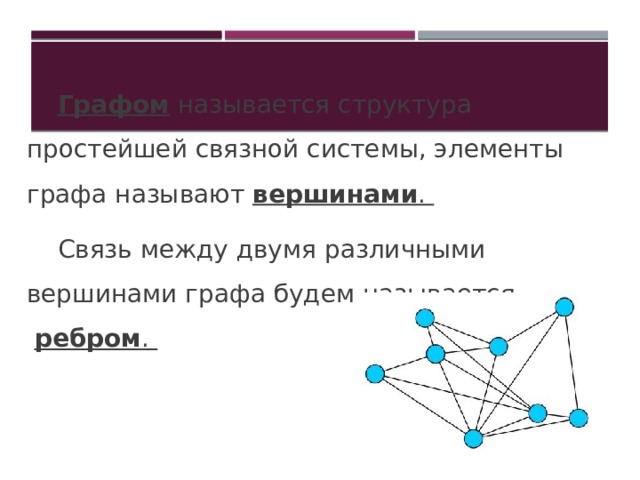
Графом  называется структура простейшей связной системы, элементы графа называют вершинами .

Связь между двумя различными вершинами графа будем называется   ребром .

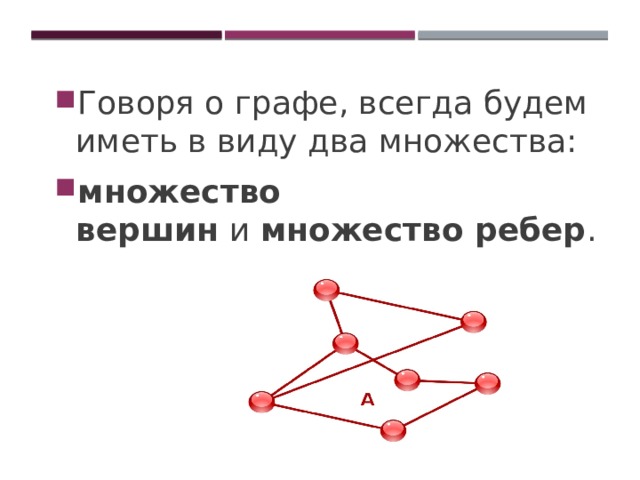
• Говоря о графе, всегда будем иметь в виду два множества:
• множество вершин  и  множество ребер .

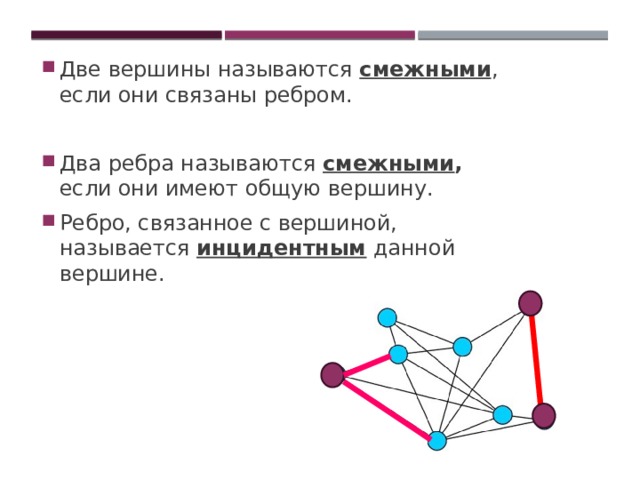
• Две вершины называются смежными , если они связаны ребром.

• Два ребра называются смежными , если они имеют общую вершину.
• Ребро, связанное с вершиной, называется  инцидентным  данной вершине.

Степень вершины графа

• Число ребер инцидентных данной вершине называется её  степенью .
• Степень вершины  vi  обычно обозначают как  degvi

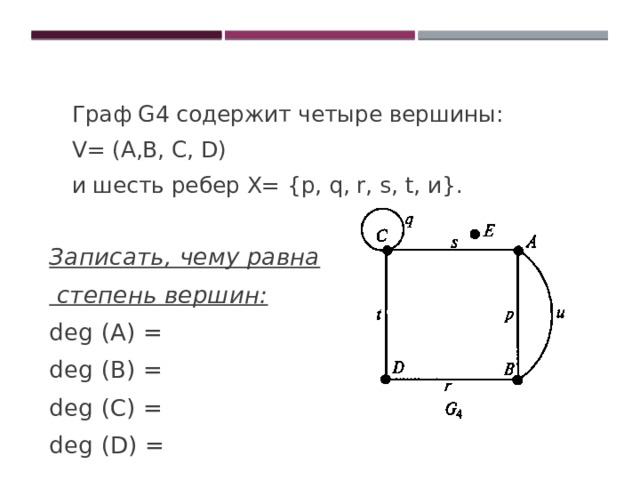
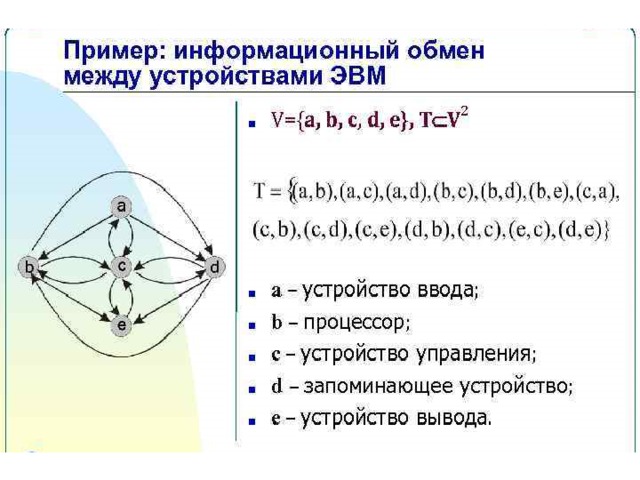
Граф G4 содержит четыре вершины:

V= (A,В, С, D)

и шесть ребер Х= {р, q, r, s, t, и}.

Записать, чему равна

степень вершин:

deg (A) =

deg (В) =

deg (С) =

deg (D) =

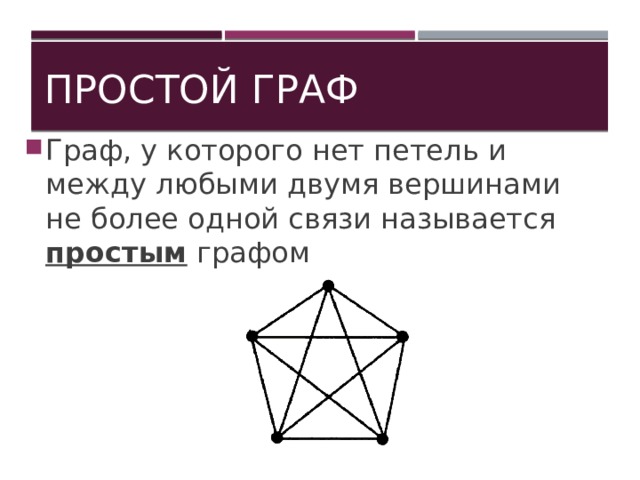
Простой граф

• Граф, у которого нет петель и между любыми двумя вершинами не более одной связи называется простым графом

Если граф имеет ребро, у которого начало и конец совпадают, то это ребро называется петлей.

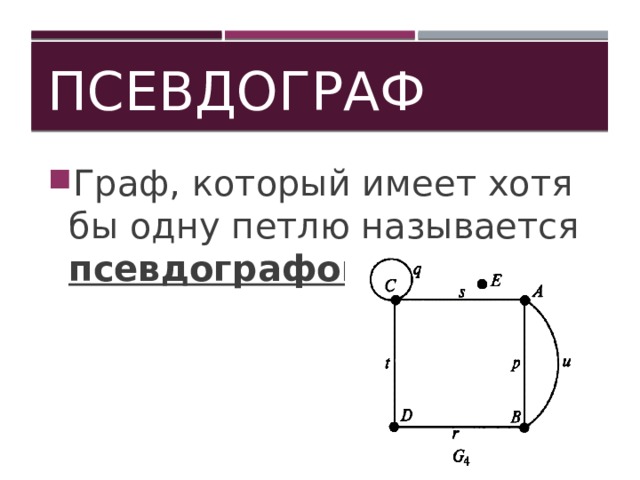
• Граф, который имеет хотя бы одну петлю называется псевдографом

Псевдограф

Мультиграф

• Граф, у которого между двумя вершинами существует более одной связи называется мультиграфом

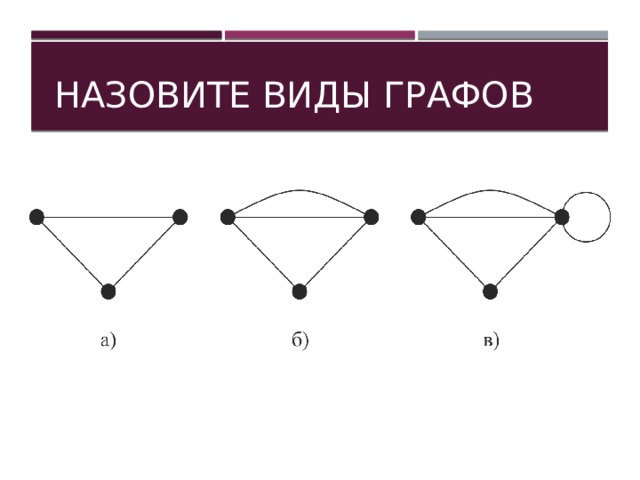
Назовите виды графов

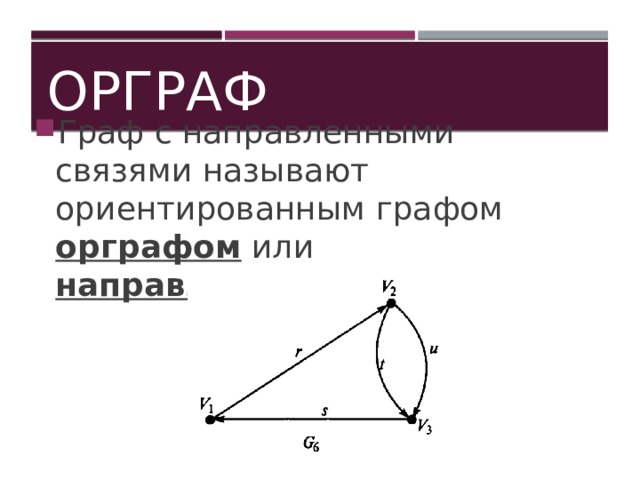
Орграф

• Граф с направленными связями называют ориентированным графом орграфом или направленным.

Матрица смежности

• Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1.
• Когда из одной вершины в другую проход свободен (имеется ребро), тогда в ячейку заноситься 1, иначе – 0.

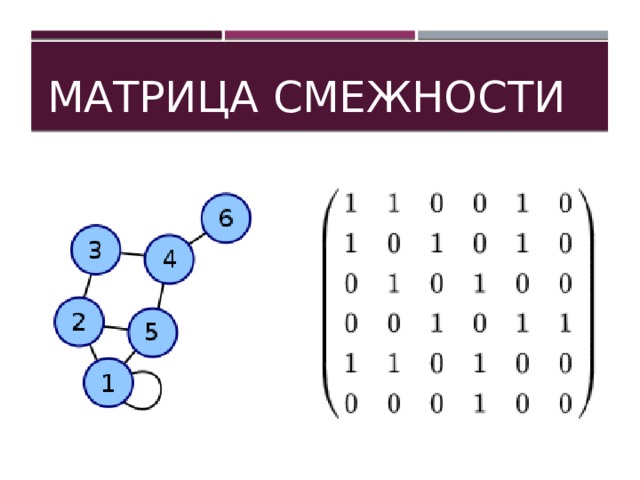
Матрица смежности

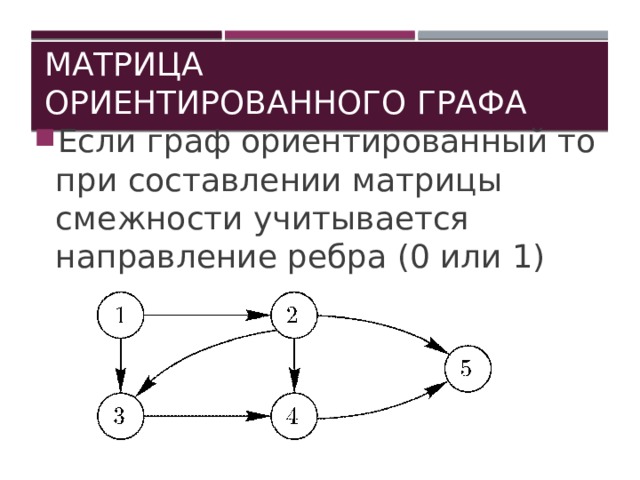
Матрица ориентированного графа

• Если граф ориентированный то при составлении матрицы смежности учитывается направление ребра (0 или 1)

Обратным отношением

• называется отношение α, определяемое обратным условием и обозначается α -1

Пример . Пусть α – отношение "делит", тогда

α -1 – отношение "делится".

Обратное отношение

.

.

• Пусть А ={1,2,3,4,5}, В ={6,7,8,9},

С ={10,11,12,13}.

• Пусть

определены следующим образом:

R ={(1,7), (4,6), (5,6), (2,8)},

S={(6,10), (6,11), (7,10), (8,13)}.

Определить отношения S -1 , R -1

Ответ: R -1 ={(7,1), (6,4), (6,5), (8,2)},

S -1 ={10,6), (11,6), (10,7), (13,8)}

Составное отношение

• Составное отношение (композиция ) это отношение, определяемое как произведение отношений (выполняются одновременно)
• Обозначается:

Составное отношение

Пример 1 . Пусть α – отношение "быть женой", а β – отношение "быть отцом".

Существует такой z, что "x - жена z" и "z - отец y".

Другими словами, "x есть жена отца y", т.е. "x - мать или мачеха y ".

Составное отношение

• Пример 2. Пусть α – отношение "быть братом", а β – отношение "быть родителем".
• Тогда произведение αβ есть отношение "быть братом одного из родителей", т.е. "быть дядей".

Инверсивное отношение

• Инверсивное отношение (отрицание ) - это отношение, определяемое как отрицающее исходное отношение
• Обозначается:

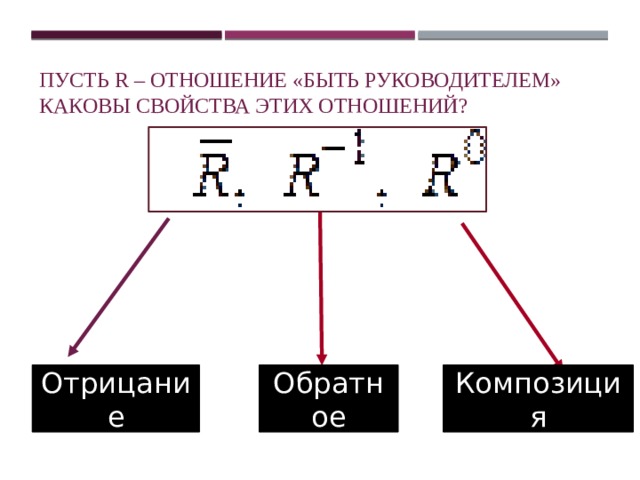
Пусть R – отношение «быть руководителем» Каковы свойства этих отношений?

Отрицание

Обратное

Композиция