Муниципальное бюджетное общеобразовательное учреждение
«Костровская среднея образовательная школа»
Рыльского района Курской области
Проектная работа
по математике
«Коперник геометрии»

Выполнил: Мазотов Михаил, ученик 7 класса
Руководитель: Паневкина Т.М., учитель математики
Кострова 2018
Содержание проекта:
I.Паспорт проекта.
II. Аннотация проекта.
III.План проекта.
IV. Теоретическая часть.
1.Введение
2.Коперник геометрии
1)Биография
2)Геометрия Лобачевского
3)Модели
V.Исследовательская часть.
Области применения геометрии Лобачевского
1) Применения в науке
2) Практические применения геметрии Лобачевского
VI.Заключение
VII.Учебно-методический комплекс.
Паспорт проекта
| Тема | Коперник геометрии |
| Руководитель | Паневкина Татьяна Михайловна |
| Тип | Исследовательский практико-ориентированный |
| Основная учебная дисциплина | геометрия |
| Дополнительные дисциплины | История, математика, физика |
| Объект | геометрия Лобачевского.
|
| Предмет | применение геометрии Лобачевского в окружающеммире.
|
| Цель | изучить возможности применения геометрии Лобачевского в жизни.
|
| Задачи | - изучить и проанализировать учебную литературу, связанную с жизнью Лобачевского; - ознакомиться с особенностями его теории; - рассмотреть применение неевклидовой геометрии в современной жизни.
|
| Гипотеза | применение геометрии Лобачевского не ограничивается математикой, она используется в других науках, в окружающем нас мире.
|
| Оборудование | Книги, компьютер |
| Состав проектной группы | Мазотов Михаил |
II. АННОТАЦИЯ ПРОЕКТА
Данный проект предназначен для знакомства с новой геометрией, с применением её в науке и в современном мире.
Объект исследования – геометрия Лобачевского.
Предмет исследования – применение геометрии Лобачевского в
окружающем мире.
Цель исследования- изучить возможности применения геометрии
Лобачевского в жизни.
Задачи:
- изучить и проанализировать учебную литературу, связанную с жизнью
Лобачевского;
- ознакомиться с особенностями его теории;
- рассмотреть применение неевклидовой геометрии в современной жизни.
Гипотеза: применение геометрии Лобачевского не
ограничивается математикой, она используется в других науках, в
окружающем нас мире.
III. ПЛАН ПРОЕКТА
| № | Этап | Направление работы | Сроки | Планируемый результат |
| 1 | подготовительный | Выбор проблемы, источников литературы, составление плана
| сентябрь 2018
| Определение поля деятельности и структуры работы.
|
| 2 | Деятельностный | Формулирование гипотезы, проведение исследовательской работы.
| сентябрь 2018
| Научное обоснование темы данного проекта и глубины освещения исследуемого вопроса.
|
| 3 | Ход исследования | Работа с литературой и другими источниками
| сентябрь - декабрь 2018 | Подготовка теоретических выкладок и материала.
|
| 4 | Рефлексивный | Обработка полученных данных
| ноябрь 2018
| Окончательное определение содержательной и практической составляющих проекта
|
| 5 | Аналитический | Анализ результатов, формулирование выводов
| ноябрь-декабрь2018
| Формулировка заключения и практических выкладок по проекту
|
| 6 | Презентационный | Мультимедийная подготовка
| декабрь 2018 |
|
IV. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.
Введение
В настоящее время геометрия широко применяется в самых разных
областях: физике, химии, биологии и т.д. Неоценимо ее значение в
прикладныхнауках: машиностроении, геодезии, картографии. Геометрия –
часть нашей жизни. Но так было не всегда. Становлении геометрии как
математической науки произошло позднее и связано с именами греческих
ученых Фалеса (625 – 547 гг. до н.э.), Пифагора (580 – 500 гг. до н.э.),
Демокрита (460 – 370 гг. до н.э.), Евклида (III век до н.э.) и др. [4]
В знаменитом сочинении Евклида «Начала» был развит
аксиоматический подход к построению геометрии, который состоит в том,
что сначала формулируются основные положения (аксиомы), а затем наих
основе посредством рассуждений доказываются другие утверждения
(теоремы). Сегодня мы используем большинство этих аксиом при решении
задач. Много вопросов было по поводу пятого постулата, формулировку
которого обычно заменяют аксиомой параллельных прямых.
Много веков усилия большого числа ученых были направленына
доказательство данного утверждения, у некоторых математиков возникала
мысль о невозможности доказательства пятого постулата. Решение этого
вопроса было найдено великим русским математиком Николаем
Ивановичем Лобачевским (1792—1856). Более того, он сделал
замечательный вывод: можно построить другую геометрию, отличную от
геометрии Евклида. И такая геометрия была построена – геометрия
Лобачевского. Но возникает вопрос: после открытия геометрии
Лобачевского применяется ли она в современной жизни?
Объект исследования – геометрия Лобачевского.
Предмет исследования – применение геометрии Лобачевского в
окружающем мире.
Цель исследования- изучить возможности применения геометрии
Лобачевского в жизни.
Задачи:
- изучить и проанализировать учебную литературу, связанную с жизнью
Лобачевского;
- ознакомиться с особенностями его теории;
- рассмотреть применение неевклидовой геометрии в современной жизни.
Гипотеза: применение геометрии Лобачевского не
ограничивается математикой, она используется в других науках, в
окружающем нас мире.
Коперник геометрии
Биография
Николай Иванович Лобачевский, один из гениальных математиков 19 века. «Человек обязан перед собой и другим людьми стремиться к гармоничному совершенствованию всех своих способностей - в этом состоит его честь, достоинство и слава, этого требует его патриотический долг», - говорил Лобачевский, инее только говорил, но и доказал всей своей жизнью, работой и общественной деятельностью, что он гармонически совершенен.
Сын мелкого чиновника родился в Нижнем Новгороде в 1792 г. Через 5 лет умирает его отец. Семьястоявшая из матери и трех сыновей переезжает в Казань, в город, где потом протекла полная творческих устремлений жизнь Лобачевского. Мать Николая Ивановича, женщина исключительной энергии, устраивает своих детей в Казанскую гимназию на казенный счет.
Поступив в гимназию в 1802 г., Лобачевский уже через пять лет, пятнадцатилетнем юношей, кончает ее и становится студентом Казанского университета. В университете Лобачевский быстро выдвигается как лучший по математике студент. В 1811 г. он производится в магистры, а в 1816 г. Лобачевский уже профессор математики.
Начиная с 1818 г., помимо работы университете, Лобачевский ведет большую просветительную работу. В течение нескольких десятилетий он руководит всей учебной работой обширного Казанского округа. Николай Иванович лично детально знакомится с постановкой преподавания в школах и добивается коренного улучшения преподавания вообще и математики в особенности.
Исключительно много сделал Лобачевский и для Казанского университета.
В 1819 г. на него возложено было приведение в порядок крайне расстроенной университетской библиотеки.
В 1820 году Лобачевский назвался деканатом физико-математического факультета.
За какую работу он не брался в любую вкладывал много сил, любви и не жалел сил. В 1827 Лобачевского избрали редактором Казанского университета. На этом посту пробыл почти 20 лет.
Умер Лобачевский 12 февраля 1856 года. Один из английских математиков назвал Лобачевского «Коперником геометрии»
Геометрия Лобачевского
В 1898 при составлении истории Казанского университета в архивах его была обнаружена рукопись Николая Ивановича Лобачевского, написанная им в 1823. Рукопись носила название « Геометрия». Первые пять глав объединяют материал той части ее, которая не зависит от аксиом Евклида.
Первая глава посвящена измерению линий и в том числе дуг окружности. При измерении длины окружности указывается на известный нам предельный переход от длины ломаной к длине кривой.
Вторая глава содержит измерение углов, причем вслед за измерением прямолинейных углов дается измерение углов двугранных и многогранных.
В третей говорится о перпендикулярах и опять, как и во второй главе, вслед за перпендикулярными прямыми дается учение о перпендикулярных плоскостях и о прямой, перпендикулярной к плоскости.
Четвертая посвящена измерению телесных углов. Здесь же после общих свойств правильных многоугольников рассматриваются свойства правильных многогранников. В этой главе Лобачевский дает ряд весьма своеобразных доказательств, часто более сложных, чем общепринятые, но, что важно, свободных от теории параллельных.
Только в пятой главе Лобачевский рассматривает признаки равенства треугольников и теоремы.
В шестой главе учение о параллельных линиях.
Геометрия Лобачевского (или гиперболическая геометрия) – одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных прямых, которая заменяется её отрицанием.
Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений, при наличии других аксиом) может быть сформулирована следующим образом:
На плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
В геометрии Лобачевского вместо неё принимается следующая аксиома:
Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Аксиома Лобачевского является точным отрицанием аксиомы Евклида (при выполнении всех остальных аксиом), т.к. случай, когда через точку, не лежащую на данной прямой, не проходят ни одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её, исключается в силу остальных аксиом(аксиомы абсолютной геометрии). Так, например, сферическая геометрия и геометрия Римана, в которых любые две прямые пересекаются, и следовательно, не выполнена ни аксиома о параллельных прямых Евклида, ни аксиома Лобачевского, не совместимы с абсолютной геометрией.
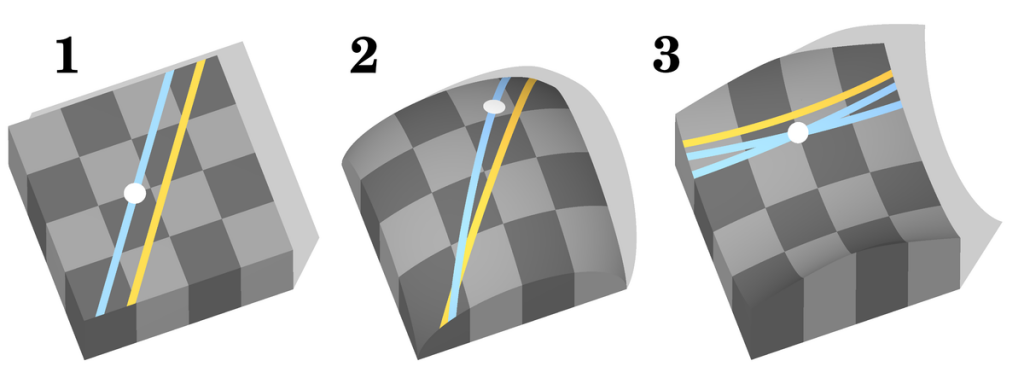
1. Евклидова геометрия – через белую точку проходит только одна прямая, которая не пересекает желтую прямую
2. Геометрия Римана – любые две прямые пересекаются( не существует параллельных прямых)
3. Геометрия Лобачевского – существует бесконечно много прямых не пересекающих желтую линию и проходящих через белую точку.
Геометрия Лобачевского имеет обширные применения . Историческое и философское её значение состоит в том, что её построением Лобачевский показал возможность геометрии отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии, математики и науки вообще.
День 11 февраля 1826 года когда с кафедры Казанского университета впервые были провозглашены Лобачевским его новые идеи, можно считать датой рождения неевклидовой геометрии.
Модели Модели геометрии Лобачевского дали доказательство её непротиворечивости точнее показали, что геометрияЛобачевского столь же непротиворечива, как геометрия Евклида.
Сам Лобачевский дал основы своей аналитической геометрии, и тем самым он уже фактически наметил такую модель. Он также заметил, что орисфера в пространстве Лобачевского изометрична евклидовой плоскости, тем самым фактически предложил обратную модель. Тем не менее, само понятие о модели прояснилось в работах Бельтрами и других.
Псевдосфера
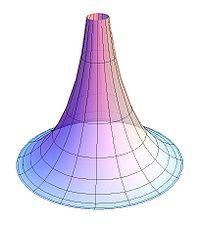 Итальянский математик Э.Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере.
Итальянский математик Э.Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере.
Однако здесь даётся только локальная интерпретация геометрии, то есть на ограниченном участке, а не на всей плоскости Лобачевского.
Только не на всей плоскости, а на той ее части, которая может быть представлена данной поверхностью. Вместе с тем доказано, что не существует (в трехмерном евклидовом пространстве) никакой поверхности, которая своей внутренней геометрией представляла бы плоскость Лобачевского.
Модель Клейна
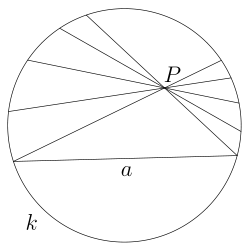 Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского.
Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского.
Пространством служит внутренность шара, прямыми - хорды с исключенными концами, наложениями - отображения шара на себя, переводящие хорды в хорды. Плоскости представляются внутренностью кругов, являющихся плоскими сечениями шара.
![]() В которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходятпо крайней мере две прямые, не пересекающие данную.
В которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходятпо крайней мере две прямые, не пересекающие данную.
Через точку Р проходит бесконечномного «прямых», не пересекающих с «прямой» а
Модель Пуанкаре
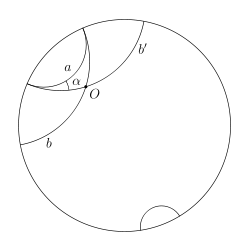
Роль плоскости Лобачевского играет в модели Пуанкаре открытая полуплоскость; роль прямых выполняют содержащиеся в ней полуокружности с центрами на ограничивающей ее прямой и лучи, перпендикулярные этой прямой. Роль наложений выполняют композиции инверсий относительно этих полуокружностей и отражений лучах.Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами.
Все аксиомы евклидовой геометрии здесь выполняются, кроме аксиомы параллельных, тем самым в этой модели выполняется геометрия Лобачевско
Области применения геометрии Лобачевского
Применения в науке
Н.И Лобачевский уже в первой работе по геометрии показал, опираясь на впервые измеренные астрономами в те годы годичные параллаксы звезд, что если в физическом пространстве реализуется его геометрии, то в пределах Солнечной системы отклонения от евклидовой геометрии будут на несколько порядков меньше возможных ошибок измерений. Таким образом, первым приложением геометрии Лобачевского явилось обоснование практической точности евклидовой геометрии.
Н.И Лобачевский применял свою геометрию в математическом анализе. Переходя от одной системы координат к другой в своем пространстве, он нашел значения около 200 различных определенных интегралов. Другие математические приложения были найдены А. Пуанкаре, который успешно применял геометрию Лобачевского при разработке теории автоморфных функций.
Значение геометрии Лобачевского для космологии было выявлено А.А.Фридманом. В 1922 году он нашел решение уравнения Энштейна, из которого следовало, что Вселенная расширяется с течением времени. Это заключение впоследствии было подтверждено наблюдениями Э.Хаббла, обнаружившего разбегание удаленных туманностей. Метрика, найденная А.А. Фридманном, дает при фиксированном времени пространство Лобачевского.
Геометрия Лобачевского с успехом используется при изучении столкновения элементарных частиц и при разработке других вопросов ядерных исследований.
Зрительное (перцептивное) восприятие близких областей пространства человеком порождает эффект обратной перспективы, объясняемый тем, что геометрия этих областей перцептивного пространства близка к геометрии Лобачевского с радиусом кривизны около 15 м.
Создание геометрии Лобачевского явилось важным этапом в развитии учения о возможных свойствах пространства. Особенное значение это имело для оснований математики, т.к. принципы современного аксиоматического метода вырабатывались в значительной степени благодаря появлению геометрии Лобачевского.
Геометрия Лобачевского находит применение также в теории чисел, в её геометрических методах, объединенных под названием « геометрия чисел». Была установлена тесная связь геометрии Лобачевского с кинематикой специальной (частной) теории относительности. Эта связь основана на том, что равенство, выражающее закон распространения света:
x+y+z=ct при делении наt, дает vx+vy+vz=c уравнение сферы с координатами vx, vy, vz- составляющие скорости по осям xyz (в «пространстве скоростей»). Преобразования Лоренца сохраняют эту эстафету и, т.к. они линейны, переводят прямые пространства скоростейв прямые. Следовательно, согласно модели Клейна, в пространстве скоростей внутри сферы радиуса с, т.е. для скоростей, меньших скорости света, имеет место геометрия Лобачевского.
Замечательное приложение геометрия Лобачевского нашла в общей теории относительности. Если считать распределение масс материи во Вселенной равномерным (это приближение в космических масштабах допустимо), то оказывается, что при определенных условиях пространство имеет геометрия Лобачевского.Таким образом, предположение Лобачевского о его геометрии как возможной теории реального пространства оправдалось. Такимобразом можно сделать вывод о том, что неевклидова геометрия представляет большой интерес не только благодаря толкованиям систематической аксиоматической природы, которые она допускает, но также и из-за того, что она тесно связана с другими областями наук, в частности с экономической сферой общества, так, что при их рассмотрении она является полезным орудием исследования и находит себе в этих областях плодотворные применения.
Практические применения геометрии Лобачевского.
Спутниковые навигационные системы (GPS и ГЛОНАСС) состоят из двух частей: орбитальная группировка из 24-29 спутников, равномерно расположенных вокруг Земли, и управленческий сегмент на Земле, обеспечивающий синхронизацию времени на спутниках и использование ими единой системы координат. На спутниках установлены очень точные атомные часы, а в приемниках (GPS-навигаторах) обычные, кварцевые. В приемниках также есть информация о координатах всех спутников в любой момент времени. Спутники с маленькими интервалами передают сигнал, содержащий данные о времени начала передачи. Получив сигнал от не менее четырех спутников, приемник может скорректировать свои часы и вычислить расстояния до этих спутников по формуле ((время отправки сигнала спутником) — (время приема сигнала от спутника)) х (скорость света) = (расстояние до спутника). Вычисленные расстояния также корректируются по встроенным в приемник формулам. Далее, приемник находит координаты точки пересечения сфер с центрами в спутниках и радиусами, равными вычисленным расстояниям до них. Очевидно, это будут координаты приемника.Известно, что, благодаря эффекту в Специальной теории относительности, из-за большой скорости спутника время на орбите идет отлично от времени на Земле. Но еще есть подобный эффект в Общей теории относительности, связанный как раз с неевклидовой геометрией пространства-времени. Опять же не будем вдаваться в математическиеподробностипоскольку они довольно таки абстрактные. Но, если перестать учитывать эти эффекты, то уже за сутки работы в показаниях навигационной системы накопится ошибка порядка 10 км.
Формулы геометрии Лобачевского также используются в физике высоких энергий, а именно, в расчетах ускорителей заряженных частиц.
Пространства в которых действуют законы гиперболической геометрии встречаются в самой природе. Вотнапример это проглядывается в структурах кораллов, в организации клеточных структур у растений, в архитектуре, у некоторых цветков и т. д.
В окружающей нас среде свойства физического пространства приблизительно таковы, какими мы их знаем из евклидовой геометрии, но для всего пространства они иные. Геометрия Лобачевского описывает искривленное пространство. Геометрия Лобачевского нашла свою реализацию в теории относительности Альберта Эйнштейна. Например, Земля создает вокруг себя искривленное пространство – время, которое называют полем тяготения. Геометрия искривленных пространств задается не аксиома как у Евклида, а способом определения расстояния между близкими точками, линейным элементом ds. Изменяются метрические коэффициенты – изменяется ds. Лобачевский проводил астрономические эксперименты. Он измерял сумму углов треугольника, вершинами которого были астрономическая обсерватория и две далёкие звезды. Более глубокое исследование выполнил российский геометр и механик А.П.Котельников (1865 – 1944). В 1923 году он ввел понятие пространство скоростей релятивистской механики, оказавшееся точнейшей реализацией геометрии Лобачевского. Пока скорости малы по сравнению со скоростью света, векторы скоростей складываются как обычные векторы в евклидовом пространстве. Но в области больших скоростей начинается странная арифметика: «любая скорость» + «скорость света» = «скорость света». Реализуется такая арифметика именно в геометрии Лобачевского. Следующий шаг сделал российский физик Н.А.Черников, который применил геометрию Лобачевского в физике высоких энергий. В расчетах современных синхрофазотронов используется формулы геометрии Лобачевского. Синхрофазотрон – это ускоритель заряженных частиц. Простейший ускоритель электронов есть в каждом доме. Это телевизор, вернее его основная деталь – электронно-лучевая трубка или кинескоп. Крупнейший российский ускоритель У-70 построенный в институте физики высоких энергий работает с 1967 года и ускоряет в 1,5 километров кольце протоны до энергии 76 ГэВ. Сегодня удалось «поймать» самые мелкие частицы, из которых состоит материя – кварки. Таким образом, «воображаемая геометрия», открытая в 19 веке замечательным русским учёным Н.И Лобачевским до сих пор сохраняет своё значение для науки и практики.
Заключение
Открытие Лобачевского поставило перед наукой по крайней мере два важных вопроса:
"Что такое геометрия вообще? Какая геометрия описывает геометрию реального мира?"
До появления геометрии Лобачевского существовала только одна геометрия - евклидова, и, соответственно, только она могла рассматриваться как описание геометрии реального мира. Ответы на оба вопроса дало последующее развитие науки. Лобачевский вошел в историю математики не только как гениальный геометр, но и как автор фундаментальных работ в области алгебры, теории бесконечных рядов и приближенного решения уравнений, в области теории вероятности, физики, механики, астрономии. Известный английский математик Уильям Клиффордназвал Лобачевского«Коперником геометрии».
Геометрия Лобачевского помогает по-другому взглянуть на окружающий мир. В этой геометрии не все просто, не все ясно, чтобы ее понять, нужно обладать фантазией. Она способствовала и способствует более глубокому пониманию окружающего нас материального мира. Изучение космического пространства, исследования в области высоких энергий и многое другое было бы невозможно без применения геометрии Лобачевского.
VII.УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС.
1. А.А. Колосов « Книга для внеклассного чтения по математике»: Москва. 1990;
2. http ://www.vuzlit.ru. Геометрия Лобачевского и ее модели;
3. http ://www.mir-znaniy.com. Практическое применение геометрии Лобачевского;
4. http ://www.studall/org. Практическое применение геометрии Лобачевского;
5.http ://www.dic.academic.ru Википедия. Геометрия Лобачевского;
6.http ://www.ru.wikipedia. org Геометрия Лобачевского – Википедия.








 Итальянский математик Э.Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере.
Итальянский математик Э.Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере. Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского.
Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского.










