Сборник олимпиадных задач для 8 класса с решениями

1

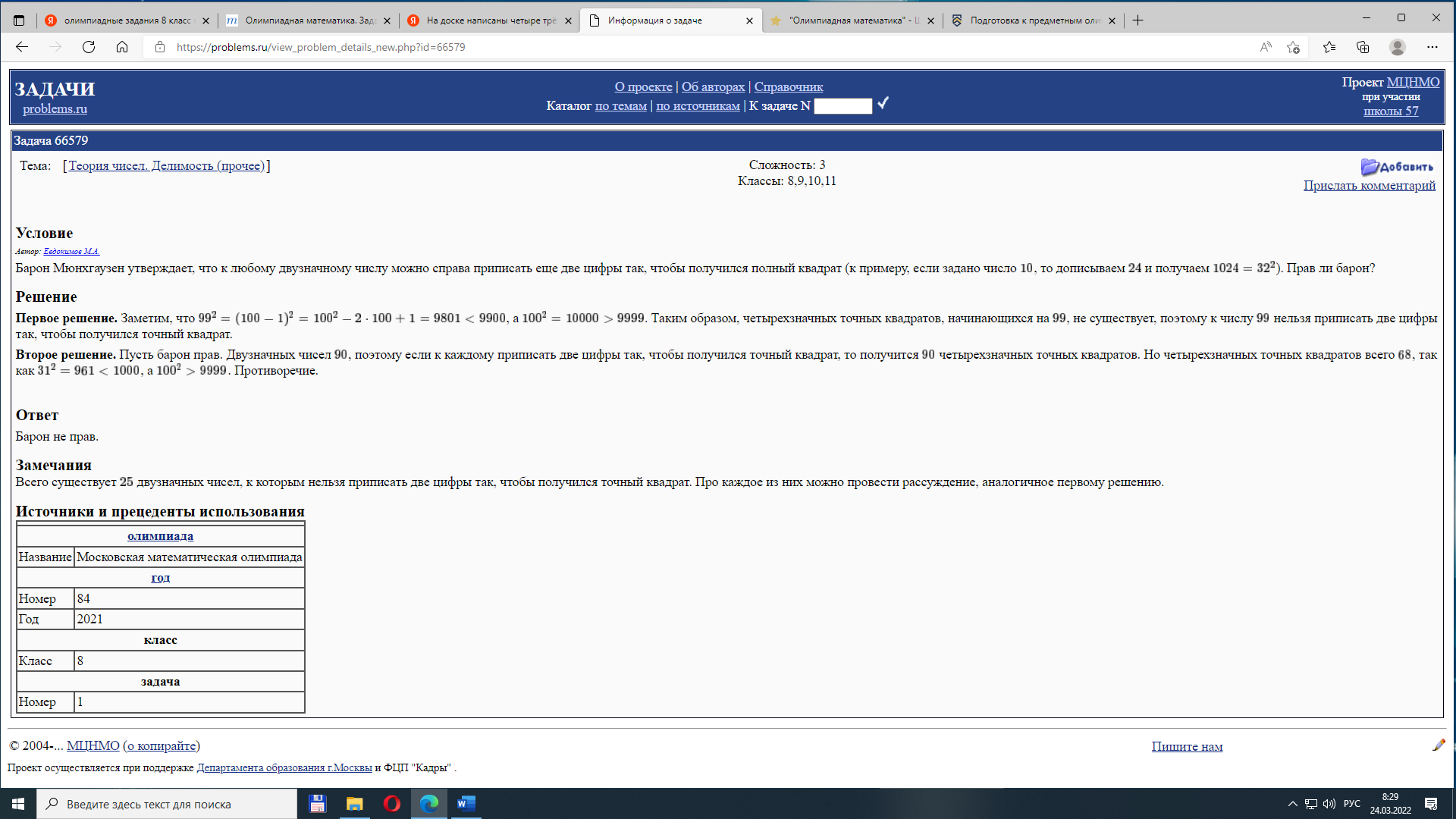
2. Митя купил на день рождения круглый торт диаметром 36 сантиметров и 13 тоненьких свечек. Мите не нравится, когда свечки стоят слишком близко, поэтому он хочет поставить их на расстоянии не меньше 10 сантиметров друг от друга. Поместятся ли все свечки на торте?

3. В комнате находится несколько детей и куча из 2021 конфеты. Каждый из них по очереди подходит к куче, делит количество конфет в ней на количество детей в комнате (включая себя), округляет (если получилось нецелое число), забирает полученное число конфет и покидает комнату. При этом мальчики округляют вверх, а девочки – вниз. Докажите, что суммарное количество конфет у мальчиков, когда все выйдут из комнаты, не зависит от порядка детей в очереди.

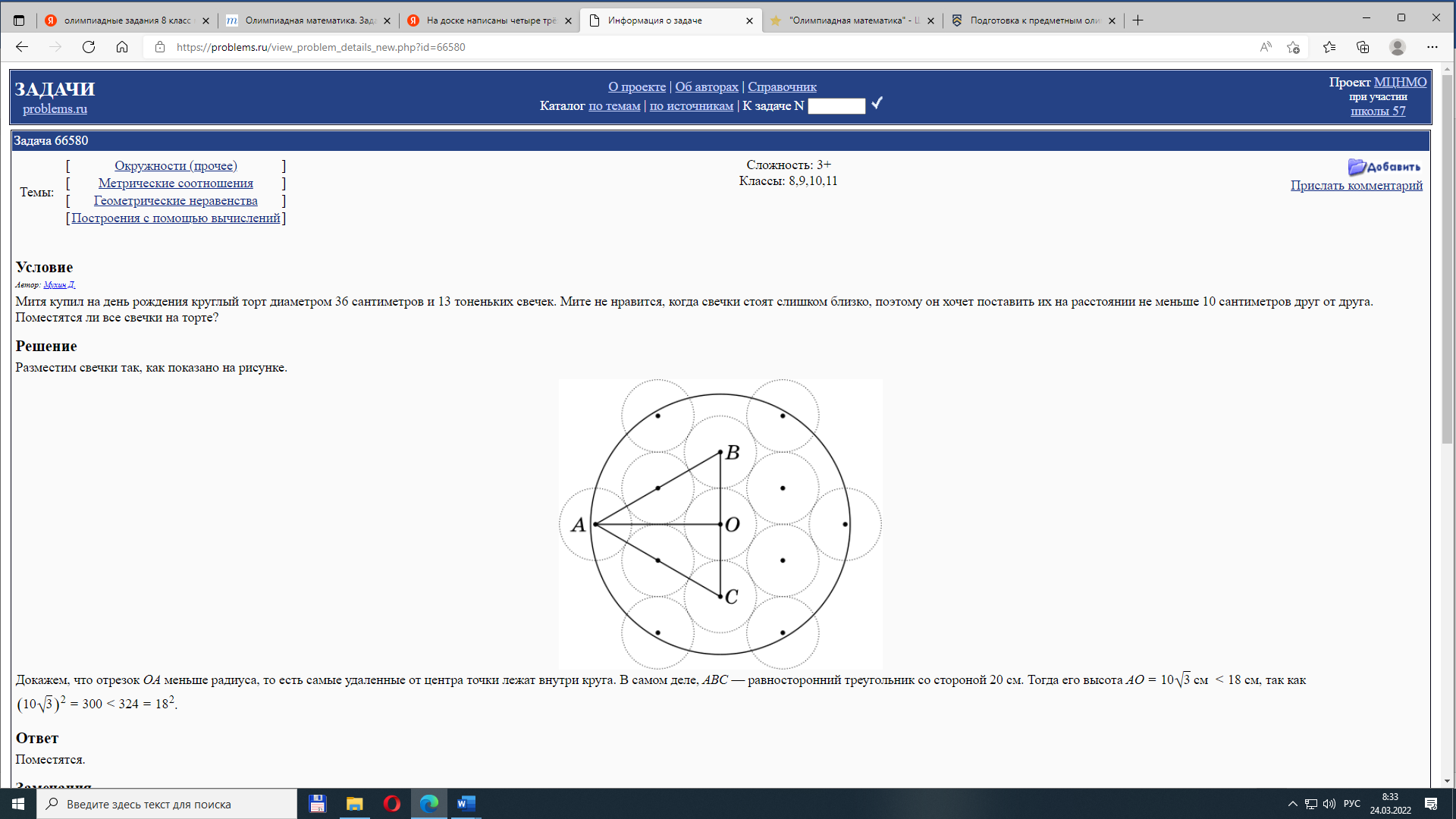
4. В правильном пятиугольнике ABCDE отмечена точка F – середина CD. Серединный перпендикуляр к AF пересекает CE в точке H. Докажите, что прямая AH перпендикулярна прямой CE.

5. В каждом из 16 отделений коробки 4×4 лежит по золотой монете. Коллекционер помнит, что какие-то две лежащие рядом монеты (соседние по стороне) весят по 9 грамм, а остальные по 10 грамм. За какое наименьшее число взвешиваний на весах, показывающих общий вес в граммах, можно определить эти две монеты?

6. В некотором государстве 32 города, каждые два из которых соединены дорогой с односторонним движением. Министр путей сообщения, тайный злодей, решил так организовать движение, что, покинув любой город, в него нельзя будет вернуться. Для этого он каждый день, начиная с 1 июня 2021 года, может менять направление движения на одной из дорог. Докажите, что он сможет добиться своего к 2022 году (то есть за 214 дней).

Условие

В комнате находится несколько детей и куча из 2021 конфеты. Каждый из них по очереди подходит к куче, делит количество конфет в ней на количество детей в комнате (включая себя), округляет (если получилось нецелое число), забирает полученное число конфет и покидает комнату. При этом мальчики округляют вверх, а девочки – вниз. Докажите, что суммарное количество конфет у мальчиков, когда все выйдут из комнаты, не зависит от порядка детей в очереди.

Решение

Первое решение. Докажем, что если поменять местами любых двух соседних детей, то количество конфет у мальчиков и у девочек не изменится. Так как такими перестановками можно добиться любого порядка детей в очереди, то это и будет означать, что общее количество конфет у мальчиков не зависит от этого порядка.

В самом деле, ясно, что если поменять местами двух девочек или двух мальчиков, то для детей ни до, ни после этой пары ничего изменится, не изменится и общее количество конфет у мальчиков.

Теперь пусть осталось всего k детей, и перед кучей из n конфет стоит пара мальчик и девочка. Если n делится на k, то легко видеть, что они оба возьмут по nk конфет вне зависимости от порядка. Далее будем считать, что n делится на k с остатком r0. Тогда n=kq+r, мальчик возьмет q+1 конфету и оставит  (k−1)q+r−1 конфет, девочка за ним возьмет q конфет. А если бы сначала подошла девочка, то она бы взяла q конфет и оставила бы  (k−1)q+r, а мальчик за ней взял бы q+1 конфету. Таким образом, эта пара берет одно и тоже количество конфет вне зависимости от порядка, а значит, ни для них, ни для детей за ними ничего не изменится, что и требовалось.

Второе решение. Пусть всего в комнате n детей, причем 2021=an+r, 0≤r. К куче подходит первый ребенок и делит ее на кучки размером a и кучки размером a+1 (общее количество кучек равно n, а кучек размером a+1 ровно r), причем все большие кучки лежат правее маленьких.

Пусть первый ребенок – мальчик, тогда он берет себе самую правую кучку и уходит. Если же это оказалась девочка, она возьмет себе самую левую кучку и тоже уйдет. Потом к конфетам подойдет следующий ребенок; перед ним лежит n−1 кучка из a или a+1 конфет.

Если остались кучки обоих видов, то это означает, что неполное частное от деления количества конфет на число детей равно a, и далее процесс продолжается аналогично: мальчики, округляя вверх, берут себе кучки справа, девочки, округляя вниз, – слева.

Если же остались только кучки одного вида, то количество конфет делится на количество детей, и любому ребенку подходит любая кучка, то есть и в этом случае мальчики могут брать кучки справа, а девочки – слева.

Тогда в итоге мальчики заберут все правые кучки (столько, сколько было мальчиков) независимо от того, в каком порядке дети подходили за конфетами.

4.

В каждом из 16 отделений коробки 4×4 лежит по золотой монете. Коллекционер помнит, что какие-то две лежащие рядом монеты (соседние по стороне) весят по 9 грамм, а остальные по 10 грамм. За какое наименьшее число взвешиваний на весах, показывающих общий вес в граммах, можно определить эти две монеты?

Отметим, что взвешивание любой группы монет может показать один из трех исходов: 0, 1 или 2 легкие монеты среди взвешенных. Действительно, эти исходы соответствуют показаниям весов в 10k, 10k−1 и 10k−2 граммов, где k – количество монет на весах, а ничего другого при взвешивании k монет весы показать не могут.

Теперь докажем, что менее чем тремя взвешиваниями обойтись не получится. Всего пар монет, которые могут быть легкими, 24: по 3 пары соседних монет в каждой строчке и в каждом столбце. Так как одно взвешивание дает три разных исхода, то два взвешивания дадут лишь 32=9 различных исходов.

Покажем, как определить легкие монеты за три взвешивания.

Первое взвешивание. Разобьем монеты на две группы так, как показано на рисунке, и взвесим одну них. Так как группы симметричны, то возможны два различных случая: легкие монеты в одной группе и легкие монеты в разных группах.

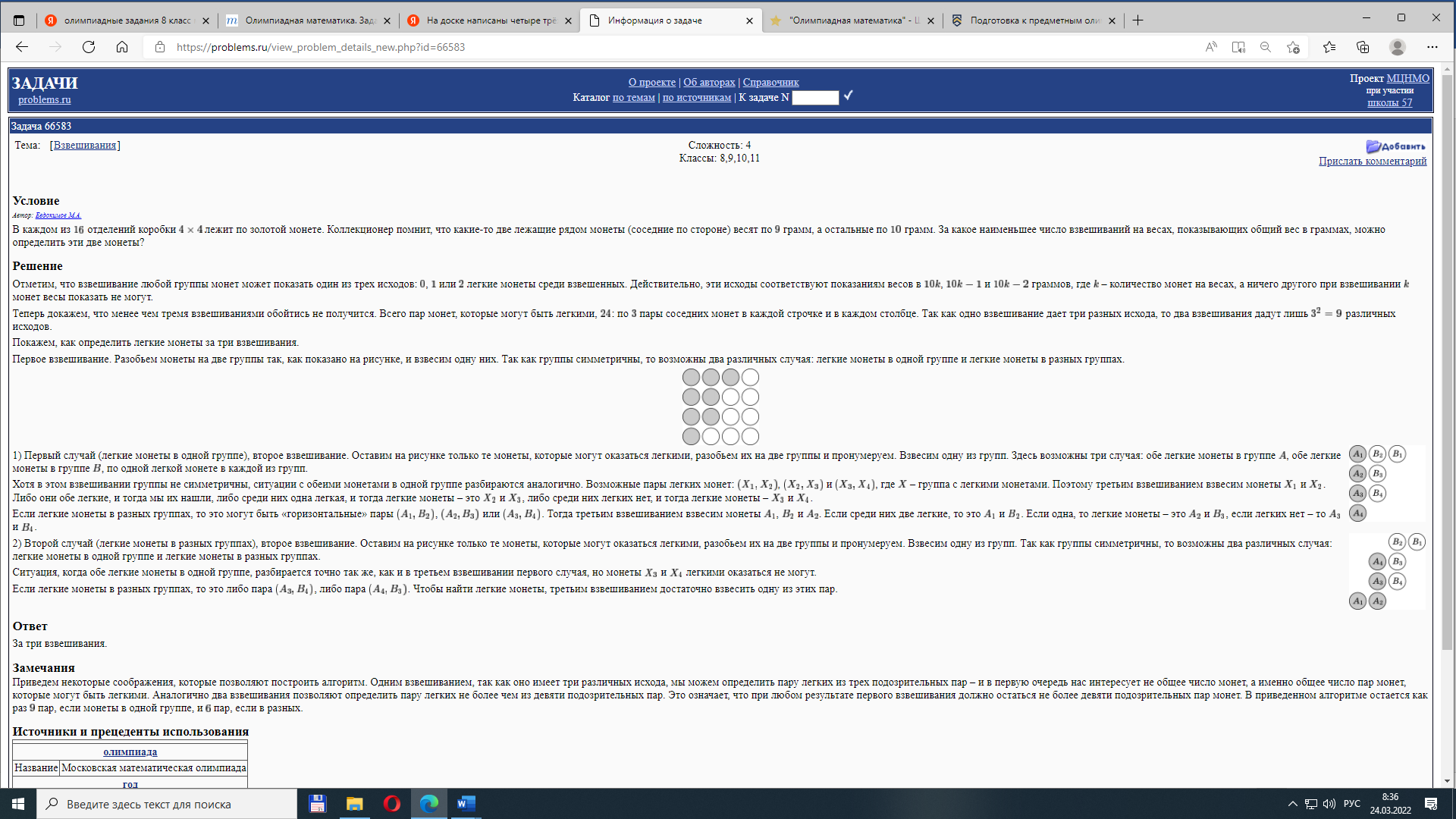
1) Первый случай (легкие монеты в одной группе), второе взвешивание. Оставим на рисунке только те монеты, которые могут оказаться легкими, разобьем их на две группы и пронумеруем. Взвесим одну из групп. Здесь возможны три случая: обе легкие монеты в группе A, обе легкие монеты в группе B, по одной легкой монете в каждой из групп.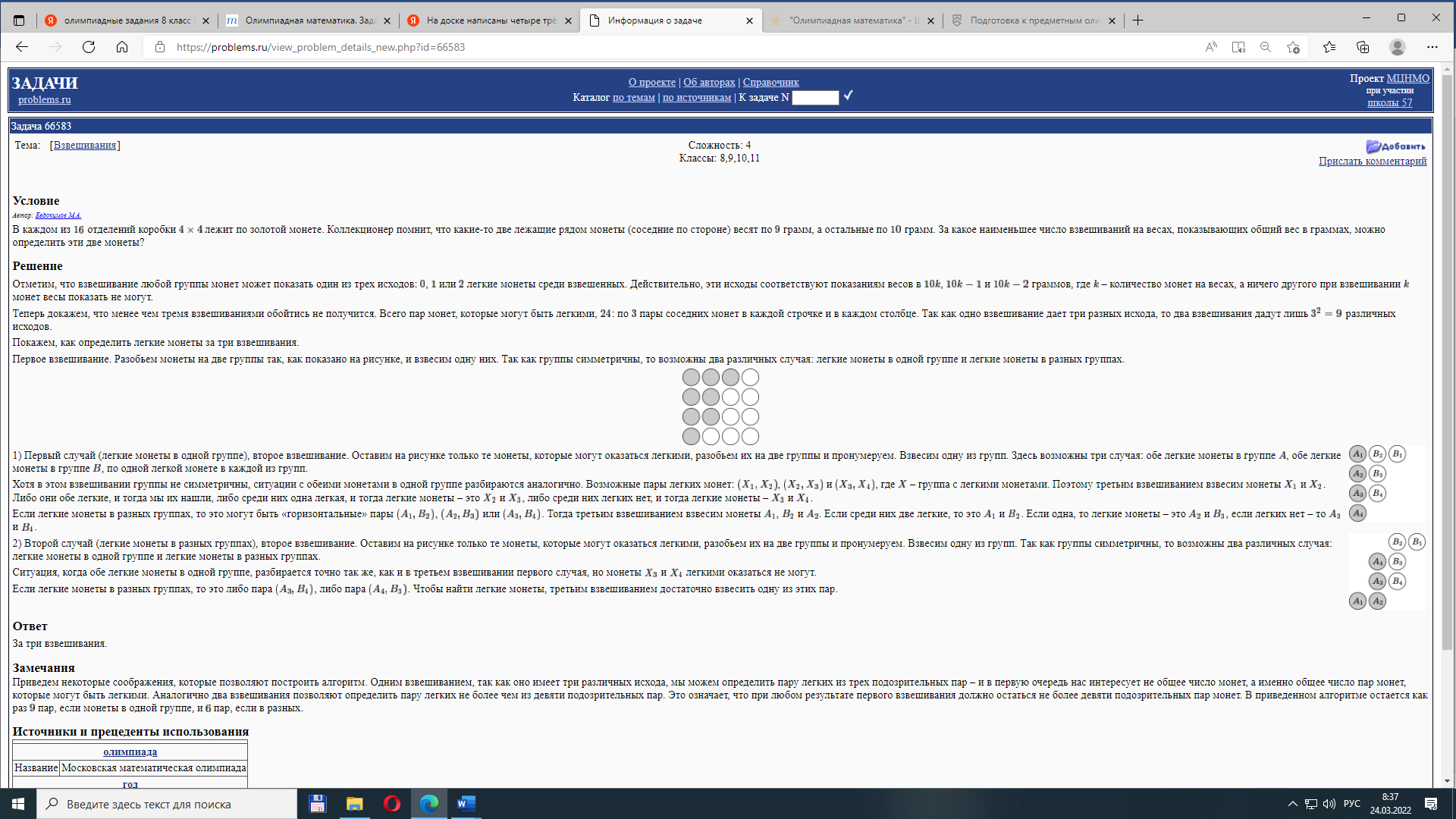

Хотя в этом взвешивании группы не симметричны, ситуации с обеими монетами в одной группе разбираются аналогично. Возможные пары легких монет: X1,X2), (X2,X3) и (X3,X4), где X – группа с легкими монетами. Поэтому третьим взвешиванием взвесим монеты X1 и X2. Либо они обе легкие, и тогда мы их нашли, либо среди них одна легкая, и тогда легкие монеты – это X2 и X3, либо среди них легких нет, и тогда легкие монеты – X3 и X4.

Если легкие монеты в разных группах, то это могут быть «горизонтальные» пары (A1,B2), (A2,B3) или A3,B4). Тогда третьим взвешиванием взвесим монеты A1, B2 и A2. Если среди них две легкие, то это A1 и B2. Если одна, то легкие монеты – это A2 и B3, если легких нет – то A3 и B4.

2) Второй случай (легкие монеты в разных группах), второе взвешивание. Оставим на рисунке только те монеты, которые могут оказаться легкими, разобьем их на две группы и пронумеруем. Взвесим одну из групп. Так как группы симметричны, то возможны два различных случая: легкие монеты в одной группе и легкие монеты в разных группах.

Ситуация, когда обе легкие монеты в одной группе, разбирается точно так же, как и в третьем взвешивании первого случая, но 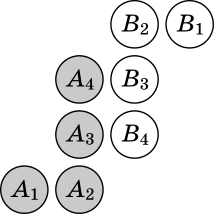монеты X3 и X4 легкими оказаться не могут.

Если легкие монеты в разных группах, то это либо пара ква (A3,B4), либо пара  (A4,B3). Чтобы найти легкие монеты, третьим взвешиванием достаточно взвесить одну из этих пар.

Ответ

За три взвешивания.

В некотором государстве 32 города, каждые два из которых соединены дорогой с односторонним движением. Министр путей сообщения, тайный злодей, решил так организовать движение, что, покинув любой город, в него нельзя будет вернуться. Для этого он каждый день, начиная с 1 июня 2021 года, может менять направление движения на одной из дорог. Докажите, что он сможет добиться своего к 2022 году (то есть за 214 дней).

Решение

Докажем общую формулу. Пусть в государстве 2n городов. Тогда министр сможет добиться желаемого не более чем 2n−2(2n−n−1) дней.

Лемма. Пусть в государстве 2k городов, каждые два из которых соединены дорогой с односторонним движением. Выберем из них половину с наибольшим числом исходящих дорог. Тогда всего из выбранных городов исходит суммарно не менее k2 дорог.

Доказательство. Пусть из k выбранных городов исходит менее k2 дорог, тогда по принципу Дирихле найдется город, из которого исходит не более k−1 дороги. Тогда, так как выбраны города с наибольшим числом исходящих дорог, из каждого из оставшихся k городов исходит также не более k−1 дороги. Суммарно исходит менее k2+k(k−1)=2k2−k дорог, при том, что общее число дорог в точности 2k(2k−1)2=2k2−k. Противоречие, лемма доказана.

Теперь перейдем к доказательству основной формулы. Докажем ее по индукции.

База n=1: между двумя городами только одна дорога и она уже и так в одном направлении. Ничего менять не придется.

Шаг индукции. Пусть для 2n городов утверждение верно. Докажем для n+1. Разделим города на две группы по 2n городов. В первую группу поместим города с наибольшим количеством исходящих дорог. В соответствии с леммой из всех городов этой группы суммарно исходит не менее 22n дорог.

Из этих дорог2n(2n−1)2 – дороги внутри группы, поэтому из первой группы во вторую ведет не менее2n−1(2n+1) дорог. Тогда из 22n дорог между первой и второй группами в первую направлено не более2n−1(2n−1). Не более чем за 2n−1(2n−1) дней министр направит все эти дороги во вторую группу. И еще не более чем за2⋅2n−2(2n−n−1) дней он добьется того, чтобы в каждой группе нельзя было выехать из города и в него вернуться. Тогда всего потребуется не более2n−1(2n+1−n−2) дней.

Так как 32=25, то на осуществление желаемого министру потребуется не более 23(25−5−1)=208 дней, что меньше 214 дней, оставшихся до 2022 года.

Замечания

Если в стране n городов, то оценку для числа f(n) замен можно получить из соотношений f(2n)≤n(n−1)2+2f(n) (фактически доказано в задаче) и f(2n+1)≤n+f(2n) (очевидно). Жюри неизвестно, является ли эта оценка точной.