Тригонометрическая окружность. Радианная мера угла

Тригонометрическая окружность, радианная мера угла. Тригонометрические функции произвольного угла

Синус, косинус произвольного угла

Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом. Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР, который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ. Так как окружность имеет радиус, равный единице, то ОР = R = 1.

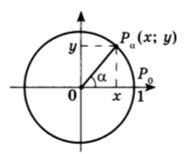
Если с точки Р опустить перпендикуляр на ось ОХ, то получим прямоугольный треугольник с гипотенузой, равной единице.

Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным, если же он двигается против движения часовой стрелки - положительным.

Синусом угла данной окружности, образованного радиусом-вектором ОР, является ордината точки Р вектора на окружности. 

То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.

Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике - это отношение противолежащего катета к гипотенузе, получим, что

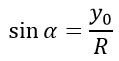
А так как R = 1, то sin(α) = y₀.

В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,

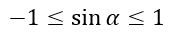
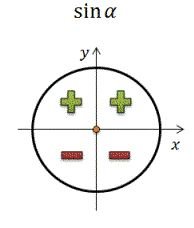
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой - отрицательное.

Косинусом угла данной окружности, образованного радиусом-вектором ОР, является абсцисса точки Р вектора на окружности.

То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.

Косинус произвольного угла в прямоугольном треугольнике - это отношение прилежащего катета к гипотенузе, получим, что

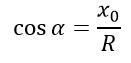
А так как R = 1, то cos(α) = x₀.

В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,

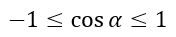
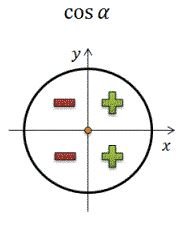
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей - отрицательное.

Тангенсом произвольного угла считается отношение синуса к косинусу. 

Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.

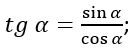
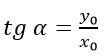
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.

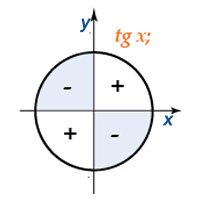
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.

Котангенсом произвольного угла называется отношение косинуса к синусу.

Рассматривая прямоугольный треугольник - отношение прилежащего катета к противолежащему, то есть абсциссы к ординате.

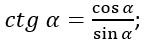
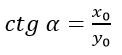
Так как ордината находится в знаменателе дроби, то котангенс не может существовать при угле альфа, равном нулю градусов.

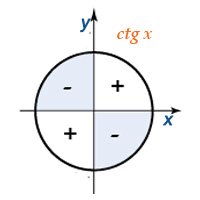
Котангенс принимает те же значения в четвертях единичной окружности, что и тангенс.

Все перечисленные функции являются периодичными. Косинус и синус имеют период 360 градусов, то есть 2Пи, а тангенс и котангенс 180 градусов, то есть Пи.

Радианная мера угла

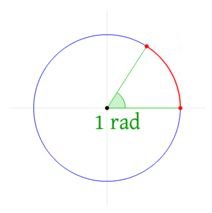
Радианной мерой произвольного угла в единичной окружности является отношение длины дуги центрального угла к радиусу окружности. 

Данное определение применимо к окружностям с произвольной длиной радиуса.

Радианная мера связана с градусной мерой простым соотношением:

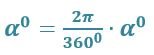
При этом для получения величины 1 рад, следует 180 градусов разделить на значение числа π.

Например, давайте получим радианную меру угла в 30 градусов:

2 * π * 30 : 360 = π/6 ≈ 0,52.

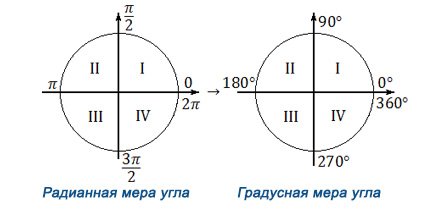
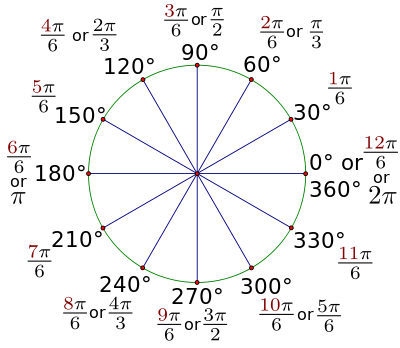
Существуют таблицы, которые позволяют без расчетов определить радианную меру основных углов:

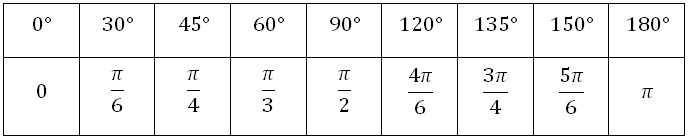
Итак, напоминаем, что при рассмотрении тригонометрических функций мы рассматриваем окружность, которая имеет единичный радиус. Данное упрощение используется для удобства. Все отношения справедливы для произвольных окружностей, с произвольным радиусом.

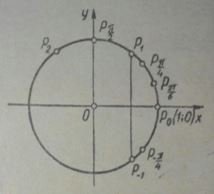
Пример. Давайте построим точки на единичной окружности, которые будут соответствовать повороту радиус-вектора на угол  

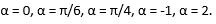
Решение. За начало отсчета принимаем точку Р₀. Угол, равный нулю радиан совпадает с данной точкой.

Мы знаем, что граничными считаются углы 0, π/2, π, 3π/2, 2π. Если использовать угол π/2 и разделить первую четверть на 3 равных части, то первое от начала отсчета разделение будет соответствовать углу π/6. На графике данная точка имеет место Р_π/6.

Чтобы получить угол π/4, необходимо прямой угол разделить на две части. Если необходимо отметить угол с отрицательным аргументом, необходимо пойти по часовой стрелке от начальной точки. Например, точка - π/4 будет находиться симметрично относительно оси ОХ в 4 четверти.

Давайте теперь вспомним, каким образом исчисляются углы, выраженные в радианной мере. Чему, например, соответствует в радианах π/4? Чтобы это узнать, следует числовое значение числа π разделить на 4.

3,14 : 4 = 0,78, если углу π/2 соответствует 3,14 : 2 = 1,57. Следовательно, на окружности угол, равный единице будет лежать выше π/4, но ниже π/2. Отрицательное значение угла симметрично положительному относительно оси ОХ.

Таким же образом следует найти и местонахождение угла, равного 2. Так как граничному прямому углу соответствует значение 1,57, то угол, равный двум, будет находиться во второй четверти.

Можно убедиться, что каждому числу соответствует своя ордината и абсцисса на плоскости.

Отсюда можно сделать вывод, что: 

Синус некоторого числа - это значение ординаты на плоскости, которая соответствует точке этого числа на единичной окружности.

Косинус некоторого числа - это значение абсциссы на плоскости, которая соответствует точке этого числа на единичной окружности.

Тангенс некоторого числа - это значение, полученное в результате отношения синуса к косинусу, иначе говоря, отношение ординаты к абсциссе.

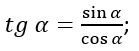
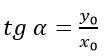
Котангенс некоторого числа - это значение, полученное в результате отношения косинуса к синусу, иначе говоря, отношение абсциссы к ординате.

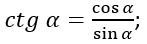
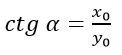
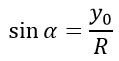
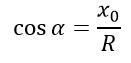
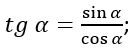
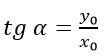
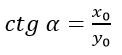
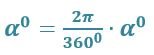
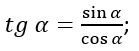
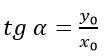
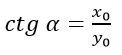
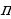Синус и косинус имеют период, равный 6,28 (2 ). Тангенс и котангенс имеет период, равный 3,14 ( ).