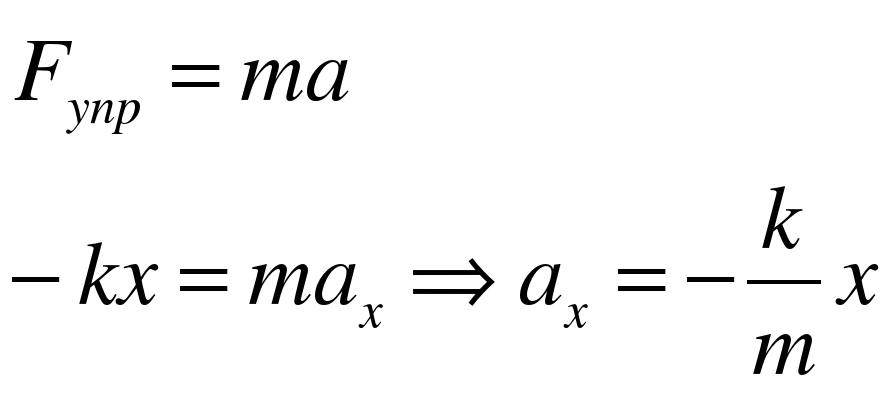11 класс физика учитель: А. В. Шилько
Урок 17-18/1-2
Тема: Свободные и вынужденные колебания. Гармонические колебания. Гармонические колебания пружинного и математического маятников.
Цель: продемонстрировать особенности колебательного движения, рассмотреть примеры механических колебаний систем и определить основные параметры колебаний и причину их возникновения, выяснить, чем отличаются различные типы колебаний, получить решение основной задачи механики для колебательных движений;
развивать умения анализировать увиденные физические явления, сопоставлять теорию физического явления с экспериментом, умение делать выводы, способность к созданию межпредметных связей;
воспитывать критичное отношение к собственным знаниям, интерес к физике.
Тип урока: урок изучение нового материала.
Оборудование: математический маятник, вертикальный и горизонтальный пружинные маятники, компьютер.
Ход урока
Активизация познавательной деятельности.
Каждый из учеников получают три карточки разного цвета (красную, желтую и зеленую). Учитель читает физические термины и понятия, в это время ученики поднимают поочередно карточки в зависимости от степени знакомства с понятием (красная – с понятием не знаком, слышу впервые, желтая – слышал такой термин, но что он означает, не помню, частично помню, зеленая – я знаком с этим понятием, знаю, что означает этот термин).
Понятия: маятник, колебания, амплитуда, период, частота, гармония, пружина, сила упругости, закон сохранения механической энергии, второй закон Ньютона, кинетическая энергия, потенциальная энергия.
Желательно на каждой карточке отметить сколько раз она была поднята.
Мотивация учебной деятельности.
В природе существует бесконечное количество примеров движений, которые можно отнести к колебательным. Большинство видов движений приближаются к математическим моделям равномерного, равнопеременного движения. Но при более тщательном рассмотрении содержат элементы колебательного движения. Например, движение автомобиля по реальной дороге, характеризуется не только постоянной или переменной скоростью его движения, но и толчками, обусловленными неровностью дорожного покрытия, которые приводят к возникновению колебаний корпуса автомобиля. При этом, наверное, каждый из вас ощущал мерное покачивание при езде в автомобиле. Это и есть пример колебательного движения.
Все макроскопические тела обычно совершают сложные колебательные движения, которые сложно описать на языке математического анализа. Несмотря на это, пренебрегая целым набором факторов, можно создать математические модели колебательных систем, которые в первом приближении соответствуют колебательным движениям этих тел.
Итак, при изучении физики мы опять столкнулись с необходимостью создания модели, в которой мы откажемся от учета некоторых факторов.
Восприятие и осознание нового материала.
Демонстрация колебательного движения.
Рассмотрим колебательные системы, которые лучше всего поддаются математическому анализу:
демонстрация колебаний груза на длинной нити (модель математического маятника);
демонстрация колебания груза на вертикальной пружине (модель вертикального пружинного маятника);
демонстрация колебания груза, закрепленного на горизонтальной пружине вдоль горизонтальной направляющей (модель горизонтального пружинного маятника);
демонстрация хода маятниковых часов (видеоролик).
Формирование понятийного аппарата.
Математическая модель, которая состоит из массивного тела соединенного с длинной, невесомой, нерастяжимой нитью, называется математическим маятником.
Математическая модель, которая состоит из массивного тела, соединенного с невесомой пружиной, называется пружинным маятником.
Рассмотрим горизонтальный пружинный маятник и познакомимся с основными параметрами, характеризующими колебания.
Максимальное отклонение маятника от положения равновесия, называют амплитудой колебания маятника Xmax. (компьютерная демонстрация)
Время, в течение которого маятник совершает одно полное колебание, называется периодом колебаний Т. (компьютерная демонстрация)
Количество колебаний маятника, происходящих за 1 с, называется частотой колебаний ν. (компьютерная демонстрация)
Произведение частоты колебаний на число 2π называется циклической частотой колебаний  .
.
Единицей измерения частоты колебаний является Герц.
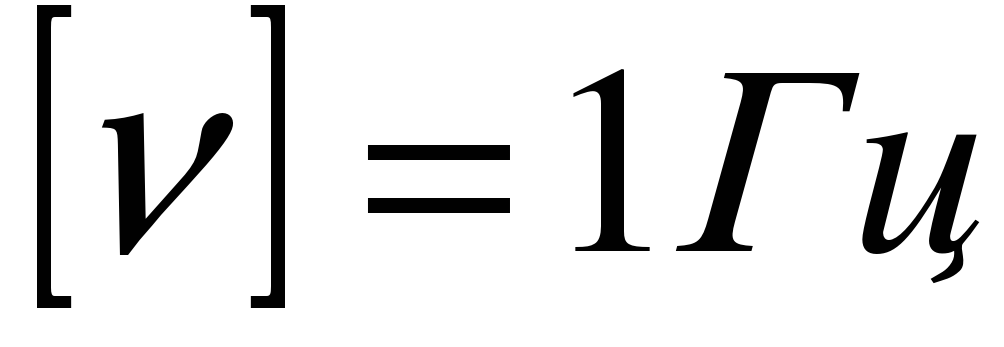
Между периодом колебаний и их частотой существует простая связь, которая определяется формулой:
 .
.
Иначе говоря, частота является величиной обратной периоду и наоборот.
Главная причина возникновения колебаний – это сила упругости, которая направлена к положению равновесия маятника. Эта сила является внутренней силой системы. Аналогично причиной возникновения колебаний в других системах являются силы, которые будут возвращать маятник в положение равновесия.
Решение основной задачи механики для колебательного движения.
Вспомним, что основная задача механики заключается в том, чтобы определить положение тела в любой момент времени, т.е. получить зависимость координаты тела от времени x(t). Рассмотрим пример колебаний математического маятника.
К омпьютерная демонстрация графической зависимости координаты математического маятника от времени.
омпьютерная демонстрация графической зависимости координаты математического маятника от времени.
Вопрос: Какой вид имеет зависимость координаты маятника от времени?
Ответ: эта зависимость отвечает функциям типа  или
или  .
.
Колебания, которые происходят по закону  или
или  , называют гармоническими колебаниями.
, называют гармоническими колебаниями.
Теперь рассмотрим колебания пружинного маятника.
К омпьютерная демонстрация графической зависимости координаты пружинного маятника от времени.
омпьютерная демонстрация графической зависимости координаты пружинного маятника от времени.
Рассмотрим силы, действующие в системе, и запишем второй закон Ньютона. Т. к.
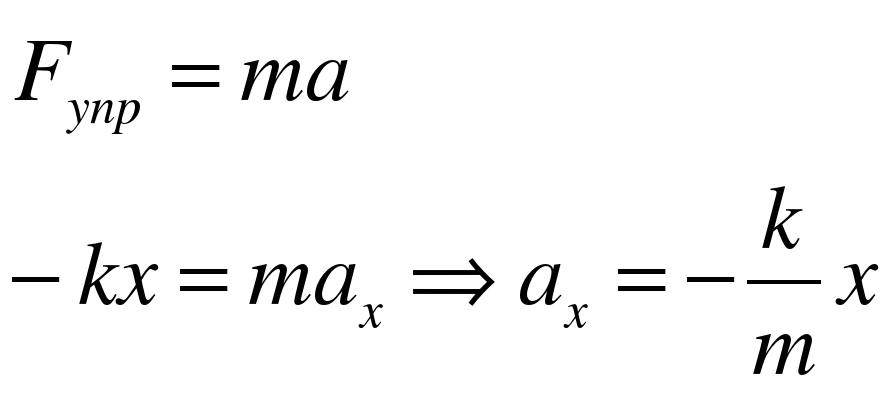
Вывод: ускорение маятника зависит от его координаты. Для анализа этой ситуации применим закон сохранения энергии. Рассмотрим положение маятника при максимальном отклонении с координатой  и промежуточное положение с координатой х2 между максимальным отклонением и положением равновесия. (обращаем внимание на преобразование энергии в компьютерной демонстрации).
и промежуточное положение с координатой х2 между максимальным отклонением и положением равновесия. (обращаем внимание на преобразование энергии в компьютерной демонстрации).
Вопрос: Какими энергиями будет обладать тело в указанных положениях? Почему?
В первом положении  , во втором положении
, во втором положении  .
.
По закону сохранения механической энергии получим:

Полученное соотношение имеет форму зависимости длин сторон прямоугольного треугольника (теорема Пифагора). Построим треугольник с указанными сторонами.

Угол φ назовем фазой колебаний.
Из треугольника следует: .
.
По мере совершения маятником полного колебания этот треугольник будет деформироваться так, что одна из его вершин опишет окружность. Происходит это в течение периода колебания Т, угол φ изменяется со временем от 0 до 2π по закону:
 .
.
Использовав это соотношение, получим закон изменения координаты маятника со временем:
 .
.
По этому закону определяется координата в случае, если маятник начинает двигаться из положения максимального отклонения. Учитывая произвольность выбора катетов треугольника, необходимо отметить и справедливость соотношения, в котором вместо функции cos будет использована функция sin. Это соотношение для определения координаты при условии начала движения из положения равновесия. Для однозначности выражения в дальнейшем будем использовать выражение, в котором будет задаваться начальная фаза колебаний φ0, прибавляемая к выражению  :
:
 .
.
Данное выражение получено для математической модели горизонтального пружинного маятника. Несмотря на это, оно может быть применено и к другим моделям, т.к. их динамические уравнения движения будут иметь сходную форму.
Предварительный контроль усвоенного материала.
Контроль осуществляется по карточке тестового контроля (Приложение 1). Карточка используется дважды: в конце текущего и начале следующего урока. Контроль построен на принципе определения индивидуальных недостатков при усвоении материала. Оценивание производится по результатам окончательных ответов. По предварительным ответам делается вывод об эффективности изложения материала.
Подведение итогов урока. Рефлексия.
Учащимся предлагается повторить оценку тех же понятий, что и в начале урока с помощью разноцветных карточек. Учащиеся вместе с учителем делают вывод о степени усвоения материала.
Домашнее задание.
П.8 с. 27-31, П.9-10 с. 32-37, п. 13 с. 42-42 проработать, упр. 5 с. 45 выполнить, выучить конспект, получить уравнение колебаний для математического маятника*
Карточка контроля. Вариант 1.
| Фамилия, имя________________________________ |
| № | Вопрос | Варианты ответа | Предварит ответ | Окончат ответ |
| 1 | Выберите движение, являющееся колебательным | А) Автомобиль набирает скорость; Б) автомобиль поворачивает; В) автомобиль движется после попадания во впадину нВ дороге; Г) автомобиль тормозит. |
|
|
| 2 | Какое из движений относится к свободным колебаниям? | А) Ребенок качается на качели; Б) поплавок колеблется на волнах воды; В) тяжелый предмет колеблется на длинном шнуре; Г) листок дрожит на ветру. |
|
|
| 3 | Какая модель лучше всего описывает катание ребенка на качели? | А) Математический маятник; Б) вертикальный пружинный маятник; В) горизонтальный пружинный маятник; Г) ни одна модель. |
|
|
| 4 | Частотой колебаний маятника называется… | А) Число колебаний, совершенных тело; Б) число колебаний, совершенных за 1 с; В) число прохождений телом положения равновесия; Г) полное время колебаний.. |
|
|
| 5 | Найдите период колебаний, если тело за 6 с совершило 15 полных колебаний. | А) 2/5 с; Б) 3/2 с: В) 1,5 с; Г) 6 с. |
|
|
| 6 | Какой частоте соответствует период колебаний маятника 1 с? | А) 0,1 Гц; Б)10 Гц: В) 1 Гц; Г) 0,01 Гц. |
|
|
| 7 | Какой вид имеет уравнение гармонических колебаний? | А)  ; ; Б)  В)  Г)  |
|
|
| 8 | С каой амплитудой происходит колебание, описываемое уравнением | А) 0,2π; Б) 0,2: В) 5π; Г) 5. |
|
|
| 9 | Сколько полных колебаний совершит маятник в течение 5 с, если его частота 0,6 Гц? | А)6; Б)10: В)3; Г)1. |
|
|
| 10 | Чему равна циклическая частота колебаний с периодом 0,5 с? | А) 40π; Б) 4π: В) 5π; Г) 2π. |
|
|
| 11 | Какой путь пройдет маятник в течение 2 с, если его максимальное смещение 4 см, а период колебаний 0,2 с? | А) 80 см; Б) 32 см: В) 40 см; Г) 4 см. |
|
|
| 12 | Какое перемещение совершит маятник в течение 4 с, если его период 0,5 с, а максимальное смещение 2 см? | А) 0см; Б) 2см: В) 4 см; Г) 1см. |
|
|
| Итоговый балл |
|
|
Карточка контроля. Вариант 2.
| Фамилия, имя________________________________ |
| № | Вопрос | Варианты ответа | Предварит ответ | Окончат ответ |
| 1 | Выберите движение, являющееся колебательным | А) Движение качелей; Б) движение мяча, падающего на землю; В) движение звучащей струны гитары; Г)движение автомодиля на дороге. |
|
|
| 2 | Какое из движений относится к свободным колебаниям? | А) Ребенок качается на качели; Б) колебания мембраны микрофона; В) движение лопастей вентичлятора; Г) листок дрожит на ветру. |
|
|
| 3 | Какая модель лучше всего описывает катание ребенка на качели? | А) Математический маятник; Б) вертикальный пружинный маятник; В) горизонтальный пружинный маятник; Г) ни одна модель. |
|
|
| 4 | Периодом колебаний маятника называется… | А) Время между двумя одинаковыми положениями маятника; Б) время, за которое маятник приходит в положение равновесия; В) время одного полного колебания; Г) время колебаний маятника. |
|
|
| 5 | Найдите период колебаний, если тело за 8 с совершило 12 полных колебаний. | А) 2/3 с; Б) 3/2 с: В) 1,5 с; Г) 8 с. |
|
|
| 6 | Какой частоте соответствует период колебаний маятника 10 с? | А) 0,1 Гц; Б)10 Гц: В) 1 Гц; Г) 0,01 Гц. |
|
|
| 7 | Какой вид имеет уравнение гармонических колебаний? | А)  ; ; Б)  В)  Г)  |
|
|
| 8 | С каой амплитудой происходит колебание, описываемое уравнением | А) 10π; Б) 10: В) 25π; Г) 25. |
|
|
| 9 | Сколько полных колебаний совершит маятник в течение 3 с, если его частота 0,2 Гц? | А)6; Б)10: В)0,5; Г)1. |
|
|
| 10 | Чему равна циклическая частота колебаний с периодом 0,2 с? | А) 10π; Б) 20π: В) 5π; Г) 2π. |
|
|
| 11 | Какой путь пройдет маятник в течение 2 с, если его максимальное смещение 2 см, а период колебаний 0,5 с? | А) 16 см; Б) 32 см: В) 4 см; Г) 2 см. |
|
|
| 12 | Какое перемещение совершит маятник в течение 4 с, если его период 0,5 с, а максимальное смещение 1 см? | А) 0см; Б) 2см: В) 4 см; Г) 1см. |
|
|
| Итоговый балл |
|
|
11 класс физика учитель: А. В. Шилько
Урок 19-20/3-4
Тема: Период математического и пружинного маятника. Преобразование энергии в процессе колебания. Решение задач.
Цель: закрепить понятия частоты и периода колебаний, получить формулы для периода и частоты колебаний пружинного и математического маятников, рассмотреть преобразование энергии в процессе механических колебаний, использовать полученные формулы в процессе решения задач, формировать навыки работы с уравнением гармонических колебаний;
развивать умения анализировать увиденные физические явления, умение сравнивать и делать выводы, способность к формированию межпредметных связей, умение применять полученные теоретические сведения на практике;
воспитывать критичное отношение к собственным знаниям, интерес к физике.
Тип урока: комбинированный урок.
Оборудование: математический маятник, вертикальный и горизонтальный пружинные маятники, компьютер.
Ход урока
Организационный момент.
Проверка домашнего задания.
Окончательный контроль по карточкам, которые были использованы в конце предыдущего урока.
Активизация познавательной деятельности.
Двадцатилетний Галилей, находясь в одном из соборов, обратил внимание на канделябр, подвешенный к потолку. Канделябр ритмично раскачивался. Нащупав собственный пульс, он убедился в том, что период колебаний канделябра со временем не изменяется. (Что такое период колебаний? С какой характеристикой колебаний связан период?) Это свойство со временем будет названо изохорностью математического маятника. Пригодилось оно Галилею уже в зрелом возрасте, когда перед ним стала проблема создания прибора для измерения времени, который можно было бы использовать на корабле. Определение точных координат корабля в открытом океане невозможно без точного определения момента времени. Водяные и песочные часы того времени не удовлетворяли нужд моряков, хотя и оставались основными приборами измерения времени. Вспомнив, свойства изохорности маятника, Галилей изобретает прототип современных маятниковых часов. (Видели ли вы маятниковые часы? В чем заключается идея работы маятниковых часов сегодня? С помощь какой математической модели можно описать движения маятника в часах?) Но, находясь под пристальным вниманием инквизиции и учитывая недоброжелательное отношение Венецианских властей, Галилей делится своей идеей со своим старым другом – послом Нидерландов в Индии Константином Гюйгенсом, послав ему зашифрованное письмо. Константин Гюйгенс поставил в известность правительство своей страны о стратегическом изобретении Галилея. Реакция не заставила себя ждать – правительство Нидерландов предлагает Галилею немалую сумму денег и дорогой подарок в надежде на сотрудничество. Галилей, понимая, что это может быть расценено как измена государственным интересам, отказывается от предложения. Но со временем идея Галилея нашла конкретное воплощение в изобретении, созданном сыном Константина Гюйгенса – Кристианом Гюйгенсом, известным математиком и естествознавцем своего времени. Именно Гюйгенсу принадлежит изобретение часов, в которых отсчет одинаковых интервалов времени основан на использовании свойства изохорности маятника. Ему принадлежит приоритет изобретения и в его честь названо соотношение для определения периода колебаний математического маятника, которое мы получим на сегодняшнем уроке.
Восприятие и осознание нового материала.
Понятие производной функции (повторение понятия полученного на уроках алгебры).
Отношение прироста функции к приросту аргумента, при условии, что прирост аргумента стремится к нулю, называется производной функции.
Вспомним определение понятия мгновенной скорости. Мгновенная скорость – это отношение прироста координаты тела к приросту промежутка времени, за которое это изменение произошло, при условии, что этот промежуток времени бесконечно мал (или стремится к нулю).
,
Но это ест ни что иное, как определение производной. Поэтому . Т.е. мгновенная скорость – это производная от координаты по времени.
Анализ уравнения колебательного движения.
Продифференцируем уравнение колебаний и получим уравнение для скорости колебаний.
.
Видим, что скорость движения колеблющегося тела также как и координата изменяется по гармоническому закону. Максимальной скорости тело достигнет в момент прохождения положения равновесия, а значит, в этот момент оно будет обладать максимальной кинетической энергией.
Продифференцировав полученное уравнение, получим уравнение для ускорения.
.
Полученное уравнение - это динамическое уравнение гармонических колебаний.
Формулы для частоты и периода колебаний пружинного и математического маятника.
Вспомним динамическое уравнение записанное для пружинного маятника на предыдущем у роке:
,
и учтем, что ускорение является второй производной от координаты . Тогда получим:
.
Сравним это выражение с динамическим уравнением гармонических колебаний. Видим, что .
Аналогично получим выражение для математического маятника .
Теперь использовав, соотношение , получим интересующие нас формулы для периода колебаний пружинного и математического маятников.
и
Последнее выражение называется формулой Гюйгенса, о которой мы упоминали в начале урока.
Преобразование энергии в процессе колебания.
Коппьютерная демонстрация преоразования энергии в процессе колебания математического маятника.
При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругих деформаций пружины. Для математического маятника – это энергия в поле тяготения Земли.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по закону инерции. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.
Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.
Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.
Обобщение и систематизация изученного материала. Решение задач.
Написать закон гармонических колебаний. Если амплитуда колебаний 0,2 м, а частота колебаний 2 Гц. ()
Тело совершает колебания по закону . Определите частоту, период колебаний тела, его координату на 2 с движения. (5 Гц, 0,2 с, -0,25м)
По графику приведенному на рисунке найти амплитуду, период и частоту колебаний. Написать уравнение гармонических колебаний. Вычислить кинетическую и потенциальную энергии в момент времени 3 с, если масса колеблющегося равна 200 г. (20 см, 4 с, 0,25 Гц, , 0,1 мДж, 0 Дж)
Определите ускорение свободного падения на Луне, если маятниковые часы идут на ее поверхности в 2.46 раза медленнее, чем на Земле.(1,62 м/с2)
С каким ускорением и в каком направлении должна двигаться кабина лифта, чтобы находящийся в не секундный маятник за 2 мин 30 с совершил 100 колебаний. (4,4 м/с2, вверх)








 омпьютерная демонстрация графической зависимости координаты математического маятника от времени.
омпьютерная демонстрация графической зависимости координаты математического маятника от времени. омпьютерная демонстрация графической зависимости координаты пружинного маятника от времени.
омпьютерная демонстрация графической зависимости координаты пружинного маятника от времени.