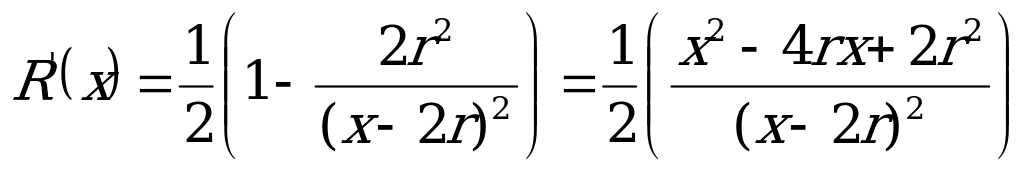ФЕДЕРАЛЬНЫЙ ПРОЕКТ «КАДРЫ ДЛЯ ЦИФРОВОЙ ЭКОНОМИКИ»
ФЕДЕРАЛЬНЫЙ ПРОЕКТ «КАДРЫ ДЛЯ ЦИФРОВОЙ ЭКОНОМИКИ»
НАЦИОНАЛЬНОЙ ПРОГРАММЫ «ЦИФРОВАЯ ЭКОНОМИКА» ГОСУДАРСТВЕННОЙ ПРОГРАММЫ РОССИЙСКОЙ ФЕДЕРАЦИИ «РАЗВИТИЕ ОБРАЗОВАНИЯ»
ПРОЕКТ «ЦИФРОШКОЛА68»
Муниципальное общеобразовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М.Кузьмина»
Н.А. Курьянова
Задачи по стереометрии
для подготовки к олимпиадам и ЕГЭ
Учебно-методическое пособие для учащихся
ТАМБОВ 2022
Автор-составитель:
Рецензенты:
Курьянова Н.А. - учитель математики высшей категории МАОУ «Лицей №14 имени Заслуженного учителя Российской Федерации А.М.Кузьмина» г.Тамбова
Андрющенко А.Р., кандидат педагогических наук, учитель математики высшей категории МАОУ «Лицей
№14 имени Заслуженного учителя Российской Федерации А.М.Кузьмина» г. Тамбов
В данном учебно-методическом пособии рассмотрены аналитические и графические методы решения задач по стереометрии. По каждому методу приведены примеры с решениями. В пособии содержатся задачи для самостоятельного решения.
Пособие будет полезным для учащихся и учителей классов с углубленным преподаванием математики при подготовке к единому государственному экзамену по математике, а также может быть использовано для проведения занятий в математических кружках.
КОМБИНАЦИЯ ШАРА С ДРУГИМИ ТЕЛАМИ
I. Некоторые геометрические места точек
Перед тем, как приступать к вопросу о комбинации шара с другими телами, следует повторить некоторые геометрические места точек, изученные в курсе геометрии .
ГМТ-1. Геометрическое место точек, равноудалённых от двух данных точек, есть плоскость, перпендикулярная к отрезку с концами в данных точках и проходящая через его середину.
ГМТ-2. Геометрическое место точек, равноудалённых от двух параллельных между собой плоскостей, есть плоскость, параллельная данным и проходящая через середину расстояния между ними.
ГМТ-3. Геометрическое место точек, равноудалённых от граней двугранного угла, есть плоскость, делящая этот двугранный угол пополам. Такая плоскость называется биссекторной.
ГМТ-4. Геометрическое место точек, равноудалённых от всех точек окружности, есть прямая, перпендикулярная плоскости этой окружности, проходящая через её центр.
Следствие. Геометрическое место точек, равноудалённых от всех вершин многоугольника, вписанного в окружность, есть прямая, перпендикулярная плоскости этого многоугольника и проходящая через центр окружности
II. Определения
Шар называется вписанным в многогранник, а многогранник описанным около шара, если поверхность шара касается всех граней многогранника.
Шар называется описанным около многогранника, а многогранник вписанным в шар, если поверхность шара проходит через все вершины многогранника
Шар называется вписанным в цилиндр, усеченный конус (конус), а цилиндр, усеченный конус (конус) – описанным около шара, если поверхность шара касается оснований (основания) и всех образующих цилиндра, усеченного конуса (конуса).
(Из этого определения следует, что в любое осевое сечение этих тел может быть вписана окружность большего круга шара).
Шар называется описанным около цилиндра, усеченного конуса (конуса), если окружности оснований (окружность основания и вершина) принадлежат поверхности шара. (Из этого определения следует, что около любого осевого сечения этих тел может быть описана окружность большего круга шара).
III. Общие замечания о положении центра шара
Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника
Центр шара, описанного около многогранника, лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может быть расположен внутри, на поверхности и вне многогранника.
IV. Комбинация шара с призмой
1. Шар, вписанный в прямую призму
Теорема 1. Шар можно вписать в прямую призму в том и только в том случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.
Доказательство необходимости
Д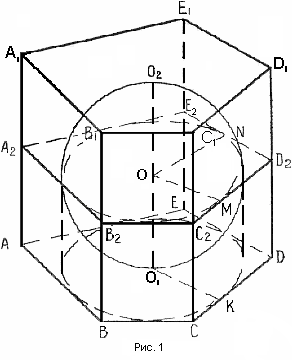 опустим, что в некоторую прямую призму вписан шар (рис. №1).Докажем, что в основание этой призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. Из центра шара, точки О, проведём радиусы OM и ON в точки касания шара с гранями
опустим, что в некоторую прямую призму вписан шар (рис. №1).Докажем, что в основание этой призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. Из центра шара, точки О, проведём радиусы OM и ON в точки касания шара с гранями 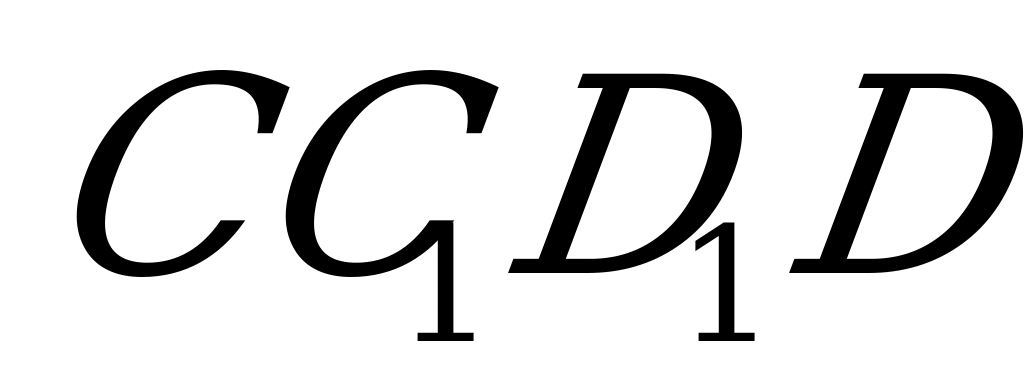 и
и 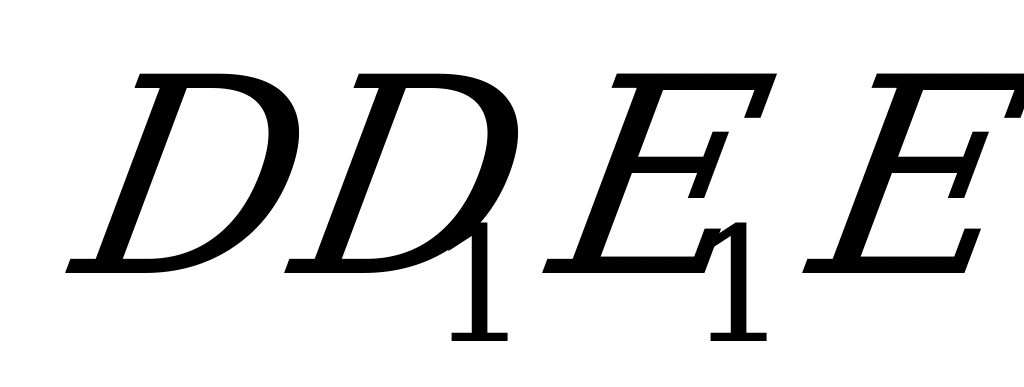 . Тогда эти радиусы будут перпендикулярны боковым граням (теорема о свойстве радиуса, проведённого в точку касания шара с плоскостью). Через OM и ON проведём плоскость
. Тогда эти радиусы будут перпендикулярны боковым граням (теорема о свойстве радиуса, проведённого в точку касания шара с плоскостью). Через OM и ON проведём плоскость  . Эта плоскость перпендикулярна указанным граням (признак перпендикулярности плоскостей) и линии их пересечения
. Эта плоскость перпендикулярна указанным граням (признак перпендикулярности плоскостей) и линии их пересечения  (следствие из признака перпендикулярности плоскостей), а следовательно, перпендикулярна остальным боковым ребрам как параллельным
(следствие из признака перпендикулярности плоскостей), а следовательно, перпендикулярна остальным боковым ребрам как параллельным  , а потому перпендикулярна и всем боковым граням.
, а потому перпендикулярна и всем боковым граням.
Если из точки О опустим перпендикуляры на остальные боковые грани, то все они будут лежать в плоскости  (теорема о прямой, перпендикулярной к одной из перпендикулярных плоскостей, имеющей общую точку с другой).
(теорема о прямой, перпендикулярной к одной из перпендикулярных плоскостей, имеющей общую точку с другой).
Таким образом, точка О равноудалена от всех сторон перпендикулярного сечения, т. е. служит центром окружности, вписанной в перпендикулярное сечение. Но это сечение равно основанию. Поэтому в основание тоже можно вписать окружность с радиусом, равным радиусу шара. Радиусы  и
и  , где точки
, где точки  и
и  - точки касания шара с основанием, будучи перпендикулярными к параллельным между собой плоскостям, составят отрезок
- точки касания шара с основанием, будучи перпендикулярными к параллельным между собой плоскостям, составят отрезок  , перпендикулярный основаниям, а потому высота призмы равна диаметру шара или диаметру окружности, вписанной в основание.
, перпендикулярный основаниям, а потому высота призмы равна диаметру шара или диаметру окружности, вписанной в основание.
Доказательство достаточности
Допустим, что в основание прямой призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. Докажем, что в эту призму можно вписать шар, т. е. существует точка, равноудаленная от всех граней этой призмы.
Проведём прямую  через центр окружности, вписанной в основание призмы, перпендикулярно этому основанию. Прямая
через центр окружности, вписанной в основание призмы, перпендикулярно этому основанию. Прямая параллельна каждому боковому ребру (теорема о двух прямых, перпендикулярных к одной плоскости), а потому она параллельна каждой боковой грани (признак параллельности прямой и плоскости). Радиус
параллельна каждому боковому ребру (теорема о двух прямых, перпендикулярных к одной плоскости), а потому она параллельна каждой боковой грани (признак параллельности прямой и плоскости). Радиус  , проведённый в точку касания К, перпендикулярен CD и
, проведённый в точку касания К, перпендикулярен CD и 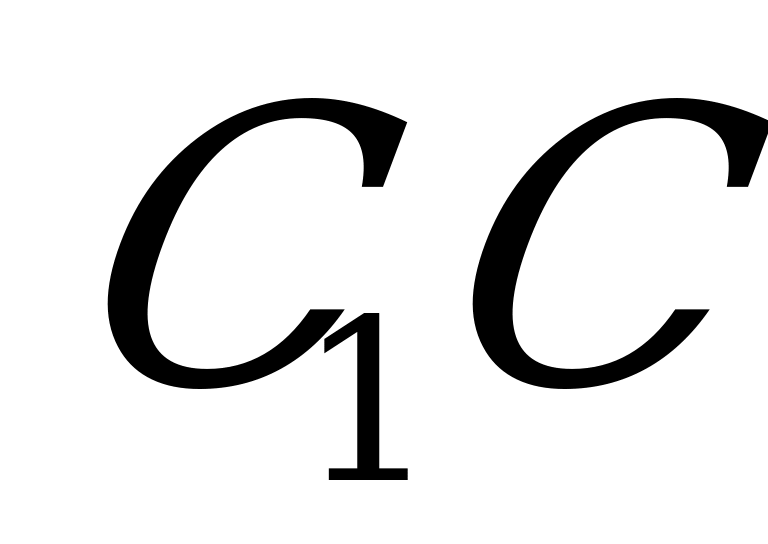 , а потому перпендикулярен грани
, а потому перпендикулярен грани 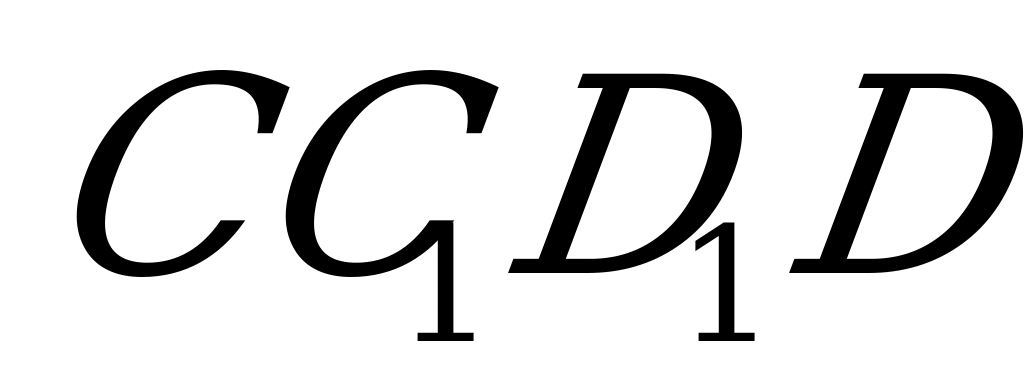 (признак перпендикулярности прямой и плоскости). Следовательно, прямая
(признак перпендикулярности прямой и плоскости). Следовательно, прямая  удалена от каждой боковой грани на величину радиуса окружности, вписанной в основание призмы. Поэтому, если существует точка, равноудаленная от всех граней призмы, то она должна принадлежать отрезку
удалена от каждой боковой грани на величину радиуса окружности, вписанной в основание призмы. Поэтому, если существует точка, равноудаленная от всех граней призмы, то она должна принадлежать отрезку  .
.
По условию высота призмы 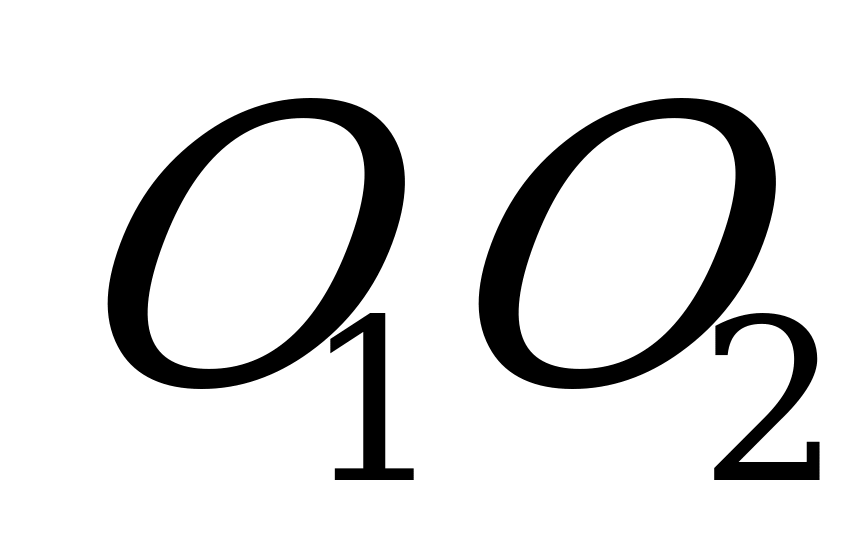 равна диаметру окружности, вписанной в основание призмы, а потому середина отрезка
равна диаметру окружности, вписанной в основание призмы, а потому середина отрезка 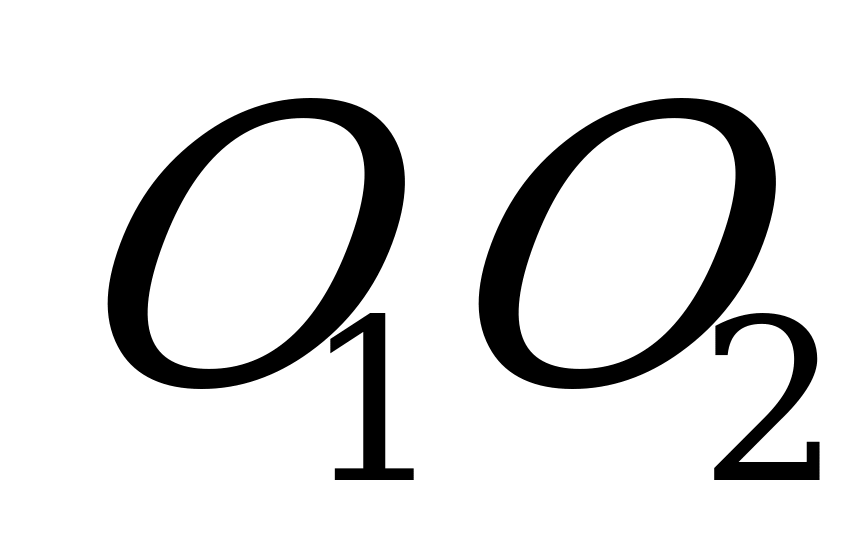 и есть точка, равноудаленная от всех граней призмы, т. е. будет служить центром шара, вписанного в эту призму. Эта точка единственная. Это доказательство справедливо для призм с любым числом сторон основания.
и есть точка, равноудаленная от всех граней призмы, т. е. будет служить центром шара, вписанного в эту призму. Эта точка единственная. Это доказательство справедливо для призм с любым числом сторон основания.
Следствие 1. Центр шара, вписанного в прямую призму, лежит в середине высоты призмы, проходящей через центр окружности, вписанной в основание.
Следствие 2. Шар, в частности, можно вписать в прямые призмы: треугольную, правильную, четырехугольную (у которой суммы противоположных сторон основания равны между собой) при условии H=2r, где Н – высота призмы, r – радиус круга, вписанного в основание.
Шар, описанный около призмы
Теорема 2. Шар можно описать около призмы в том и только в том случае, если призма прямая и около её основания можно описать окружность.
Доказательство необходимости
Д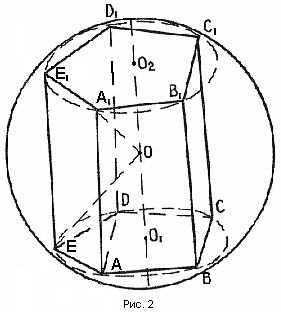 опустим, что шар описан около призмы (рис. №2). Докажем, что призма прямая и что около её основания можно описать окружность.
опустим, что шар описан около призмы (рис. №2). Докажем, что призма прямая и что около её основания можно описать окружность.
Плоскость основания призмы (теорема о сечении шара плоскостью) пересечет поверхность шара по окружности, на которой лежат все вершины основания. Таким образом, около основания призмы можно описать окружность.
Плоскости любых боковых граней призмы также пересекут поверхность шара по окружностям, а так как из параллелограммов можно вписать в окружность только прямоугольник, то, следовательно, все боковые грани призмы – прямоугольники. Тогда боковое ребро, например 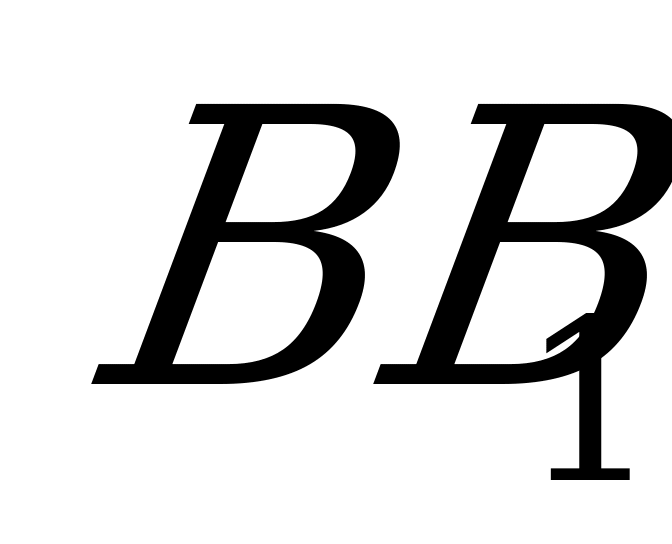 , перпендикулярно к АВ и ВС, а потому (признак перпендикулярности прямой и плоскости)
, перпендикулярно к АВ и ВС, а потому (признак перпендикулярности прямой и плоскости) 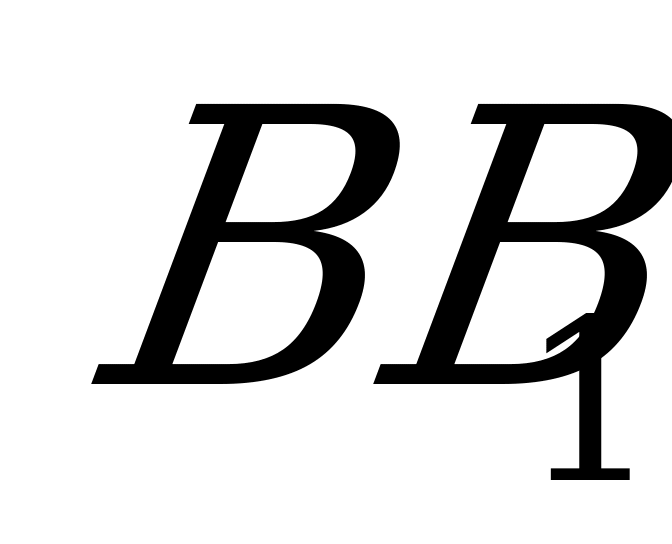 перпендикулярно к плоскости основания. Значит, призма прямая.
перпендикулярно к плоскости основания. Значит, призма прямая.
Доказательство достаточности
Допустим, что около основания прямой призмы можно описать окружность, и докажем, что около такой призмы можно описать шар, т. е. существует точка, равноудаленная от всех вершин этой призмы. Так как основания призмы равны, то и окружности, описанные около них, равны. Из центра окружности, описанной около верхнего основания 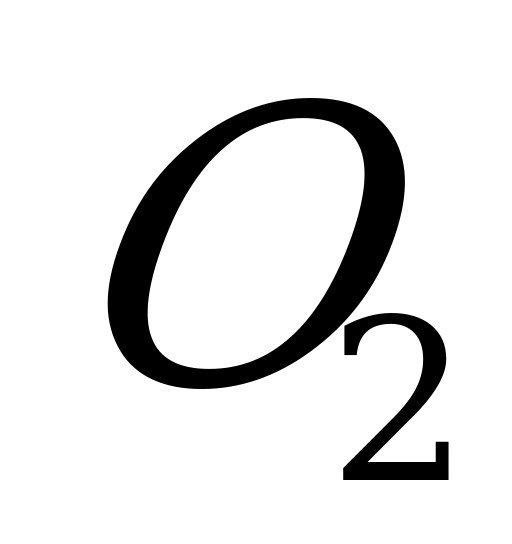 , опустим перпендикуляр на нижнее основание
, опустим перпендикуляр на нижнее основание 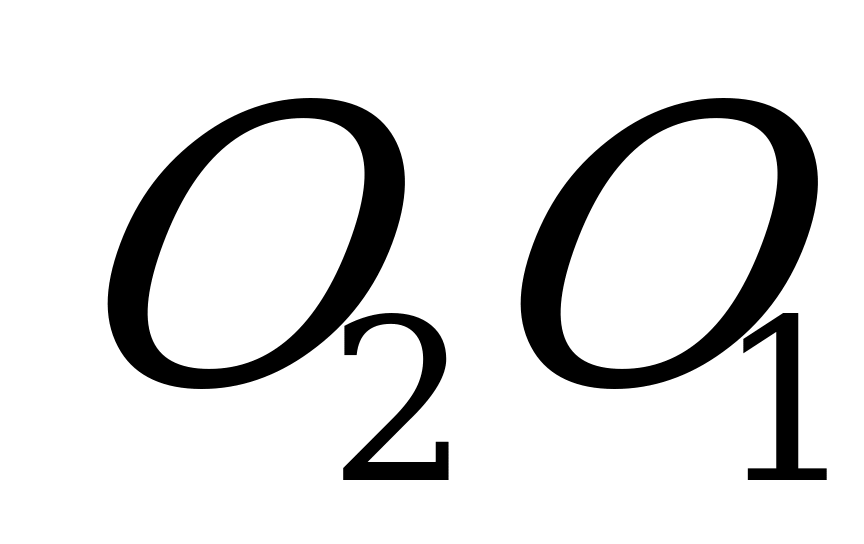 . Четырехугольники
. Четырехугольники 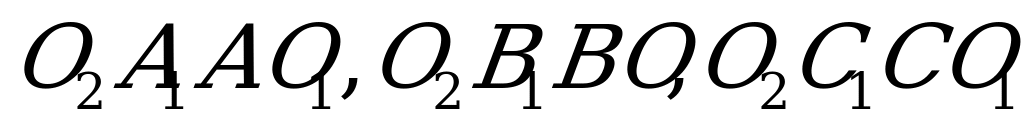 и т.д. – прямоугольники, а потому из равенства:
и т.д. – прямоугольники, а потому из равенства: 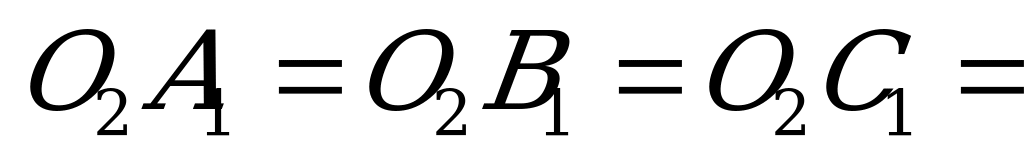 … следуют равенства:
… следуют равенства: 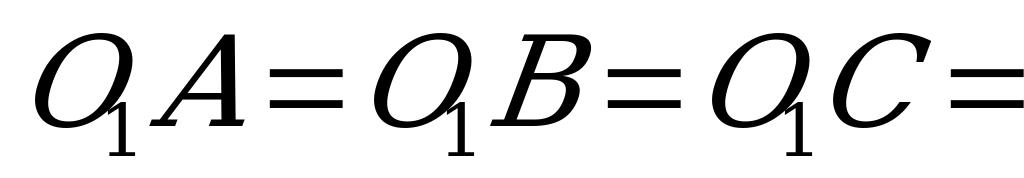 … , т.е. точка
… , т.е. точка 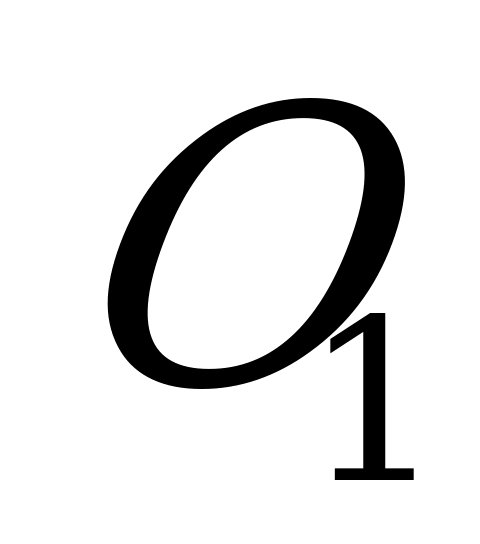 является центром окружности, описанной около нижнего основания. Поэтому прямая
является центром окружности, описанной около нижнего основания. Поэтому прямая 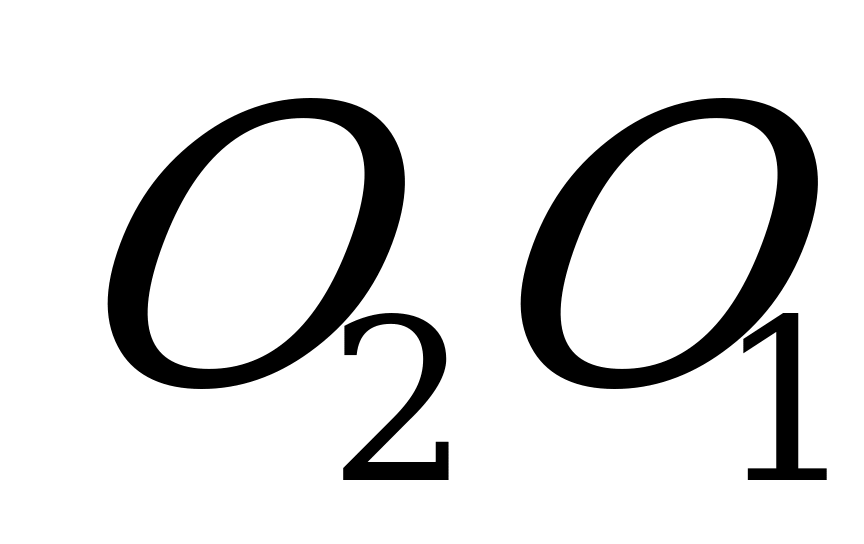 , проходящая через центры окружностей, описанных около оснований, перпендикулярна основаниям. Все точки прямой
, проходящая через центры окружностей, описанных около оснований, перпендикулярна основаниям. Все точки прямой  равноудалены от вершины каждого основания (следствие из ГМТ-4). С другой стороны, все точки плоскости, проведенной через середины боковых ребер равноудалены от каждой пары вершин одного бокового ребра призмы, например,
равноудалены от вершины каждого основания (следствие из ГМТ-4). С другой стороны, все точки плоскости, проведенной через середины боковых ребер равноудалены от каждой пары вершин одного бокового ребра призмы, например,  (ГМТ-1).
(ГМТ-1).
Пересечение этих геометрических мест даст единственную точку О, равноудаленную от всех вершин призмы, т.е. центр шара, описанного около призмы.
Следствие 1. Центр шара, описанного около прямой призмы, лежит на середине высоты призмы, проведенной через центр круга, описанного около основания.
Следствие 2. Шар, в частности можно описать: около прямой треугольной призмы, около правильной призмы, около прямоугольного параллелепипеда, около прямой четырехугольной призмы, у которой сумма противоположных углов основания равна 180.
V. Комбинация шара с пирамидой
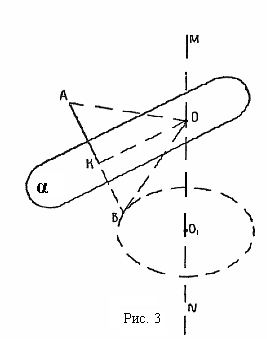
Лемма. Через окружность и точку, не принадлежащую плоскости этой окружности, можно провести сферу и притом только одну.
Геометрическое место точек, равноудаленных от всех точек окружности (ГМТ-4), есть прямая MN, перпендикулярная плоскости этой окружности и проходящая через ее центр (см. рис. № 3).
Возьмем на данной окружности произвольную точку В. Геометрическое место точек, равноудаленных от точек А и В (ГМТ-1), есть плоскость , перпендикулярная отрезку АВ и проходящая через его середину – точку К.
Точка пересечения этой плоскости с MN – точка О, равноудалена от всех точек окружности и точки А, а потому является центром сферы, проходящей через окружность и точку А. Точка О есть единственная точка, обладающая этим свойством. Так как плоскость пересекается с MN только в одной точке, а следовательно, через окружность и точку, не принадлежащую плоскости этой окружности, можно провести сферу и притом только одну.
Шар, описанный около пирамиды
Теорема 3. Около пирамиды можно описать шар в том и только в том случае, если около ее основания можно описать окружность
Доказательство необходимости
Допустим, что шар описан около пирамиды (рис. № 4). 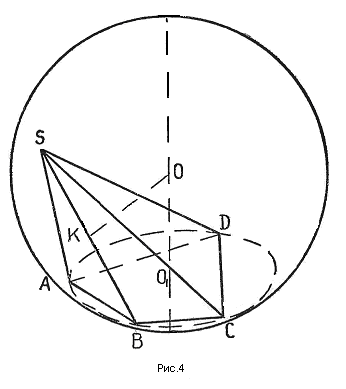 Докажем, что около основания этой пирамиды можно описать окружность. Плоскость основания пересекает поверхность сферы по окружности (теорем о сечении шара плоскостью). Вершины основания лежат на поверхности шара и на плоскости основания, следовательно, они лежат на линии пересечения их, т.е. на окружности. Поэтому около основания можно описать окружность.
Докажем, что около основания этой пирамиды можно описать окружность. Плоскость основания пересекает поверхность сферы по окружности (теорем о сечении шара плоскостью). Вершины основания лежат на поверхности шара и на плоскости основания, следовательно, они лежат на линии пересечения их, т.е. на окружности. Поэтому около основания можно описать окружность.
Доказательство достаточности
Допустим, что около основания пирамиды можно описать окружность.
Докажем, что около такой пирамиды можно описать шар. Вершины основания принадлежат окружности, а через окружность и точку S, расположенную вне плоскости этой окружности, на основании леммы, можно описать сферу и притом только одну. Следовательно, около этой пирамиды можно описать шар.
Следствие 1. Центр шара, описанного около пирамиды, лежит в точке пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр окружности, описанной около этого основания, и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.
С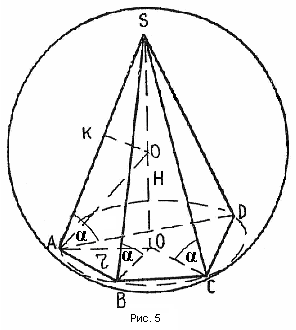 ледствие 2. Если боковые ребра пирамиды равны между собой (или равнонаклонены к плоскости основания), то около такой пирамиды можно описать шар (рис. № 5). Центр шара в этом случае лежит в точке пересечения высоты пирамиды (или ее продолжения) с осью симметрии бокового ребра, лежащей в плоскости бокового ребра и высоты.
ледствие 2. Если боковые ребра пирамиды равны между собой (или равнонаклонены к плоскости основания), то около такой пирамиды можно описать шар (рис. № 5). Центр шара в этом случае лежит в точке пересечения высоты пирамиды (или ее продолжения) с осью симметрии бокового ребра, лежащей в плоскости бокового ребра и высоты.
Известно, что если боковые ребра пирамиды равны, то вершина пирамиды проектируется в центр круга, описанного около основания. А так как около основания пирамиды можно описать окружность, то по доказанному выше, около такой пирамиды можно описать шар.
В этом случае полезно пользоваться формулами:
1) 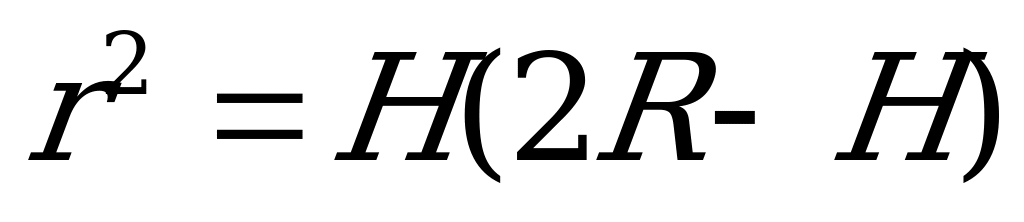
2) 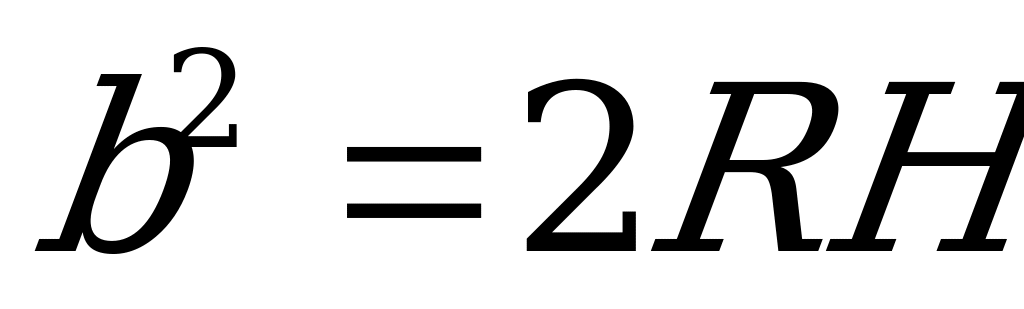
3) 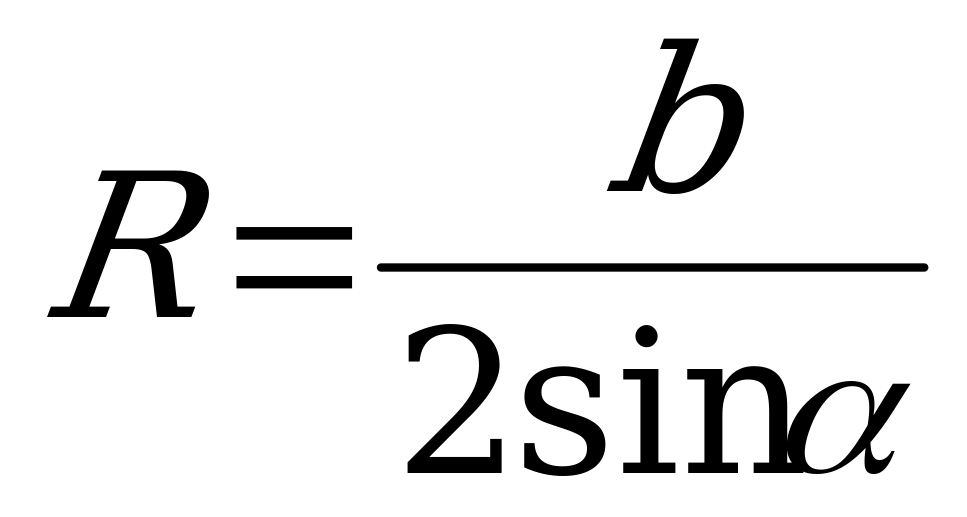
4) 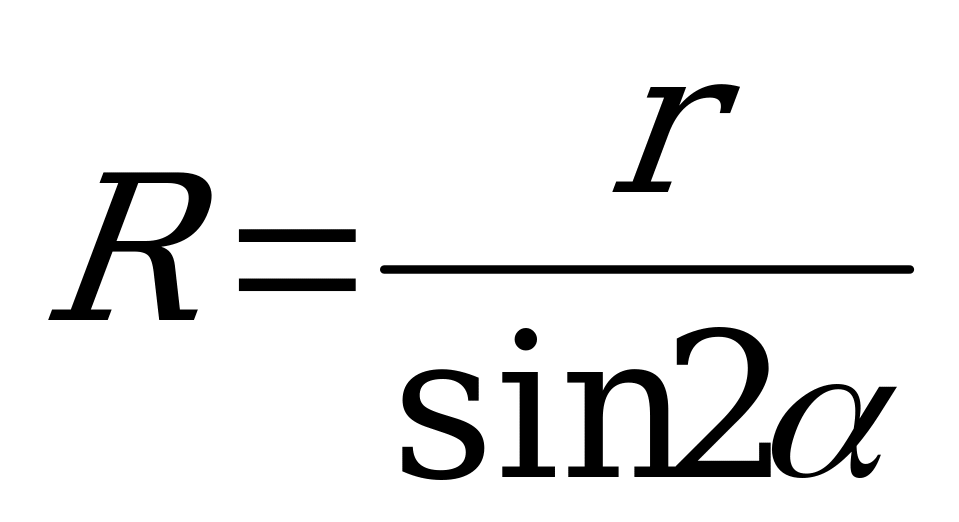 ,
,
где R – радиус шара, r – радиус окружности, описанной около основания пирамиды, b – боковое ребро, Н – высота пирамиды, α – угол наклона бокового ребра к плоскости основания.
Следствие 3. Шар, в частности, можно описать: около треугольной пирамиды, около правильной пирамиды, около четырехугольной пирамиды, у которой сумма противоположных углов равна 180.
Шар, вписанный в пирамиду
Шар можно вписать в выпуклую пирамиду в том и только в том случае, если биссекторные плоскости двугранных углов при всех боковых ребрах пересекаются по одной прямой или биссекторные плоскости всех двугранных углов при основании пирамиды проходят через одну точку.
Следствие 1. Шар можно вписать в любую треугольную пирамиду.
Следствие 2. Для того, чтобы шар можно было вписать в выпуклую четырехугольную пирамиду, необходимо и достаточно чтобы сумма плоских углов противоположных боковых граней пирамиды были равны между собой.
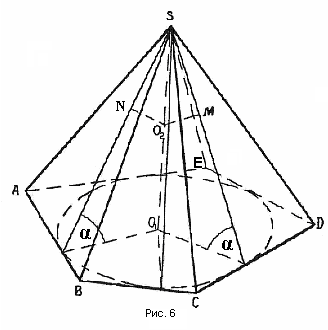
Теорема № 4. Если боковые грани пирамиды одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.
Замечание. Это условие – достаточное и не является необходимым.
Доказательство
Докажем, что любая точка (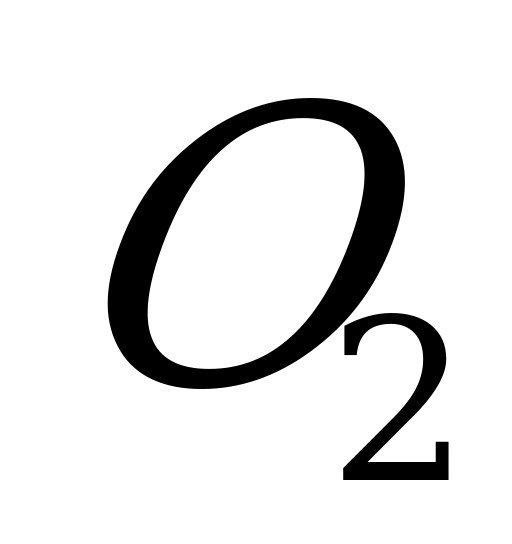 ) (рис.6) высоты такой пирамиды равноудалена от всех боковых граней. Плоскости линейных углов двугранных углов при основании перпендикулярны боковым граням (т.к. плоскость боковой грани проходит через ребро основания, которое перпендикулярно плоскости линейного угла), а потому, если мы опустим на боковые грани перпендикуляры
) (рис.6) высоты такой пирамиды равноудалена от всех боковых граней. Плоскости линейных углов двугранных углов при основании перпендикулярны боковым граням (т.к. плоскость боковой грани проходит через ребро основания, которое перпендикулярно плоскости линейного угла), а потому, если мы опустим на боковые грани перпендикуляры 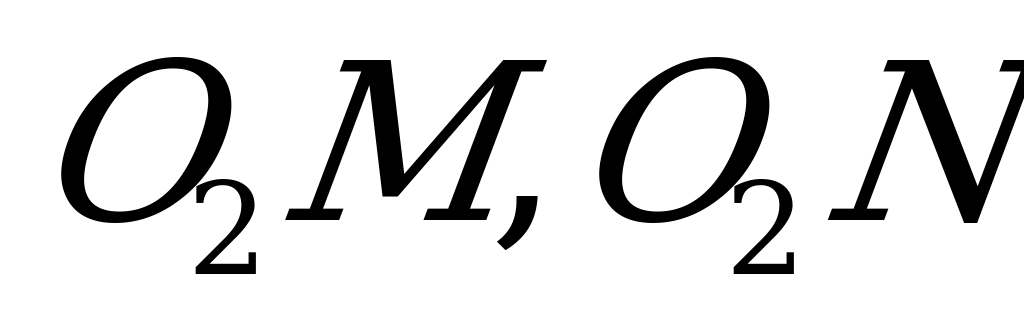 и т.д., то они будут лежать в плоскостях линейных углов, а точки M, N и т.д. окажутся на высотах боковых граней, опущенных из вершины пирамиды.
и т.д., то они будут лежать в плоскостях линейных углов, а точки M, N и т.д. окажутся на высотах боковых граней, опущенных из вершины пирамиды.
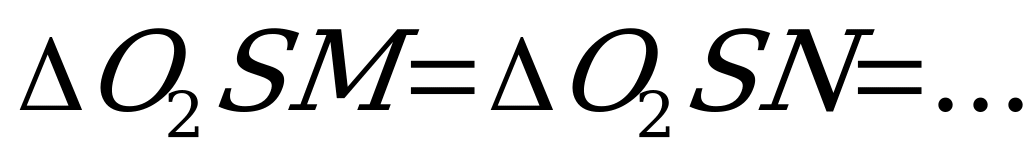 (по гипотенузе и острому углу), а потому ОМ=ON=… , т.е. точка
(по гипотенузе и острому углу), а потому ОМ=ON=… , т.е. точка 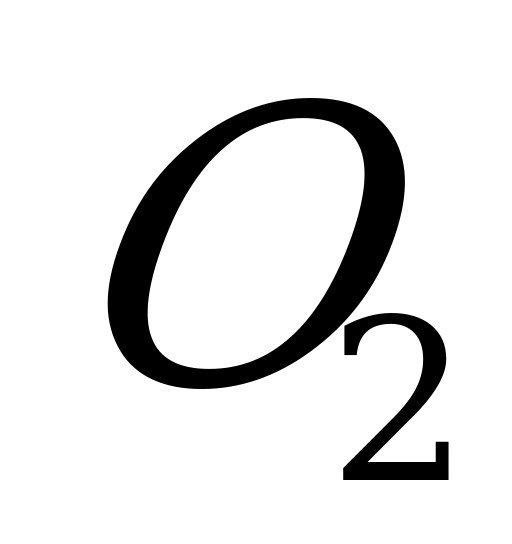 равноудалена от всех боковых граней. Из этого следует, что центр шара, вписанного в такую пирамиду, лежит на высоте пирамиды. Точка пересечения высоты пирамиды с биссектрисой линейного угла двугранного угла при основании пирамиды, в плоскости которого расположена высота пирамиды, есть центр шара, вписанного в пирамиду, и притом единственного.
равноудалена от всех боковых граней. Из этого следует, что центр шара, вписанного в такую пирамиду, лежит на высоте пирамиды. Точка пересечения высоты пирамиды с биссектрисой линейного угла двугранного угла при основании пирамиды, в плоскости которого расположена высота пирамиды, есть центр шара, вписанного в пирамиду, и притом единственного.
Следствие 1. Центр шара, вписанного в пирамиду, у которой боковые грани одинаково наклонены к основанию, лежит в точке пересечения высоты пирамиды с биссектрисой линейного угла любого двугранного угла при основании пирамиды, стороной которого служит высота боковой грани, проведенная из вершины пирамиды.
Следствие 2. В правильную пирамиду можно вписать шар.
VI. Комбинация шара с усеченной пирамидой
1. Шар, описанный около правильной усеченной пирамиды
Теорема. Около усеченной пирамиды можно описать шар в том и только в том случае, если около ее оснований можно описать окружности, и прямая, проведенная через их центры, перпендикулярна плоскости основания (рис. 7).
Т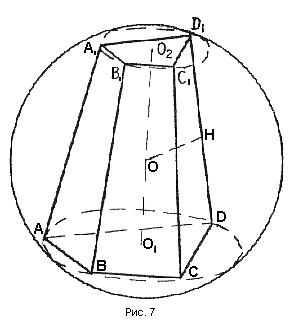 еорема 5. Около любой правильной усеченной пирамиды можно описать шар.
еорема 5. Около любой правильной усеченной пирамиды можно описать шар.
Замечание. Это условие является достаточным, но не является необходимым.
Доказательство
Известно, что около оснований правильной усеченной пирамиды можно описать окружности и что прямая, проходящая через центры этих окружностей, перпендикулярна основаниям. Следовательно, все точки, равноудаленные от вершины каждого основания (следствие из геометрического места точек № 4), лежат на этой прямой. Точка пересечения этой прямой с осью симметрии любого бокового ребра, лежащей в плоскости этой прямой и бокового ребра, есть центр шара, описанного около правильной усеченной пирамиды. Легко показать, что эта точка единственная.
Следующие теоремы без доказательства..
2. Шар, вписанный в правильную усеченную пирамиду
Теорема. В усеченную пирамиду можно вписать шар в том и только в том случае, если биссекторные плоскости всех двугранных углов при боковых ребрах пересекаются по одной прямой, а отрезок ее, отсеченный основаниями усеченной пирамиды, делится пополам биссекторной плоскостью любого двугранного угла при основании.
Т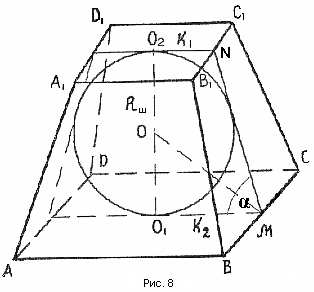 еорема 6. В правильную усеченную пирамиду можно вписать шар в том и только в том случае, если апофема пирамиды равна сумме апофем оснований (рис.8).
еорема 6. В правильную усеченную пирамиду можно вписать шар в том и только в том случае, если апофема пирамиды равна сумме апофем оснований (рис.8).
Центр шара есть точка пересечения высоты правильной усеченной пирамиды, проходящей через центр основания 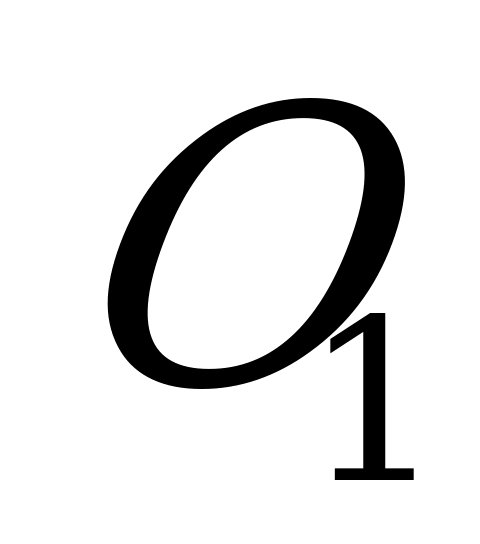 и биссектрисы линейного угла двугранного угла при основании
и биссектрисы линейного угла двугранного угла при основании  .
.
VII. Комбинация шара с круглыми телами
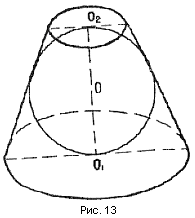
Теорема 7. Около цилиндра, усеченного конуса, конуса (прямых круговых), можно описать шар. (рис. №№ 9,10, 11).
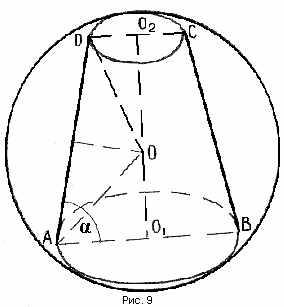
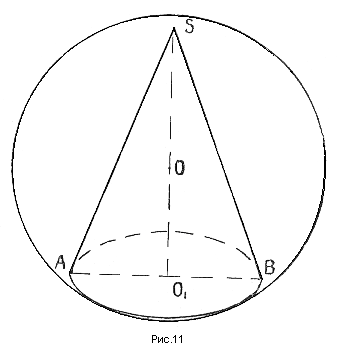
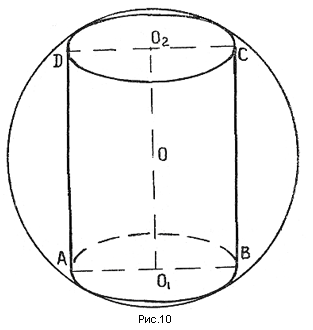
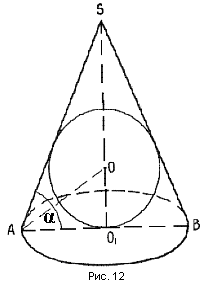
Теорема 8. В любой конус (прямой круговой) можно вписать шар (рис. № 12).
Теорема 9. В усеченный конус (прямой, круговой) можно вписать шар в том и только в том случае, если его образующая равна
сумме радиусов оснований (рис. № 13).
ФОРМУЛЫ ПЕРЕХОДА
Рассмотрим углы в правильной пирамиде, наиболее часто встречаются в задачах:
а) угол наклона бокового ребра к плоскости основания пирамиды, его величину условимся обозначать буквой  ;
;
б) угол наклона боковой грани к плоскости основания  ;
;
в) плоский угол при вершине пирамиды 

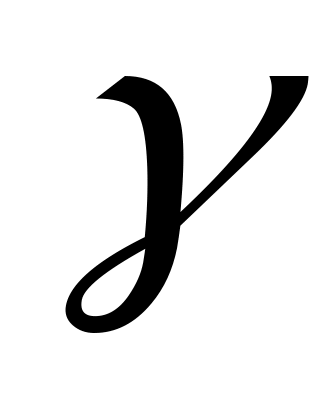 ;
;
г) двугранный угол при боковом ребре пирамиды 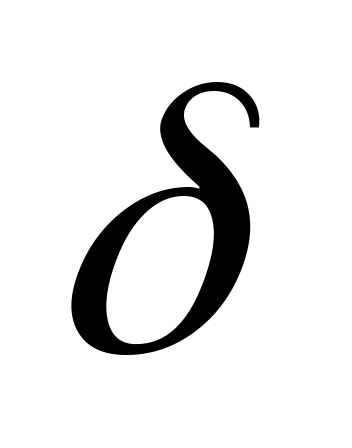 .
.
Все перечисленные выше углы, называемые иногда основными, лежат в разных плоскостях. Зная величину любого из них, можно определить величину всех остальных углов. Эти зависимости мы назовем формулами перехода.
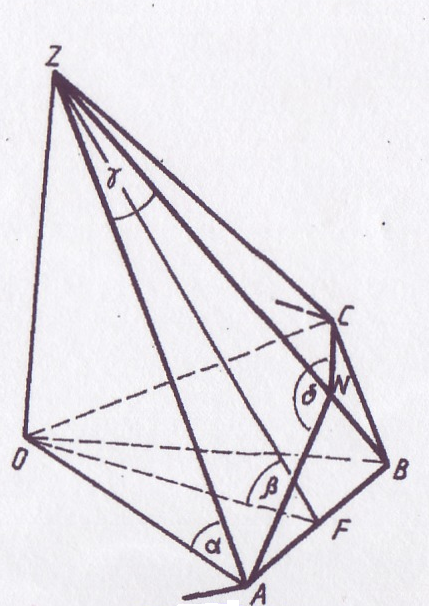
Дана правильная  n-угольная пирамида с обозначенными выше углами
n-угольная пирамида с обозначенными выше углами  ,
, ,
,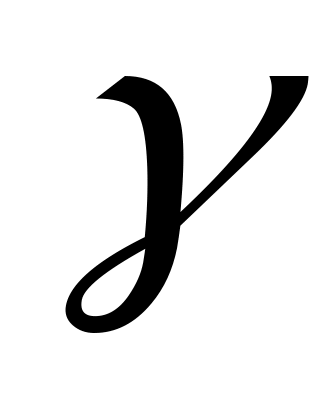 и
и 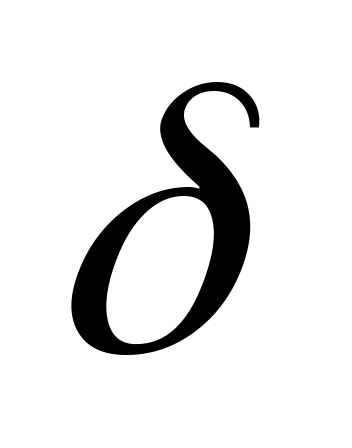 . Вывести формулы перехода, связывающие эти углы между собой.
. Вывести формулы перехода, связывающие эти углы между собой.
Примечание. Поскольку для решения многих задач желательно знать величину угла наклона бокового ребра к плоскости основания пирамиды либо угла наклона боковой грани к плоскости основания, то мы будем выводить формулы перехода только к этим углам.
 Решение. Обозначим через x длину отрезка в правильной пирамиде, входящего как в прямоугольный треугольник, содержащий данный угол, так и в треугольник, содержащий искомый угол. Выразим далее через x и функции данного угла одну из двух других сторон в том треугольнике, который содержит искомый угол. Затем найдём функцию искомого угла.
Решение. Обозначим через x длину отрезка в правильной пирамиде, входящего как в прямоугольный треугольник, содержащий данный угол, так и в треугольник, содержащий искомый угол. Выразим далее через x и функции данного угла одну из двух других сторон в том треугольнике, который содержит искомый угол. Затем найдём функцию искомого угла.
Вывод формул перехода для правильной четырёхугольной пирамиды.
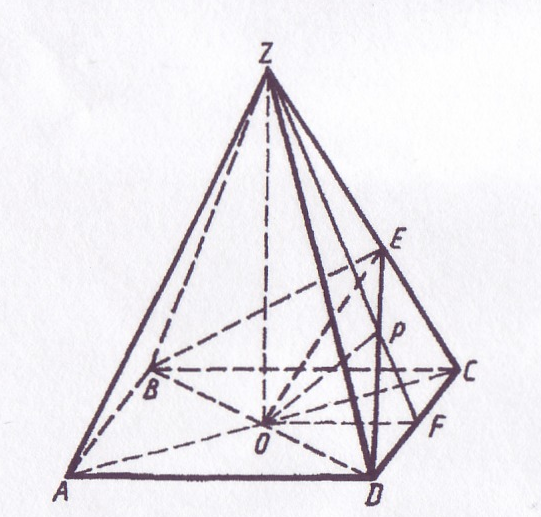
В правильной четырёхугольной пирамиде ZABCD как было обусловлено выше, обозначим:
 ZAO =
ZAO =  ZBO =
ZBO =  ZCO =
ZCO =  ZDO =
ZDO = ,
,
 CZD =
CZD =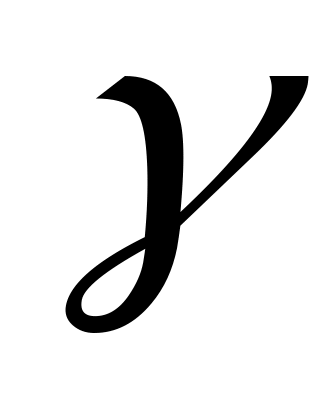 ,
,  ZFO =
ZFO =  и
и  BED =
BED = .
.
Опишем построение  BED – линейного угла двугранного угла при боковом ребре ZC.
BED – линейного угла двугранного угла при боковом ребре ZC.
В грани ZCD проводим DE  ZC и соединяем точку Е с вершиной основания В. Треугольники ВЕС и DEC равны. Из этого следует, что ВЕ = ED и
ZC и соединяем точку Е с вершиной основания В. Треугольники ВЕС и DEC равны. Из этого следует, что ВЕ = ED и  BEC =
BEC =  DEC =
DEC = /2. Таким образом,
/2. Таким образом,  BED – линейный угол двугранного угла при ребре ZC. Отрезок ОЕ – медиана равнобедренного треугольника BED, следовательно, и биссектриса и высота этого треугольника. Поэтому
BED – линейный угол двугранного угла при ребре ZC. Отрезок ОЕ – медиана равнобедренного треугольника BED, следовательно, и биссектриса и высота этого треугольника. Поэтому  OED =
OED =  /2.
/2.
Отрезок ОР принадлежит линии пересечения плоскостей линейных углов BED и ZFO. Так как плоскость линейного угла перпендикулярна граням двугранного угла, то каждая из плоскостей – BED и ZOF - перпендикулярна плоскости ZCD. Можно показать, что линия пересечения двух плоскостей, каждая из которых перпендикулярна третьей плоскости, перпендикулярна к этой третьей плоскости. Поэтому OP ZCD. Из этого, в частности, следует, что треугольники OPF и OPD прямоугольные и
ZCD. Из этого, в частности, следует, что треугольники OPF и OPD прямоугольные и  DOP =
DOP =  /2.
/2.
Перейдём теперь к выводу формул перехода:
а) от  к
к  .
.
Положим ZO = x.
Из  ZOF
ZOF
OF = x ctg .
.
Из  OFD
OFD
OD = x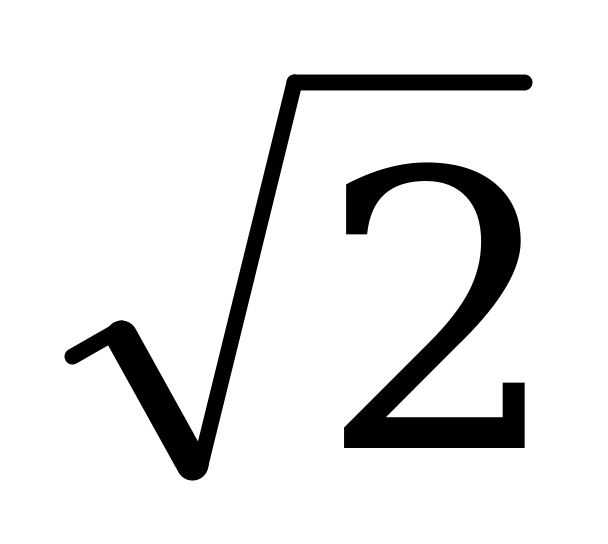 ctg
ctg .
.
Из  ZOD
ZOD
tg =
=  =
=  tg
tg .
.
tg =
= 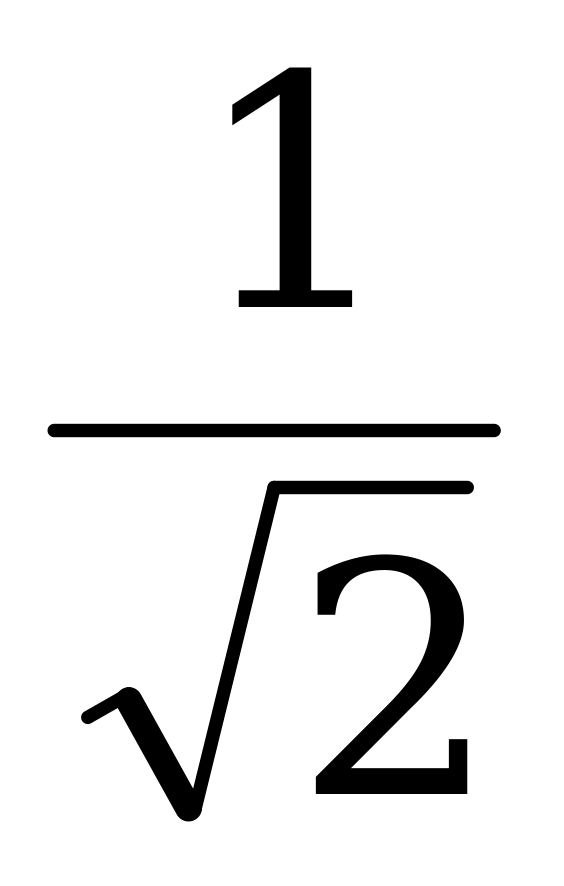 tg
tg ; (I)
; (I)
б) от  к
к  .
.
Положим ZD = x.
Из  ZDF
ZDF
DF = x sin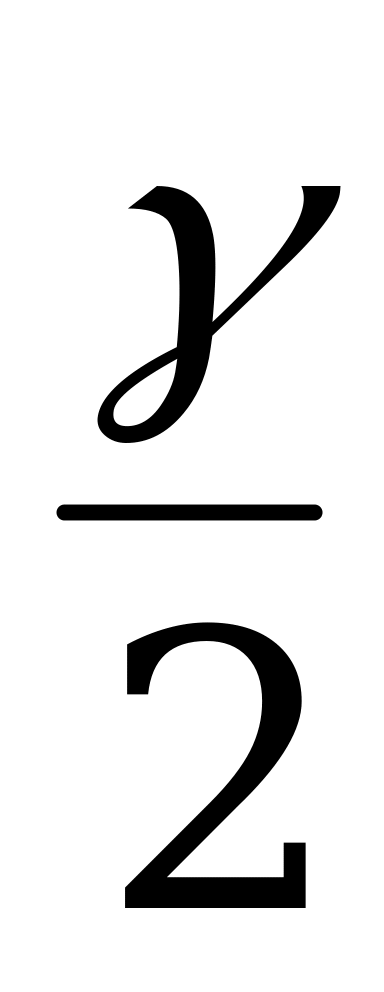 .
.
Из  OFD
OFD
OD = x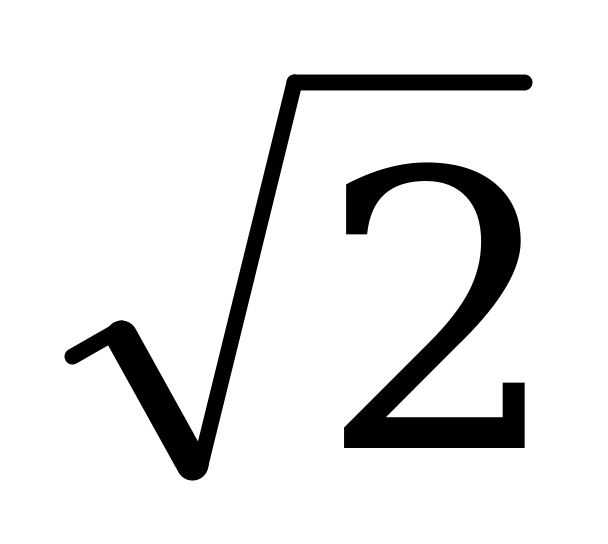 sin
sin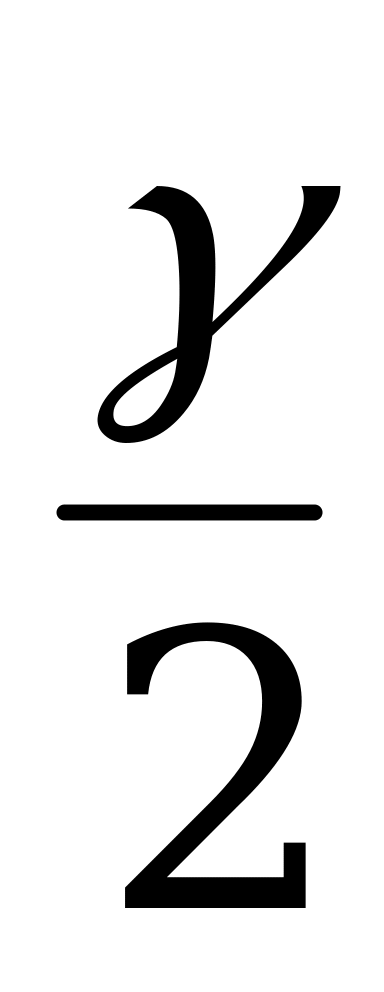 .
.
Из  ZOD
ZOD
cos  =
= 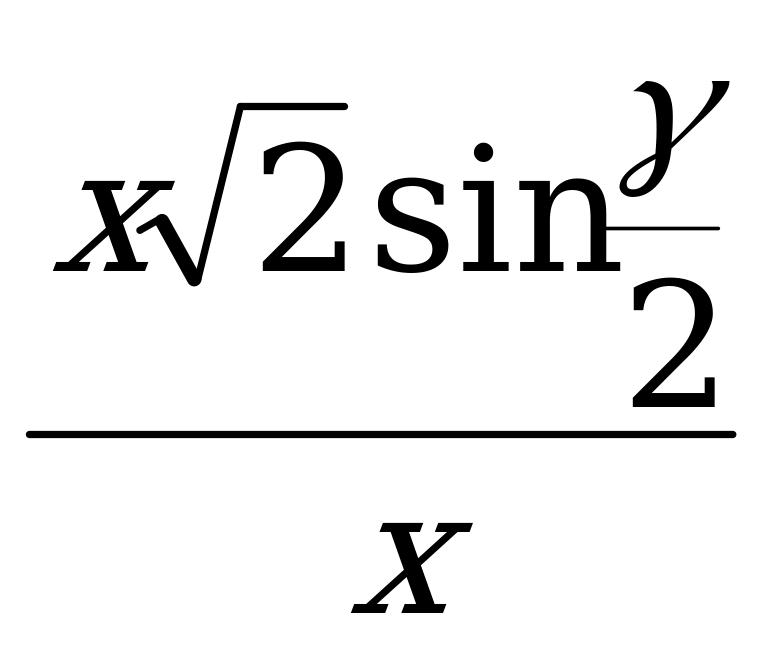 =
= 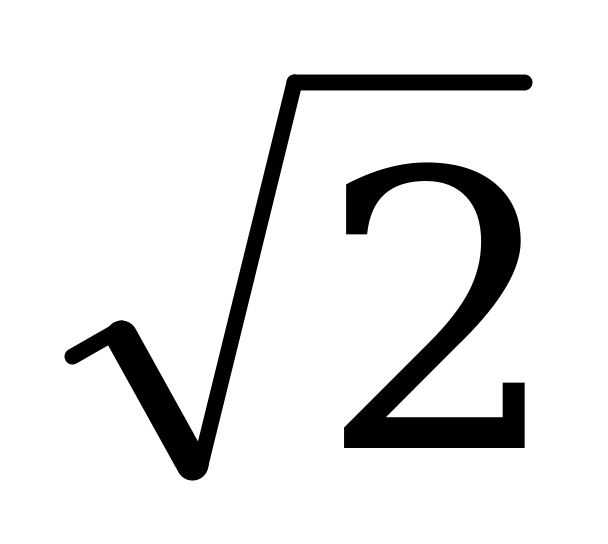 sin
sin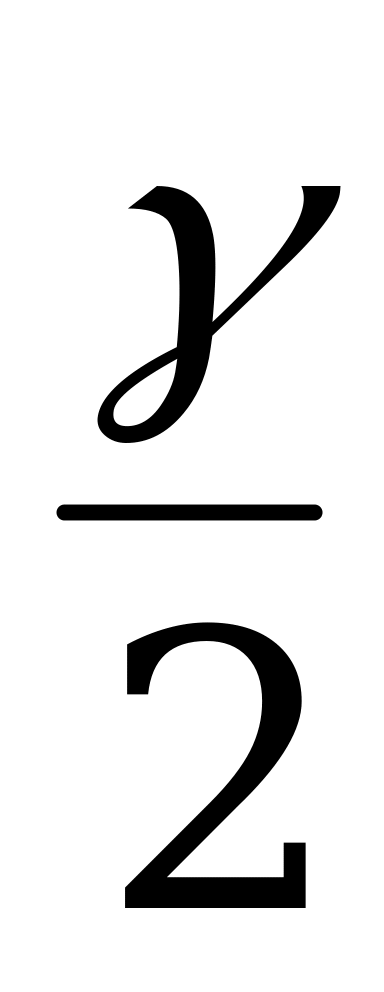 ;
;
cos  =
= 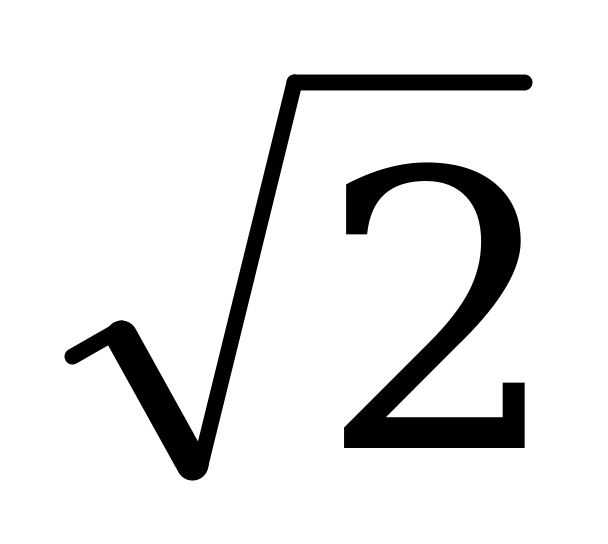 sin
sin 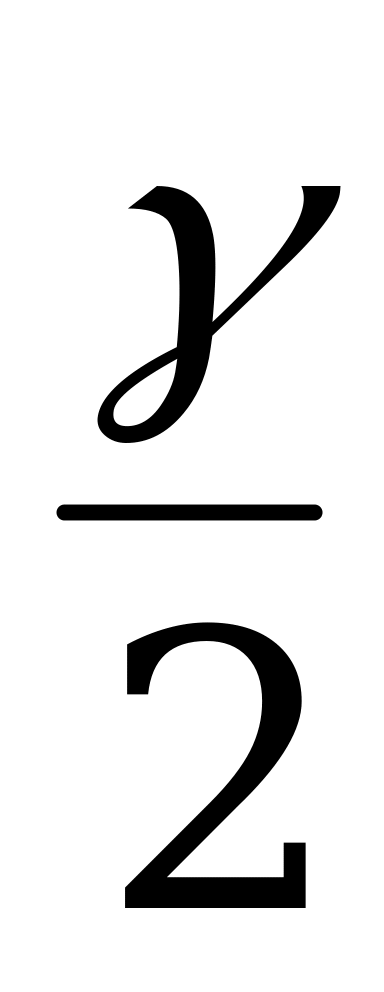 ; (II)
; (II)
в) от  к
к  .
.
Положим EO = x.
Из  EOD
EOD
OD – x tg  , OC = OD = x tg
, OC = OD = x tg .
.
Из  EOC
EOC
sin  =
= 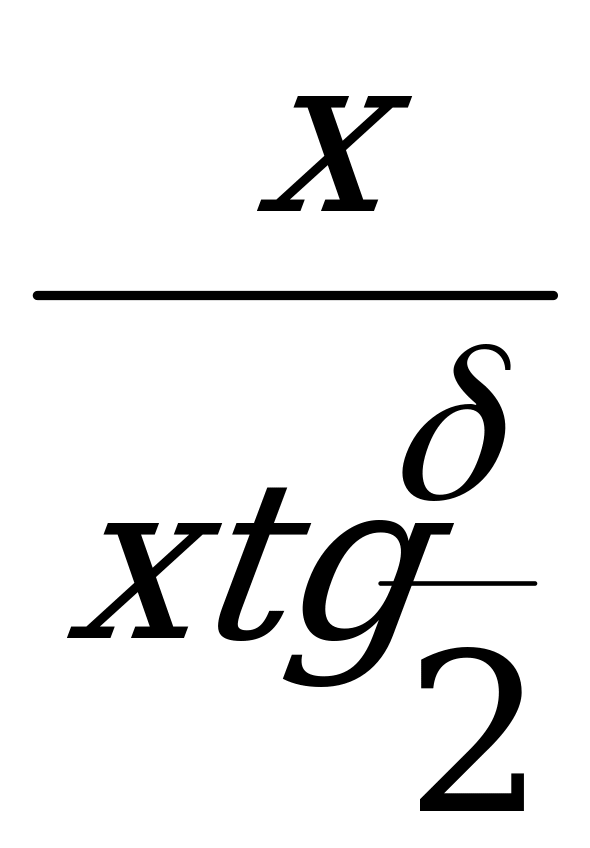 = ctg
= ctg ,
,
sin = ctg
= ctg ; (III)
; (III)
г) от  к
к  .
.
Формулу перехода для этой задачи получаем из (I):
tg  =
=  tg
tg ; (IV)
; (IV)
д) от  к
к  .
.
Эта задача решается аналогично задаче б). Запишем получающуюся при этом формулу перехода:
cos  = tg
= tg  ; (V)
; (V)
е) от  к
к  .
.
Выше было, в частности, показано, что треугольники OPD и OPF прямоугольные и что  DOP =
DOP =  . Поэтому переходим непосредственно к выводу формулы.
. Поэтому переходим непосредственно к выводу формулы.
Положим OP = x.
Из  OPD OD =
OPD OD = 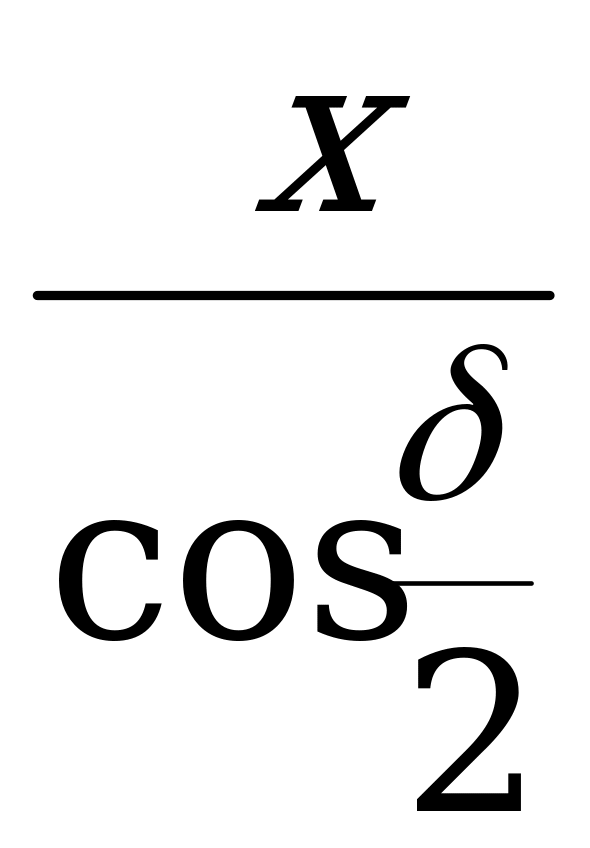 . Из
. Из  OFD OF =
OFD OF = 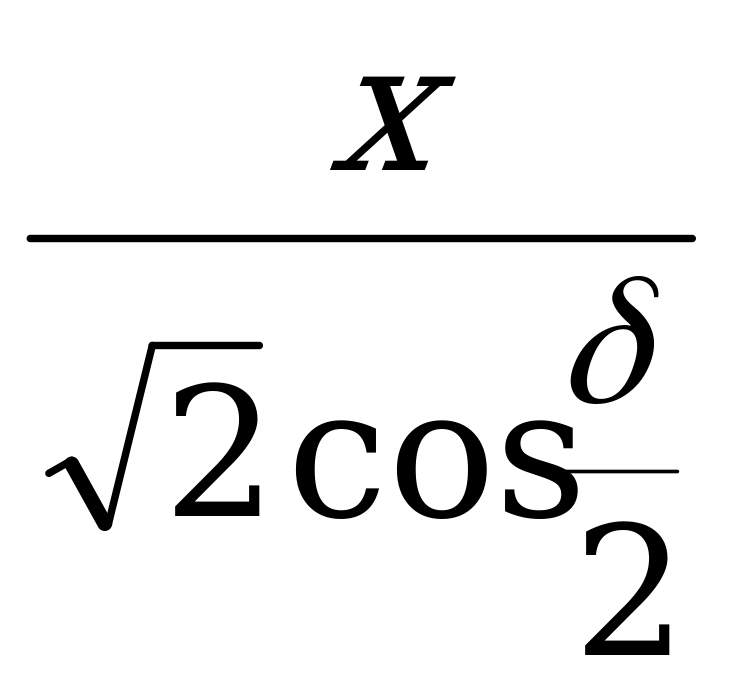 .
.
Из  OPF
OPF
sin  =
= 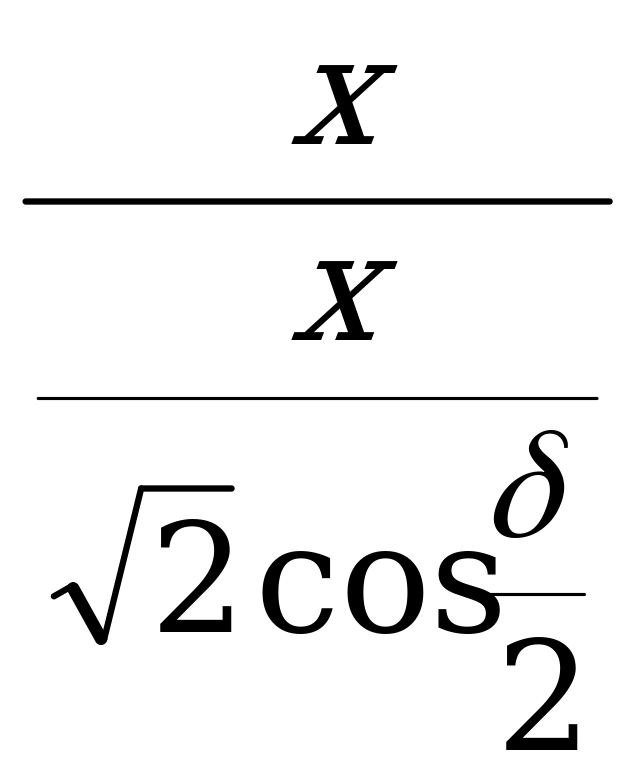 =
=  cos
cos  ,
,
sin  =
=  cos
cos  . (VI)
. (VI)
В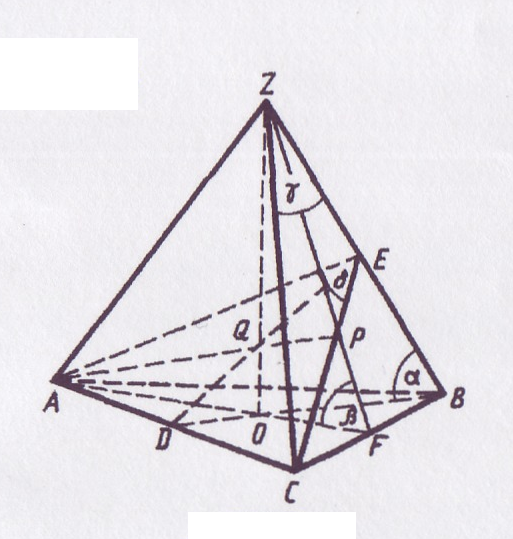 ывод формул перехода для правильной треугольной пирамиды.
ывод формул перехода для правильной треугольной пирамиды.
В правильной треугольной пирамиде  ZFO – линейный угол при основании пирамиды. Описание построения
ZFO – линейный угол при основании пирамиды. Описание построения  AEC – линейного угла двугранного угла при боковом ребре ZB – опускаем, поскольку оно аналогично описанию соответствующего угла в правильной четырёхугольной пирамиде, приведённому выше. Из рисунка видно, что АР – линия пересечения плоскостей AZF и AEC. Аналогично тому, как было сделано для правильной четырёхугольной пирамиды, доказывается, что АР
AEC – линейного угла двугранного угла при боковом ребре ZB – опускаем, поскольку оно аналогично описанию соответствующего угла в правильной четырёхугольной пирамиде, приведённому выше. Из рисунка видно, что АР – линия пересечения плоскостей AZF и AEC. Аналогично тому, как было сделано для правильной четырёхугольной пирамиды, доказывается, что АР  пл.ZBC. Следовательно, треугольники АРС и APF – прямоугольные и
пл.ZBC. Следовательно, треугольники АРС и APF – прямоугольные и  САР =
САР =  .
.
Для обозначения величин основных углов в правильной треугольной пирамиде употребим те же буквы, которыми обозначались величины этих углов в правильной четырёхугольной пирамиде:  ,
,  ,
,  и
и 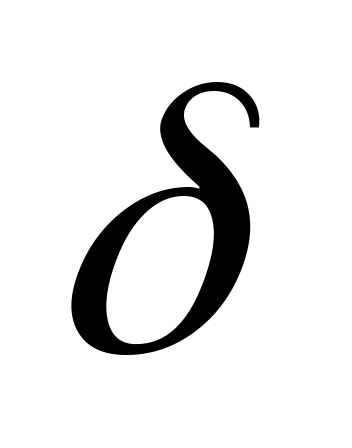 .
.
Перейдём к выводу формулы перехода:
а) от к
к  .
.
Положим ZO = x.
Из  ZOF
ZOF
OF = x ctg  .
.
Из  OFB
OFB
OB = 2x ctg  .
.
Из  ZOB
ZOB
tg  =
= 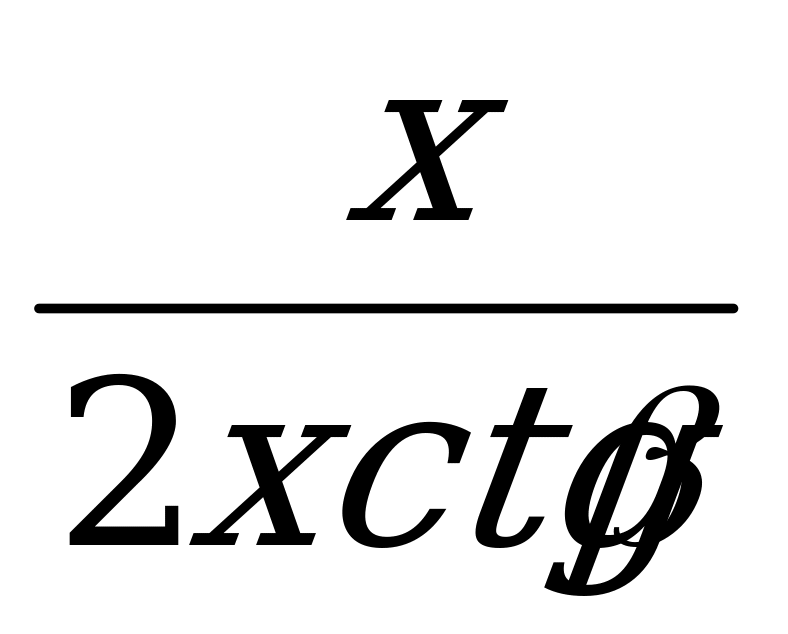 =
= 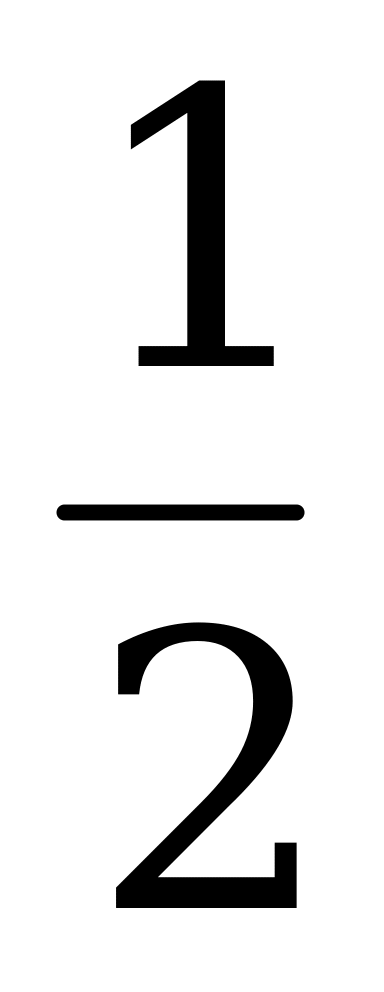 tg
tg  ,
,
tg  =
= 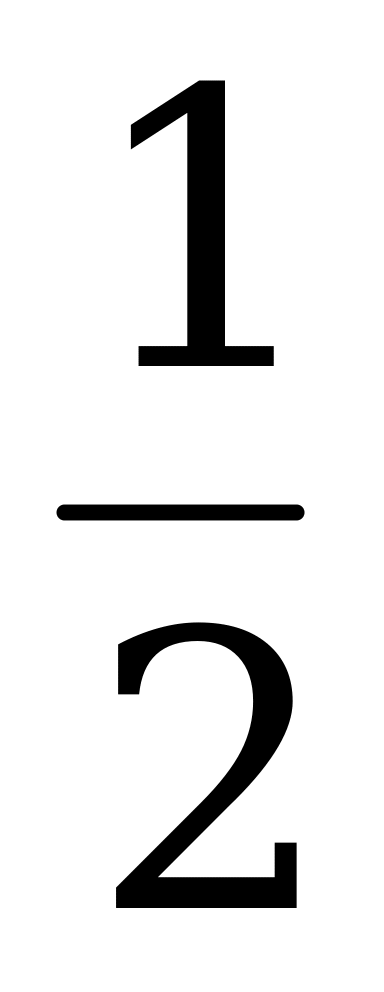 tg
tg  . (VII)
. (VII)
Решение задачи аналогично решению задачи для правильной четырёхугольной пирамиды.
б) cos =
= 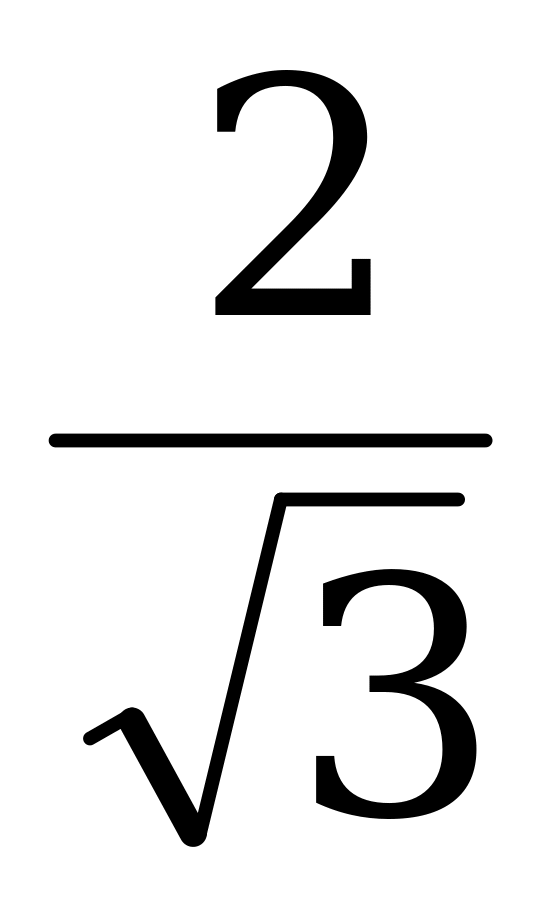 sin
sin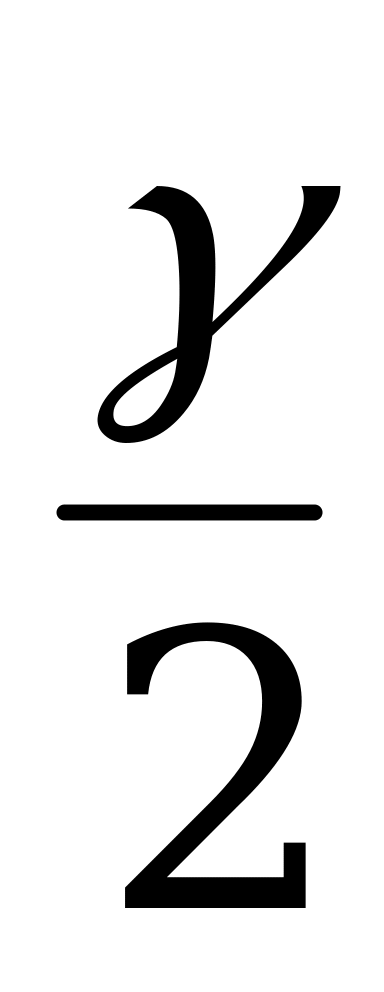 ; (VIII)
; (VIII)
в) sin =
= 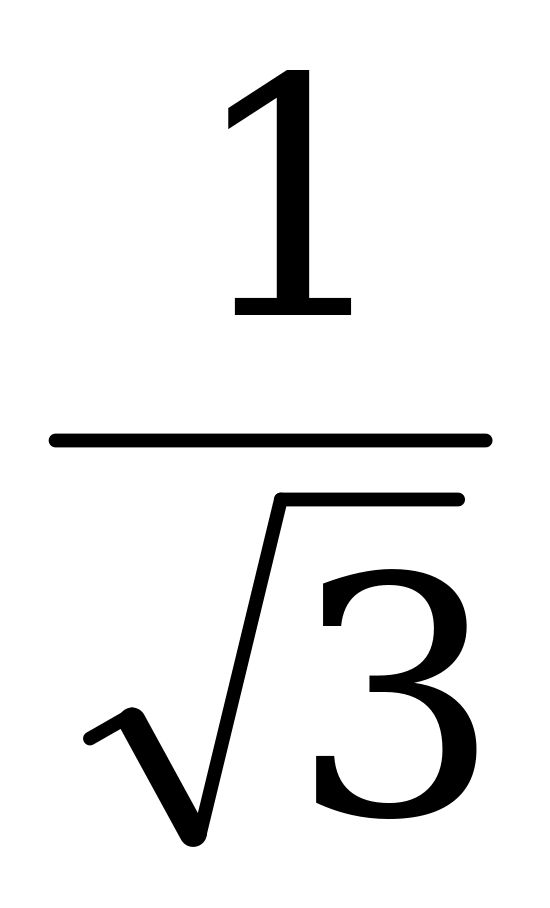 ctg
ctg ; (IX)
; (IX)
г) tg = 2tg
= 2tg ; (X)
; (X)
д) cos =
= 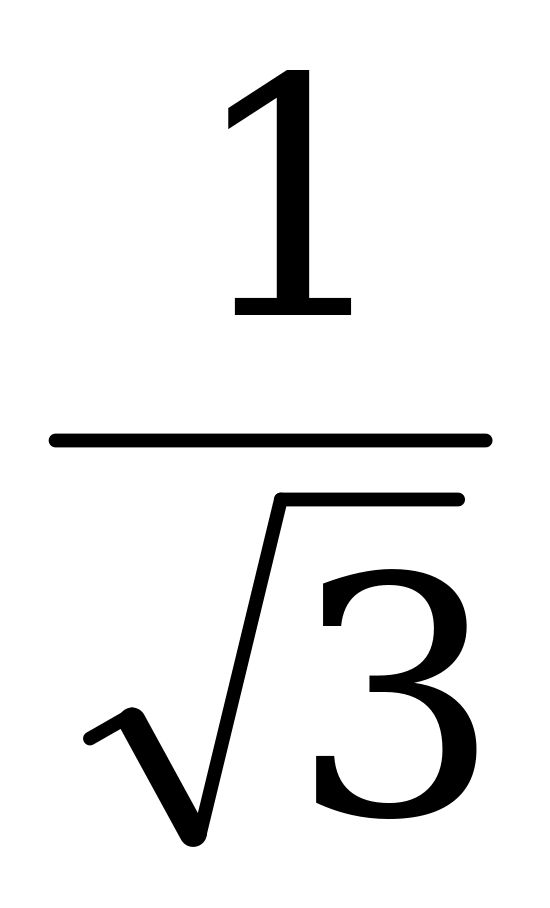 tg
tg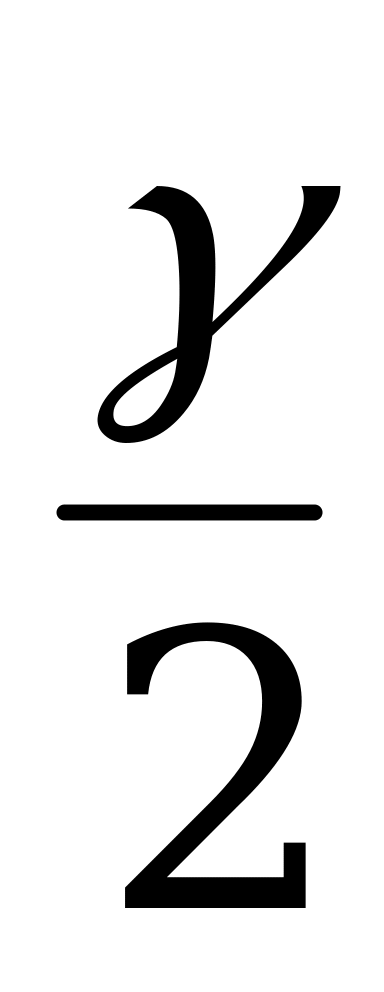 ; (XI)
; (XI)
е) sin =
= 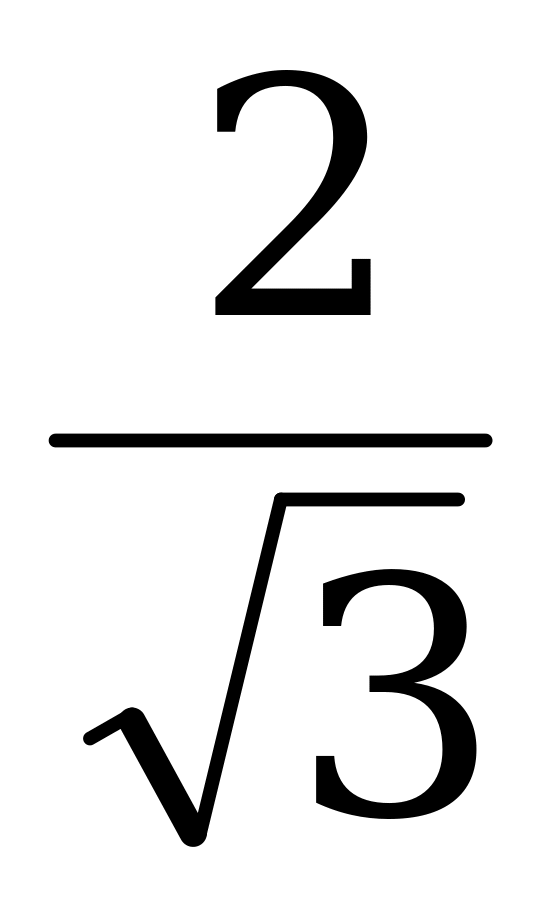 cos
cos . (XII)
. (XII)
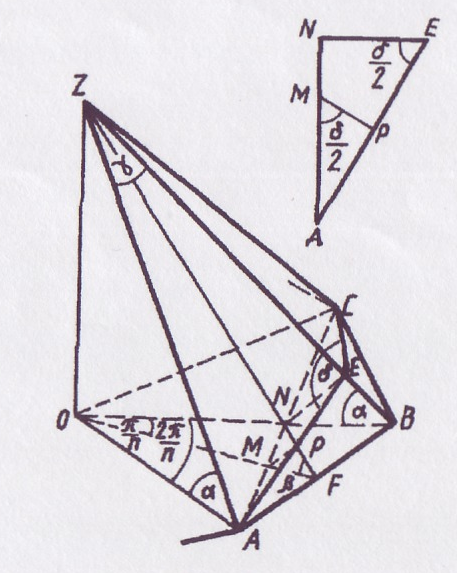 Формулы перехода для правильной n-угольной пирамиды.
Формулы перехода для правильной n-угольной пирамиды.
На рисунке изображена часть правильной n-угольной пирамиды ZFDC… . Величины основных углов обозначены, как и ранее, буквами  ,
,  ,
,  и
и 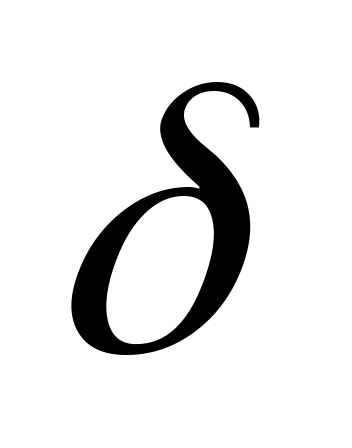 .
.  ZFO – линейный угол двугранного угла при ребре основания АВ:
ZFO – линейный угол двугранного угла при ребре основания АВ:  ZFO =
ZFO = . Построение
. Построение  АЕС – линейного угла двугранного угла при боковом ребре ZB, как и в случае правильной треугольной пирамиды, опускаем.
АЕС – линейного угла двугранного угла при боковом ребре ZB, как и в случае правильной треугольной пирамиды, опускаем.
ВО – биссектриса  АВС и поэтому в равнобедренном треугольнике АВС отрезок BN – биссектриса, медиана и высота. Следовательно, N – середина АС. Очевидно, что АЕ = ЕС и поэтому треугольник АЕС равнобедренный и EN – его медиана, биссектриса и высота. Поэтому
АВС и поэтому в равнобедренном треугольнике АВС отрезок BN – биссектриса, медиана и высота. Следовательно, N – середина АС. Очевидно, что АЕ = ЕС и поэтому треугольник АЕС равнобедренный и EN – его медиана, биссектриса и высота. Поэтому  AEN =
AEN =  .
.
Отрезок МР принадлежит линии пересечения плоскостей линейных углов ZFO b AEC, и поэтому, как уже упоминалось выше при рассмотрении правильной четырёхугольной пирамиды, МР 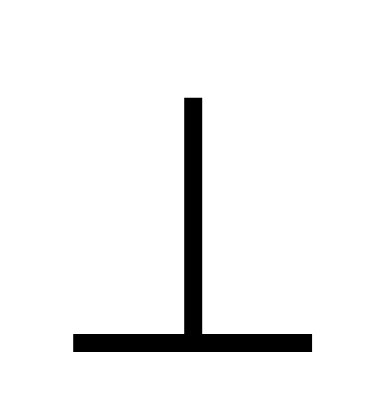 пл.ZAB. Из этого непосредственно следует, что треугольники АМР и МPF прямоугольные и
пл.ZAB. Из этого непосредственно следует, что треугольники АМР и МPF прямоугольные и  АМР =
АМР = АЕN =
АЕN = .
.
Поскольку ВN – высота треугольника АВС, то  ВАN =
ВАN = BOF =
BOF =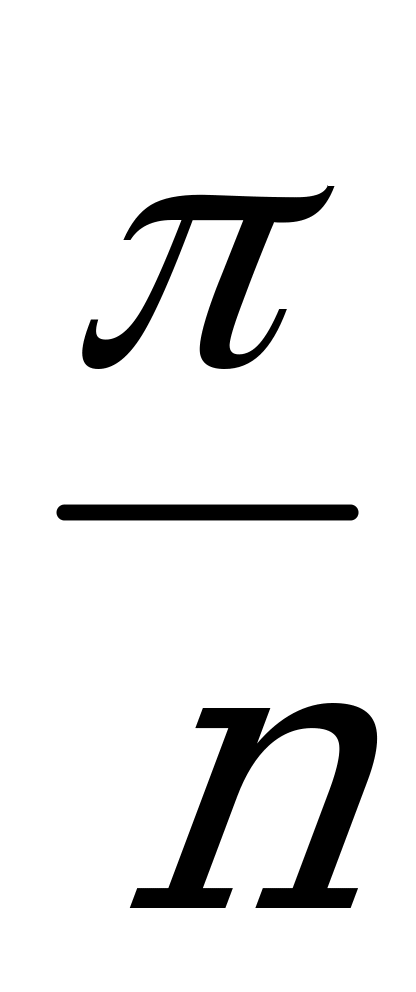 как острые углы с соответственно перпендикулярными сторонами.
как острые углы с соответственно перпендикулярными сторонами.
Из шести формул перехода для правильной n-угольной пирамиды первые пять мы приведём без доказательств, поскольку их вывод аналогичен выводу соответствующих формул перехода правильных четырёхугольной и треугольной пирамид, и докажем лишь одну: от 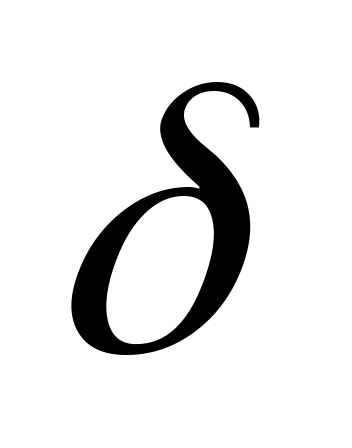 к
к  .
.
а) tg = tg
= tg cos
cos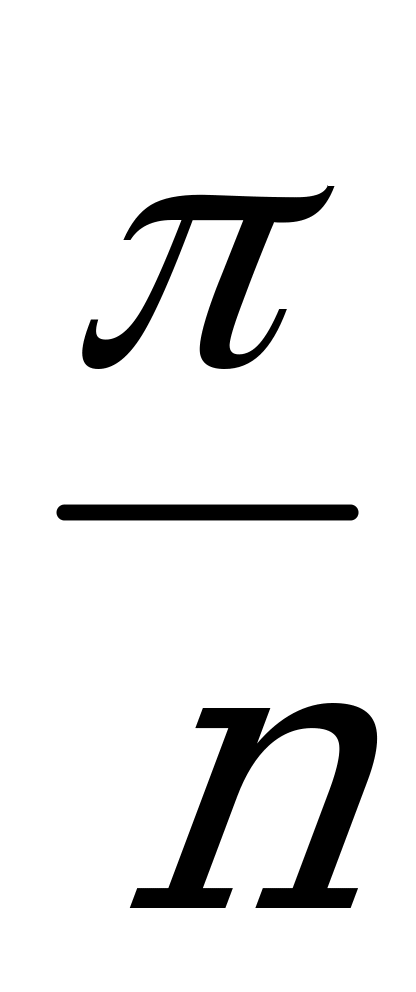 ; (XIII)
; (XIII)
б) cos =
=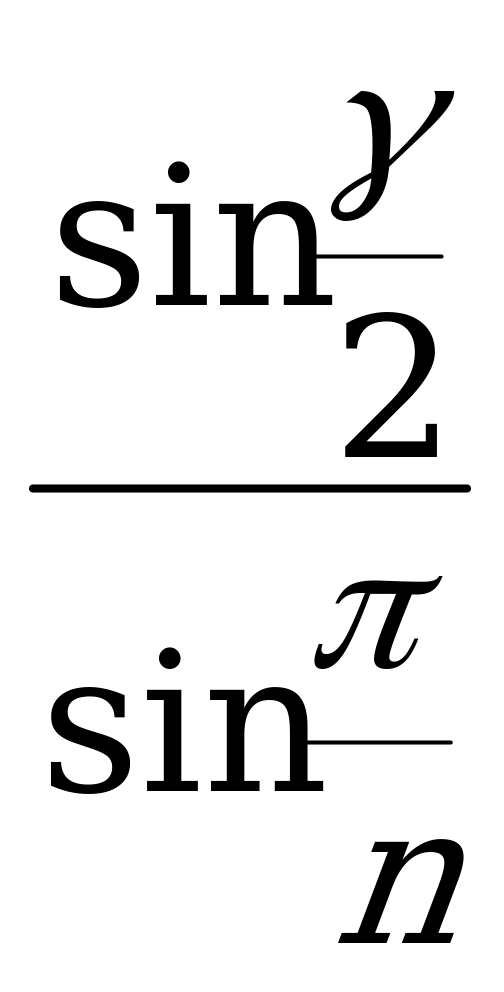 ; (XIV)
; (XIV)
в) sin = ctg
= ctg ctg
ctg
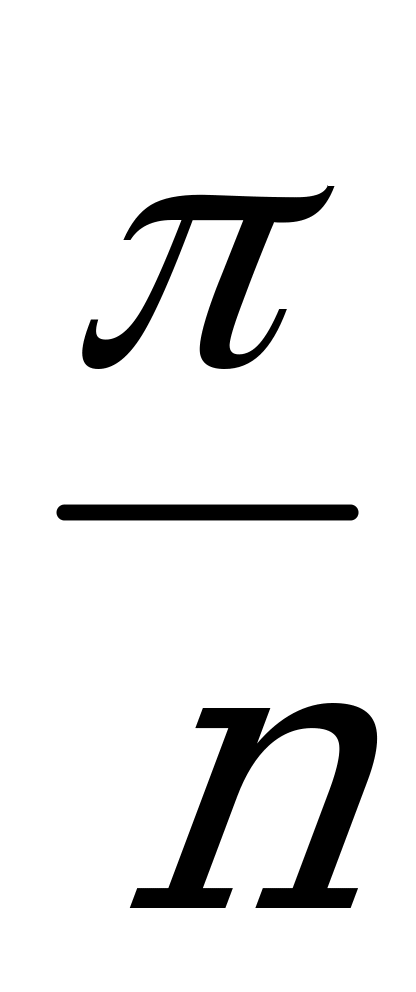 ; (XV)
; (XV)
г) tg =
= 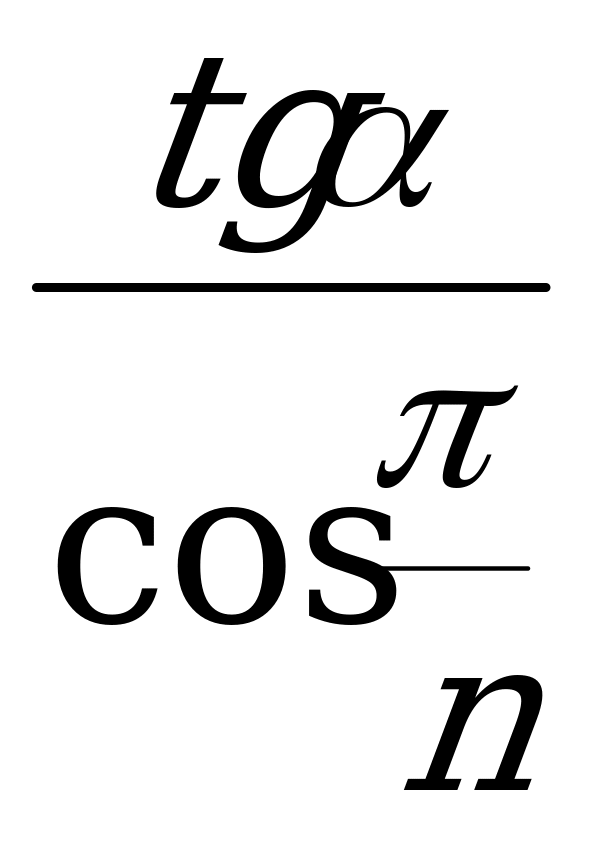 ; (XVI)
; (XVI)
д) cos = tg
= tg ctg
ctg ; (XVII)
; (XVII)
е) от  к
к  .
.
Положим MP = x.
Из  АМР
АМР
АМ =  .
.
Из  AMF
AMF
MF = 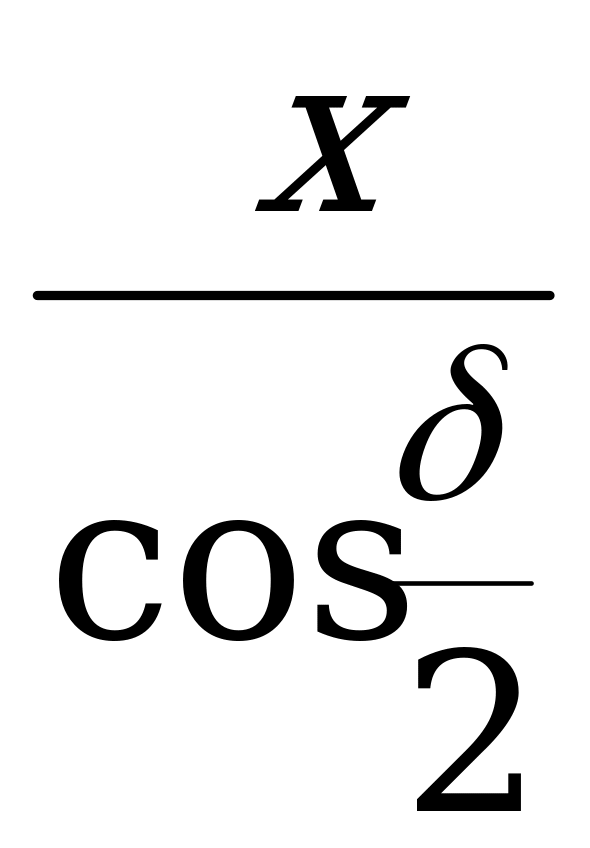 sin
sin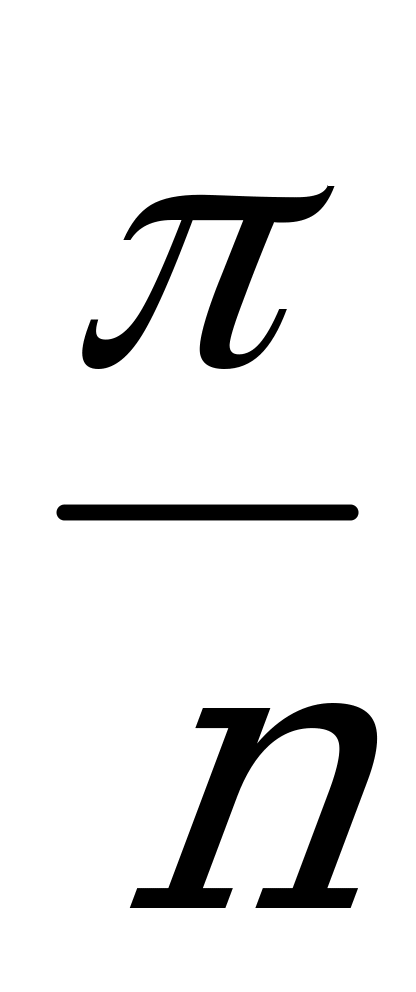 .
.
Из  MPF
MPF
sin =
= 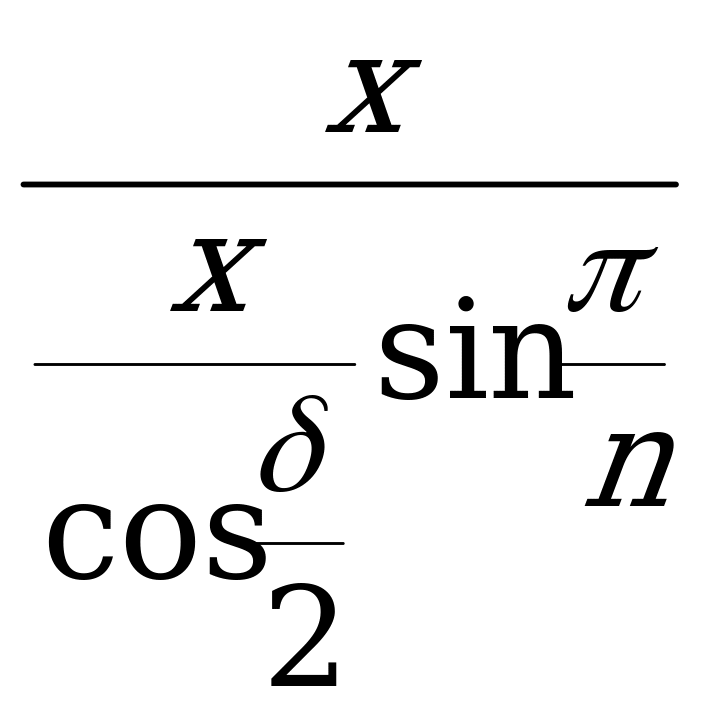 =
= 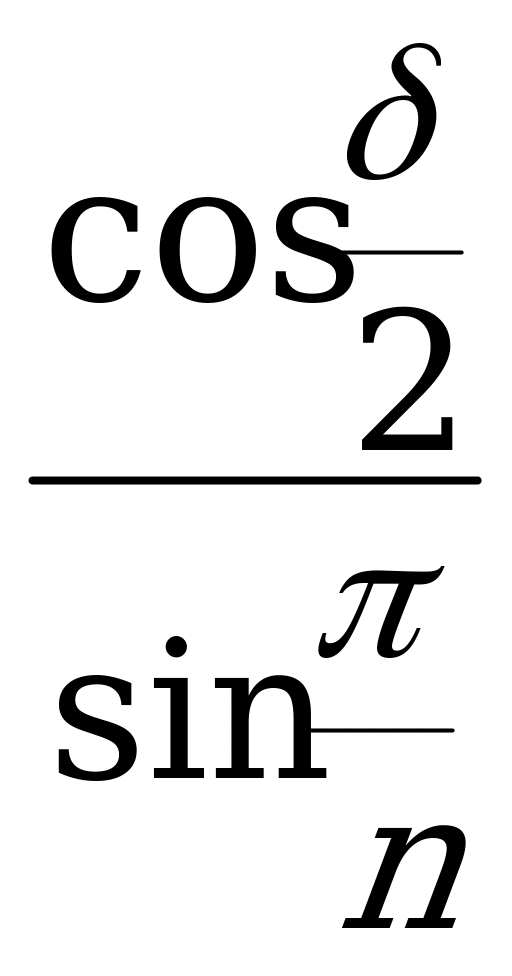 ,
,
sin =
= 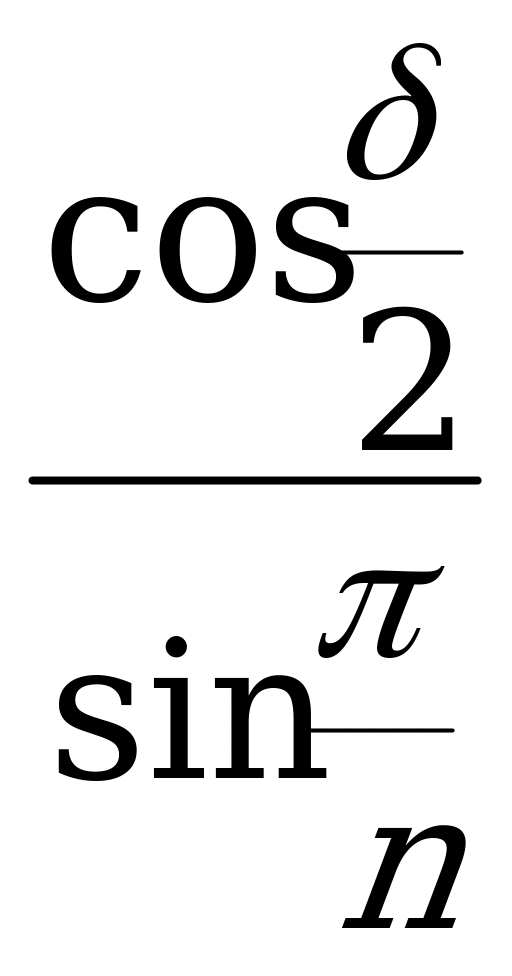 . (XVIII)
. (XVIII)
Формулы перехода включены в таблицу. Они эффективно используются при решении многих геометрических задач, но запоминать их, разумеется, не нужно. Достаточно знать идею их вывода.
| Переход/n | 3 | 4 | n |
| От  к к  | 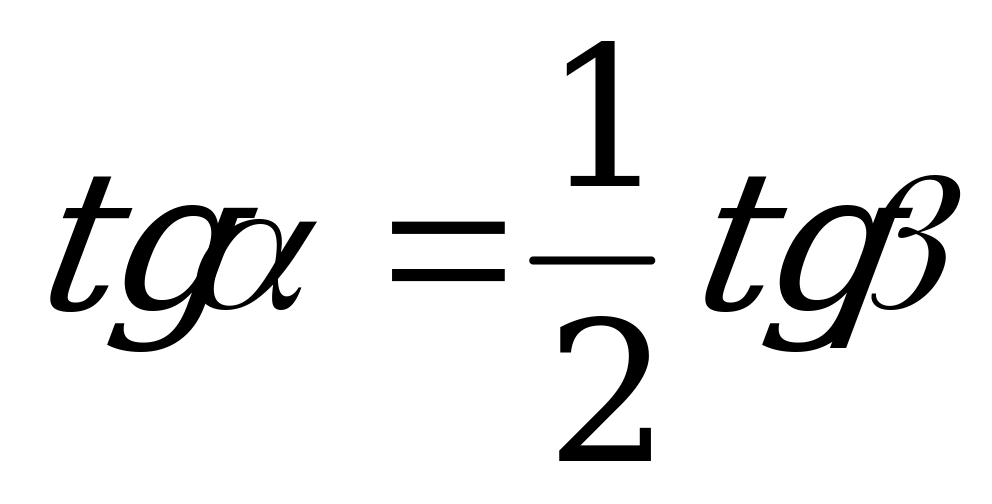 | 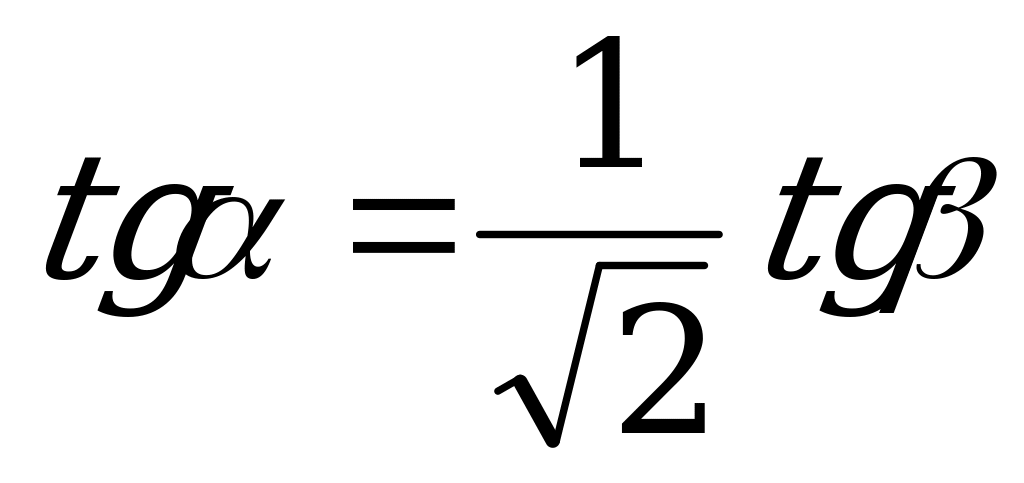 | 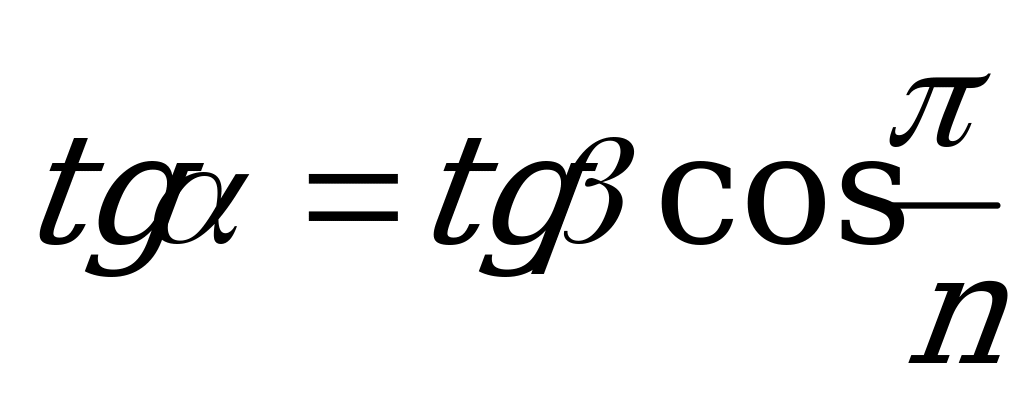 |
| От 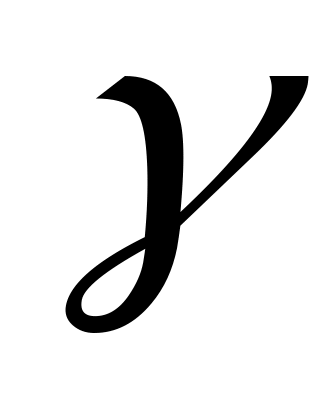 к к  | 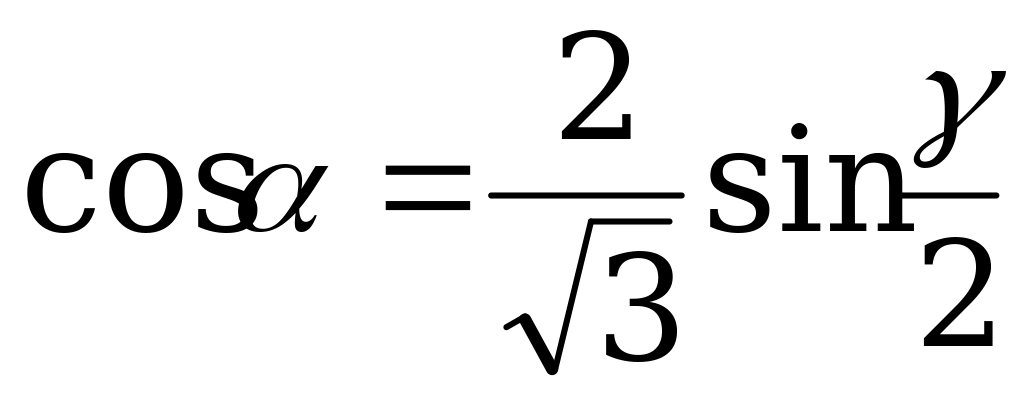 | 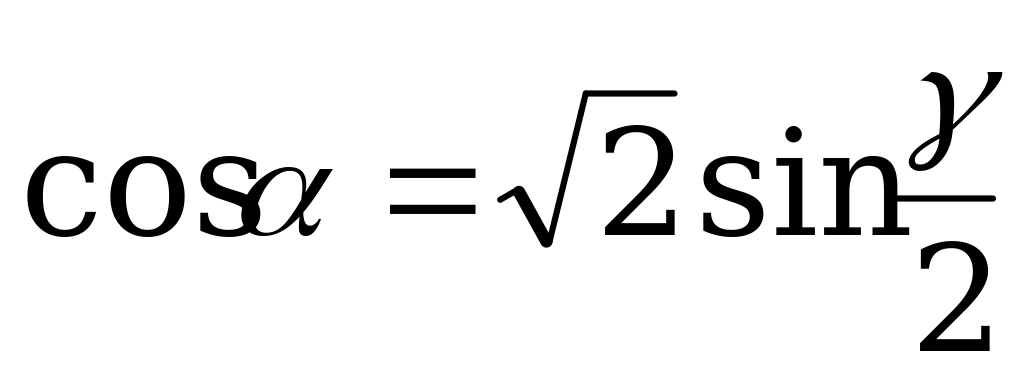 | 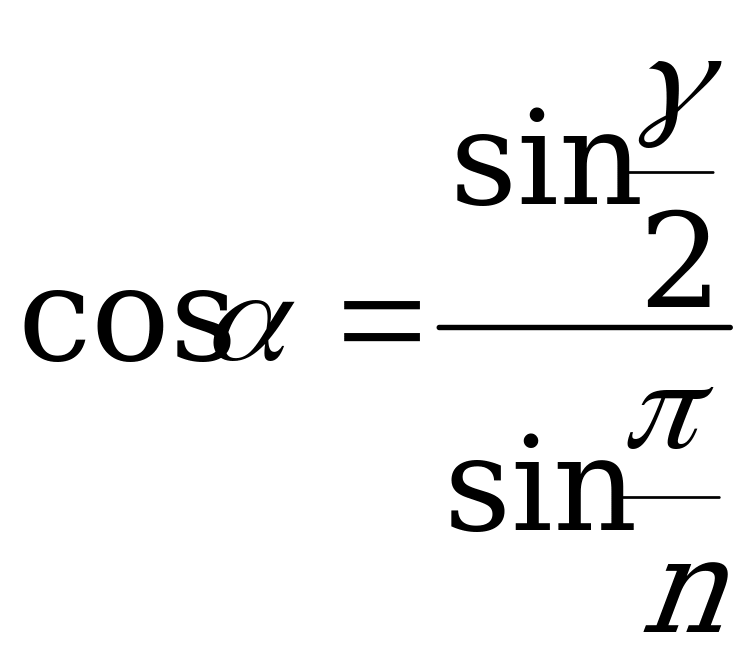
|
| От 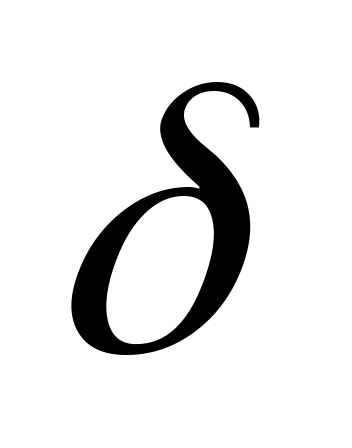 к к  | 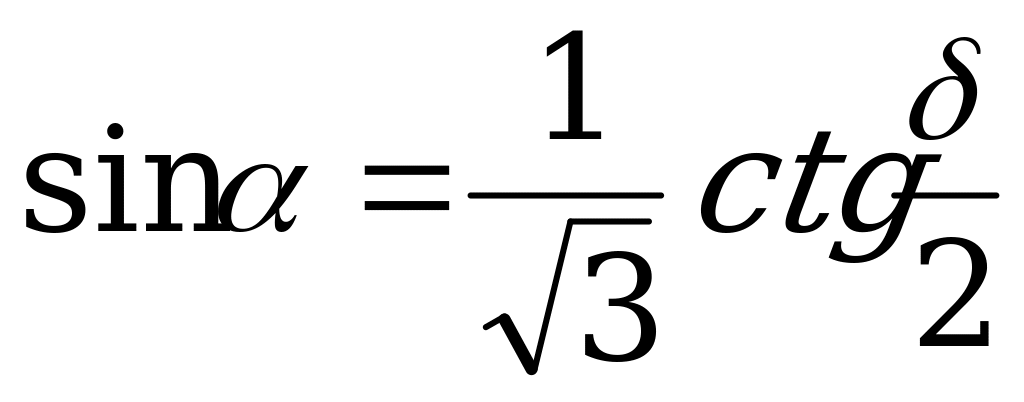 | 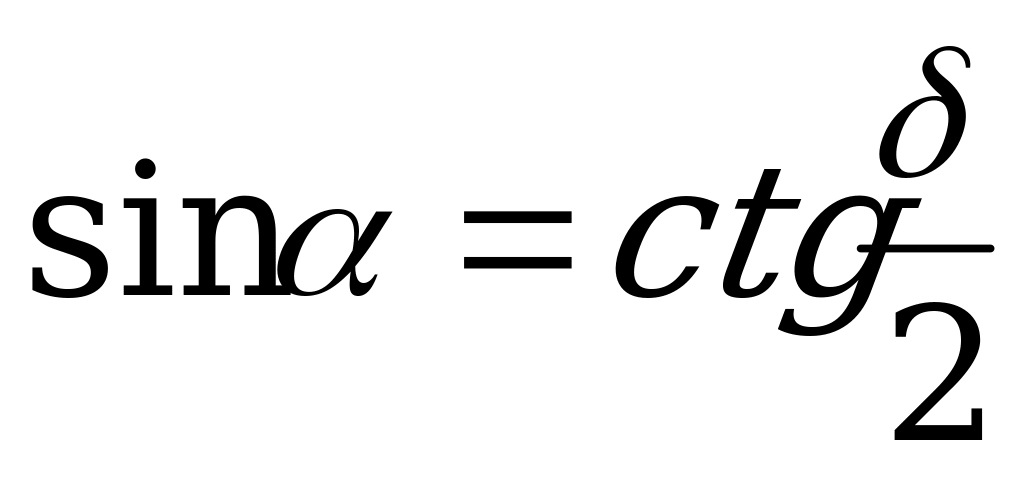 |  |
| От  к к  | 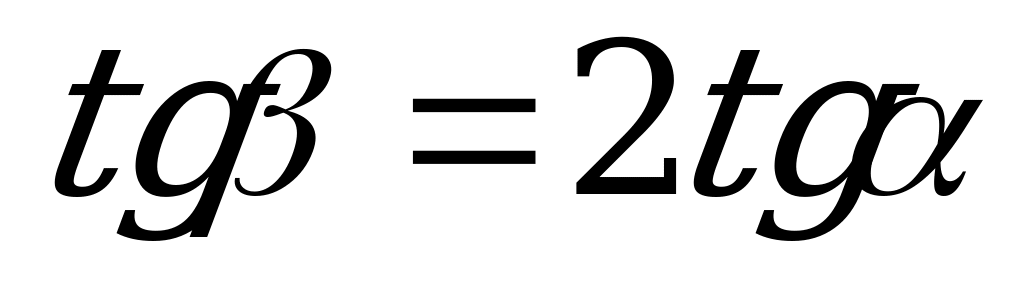 | 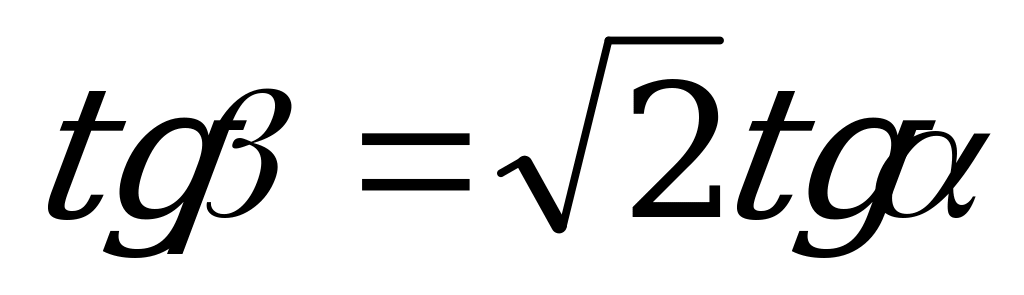 | 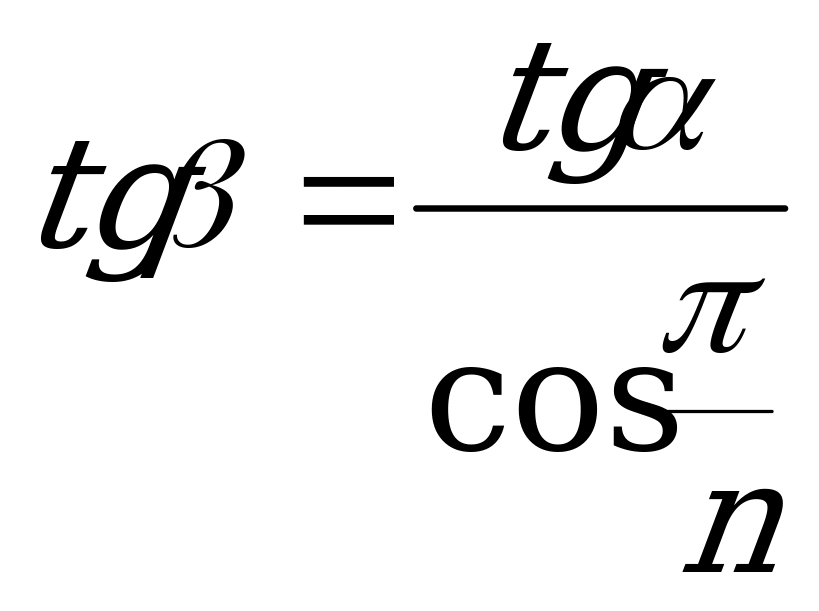 |
| От 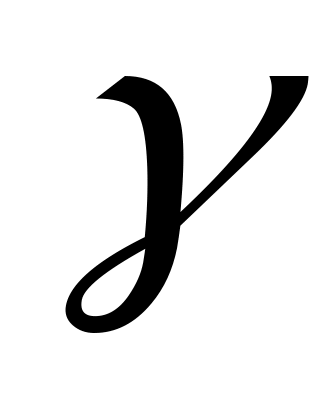 к к  | 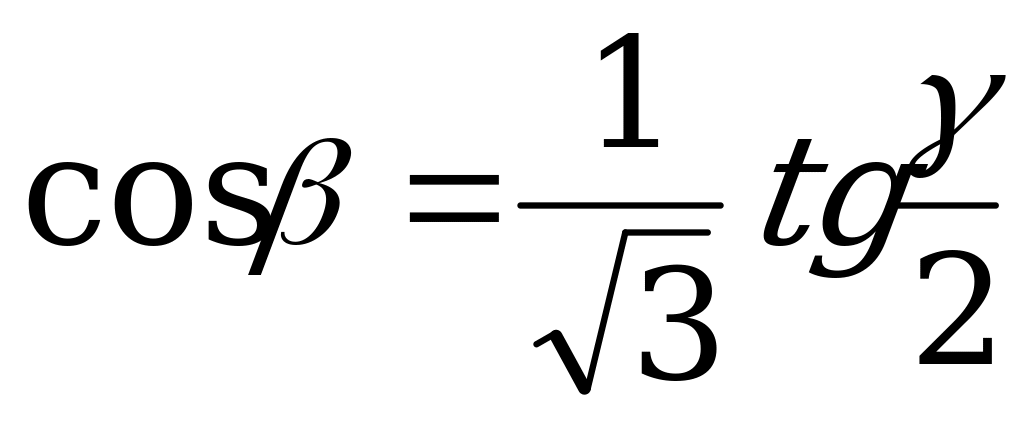 | 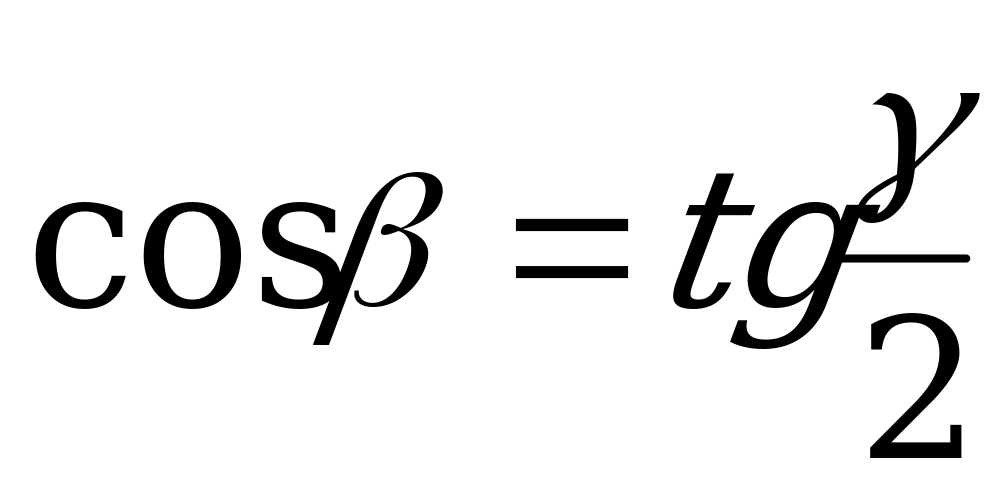 | 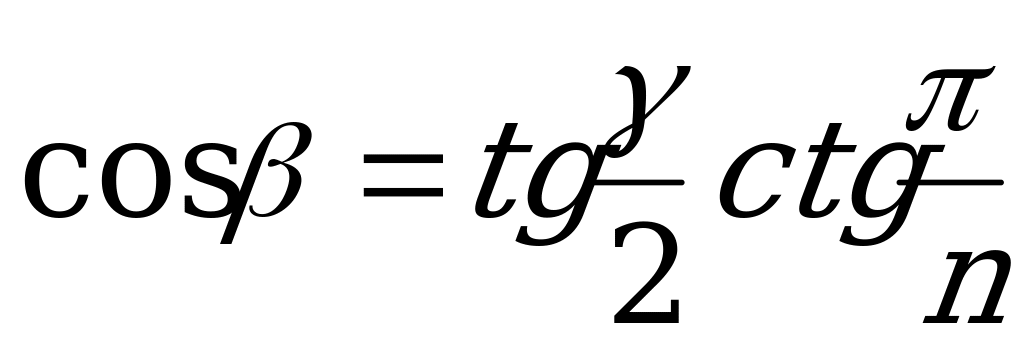 |
| От 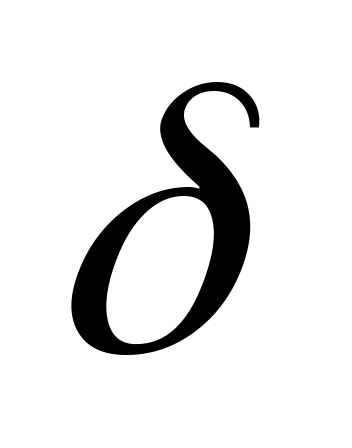 к к  | 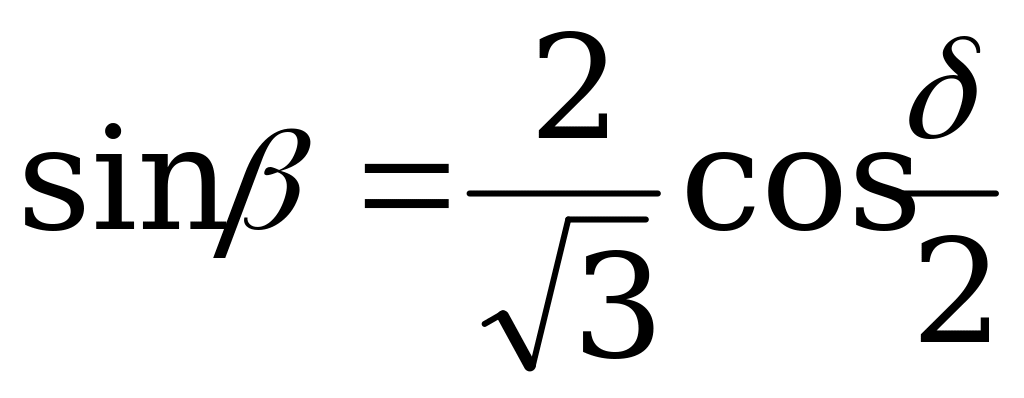 | 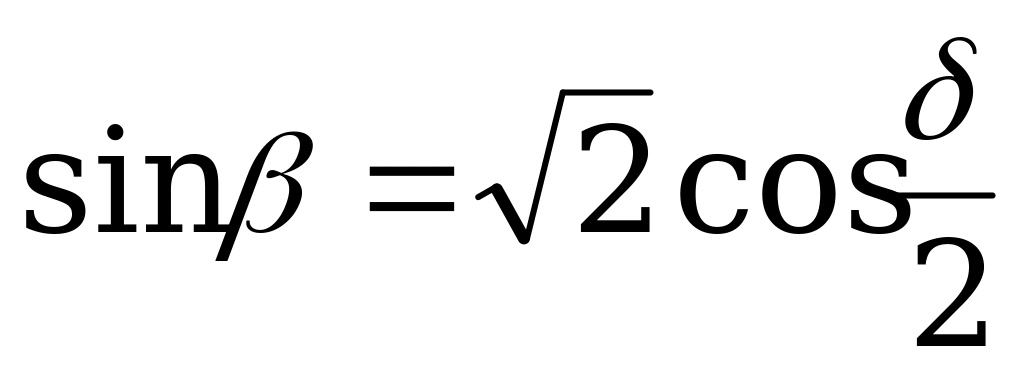 | 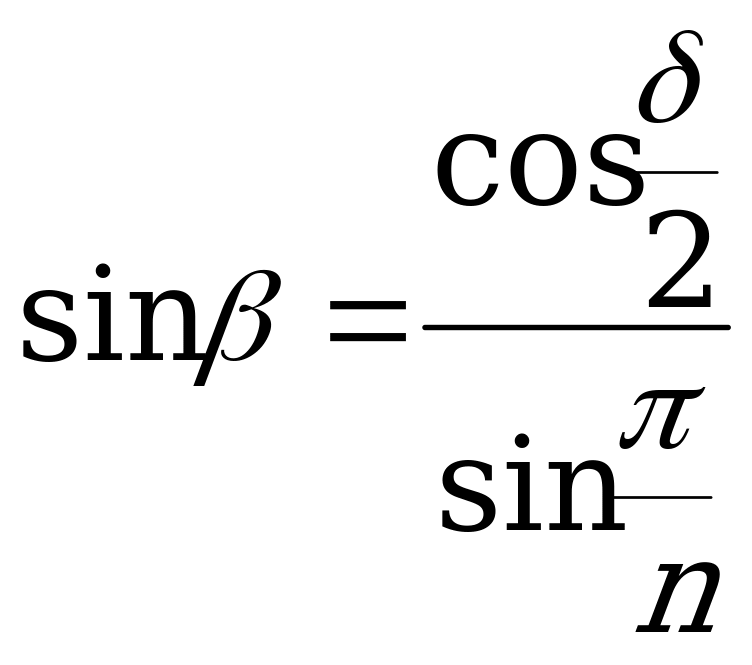 |
Задача №1
Гипотенуза прямоугольного треугольника лежит в некоторой плоскости  , а катеты составляют с этой плоскостью углы
, а катеты составляют с этой плоскостью углы  и
и  соответственно. Определить угол между плоскостью
соответственно. Определить угол между плоскостью  и плоскостью треугольника.
и плоскостью треугольника. 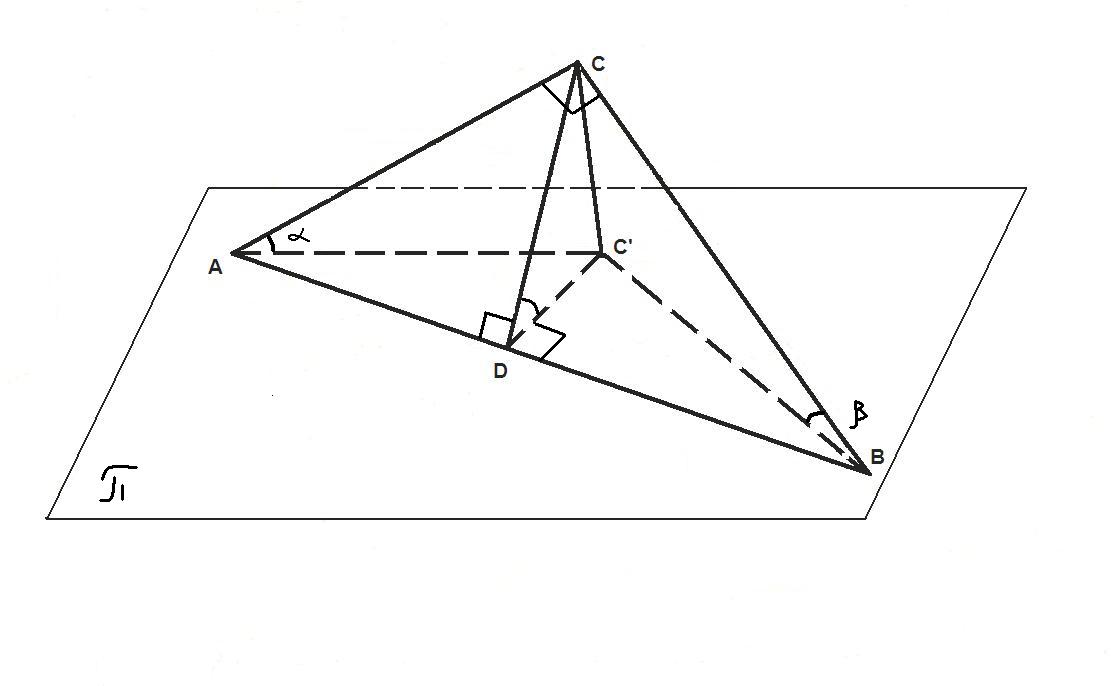
Решение. Обозначим вершины треугольника буквами A,B,C так, что C-вершина прямого угла.
Проведём через точку С плоскость, перпендикулярную прямой АВ. Пусть D точка пересечения этой плоскости с прямой АВ , а  - основание перпендикуляра, опущенного из точки С на плоскость
- основание перпендикуляра, опущенного из точки С на плоскость  .Так как CD и D
.Так как CD и D перпендикулярны АВ , то
перпендикулярны АВ , то  CD
CD является углом между плоскостью
является углом между плоскостью  и плоскостью АВС и
и плоскостью АВС и  CD
CD =φ. Обозначим C
=φ. Обозначим C =
=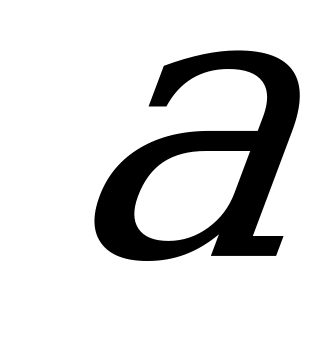 .
.
Из ∆ CВ выразим СВ: СВ=
выразим СВ: СВ=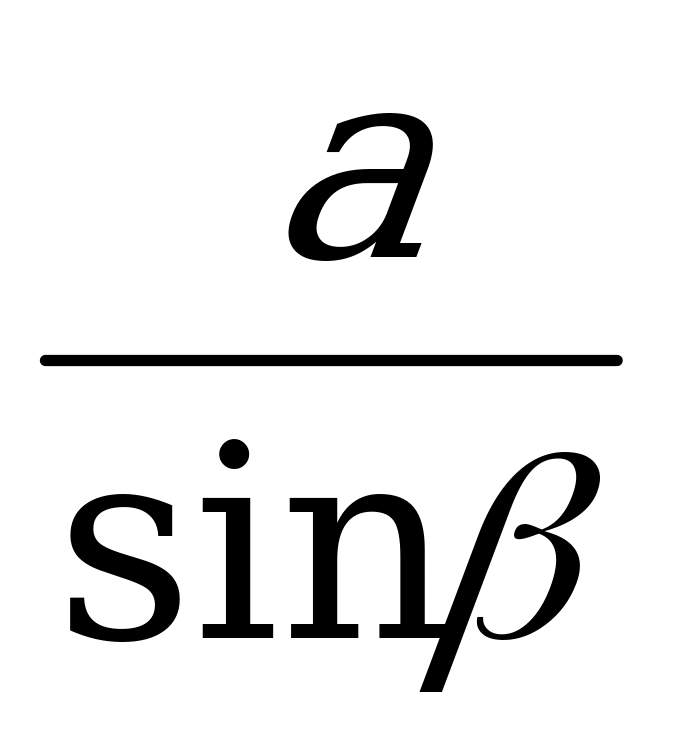 . Из ∆ СА
. Из ∆ СА выразим СА: СА=
выразим СА: СА=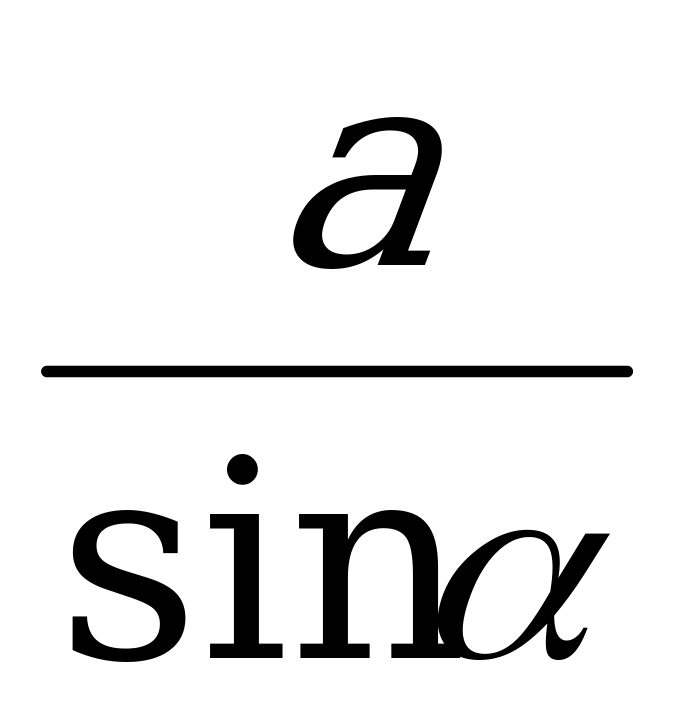 . Из ∆ ABC:
. Из ∆ ABC:
CD=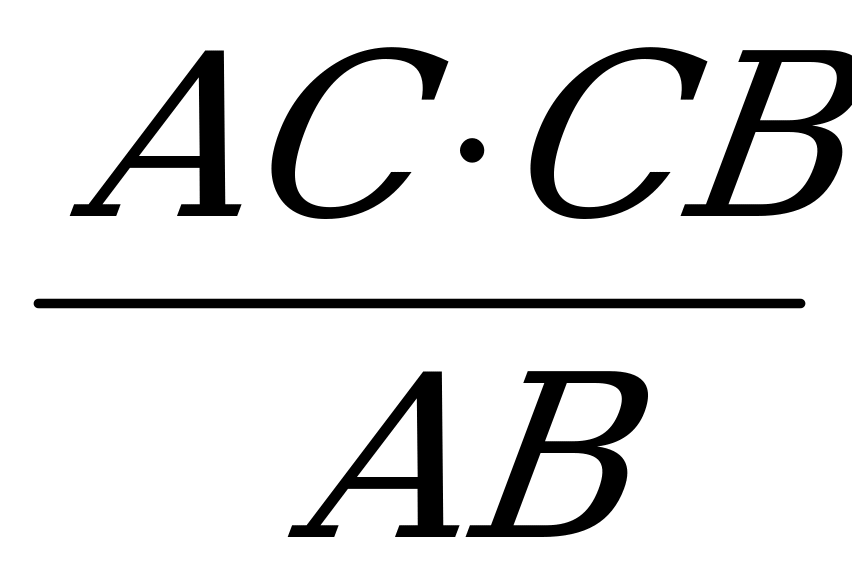 , т.е.
, т.е.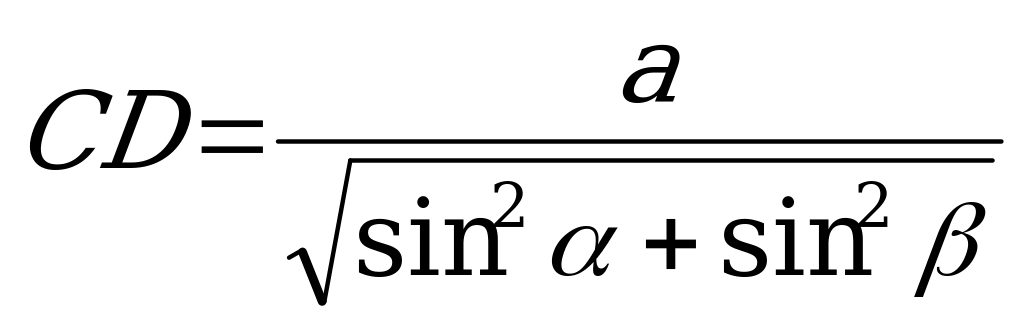 .
.
Из ∆ CD :
: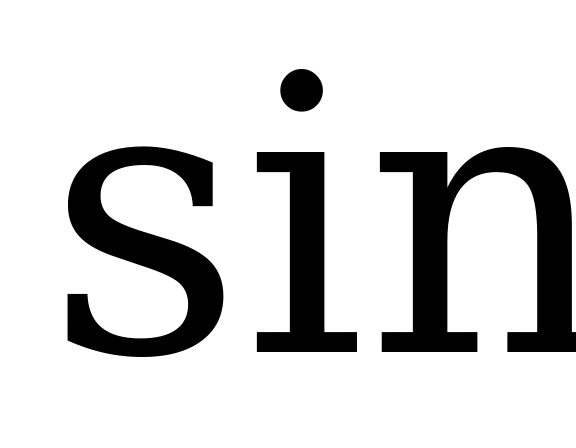 φ=
φ=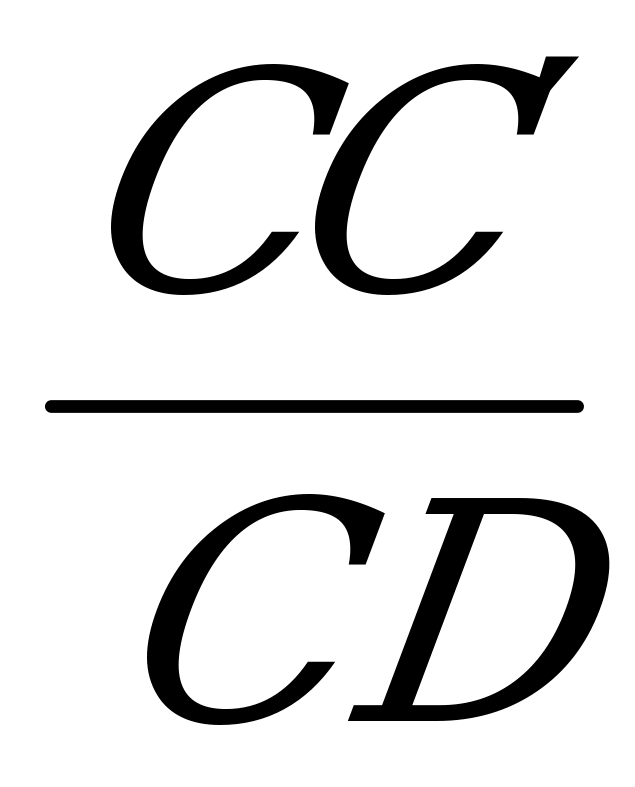 , sinφ=
, sinφ=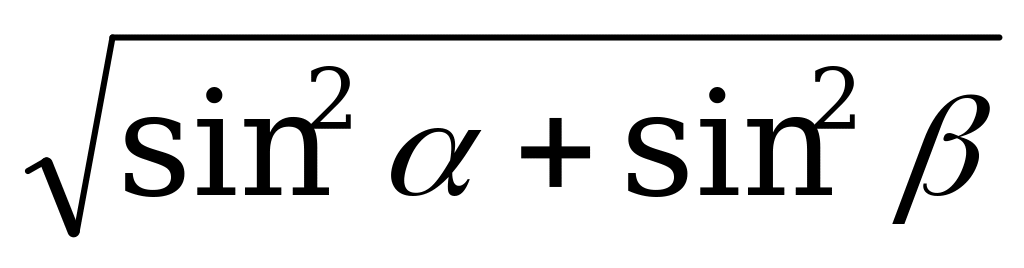 ,
,  φ
φ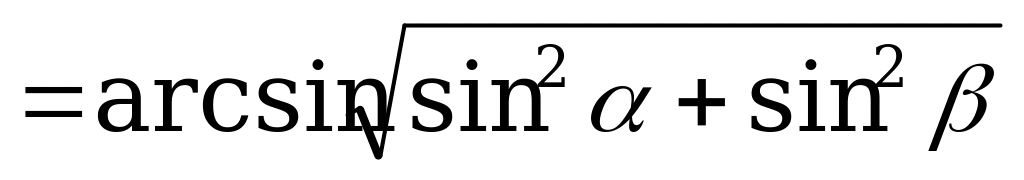 .
.
Ответ: arcsin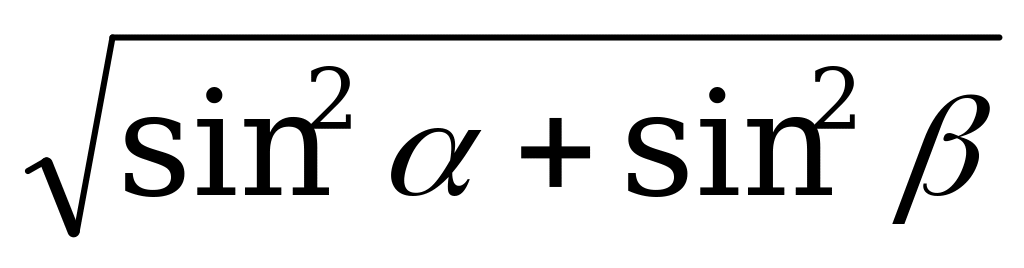 .
.
2. Дан куб АВСDA1B1C1D1.
Найти угол между плоскостью, проходящей через вершину А и середины рёбер СС1 и С1D1 и плоскостью основания.

Решение. Построим сечение методом следов. Опустим перпендикуляр из точки S на AL.
По теореме о трёх перпендикулярах DE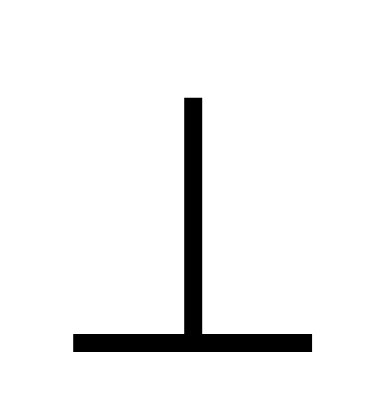 AL.Угол SED – угол между плоскостью сечения и плоскостью основания. Пусть
AL.Угол SED – угол между плоскостью сечения и плоскостью основания. Пусть  SED=
SED=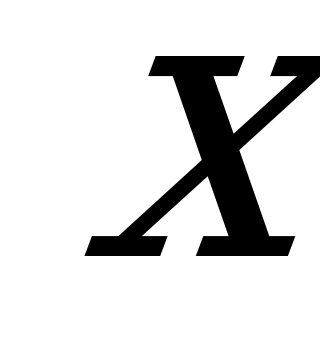 .Обозначим ребро куба
.Обозначим ребро куба 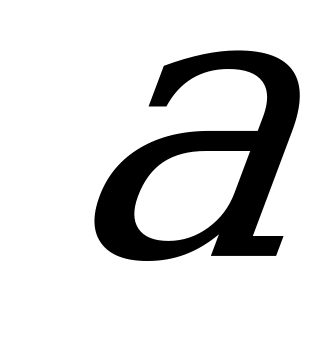 , тогда МС1=С1N=
, тогда МС1=С1N=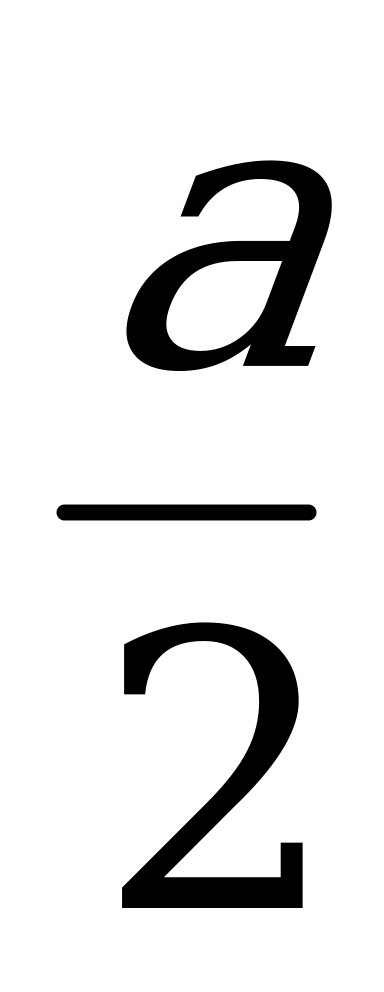 . Треугольник NCL равен треугольнику MC1N, значит CL=
. Треугольник NCL равен треугольнику MC1N, значит CL=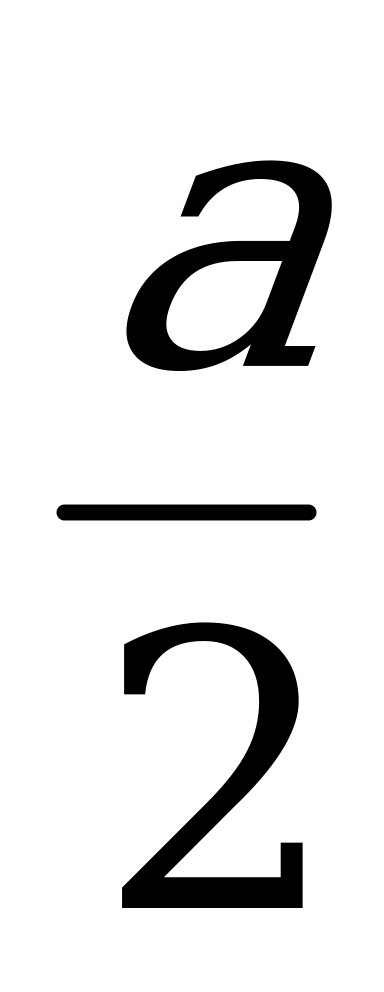 , тогда DL=
, тогда DL=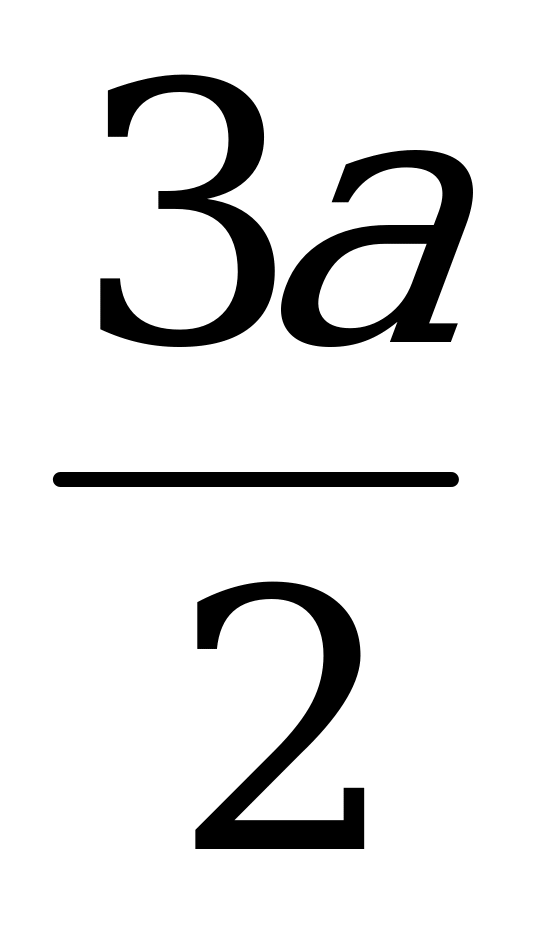 . Из треугольника ADL найдем DE: DE=
. Из треугольника ADL найдем DE: DE= =
=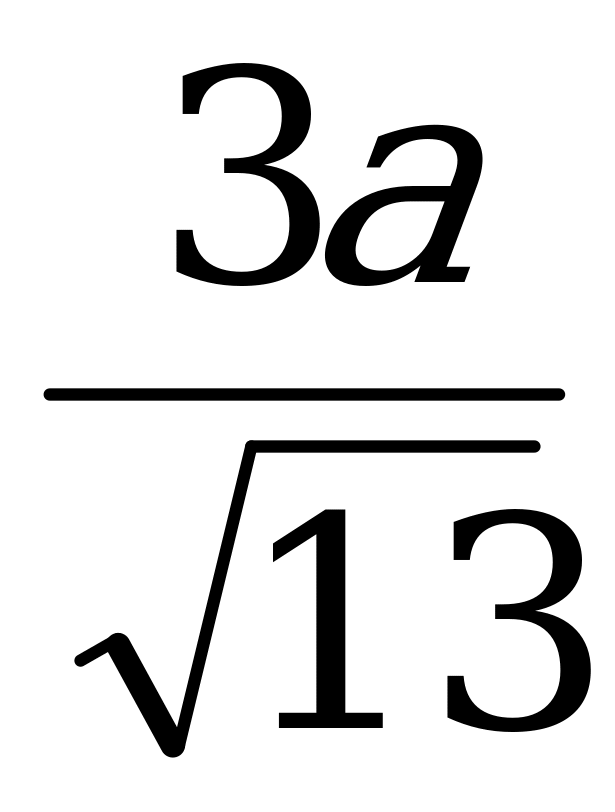 .Треугольник SD1M подобен треугольнику SDL, отсюда
.Треугольник SD1M подобен треугольнику SDL, отсюда 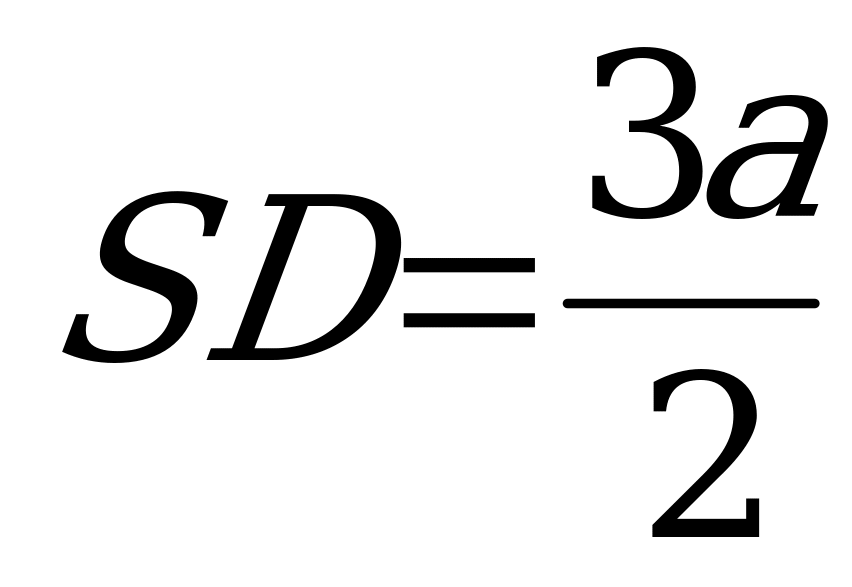 .
.
Угол 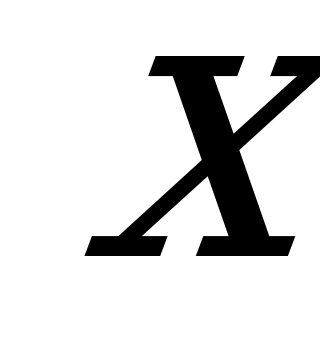 найдём из треугольника SDE:
найдём из треугольника SDE: 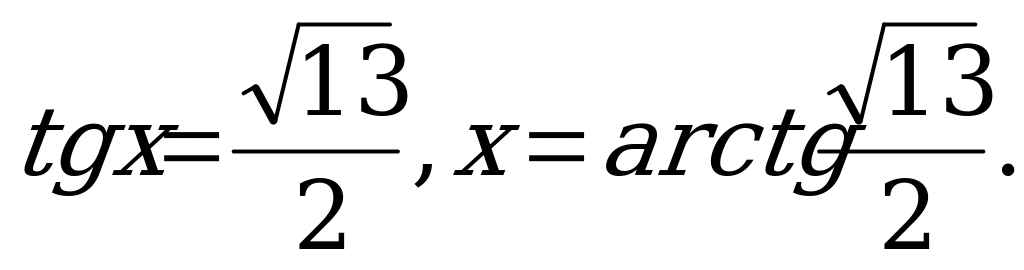
Ответ: 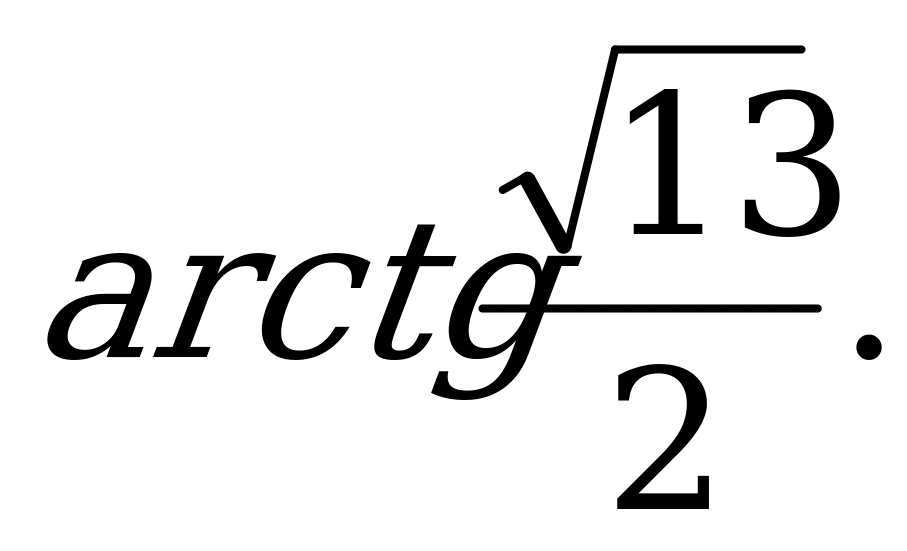
Задачи для самостоятельного решения.
Через точку, лежащую на ребре двугранного угла  (
(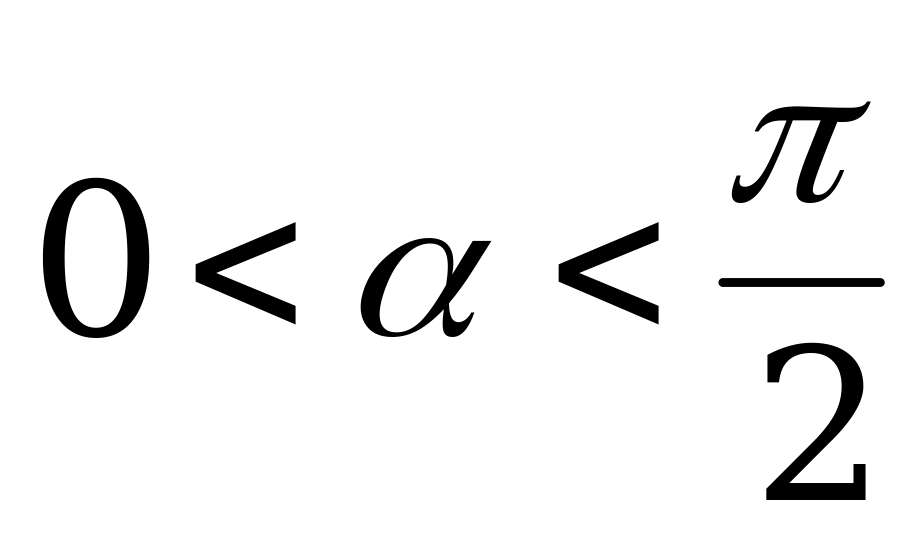 ) проходят два луча , расположенные в различных плоскостях. Один луч перпендикулярен ребру, а другой образует с ребром острый угол
) проходят два луча , расположенные в различных плоскостях. Один луч перпендикулярен ребру, а другой образует с ребром острый угол  . Найти угол между данными лучами. Ответ:
. Найти угол между данными лучами. Ответ:
Дан куб ABCDA1B1C1D1.Через вершину А, точку М- середину ребра C1D1 и точку N- середину ребра BC проведена плоскость. Найти угол наклона этой плоскости к плоскости основания.
Ответ: 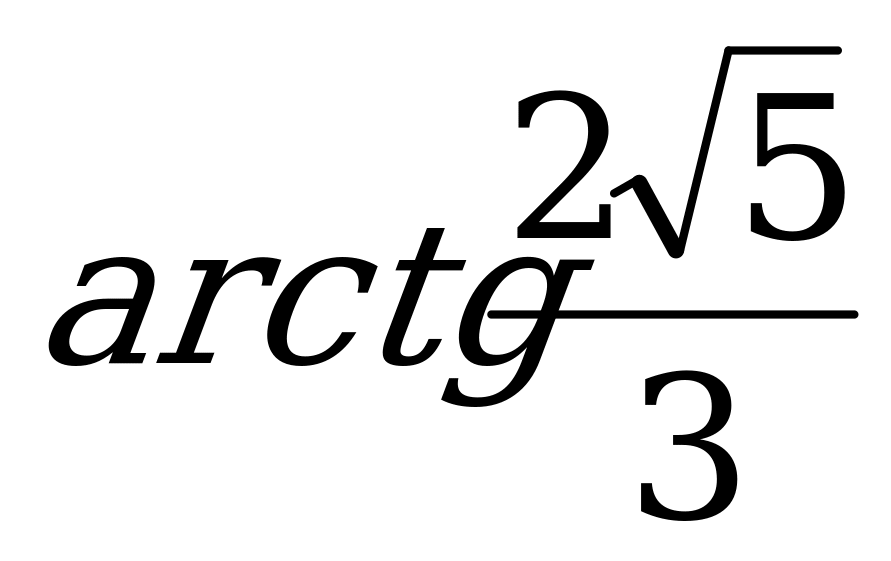 .
.
Плоскость прямоугольного треугольника, катеты которого равны 3 и 4 см, образует с плоскостью  угол
угол  . Гипотенуза этого треугольника лежит в плоскости
. Гипотенуза этого треугольника лежит в плоскости . Вычислить угол, который образует меньший катет с плоскостью
. Вычислить угол, который образует меньший катет с плоскостью .
.
Ответ: 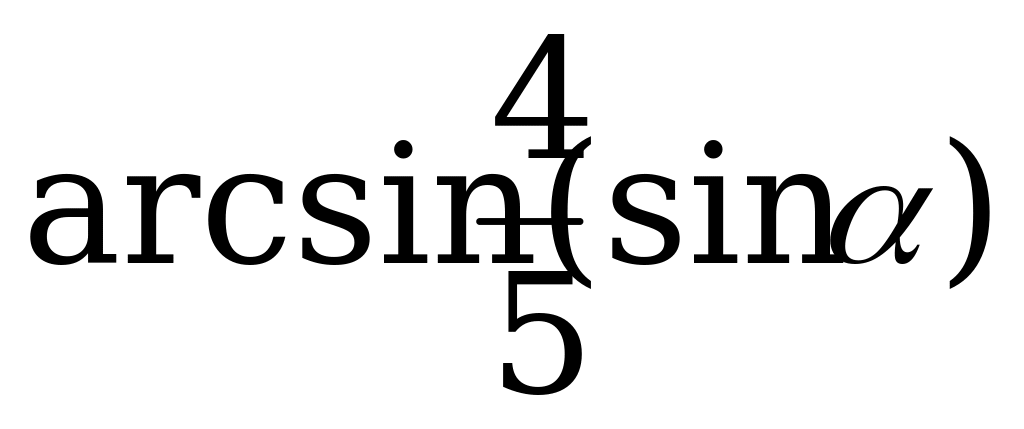 .
.
В прямоугольном параллелепипеде точка пересечения диагоналей нижнего основания соединена с серединой бокового ребра отрезком 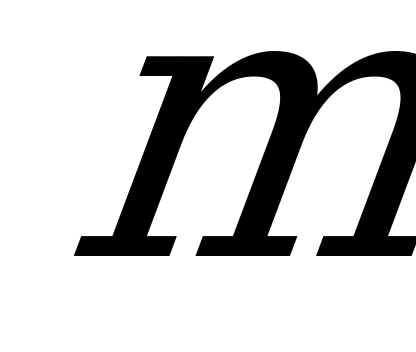 . Этот отрезок образует с основанием параллелепипеда угол
. Этот отрезок образует с основанием параллелепипеда угол  и с боковой гранью угол
и с боковой гранью угол 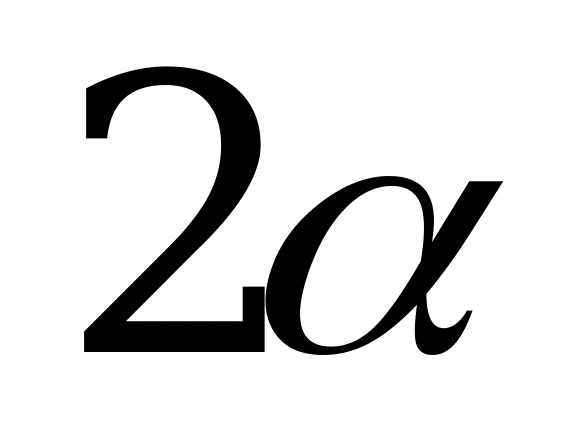 . Вычислить объём параллелепипеда.
. Вычислить объём параллелепипеда.
Ответ: 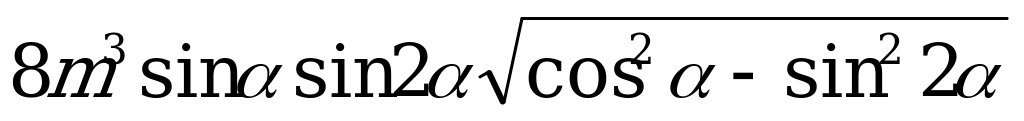 .
.
Основанием пирамиды служит правильный треугольник. Из трёх боковых граней этой пирамиды одна перпендикулярна основанию, а две другие наклонены к нему под углом  . Под каким углом наклонены к основанию боковые ребра?
. Под каким углом наклонены к основанию боковые ребра?
Ответ: 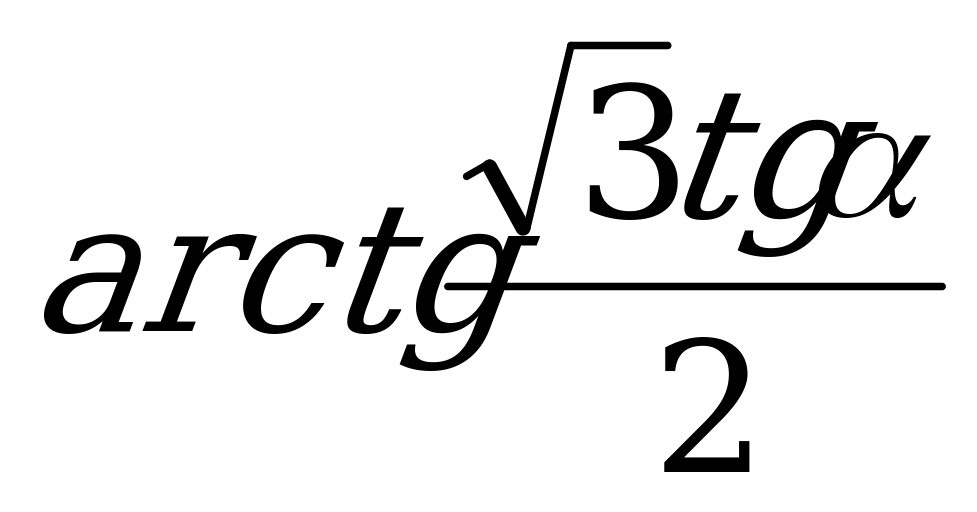 ;
; 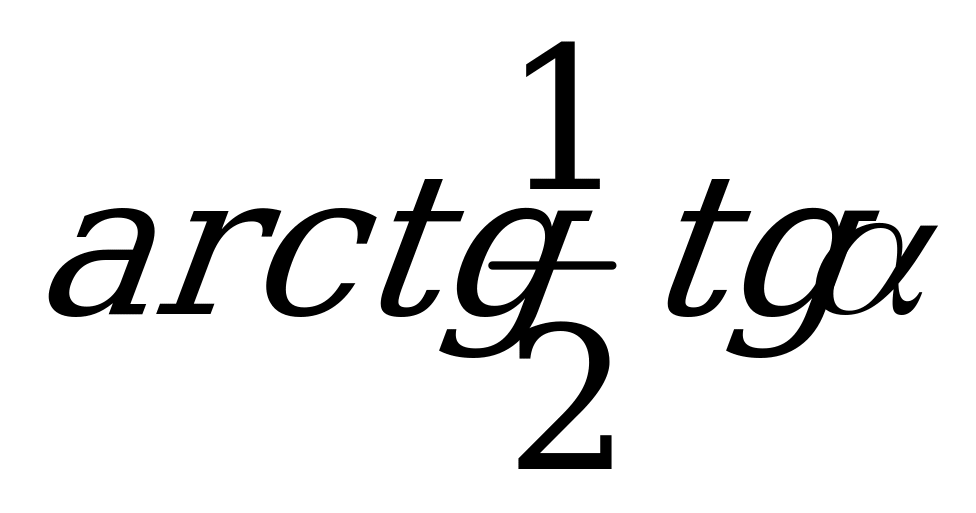 .
.
. В прямоугольном параллелепипеде 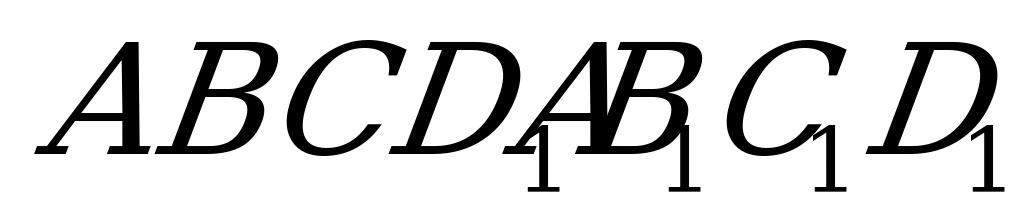 :
: 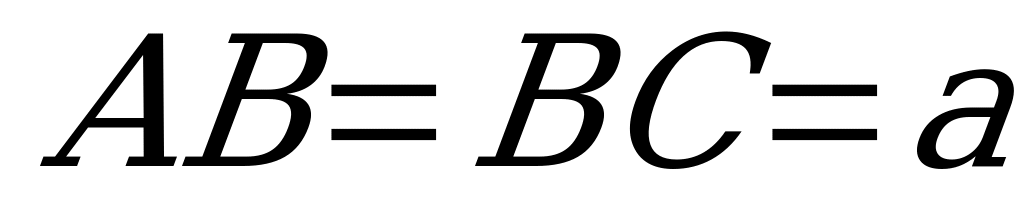 ,
, 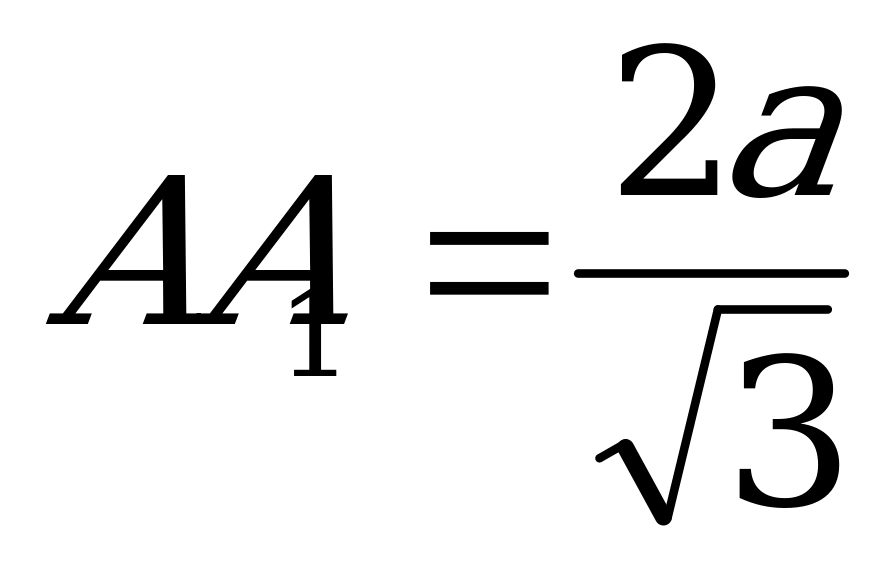 . Через вершину
. Через вершину  и середину
и середину 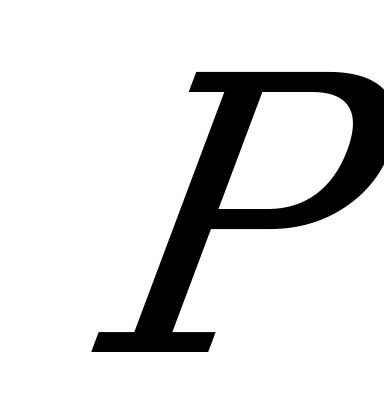 ребра
ребра  проведена плоскость, параллельная диагонали
проведена плоскость, параллельная диагонали 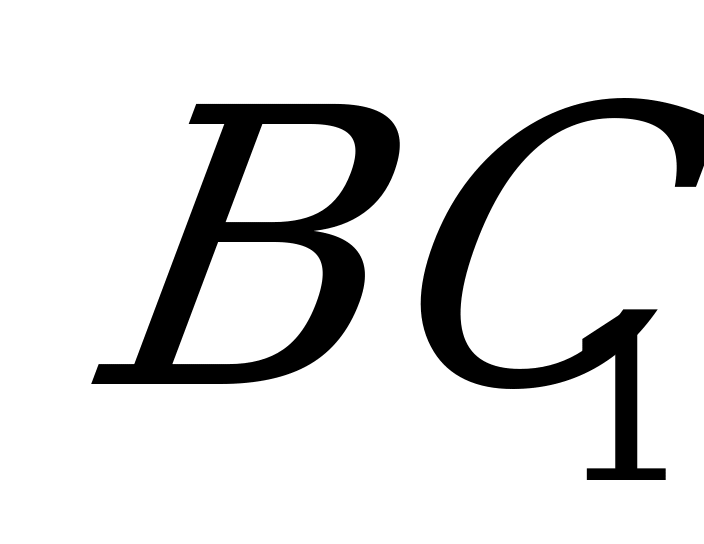 грани
грани 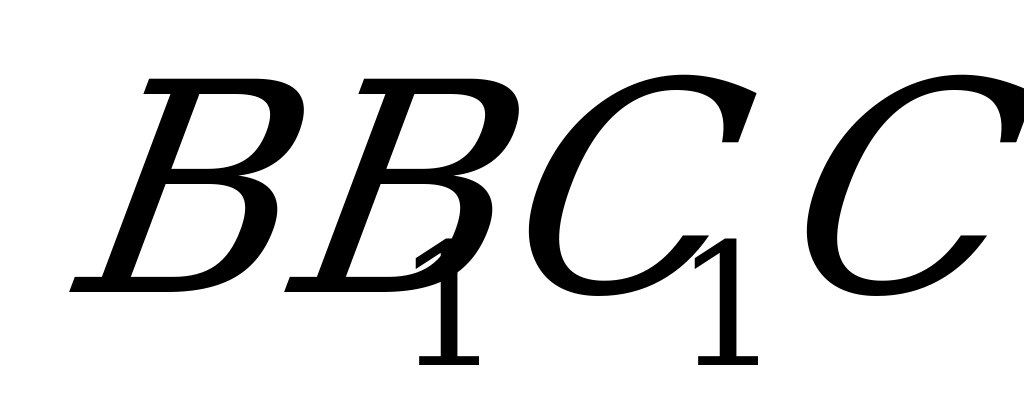 .Постройте сечение параллелепипеда этой плоскостью. Вычислите площадь сечения и расстояние от вершины
.Постройте сечение параллелепипеда этой плоскостью. Вычислите площадь сечения и расстояние от вершины 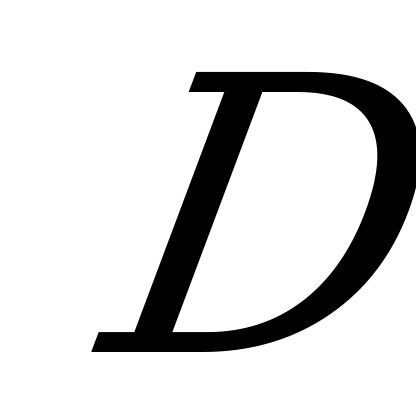 до плоскости сечения.
до плоскости сечения.
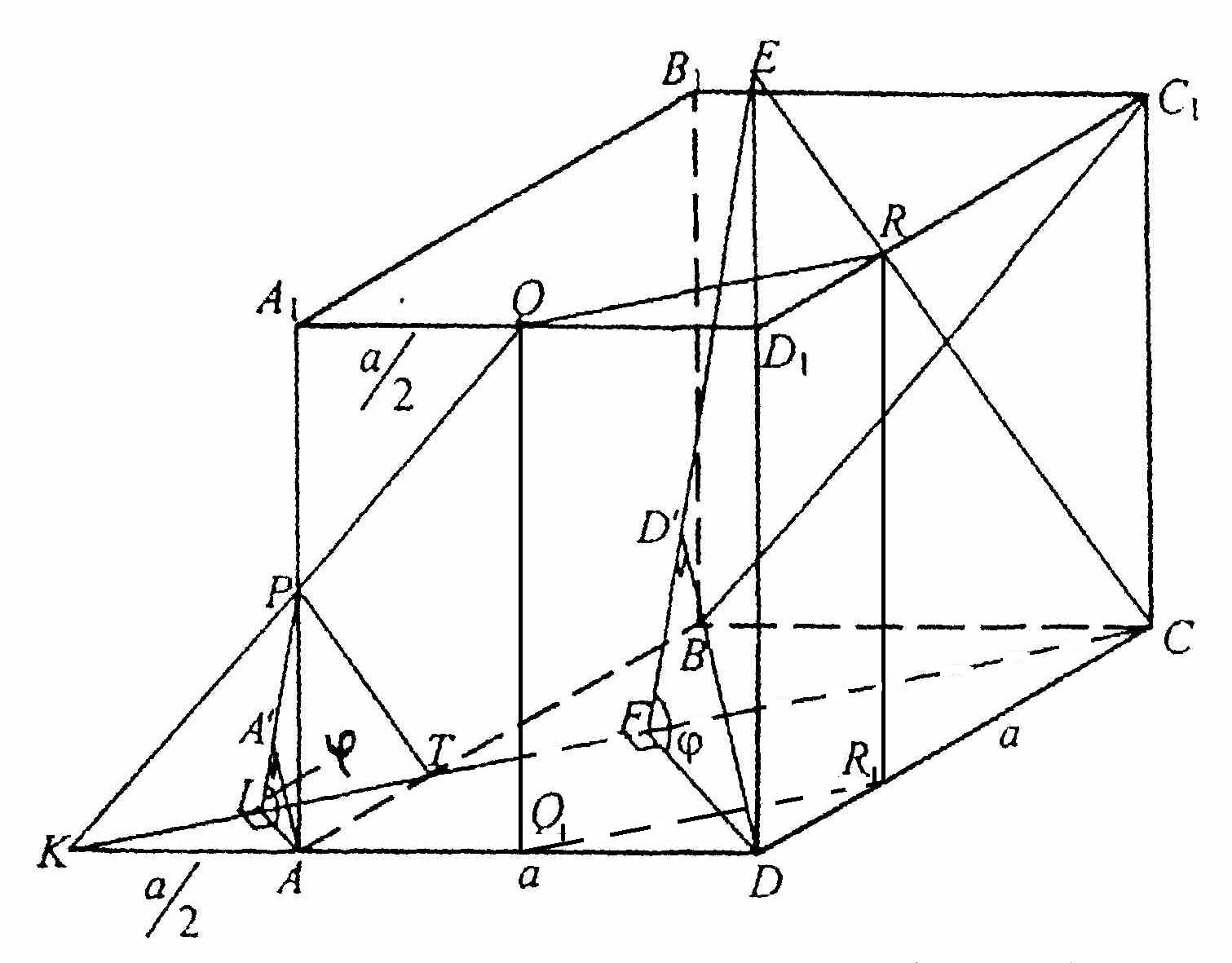
Решение. Построим сечение параллелепипеда. В плоскости 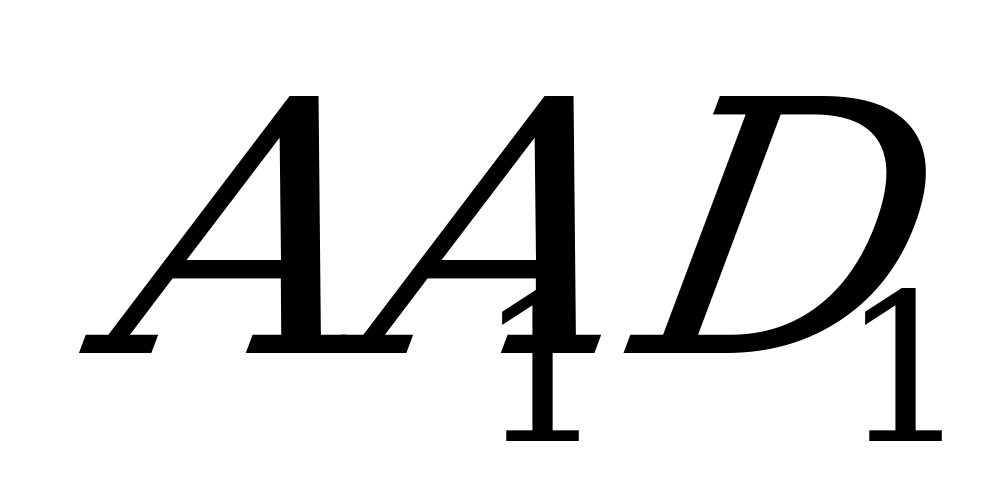 через точку
через точку 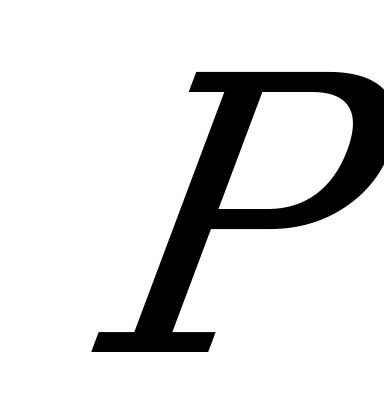 проведем прямую, параллельную ВС 1 до пересечения с прямыми
проведем прямую, параллельную ВС 1 до пересечения с прямыми 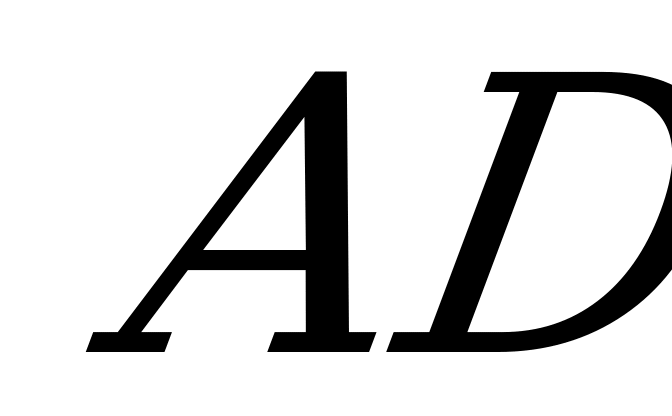 и
и  в точках
в точках 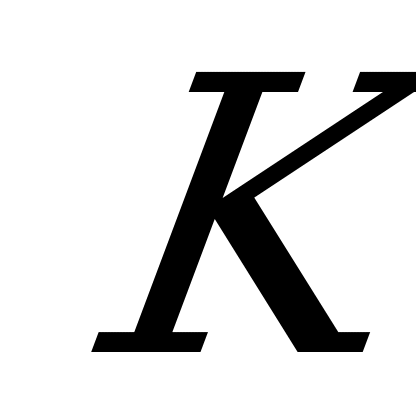 и
и  , соответственно:
, соответственно:  .
.
В плоскости  ,
,  - точка пересечения прямых
- точка пересечения прямых 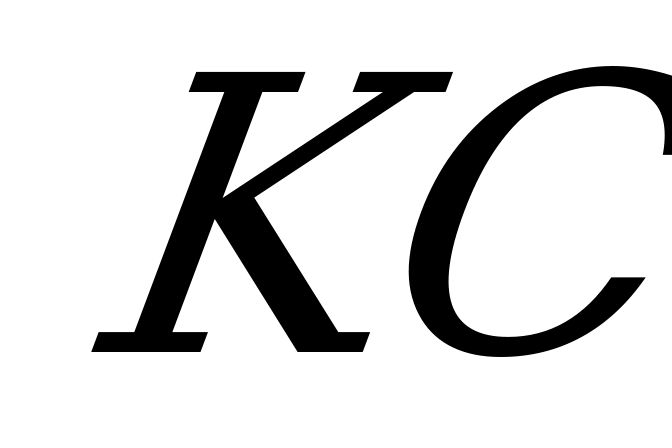 и
и 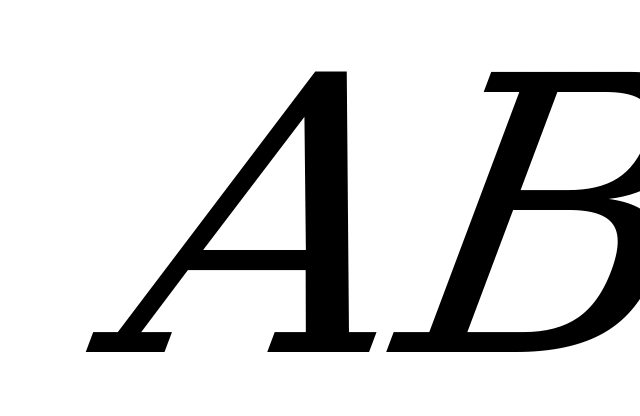 ,
, 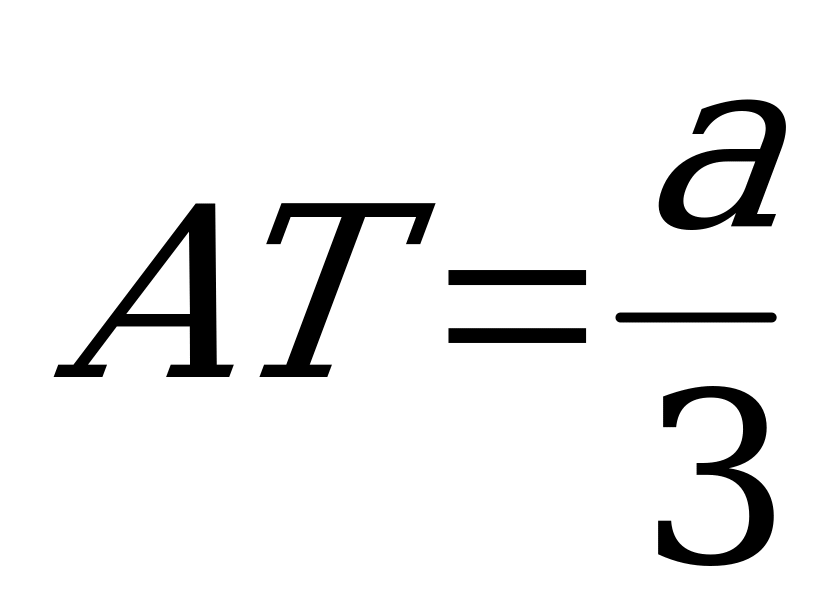 (
( ~
~  ).
).
Прямые  и
и  параллельны , точка R принадлежит ребру C1D1, RD1=
параллельны , точка R принадлежит ребру C1D1, RD1= (
( ~
~
 ).
).
Искомое сечение: 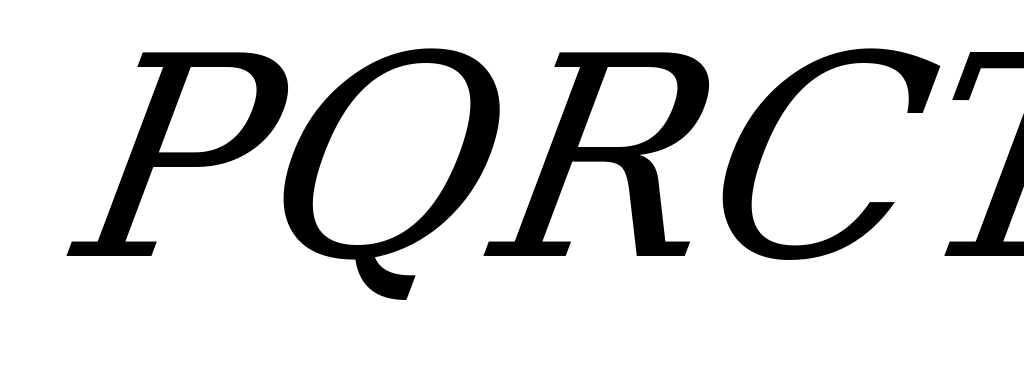 . Площадь S этого сечения вычислим по формуле:
. Площадь S этого сечения вычислим по формуле:
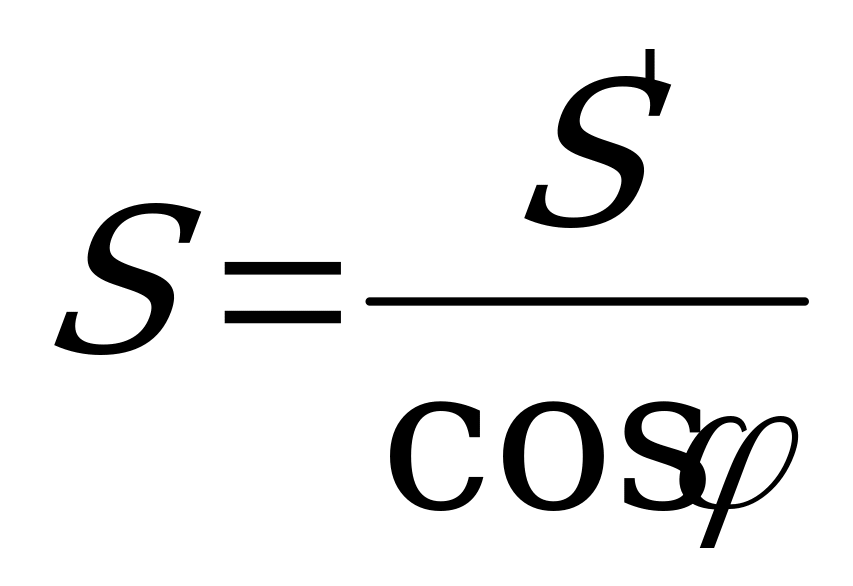 , где
, где 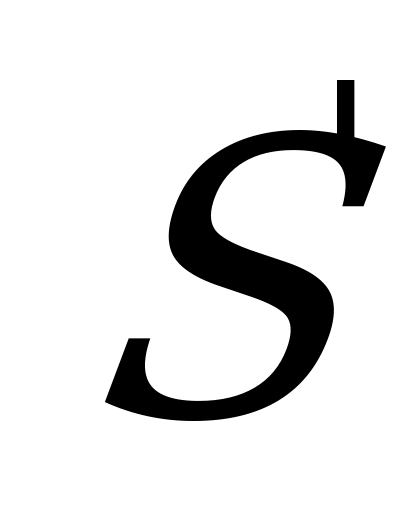 проекция сечения на плоскость (АВС). Проекцией сечения является пятиугольник
проекция сечения на плоскость (АВС). Проекцией сечения является пятиугольник 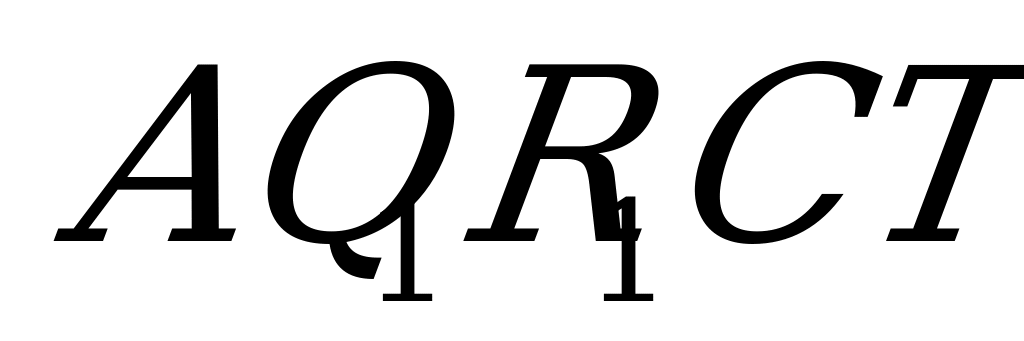 .
.
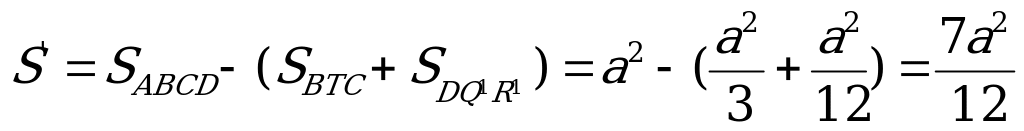
 . Найдём угол
. Найдём угол 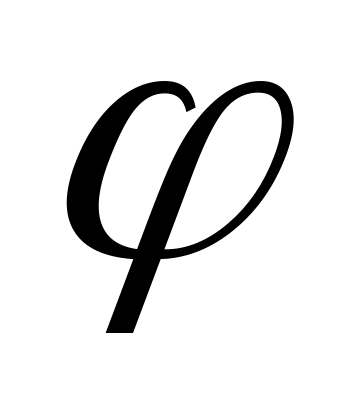 между плоскостью сечения и плоскостью АВС. Через точку
между плоскостью сечения и плоскостью АВС. Через точку  проведём плоскость
проведём плоскость 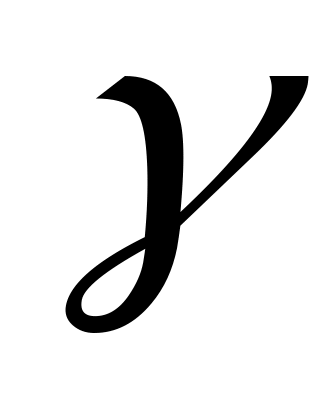 , перпендикулярную линии пересечения плоскостей :
, перпендикулярную линии пересечения плоскостей :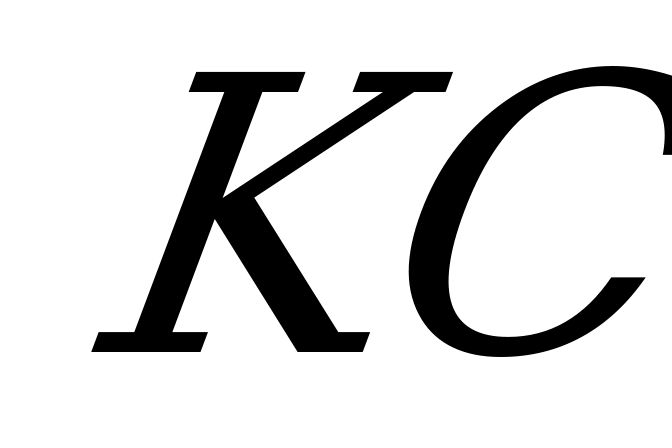 .Опустим перпендикуляр
.Опустим перпендикуляр 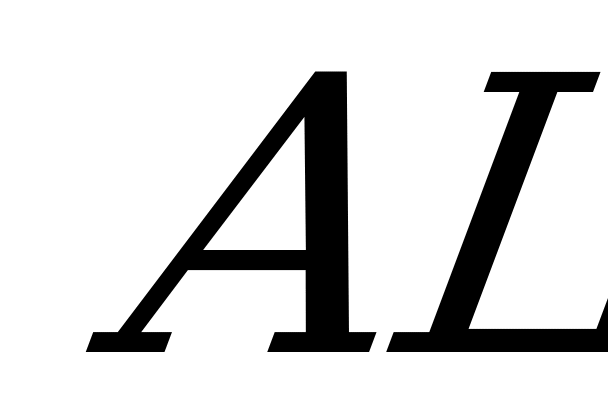 на
на 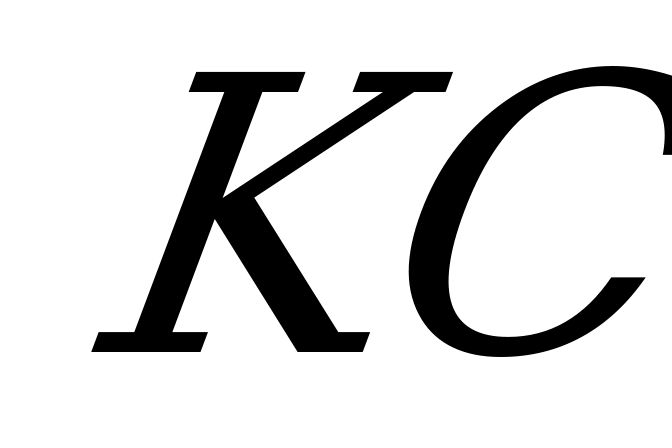 ,
, 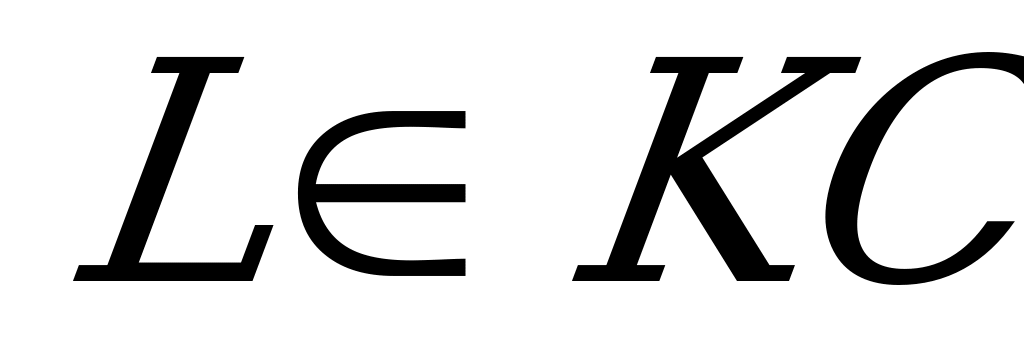 ,гипотенуза
,гипотенуза 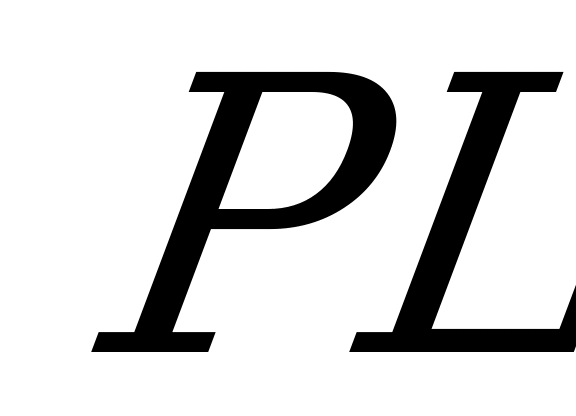 прямоугольного треугольника
прямоугольного треугольника 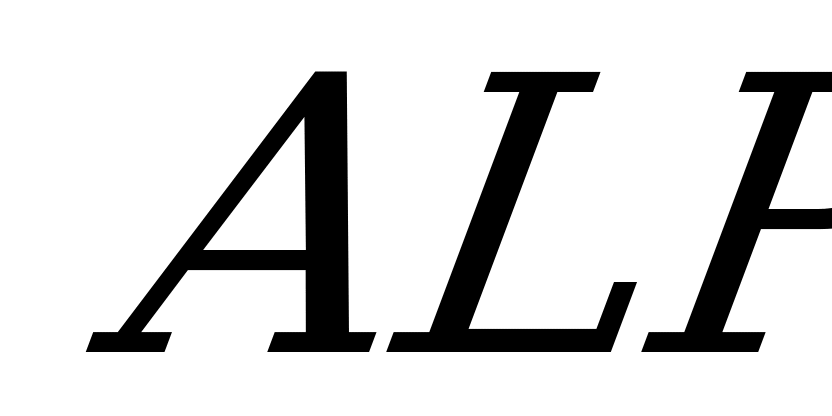 перпендикулярна
перпендикулярна 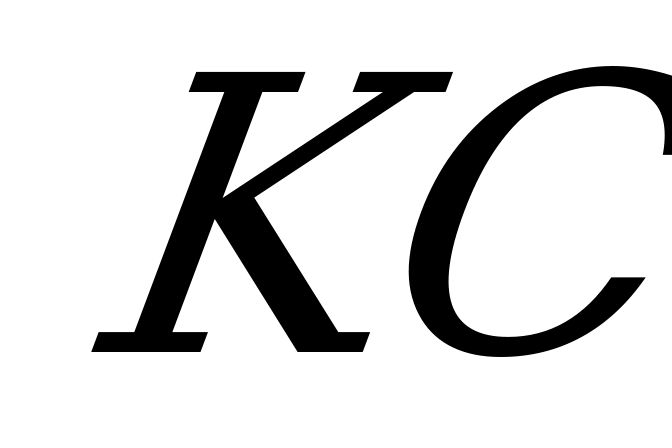 ,значит
,значит  тогда
тогда 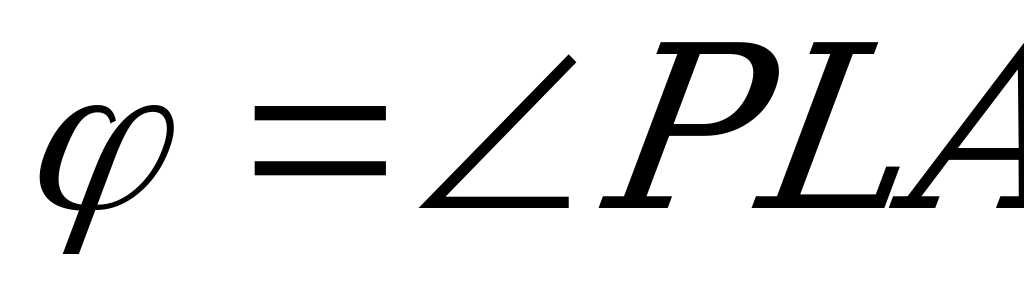 и поскольку
и поскольку 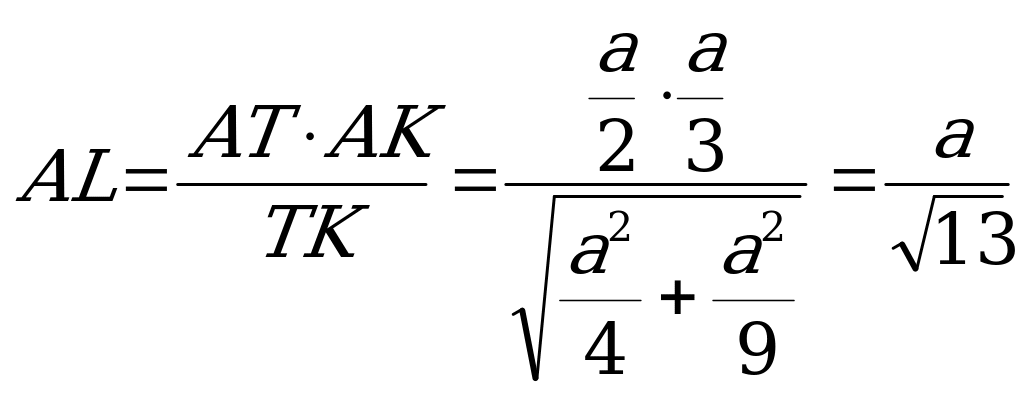 , то
, то 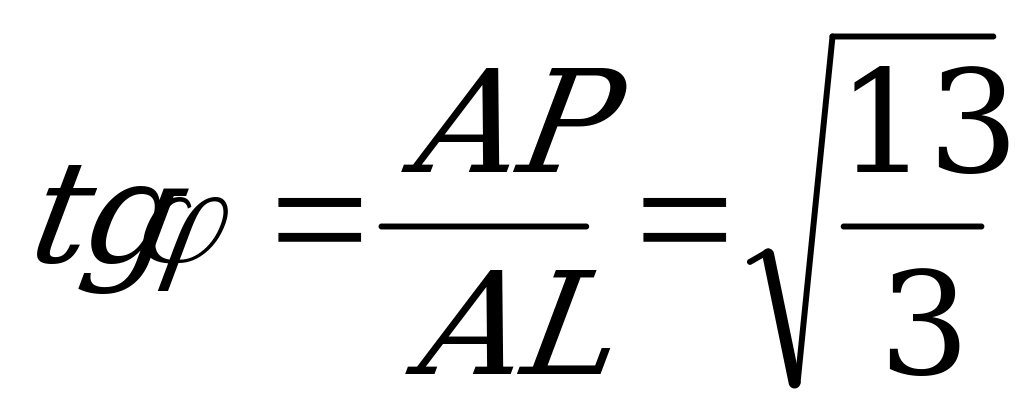 .
.
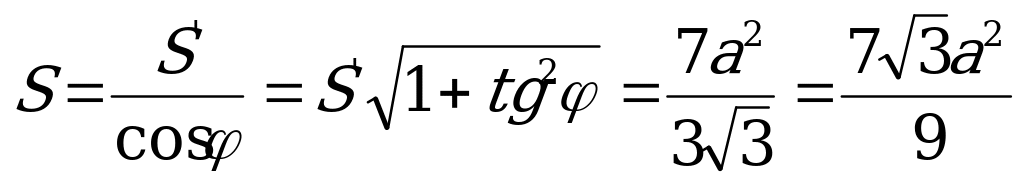 . Найдём расстояние от точки
. Найдём расстояние от точки  до плоскости сечения.
до плоскости сечения. 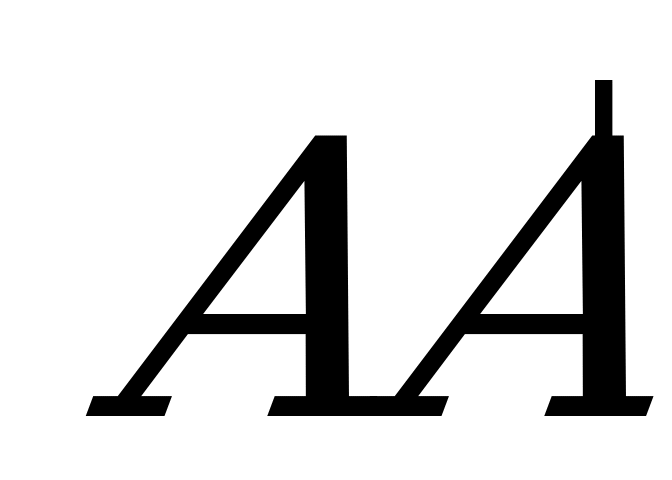 - перпендикуляр, опущенный из
- перпендикуляр, опущенный из  на гипотенузу
на гипотенузу 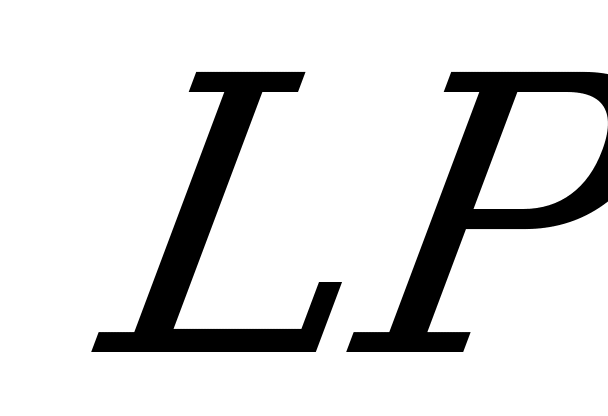 треугольника
треугольника 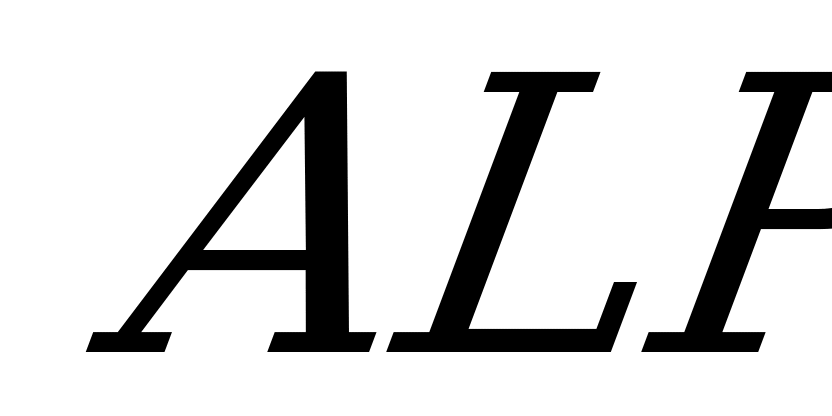 .
.  -расстояние от точки А до плоскости сечения. Через
-расстояние от точки А до плоскости сечения. Через 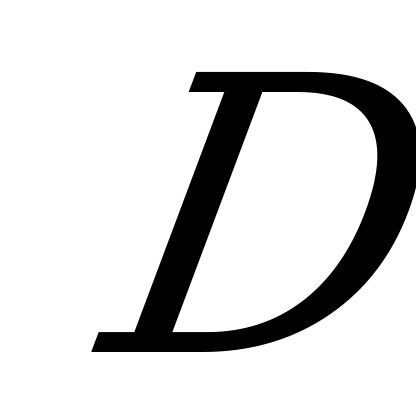 проведём
проведём  ║
║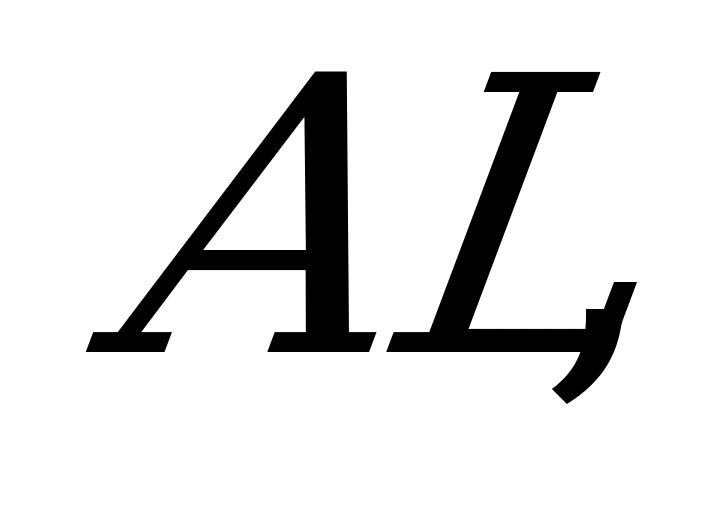
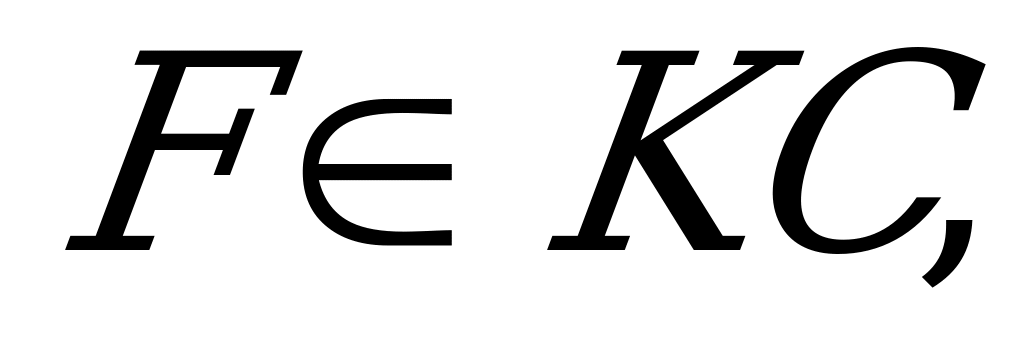 и FE║LP
и FE║LP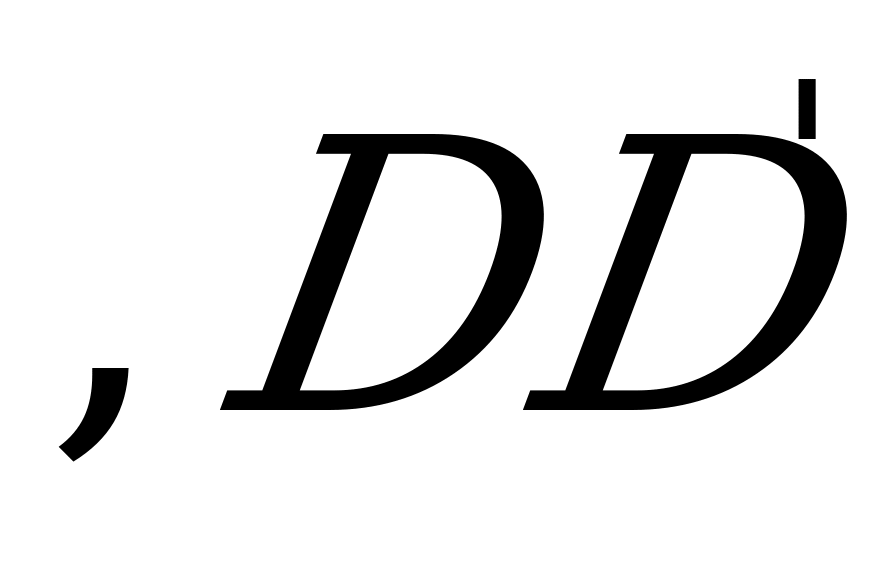 ║
║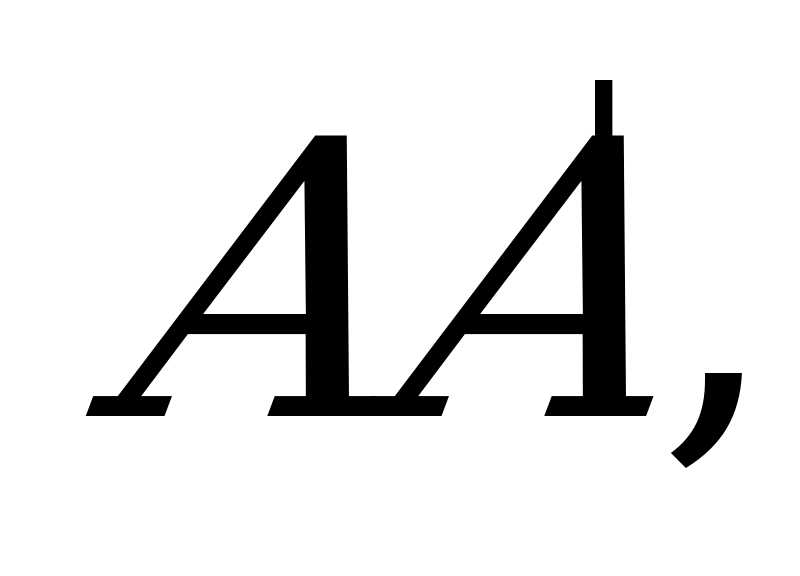
 Тогда
Тогда 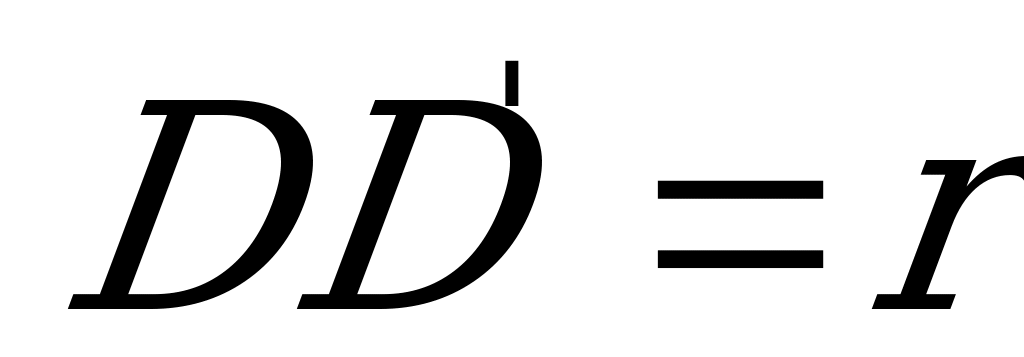 - расстояние от
- расстояние от  до плоскости сечения, и поскольку
до плоскости сечения, и поскольку 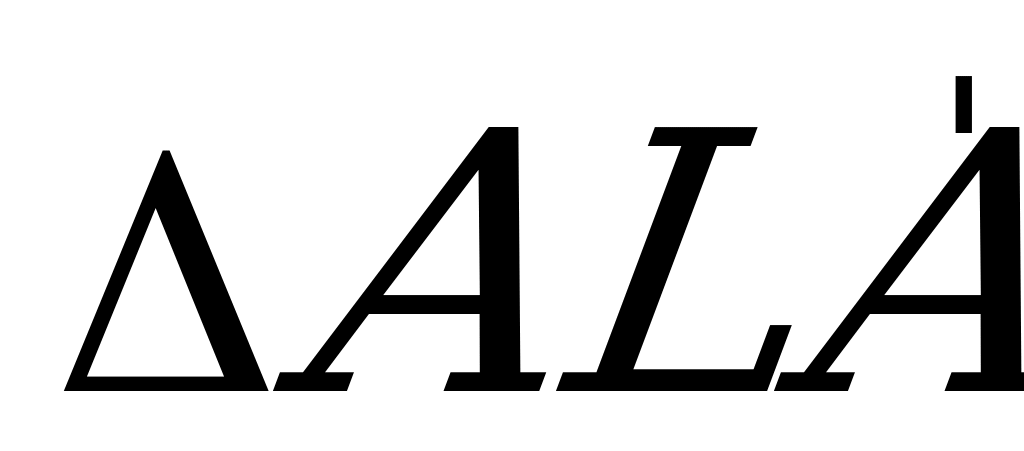 подобен
подобен  , то
, то 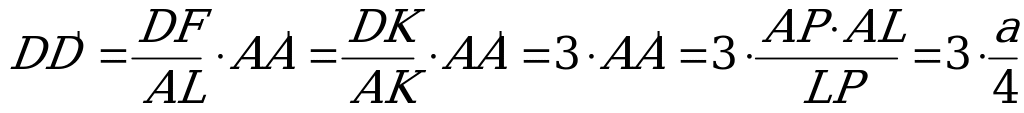 .
.
Ответ: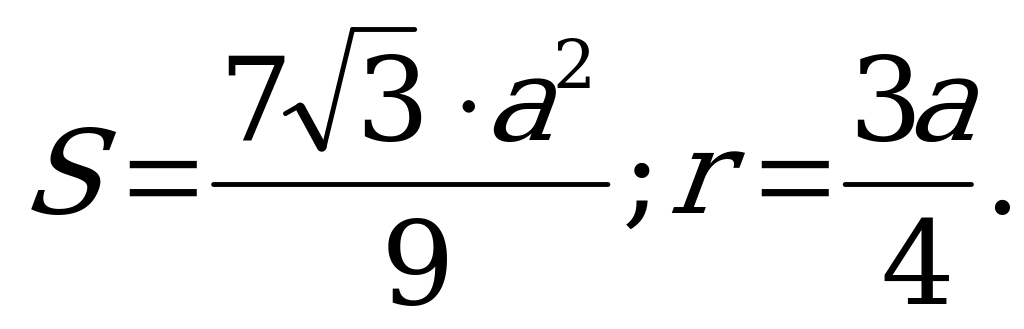
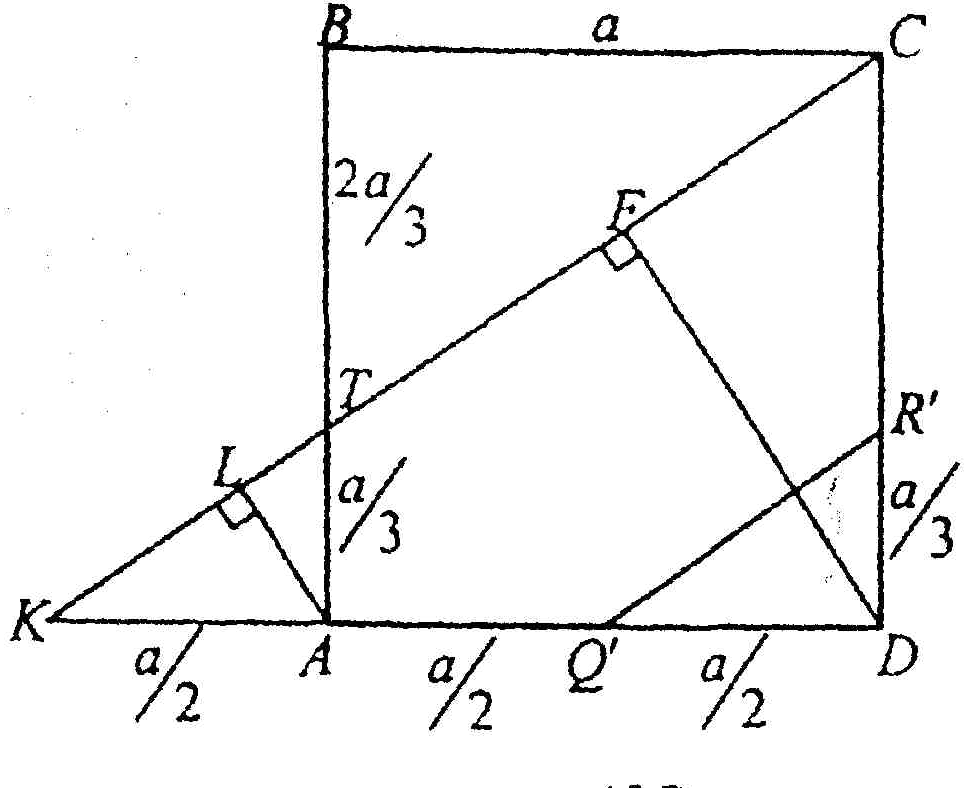
5. В правильной треугольной призме  через ребро
через ребро 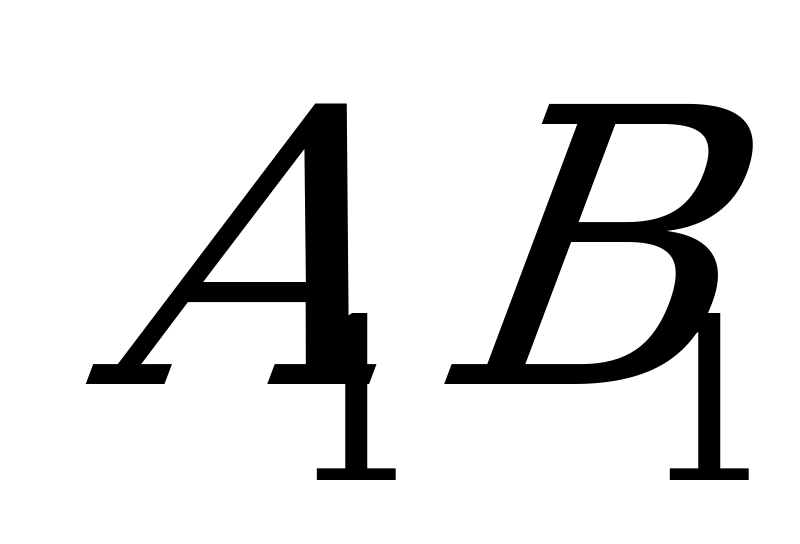 верхнего основания
верхнего основания 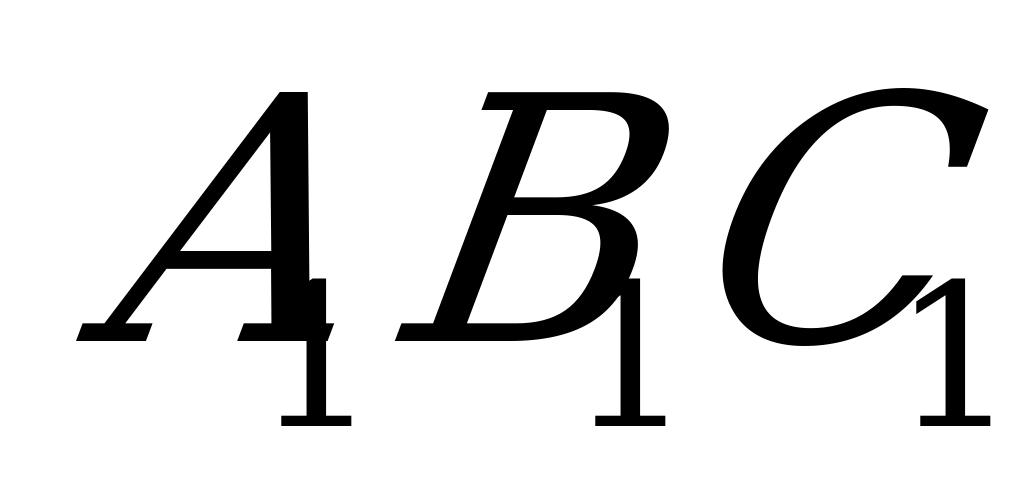 и середину M бокового ребра
и середину M бокового ребра 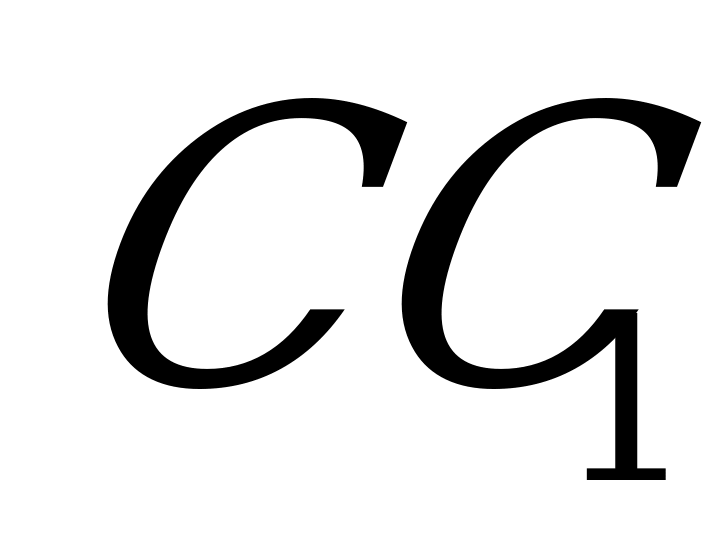 проведено сечение.
проведено сечение.
Н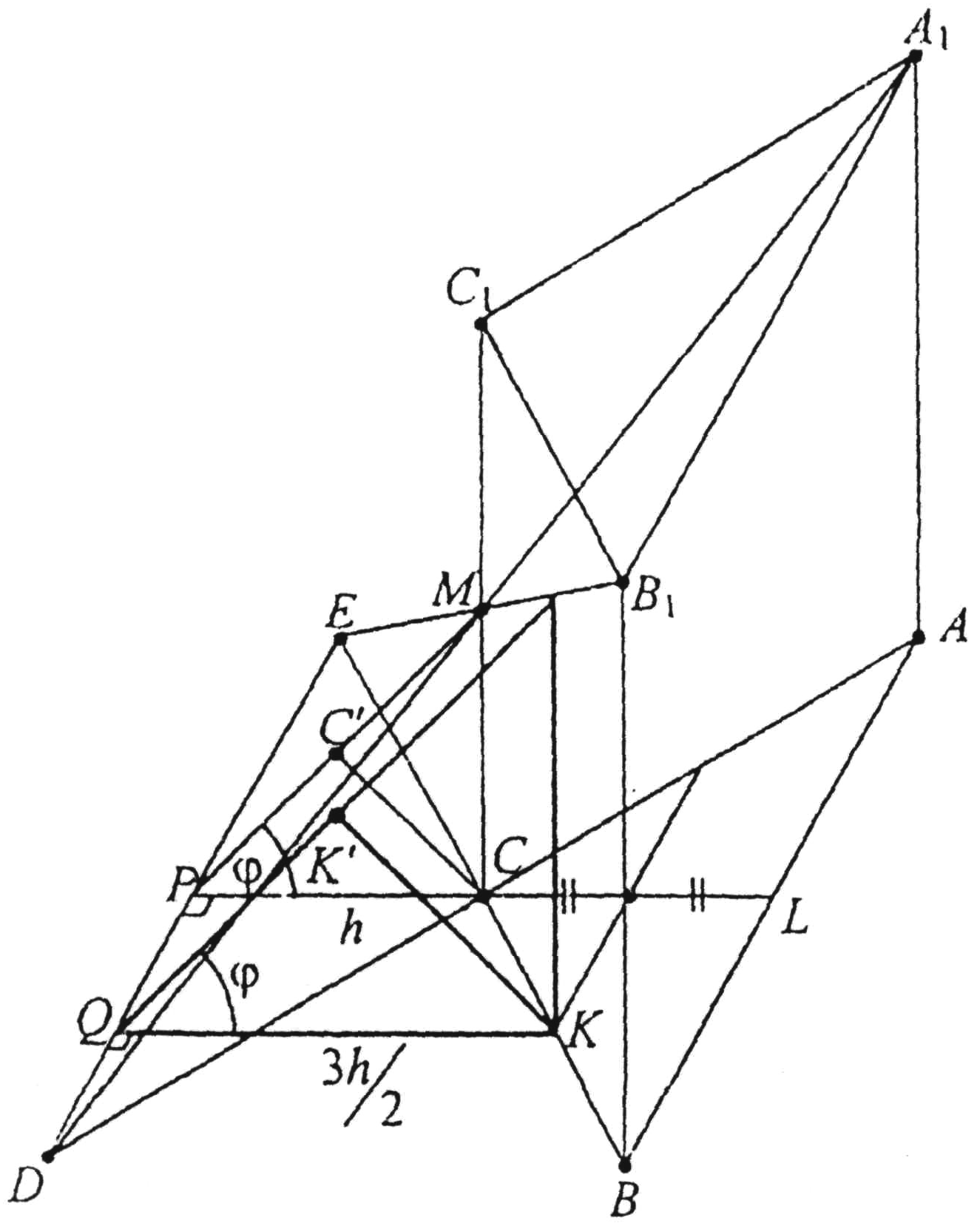 айдите :1) угол между плоскостью сечения и плоскостью основания; 2) площадь данного сечения; 3) расстояние от середины
айдите :1) угол между плоскостью сечения и плоскостью основания; 2) площадь данного сечения; 3) расстояние от середины 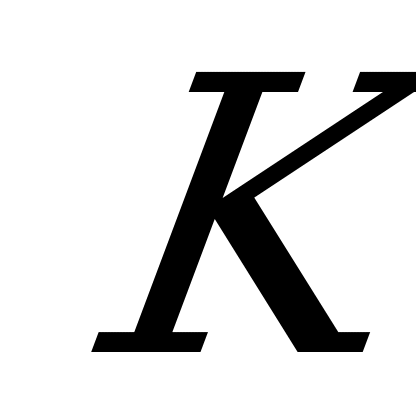 ребра
ребра  до плоскости сечения. Известно, что высота призмы
до плоскости сечения. Известно, что высота призмы  , а сторона основания
, а сторона основания 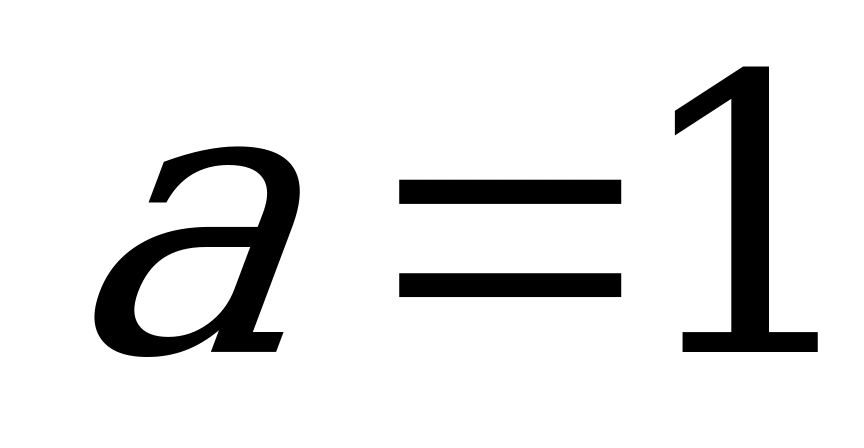 .
.
Решение. Построим линию пересечения плоскости  данного сечения с плоскостью основания. Прямую
данного сечения с плоскостью основания. Прямую 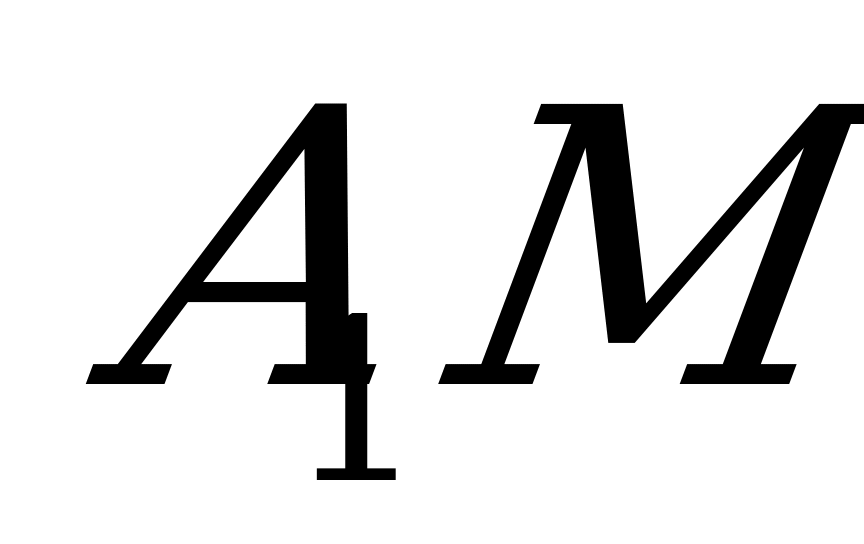 продолжаем до пересечения с прямой
продолжаем до пересечения с прямой  в точке
в точке  , прямую
, прямую  - до пересечения с прямой
- до пересечения с прямой  в точке
в точке  .
.  - искомая прямая. Через точку
- искомая прямая. Через точку 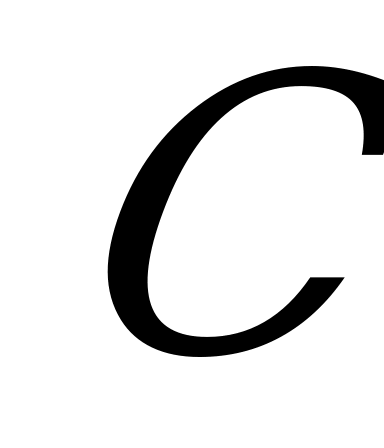 проводим плоскость
проводим плоскость 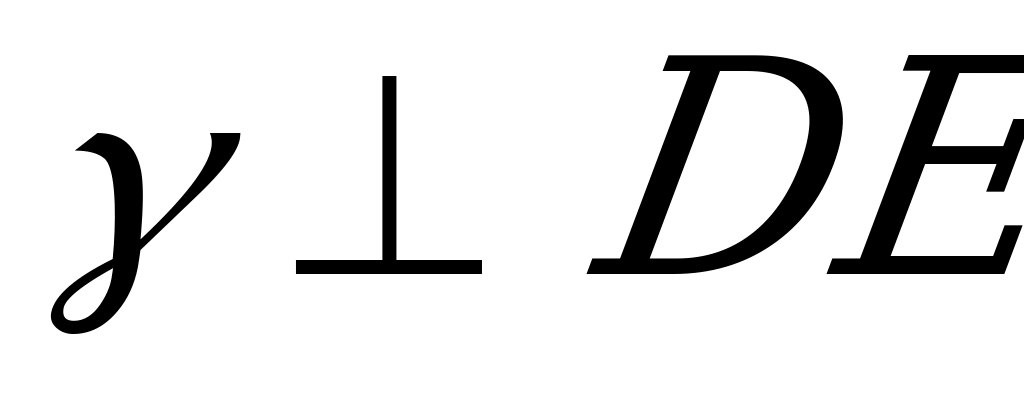 ,
, 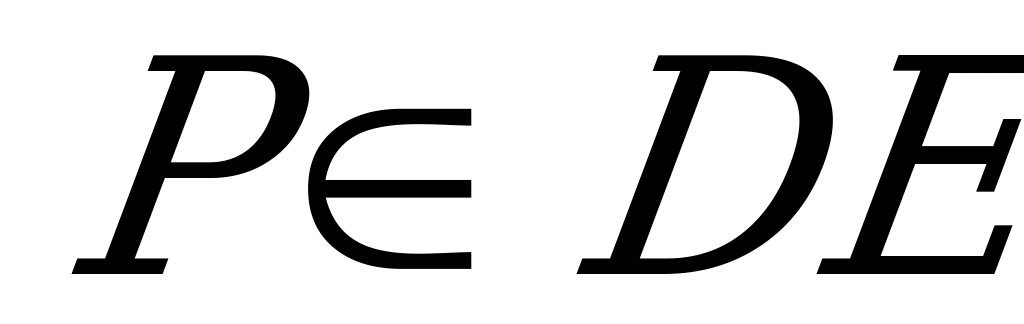 ,
, 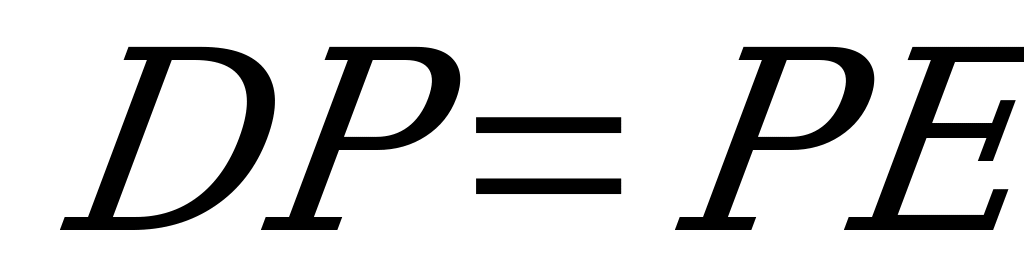 . Прямые
. Прямые  и
и 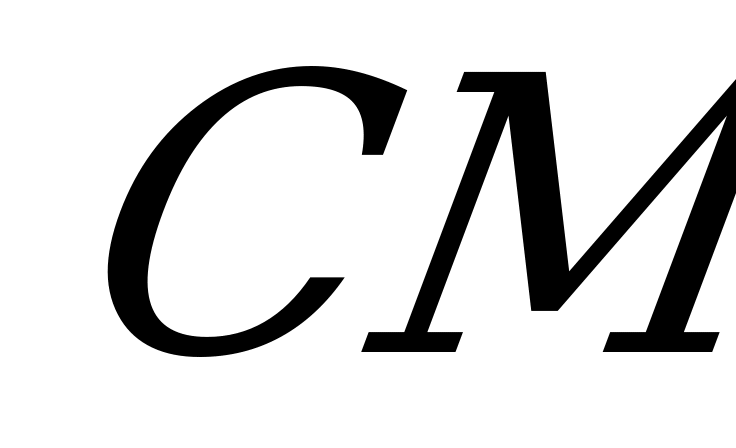 перпендикулярны
перпендикулярны  и проходят через C, следовательно
и проходят через C, следовательно  , треугольник
, треугольник  - прямоугольный и его гипотенуза
- прямоугольный и его гипотенуза 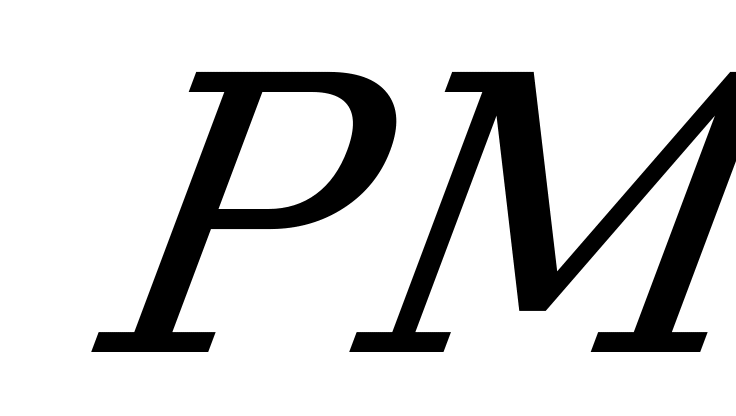 лежит в плоскостях
лежит в плоскостях  и
и 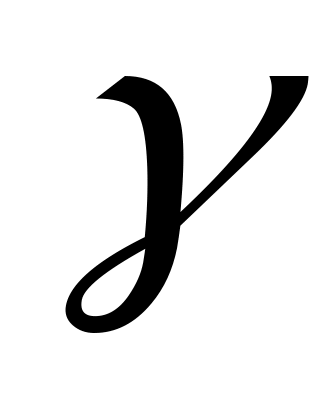 и ,следовательно,
и ,следовательно, 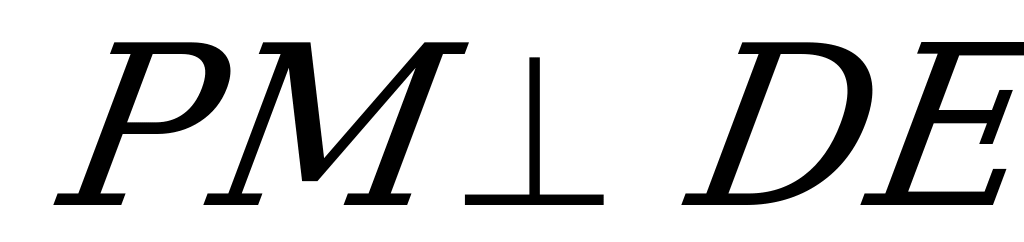 . Так как
. Так как 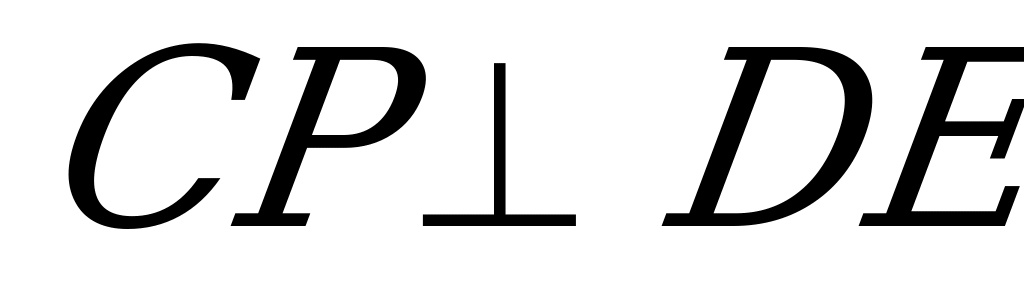 и
и  , то
, то 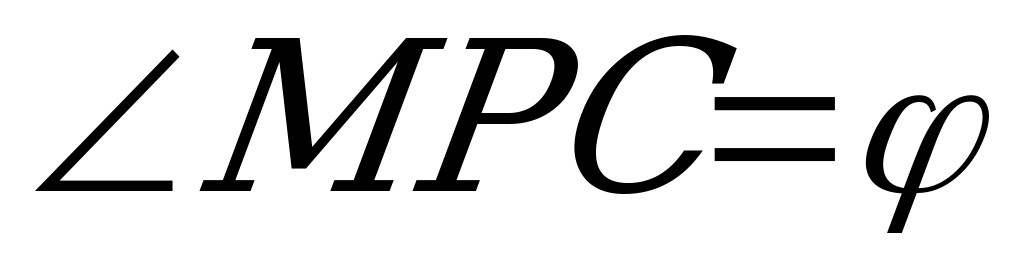 - угол между
- угол между  и плоскостью(ABC),
и плоскостью(ABC), 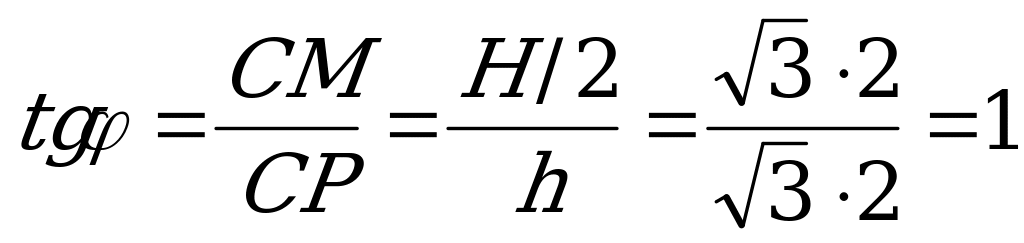 ,где h – высота
,где h – высота 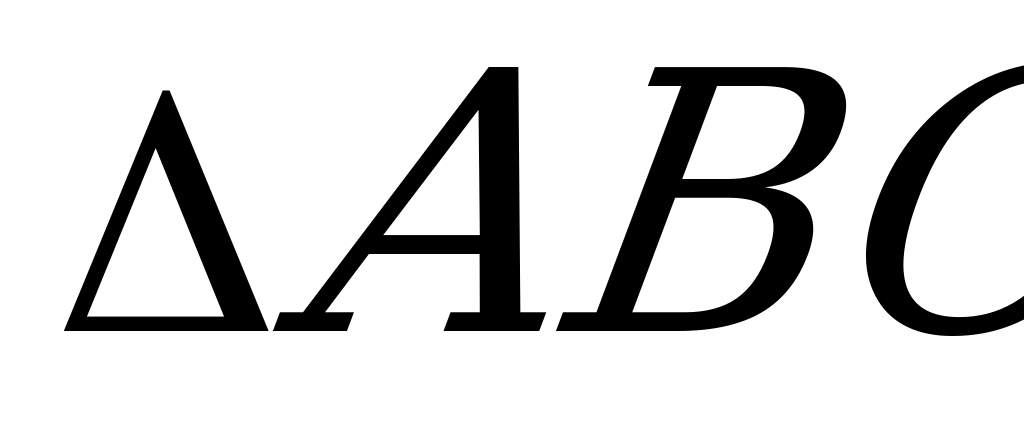 . Очевидно
. Очевидно 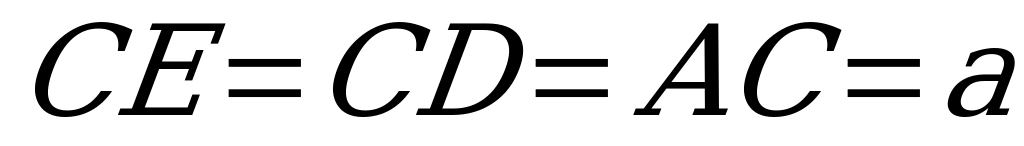 и
и  равен высоте
равен высоте 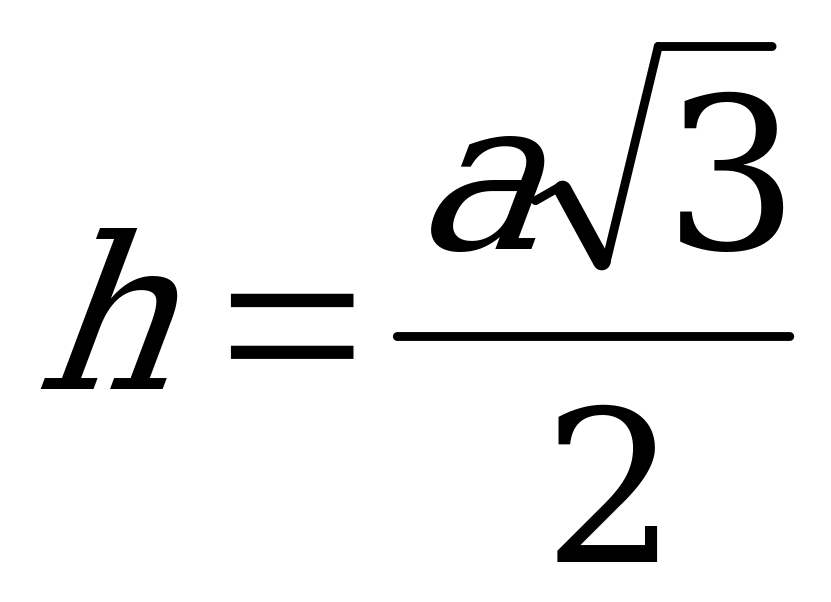 треугольника ABC. Следовательно,
треугольника ABC. Следовательно, 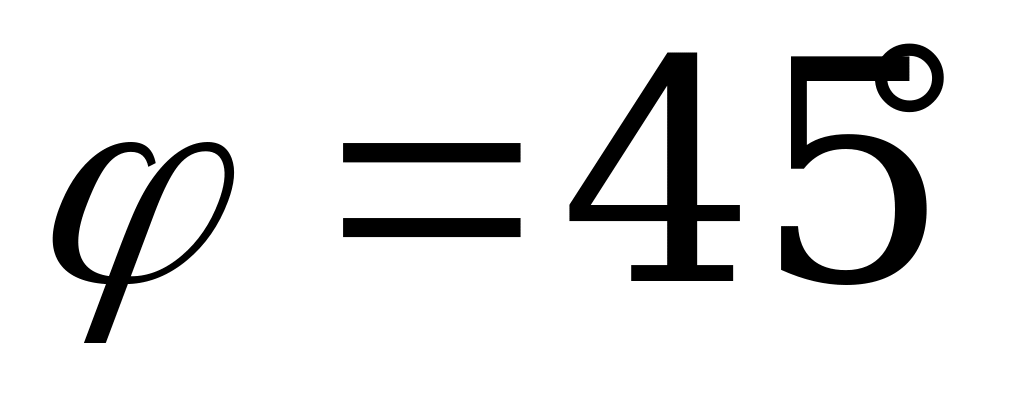 .
.
Площадь треугольника 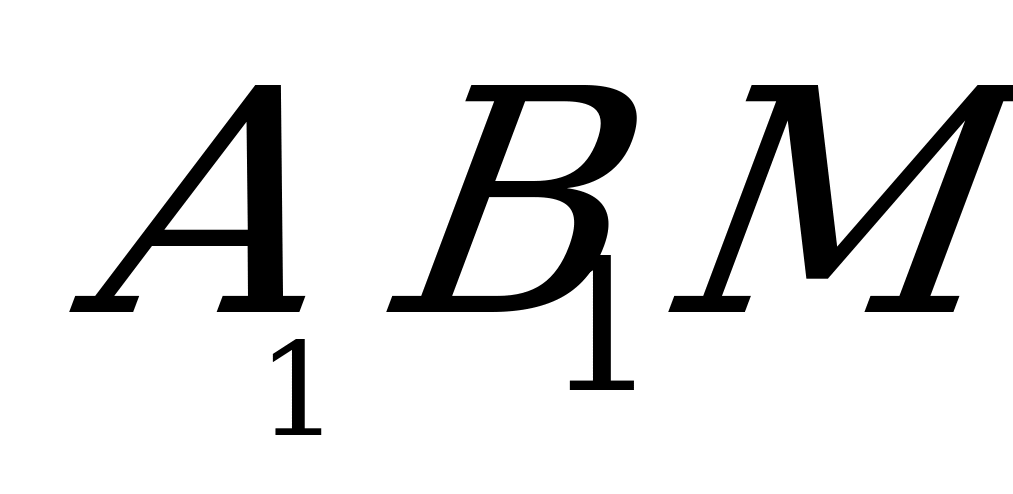 равна
равна 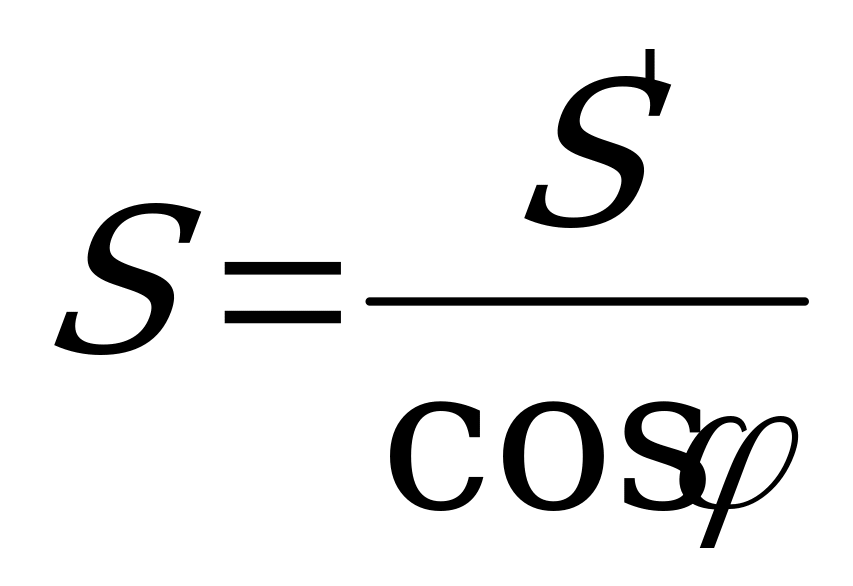 , где
, где  - площадь проекции
- площадь проекции 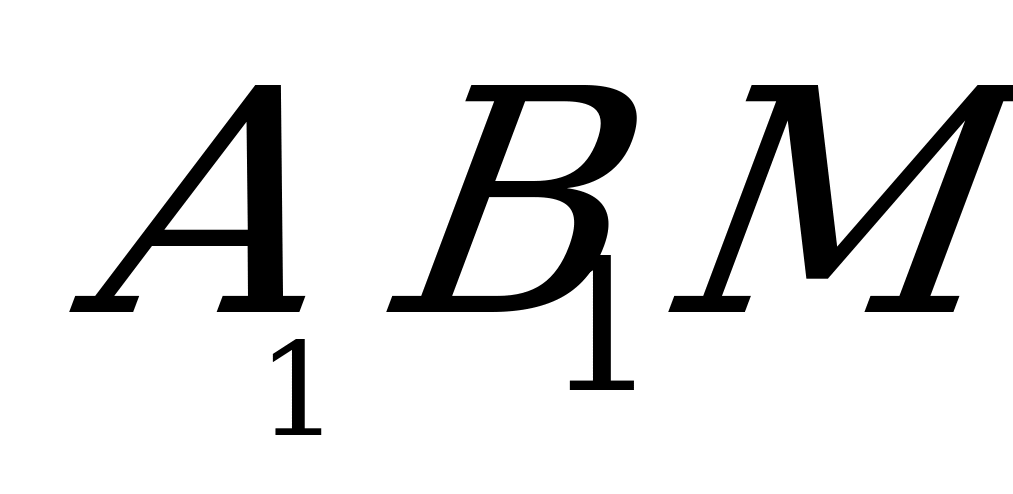 на плоскость (АВС), т.е.
на плоскость (АВС), т.е. 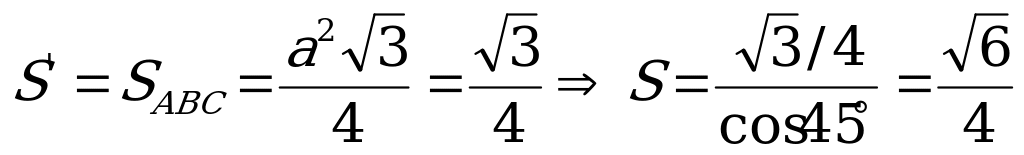 .
.
Найдём расстояние от точки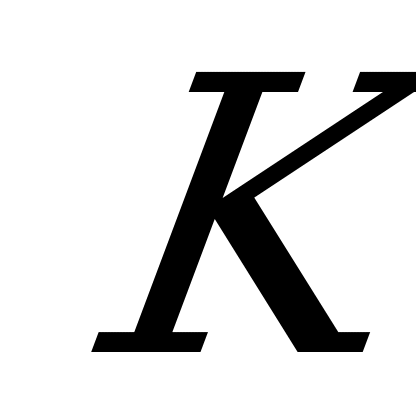 до
до . Расстояние от
. Расстояние от 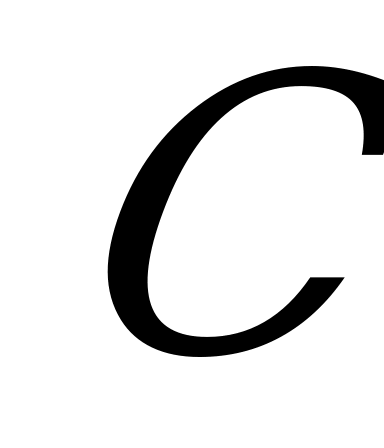 до
до  равно высоте
равно высоте  , опущенной на гипотенузу
, опущенной на гипотенузу 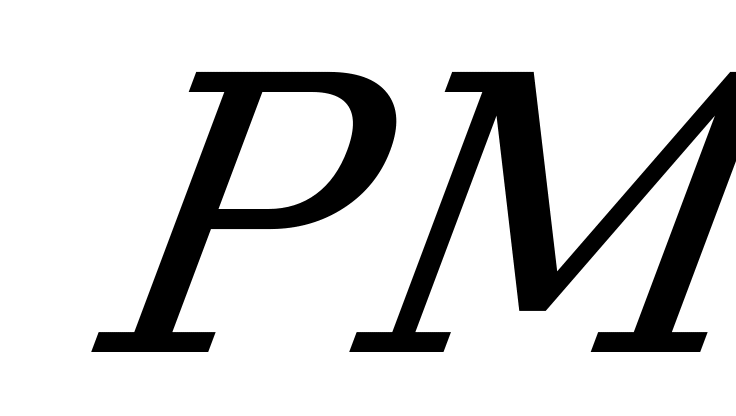 . (Действительно,
. (Действительно, 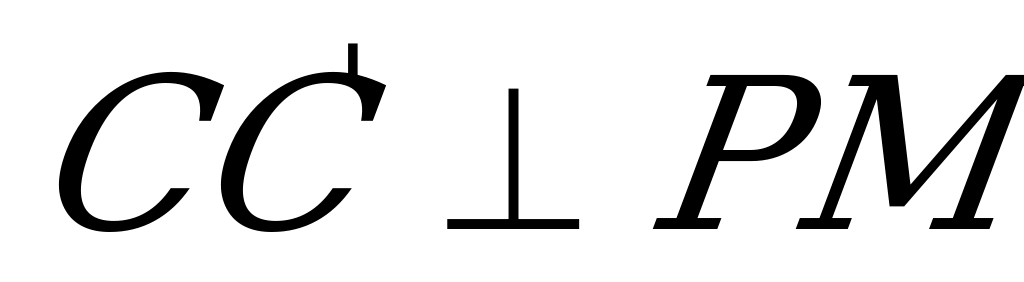 по построению и
по построению и 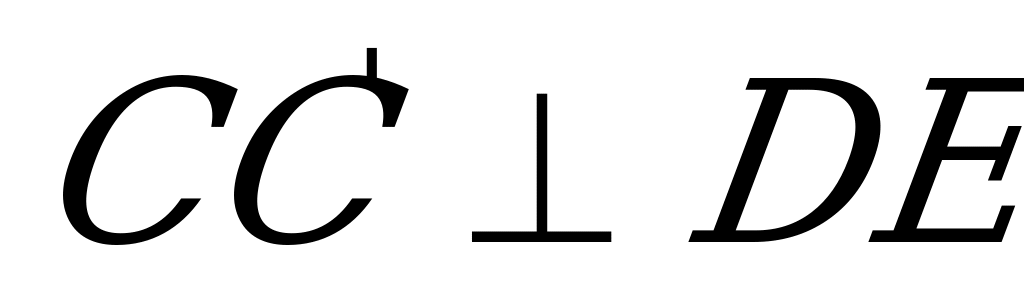 , т.к.
, т.к. 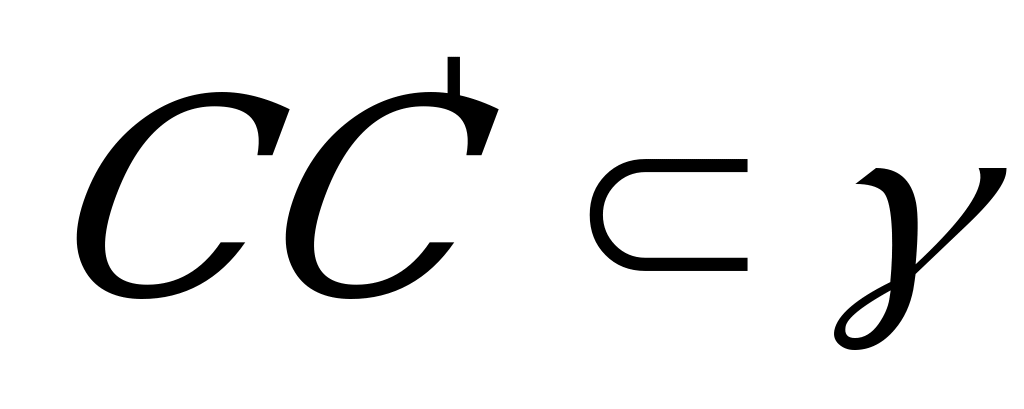 и
и 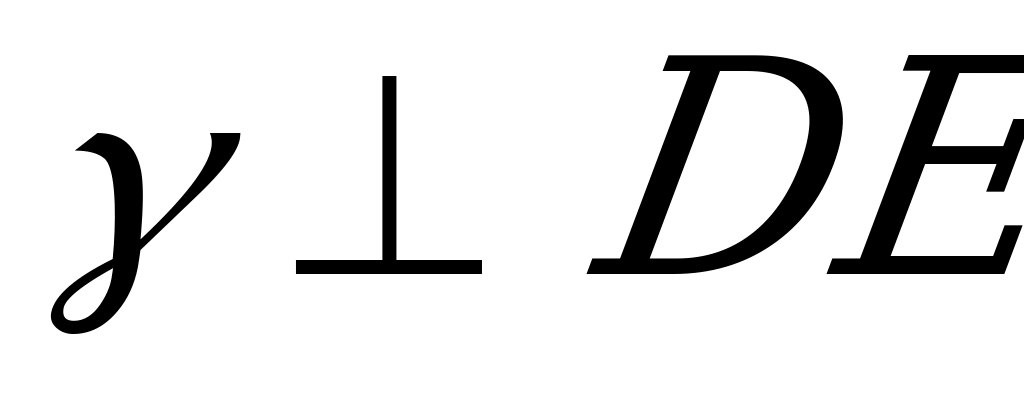 , то
, то  перпендикулярна двум пересекающимся прямым , лежащим в плоскости
перпендикулярна двум пересекающимся прямым , лежащим в плоскости  ). Значит расстояние от
). Значит расстояние от  до
до  равно
равно  . Через точку
. Через точку  проведём
проведём 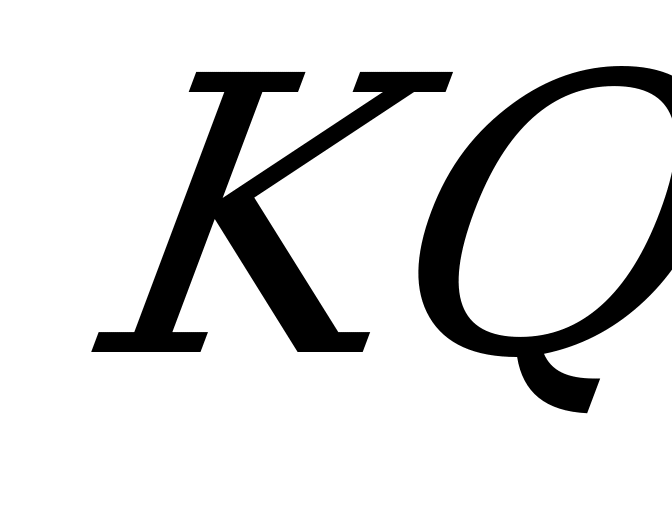 ║
║ ,
, 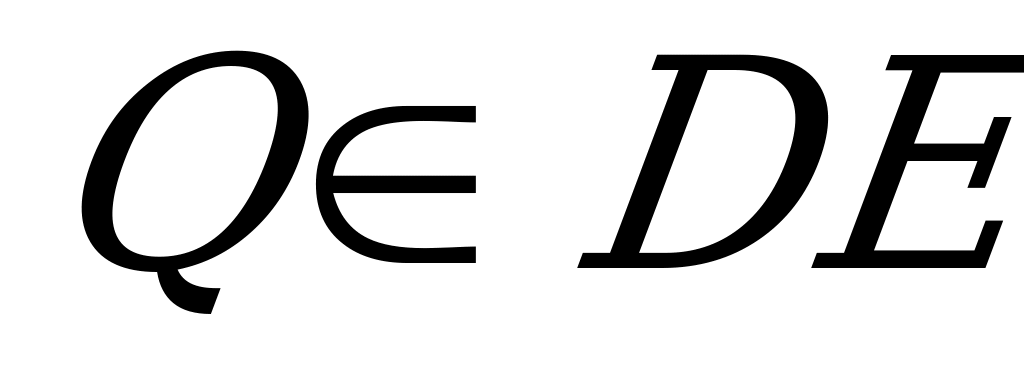 ,
,  ║
║ ,
, 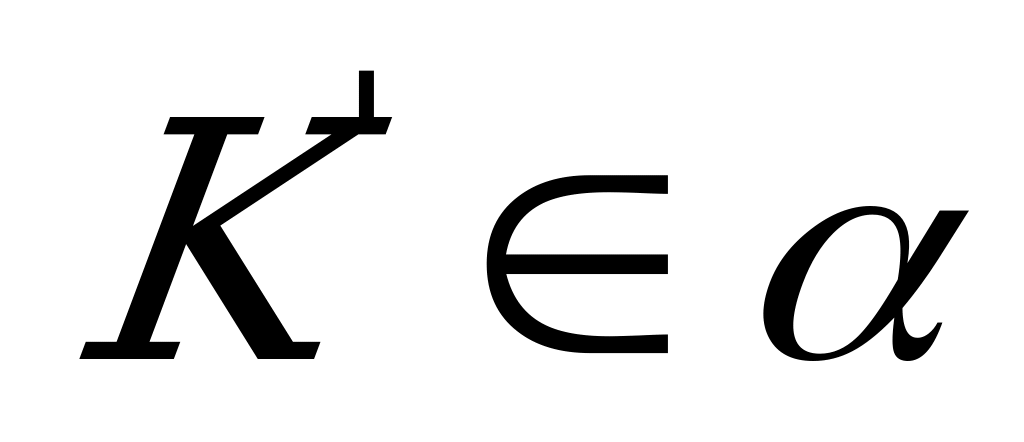 . Тогда
. Тогда 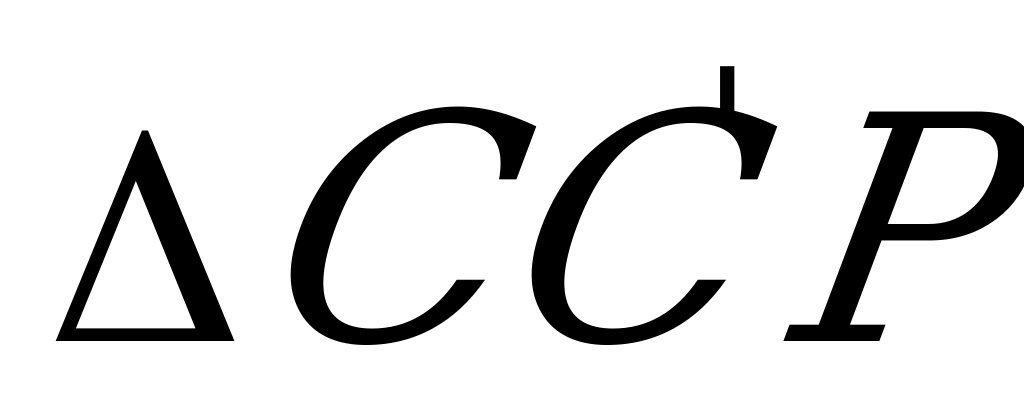 ~
~ 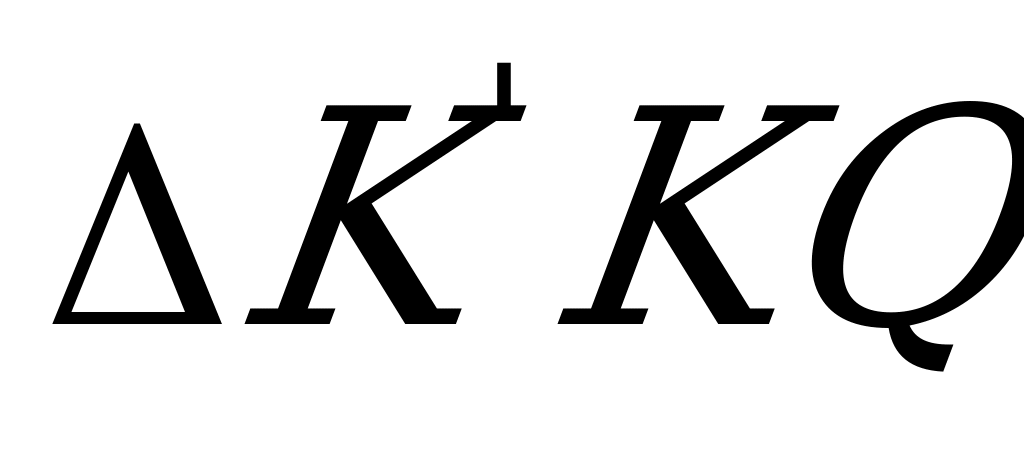 и искомое расстояние
и искомое расстояние 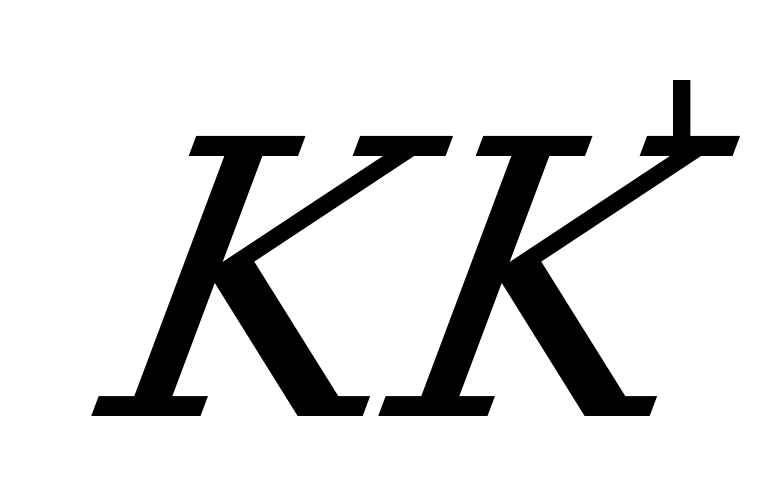 находим из условия:
находим из условия: 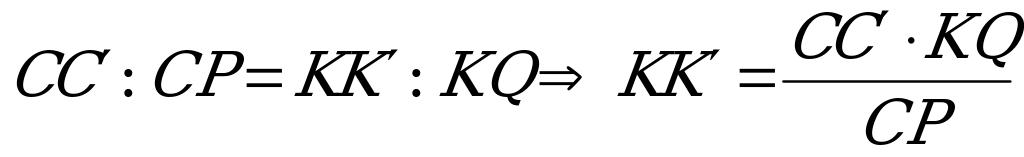 ,
, 
Ответ: 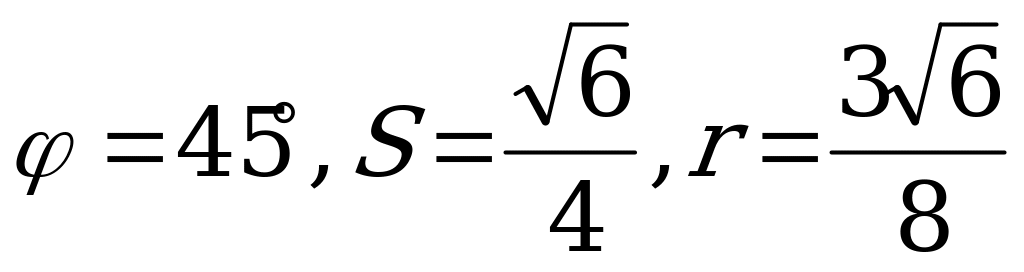 .
.
3. Высота правильной четырёхугольной пирамиды TABCD в два раза меньше стороны основания. Найдите угол  между плоскостью основания и плоскостью боковой грани и угол
между плоскостью основания и плоскостью боковой грани и угол  между диагональю основания и плоскостью боковой грани.
между диагональю основания и плоскостью боковой грани.
Р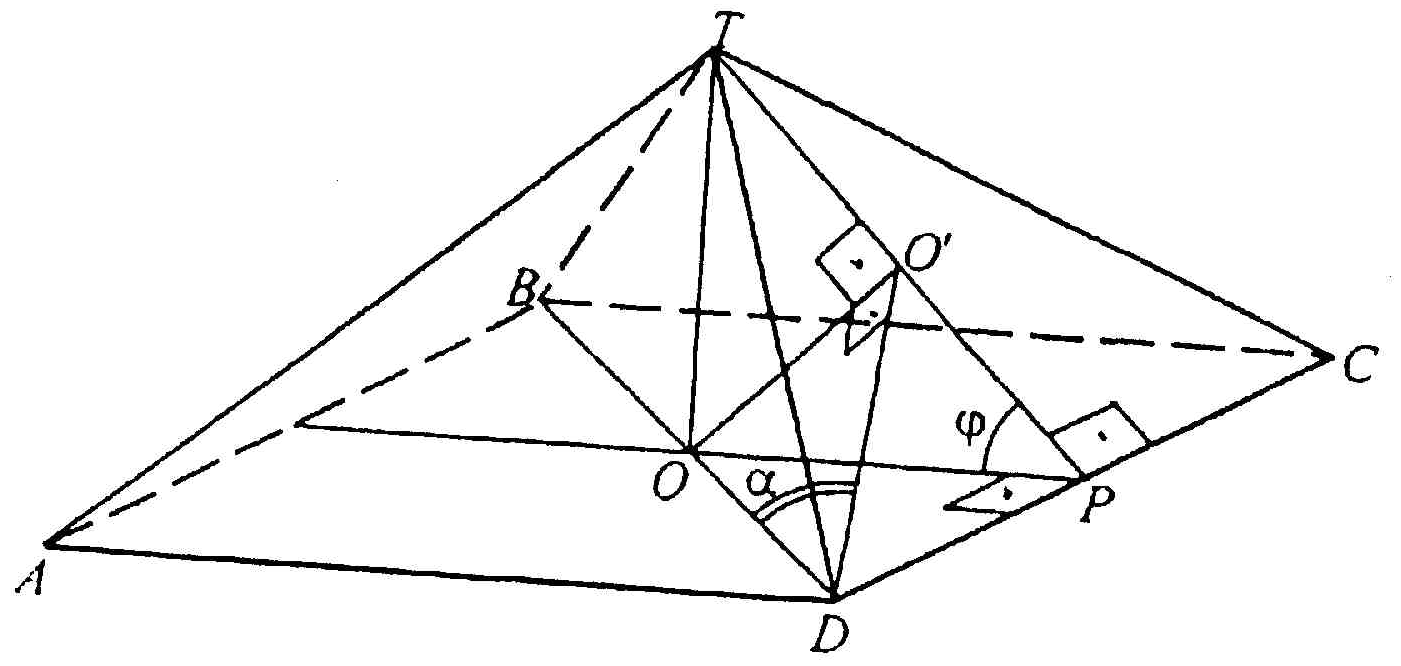 ешение. Через центр основания O проведём плоскость
ешение. Через центр основания O проведём плоскость  , перпендикулярную линии пересечения
, перпендикулярную линии пересечения  грани
грани  и плоскости основания. Для этого в плоскости (ABC) опустим перпендикуляр
и плоскости основания. Для этого в плоскости (ABC) опустим перпендикуляр  на
на 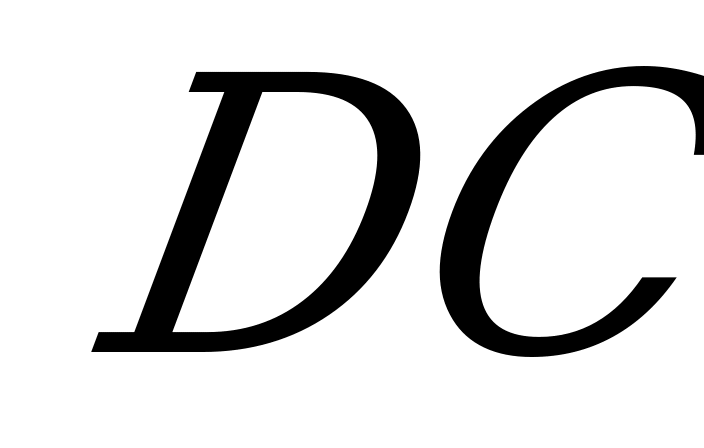 . Если AB=BC=
. Если AB=BC=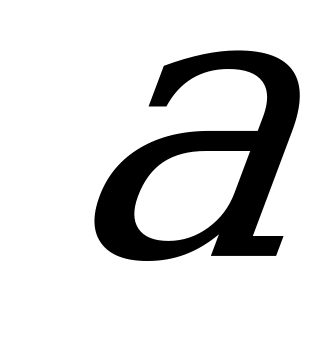 , то
, то 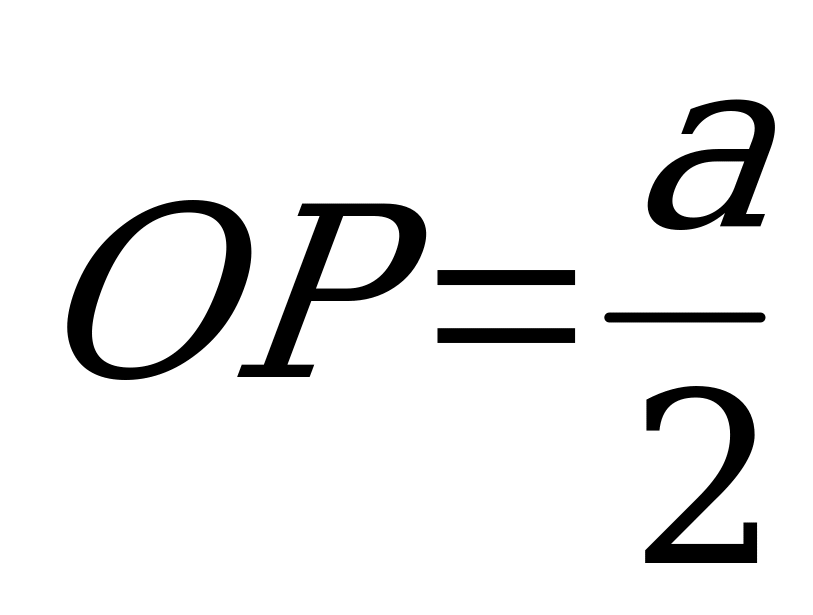 и, по условию, высота
и, по условию, высота 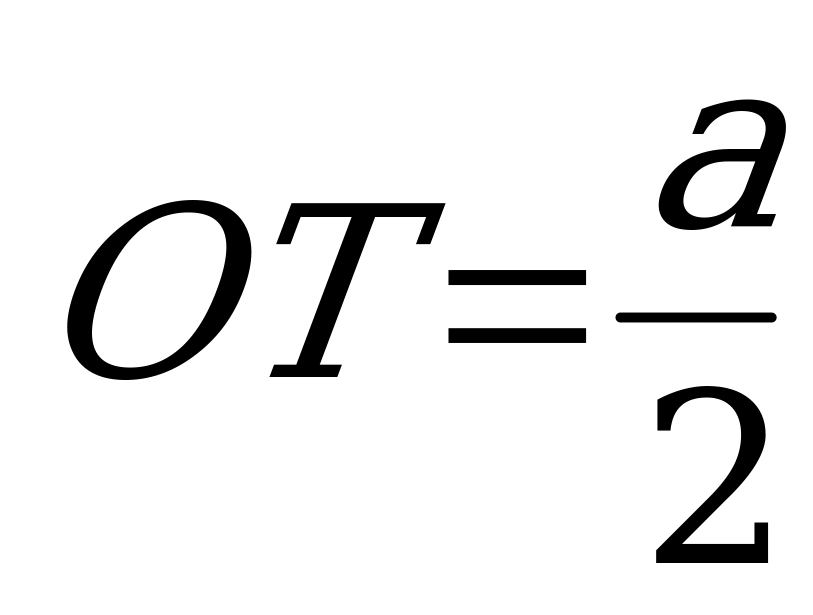 . Плоскость прямоугольного равнобедренного треугольника
. Плоскость прямоугольного равнобедренного треугольника  и является плоскостью
и является плоскостью 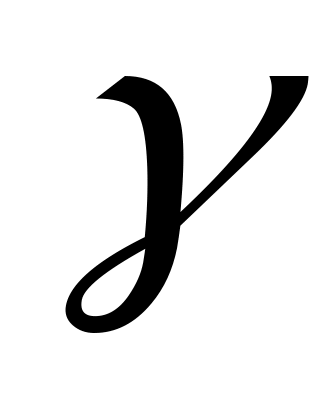 (по признаку перпендикулярности прямой и плоскости).Так как
(по признаку перпендикулярности прямой и плоскости).Так как  - ортогональная проекция
- ортогональная проекция  на плоскость основания, то
на плоскость основания, то  . Поэтому
. Поэтому 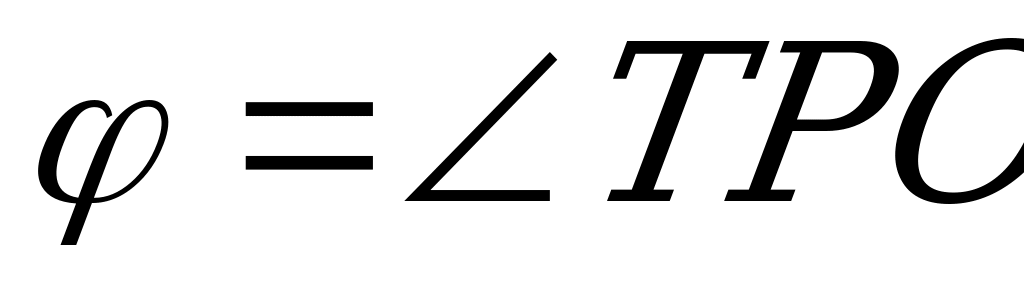 - линейный угол двугранного угла, образованного плоскостью основания и грани
- линейный угол двугранного угла, образованного плоскостью основания и грани  . Поскольку
. Поскольку  , то
, то 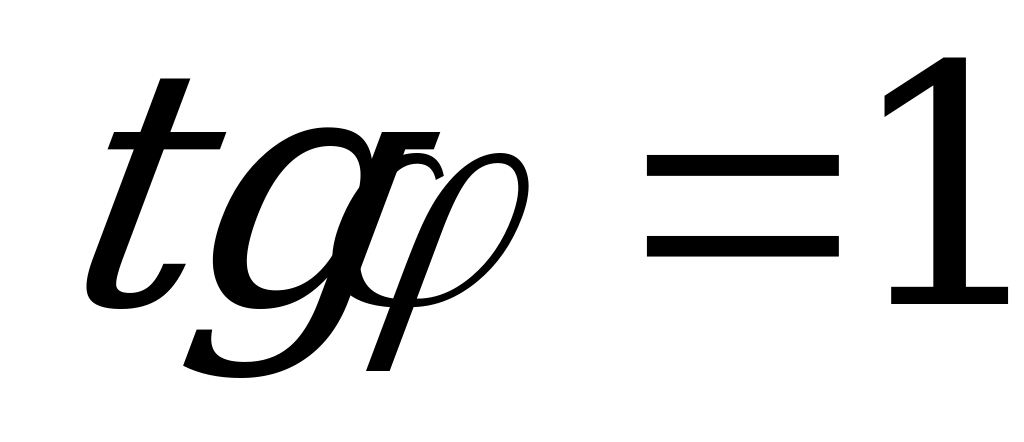 и
и 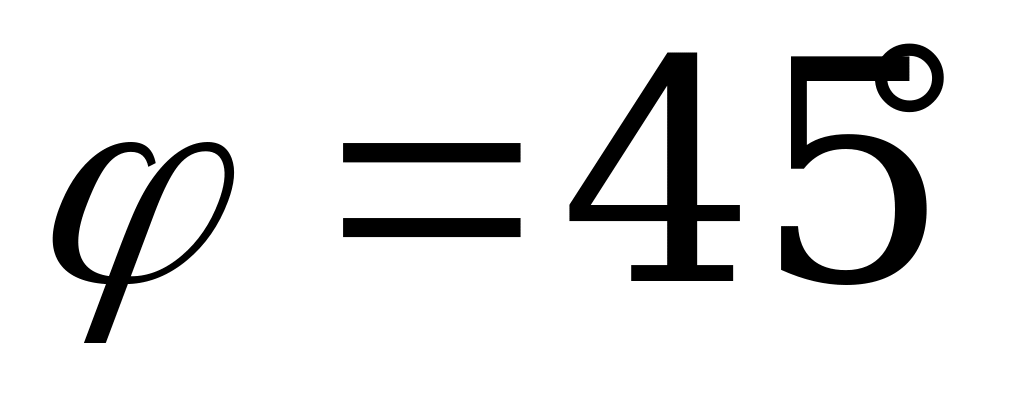 .
.
Угол между прямой  и плоскостью
и плоскостью  равен углу между прямой
равен углу между прямой  и её ортогональной проекцией на плоскость
и её ортогональной проекцией на плоскость  , Проекцией
, Проекцией  на
на  является основание
является основание  высоты
высоты  прямоугольного треугольника
прямоугольного треугольника  , опущенной на гипотенузу
, опущенной на гипотенузу  . Действительно,
. Действительно, 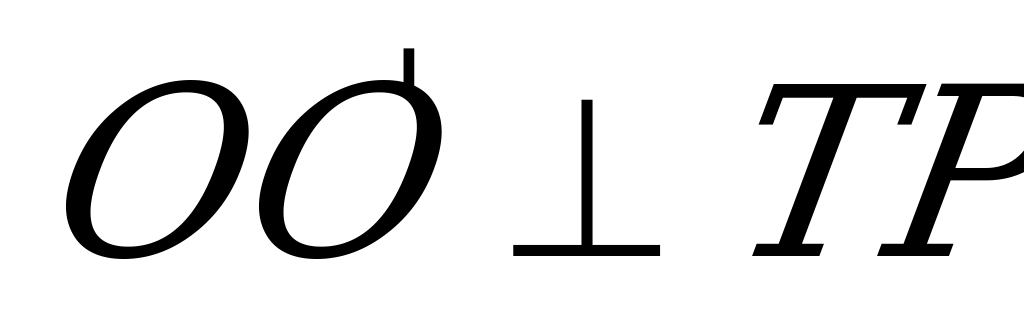 по построению и
по построению и 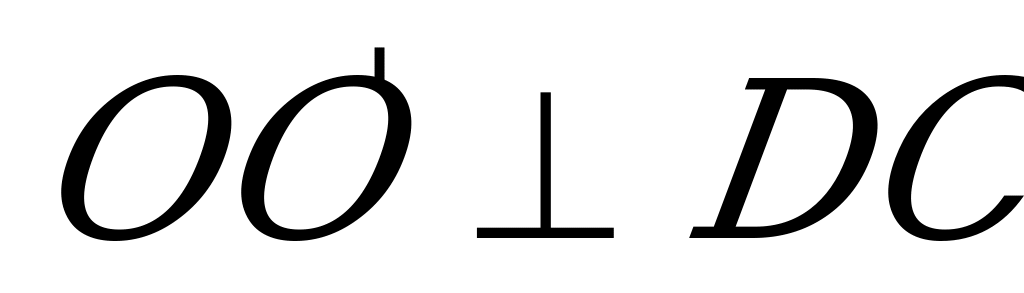 , т.к.
, т.к. 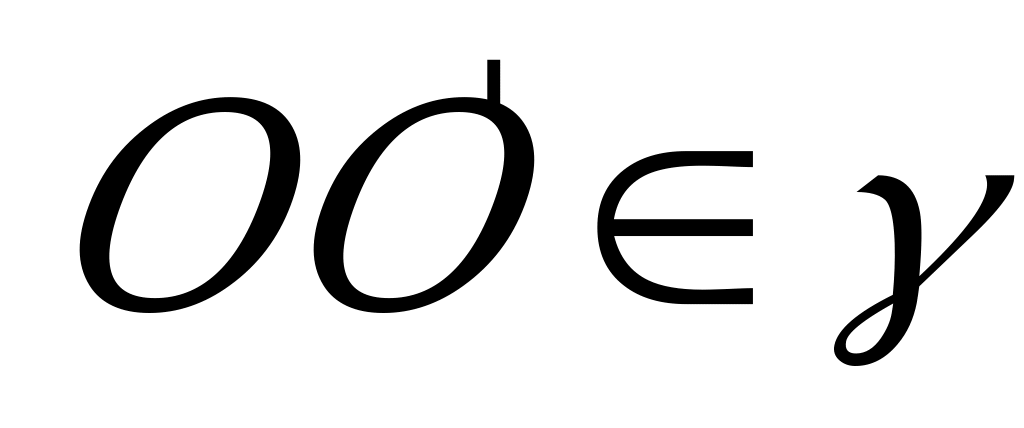 и
и 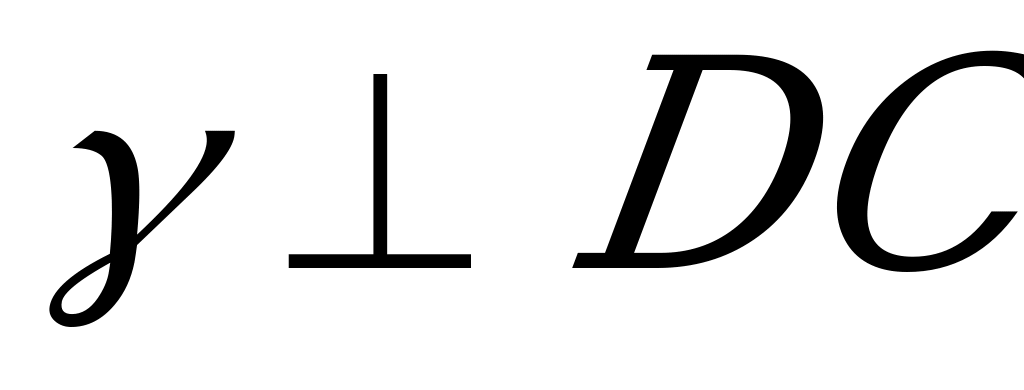 . Итак
. Итак  перпендикулярно двум пересекающимся прямым
перпендикулярно двум пересекающимся прямым  и
и  грани
грани  , поэтому
, поэтому  . Следовательно, ортогональной проекцией
. Следовательно, ортогональной проекцией  на плоскость
на плоскость  является прямая
является прямая  и угол
и угол  между
между  и
и 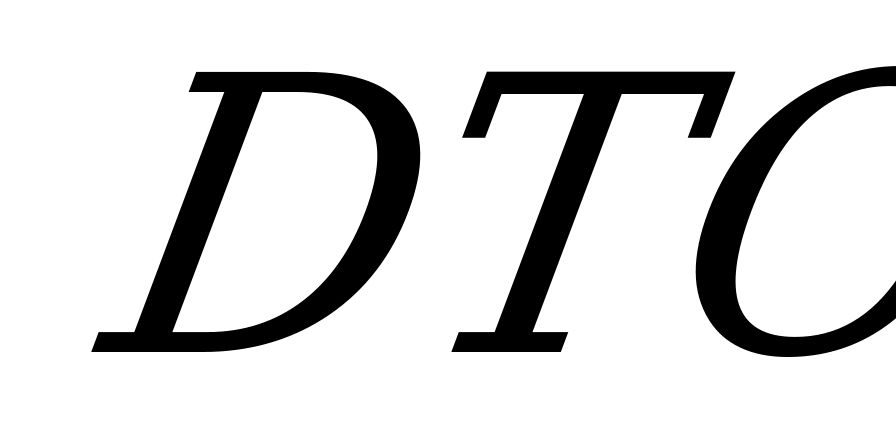 равен
равен  .Т.к.
.Т.к. 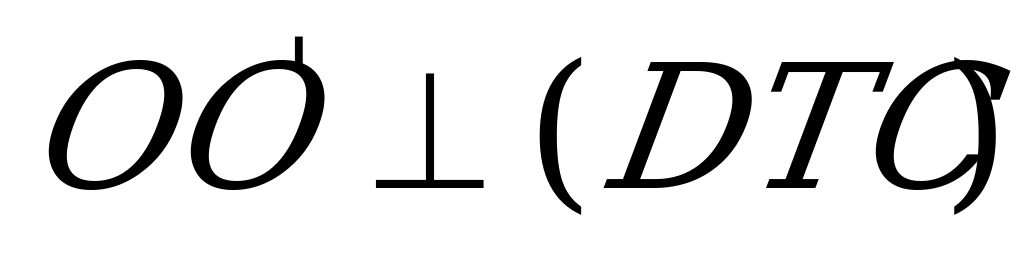 , то
, то 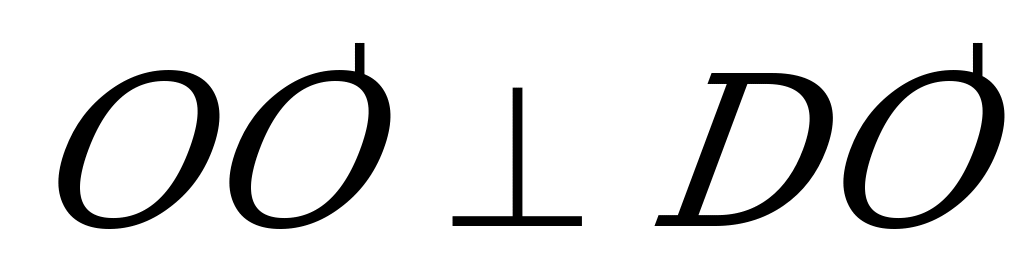 и , следовательно,
и , следовательно, 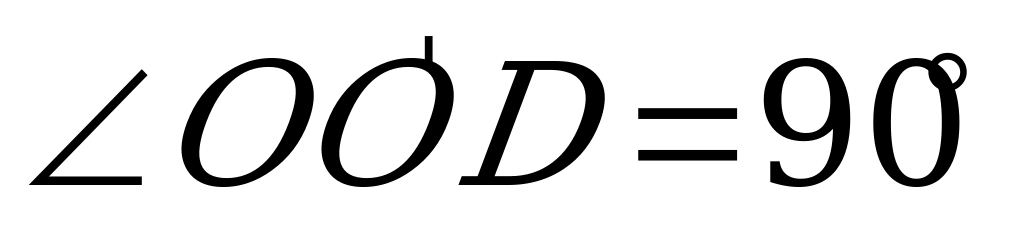 ,
, 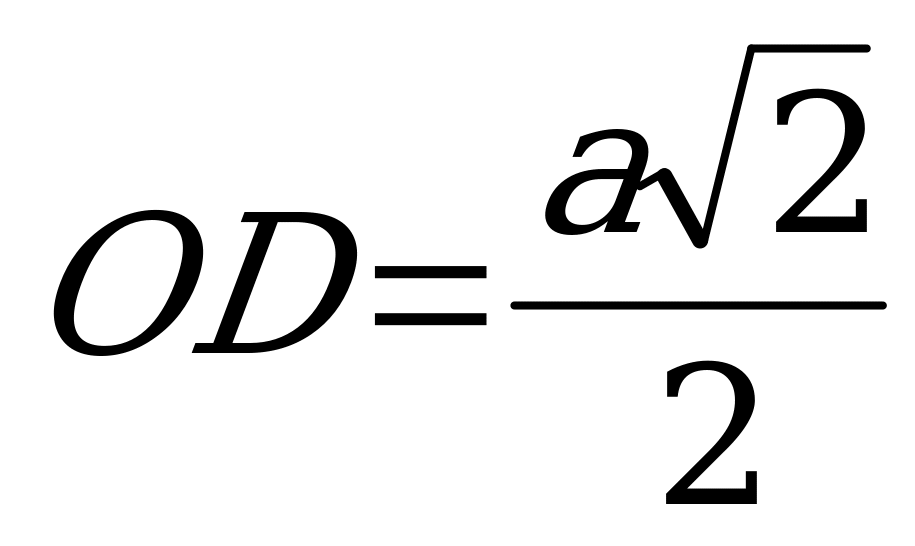 , откуда
, откуда 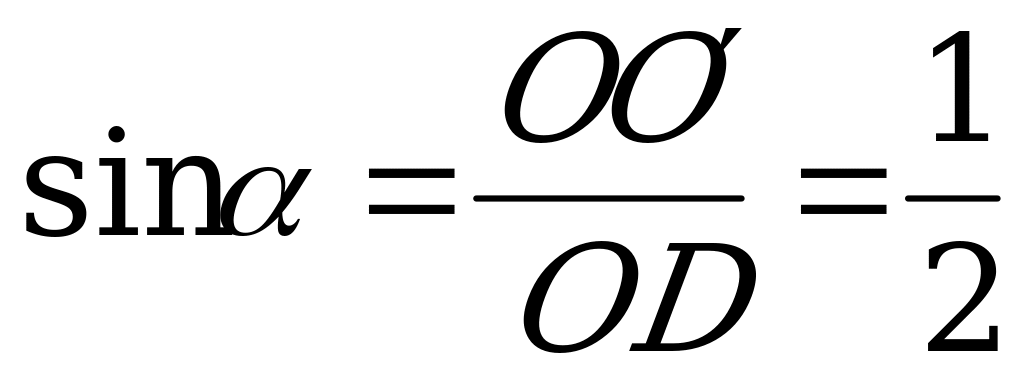 , значит
, значит  .
.
Ответ: 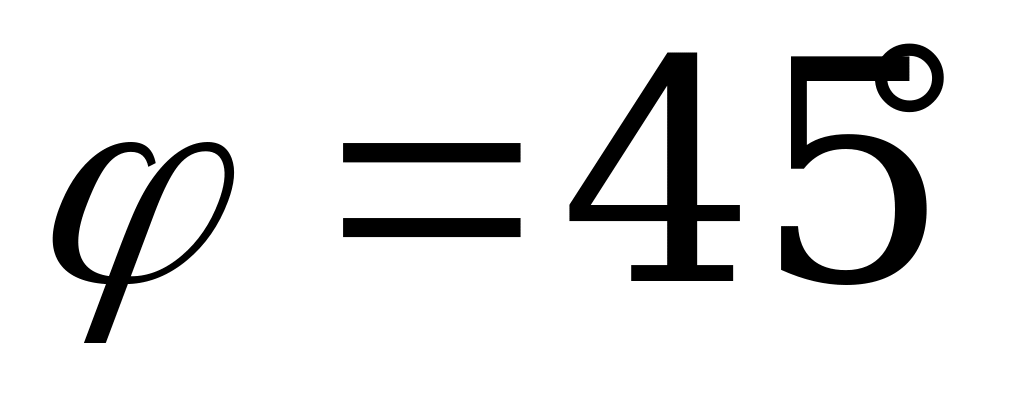 ,
, 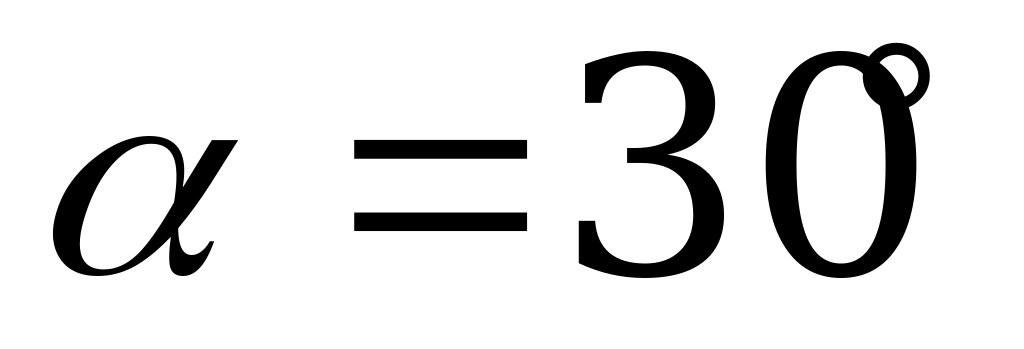 .
.
6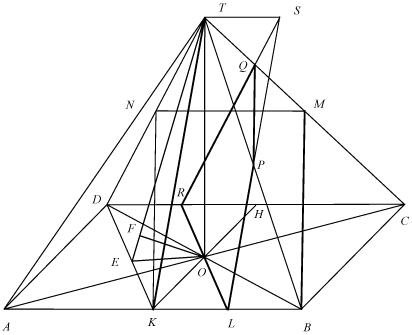 .Найдите площадь сечения правильной четырехугольной пирамиды TABCD плоскостью, проходящей через центр ее основания параллельно апофеме TK боковой грани TAB и медиане BM боковой грани TBC, если сторона основания равна 8, а
.Найдите площадь сечения правильной четырехугольной пирамиды TABCD плоскостью, проходящей через центр ее основания параллельно апофеме TK боковой грани TAB и медиане BM боковой грани TBC, если сторона основания равна 8, а
расстояние от вершины пирамиды T до секущей плоскости равно r=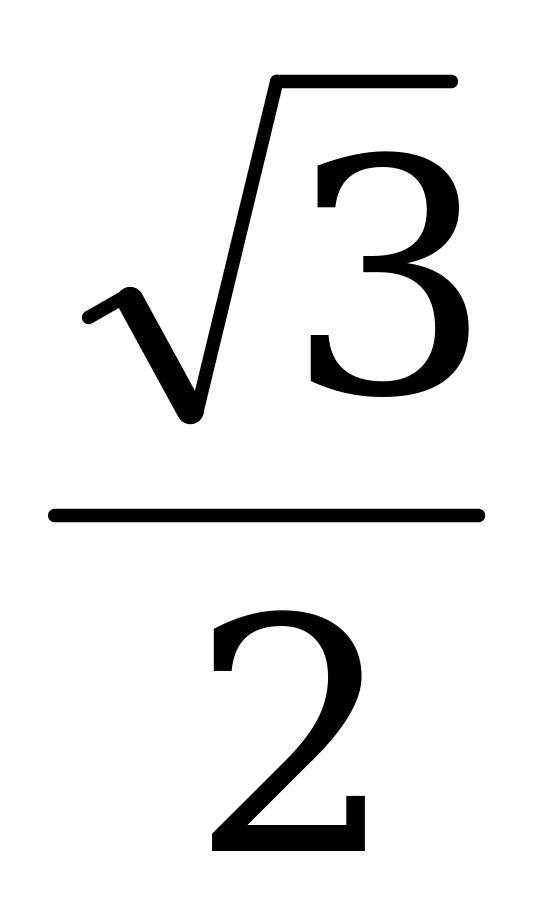 .
.
РЕШЕНИЕ:
Построим сечение.
Проведем 
 ,тогда
,тогда  и
и 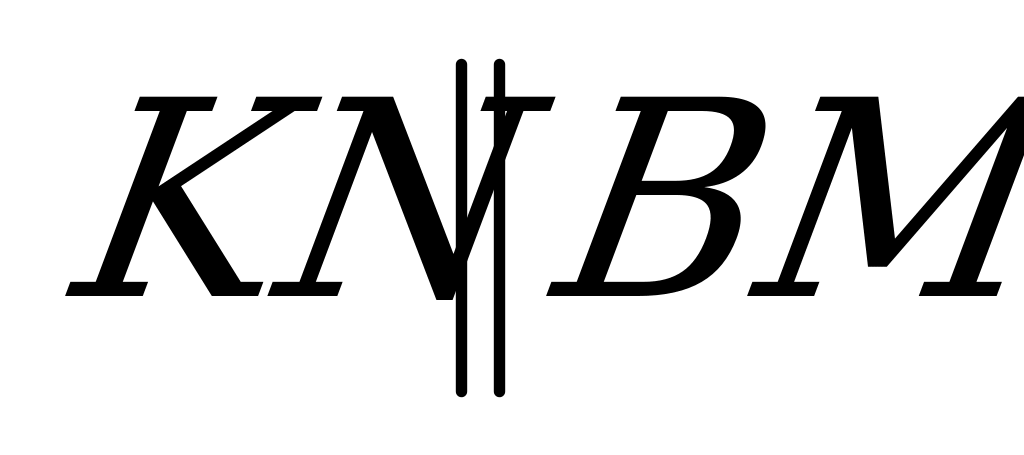 .
.
Плоскость TKD проходит через апофему TK и параллельна медиане ВM. Затем выполним параллельный перенос плоскости TKD в направлении АВ на величину  (KL=LB=
(KL=LB=
Полученная плоскость SLR проходит через центр основания пирамиды, параллельна апофеме TK и медиане ВM, т.е. является заданной в условии секущей плоскостью.
Если 
 , то четырехугольник LPQR - искомое сечение.
, то четырехугольник LPQR - искомое сечение.
Из подобия треугольников TSP и BLP следует SP = SL/2, а из подобия треугольников
TSQ и CRQ - SQ = SR/4, так как TS = KL = 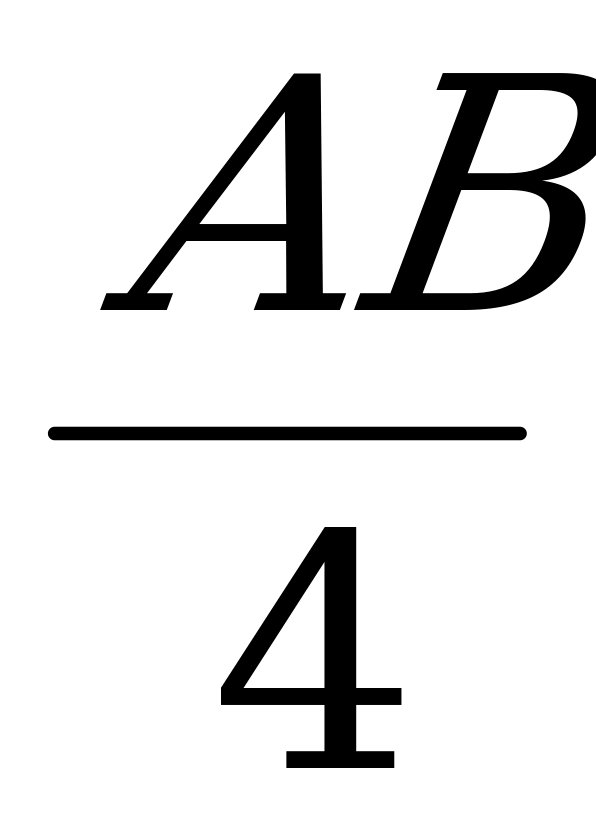 , а CR =
, а CR = 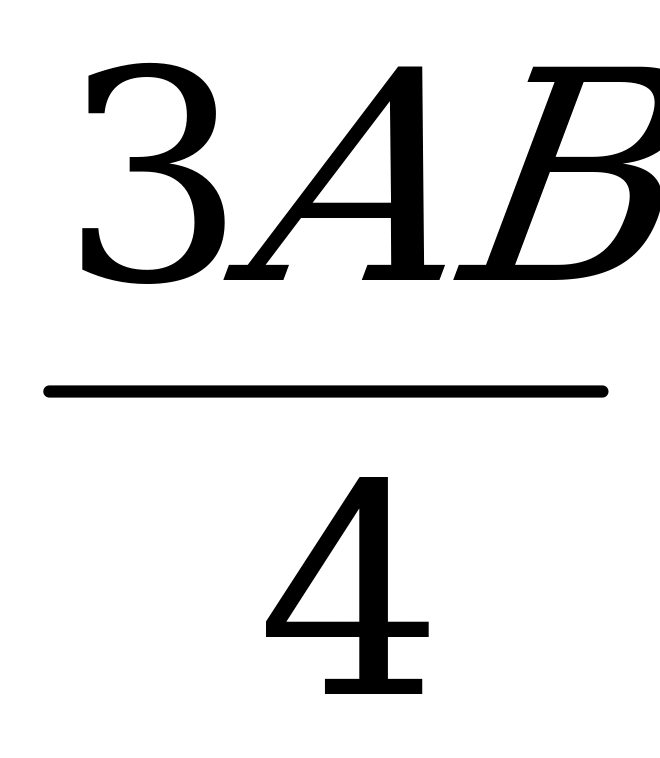 .
.
Тогда площадь треугольника PSQ равна:
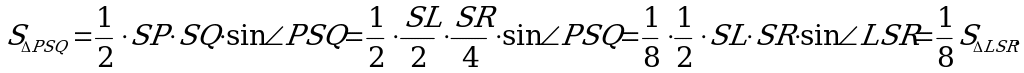
Следовательно, площадь сечения LPQR равна 7/8 площади треугольника LSR, или
равного ему треугольника KTD. Проведем  и
и . Длина OF равна расстоянию от центра основания пирамиды до плоскости TKD и равна заданному в условии задачи расстоянию от вершины пирамиды до секущей плоскости SLR.
. Длина OF равна расстоянию от центра основания пирамиды до плоскости TKD и равна заданному в условии задачи расстоянию от вершины пирамиды до секущей плоскости SLR.
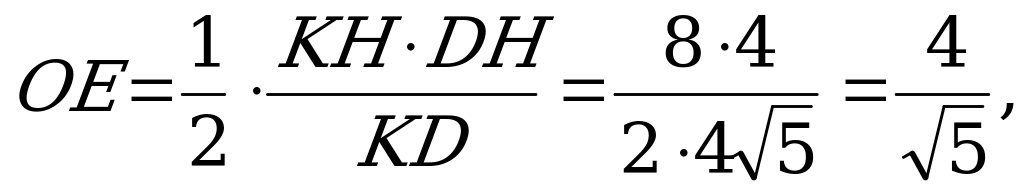
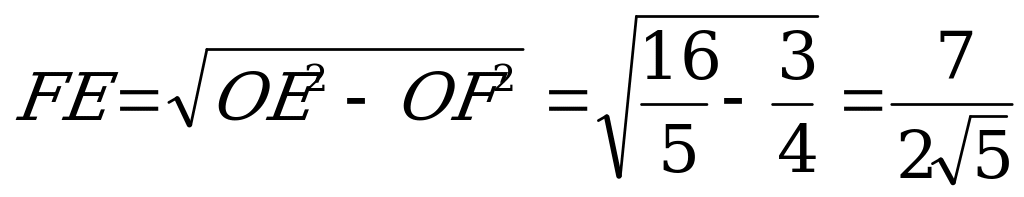
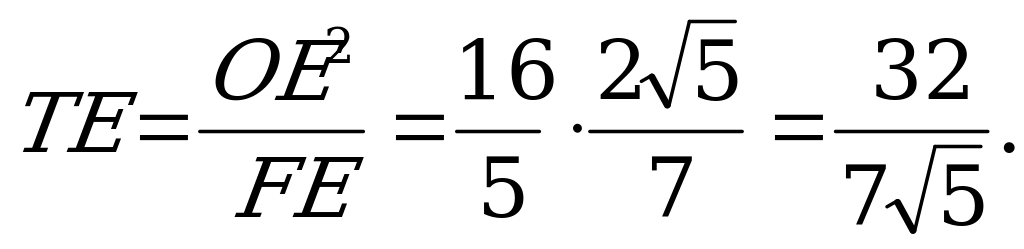
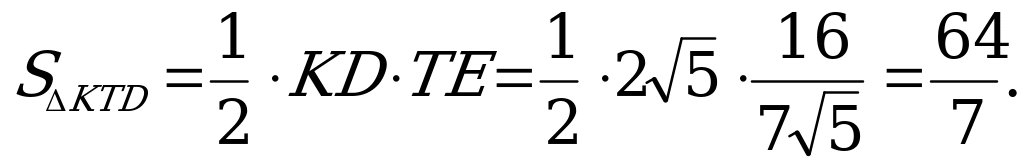
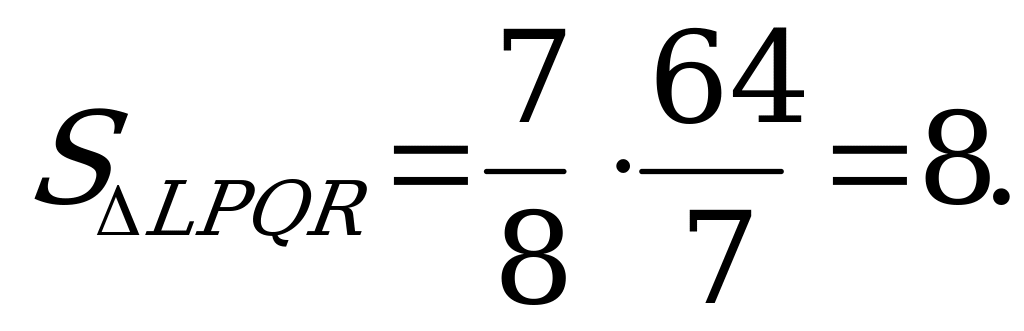
ОТВЕТ: 8.
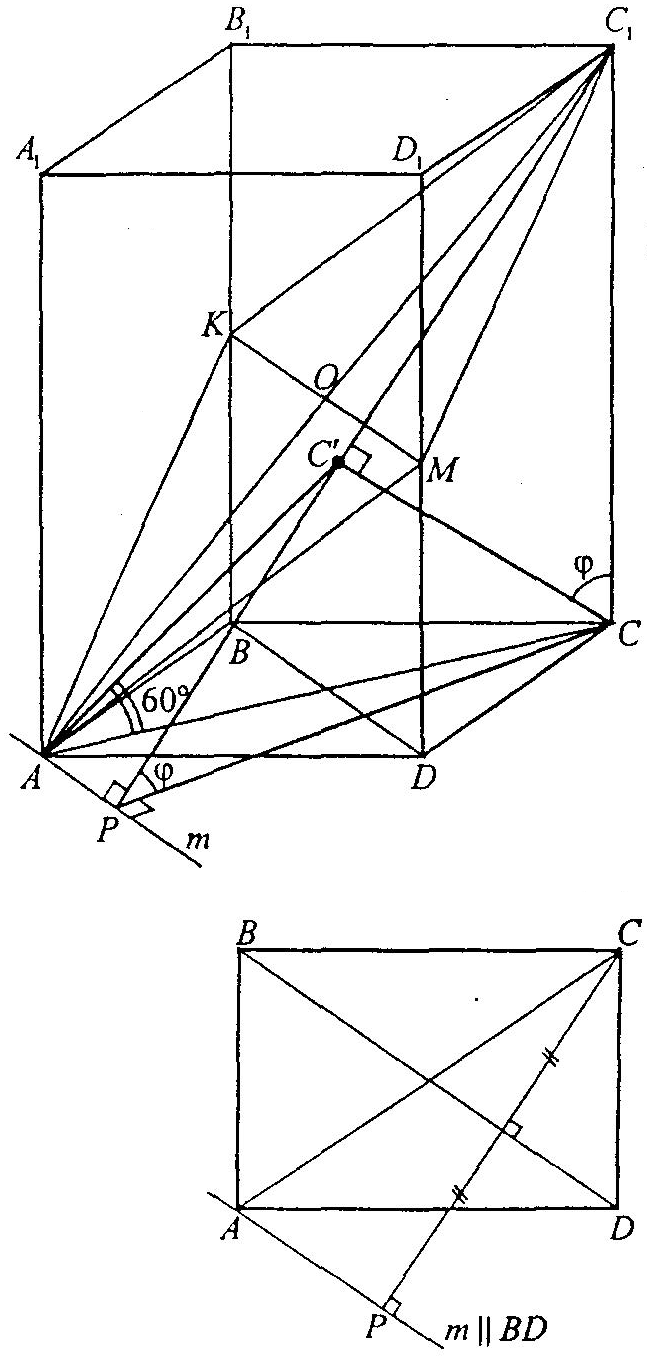
7. В прямоугольном параллелепипеде через диагональ
через диагональ 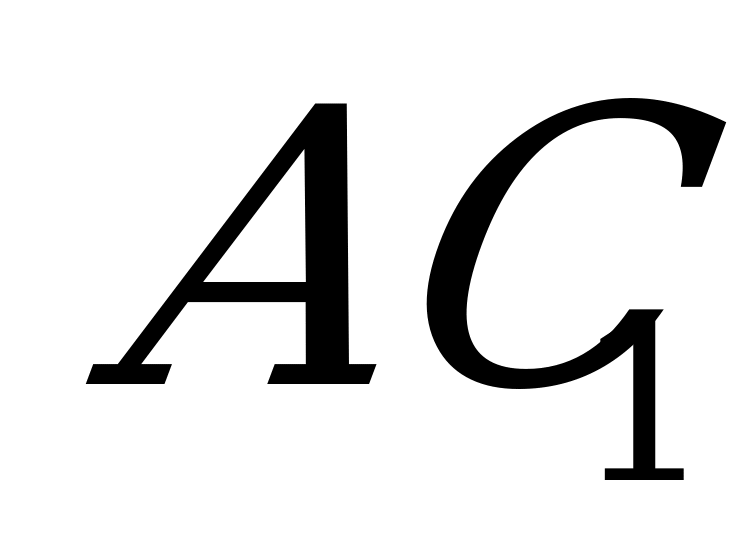 проведено сечение, параллельное диагонали основания
проведено сечение, параллельное диагонали основания 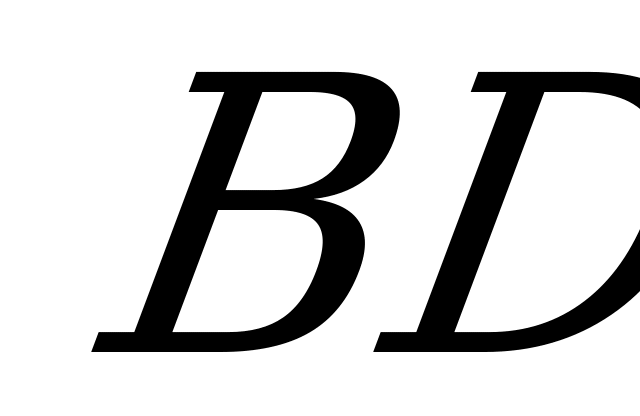 и образующее с диагональю основания
и образующее с диагональю основания 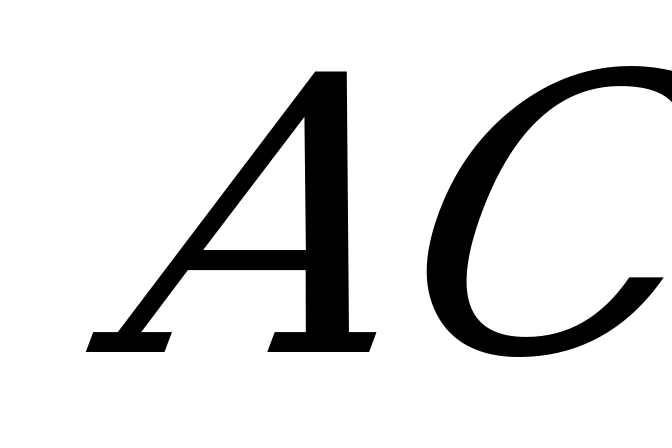 угол
угол 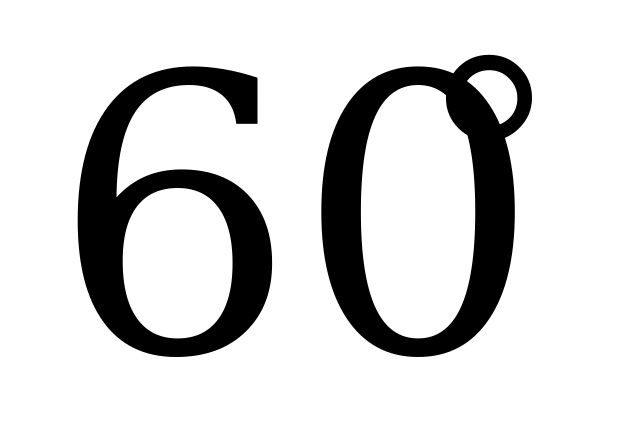 . Найдите площадь поверхности сферы, описанной вокруг параллелепипеда, если его высота в два раза больше диагонали основания, а площадь сечения равна
. Найдите площадь поверхности сферы, описанной вокруг параллелепипеда, если его высота в два раза больше диагонали основания, а площадь сечения равна 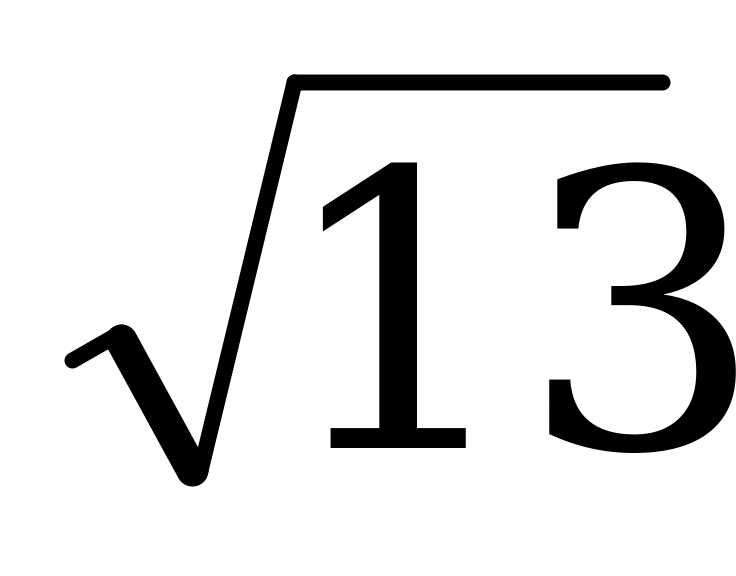 .
.
Решение:
Данное сечение проходит через середины 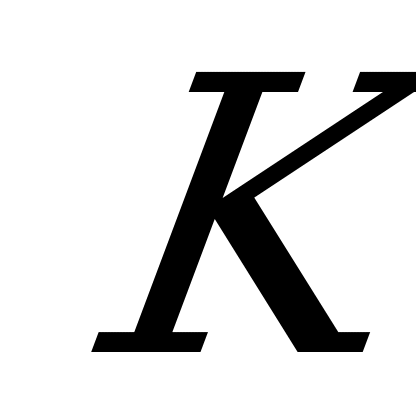 и
и 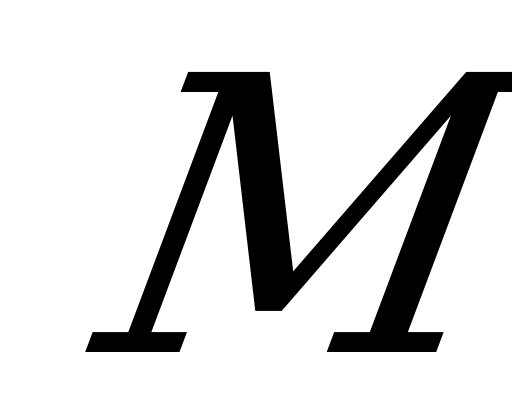 рёбер
рёбер 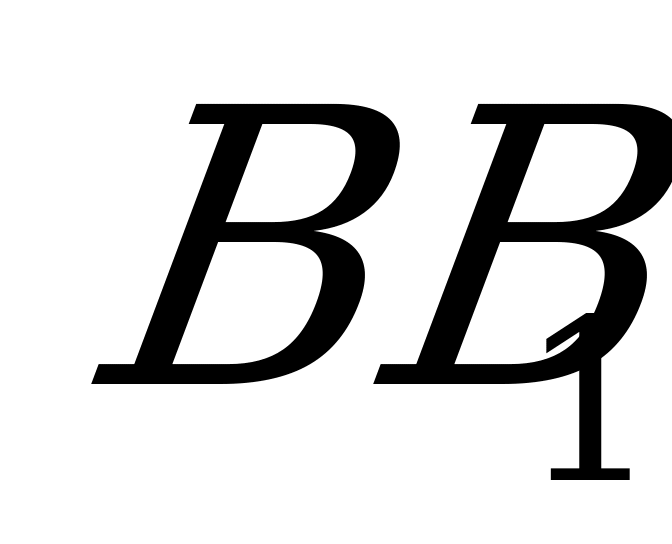 и
и 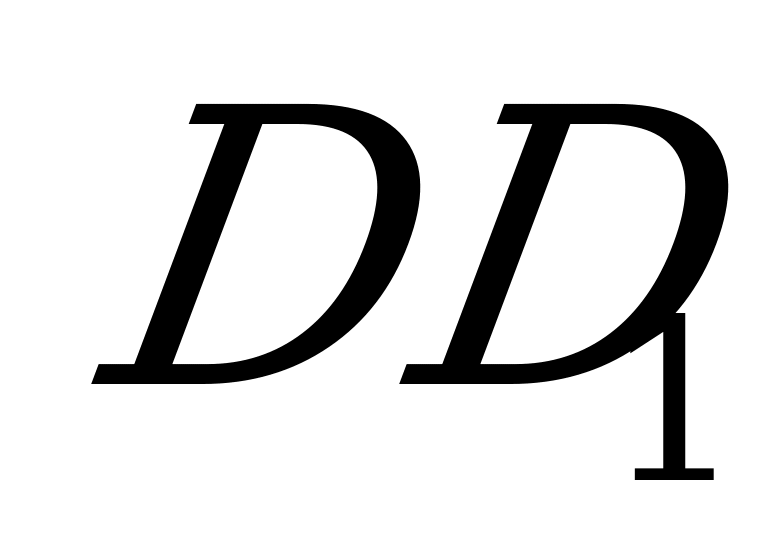 , соответственно, т.к. прямая
, соответственно, т.к. прямая  пересекается с диагональю
пересекается с диагональю 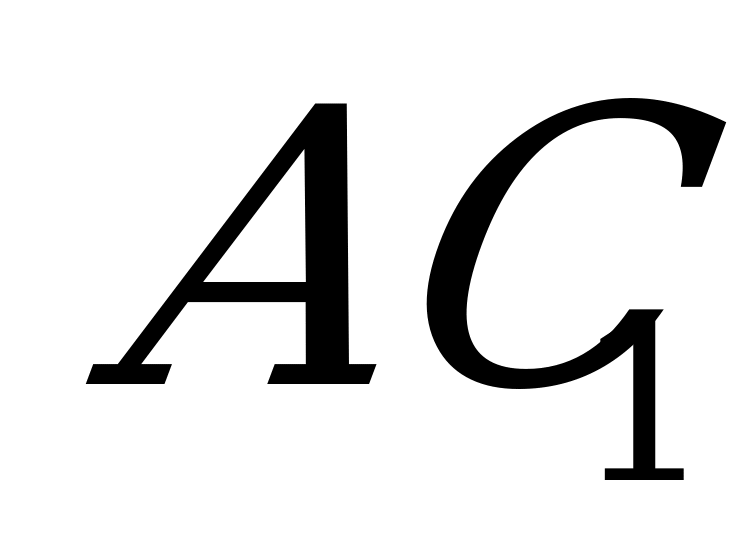 в центре
в центре  параллелепипеда и
параллелепипеда и  ║
║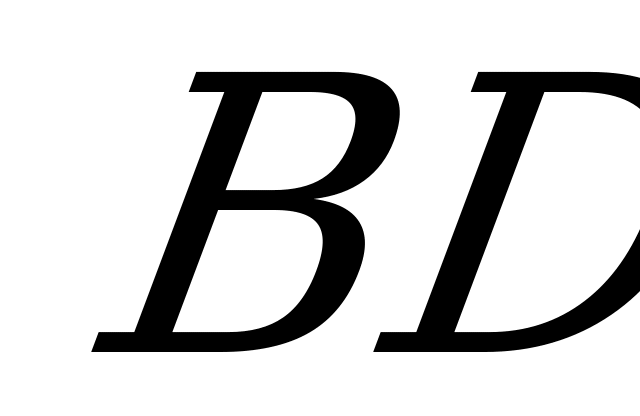 .
.
Пусть 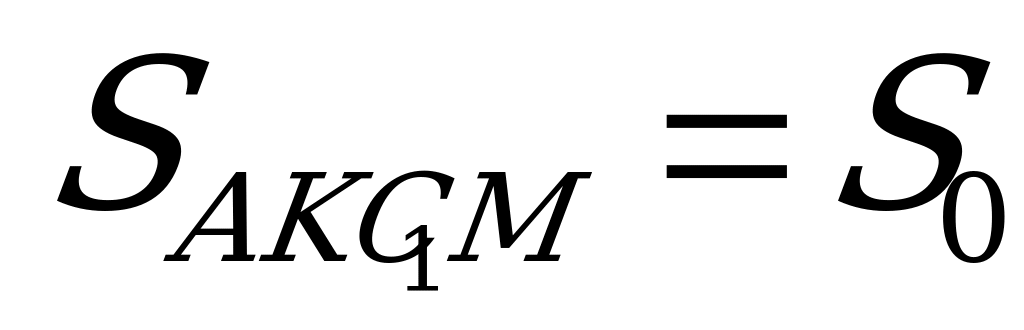 . Тогда
. Тогда 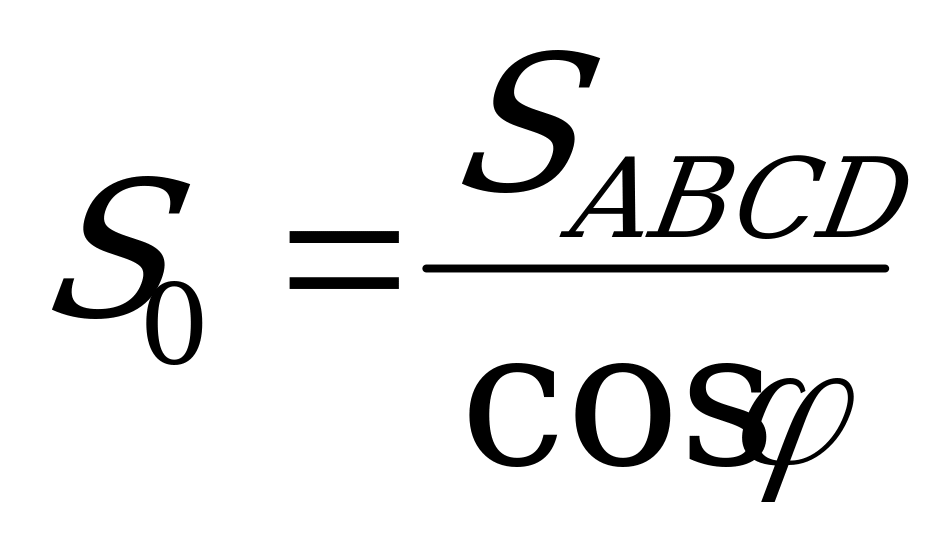 , где
, где 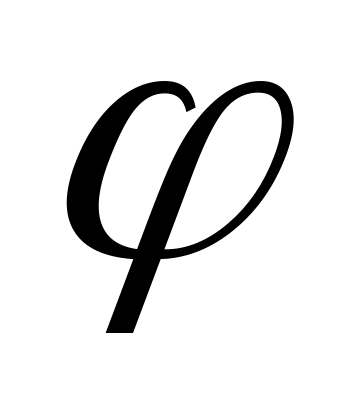 - угол между плоскостью сечения и плоскостьюABC.Проведём через точку А прямую m║ BD.Тогда
- угол между плоскостью сечения и плоскостьюABC.Проведём через точку А прямую m║ BD.Тогда 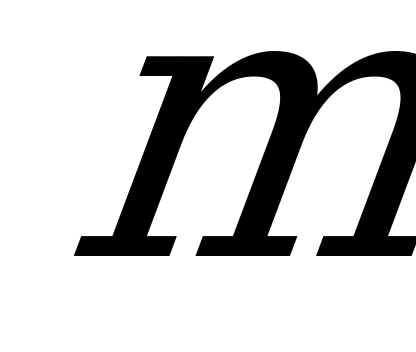 -линия пересечения плоскостей АКС1 и АВС. Из точки
-линия пересечения плоскостей АКС1 и АВС. Из точки 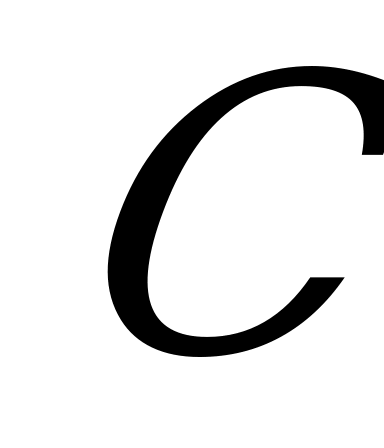 опустим перпендикуляр
опустим перпендикуляр  на
на 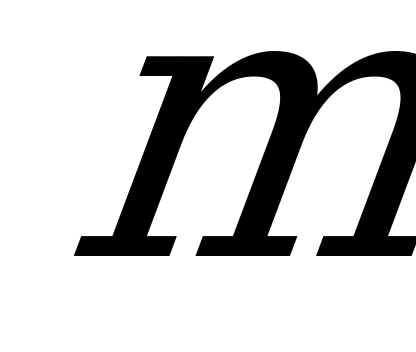 . Тогда
. Тогда 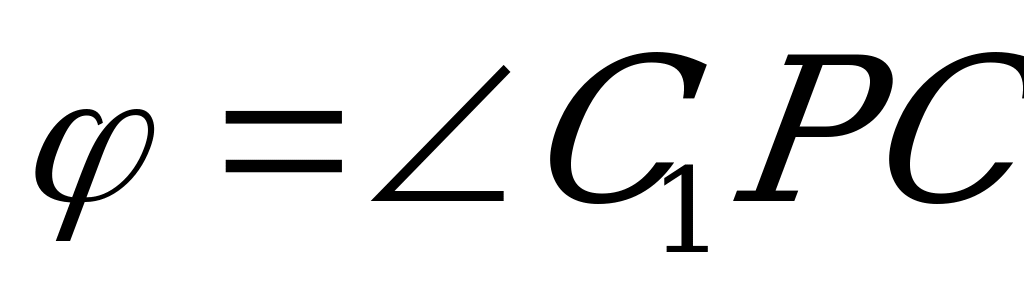 .
.
Поскольку плоскость С1РС перпендикулярна 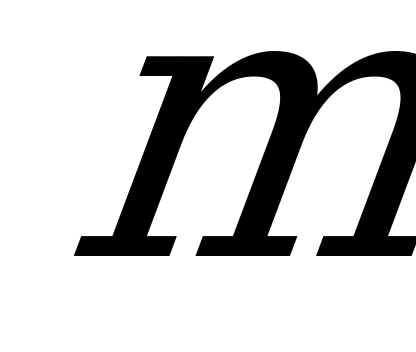 , то перпендикуляр
, то перпендикуляр  , опущенный из вершины прямого угла треугольника С1СР на гипотенузу
, опущенный из вершины прямого угла треугольника С1СР на гипотенузу  является перпендикуляром к плоскости АКС1 и
является перпендикуляром к плоскости АКС1 и  - ортогональная проекция точки
- ортогональная проекция точки 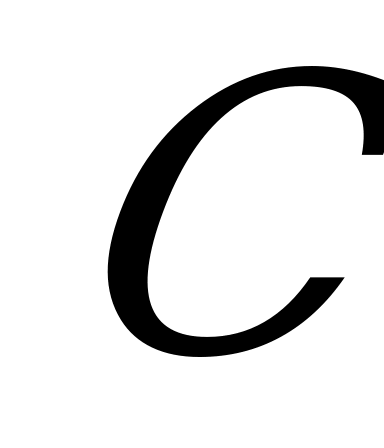 на эту плоскость. Поэтому
на эту плоскость. Поэтому  является углом между диагональю
является углом между диагональю 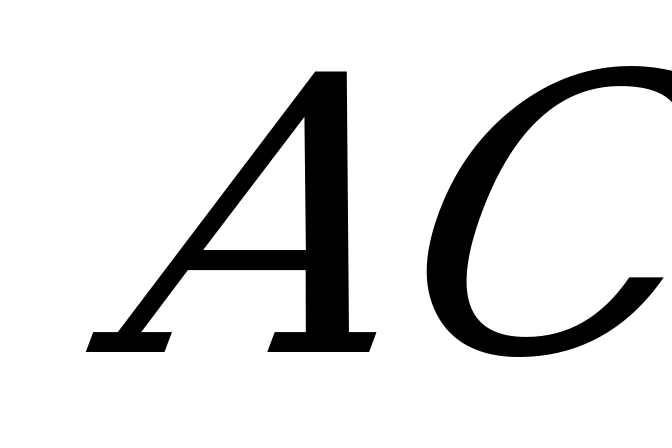 и плоскостью АКС1, т.е.
и плоскостью АКС1, т.е. 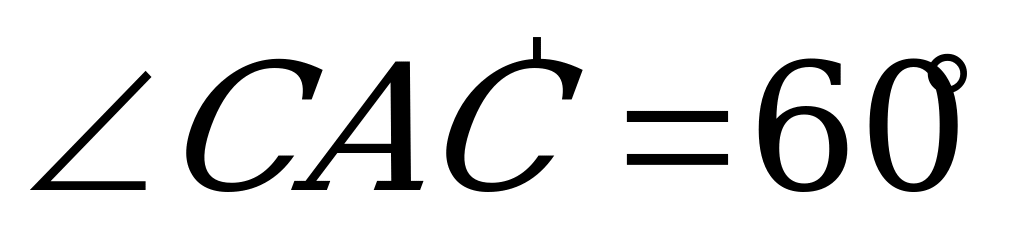 .
.
Пусть АС= d .Тогда из 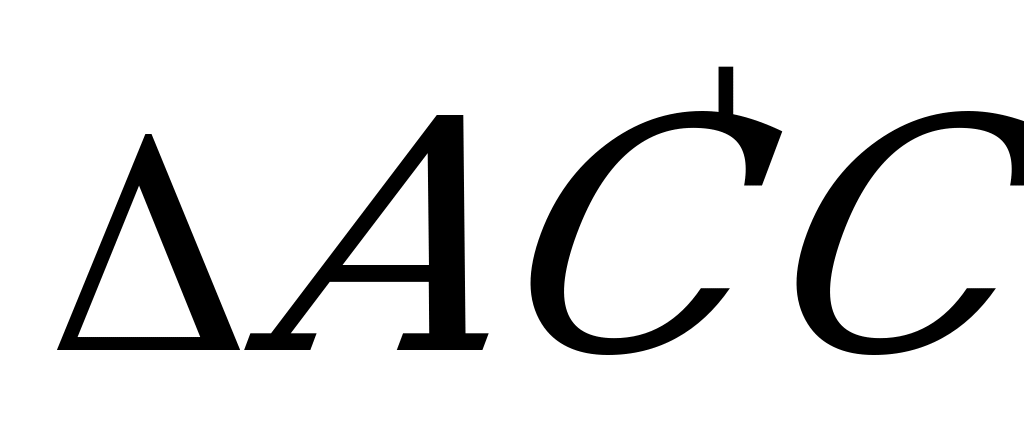 имеем:
имеем: 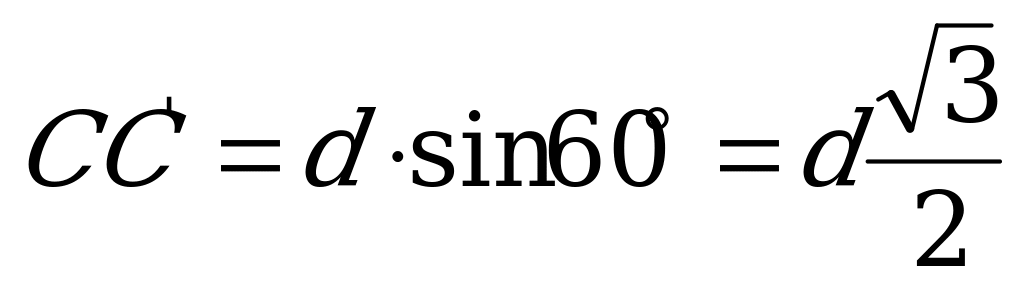 . Поскольку по условию
. Поскольку по условию 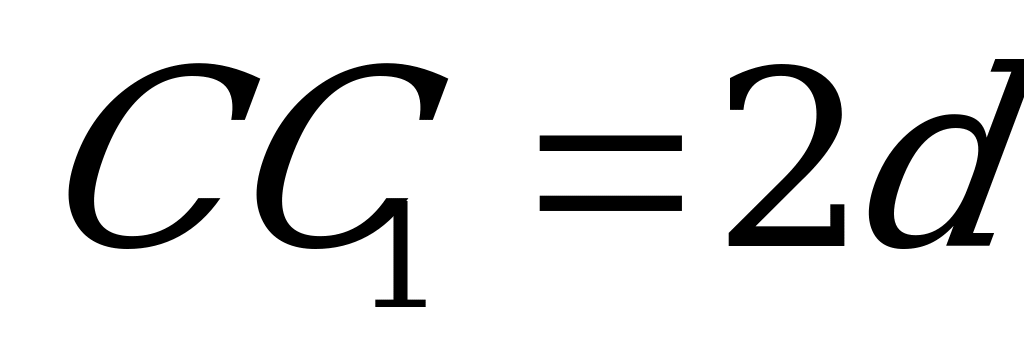 , то
, то 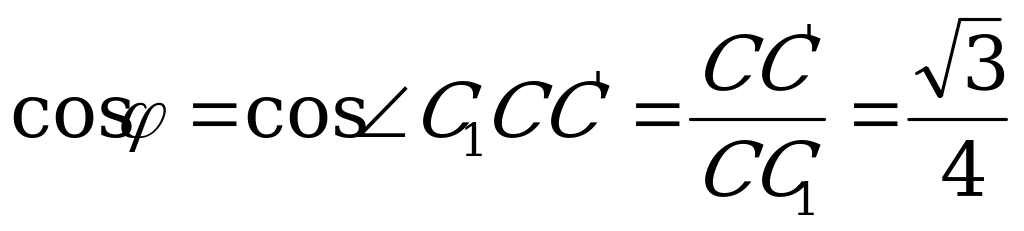 ,
, 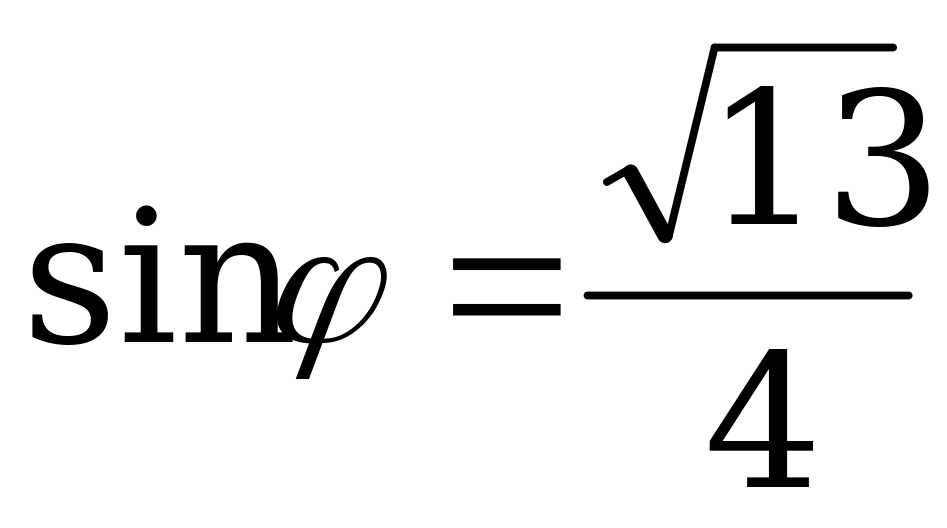 ,
, 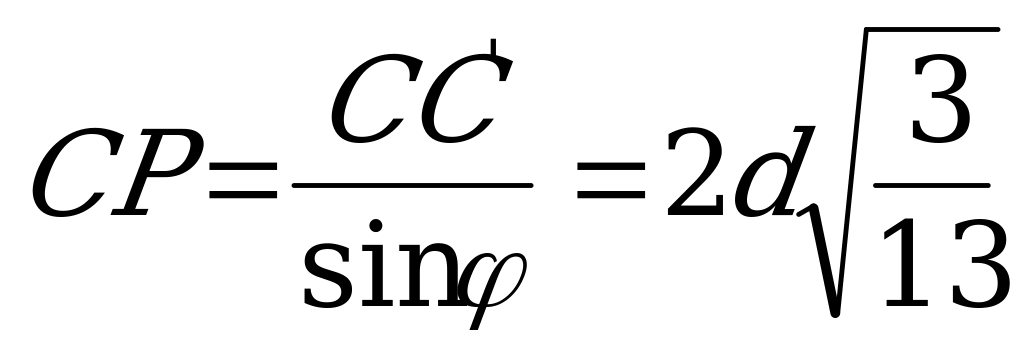 .
.
Так как  равно удвоенной высоте треугольника
равно удвоенной высоте треугольника 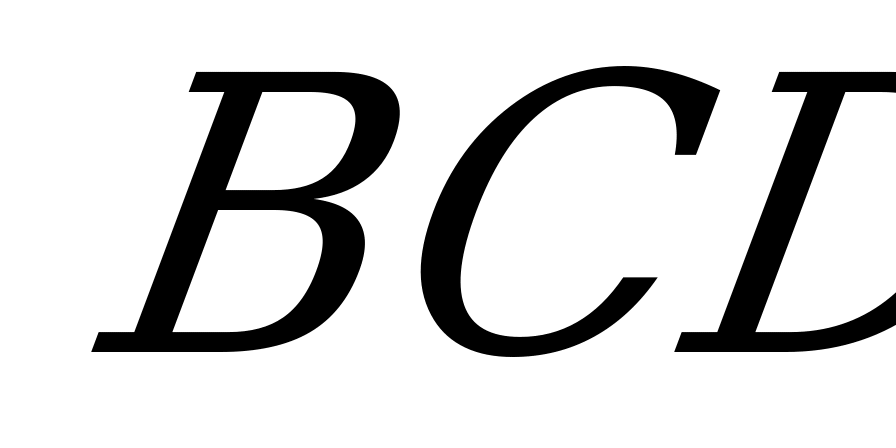 , опущенной на гипотенузу
, опущенной на гипотенузу  , то
, то 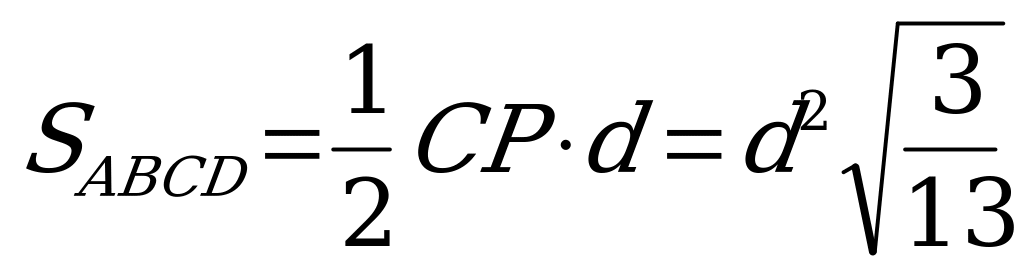 . По условию
. По условию 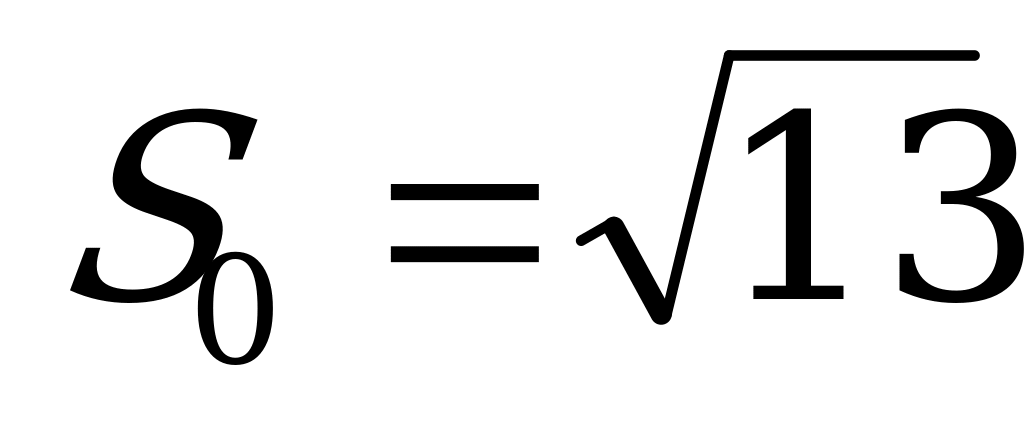 и
и 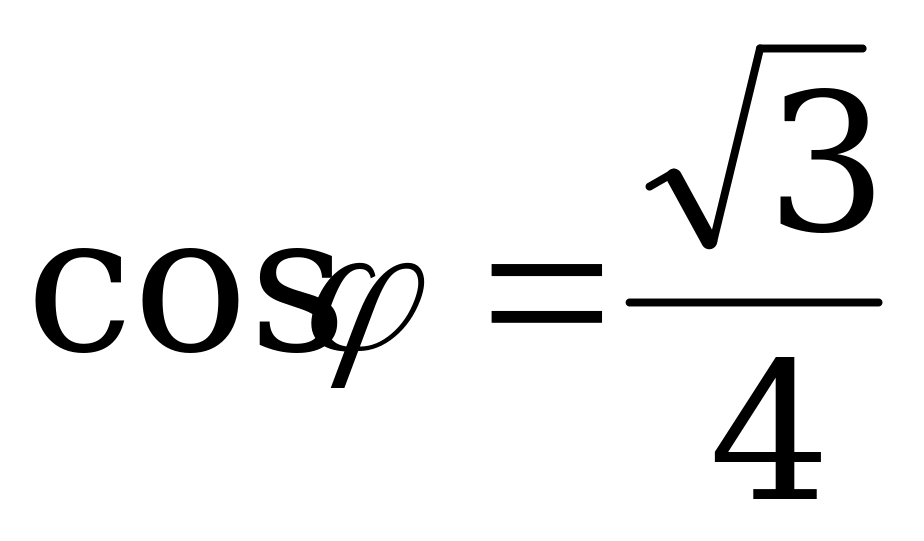 , то d находим из условия:
, то d находим из условия: 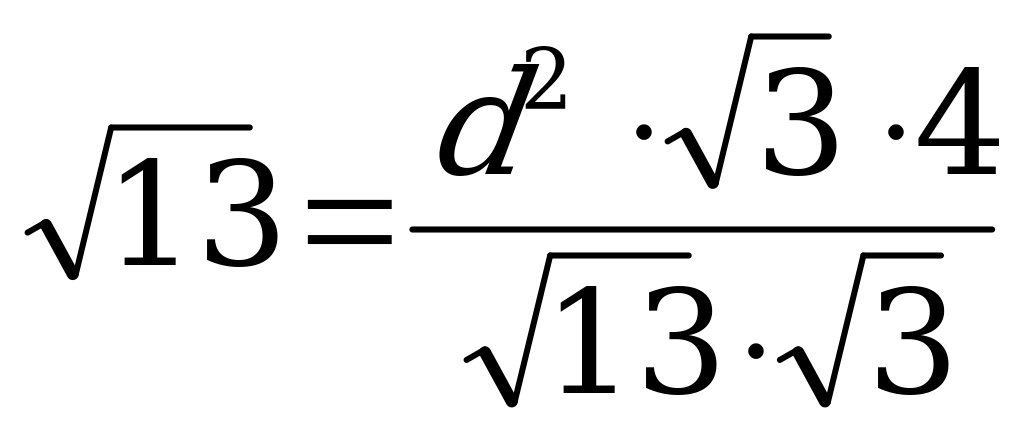 , т.е.
, т.е. 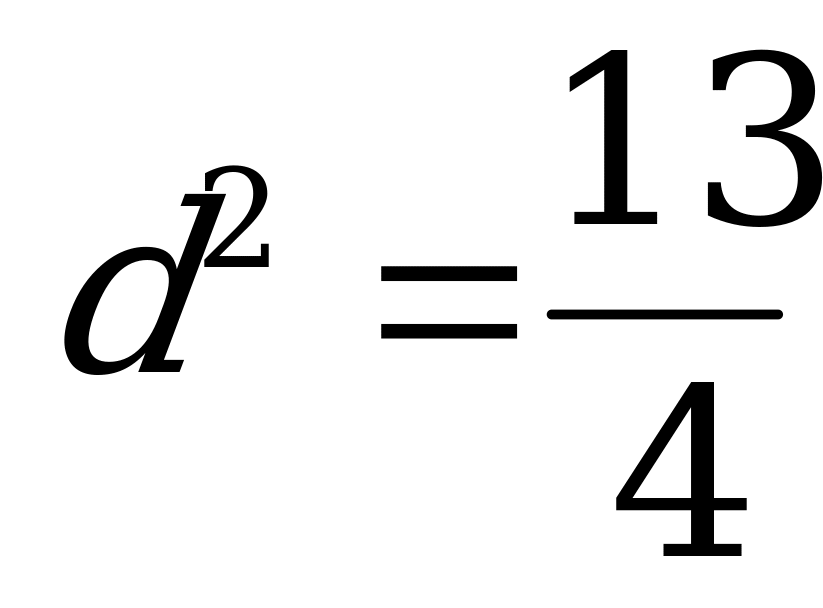 .
.
Поскольку центр описанной сферы лежит в центре  параллелепипеда, то её диаметр АС1=2R,
параллелепипеда, то её диаметр АС1=2R, 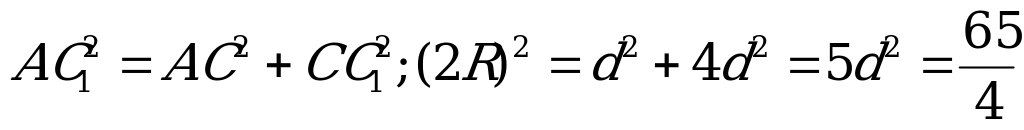 , а площадь поверхности сферы равна
, а площадь поверхности сферы равна 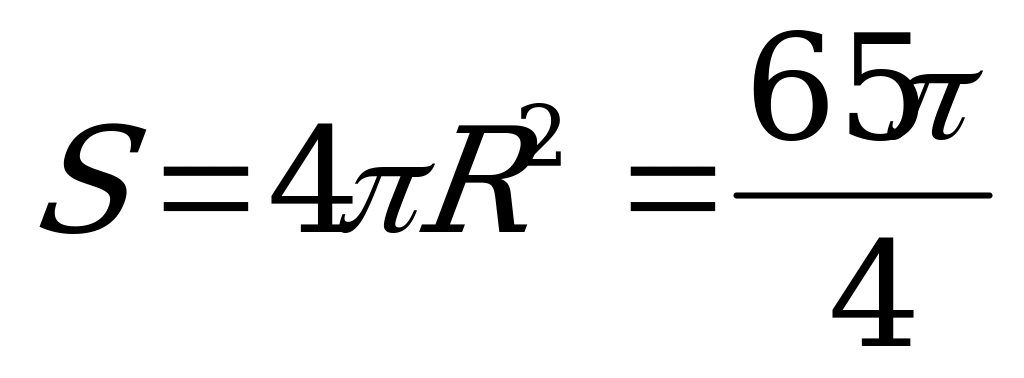 .
.
Ответ: 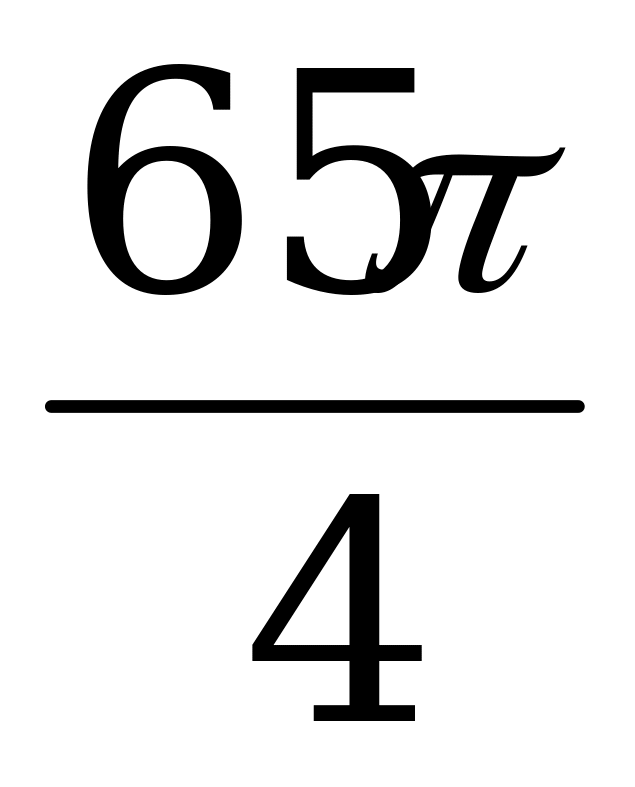 .
.
8 . Найдите площадь сечения правильной треугольной пирамиды
. Найдите площадь сечения правильной треугольной пирамиды  плоскостью, проходящей через середину ребра
плоскостью, проходящей через середину ребра  , середину ребра
, середину ребра  и параллельной медиане
и параллельной медиане 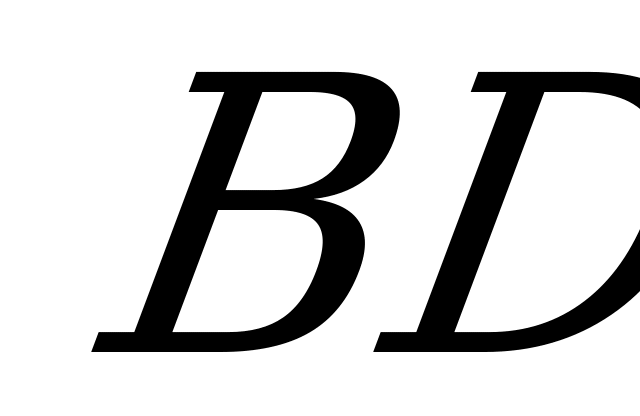 основания. Сторона основания
основания. Сторона основания 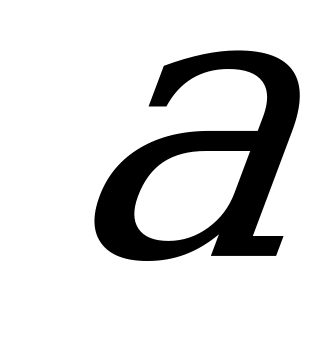 равна высоте пирамиды
равна высоте пирамиды  и равна
и равна 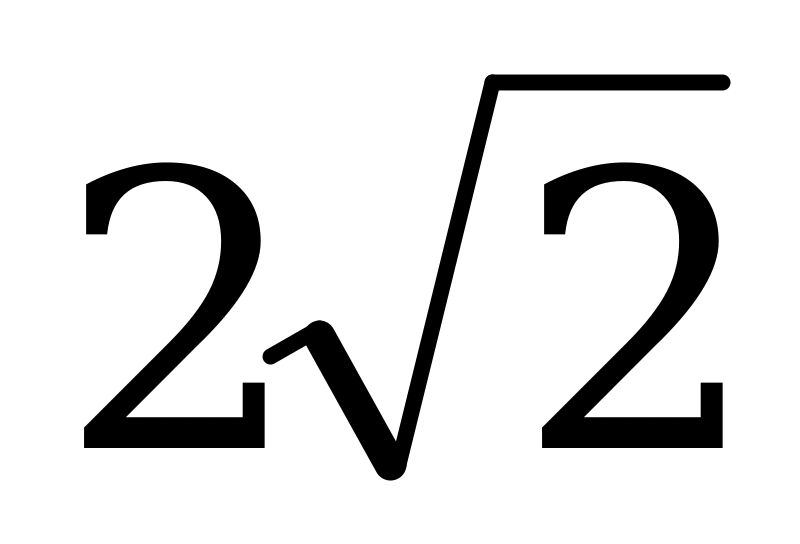 .
.
Решение:
Построим сечение. Через середину 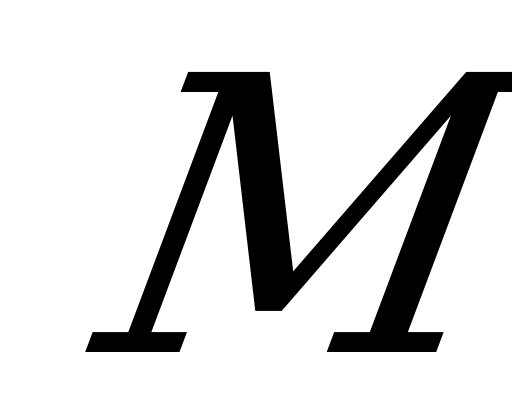 стороны
стороны  проведём
проведём  ║
║ ,
,  и обозначим через
и обозначим через  точку пересечении прямой
точку пересечении прямой  с прямой
с прямой  . Прямая
. Прямая  , лежащая в пл.
, лежащая в пл. , пересекает
, пересекает  в точке
в точке  .
.  - искомое сечение.
- искомое сечение.
Очевидно, 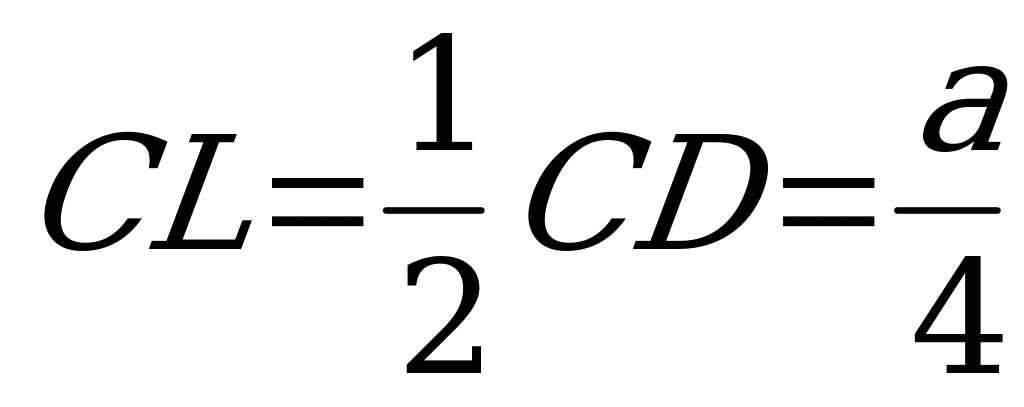 .
. 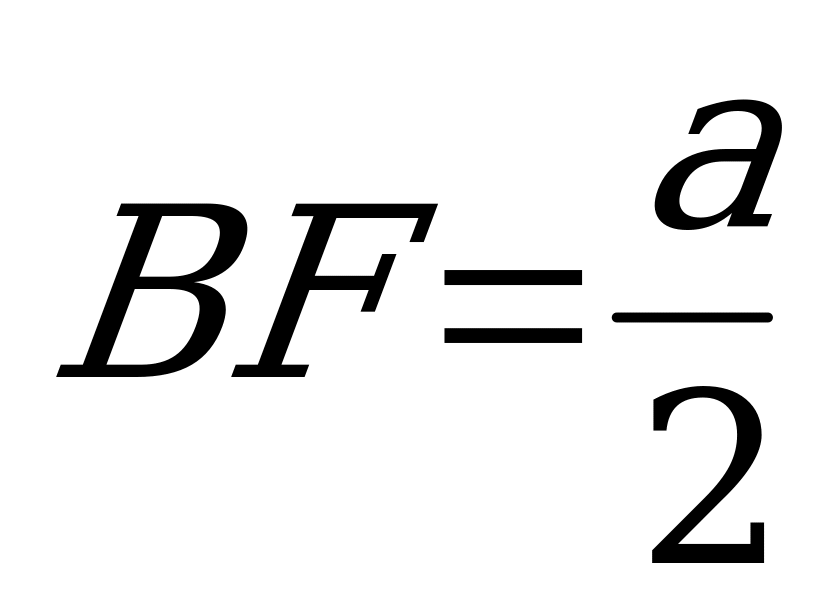 поскольку
поскольку  ║ и, следовательно,
║ и, следовательно, 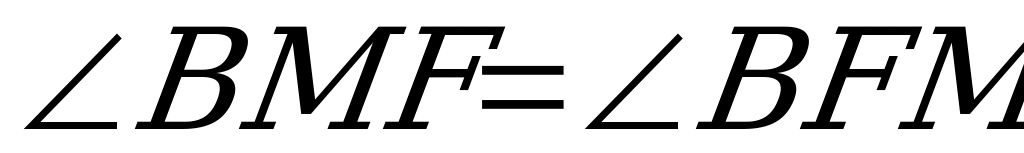 , т.е.
, т.е.  - равнобедренный:
- равнобедренный: 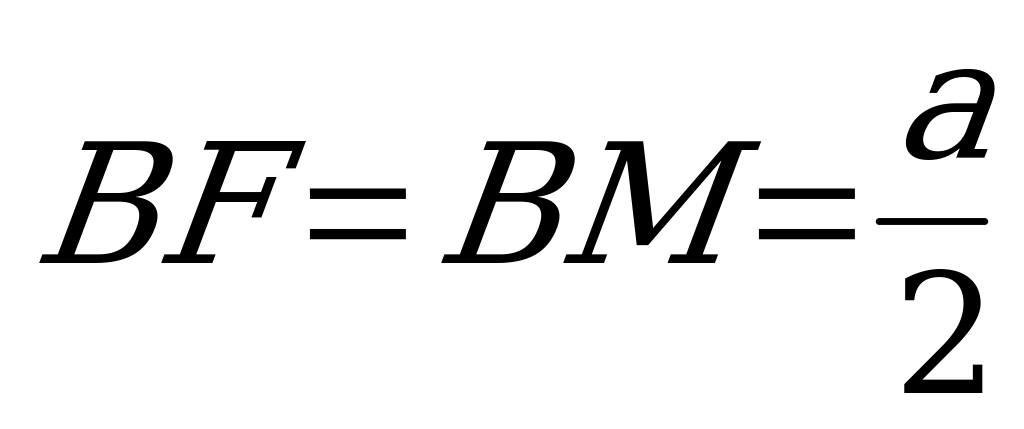 .
.
 Найдём положение
Найдём положение  на
на 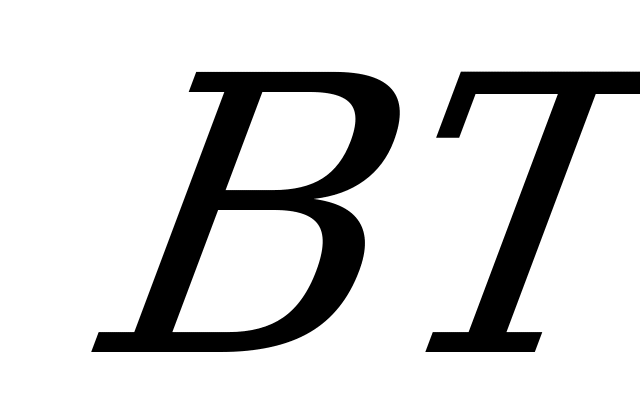 . В
. В  через
через 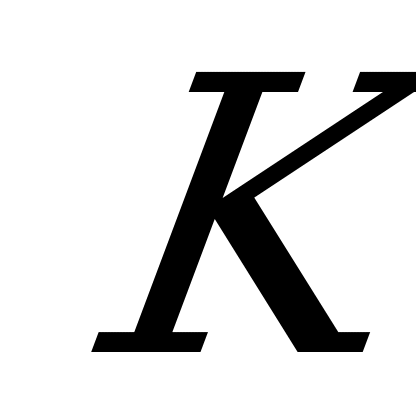 проведём среднюю линию
проведём среднюю линию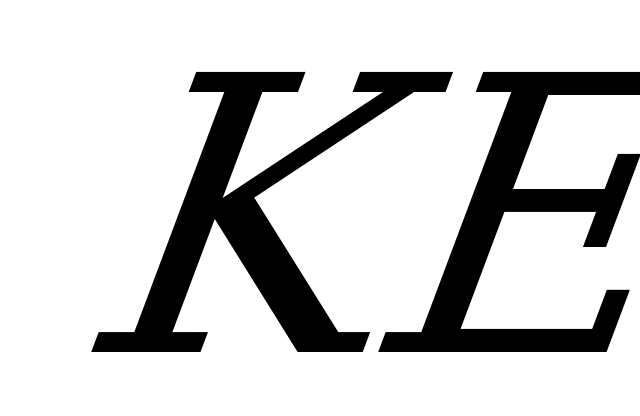 ║
║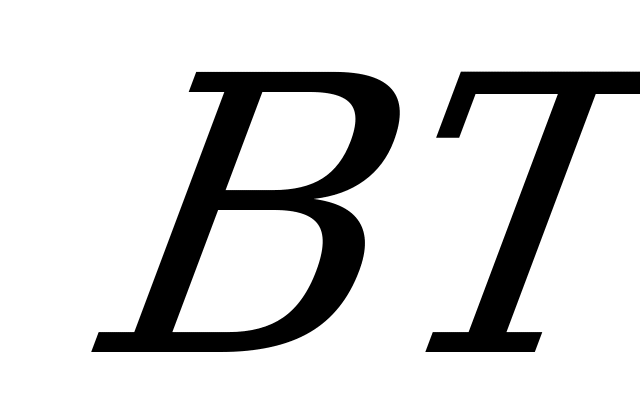 . Тогда
. Тогда  подобен
подобен , откуда
, откуда  и, поскольку
и, поскольку 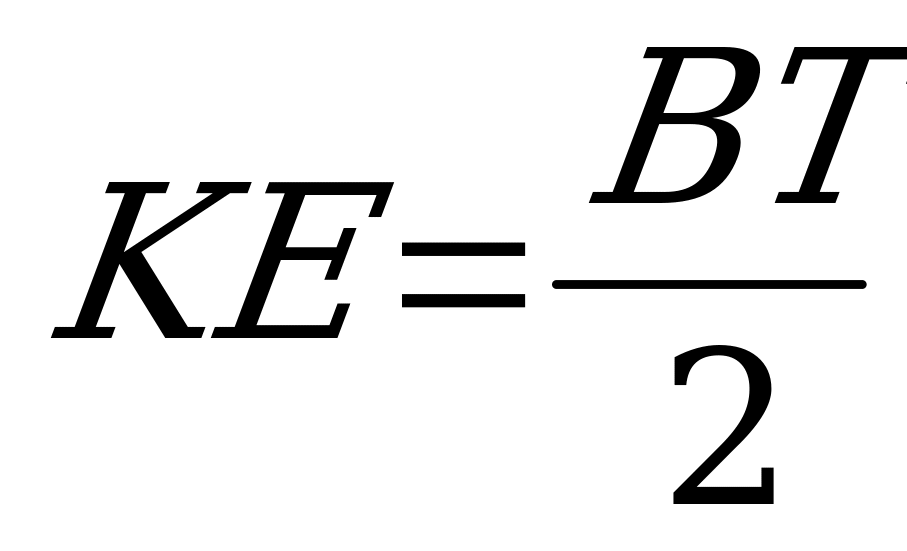 , то
, то 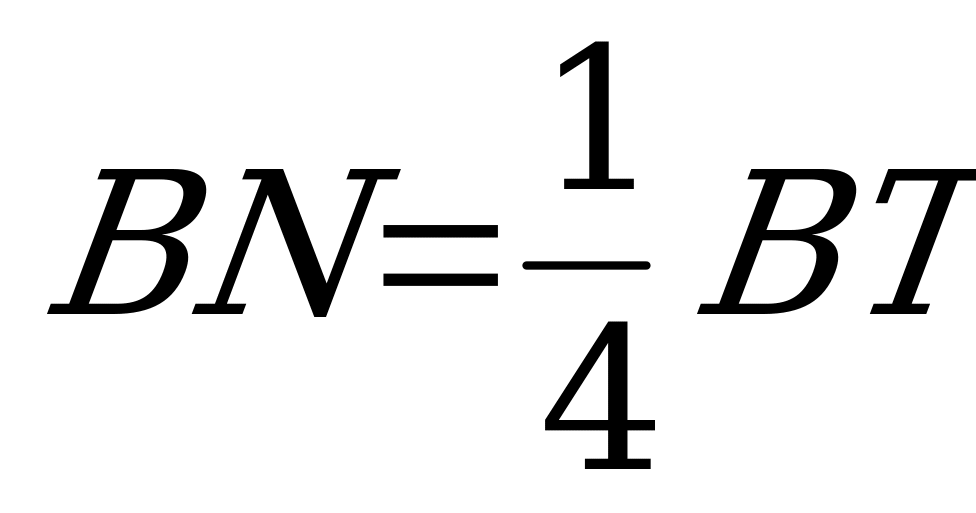 .
.
Пусть 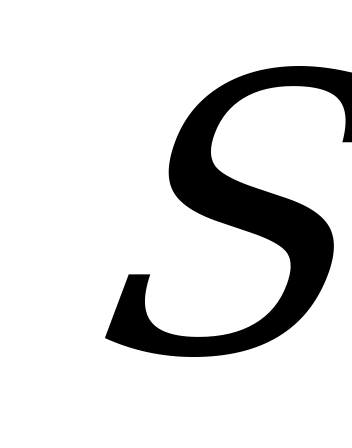 - площадь сечения ,и
- площадь сечения ,и 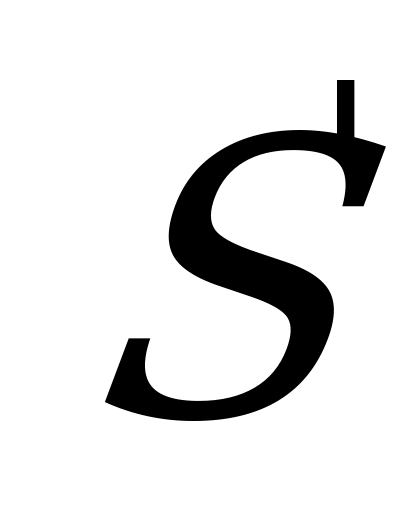 - площадь его проекции
- площадь его проекции  на пл.(ABC) и
на пл.(ABC) и 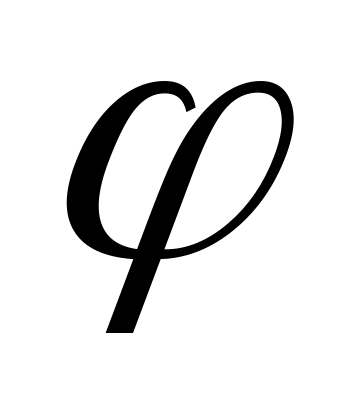 - угол между плоскостью (ABC). Тогда
- угол между плоскостью (ABC). Тогда 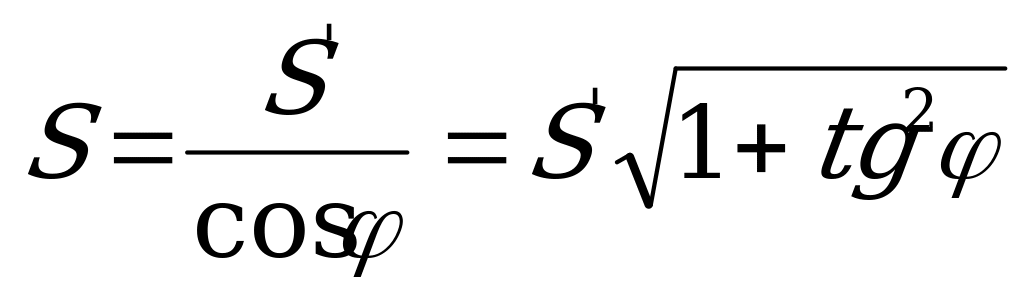 .
.
Для вычисления 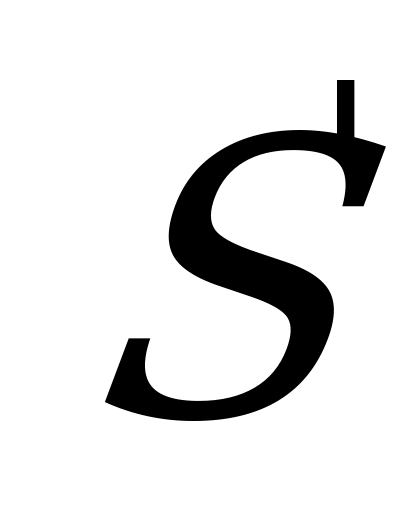 и
и 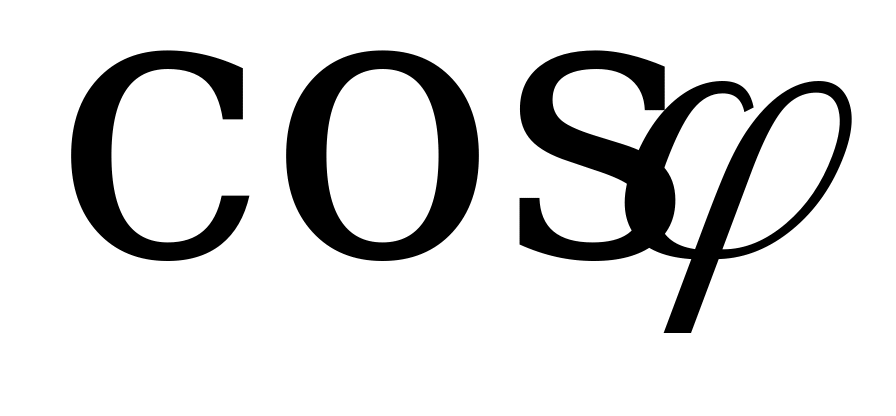 обозначим высоту основания через
обозначим высоту основания через 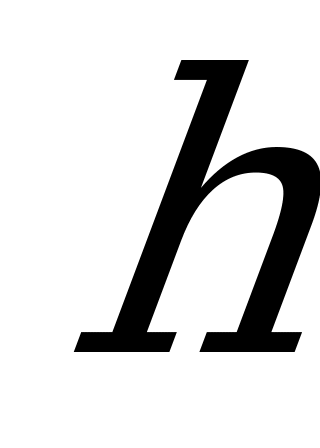 . Заметим, что т.к.
. Заметим, что т.к.  , то
, то 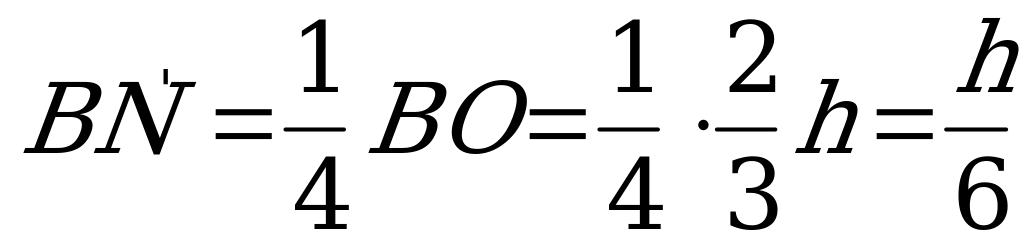 . А т.к.
. А т.к. 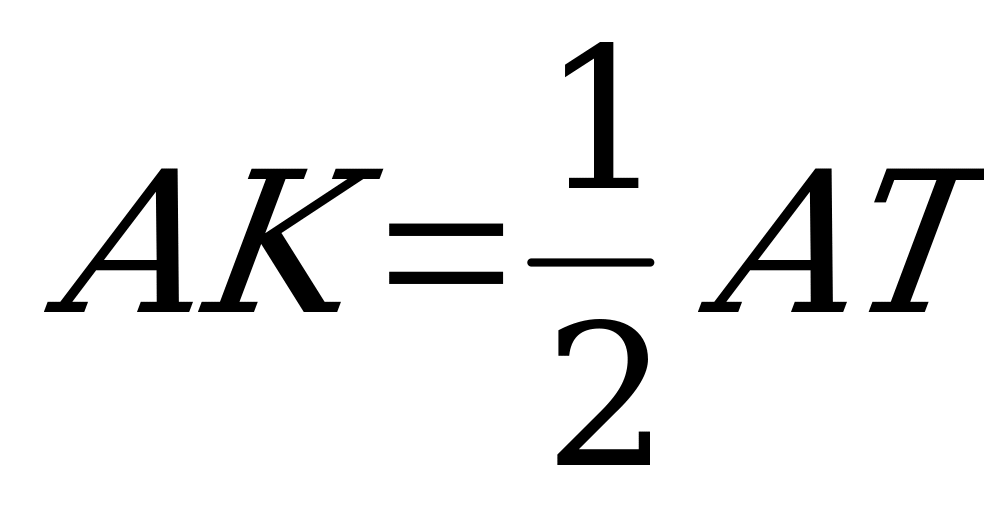 , то
, то 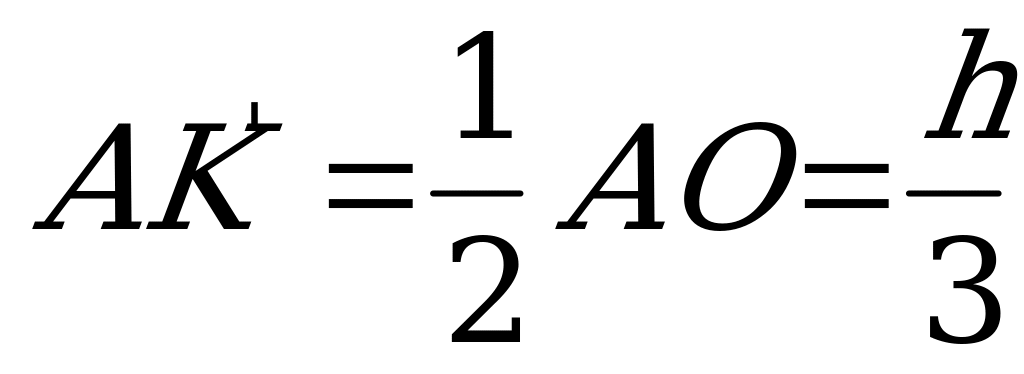 .
. 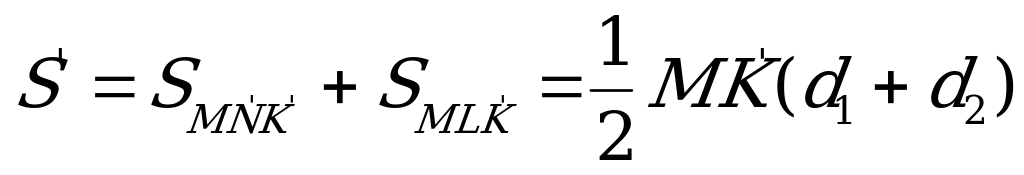 , где
, где 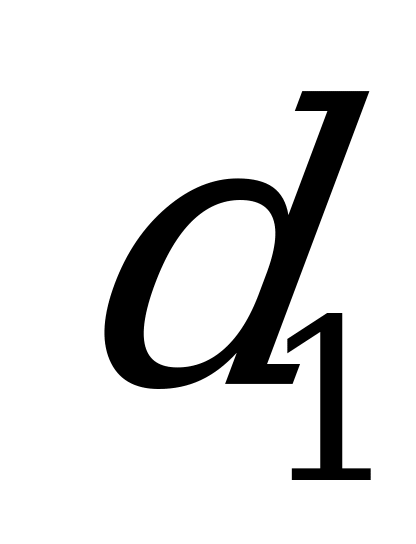 и
и  - высоты
- высоты  и
и  , соответственно, опущенные на
, соответственно, опущенные на 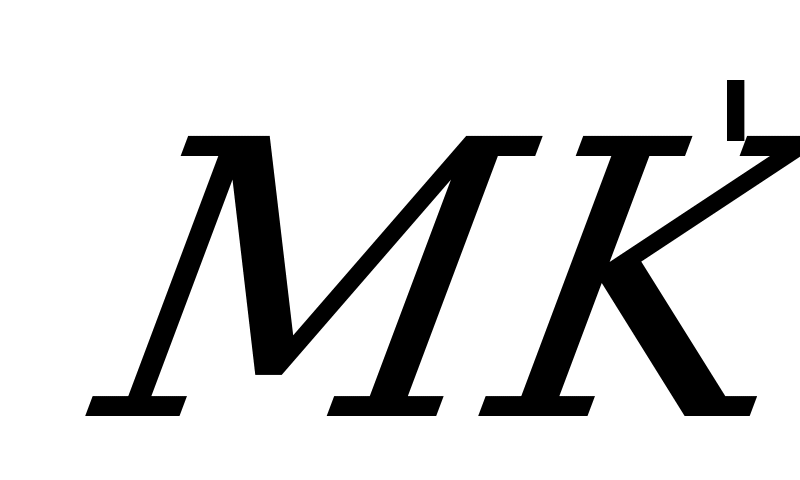 . Т.к. эти высоты параллельны
. Т.к. эти высоты параллельны  и
и 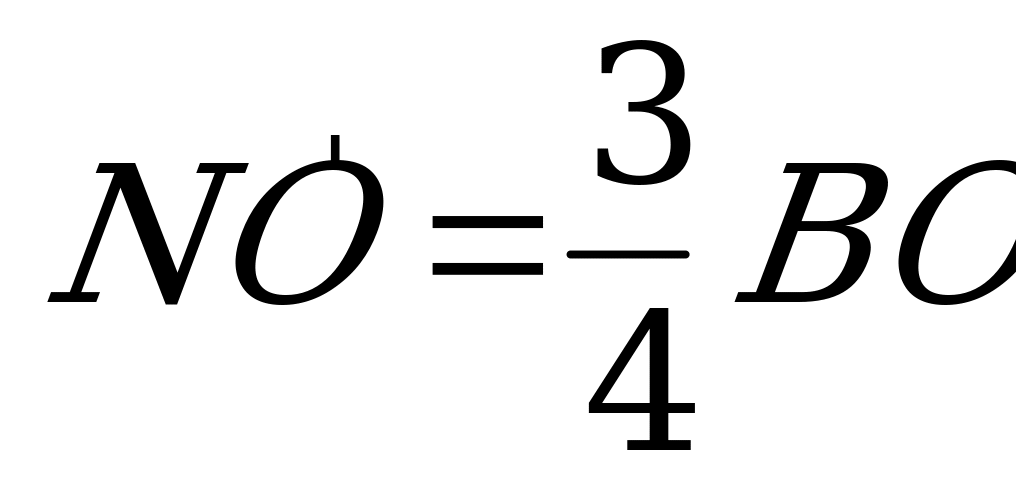 ,
,
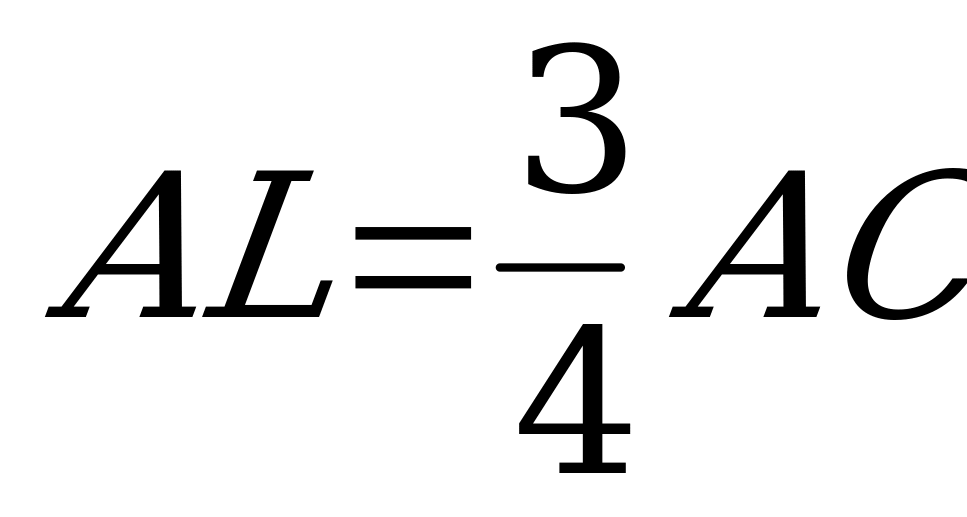 , то
, то 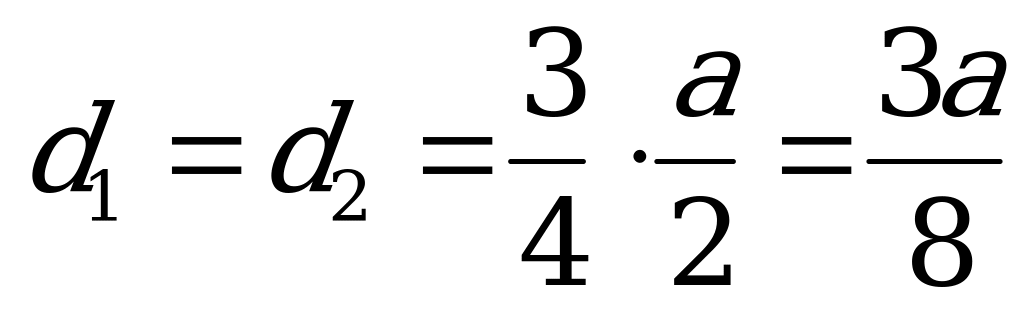 .
. 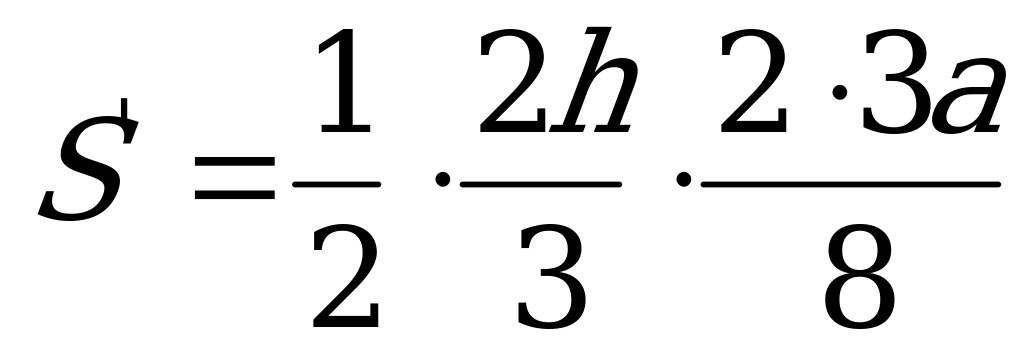 .
.
Для нахождения 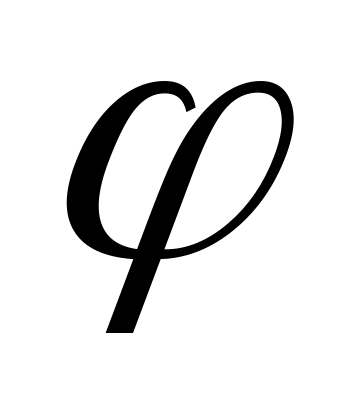 опускаем перпендикуляр
опускаем перпендикуляр  из точки
из точки 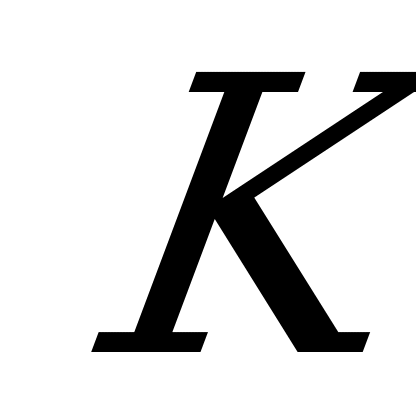 на плоскость основания и затем из
на плоскость основания и затем из 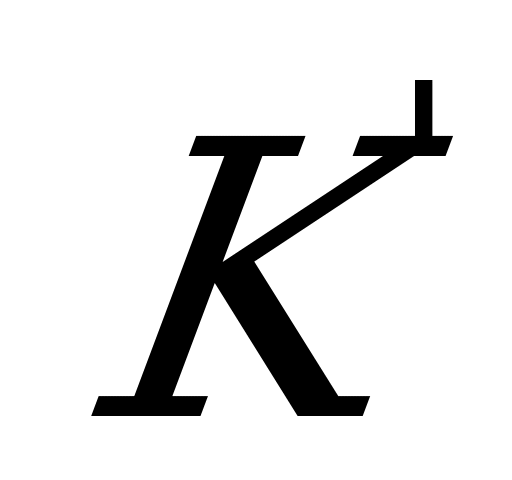 опускаем перпендикуляр
опускаем перпендикуляр  и
и  - линию пересечения плоскости основания. Т.к.
- линию пересечения плоскости основания. Т.к.  - ортогональная проекция
- ортогональная проекция 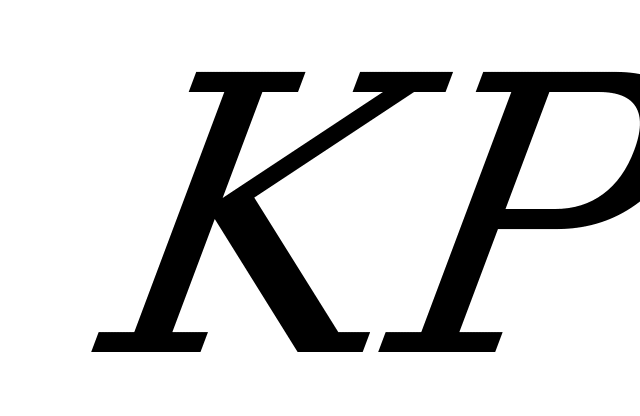 на плоскость ABC, то по теореме о трёх перпендикулярах
на плоскость ABC, то по теореме о трёх перпендикулярах 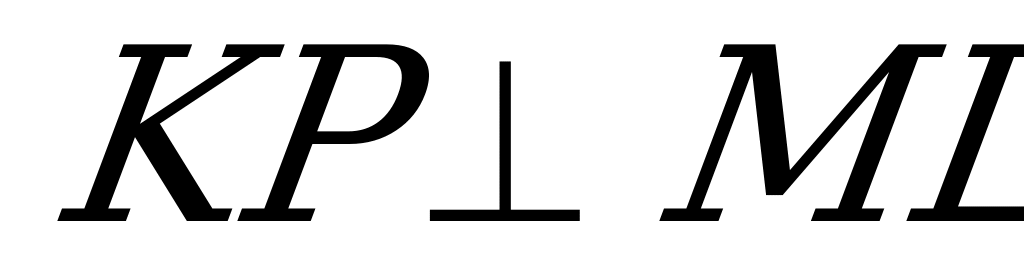 . Т.к.
. Т.к.  по построению, то
по построению, то  и
и  т.е.
т.е. 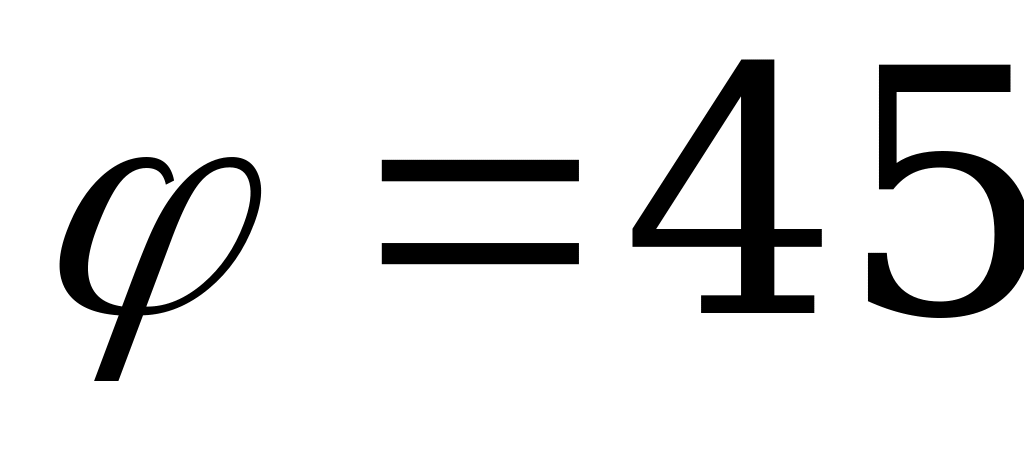 ,
, 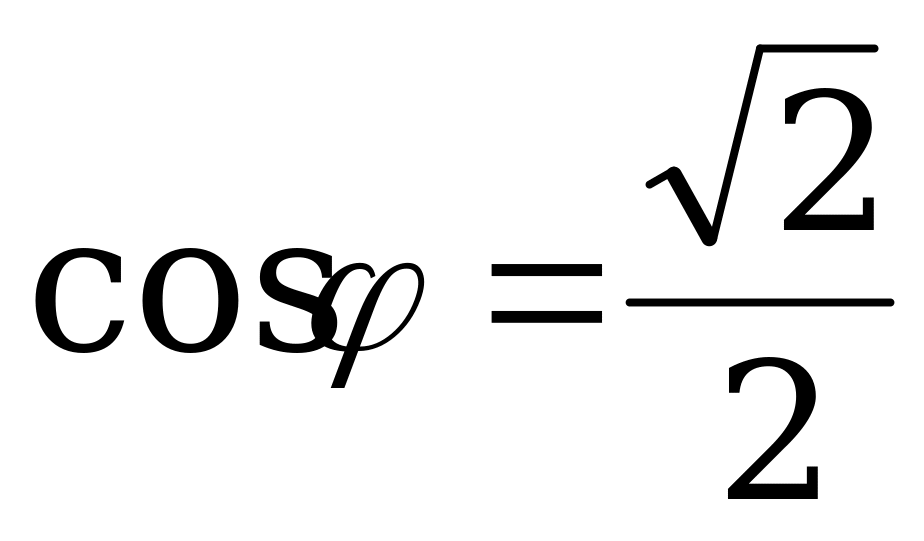 ,
, 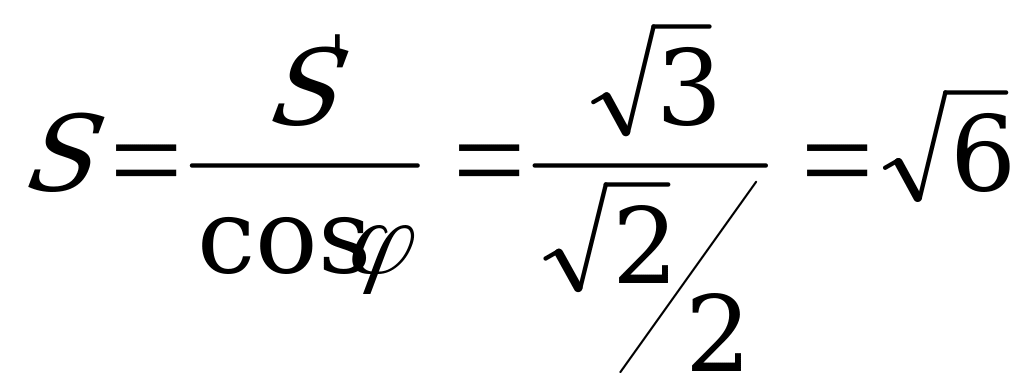 .
.
Ответ: 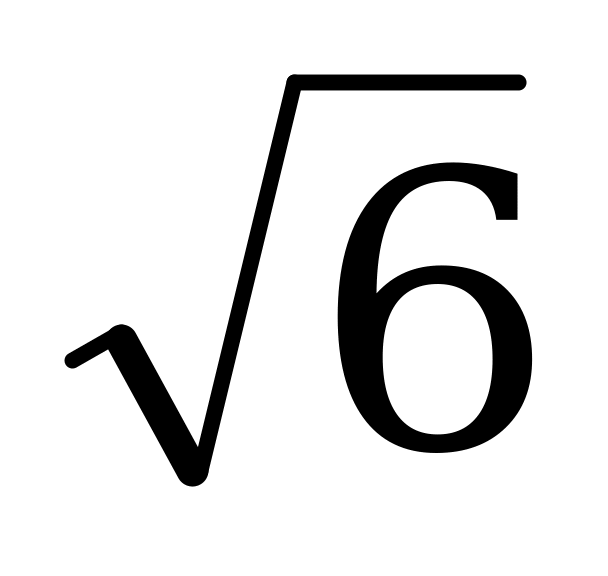 .
.
9 . В основании пирамиды лежит ромб со стороной
. В основании пирамиды лежит ромб со стороной 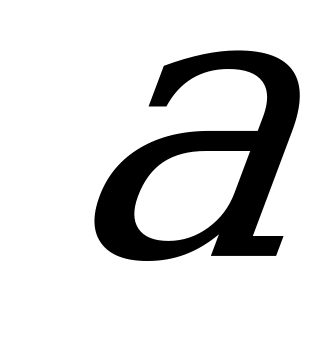 и острым углом
и острым углом  . Каждый из двугранных углов при основании равен
. Каждый из двугранных углов при основании равен 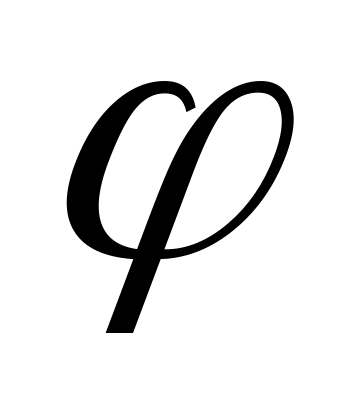 . Определить объём шара, вписанного в пирамиду.
. Определить объём шара, вписанного в пирамиду.
Решение.
Пусть SABCD – данная пирамида. Высота пирамиды SE пересекает основание пирамиды в точке пересечения диагоналей ромба(являющейся центром вписанной окружности) и центр вписанного шара O лежит на высоте пирамиды. Угол SKE – линейный угол двугранного угла, который грань SAB образует с основанием. Согласно условию 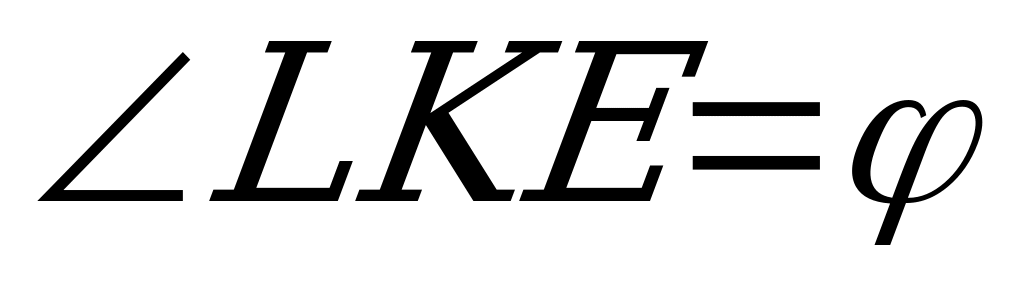 , L и E – точки касания шара с гранями SAB и ABC соответственно, EF=EK, KO – биссектриса угла
, L и E – точки касания шара с гранями SAB и ABC соответственно, EF=EK, KO – биссектриса угла  и потому
и потому 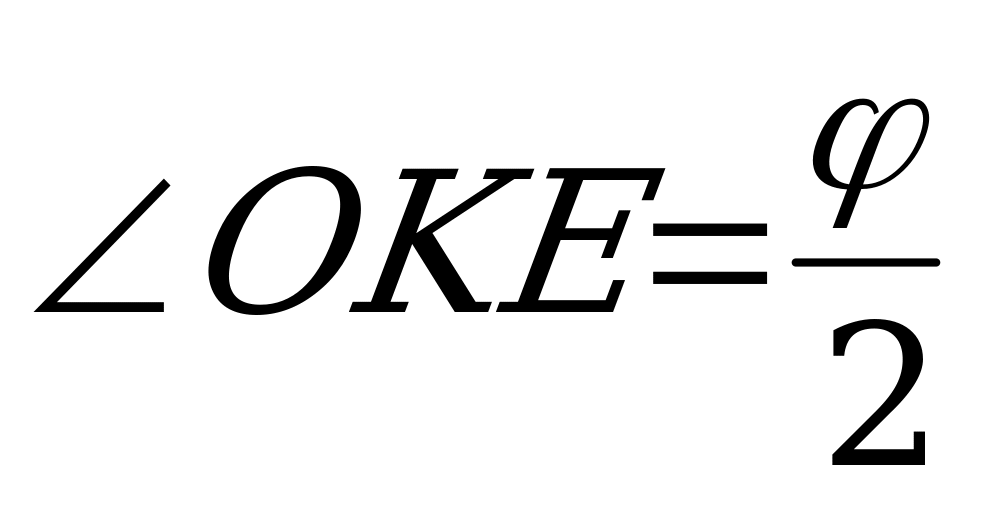 , OE – радиус вписанного шара.
, OE – радиус вписанного шара.
Из  выразим
выразим 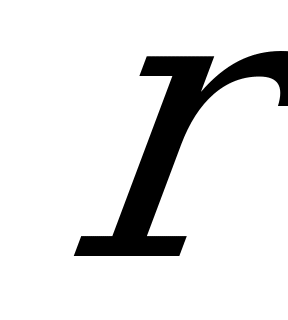 =ОЕ:
=ОЕ:
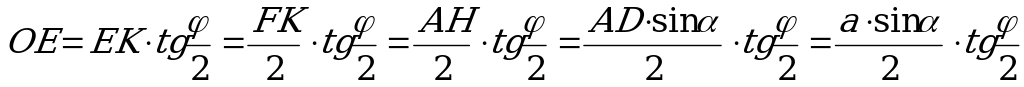 .
.
Найдём объём шара:

Ответ: 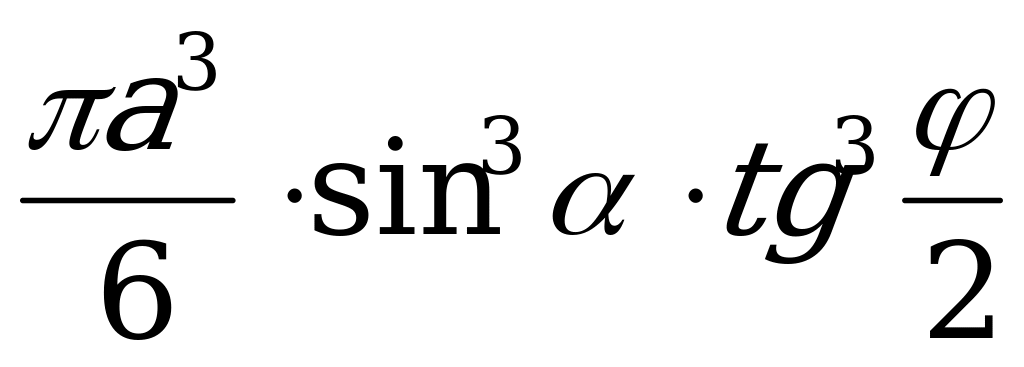 .
.
10.Для самостоятельного решения.
Основанием пирамиды служит ромб с острым углом  . Найти объём пирамиды, зная, что её боковые грани образуют с основанием один и тот же угол
. Найти объём пирамиды, зная, что её боковые грани образуют с основанием один и тот же угол  и радиус вписанного в неё шара равен r.
и радиус вписанного в неё шара равен r.
Ответ: 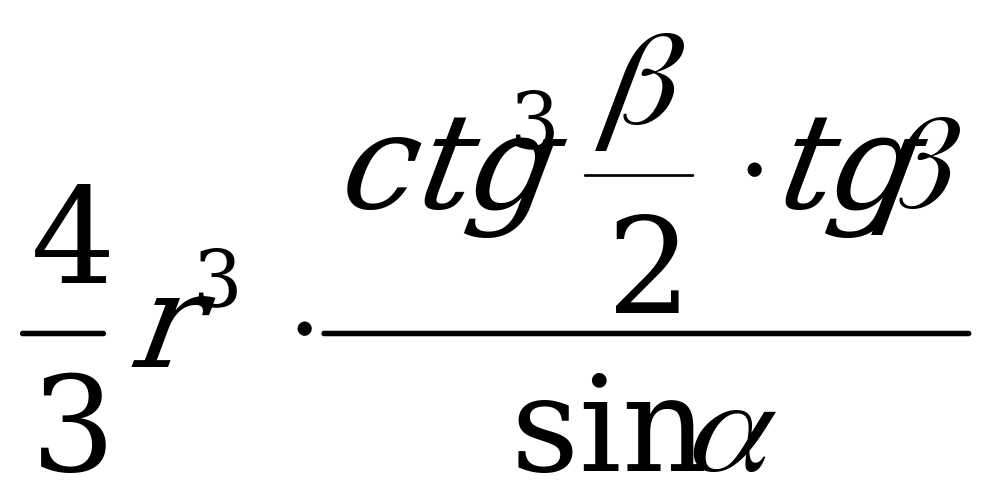 .
.
11.Основанием пирамиды служит прямоугольник, диагонали которого образуют угол  , а боковые рёбра составляют с основанием угол
, а боковые рёбра составляют с основанием угол 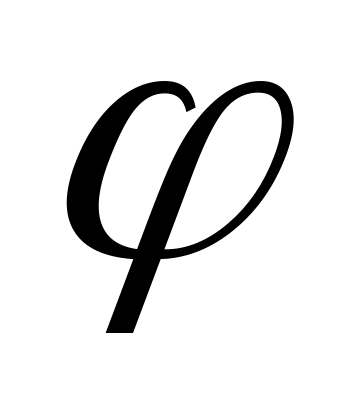 . Определить объём пирамиды, если радиус описанного около неё шара равен R.
. Определить объём пирамиды, если радиус описанного около неё шара равен R.
Решение.
Пусть дана пирамида SABCD с прямоугольным основанием ABCD, SO-её высота; тогда по условию 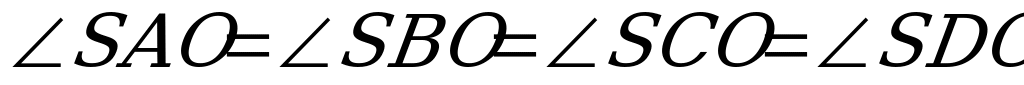
(т.к. 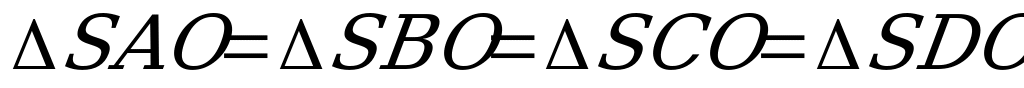 ), а поэтому все боковые рёбра равны между собой и
), а поэтому все боковые рёбра равны между собой и  является точкой пересечения диагоналей прямоугольника. Центр описанного шара должен лежать на перпендикуляре к плоскости ABCD, восстановленном в центре прямоугольника, т.е. на высоте SO.
является точкой пересечения диагоналей прямоугольника. Центр описанного шара должен лежать на перпендикуляре к плоскости ABCD, восстановленном в центре прямоугольника, т.е. на высоте SO.
Рассмотрим  и
и  .
.
Из  выразим AC:
выразим AC: 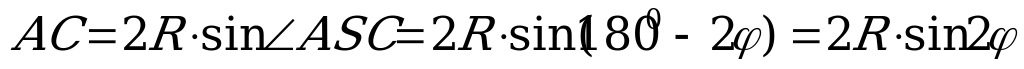 .
.
Из  :
: 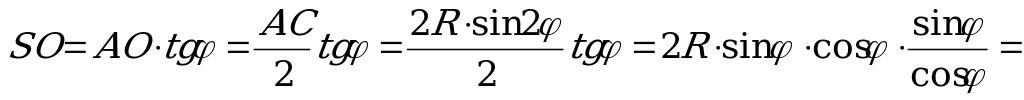
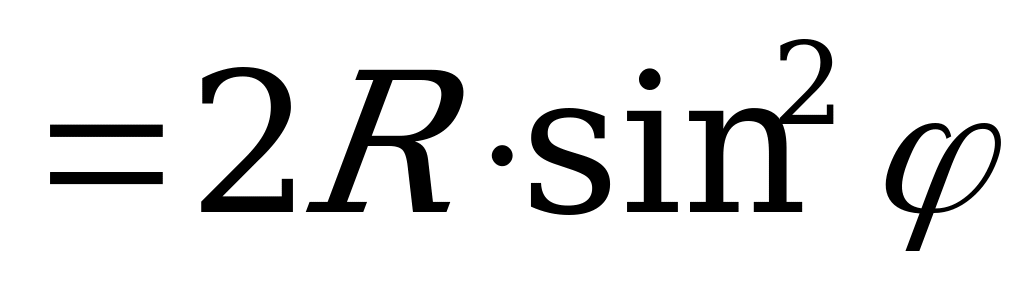 .
.
Вычислим объём пирамиды:
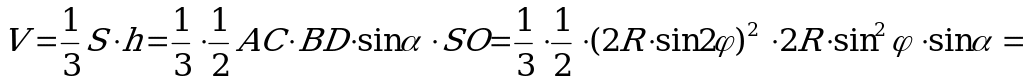
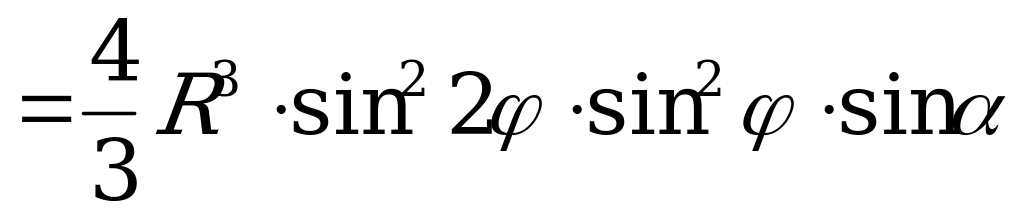 .
.
Ответ: 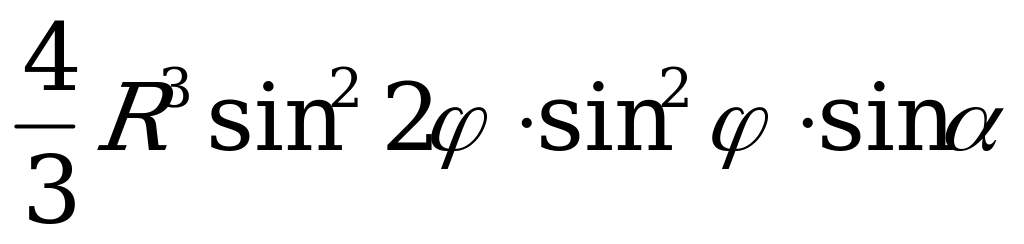 .
.
Одно из оснований правильной треугольной призмы принадлежит большому кругу шара принадлежит большому кругу радиуса R, а вершины другого основания принадлежат поверхности этого шара. Определить высоту призмы, при которой объём призмы будет наибольшим. Найти объём призмы.
Р ешение.
ешение.
Пусть ABCA1B1C1 правильная треугольная призма. O – центр шара. Обозначим высоту призмы 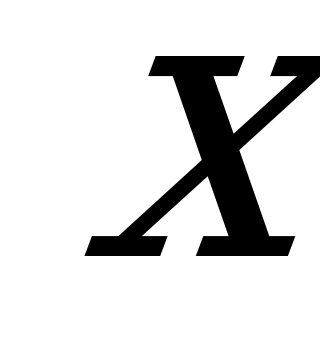 ,где
,где 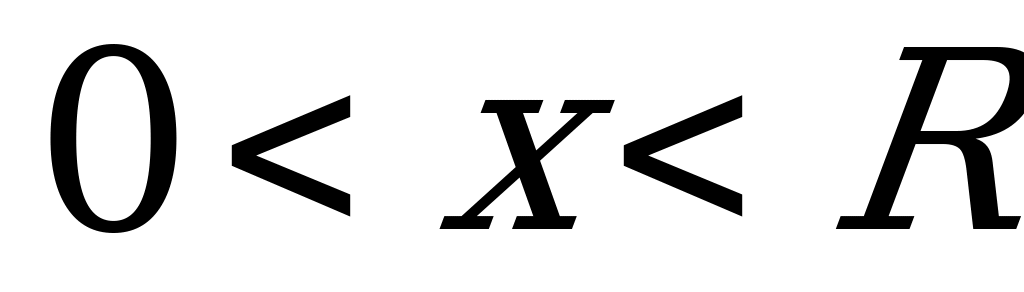 а сторону основания -
а сторону основания -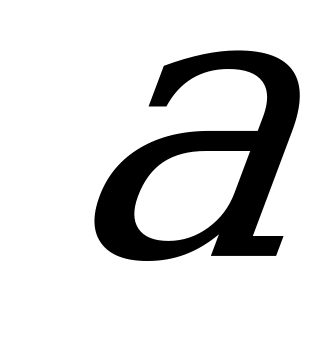 . Тогда объем призмы
. Тогда объем призмы 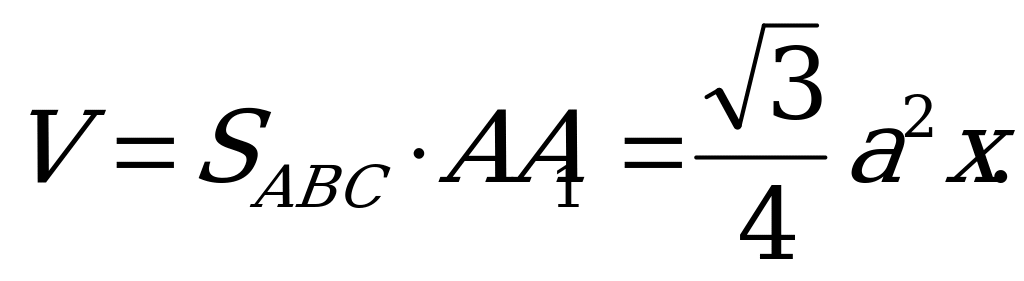 Из
Из 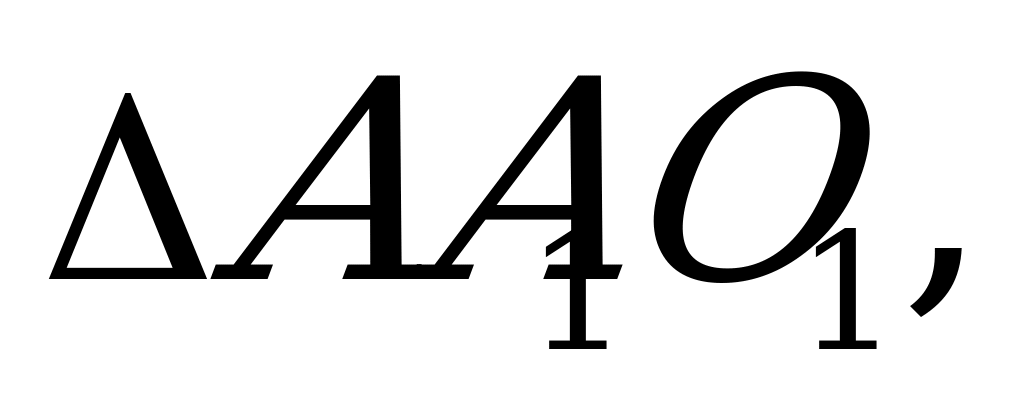 где А1О=R,АА1=x ,АО=
где А1О=R,АА1=x ,АО=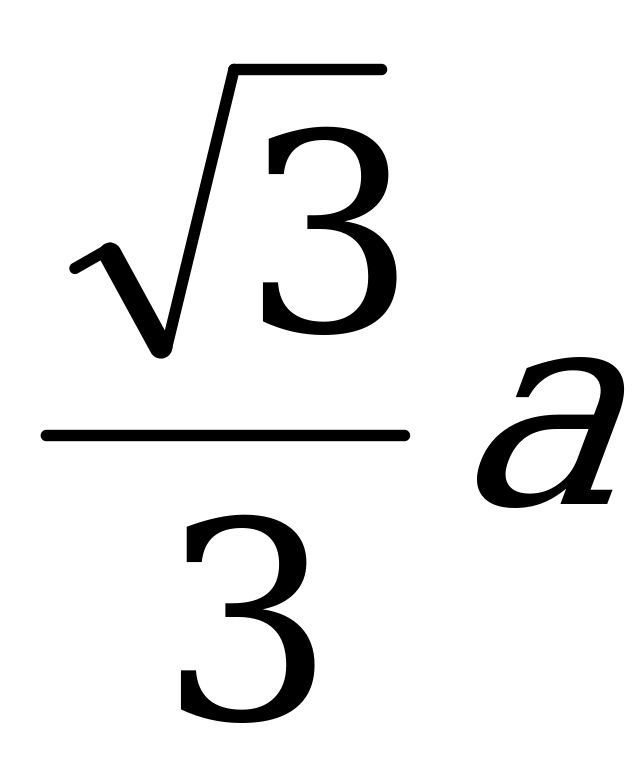 получим
получим 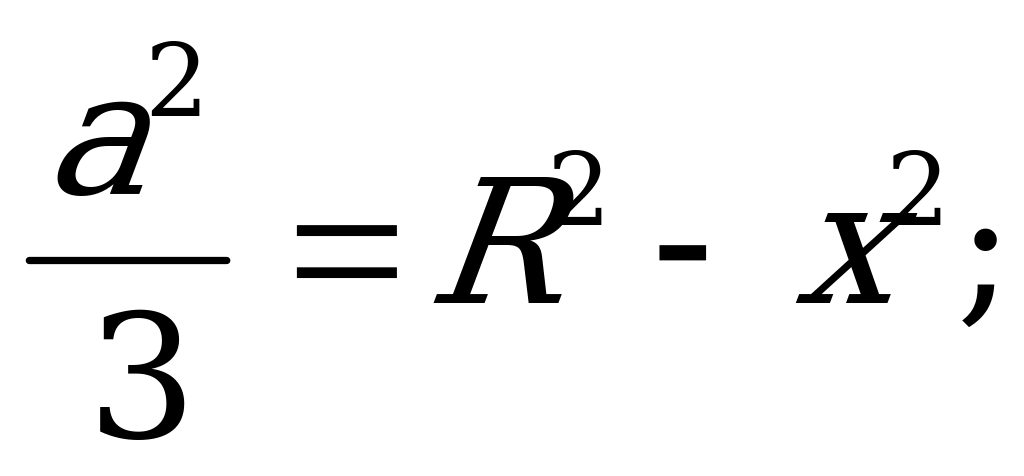
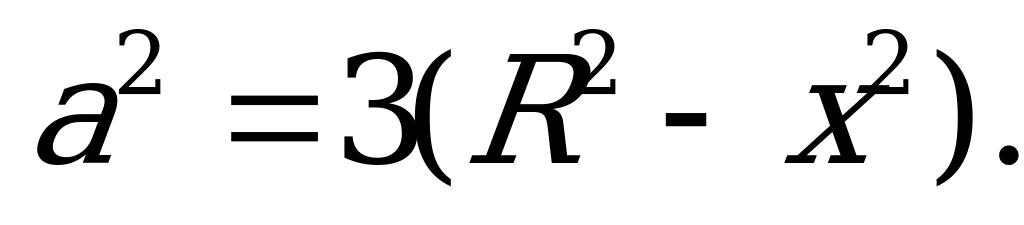
Тогда 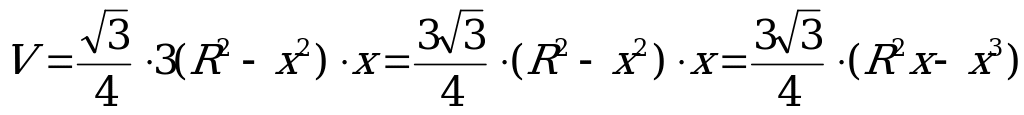 .
.
Для определения значений x, при которых объём призмы будет наибольшим, найдём производную функции 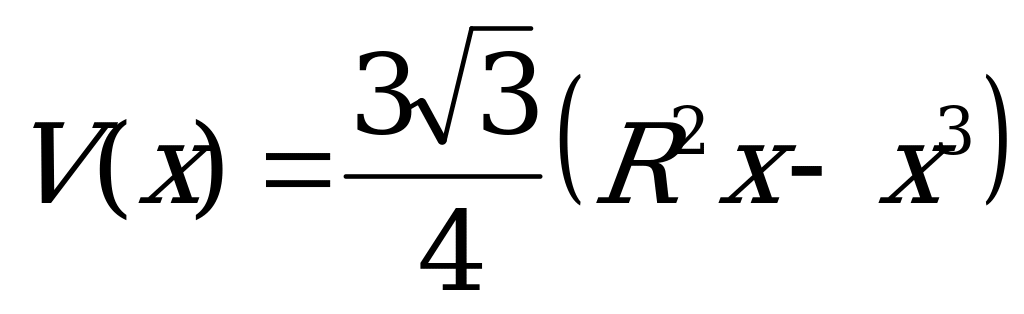 и её критические точки:
и её критические точки:
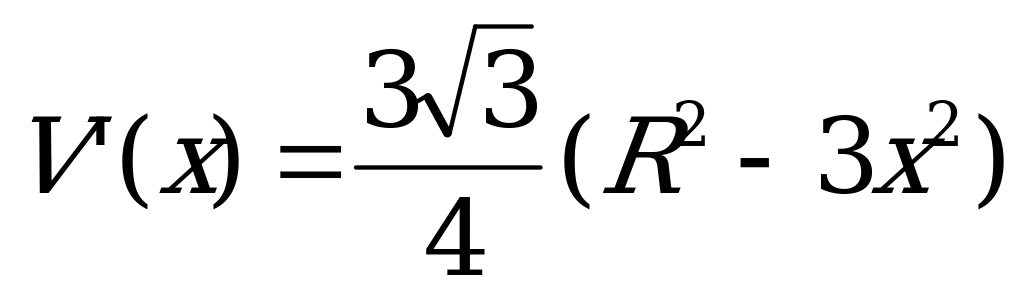 .
.
Приравняв производную к нулю, найдём, что 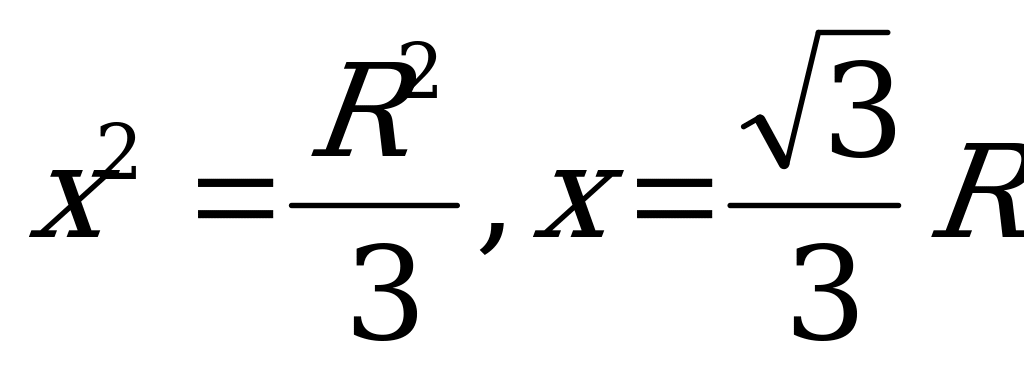 .
.
Покажем, что точка x=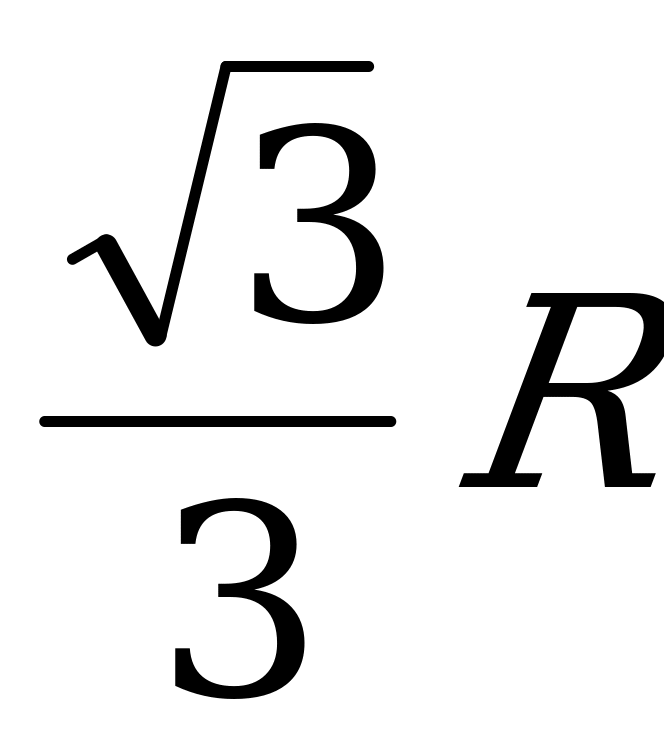 — точка максимума функции V(x).
— точка максимума функции V(x).
Очевидно, что V’(x) при переходе через 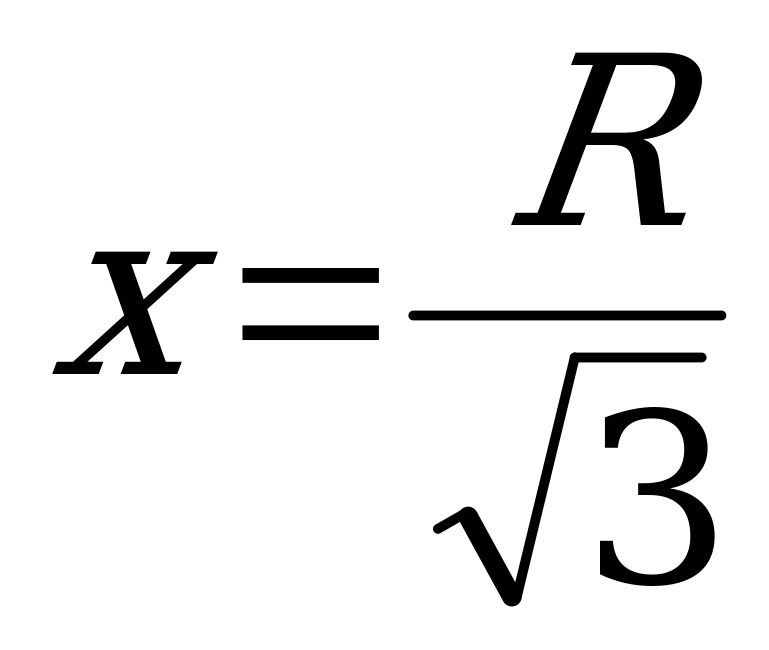 меняет знак с плюса на минус. Тогда
меняет знак с плюса на минус. Тогда 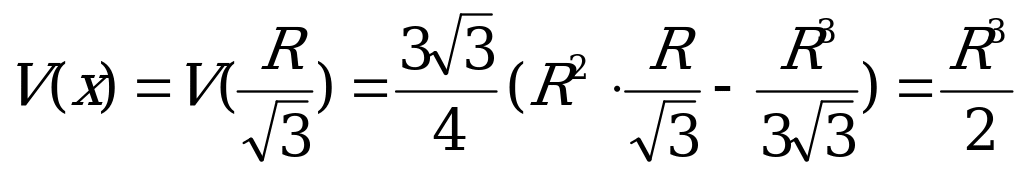 .
.
Ответ: 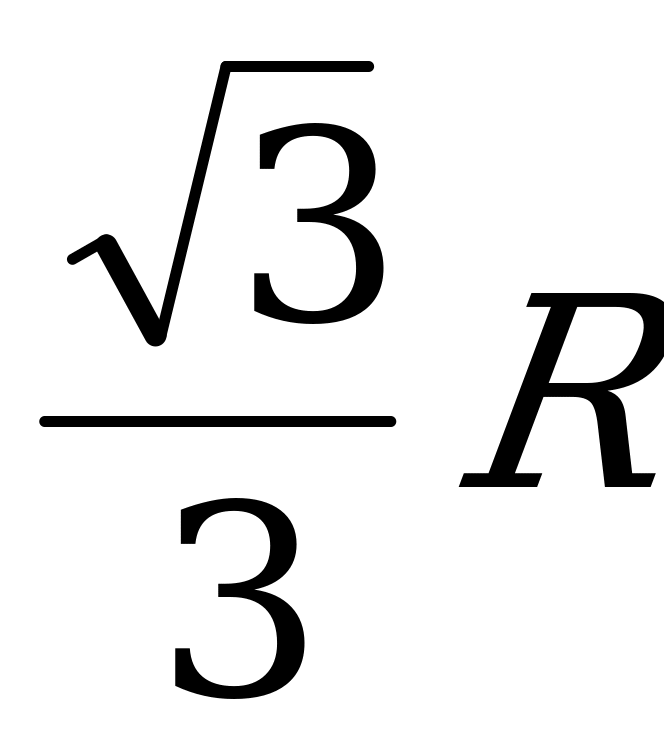 ;
; 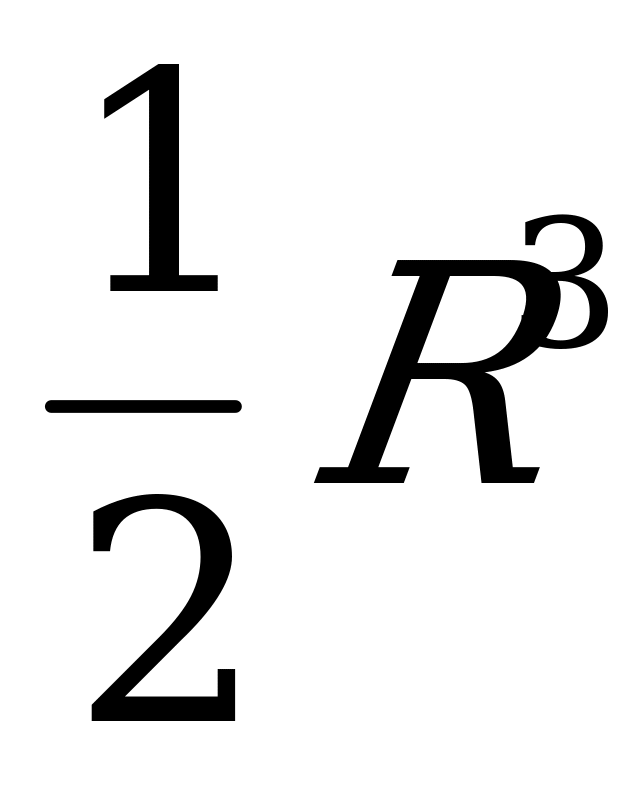 .
.
В сфере расположена правильная четырёхугольная пирамида так, что её вершина совпадает с центром сферы, а вершины основания лежат на сфере. Сечение пирамиды, параллельное основанию, является гранью куба, а вершины противоположной его грани лежат на сфере. Вычислить высоту пирамиды, если известно, что длина диагонали куба и ребра основания пирамиды одинакова и равна в . Определить отношение объема пирамиды к объему куба.
Ответ: в, 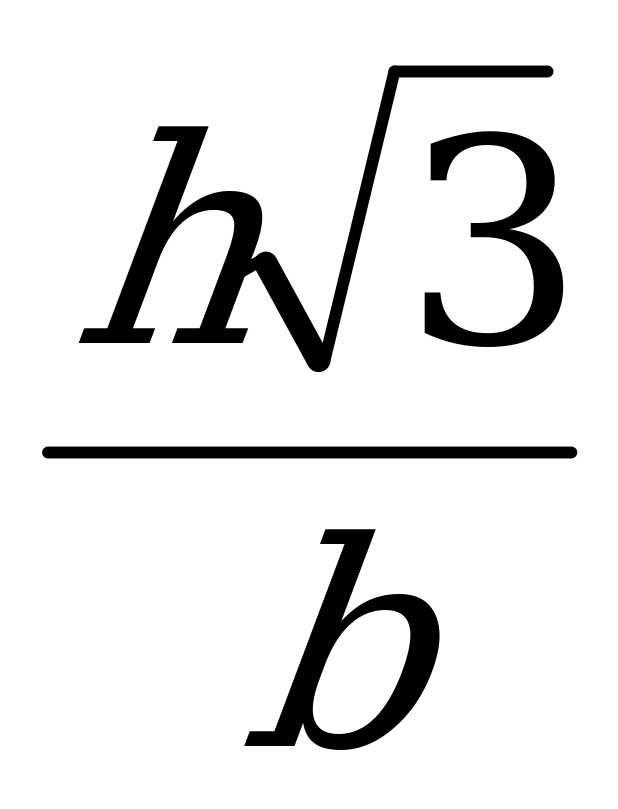 .
.
В сферу радиуса R вписана пирамида, основание которой – правильный треугольник. Одно из боковых рёбер перпендикулярно основанию и равно 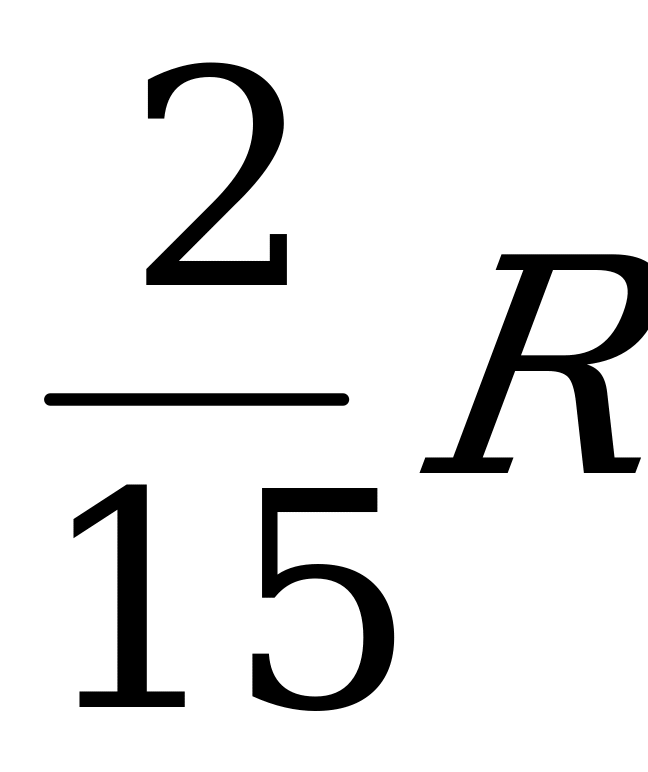 . Между сферой и пирамидой расположена правильная треугольная призма, одно из оснований которой лежит в плоскости основания пирамиды, а вершины другого основания принадлежат сфере. Какой наибольший объём может иметь призма?
. Между сферой и пирамидой расположена правильная треугольная призма, одно из оснований которой лежит в плоскости основания пирамиды, а вершины другого основания принадлежат сфере. Какой наибольший объём может иметь призма?
Р ешение.
ешение.
Центры оснований пирамиды и призмы совпадают. Это следует из того, что вершины основания пирамиды и призмы принадлежат сфере, и грани, их содержащие, параллельны, значит , центры оснований лежат на одном диаметре сферы.
Пусть сторона основания призмы a,О1О2=x, где x0, 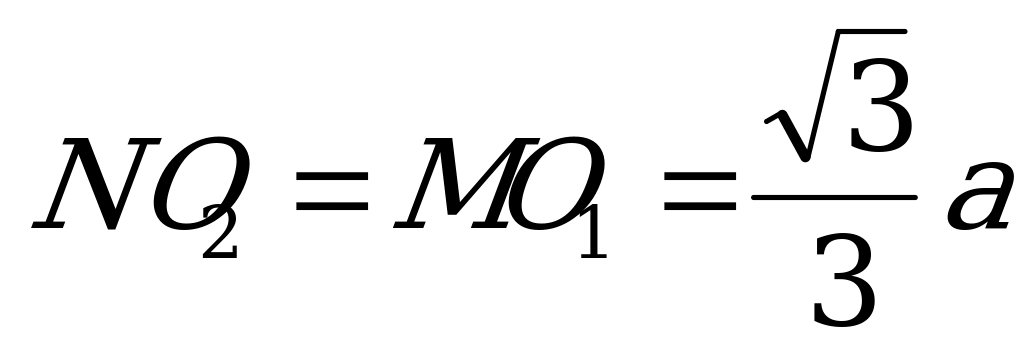 .
.
В 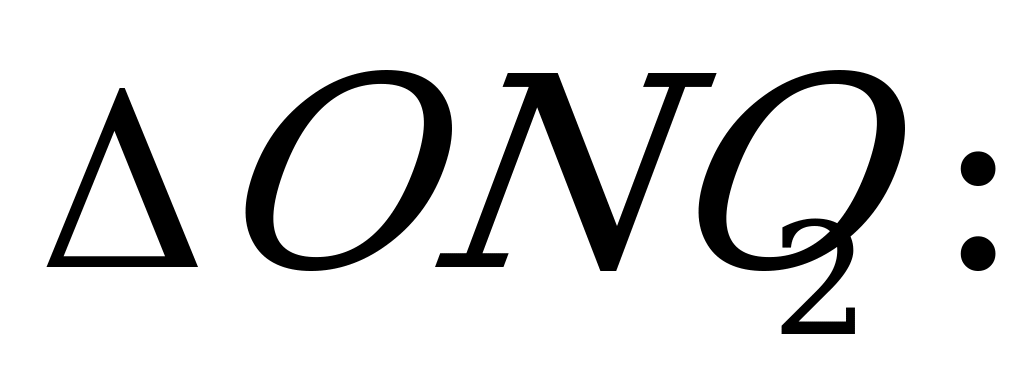
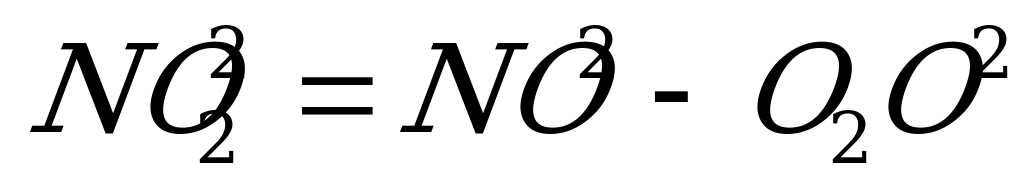 , а
, а 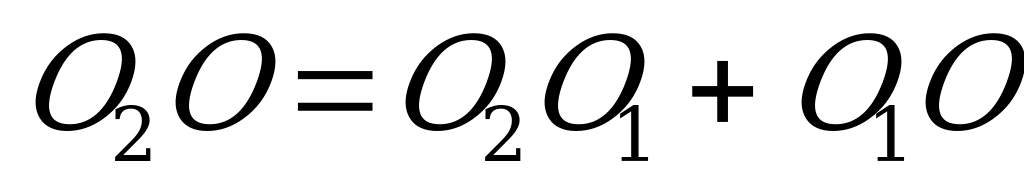 , так как ОА=ОS как радиусы сферы, то О1О=
, так как ОА=ОS как радиусы сферы, то О1О=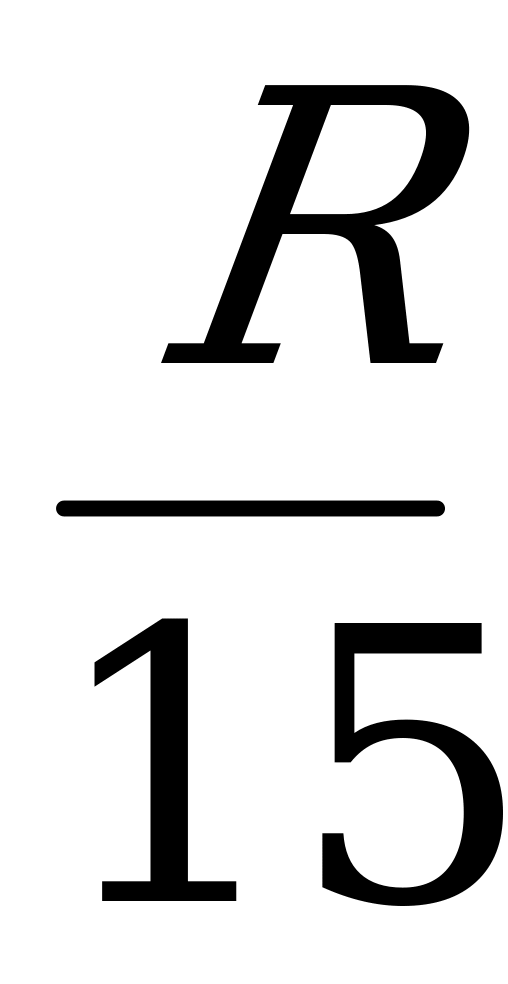 ,тогда
,тогда 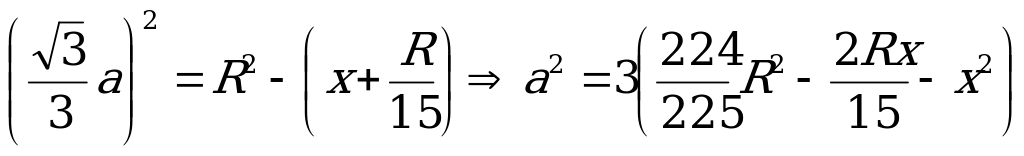 .
.
Вычислим объём призмы: 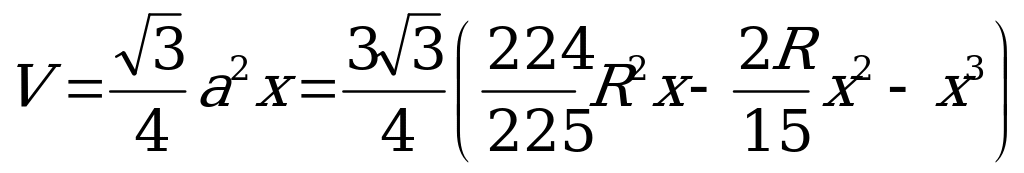 .Итак, получили объем призмы как функцию переменной x.Найдём производную функции
.Итак, получили объем призмы как функцию переменной x.Найдём производную функции  :
: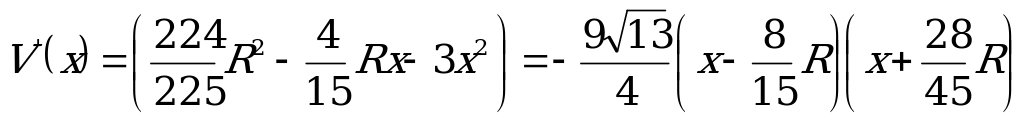 ;
; 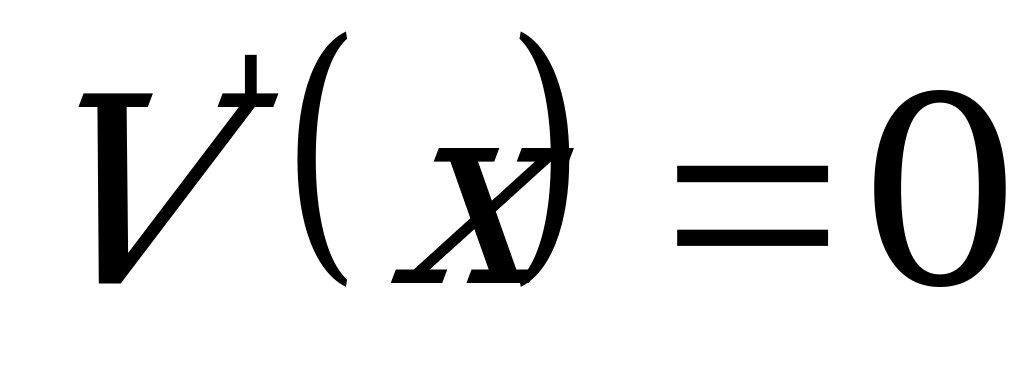 при
при  ,x0.
,x0. 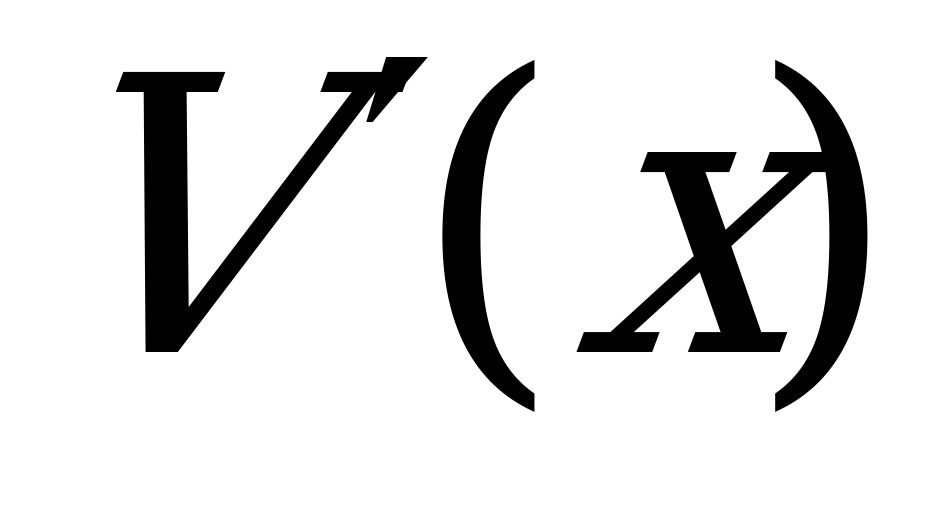 при переходе через точку
при переходе через точку 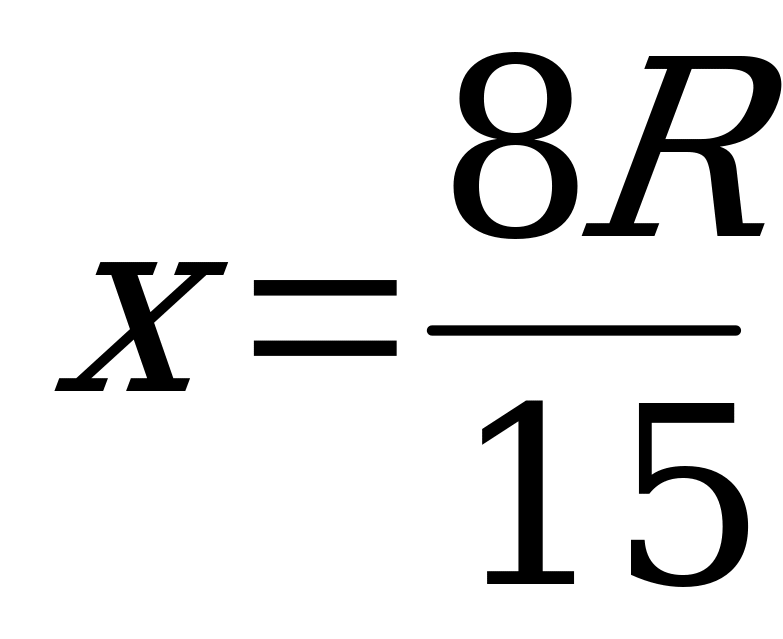 меняет знак с
меняет знак с «+» на «-« , значит это точка максимума .
«+» на «-« , значит это точка максимума .
Итак, 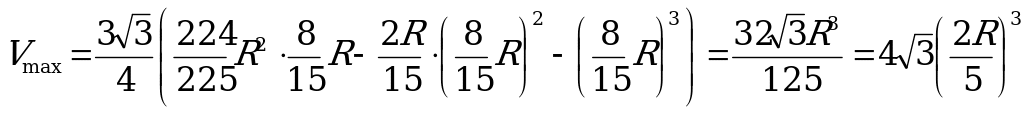 .
.
Ответ: 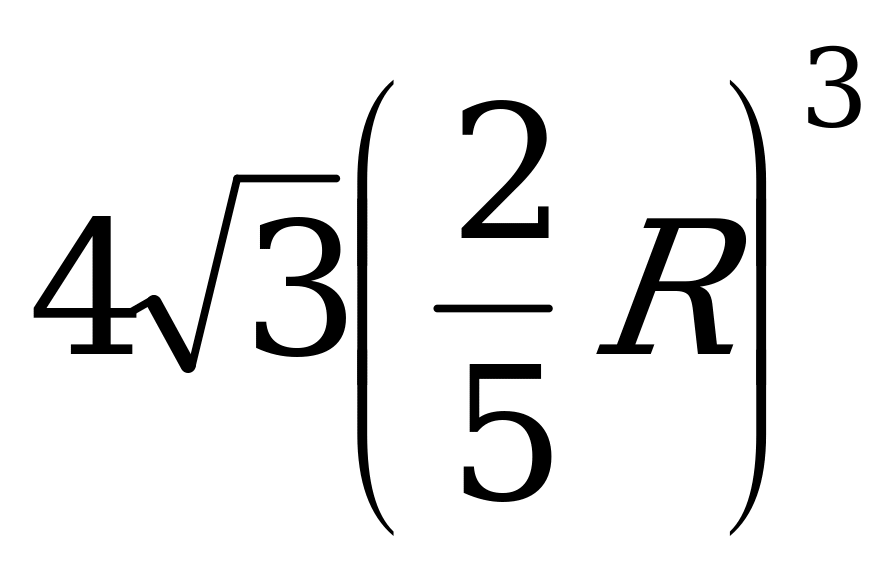
В сферу вписана правильная треугольная призма, все рёбра которой имеют одну и ту же длину а. Подобная ей призма одним основанием лежит на боковой грани данной призмы, а вершины ее верхнего основания расположены на сфере. Вычислить длину ребра второй призмы. Определить отношение объема второй призмы к объему шара, ограниченного сферой.
Ответ: 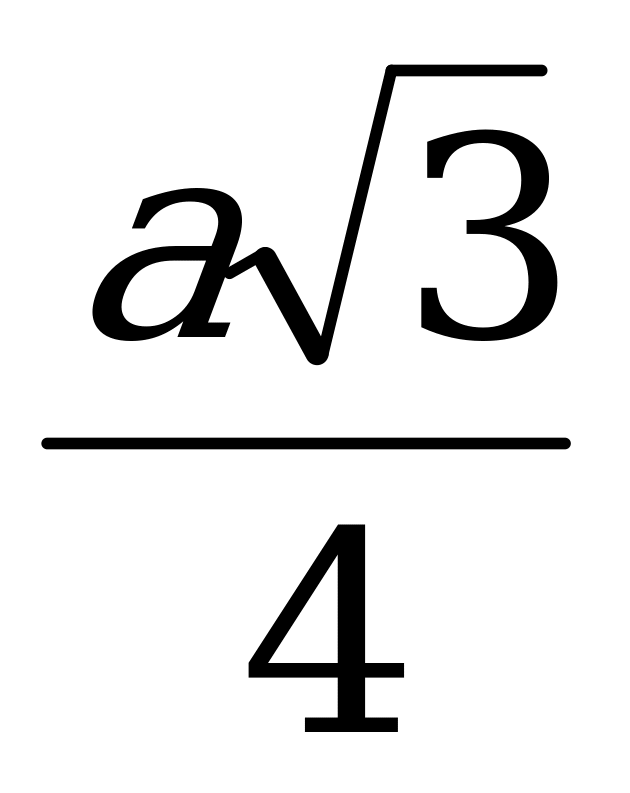 ;
; 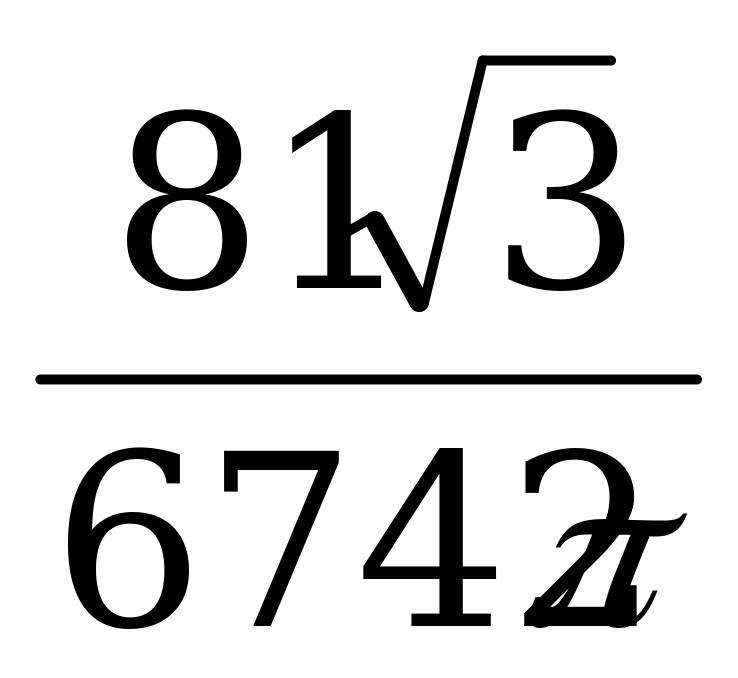 .
.
Шар радиуса r вписан в правильную четырёхугольную пирамиду, которая, в свою очередь, вписана в сферу. Определить, какой должна быть высота пирамиды, чтобы радиус описанной сферы был наименьшим? Найти это наименьшее значение радиуса. Докажите, что в этом случае центры вписанного шара и описанной сферы совпадают.
Р
 ешение.
ешение.
Пусть высота пирамиды 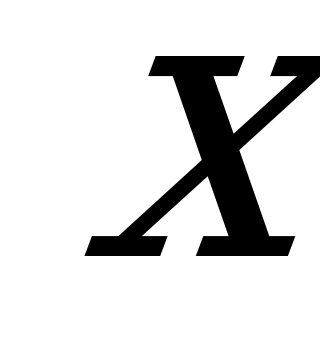 , где
, где  ,R-радиус описанной сферы, а- сторона основания пирамиды О-центр описанной сферы,
,R-радиус описанной сферы, а- сторона основания пирамиды О-центр описанной сферы,
О1- центр вписанного шара.
Треугольник  подобен треугольнику SBC, отсюда :
подобен треугольнику SBC, отсюда : 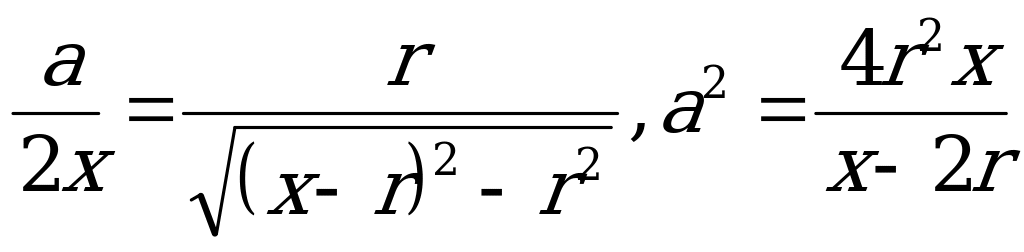 . Из
. Из 
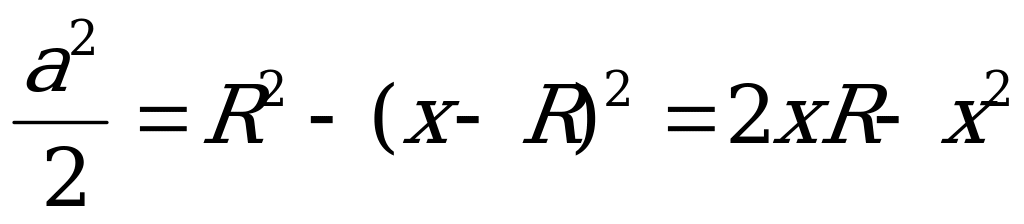 ;
; 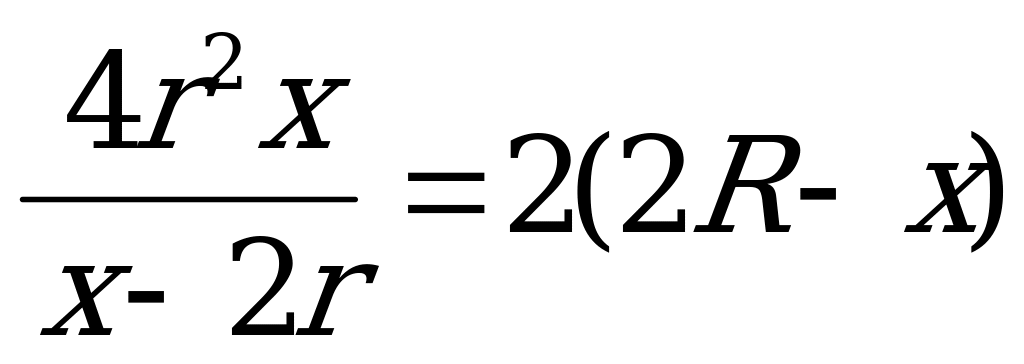 ;
;  ;
; 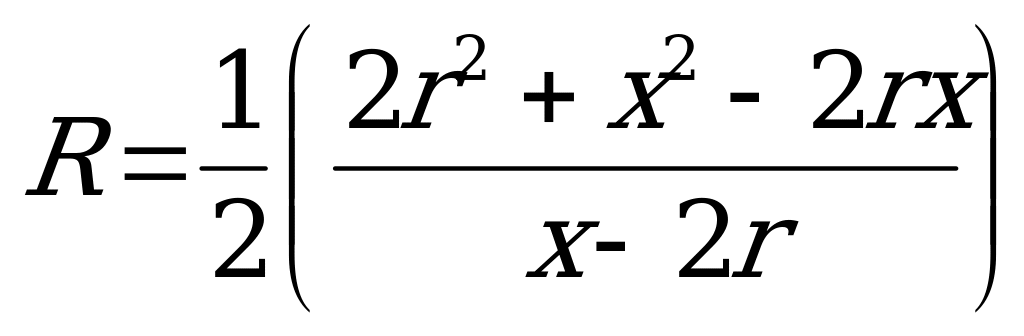
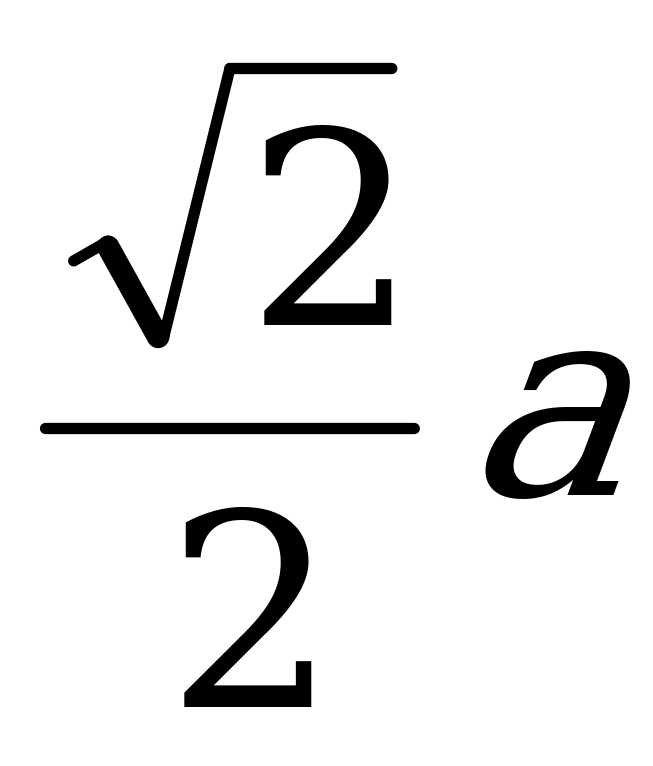 ;
; 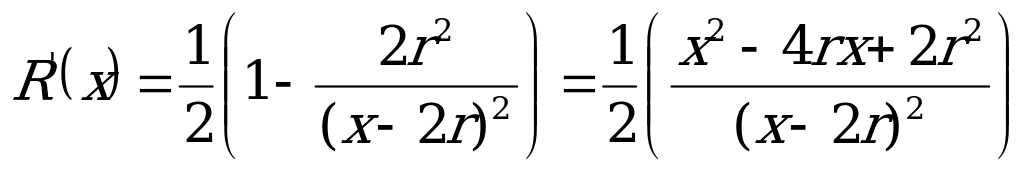
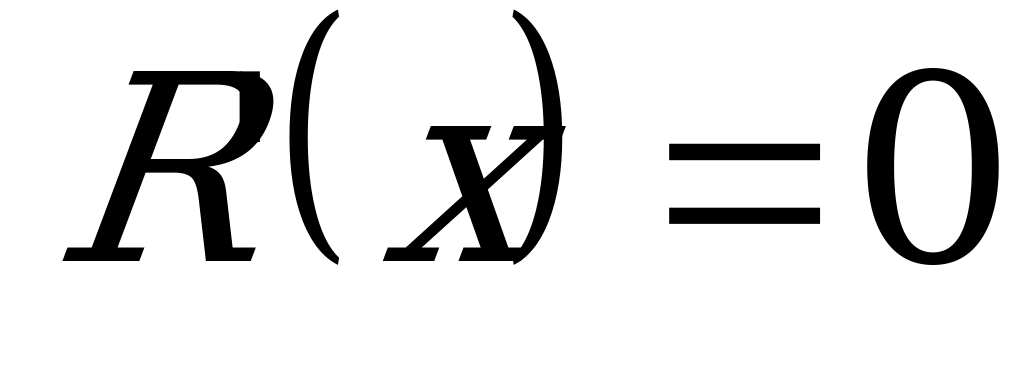 при
при 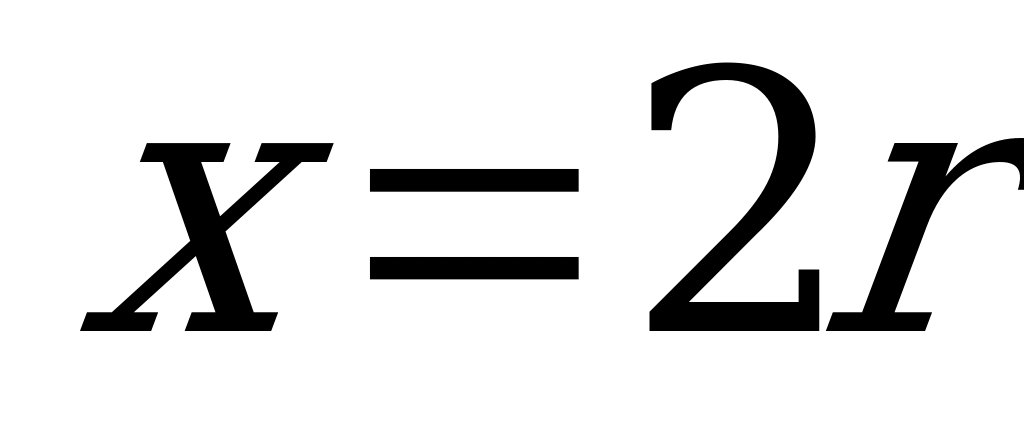 ±
±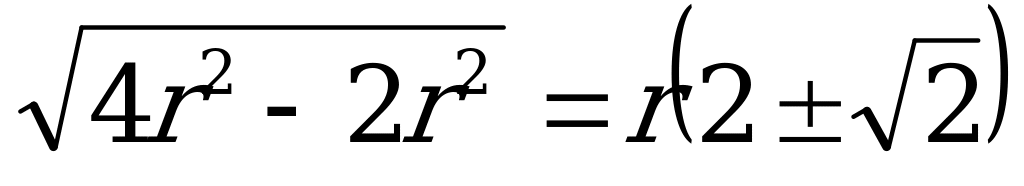 . Т.к.
. Т.к.  , то
, то 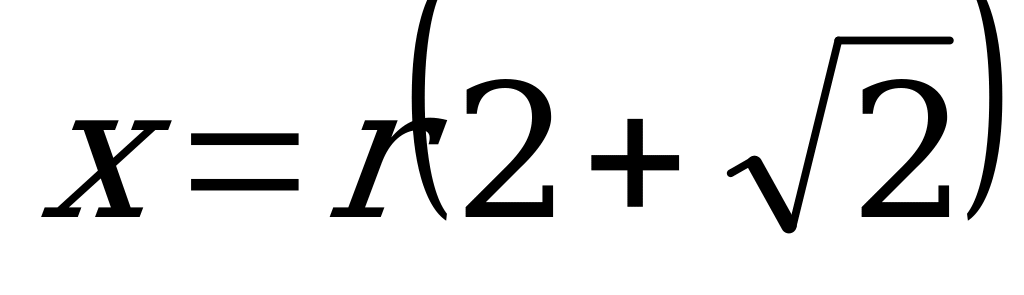 .Вокруг точки
.Вокруг точки 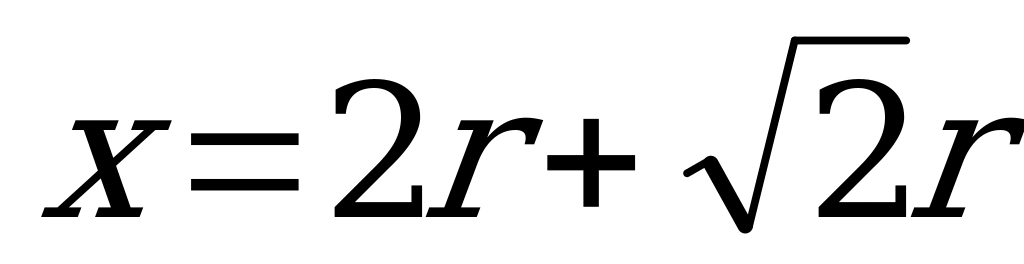 производная меняет свой знак с минуса на плюс, значит это точка минимума. Найдём наименьшее значение радиуса:
производная меняет свой знак с минуса на плюс, значит это точка минимума. Найдём наименьшее значение радиуса:
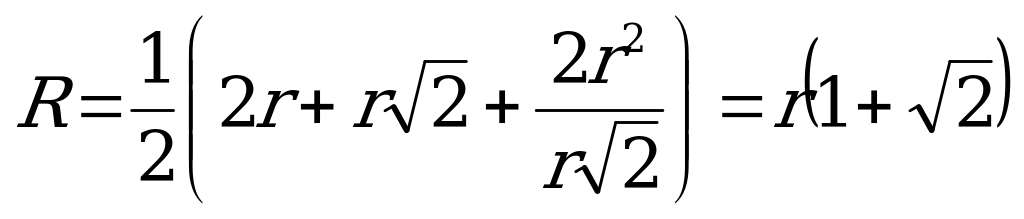 .
.
Центры  и
и  совпадают, если
совпадают, если 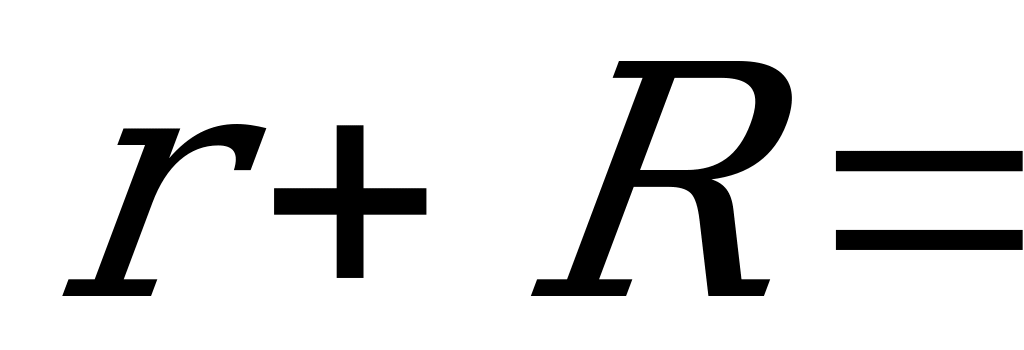 x, проверим это:
x, проверим это:
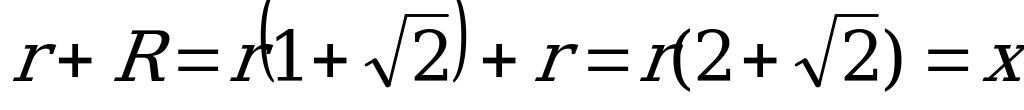 - значит центры описанной сферы и вписанного шара совпадают.
- значит центры описанной сферы и вписанного шара совпадают.
Ответ: 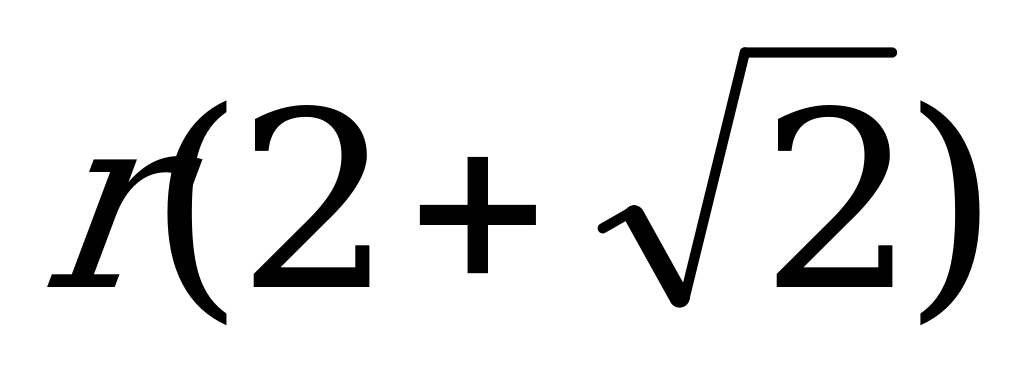 .
.
Основание параллелепипеда – квадрат со стороной 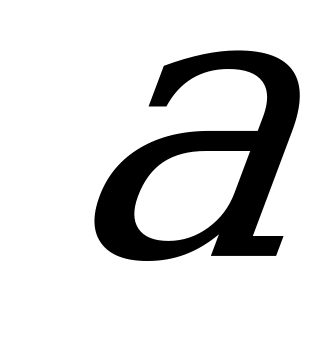 . Одна из вершин верхнего основании одинаково удалена от всех вершин нижнего основания. Известно, что в параллелепипед можно вписать шар, касающийся всех его граней. Найти длину боковых рёбер параллелепипеда и радиус вписанного шара.
. Одна из вершин верхнего основании одинаково удалена от всех вершин нижнего основания. Известно, что в параллелепипед можно вписать шар, касающийся всех его граней. Найти длину боковых рёбер параллелепипеда и радиус вписанного шара.
Ответ: 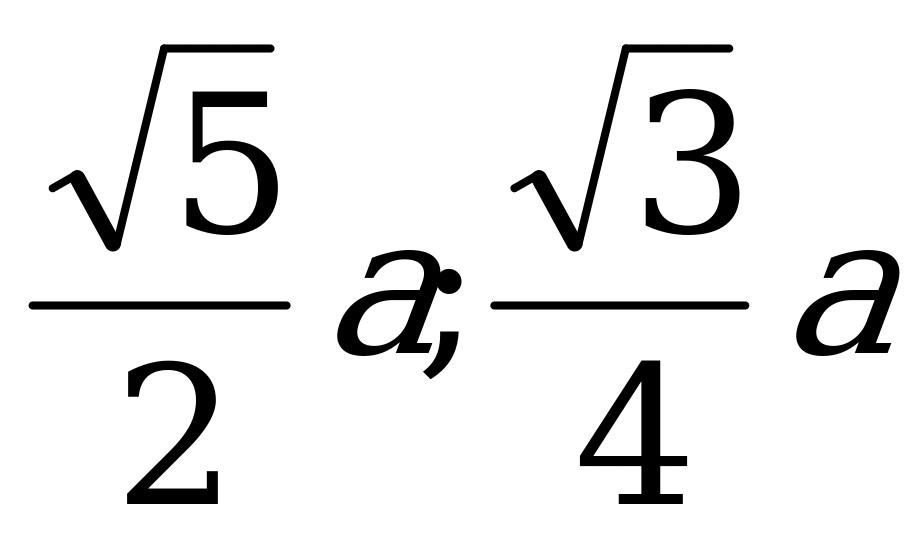 .
.







 ФЕДЕРАЛЬНЫЙ ПРОЕКТ «КАДРЫ ДЛЯ ЦИФРОВОЙ ЭКОНОМИКИ»
ФЕДЕРАЛЬНЫЙ ПРОЕКТ «КАДРЫ ДЛЯ ЦИФРОВОЙ ЭКОНОМИКИ» опустим, что в некоторую прямую призму вписан шар (рис. №1).Докажем, что в основание этой призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. Из центра шара, точки О, проведём радиусы OM и ON в точки касания шара с гранями
опустим, что в некоторую прямую призму вписан шар (рис. №1).Докажем, что в основание этой призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. Из центра шара, точки О, проведём радиусы OM и ON в точки касания шара с гранями  опустим, что шар описан около призмы (рис. №2). Докажем, что призма прямая и что около её основания можно описать окружность.
опустим, что шар описан около призмы (рис. №2). Докажем, что призма прямая и что около её основания можно описать окружность.
 Докажем, что около основания этой пирамиды можно описать окружность. Плоскость основания пересекает поверхность сферы по окружности (теорем о сечении шара плоскостью). Вершины основания лежат на поверхности шара и на плоскости основания, следовательно, они лежат на линии пересечения их, т.е. на окружности. Поэтому около основания можно описать окружность.
Докажем, что около основания этой пирамиды можно описать окружность. Плоскость основания пересекает поверхность сферы по окружности (теорем о сечении шара плоскостью). Вершины основания лежат на поверхности шара и на плоскости основания, следовательно, они лежат на линии пересечения их, т.е. на окружности. Поэтому около основания можно описать окружность. ледствие 2. Если боковые ребра пирамиды равны между собой (или равнонаклонены к плоскости основания), то около такой пирамиды можно описать шар (рис. № 5). Центр шара в этом случае лежит в точке пересечения высоты пирамиды (или ее продолжения) с осью симметрии бокового ребра, лежащей в плоскости бокового ребра и высоты.
ледствие 2. Если боковые ребра пирамиды равны между собой (или равнонаклонены к плоскости основания), то около такой пирамиды можно описать шар (рис. № 5). Центр шара в этом случае лежит в точке пересечения высоты пирамиды (или ее продолжения) с осью симметрии бокового ребра, лежащей в плоскости бокового ребра и высоты. 
 еорема 5. Около любой правильной усеченной пирамиды можно описать шар.
еорема 5. Около любой правильной усеченной пирамиды можно описать шар.  еорема 6. В правильную усеченную пирамиду можно вписать шар в том и только в том случае, если апофема пирамиды равна сумме апофем оснований (рис.8).
еорема 6. В правильную усеченную пирамиду можно вписать шар в том и только в том случае, если апофема пирамиды равна сумме апофем оснований (рис.8). 





 Решение. Обозначим через x длину отрезка в правильной пирамиде, входящего как в прямоугольный треугольник, содержащий данный угол, так и в треугольник, содержащий искомый угол. Выразим далее через x и функции данного угла одну из двух других сторон в том треугольнике, который содержит искомый угол. Затем найдём функцию искомого угла.
Решение. Обозначим через x длину отрезка в правильной пирамиде, входящего как в прямоугольный треугольник, содержащий данный угол, так и в треугольник, содержащий искомый угол. Выразим далее через x и функции данного угла одну из двух других сторон в том треугольнике, который содержит искомый угол. Затем найдём функцию искомого угла.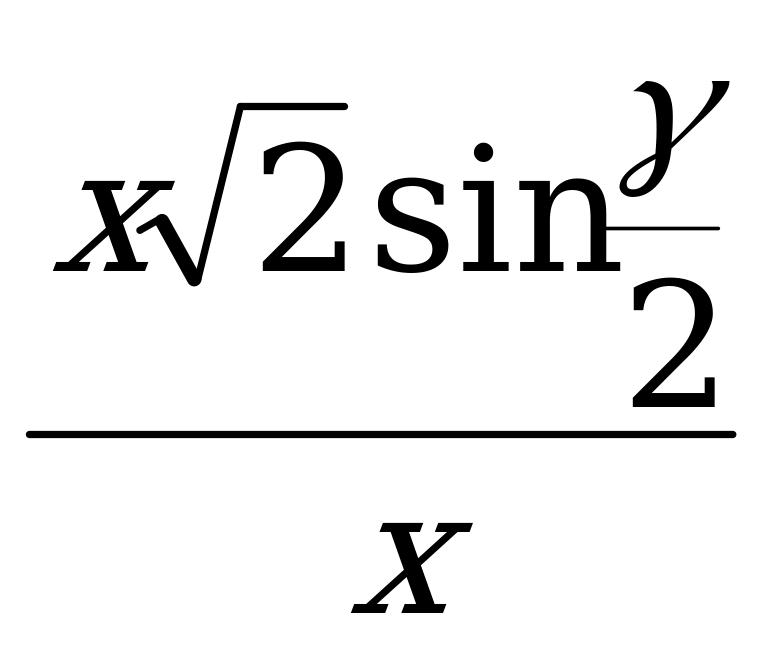 =
= 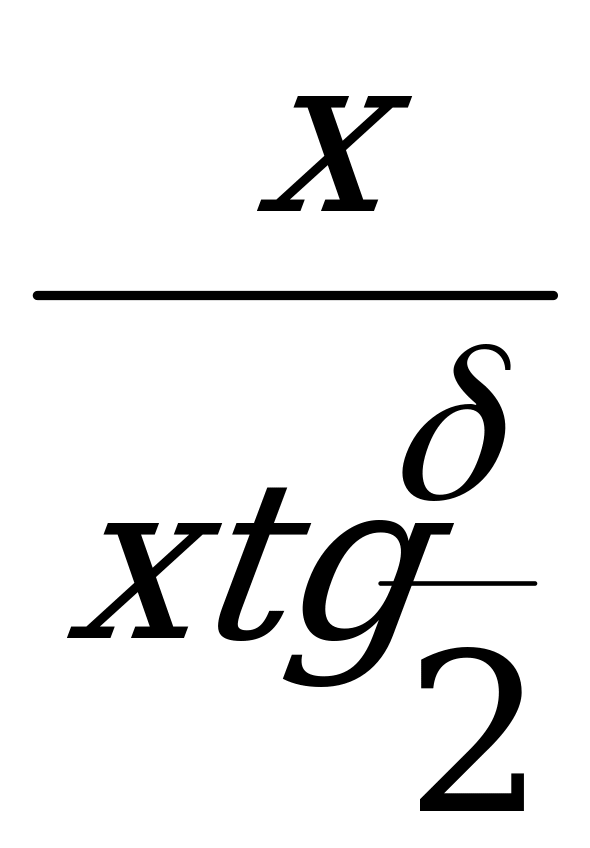 = ctg
= ctg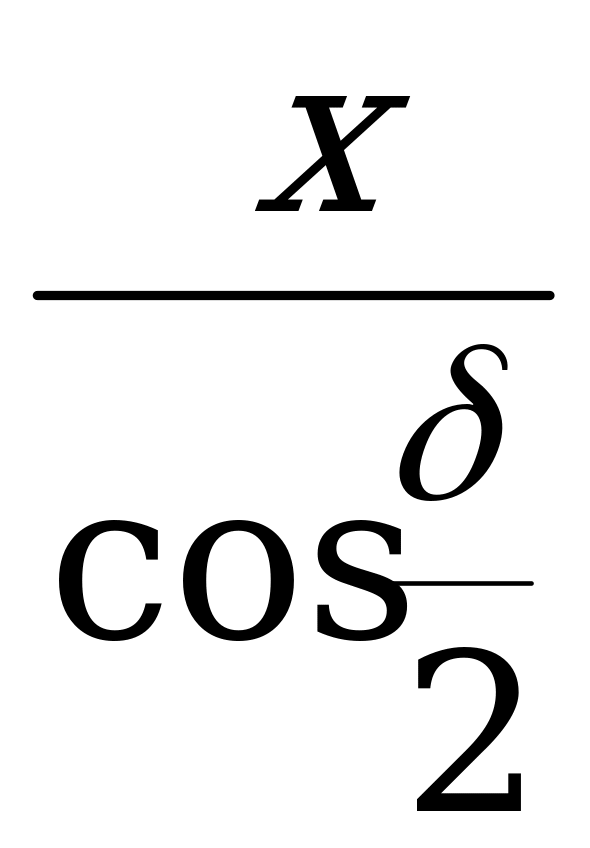 . Из
. Из 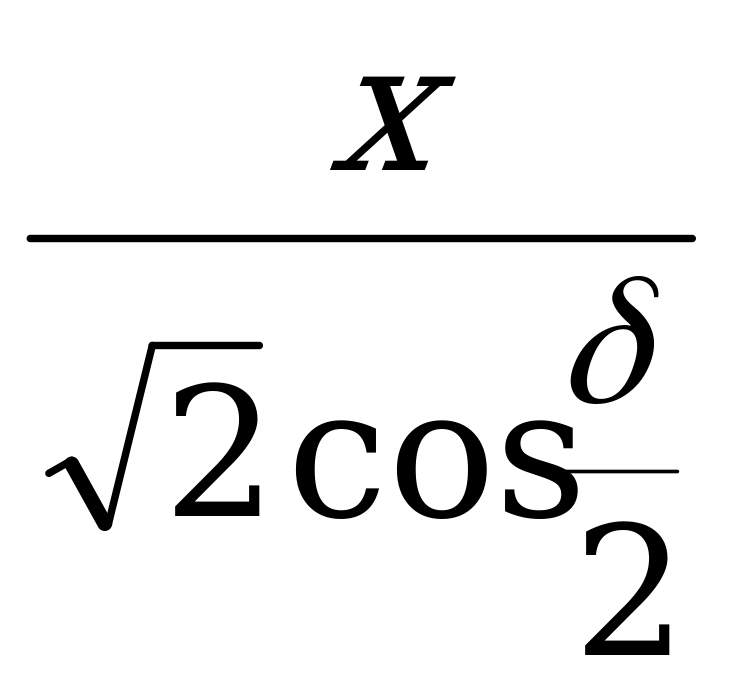 .
.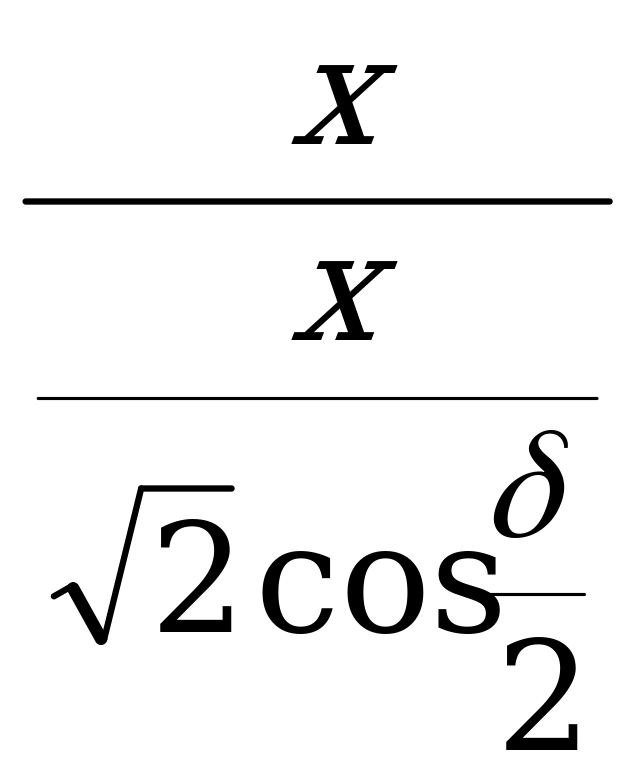 =
=  ывод формул перехода для правильной треугольной пирамиды.
ывод формул перехода для правильной треугольной пирамиды. Формулы перехода для правильной n-угольной пирамиды.
Формулы перехода для правильной n-угольной пирамиды.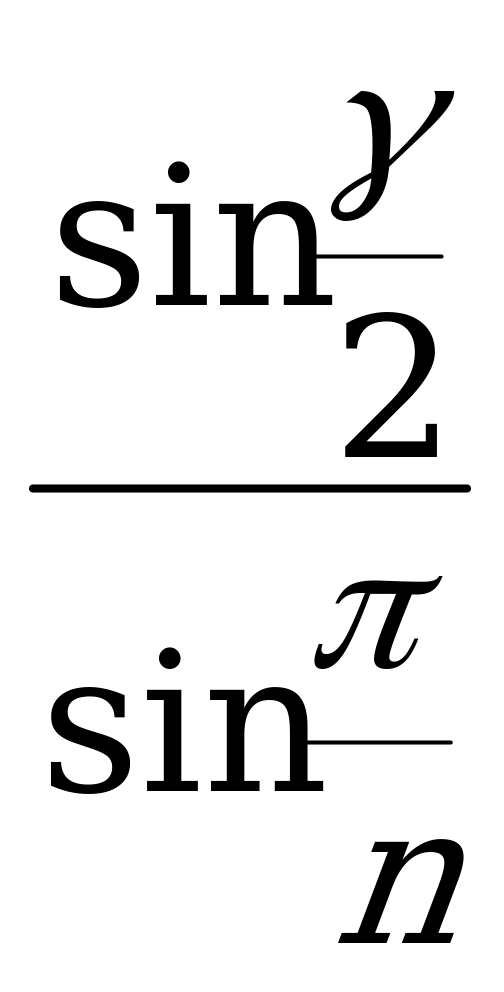 ; (XIV)
; (XIV)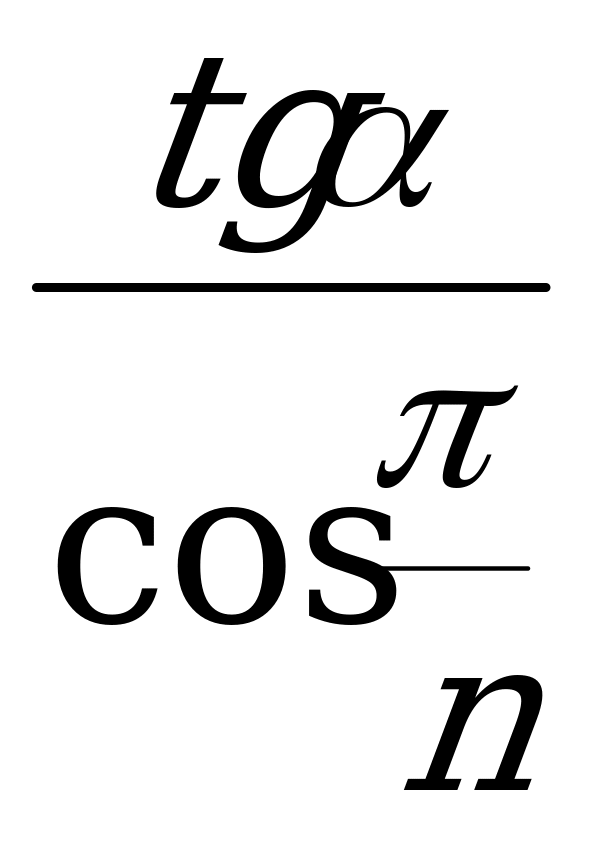 ; (XVI)
; (XVI)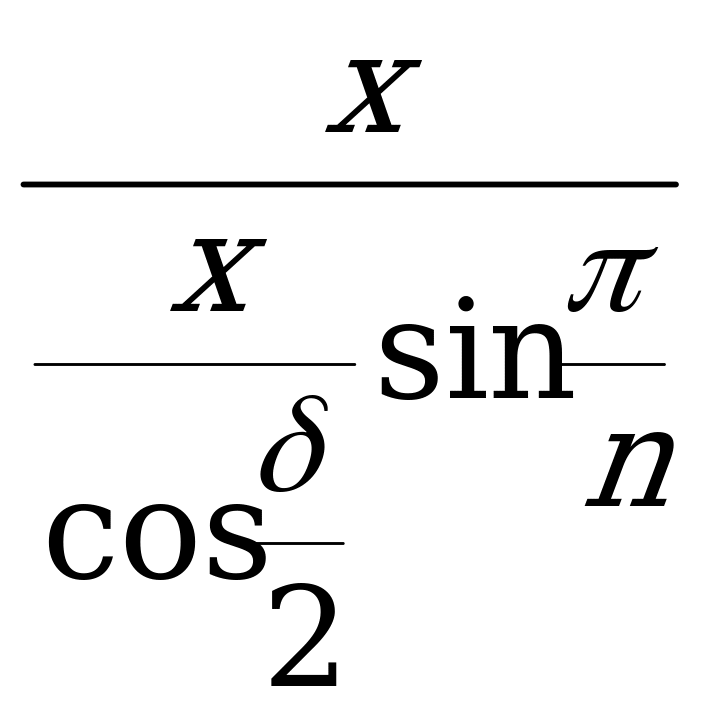 =
= 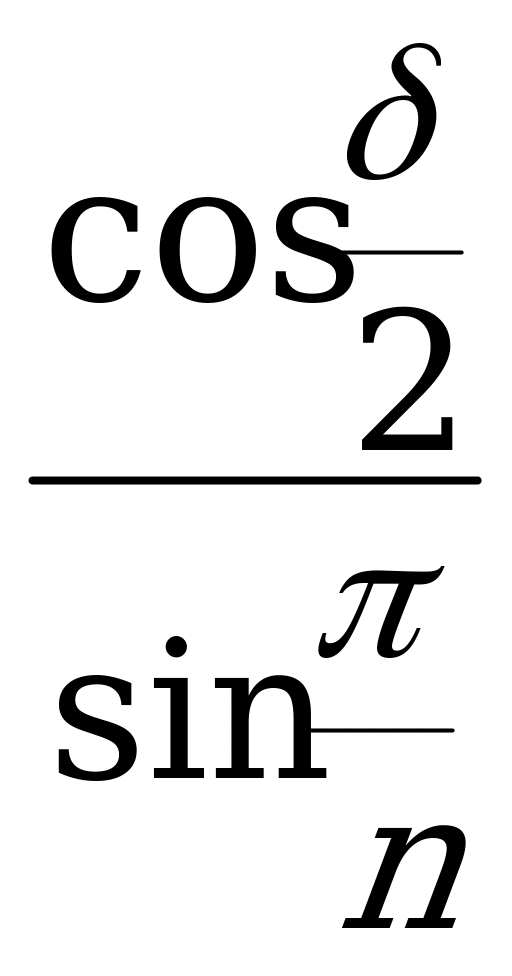 ,
,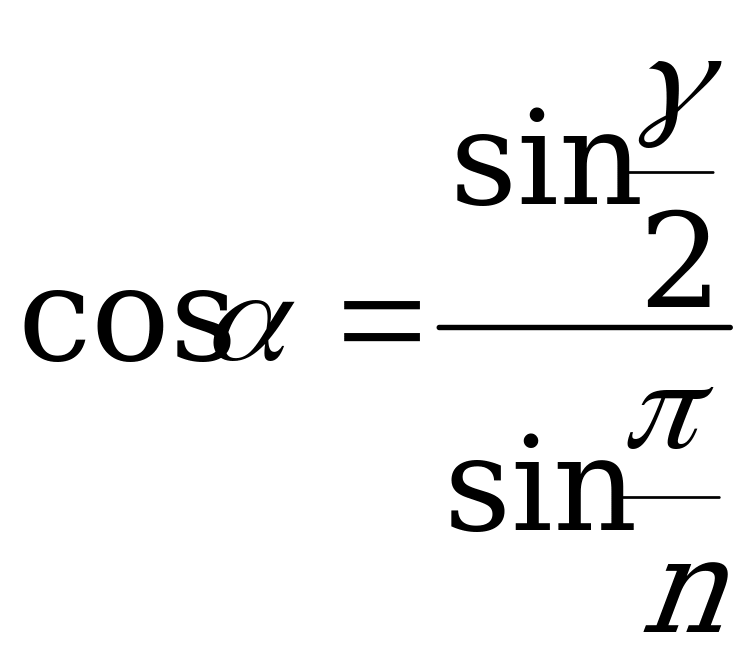
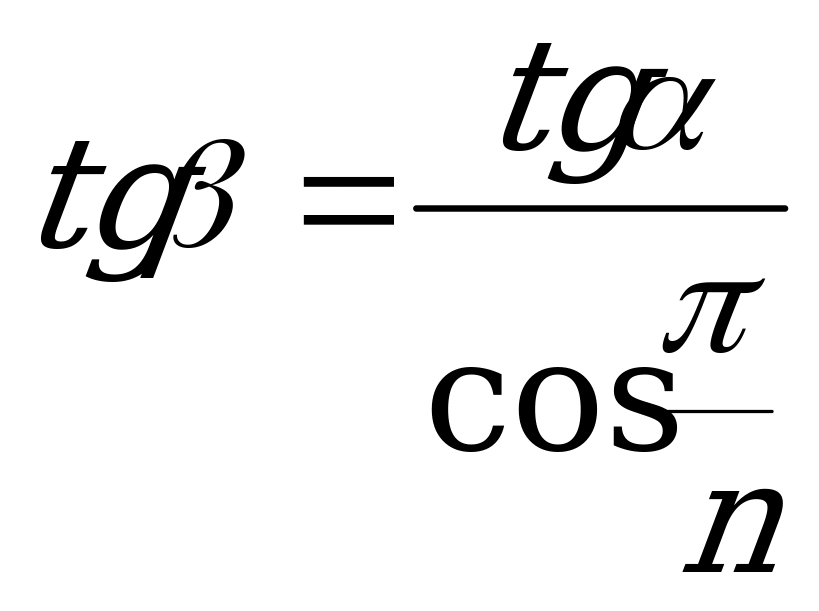
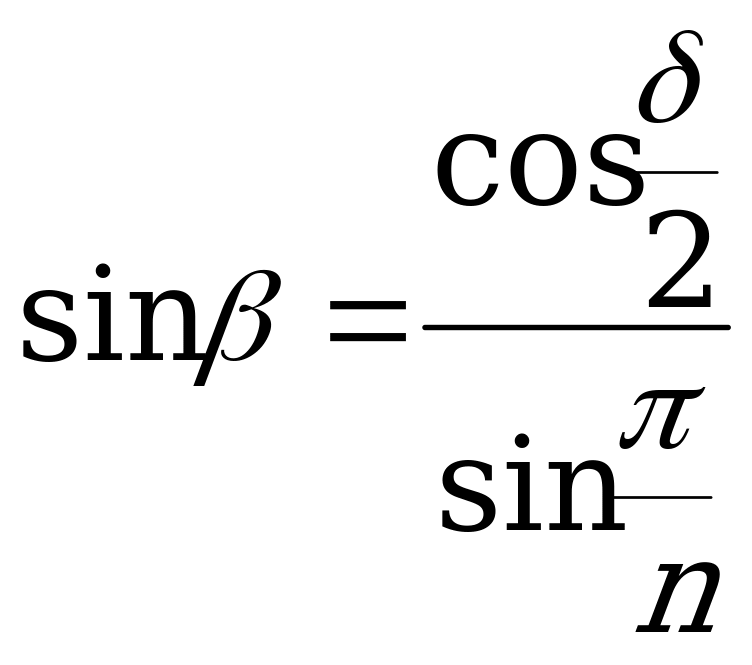



 . Найдём угол
. Найдём угол 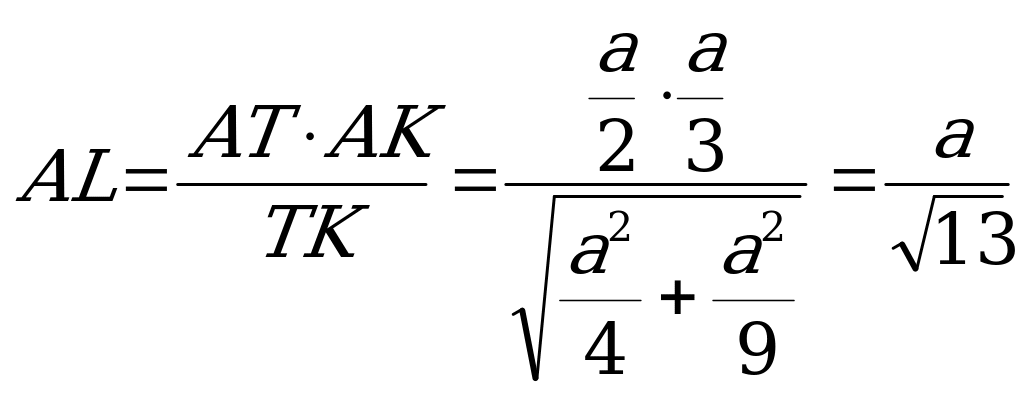 , то
, то  айдите :1) угол между плоскостью сечения и плоскостью основания; 2) площадь данного сечения; 3) расстояние от середины
айдите :1) угол между плоскостью сечения и плоскостью основания; 2) площадь данного сечения; 3) расстояние от середины  ешение. Через центр основания O проведём плоскость
ешение. Через центр основания O проведём плоскость  .Найдите площадь сечения правильной четырехугольной пирамиды TABCD плоскостью, проходящей через центр ее основания параллельно апофеме TK боковой грани TAB и медиане BM боковой грани TBC, если сторона основания равна 8, а
.Найдите площадь сечения правильной четырехугольной пирамиды TABCD плоскостью, проходящей через центр ее основания параллельно апофеме TK боковой грани TAB и медиане BM боковой грани TBC, если сторона основания равна 8, а
 . Найдите площадь сечения правильной треугольной пирамиды
. Найдите площадь сечения правильной треугольной пирамиды  Найдём положение
Найдём положение 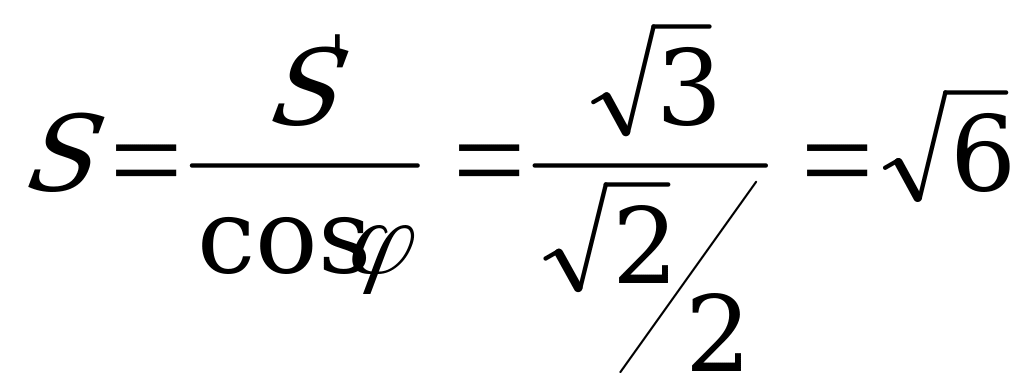 .
. . В основании пирамиды лежит ромб со стороной
. В основании пирамиды лежит ромб со стороной 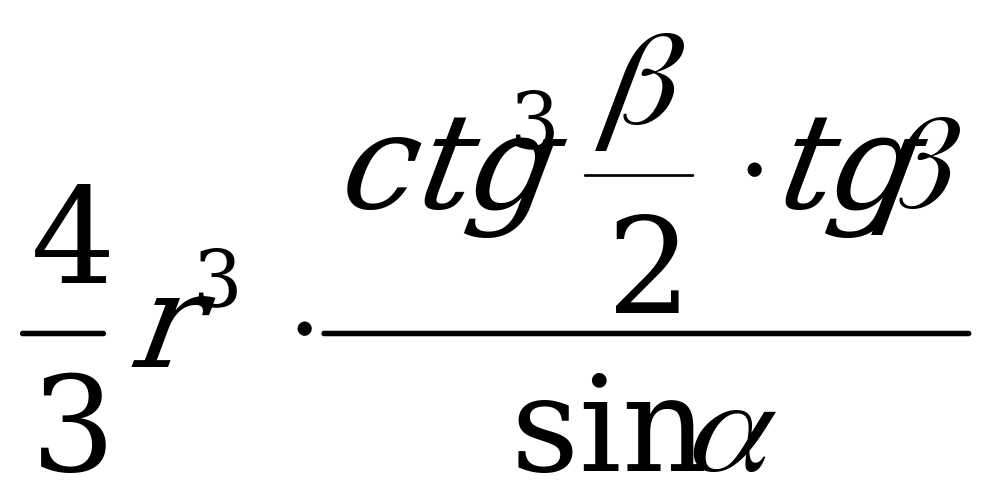 .
.
 ешение.
ешение. ешение.
ешение.