Просмотр содержимого документа
«№3 8_б Теорема о пересечении высот треугольника»
7.04.20. для 8-Б геометрия Урок № 3
Тема: Теорема о пересечении высот треугольника.
Цели: 1) Рассмотреть теорему о точке пересечения высот и следствие из неё;
2) Формировать умения применять известные знания для решения задач.
Скачиваем файл, чтобы не потерять данные
https://www.youtube.com/watch?v=qbp1dh1tCp88 класс, 37 урок, Теорема о пересечении высот треугольника
https://www.youtube.com/watch?v=qgnCyeoDHIQеометрия 8 класс (Урок№31 - Теорема о пересечении высот треугольника.)
https://www.yaklass.ru/p/geometria/8-klass/okruzhnost-9230/chetyre-zamechatelnye-tochki-treugolnika-9279Четыре замечательные точки треугольника (эту ссылку копируйте и в поиск Яндекс вставить)
1. Организационный момент.
Записываем число. Тему урока и начинаем выполнять задания.
2. Актуализация
1. Сформулировать и доказать теоремы о свойстве биссектрисы и серединном перпендикуляре. Устно. Проговаривая доказательство, все делаем с помощью учебника.
2. Решить ПРОВЕРЯЕТСЯ.
А)
| 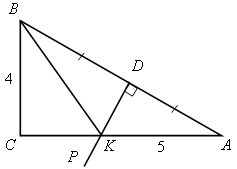
| Найти: РВKС, РАВС. Вспоминаем свойства серединного перпендикуляра и египетский треугольник 5; 4; 3. Ответ: 12 и 20
|
| Б) |
| 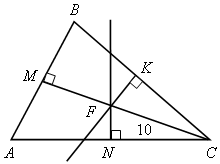
| FK, FN серединные перпендикуляры. АВ = 16 СF = 10 Найти расстояние от точки F до стороны АВ. Вспоминаем серединные перпендикуляры, их свойства. Ответ: 6
|
3. Новый материал
Мы продолжим изучение темы «Замечательные точки треугольника» и познакомимся с теоремой о точке пересечения высот в треугольнике.
Как определяется высота в треугольнике? Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
2. Практическая работа. Выполняем в рабочей тетради. ПРОВЕРЯЕТСЯ
Постройте остроугольный треугольник АВС.
| 1. Проведите ВК АС 2. Проведите AN ВС. 3. Проведите CM AB.
| 
|
|
Все высоты пересеклись в одной точке О.
|
| Вывод: В остроугольном треугольнике все три высоты пересеклись в одной точке. Эта точка расположена в плоскости треугольника.
|
Постройте тупоугольный треугольник KMN
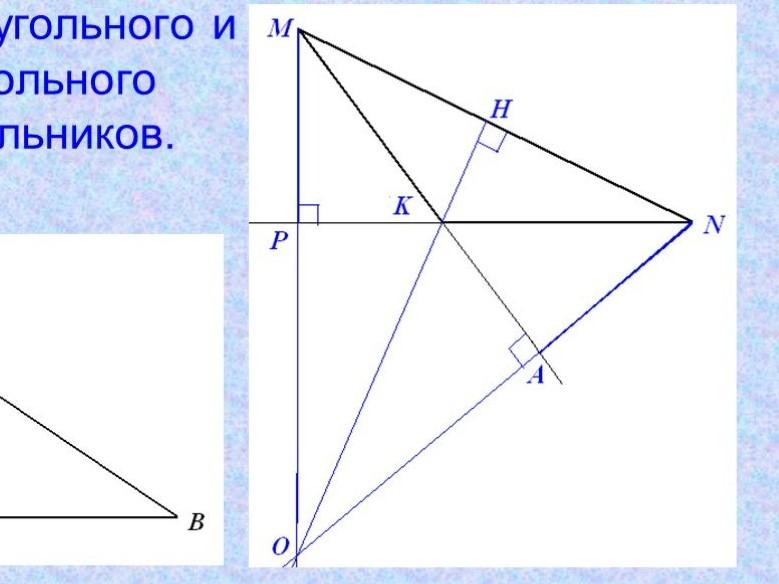
| 1. Проведите MP NK, основание высоты лежит на продолжении NK.
2. Проведите AN MK, основание высоты лежит на продолжении MK.
3. Проведите KH MN. |
|
|
Продолжения высот тупоугольного треугольника пересеклись в одной точке О.
|
| Вывод: В тупоугольном треугольнике все три высоты пересеклись в одной точке. Эта точка расположена вне плоскости треугольника.
|
Постройте высоты в прямоугольном треугольнике (самостоятельно) и убедитесь: ПРОВЕРЯЕТСЯ
|
Высоты прямоугольного треугольника пересеклись в одной точке О.
|
| В прямоугольном треугольнике все три высоты пересеклись в одной точке. Эта точка лежит в плоскости треугольника и совпадает с вершиной прямого угла треугольника.
|
Теорема о пересечении высот треугольника:
Высоты треугольника (или их продолжения) пересекаются в одной точке.
(доказательство смотрим в ссылках)
Закрепление изученного материала. Делаем в тетради
| 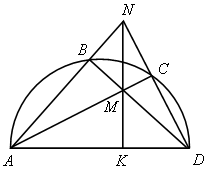
| 1. Решить устно: Дуга АD – полуокружность. Доказать MN АD. АD.
|
| Решение: 1. Δ ABD: B=90˚-опирается на диаметр. Δ AСD: M=ACÇBDÇNKÞNK-высота ΔANDÞ MN АD. АD.
|
| 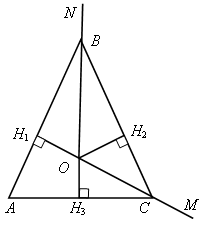
| | № 677. Решение 1)  АВО = 180° – АВО = 180° –  АВN = АВN = 180°–  СВN = СВN =  CВО, то есть ВО – биссектриса CВО, то есть ВО – биссектриса  АВС, АВС, аналогично СО – биссектриса  АСВ. АСВ. 2) По теореме о биссектрисе угла, точка О равноудалена от сторон АВ, ВС, АС. Таким образом, ОН1 = ОН2 = ОН3, где ОН1 АВ, ОН2 АВ, ОН2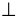 ВС, ОН3 ВС, ОН3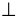 АС. АС. |
| 2. Получили, что АВ, ВС, АС – касательные к окружности с центром в точке О и радиусом, равным ОН1. |
Домашнее задание. Рефлексия.
Заполнить таблицу
| Тема занятия | Мои действия на занятии (слушал, выполнял эксперимент, общался...) | Я на занятии научился, узнал.. (оценивать свои действия, приобретать знания caмостоятельно и т.д.) | В чем ценность занятия для меня? | Что вызвало затруднения и почему? | Свою работу я оценил бы на оценку ..., потому что ... | Класс (учитель) выставил мне за работу оценку ... | Меня порадовало (огорчило) |
Д/з
Стр. 184 №1– 20, вопросы. Проговорить вслух, запомнить.
п. 76 № 681, 688





















