823, 26.03.2020 "Решение дифференциальных уравнений 2-го порядка".

Практическая работа по теме: «Решение дифференциальных уравнений II-го порядка»

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

В теории и практике различают два типа таких уравнений – однородное уравнение и неоднородное уравнение.

Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:

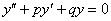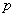, где   и 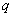  – константы (числа), а в правой части – строго ноль.

Неоднородное ДУ второго порядка с постоянными коэффициентами имеет вид:
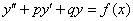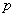, где   и 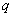  – константы, а  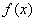 – функция, зависящая только от «икс». В простейшем случае функция  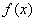 может быть числом, отличным от нуля.

Какая мысль приходит в голову после беглого взгляда? Неоднородное уравнение кажется сложнее. На этот раз первое впечатление не подводит!

Кроме того, чтобы научиться решать неоднородные уравнения необходимо уметь решать однородные уравнения. По этой причине сначала рассмотрим алгоритм решения линейного однородного уравнения второго порядка:

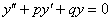
Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

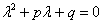
По какому принципу составлено характеристическое уравнение, отчётливо видно: 
вместо второй производной записываем  ;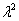
вместо первой производной записываем просто «лямбду»;
вместо функции 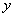  ничего не записываем.

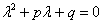 – это обычное квадратное уравнение, которое предстоит решить.

Существуют три варианта развития событий. 
Они доказаны в курсе математического анализа, и на практике мы будет использовать готовые формулы.

Характеристическое уравнение имеет два различных действительных корня

Если характеристическое уравнение 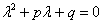  имеет два различных действительных корня  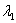,  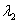 (т.е., если дискриминант  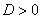), то общее решение однородного уравнения выглядит так: 
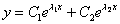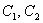, где   – константы.

В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например, 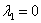 , тогда общее решение: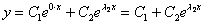 

Пример 5

Решить дифференциальное уравнение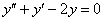 

Решение: составим и решим характеристическое уравнение:

, 

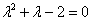
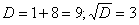
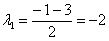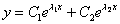
Ответ: общее решение: 

Характеристическое уравнение имеет два кратных действительных корня

Если характеристическое уравнение 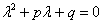  имеет два кратных (совпавших) действительных корня   (дискриминант  ), то общее решение однородного уравнения принимает вид: 
, где 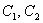  – константы. 
Вместо 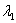  в формуле можно было нарисовать  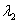, корни всё равно одинаковы.

Если оба корня равны нулю  , то общее решение опять же упрощается:  . Кстати,   является общим решением того самого примитивного уравнения  , о котором я упоминал в начале урока. Почему? Составим характеристическое уравнение:   – действительно, данное уравнение как раз и имеет совпавшие нулевые корни  .

Пример 6

Решить дифференциальное уравнение 

Решение: составим и решим характеристическое уравнение:

Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно невозбранно применить известную школьную формулу сокращенного умножения:

Получены два кратных действительных корня 

Ответ: общее решение: 

Характеристическое уравнение имеет сопряженные комплексные корни

Если характеристическое уравнение 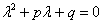  имеет сопряженные комплексные корни  ,   (дискриминант  ), то общее решение однородного уравнения принимает вид: 
, где 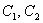  – константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом: 

Если получаются чисто мнимые сопряженные комплексные корни:  , то общее решение упрощается:

Пример 7

Решить однородное дифференциальное уравнение второго порядка

Решение: Составим и решим характеристическое уравнение:


 – получены сопряженные комплексные корни

Ответ: общее решение: 

Пример 8

Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям  , 

Решение: составим и решим характеристическое уравнение:

, 
Получены два различных действительных корня, поэтому общее решение:

Алгоритм нахождения частного решения следующий:

Сначала используем начальное условие  :

Согласно начальному условию, получаем первое уравнение:   или просто 

Далее берём наше общее решение   и находим производную:

Используем второе начальное условие  :

Согласно второму начальному условию, получаем второе уравнение:   или просто 

Составим и решим систему из двух найденных уравнений:

Подставим найденные значения констант   в общее решение  :

Ответ: частное решение: 

ЗАДАНИЯ:

1. Найти общее решение дифференциального уравнения 2-го порядка.

А) ; Б) ;

1. Найти частное решение дифференциального уравнения 2-го порядка.

А)

Б)