Министерство образования и науки Хабаровского края
Краевое государственное бюджетное
профессиональное образовательное учреждение
«Комсомольский-на-Амуре авиастроительный лицей»
СОГЛАСОВАНО УТВЕРЖДАЮ
Председатель ЦК Зам. директора по УМР
__________Н.А. Ржевская _________ А.В.Барышникова
«_____»______________2015 г. «____»____________2015 г.
Контрольно-оценочные средства
для промежуточной аттестации
по ОУД. 03 МАТЕМАТИКА
за 1 семестр I курса
по профессии: 24.01.01 Слесарь-сборщик авиационной техники
г. Комсомольск-на-Амуре
2015 г.
Разработчики:
КГБ ПОУ КАСЛ преподаватель М.В. Дробашко
(место работы)(занимаемая должность)(инициалы, фамилия)
Паспорт комплекта контрольно-оценочных средств
Комплект контрольно-оценочных средств предназначен для оценки результатов освоения программы УД «Математика» за 1 семестр 1 курса
Объектами проверки выступают элементы содержания, а также умения, способы познавательной деятельности, определенные требованиями ФГОС НПО.
Для достижения поставленной цели разработан и используется комплекс заданий, различающихся по характеру, направленности, уровню сложности.
Контрольно-измерительный материал состоит из 2 частей.
Часть 1 включает 15 заданий (1-15) 1 уровня освоения учебного материала. Решение и ответы к этим заданиям должны быть выбраны из вариантов предложенных ответов.
Часть 2 состоит из 5 заданий (ПЗ1 ̶ ПЗ5) 2 и 3 уровня освоения учебного материала. Решение и ответы к этим заданиям должны быть сформулированы самостоятельно.
Время выполнения – 45 минут, место выполнения – учебная аудитория.
Правильность решения и ответ в зависимости от сложности каждого задания оценивается одним или несколькими баллами. Баллы, полученные при выполнении задания, суммируются.
Структура и содержание контрольно-измерительного материала
| Части работы | Число заданий | Максимальный балл |
| Часть 1 | 15 | 15 |
| Часть 2 | 5 | 10 |
| Итого | 20 | 25 |
|
|
|
|
В результате оценки осуществляется проверка следующих объектов:
| Объекты оценивания | Показатели | Критерии | Форма аттестации (в соответствии с учебным планом) |
| 1.1.Знать корни и степени. Корни натуральной степени из числа и их свойства. Степени с рацио-нальными показателями, их свойства. Степени с действительными пока-зателями. Свойства степени с действи-тельным показателем. 1.2. Знать логарифмы. Логарифм числа. Основное логарифми-ческое тождество. Десятичные и натураль-ные логарифмы. Правила действий с логарифмами. Переход к новому основанию. 1.3.Уметь преобразо-вывать алгебраические выражения. 1.4.Уметь преобразо-вывать рациональные, иррациональные степен-ные, показательные и логарифмические выражения.
| Правильно дает определение корня п-ой степени из натурального числа, правильно дает определение степени с рациональным и действительным показателем.
Верно и полно формулирует свойства степени. Правильно дает определение логарифма, десятичного и натурального логарифма. Правильно производит действия с логарифмами. Правильно переводит логарифм к новому основанию. Правильно применяет формулы для преобразования алгебраических выражений, иррациональных, степенных, показательных и логарифмических выражений. | Может произвести простейшие вычисления корня второй, третьей и четвертой степени соответствующих натуральных чисел.
Может перечислить все свойства степени. Может привести несколько примеров определения логарифма и виды (десятичного, натурального). Может произвести действия с логарифмами. Может перевести логарифм от одного основания к другому. Может выполнить преобразования алгебраических выражений, иррациональных, степенных, показательных и логарифмических выражений | Контрольная работа |
| 2.1.Знать радианную меру угла. Вращательное движение. Синус, косинус, тангенс и котангенс числа. 2.2. Знать основные тригонометрические тождества, формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. 2.3.Уметь преобразовать суммы тригонометри-ческих функций в произведение и произве-дения в сумму. 2.4. Уметь выражать тригонометрические функции через тангенс половинного аргумента. 2.5.Уметь преобразо-вывать простейших тригонометрических выражений. 2.6. Уметь решать простейшие тригоно-метрические уравнения. Простейшие тригономет-рические неравенства. Арксинус, арккосинус, арктангенс числа. |
Знает определение радианной меры угла, делает описание вращательного движения. Дает определение синуса, косинуса, тангенса и котангенса. Выводит основное тригонометрическое тождество. Знает формулу синуса и косинуса двойного угла. Формулу половинного угла. Выражает суммы тригонометрических функций в произведение и произведения в сумму. Выражает тригонометрические функции через функции половинного аргумента. Преобразует простейшие тригонометрические выражения.
Правильно решает тригонометрические неравенства и уравнения. Дает определение арксинуса, арккосинуса, арктангенса числа.
|
Может описать радианное измерение углов, привести примеры синуса, косинуса, тангенса и котангенса. Может вывести основное тригонометрическое тождество. Может применить формулу двойного и половинного угла при решении задач.
Может выразить суммы тригонометрических функций в произведение и произведения в сумму. Может выразить тригонометрические функции через функции половинного аргумента, преобразовать простейшие тригонометрические выражения.
Решить тригонометрические неравенства и уравнения, дать определение арксинуса, арккосинуса, арктангенса числа.
| Контрольная работа |
Условия выполнения задания
Максимальное время выполнения задания: ___45__минут.
Критерии оценки выполнения работы
| Оценка | Число баллов, необходимое для получения оценки |
| «3» (удовлетворительно) | 13 - 17
|
| «4» (хорошо) | 18 - 22
|
| «5» (отлично) | 23 - 25
|
2. Комплект контрольно-оценочных средств
Вариант 1
Часть 1 Задания для проведения тестирования
(задания с 1-15 – 1 балл)
1. Токарю нужно было сделать 120 деталей, но он перевыполнил план на 10 %. Сколько деталей сделал токарь?
а) 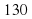 б)
б) 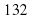 в)
в) 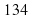 г) 140
г) 140
2. За 3 часа машина проехала 321 километр. Сколько она проедет за 5 часов, если будет двигаться с той же скоростью?
а) 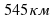 б)
б) 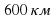 в)
в) 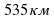 г) 635 км
г) 635 км
3. Представьте в виде степени с рациональным показателем 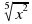
а) 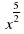 б)
б) 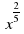 в)
в) 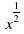 г)
г) 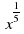
4. Вычислите: 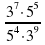
а) 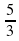 б)
б) 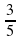 в)
в) 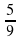 г)
г) 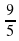
5. Упростить выражение: 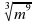
а) 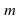 б)
б) 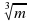 в)
в) 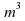 г)
г) 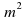
6. Вычислите: 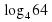
а) 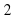 б)
б) 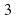 в)
в) 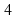 г) 5
г) 5
7. Вычислите: 
а) 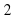 б)
б)  в)
в)  г) 5
г) 5
8. Найти радианную меру угла 20°
а)  б)
б)  в)
в)  г)
г) 
9. Выразить в градусах уголα = 
а) 16º б) 15º в) 20º г) 35º
10. Какой четверти числовой окружности принадлежит точка t = 
а) первой б) второй в) третьей г) четвёртой
11. Вычислить  .
.
а)  б)
б)  в)
в)  г) 1
г) 1
12. Вычислите:
а)  б)
б)  в)
в)  г)
г) 
13 Упростите
а)  б)
б)  в)
в)  г)
г) 
14 Синусом угла  называется ______________, полученной поворотом точки (1; 0) вокруг начала координат на угол
называется ______________, полученной поворотом точки (1; 0) вокруг начала координат на угол  .
.
а) ордината точки; б) абсцисса точки;
15 Вычислите 
а)  б)
б)  в)
в)  г) 1
г) 1
Часть 2 Практическая часть
Инструкция: выполните задания, запишите полное решение и ответ
ПЗ 1. Вычислить
ПЗ 2. Вычислить 
ПЗ 3. Найдите значение выражения:
ПЗ 4. Упростите выражение: 
ПЗ 5. Найдите  , если
, если  .
.
Вариант 2
Часть 1 Задания для проведения тестирования
(задания с 1-15 – 1 балл)
1. Ежемесячный заработок слесаря-сборщика 35 000 р., а повар-кондитер получает на 30 % меньше. Сколько зарабатывает повар-кондитер.
а)  б)
б)  в)
в)  г)
г) 
2. Из 21 кг хлопкового семени получили 6 л масла. Сколько масла получится из 7 кг хлопкового семени?
а)  б)
б)  в)
в)  г)
г) 
3. Представьте в виде степени с рациональным показателем 
а)  б)
б)  в)
в)  г)
г) 
4. Вычислите: 
а)  б)
б)  в)
в)  г)
г) 
5. Упростить выражение: 
а) 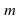 б)
б)  в)
в) 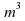 г)
г) 
6. Вычислите: 
а) 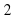 б)
б) 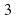 в)
в) 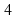 г) 5
г) 5
7. Вычислите: 
а) 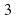 б)
б)  в)
в)  г) 2
г) 2
8. Найти радианную меру угла 40°
а)  б)
б)  в)
в)  г)
г) 
9. Выразить в градусах угол α = 
а) 150º б) 216º в) 120º г) 135º
10. Какой четверти числовой окружности принадлежит точка t = 
а) первой б) второй в) третьей г) четвёртой
11. Вычислить 
а)  б)
б)  в)
в)  г)
г) 
12. Вычислите
а)  б)
б)  в)
в)  г)
г) 
13. Вычислите
а)  б)
б)  в)
в)  г)
г) 
14. Косинусом угла  называется ______________, полученной поворотом точки (1; 0) вокруг начала координат на угол
называется ______________, полученной поворотом точки (1; 0) вокруг начала координат на угол  .
.
а) ордината точки; б) абсцисса точки;
15. Вычислите 
а)  б)
б)  в)
в)  г) 1
г) 1
Часть 2 Практическая часть
Инструкция: выполните задания, запишите полное решение и ответ
ПЗ 1. Вычислить 
ПЗ 2. Вычислить 
ПЗ 3. Найдите значение выражения:
ПЗ 4. Упростите выражение: 
ПЗ 5. Найдите  , если
, если  .
.
Ключ к контрольной работе по УД Математика
Вариант 1
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 1 |
| * |
|
| * |
|
| * |
|
| * |
| * | * | * |
| 2 | * |
| * |
|
|
| * |
| * |
|
| * |
|
|
|
| 3 |
|
|
|
|
|
|
|
|
| * |
|
|
|
|
|
| 4 |
|
|
| * |
| * |
|
|
|
|
|
|
|
|
|
Вариант 2
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 1 | * |
|
|
|
| * |
| * |
|
|
|
|
|
|
|
| 2 |
|
| * |
|
|
| * |
|
| * |
|
|
|
|
|
| 3 |
| * |
|
|
|
|
|
| * |
| * |
| * | * |
|
| 4 |
|
|
| * | * |
|
|
|
|
|
| * |
|
| * |
СОДЕРЖАНИЕ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
МАТЕМАТИКА
Тема 1. Введение.
Тема 2. Числовые и буквенные выражения.
Делимость целых чисел. Деление с остатком. Сравнения. Решение задач с целочисленными неизвестными. Комплексные числа. Формы записи комплексного числа. Действительная и мнимая часть. Геометрическая интерпретация. Модуль и аргумент комплексного числа. Действия над комплексными числами. Комплексно-сопряженные числа. Формула Муавра. Основная теорема алгебры. Многочлены от одной переменной. Делимость многочленов. Рациональные корни многочленов. Решение целых алгебраических уравнений. Схема Горнера. Теорема Безу. Число корней многочлена. Многочлены от двух переменных. Формулы сокращенного умножения для старших степеней. Бином Ньютона. Многочлены от нескольких переменных. Симметрические многочлены
В результате изучения темы учащиеся должны уметь:
- выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
- применять понятия, связанные с делимостью целых чисел, при решении математических задач;
- находить корни многочленов с одной переменной, раскладывать многочлены на множители;
- выполнять действия с комплексными числам и, пользоваться геометрической
интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
- проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
- практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.
Тема 3. Корни и степени.
Корень n-ой степени и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем.
В результате изучения темы учащиеся должны уметь:
- находить значения корня натуральной степени, степени с рациональным показателем; находить приближенные значения корня, степени с помощью калькулятора;
- проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени.
Тема 4. Логарифм.
Логарифм числа. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный логарифм. Число е. Натуральный логарифм.
Преобразования логарифмических выражений.
В результате изучения темы учащиеся должны уметь:
- находить значения и приближенные значения логарифма с помощью
калькулятора;
- проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы.
Тема 5. Тригонометрия.
Тригонометрические функции числового аргумента. Основные формулы тригонометрии. Формулы двойного аргумента. Формулы сложения. Преобразования тригонометрических выражений. Свойства и графики функций y = sinx, y = cosx, y = tgx, y = ctgx. Построение графиков. Обратные тригонометрические функции (свойства, графики). Четность, нечетность, периодичность тригонометрических функций. Возрастание убывание, экстремумы функций. Исследование тригонометрических функций.
В результате изучения темы учащиеся должны:
- знать основные формулы тригонометрии, уметь применять при преобразованиях выражений;
- знать определения тригонометрических функций (по единичной окружности) и уметь применять их для нахождения значений функций для аргументов вида π/2 + 2πn, где n- целое;
- уметь строить графики функции синус, косинус, тангенс и объяснять, используя график свойства этих функций;
- уметь определять четность, нечетность, периодичность, возрастание, убывание, экстремумы функций.
Список литературы
Ю. М. Колягин, М. В. Ткачева и др. Алгебра и начала математического анализа : учеб. Для 10 кл. общеобразовательных учреждений : базовый и профил. уровни. – М. : Просвещение, 2008.
А. Г. Мордкович, П. В. Семенов. Алгебра и начала математического анализа: учеб.для 10 кл. общеобразовательных учреждений: профил. уровень. – М.: Мнемозина, 2009.
А. Г. Мордкович и др. Алгебра и начала математического анализа: задачник для 10 кл. общеобразовательных учреждений: профил. уровень. – М.: Мнемозина, 2009.
А. В. Погорелов. Геометрия: учеб. Для 10-11 кл. общеобразовательных учреждений. – М. : Просвещение, 2008.







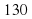 б)
б) 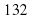 в)
в) 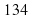 г) 140
г) 140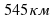 б)
б) 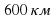 в)
в) 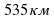 г) 635 км
г) 635 км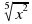
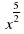 б)
б) 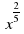 в)
в) 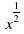 г)
г) 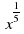
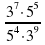
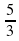 б)
б) 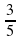 в)
в) 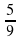 г)
г) 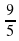
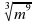
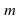 б)
б) 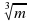 в)
в) 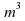 г)
г) 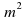
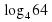
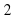 б)
б) 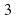 в)
в) 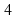 г) 5
г) 5









