Методическая разработка занятия по информатике по теме "Введение в алгебру логики".

Введение в алгебру логики

Задачи урока:

• актуализировать и углубить знания, полученные ранее по данному разделу;
• вспомнить определение логики, понятия, высказывания, умозаключения, доказательства;
• привести примеры основных форм мышления;
• познакомиться с историей развития логики.

«… .по одной капле воды …

человек, умеющий мыслить

логически, может сделать вывод о

существовании Атлантического океана

или Ниагарского водопада, даже если

он не видел ни того, ни другого и никогда о них не слыхал …

По ногтям человека, по его рукам, обуви, сгибу на коленях, по выражению лица и обшлагам рубашки – по таким мелочам нетрудно угадать его профессию.

И можно не сомневаться, что все это вместе взятое, подскажет сведущему наблюдателю верные выводы »

А. Конан Дойл

Задача Иван против Кащея бессмертного

Темница I – «Здесь Василиса Прекрасная».

Темница II – « Темница III не пустая».

Темница III – «Здесь Змей Горыныч».

Все подписи на дверях темниц неверные.

На какую дверь показать?

Иван против Кащея бессмертного

Здесь нет Василисы Прекрасной

Темница III пустая

Здесь нет

Змея

Горыныча

На какую дверь показать?

Все подписи на дверях темниц неверные

Иван против Кащея бессмертного

Здесь Змей

Здесь Василиса

Здесь пусто

На какую дверь показать?

Все подписи на дверях темниц неверные

Где же правда?

Дядюшка Скрудж попал на остров. На нем живут только правдолюбы (они всегда говорят правду) и лгуны (они всегда лгут). Скруджа сопровождал проводник – житель острова, который сказал, что знает, как найти спрятанные в горах сокровища.

Вскоре они увидели еще одного жителя острова. Скрудж послал проводника узнать, кто это житель острова –

правдолюб или лгун. Проводник вернулся и сказал , что тот говорит, что лгун.

Знает ли проводник, где спрятаны сокровища или нет, правду он сказал Скруджу нанимаясь на работу, или солгал?

Решение

• Если лгун, значит соврал

Лгун

• Если правдолюб, значит сказал правду

Правдолюб

В обоих случаях ответ должен быть

правдолюб

правдолюб

правдолюб

Человек и информация Как мы познаем мир

Формы познания

Абстрактное мышление

Чувственное познание

Суждение

Восприятие

Ощущение

Понятие

Умозаключение

Представление

Решите кроссворд

«Если у двух человек есть по одному яблоку и они обмениваются ими, у каждого из них окажется по одному яблоку. Но если у двух человек есть по одной идее и они обмениваются ими, у каждого будет по две идеи»

Б. Шоу

К россворд

Форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов.

Прием мышления, посредством которого из исходного знания получается новое знание.

Одно из двух возможных значений, которые могут принимать логические формулы; правда.

Распределение объема некоторого понятия по избранному основанию на ряд частей.

Мысленное соединение в единое целое частей объекта или его признаков, полученных в процессе анализа.

Это повествовательное предложение, о котором можно сказать, истинно оно или ложно.

Мысленное разделение объекта на составные части или выделение признаков объекта.

Мысль, в которой что-либо утверждается или отрицается.

Наука о законах и формах мышления.

Пингвины – чёрно-белые.

Старые фильмы тоже черно-белые.

Поэтому пингвины – это старые фильмы.

Пингвины – чёрно-белые.

Старые фильмы тоже черно-белые.

Поэтому пингвины – это старые фильмы.

В V до н.э. появились софисты, которые, манипулируя логической структурой речи, учили искусству выигрывать спор независимо от того, истинен обсуждаемый тезис или ложен.

Математические софизмы

4 = 5

16 - 36 = 25 – 45

16 – 36 + 20 = 25 – 45 + 20

(4 - ) 2 = (5 - ) 2

(4 - )= (5 - )

Математические софизмы

4 = 5

Математические софизмы

Математические софизмы

Дополнительное задание

5 = 1

Из числа 5 и 1 по отдельности вычтем одно и то же число 3.

5 – 3 = 2

1 – 3 = -2

При возведении в квадрат этих чисел получаются равные числа.

4 = 4

Значит, должны быть равны и

исходные числа 5 и 1 .

Где ошибка?

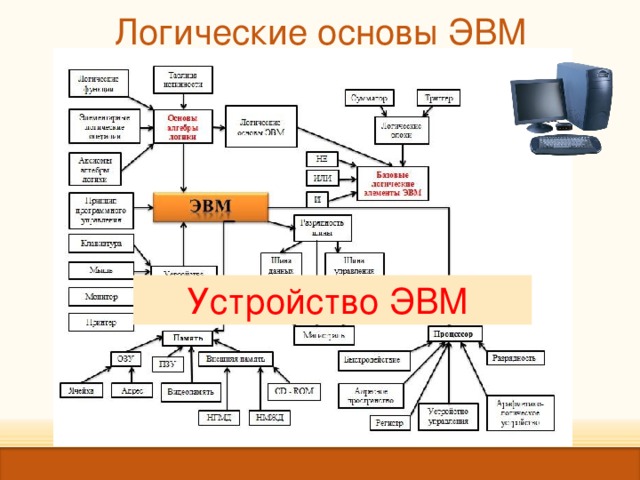
Логические основы ЭВМ

Устройство ЭВМ

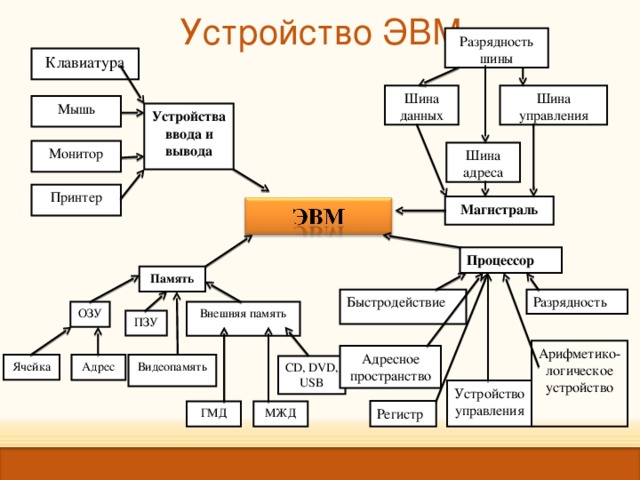
Устройство ЭВМ

Разрядность

шины

Клавиатура

Шина

данных

Шина

управления

Мышь

Устройства

ввода и

вывода

Монитор

Шина

адреса

Принтер

Магистраль

Процессор

Память

Разрядность

Быстродействие

ОЗУ

Внешняя память

ПЗУ

Арифметико-

логическое

устройство

Адресное

пространство

Ячейка

Видеопамять

Адрес

CD, DVD, USB

Устройство

управления

Регистр

МЖД

ГМД

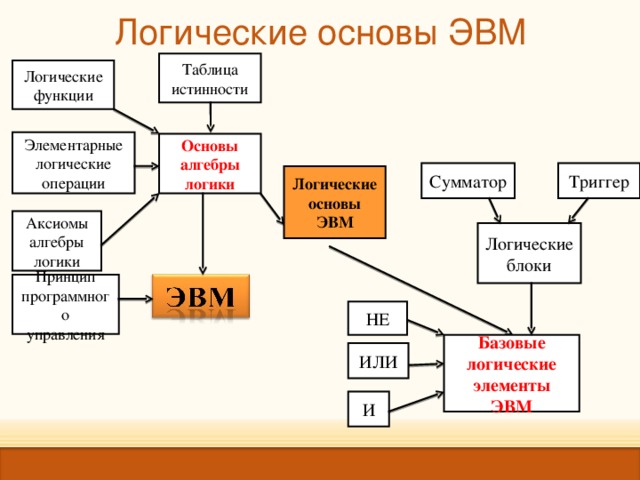
Логические основы ЭВМ

Таблица

истинности

Логические

функции

Элементарные

логические

операции

Основы

алгебры

логики

Сумматор

Триггер

Логические

основы

ЭВМ

Аксиомы

алгебры

логики

Логические

блоки

Принцип

программного

управления

НЕ

Базовые

логические

элементы ЭВМ

ИЛИ

И

На уроках алгебры

Алгебра в широком смысле этого слова – наука об общих операциях , аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами .

Для информатики важен раздел математики алгебра логики

Высказывания объекты алгебры логики

Задача « Уроки логики »

Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй.

Кто изучал логику?

«То, чем в прежние эпохи занимались лишь зрелые умы ученых мужей, в более поздние времена стало доступно пониманию мальчишек».

Гегель

Домашнее задание

Ученый

Вклад в развитие логики

Аристотель (384-322 г. до н.э.)

Френсис Бэкон (1561-1626 г.)

Дж. Ст. Милль (1806-1863 г.)

Рене Декарт (1596-1650 г.)

Готфрид Вильгельм Лейбниц (1646-1716 г.)

Иммануил Кант (1724-1804 г.)

Джон Буль (1815-1864 г.)

Георг Вильгельм Фридрих Гегель (1770-1831 г.)

Готлоб Фреге (1848-1925 г.)

Чарлз Пирс (1839-1914 г.)

Простым высказыванием  называют повествовательное предложение, относительно которого имеет смысл говорить,  истинно  оно или  ложно .

8. a*x2+b*x+c=0. Который час? " width="640"

Следующие предложения высказываниями не являются:

Давай пойдем гулять.

2*x8.

a*x2+b*x+c=0.

Который час?

Сложные (составные)  высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных  логическими операциями .

Логическое НЕ (отрицание) 1=0 0=1

Маша не умеет готовить = Маша умеет готовить

Бисквит делают из меда = бисквит не делают из меда

Пирожки удались = пирожки не получились

Дизъюнкция  - логическое сложение (ИЛИ ) 

Истинно, когда одно условие истинно!

1 V 0=1

0 V 1=1

0 V 0=0

1 V 1=1

Люся красавица и не умеет готовить

Конъюнкция - логическое умножение (И)

Истина, если оба высказывания ИСТИННЫ!

Петя ходил на все занятия, очень старался, писал конспекты и не сдал экзамен

0 & 1=0

1 & 0=0

0 & 0=0

1 & 1=1

0=0 0 = 1=1 0 = 0=1 1 = 1=1 A = B  "Из А следует В" Если выглянет солнце, то станет тепло " width="640"

Логическое следование (импликация) «если .А., то .В.»

ЛОЖЬ, когда условие (посылка  А ) - истинно, а следствие (заключение  В ) - ложно и истинно во всех остальных случаях. 

1 = 0=0

0 = 1=1

0 = 0=1

1 = 1=1

A = B 

"Из А следует В"

Если выглянет солнце, то станет тепло

Эквивалентность (логическое тождество)

тогда и только тогда, когда

A  B 

"А равносильно В"

Истина, если оба истинны или оба ложны

1   1 = 1

1   0=0

0   1=0

0  0=1