ЗАДАНИЕ 15 ЕГЭ. НЕРАВЕНСТВА С МОДУЛЕМ.
Модулем (абсолютной величиной) называется функция, которая каждому числу 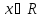 ставит в соответствие число
ставит в соответствие число
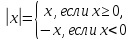
То есть, другими словами, модуль х – это расстояние от 0 (начало координат) до точки х. Т.к. расстояние – величина неотрицательная, то модуль х не может быть отрицательным: 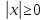 . Более общее понятие модуля:
. Более общее понятие модуля: 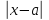 – это расстояние от точки х до точки а.
– это расстояние от точки х до точки а.
Свойства модуля:
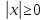
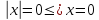
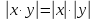
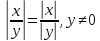
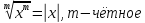
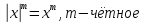
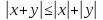
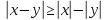
Геометрический смысл модуля:
Рассмотрим на примерах.
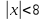 . Решениями такого неравенства являются все числа, которые удалены от начала координат на расстояние, меньшее 8.
. Решениями такого неравенства являются все числа, которые удалены от начала координат на расстояние, меньшее 8.
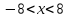 или
или 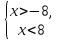

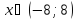
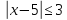 . Решением такого неравенства являются все числа, которые удалены от точки 5 на расстояние, не больше 3.
. Решением такого неравенства являются все числа, которые удалены от точки 5 на расстояние, не больше 3.
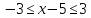 или
или 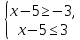
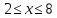 или
или 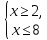

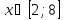
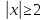 . Решением этого неравенства являются все числа, которые удалены от начала координат на расстояние, не меньшее 2.
. Решением этого неравенства являются все числа, которые удалены от начала координат на расстояние, не меньшее 2.



 . Решением этого неравенства являются все числа, которые удалены от точки
. Решением этого неравенства являются все числа, которые удалены от точки  на расстояние, большее 5.
на расстояние, большее 5.




 . Данное неравенство решений не имеет, т.к. расстояние не может быть отрицательным. Аналогично,
. Данное неравенство решений не имеет, т.к. расстояние не может быть отрицательным. Аналогично,  решений не имеет.
решений не имеет.
 . Это неравенство имеет единственное решение
. Это неравенство имеет единственное решение  .
.
 . Данное неравенство имеет бесконечно много решений, т.к. расстояние от точки х до нуля всегда больше отрицательного числа.
. Данное неравенство имеет бесконечно много решений, т.к. расстояние от точки х до нуля всегда больше отрицательного числа. 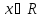 .
.
Виды неравенств, содержащих модуль:
Неравенство содержит некоторое выражение  под модулем и число вне модуля:
под модулем и число вне модуля: , где а – некоторое число.
, где а – некоторое число.
Например,  .
.
Неравенство, содержит выражение с переменной под знаком модуля и вне его:  .
.
Например,  .
.
Неравенство, которое содержит несколько модулей:
Например,  .
.
Неравенства вида , где 
Например,  .
.
Неравенства, решаемые заменой переменной.
Например,  .
.
Способы решения неравенств, содержащих модуль:
Решение неравенств с помощью геометрического свойства модуля.
Пример 1.
Решением исходного неравенства будут все значения х, которые удовлетворяют хотя бы одному неравенству из совокупности и каждому неравенству из системы.
Ответ:  .
.
Пример 2.
Решением исходного неравенства будут все значения х, которые удовлетворяют и совокупности, и двойному неравенству.

Ответ: 
Решение неравенств, используя определение модуля.
Пример. 
Воспользуемся определением модуля:


Ответ: 
Решение неравенств методом возведения в квадрат.
Пример 1. 
Левая и правая части данного неравенства являются положительными выражениями, поэтому их можно возвести в квадрат:

Так как 2 – чётный показатель степени, то по свойству 6 получаем:


Применяем формулу разности квадратов:

Значит, 
Ответ: 
Пример 2. 

Применяем формулу разности квадратов:
Умножаем обе части неравенства на 400 (каждую скобку на 20):




Ответ: 
Метод перебора вариантов (метод интервалов).
Так как этот метод достаточно сложный, приведём алгоритм его применения.
Выписать все подмодульные выражения, приравнять их к нулю и решить уравнения.
Найденные корни отметить на одной числовой прямой и на каждом получившемся участке определить знаки каждого подмодульного выражения.
Раскрыть модули согласно знакам на каждом участке и решить получившиеся неравенства.
Результаты объединить.
Пример. 
Решим согласно алгоритму.



Раскроем модули на каждом участке.




Учитывая, условие  , получаем:
, получаем: 




Учитывая условие  ,
, 



Учитывая условие  ,
, 
Объединяя решения всех трёх неравенств, получим решение исходного неравенства: 
Ответ: 
Решение неравенств методом замены переменной.
Пример 1. 
Сделаем замену переменной:  . Тогда, согласно свойству 6
. Тогда, согласно свойству 6  и неравенство примет вид:
и неравенство примет вид:



Значит,  . Возвращаемся в замену:
. Возвращаемся в замену:
Ответ:
Пример 2. 
Сделаем замену переменной:  . Тогда неравенство принимает вид:
. Тогда неравенство принимает вид:




Значит,  . Возвращаемся в замену переменной:
. Возвращаемся в замену переменной:
Ответ: 
Графический способ решения неравенств.
Пример. 
Решим это неравенство графически. Справа у нас линейная функция, графиком является прямая, проходящая через точки  . Слева под знаком модуля квадратичная функция, графиком является парабола с вершиной в точке
. Слева под знаком модуля квадратичная функция, графиком является парабола с вершиной в точке  , ветви направлены вверх. Т.к. квадратичная функция стоит под знаком модуля, то её отрицательная часть (там, где у отрицателен) отображается относительно оси Ох. Строим графики.
, ветви направлены вверх. Т.к. квадратичная функция стоит под знаком модуля, то её отрицательная часть (там, где у отрицателен) отображается относительно оси Ох. Строим графики.
Графики пересекаются в точках А и В. Для того, чтобы выполнялось исходное неравенство, необходимо, чтобы прямая располагалась выше параболы. Это заштрихованный участок. Ему соответствует  . Сами точки пересечения не включаются в промежуток, т.к. исходное неравенство строгое.
. Сами точки пересечения не включаются в промежуток, т.к. исходное неравенство строгое.
Ответ: 
Приведённые ниже задания взяты из базы данных ЕГЭ.
Решить неравенство:
Решение. Упростим неравенство:
ОДЗ:
Левая и правая части полученного неравенства имеют одинаковые знаменатели, причём положительные при всех х из области допустимых значений.
Умножая обе части неравенства на знаменатель (он положителен!!!), получаем неравенство:

Воспользуемся первым способом решения неравенств, содержащих модуль (с помощью геометрического свойства модуля).
Учитывая ОДЗ, получаем:
Ответ:
Решить неравенство:
Решение.
Упростим неравенство:

Это неравенство удобно решать методом замены переменной:
 . Тогда, учитывая 6 свойство модуля,
. Тогда, учитывая 6 свойство модуля,  . Значит, неравенство принимает вид:
. Значит, неравенство принимает вид:


Отмечаем на числовой прямой нули левой части неравенства:
Значит,  . Возвращаемся в замену переменной, т.е. вместо
. Возвращаемся в замену переменной, т.е. вместо  ставим
ставим  . Получаем двойное неравенство, которое решаем в виде системы неравенств:
. Получаем двойное неравенство, которое решаем в виде системы неравенств:
Ответ:
Решить неравенство:

Решение.
Упростим неравенство:

Воспользуемся методом перебора вариантов (методом интервалов):
Приравняем к нулю подмодульные выражения и найдём корни:


Отметим корни на числовой прямой и определим знаки подмодульных выражений на получившихся промежутках:

Раскроем модули на каждом промежутке.




Учитывая условие, что  , получаем:
, получаем: 




Учитывая условие, что  , получаем:
, получаем: 



Учитывая условие, что  , получаем:
, получаем: 
Объединяем решения всех трёх вариантов: 
Ответ: 
Решить неравенство:
Решение.
Воспользуемся первым способом решения неравенств, содержащих модуль (с помощью геометрического свойства модуля):
Ответ: 
Решить неравенство:
Решение.
Преобразуем неравенство:
Воспользуемся методом замены переменной:
. Тогда неравенство примет вид:




Значит,  . Учитывая условие
. Учитывая условие  , сделанное при замене переменной, делаем вывод, что данное неравенство имеет решения только при
, сделанное при замене переменной, делаем вывод, что данное неравенство имеет решения только при  . Вернёмся к замене переменной:
. Вернёмся к замене переменной:

Это уравнение имеет корни только в двух случаях:
Ответ: 
Решить неравенство:

Решение.
Воспользуемся методом перебора вариантов. Так как под модулем у нас только х, то вариантов всего два:
Объединяя решения обоих случаев, получаем решение исходного неравенства:
Ответ:
Решить неравенство:
Решение.
Воспользуемся методом замены переменной:
 . Тогда неравенство принимает вид:
. Тогда неравенство принимает вид:

Значит, учитывая условие  , сделанное при замене переменной, получаем:
, сделанное при замене переменной, получаем:
Вернёмся в замену переменной:
Значит, решение исходной системы имеет вид:
Ответ:
Задания для самостоятельного решения.
Решить неравенства:
-
-
-







-
-



-
Ответы на задания для самостоятельного решения.
-
-
-
-











-
8







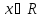 ставит в соответствие число
ставит в соответствие число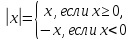
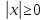 . Более общее понятие модуля:
. Более общее понятие модуля: 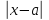 – это расстояние от точки х до точки а.
– это расстояние от точки х до точки а.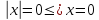
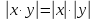
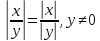
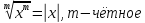
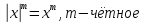
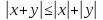
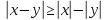
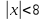 . Решениями такого неравенства являются все числа, которые удалены от начала координат на расстояние, меньшее 8.
. Решениями такого неравенства являются все числа, которые удалены от начала координат на расстояние, меньшее 8.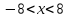 или
или 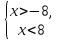
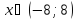
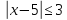 . Решением такого неравенства являются все числа, которые удалены от точки 5 на расстояние, не больше 3.
. Решением такого неравенства являются все числа, которые удалены от точки 5 на расстояние, не больше 3. 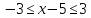 или
или 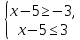
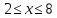 или
или 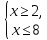
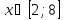
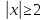 . Решением этого неравенства являются все числа, которые удалены от начала координат на расстояние, не меньшее 2.
. Решением этого неравенства являются все числа, которые удалены от начала координат на расстояние, не меньшее 2.