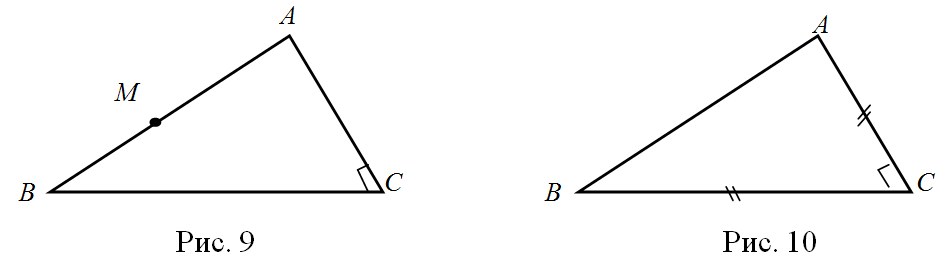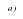Формирование графической культуры на первых уроках стереометрии

Е.П. Голованова, Т.Н. Карпова

Формирование графической культуры на первых уроках стереометрии

Аннотация: В статье раскрываются понятия «математическая культура» и «графическая культура» школьников, предложена серия задач, способствующая формированию графической культуры школьников с первых уроков стереометрии.

Ключевые слова: культура, математическая культура, графическая культура, стереометрия, формирование графической культуры.

Графические дисциплины, такие как стереометрия, являются основополагающими в формировании профессиональной и графической культуры учащихся. Поэтому необходимо, чтобы методика преподавания стереометрии была больше ориентирована на развитие образного, логического, абстрактного мышления, давала возможность формировать статические и динамические пространственные представления школьников.

Раскроем суть понятия «графическая культура», для этого рассмотрим следующую цепочку: сначала остановимся на основном понятии «культура», затем раскроем суть термина «математическая культура», и в конечном итоге обратимся к понятию «графическая культура».

В словаре философских терминов под культурой понимается «совокупность искусственных объектов (идеальных и материальных), созданных человеком в процессе освоения природы обладающих структурами, функциональными и динамическими закономерностями (общими и специальными)» [6, с.271].

В педагогическом словаре культура определяется как « исторически определенный уровень разви­тия общества, творческих сил и способностей человека, выра­женный в типах и формах организации жизни и деятельности людей, в их взаимоотношениях, а также в создаваемых ими мате­риальных и духовных ценностях. Культура в образовании высту­пает как его содержательная составляющая, источник знаний о природе, обществе, способах деятельности, эмоционально-воле­вого и ценностного отношения человека к окружающим людям, труду, общению и т. д.» [2, с. 67].

А. Я. Флиер рассматривает много подходов к определению культуры. Мы будем придерживаться следующего определения: «Культура - мир символических обозначений явлений и понятий – языков и обра­зов, созданный людь­ми с це­лью фиксации и трансляции социально значимой инфор­мации, знаний, представлений, опыта, идей и т.п.» [7].

Математика в современном мире занимает почетное месть, и ее роль в науке постоянно возрастает. Математика является мощным и универсальным методом познания. Изучение математики совершенствует общую культуру мышления, приучает логически рассуждать, воспитывает точность. Физик Н. Бор говорил что математика – это больше, чем наука, - это язык.

О. Шпенглер утверждал, что каждая культура имеет свою математику, поэтому математика призвана формировать у обучающихся свою, особую культуру – математическую.

Термин «математическая культура» появился в 20 – 30-е года ХХ века.

Дж. Икрамов говорит, что математическую культуру школьника стоит понимать как «совокупность математических знаний, умений и навыков» [1, с.5]. Он выделяет компоненты математической культуры, важнейшими из которых являются: математическое мышление и математический язык. Под «математическим языком» стоит понимать совокупность всех средств, помогающих выражать математическую мысль. Согласно Икрамову «языки математических символов, геометрических фигур, графиков, диаграмм, а также система научных терминов вместе с элементами естественного языка составляют математический язык» [1, с.6].

Дж. Икрамов под математическим мышлением, в основе которого лежат математические понятия и суждения, понимает совокупность взаимосвязанных логических операций; оперирование как свернутыми, так и развернутыми структурами; знаковыми системами математического языка, а также способность к пространственным преставлениям, запоминанию и воображению.

С. А. Розанова рассматривает математическую культуру не школьника, а студента технического университета, как выработанную систему математических знаний, умений и навыков, позволяющих использовать их в (быстро меняющихся условиях) профессиональной и общественно-поли­тической деятельности, повышающую духовно-нравственный по­тенциал и уровень развития интеллекта личности. С.А. Розанова выделяет параметры математической культуры, и разбивает их на два класса в зависимости от значимости. «В первый класс входят знания, умения, навыки, формируе­мые посредством математики и необходимые в профессиональ­ной, общественно-политической, духовно-нравственной деятель­ности и повышающие уровень развития интеллекта студента.

Ко второму классу можно отнести параметры, влияющие непосредственно на развитие интеллекта и опосредованно на другие параметры первого класса: математическое мышление, профессиональное мышление, нравственное развитие, эстети­ческое развитие, мировоззрение, способность к самообучению, качество ума (счетная способность, речевая гибкость, речевое восприятие, пространственная ориентация, память, способность к рассуждению, скорость восприятия информации и принятия решения)» [5, с.71].

С.А. Розанова утверждает, что «математическая культура – ядро профессиональной культуры специалиста» [5, с.71]. Несомненно, данный подход можно применить и к учащимся 10 – 11 классов.

Под графической культурой в широком значении понимается «совокупность достижений человечества в области создания и освоения графических способов отображения, хранения, передачи геометрической, технической и другой информации о предметном мире, а также созидательная профессиональная деятельность по развитию графического языка» [4].

А.В. Костюков в своей диссертационной работе говорит о том, что в узком значении графическая культура рассматривается как уровень совершенства, достигнутый личностью в освоении графических методов и способов передачи информации, который оценивается по качеству выполнения и чтения чертежей [3].

Мы под графической культурой будем понимать интегративное качество личности, характеризующееся единством графических знаний, умений и навыков, достижения в области освоения и применения графических методов и способов преобразования информации.

Нашей целью становится подготовить такую систему заданий, которая будет способствовать формированию графической культуры учащегося как качество личности. Мы будем рассматривать упражнения, которые можно применить на первых уроках стереометрии в профильной школе и классах углубленного изучения математики, а также на элективных занятиях.

Теперь приведем несколько упражнений способствующих формированию графической культуры.

К любому школьному чертежу предъявляют ряд требований.

1. Изображение должно быть верным, т.е. должно представлять собой фигуру, подобную параллельной проекции оригинала.

2. Изображение должно быть по возможности наглядным, т.е. должно вызывать пространственное представление о форме оригинала.

3. Изображение должно быть полным, т.е. каждая точка принадлежащая оригиналу, должна быть задана на проекционном чертеже.

4. Изображение должно быть легко выполнимым, т.е. правила построения должны быть максимально просты.

5. Изображение должно быть удобным для проведения на нем дополнительных линий.

Верность изображения являются строго определенными понятиями, наглядность, полнота, легкость выполнения, удобность относятся к числу субъективных понятий.

Все представленные на рисунке 1а, б, в, г изображения являются верными изображениями куба. Однако наглядным представляется, только изображение под буквой г.

в)

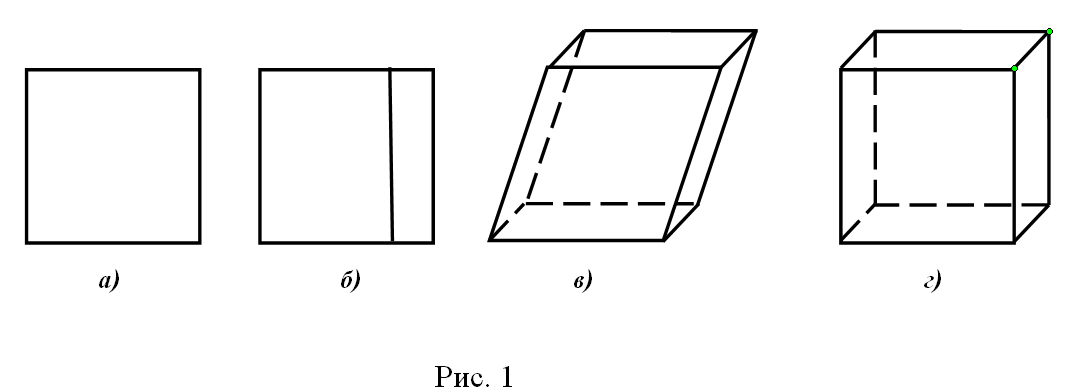
Все представленные на рисунке 2 а, б, в изображения являются верными изображениями усеченного конуса. Но наглядным является изображение 2 в. Представленные рисунки можно дополнить, например, тетраэдр, который может быть изображен в виде треугольника, цилиндр – в виде окружности, конус – в окружности, пирамида – в виде треугольника, четырехугольника и т.д.

Все представленные изображения являются верными и правильными, однако свойством наглядности обладают лишь два из них (1г, 2в).

Таково рода задания могут быть использованы как средства демонстрации изображений, полностью удовлетворяющих свойствам школьного чертежа.

Задачи неожиданного и непривычного содержания всегда надолго запоминаются учащимися, соответственно и их решение не остается забытым.

№1. Три мухи одновременно взлетели с одной лысины. В каком случае они окажутся в одной плоскости?

№2. Столяр с помощью двух нитей проверяет, будут ли устойчиво стоять на полу стол, имеющий четыре ножки. Как натянуть нити?

Задания по готовому чертежу, также могут поспособствовать развитию пространственного мышления, а значит и формированию графической культуры.

№1. На рис.3 три попарно пересекающиеся прямые а, b, с пересекают плоскость α в точках А, В, С соответственно.

Правильно ли выполнен рисунок?

№2. Найдите ошибки (если они имеются) в изображении сечений куба плоскостью на рис. 4.

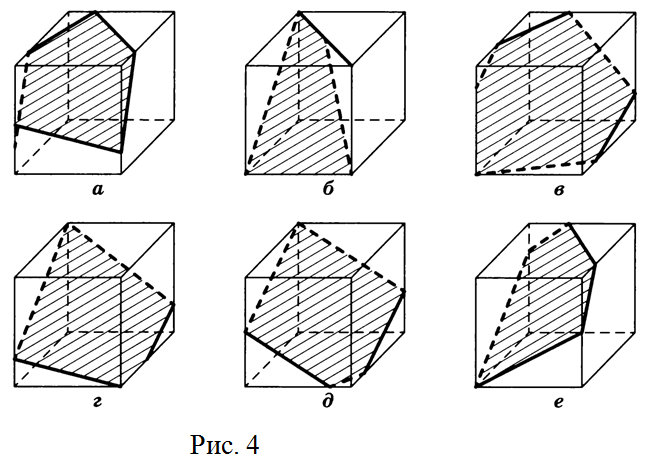
№3. Правильно ли нарисованы сечения тетраэдра (треугольной пирамиды) плоскостью на рис. 5?

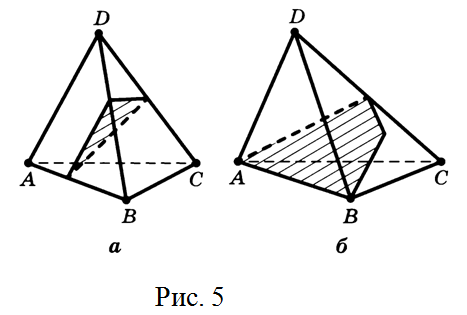
Также на первых этапах можно предложить учащимся задания на моделирования пространственных фигур.

№1. Изготовьте развертки и склейте их (рис. 6). Какие фигуры вы получили?

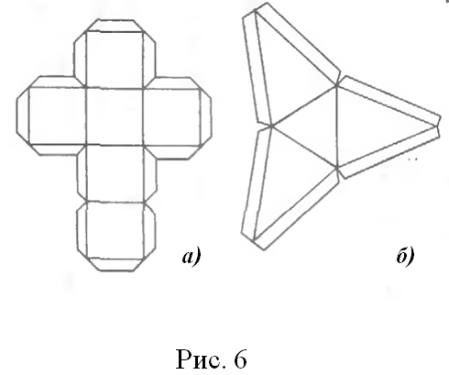
№2. Среди данных на рис. 7 разверток найдите развертки пирамид. Определите их вид.

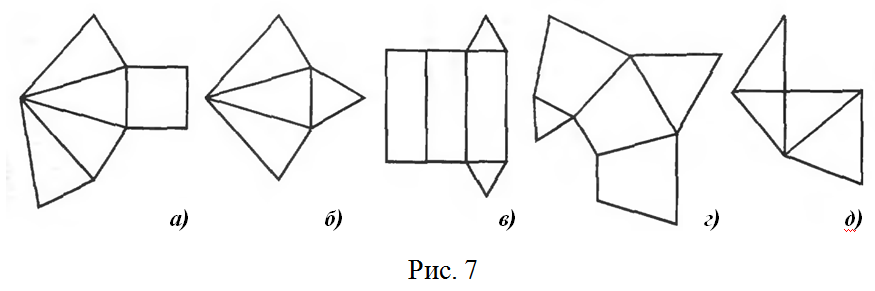
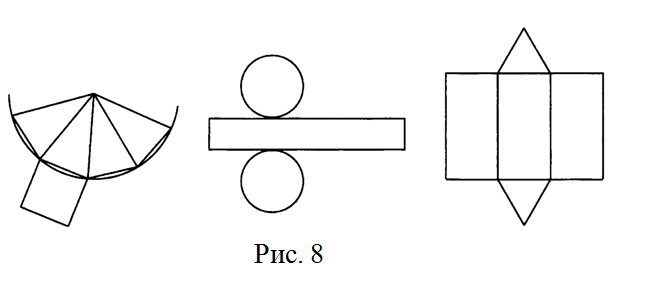
№3. Развертки каких геометрических фигур изображены на рис. 8? Нарисуйте эти геометрические фигуры.

Также большое значение имеют задания на изображение плоской фигуры, комбинации фигур в произвольной параллельной проекции на плоскости чертежа. Изображение пирамиды, призмы, цилиндра или конуса обычно начинается с изображения их основания – многоугольника или круга. Именно на этом этапе построения возникает наибольшее количество ошибок, поэтому нужно уделить внимание такого рода заданиям.

№1. Треугольник АВС прямоугольный (С = 90^о) рис. 9. Изобразите перпендикуляр, опущенный из заданной точки гипотенузы на какой – либо катет. Укажите условие его существования.

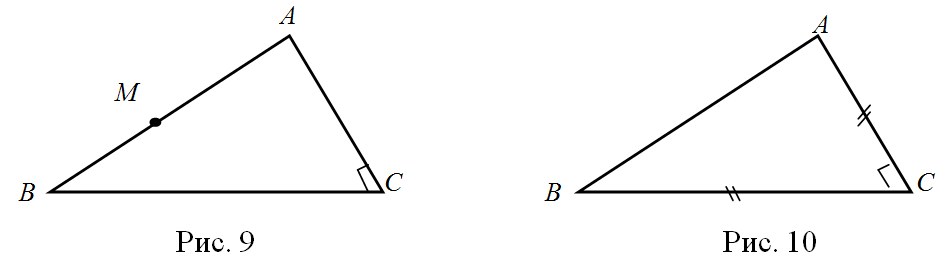
№2. Треугольник АВС прямоугольный (С = 90^о) и равнобедренный рис. 10. Изобразите биссектрису прямого угла. Объясните свое построение.

№3. Постройте равнобокую трапецию АВСD. Изобразите высоту, опущенную из вершины В. Объясните свое построение.

№4. Построить изображение правильного восьмиугольника в параллельной проекции. Записать этапы построения.

Использование подобных упражнений позволяет акцентировать внимание учащихся именно на изображении фигур. Таково рода задания позволяют повысить графическую культуру учащихся, что позволяет достичь поставленной цели.

Библиографический список:

1. Икрамов, Дж. Математическая культура школьников. Методические аспекты проблемы развития мышления и языка школьников при обучении математике [Текст] / Дж. Икрамов. – Ташкент: УКИТУВЧИ, 1981. – 280 с.

2. Коджаспирова Г.М. Педагогический словарь: для студ. высш. и сред. Пед. учеб. заведений [Текст] / Коджаспирова Г.М., Коджаспиров А.Ю. – М.; И; М.: Издательский центр «Академия», 2000. – 176 с.

3. Костюков А. В. Теоретические основы и практика формирования графической культуры у студентов технических вузов в условиях модернизации высшего профессионального образования (на примере начертательной геометрии и инженерной графики):дис. …д-ра пед.наук: Оренбург, 2004. - 328 с.

4. Лямина А.А. Графический язык – международный язык общения: мат-лы XI регион. Науч.-техн. Конф. «Вузовская наука – Северо – Кавказскому региону». Т. 2. Ставрополь: СевКавГТУ, 2007. 168 с.

5. Розанова, С.А. Математическая культура инженера как педагогическая проблема [Текст] / С.А. Розанова. – М.: ФИЗМАТ ЛИТ, 2003. – 176 с.

6. Словарь философских терминов /науч. ред. проф. В.Г. Кузнецова. - Москва : Инфра-М, 2005. - 729,[1] с. ; 24 см. - (Библиотека словарей "Инфра-М"). - Библиогр. в тексте. - Предм. указ.: с. 723-730 

7. Флиер А.Я.Культурология для культурологов: Учебное пособие для магистрантов, аспирантов и соискателей, а так же преподавателей культурологии. 2 издание, исправленное и дополненное. – М., МГУКИ, 2009. – … с.

3