Карточки по геометрии для 10 класса.
Карточка 1
1. Найдите большую диагональ ромба, сторона которого равна 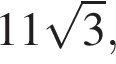 а острый угол равен 60°.
а острый угол равен 60°.
2. В четырёхугольник ABCD вписана окружность,  и
и  Найдите периметр четырёхугольника ABCD.
Найдите периметр четырёхугольника ABCD.
3. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба.
 4. В правильной шестиугольной призме
4. В правильной шестиугольной призме 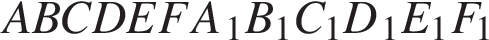 все ребра равны
все ребра равны  Найдите расстояние между точками B и
Найдите расстояние между точками B и 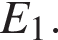
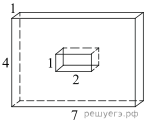
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Карточка 2.
1. В треугольнике ABC угол C равен 90°, AC = 7,  Найдите радиус описанной окружности этого треугольника.
Найдите радиус описанной окружности этого треугольника.
2. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен  Найдите высоту трапеции.
Найдите высоту трапеции.
3. Площадь поверхности правильной треугольной призмы равна 12. Какой будет площадь поверхности призмы, если все ее ребра увеличить в шесть раз?
4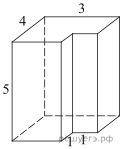 . Диагональ куба равна 13. Найдите площадь его поверхности.
. Диагональ куба равна 13. Найдите площадь его поверхности.
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Карточка 3
1. Угол ACO равен 58°. Его сторона CA касается окружности с центром в точке O. Сторона CO пересекает окружность в точках B и D (см. рис.) Найдите градусную меру дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.
2. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
3 . Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
4. В правильной четырёхугольной пирамиде все рёбра равны 18. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
5. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 12, и боковым ребром, равным 5.
Карточка 4
1. В треугольнике ABC 
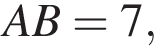
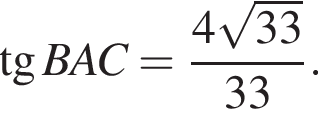 Найдите высоту
Найдите высоту 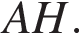
2. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.
3. Площадь поверхности куба равна 128. Найдите длину его диагонали.
 4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
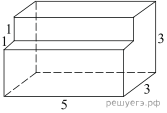
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Карточка 5.
1. Гипотенуза прямоугольного треугольника равна 28. Найдите радиус описанной окружности этого треугольника.
2. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
3. В правильной четырёхугольной пирамиде все рёбра равны 18. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
 4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10.
4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10.
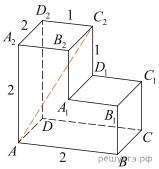
5. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите расстояние между вершинами A и  .
.
Карточка 6
1. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.
2. Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 42. Найдите радиус окружности.
3. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 43. Найдите площадь боковой поверхности исходной призмы.
 4. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба.
4. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба.
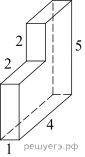
5 . Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Карточка 7
1. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 102° , угол CAD равен 46°. Найдите угол ABD. Ответ дайте в градусах.
 2. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
2. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
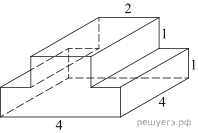
3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
4. Если каждое ребро куба увеличить на 5, то его площадь поверхности увеличится на 270. Найдите ребро куба.
5. Ребра тетраэдра равны 38. Найдите площадь сечения, проходящего через середины четырех его ребер.
Карточка 8
1. Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 4 : 2 : 3 : 6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
 2. В треугольнике ABC угол C равен 90°, CH − высота,
2. В треугольнике ABC угол C равен 90°, CH − высота, 
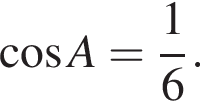 Найдите
Найдите 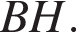
3. Найдите площадь поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.
4. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.
5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 5, найдите угол между прямыми FA и D1E1. Ответ дайте в градусах.
Карточка 9
1. Касательные CA и CB к окружности образуют угол ACB, равный 122°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
2. Сумма двух углов параллелограмма равна  Найдите один из оставшихся углов. Ответ дайте в градусах.
Найдите один из оставшихся углов. Ответ дайте в градусах.
3. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 2.
4. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 52. Найдите третье ребро, выходящее из той же вершины.
5. В правильной четырёхугольной пирамиде SABCD точка O — центр основания, S — вершина, SO = 30, SA = 34. Найдите длину отрезка AC.
Карточка 10
1. Площадь параллелограмма ABCD равна 36. Точка E — середина стороны CD. Найдите площадь трапеции ABED.
2. Хорда AB стягивает дугу окружности в 70°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
 3. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 18 и высота равна 40.
3. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 18 и высота равна 40.
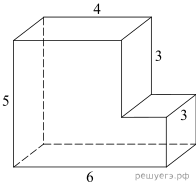
4. Найдите площадь поверхности многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
5. В правильной четырёхугольной пирамиде SABCD точка O — центр основания, S — вершина, SO = 30, SA = 34. Найдите длину отрезка AC.
Карточка 11
1. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
2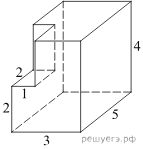 . Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.
. Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.
3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
4. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в 36 раз?
5. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB = 7, AD = 40 , AA1 = 9. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
Карточка 12
1. Угол C треугольника ABC, вписанного в окружность радиуса 36, равен 30°. Найдите сторону AB этого треугольника.
 2. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
2. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
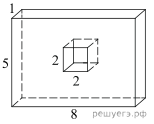
3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
4. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
5. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Карточка 13
1. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
2. Площадь параллелограмма ABCD равна 12. Точка E — середина стороны AD. Найдите площадь трапеции BCDE.
3. В кубе 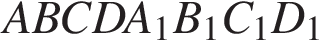 точка K — середина ребра
точка K — середина ребра 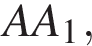 точка L — середина ребра
точка L — середина ребра 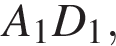 точка M — середина ребра
точка M — середина ребра 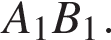 Найдите угол
Найдите угол 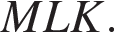 Ответ дайте в градусах.
Ответ дайте в градусах.
4. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
5. Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.
Карточка 14
1. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.
2. В треугольнике ABC угол C равен 138°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.
3. В правильной четырёхугольной пирамиде боковое ребро равно 22, а тангенс угла между боковой гранью и плоскостью основания равен 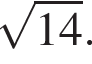 Найти сторону основания пирамиды.
Найти сторону основания пирамиды.
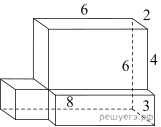 4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
5. Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 14 и высота равна 24.
Карточка 15
1. Площадь параллелограмма ABCD равна 14. Найдите площадь параллелограмма A'B'C'D', вершинами которого являются середины сторон данного параллелограмма.
2. Острый угол ромба равен 30°. Радиус вписанной в этот ромб окружности равен 9. Найдите сторону ромба.
3. Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 20 и высота равна 24.
4. Диагональ куба равна 13. Найдите площадь его поверхности.
 5. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите расстояние между вершинами A и
5. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите расстояние между вершинами A и  .
.
Карточка 16
1. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
2. На окружности по разные стороны от диаметра AB взяты точки D и C. Известно, что 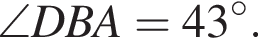 Найдите
Найдите  Ответ дайте в градусах.
Ответ дайте в градусах.
3. Площадь боковой поверхности треугольной призмы равна 43. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
4. Найдите угол 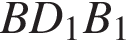 прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 

 Ответ дайте в градусах.
Ответ дайте в градусах.
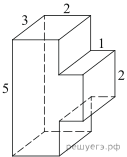 5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Карточка 17
1. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной 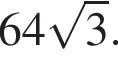
2. В треугольнике ABC AC = BC = 5, 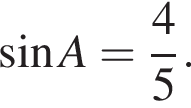 Найдите АВ.
Найдите АВ.
3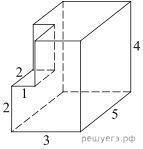 . Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
5. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в 36 раз?
Карточка 18
1. Касательные CA и CB к окружности образуют угол ACB, равный 122°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
 2. В треугольнике ABC угол C равен 90°,
2. В треугольнике ABC угол C равен 90°, 
 Найдите
Найдите 
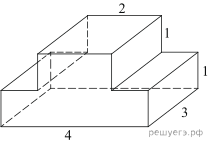
3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
4. Площадь боковой поверхности треугольной призмы равна 36. Через среднюю линию основания этой призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсечённой треугольной призмы.
5. Площадь поверхности куба равна 128. Найдите длину его диагонали.
Карточка 19
 1. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
1. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
2. Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно 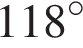 и
и 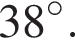 Ответ дайте в градусах.
Ответ дайте в градусах.
3. Площадь поверхности куба равна 128. Найдите длину его диагонали
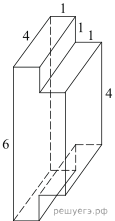 4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
5. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Карточка 20
1. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
2. В тупоугольном треугольнике ABC 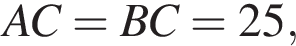 высота AH равна 20. Найдите
высота AH равна 20. Найдите 
 3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
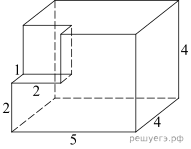
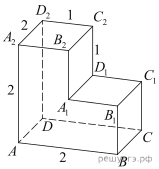
4. Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
5. В правильной четырехугольной пирамиде SABCD точка O − центр основания, S − вершина, 
 Найдите боковое ребро
Найдите боковое ребро 

|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 33 | 4 | 148 | 4 | 14 | 304 | 56 | 60 | 58 | 27 | 25 | 36 | 160 | 62 | 7 | 30 | 96 | 58 | 0,96 | 0,96 |
| 2 | 54 | 10 | 3 | 304 | 10 | 4 | 2 | 17,5 | 157 | 35 | 3,5 | 3 | 9 | 159 | 36 | 47 | 6 | 20 | 40 | -0,6 |
| 3 | 4 | 432 | 52 | 8 | 81 | 86 | 60 | 112 | 60 | 1800 | 94 | 106 | 162 | 11 | 1040 | 21,5 | 300 | 46 | 8 | 300 |
| 4 | 5 | 338 | 81 | 300 | 248 | 4 | 2 | 1 | 2 | 114 | 1296 | 4 | 4 | 152 | 338 | 45 | 94 | 18 | 84 | 60 |
| 5 | 80 | 95 | 258 | 76 | 3 | 56 | 361 | 60 | 32 | 32 | 287 | 5 | 60 | 700 | 3 | 72 | 1296 | 8 | 12 | 17 |






 4. В правильной шестиугольной призме
4. В правильной шестиугольной призме  . Диагональ куба равна 13. Найдите площадь его поверхности.
. Диагональ куба равна 13. Найдите площадь его поверхности. . Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).  4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности. 4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10.
4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10. 4. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба.
4. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба. 2. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
2. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника. 2. В треугольнике ABC угол C равен 90°, CH − высота,
2. В треугольнике ABC угол C равен 90°, CH − высота,  3. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 18 и высота равна 40.
3. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 18 и высота равна 40. . Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.
. Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности. 2. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
2. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ. 4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). . Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности. 2. В треугольнике ABC угол C равен 90°,
2. В треугольнике ABC угол C равен 90°,  1. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
1. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции. 4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).  3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.


















