План урока
Курс__, гр__
Дисциплина: Математика
Преподаватель: Амирханова А. К.
Тема урока: Производные элементарных функций.
Перечень вопросов, рассматриваемых в теме
1) определение элементарной функции;
2) производная показательной функции;
2) производные тригонометрических функций;
3) производная логарифмической функции.

Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации.
- (ex) '= ex
- (ekx+b) '=kekx+b
- (ax) '=axlna



- (sin x) '=cosx
- (cos x) '= -sinx
Теоретический материал для самостоятельного изучения
Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации. При решении многих практических задач часто приходится находить производные таких функций.
1.Производная показательной функции.
Показательная функция f(x)=ax, где а>0, a ≠1, определена на всей числовой прямой и имеет производную в каждой ее точке. Любую показательную функцию можно выразить через показательную функцию с основанием у по формуле:
ax=exln a (1)
так как exln a= (eln a)х= ах.
Стоит отметить свойств о функции ех: производная данной функции равна ей самой
(ex) '= ex. (2)
Применяя правило дифференцирования сложной функции, получим:
(ekx+b) ' = kekx+b. (3)
Производная для ax:
(ax) ' = axlna. (4)
2.Производная логарифмической функции.
Логарифмическую функцию  с любым основанием а > 0, а≠ 1 можно выразить через логарифмическую функцию с основанием е с помощью формулы перехода
с любым основанием а > 0, а≠ 1 можно выразить через логарифмическую функцию с основанием е с помощью формулы перехода
 (5)
(5)
Производная функции lnх выражается формулой
 (6)
(6)
Применяя правило дифференцирования сложной функции, получаем
 (7)
(7)
 (8)
(8)
3.Производные тригонометрических функций.
Для тригонометрических функций справедливы следующие равенства:
(sin x)’=cosx (9)
(cos x)’= -sinx (10)
Примеры и разбор решения заданий тренировочного модуля
Найти производную:
- f(x) = 3lnx
Решение: 
Ответ: 
- f(x) = 3·e2x
Решение: (3e2x) ' = 3·2· e2x = 6 ·e2x
Ответ: 6 ·e2x
- f(x) = 2x
Решение: (2x) ' = 2xln2
Ответ: 2xln2

Решение: 
Ответ: 
- f(x) = sin (2x+1) - 3cos(1-x)
Решение: (sin (2x+1) - 3cos(1-x)) ' = 2cos(2x+1) - 3sin(1-x)
Ответ: 2cos(2x+1) - 3sin(1-x)
Просмотр содержимого документа
«Тема урока: Производные элементарных функций.»
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Производные элементарных функций.
Перечень вопросов, рассматриваемых в теме
1) определение элементарной функции;
2) производная показательной функции;
2) производные тригонометрических функций;
3) производная логарифмической функции.

Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации.
(ex) '= ex
(ekx+b) '=kekx+b
(ax) '=axlna

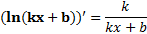

(sin x) '=cosx
(cos x) '= -sinx
Теоретический материал для самостоятельного изучения
Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации. При решении многих практических задач часто приходится находить производные таких функций.
1.Производная показательной функции.
Показательная функция f(x)=ax, где а0, a ≠1, определена на всей числовой прямой и имеет производную в каждой ее точке. Любую показательную функцию можно выразить через показательную функцию с основанием у по формуле:
ax=exln a (1)
так как exln a= (eln a)х= ах.
Стоит отметить свойств о функции ех: производная данной функции равна ей самой
(ex) '= ex. (2)
Применяя правило дифференцирования сложной функции, получим:
(ekx+b) ' = kekx+b. (3)
Производная для ax:
(ax) ' = axlna. (4)
2.Производная логарифмической функции.
Логарифмическую функцию  с любым основанием а 0, а≠ 1 можно выразить через логарифмическую функцию с основанием е с помощью формулы перехода
с любым основанием а 0, а≠ 1 можно выразить через логарифмическую функцию с основанием е с помощью формулы перехода
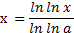 (5)
(5)
Производная функции lnх выражается формулой
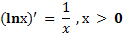 (6)
(6)
Применяя правило дифференцирования сложной функции, получаем
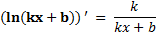 (7)
(7)
 (8)
(8)
3.Производные тригонометрических функций.
Для тригонометрических функций справедливы следующие равенства:
(sin x)’=cosx (9)
(cos x)’= -sinx (10)
Примеры и разбор решения заданий тренировочного модуля
Найти производную:
f(x) = 3lnx
Решение: 
Ответ: 
f(x) = 3·e2x
Решение: (3e2x) ' = 3·2· e2x = 6 ·e2x
Ответ: 6 ·e2x
f(x) = 2x
Решение: (2x) ' = 2xln2
Ответ: 2xln2
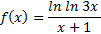
Решение: 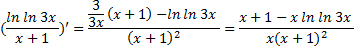
Ответ: 
f(x) = sin (2x+1) - 3cos(1-x)
Решение: (sin (2x+1) - 3cos(1-x)) ' = 2cos(2x+1) - 3sin(1-x)
Ответ: 2cos(2x+1) - 3sin(1-x)










 с любым основанием а > 0, а≠ 1 можно выразить через логарифмическую функцию с основанием е с помощью формулы перехода
с любым основанием а > 0, а≠ 1 можно выразить через логарифмическую функцию с основанием е с помощью формулы перехода (5)
(5) (6)
(6) (7)
(7) (8)
(8)





















