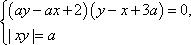Вариант 8.
Задание 1. Флакон шампуня стоит 190 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 35%?
Задание 2.
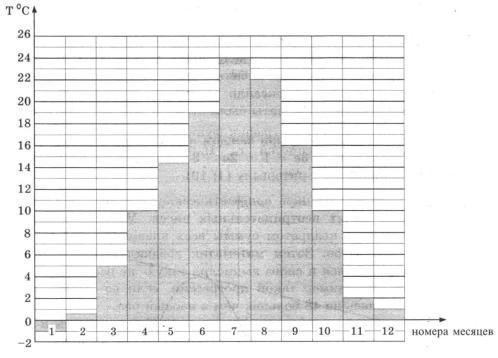
На диаграмме показана средняя температура воздуха в Симферополе за каждый номера месяцев 1988 года. По горизонтали указываются месяцы, по вертикали — средняя температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с отрицательной средней температурой в Симферополе в 1988 году.
Задание 3.
| 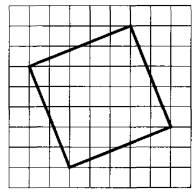
| На клетчатой бумаге с размером клетки 1x1 изображён квадрат. Найдите его площадь.
|
Задание 4. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.
Задание 5. Найдите корень уравнения log3(14–x) = 2log3 5
Задание 6.
| 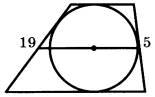
| Боковые стороны трапеции, описанной около окружности, равны 19 и 5. Найдите среднюю линию трапеции.
|
Задание 7.
| 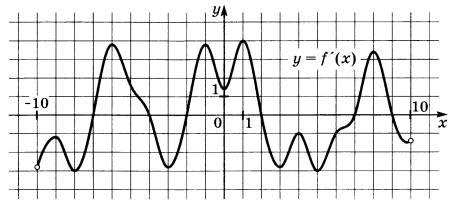
| На рисунке изображён график у = f(x) .Сколько корней имеет уравнение f(x)=0. |
Задание 8. Во сколько раз увеличится площадь поверхности куба, если все его ребра увеличить в 15 раз?
Задание 9. Найдите значение выражения 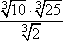
Задание 10. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 20 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 15 до 40 см, а расстояние d2 от линзы до экрана — в пределах от 100 до 120 см. Изображение на экране будет чётким, если выполнено соотношение
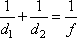 .
.
Укажите, на каком наименьшем расстоянии от линзы нужно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах.
Задание 11. Два гонщика участвуют в гонках. Им предстоит проехать 70 кругов по кольцевой трассе протяжённостью 4,4 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 30 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 24 минуты? Ответ дайте в км/ч.
Задание 12. Найдите наибольшее значение функции у=х2-20х-13 на отрезке [-8; 0].
Задание 13. а) Решите уравнение 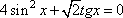 .
.
б) Найдите все корни этого уравнения, принадлежащие промежутку [-3π; -2π].
Задание 14. Задание 14. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра АВ = 35, AD = 12, СС1 = 21.
а) Докажите, что высоты треугольников ABD и A1BD, проведённые к стороне BD, имеют общее основание.
б) Найдите угол между плоскостями ABC и A1DB.
Задание 15. Решите неравенство 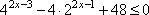 .
.
Задание 16. Дан выпуклый четырёхугольник ABCD со сторонами АВ = 3, ВС = CD = 5, AD = 8 и диагональю АС = 7.
а) Докажите, что около него можно описать окружность.
б) Найдите диагональ BD.
Задание 17. 15-го января планируется взять кредит в банке на 12 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования на 13% больше, чем сумма, взятая в кредит. Найдите r.
Задание 18. Найдите все значения a, при каждом из которых система уравнений
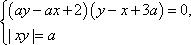
имеет ровно шесть решений.
Задание 19. Учитель пишет примеры на сложение трёх натуральных чисел так, чтобы во всех примерах ответ был один и тот же N, при этом он хочет, чтобы все слагаемые во всех примерах (даже в различных примерах) были различны.
а) Можно ли написать два таких примера, если N = 14?
б) Можно ли написать 7 таких примеров, если N = 51?
в) Можно ли написать 13 таких примеров, если N = 51?