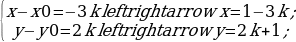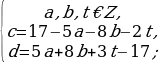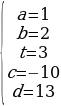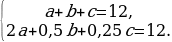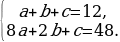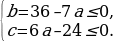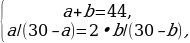Упражнения для подготовки к профильному ЕГЭ по математике

Упражнения для подготовки к заданию №18 профильного ЕГЭ по математике

Диофантовы уравнения:

1. Для каждого целого z решите в целых числах уравнение 2x+3y=5z.

1. Решить линейное уравнение в целых числах:

5a+8b+3c+2d=17

Задачи на составление диофантовых уравнений:

Задача 1.

Парикмахер получал за стрижку женщины по 2 рубля, за стрижку мужчины – по 50 копеек, а ребенка – по 25 копеек. За 12 рублей он подстриг 12 человек. Сколько женщин, мужчин и детей он подстриг?

Задача 2.

Каждый из двух стрелков сделал по 30 выстрелов. Всего было 44 попадания, а остальные – промахи. Сколько раз попал каждый, если известно, что у первого стрелка на каждый промах приходилось в 2 раза больше попаданий, чем у второго?

Задача 3.

В школьной столовой нужно рассадить группу учеников. За один стол можно усадить 3 человека. Если сажать за стол по 2 девочки, то окажется 3 стола, где сидят одни мальчики. Если сажать за стол по 2 мальчика, то будет 2 стола, где сидят одни девочки. Сколько девочек было в группе?

Задача 4.

В первой коробке находились красные шары, а во второй – синие. Число красных шаров составляло 15/19 от числа синих. Когда из коробки забрали 3/7 красных шаров и 2/5 синих, то в первой коробке осталось шаров менее 1000, а во второй коробке – более 1000. Сколько изначально было шаров в каждой из двух коробок?

Задача 5.

Определенное количество одинаковых шаров можно уложить в виде квадрата или в виде равностороннего треугольника. Найдите число этих шаров, если известно, что, если расположить их треугольником, то сторона этого треугольника будет содержать на 2 шара больше, чем сторона квадрата, составленного из этих же шаров. Причем, шары располагаются не только по контуру квадрата или треугольника, но и заполняют их внутреннюю часть.

Задачи в целых числах:

Задача 1. В группе учится меньше 50 студентов. За индивидуальную работу 1/7 часть студентов получила оценку «5», 1/3 «4», а половина студентов получила оценку «3». Остальные работы были оценены оценкой «2». Сколько было студентов, индивидуальные работы которых были оценены неудовлетворительной оценкой?

Задача 2. Три друга купили 13 пирожков, причем Алексей купил в два раза меньше Ивана, а Володя – больше Алексея, но меньше Ивана. Сколько пирожков купил каждый из них?

Задача 3. В аудитории присутствуют преподаватель и несколько обучающихся. Найти число обучающихся, если известно, что возраст преподавателя на 24 года больше среднего возраста обучающихся и на 20 лет больше среднего возраста всех присутствующих в аудитории.

Задача* (из Демоверсии профильного ЕГЭ по математике).

В школах №1 и №2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы №1 в школу №2, а средние баллы были пересчитаны в обеих школах.

1. Мог ли средний балл в школе №1 уменьшиться в 10 раз?

2. Средний балл в школе №1 уменьшился на 10 %, средний балл в коле №2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе №2 равняться 7?

3. Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего бала в школе №2.

Решения и ответы

Диофантовы уравнения:

1. Решение:

Итак, подберём по одному значению для x и y, если z=1:

2*1+3*1=5 ↔ x0=1, y0=1

Получим два уравнения:

2x+3y=5 и 2x0+3y0=5

Вычтем из первого уравнения второе:

2(x-x0) + 3(y-y0) = 0

Пусть, x-x0=a; y-y0=b.

Получим:

2a+3b=0

2a=-3b ↔ a кратно 3, b кратно 2:

↔

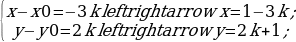
k-целое число.

1. Как же решить это уравнение исключительно в целых числах?

Сделаем некоторые элементарные преобразования искомого уравнения:

5a+8b+3c+2d=17 ↔ 5a+8b+2(c+d) + c=17

Теперь сделаем замену:

c+d=t;

Получим: 5a+8b+2t+c=17

Коэффициент при c у нас сейчас равен единице, а это значит, что мы с вами можем выразить эту неизвестную через остальные неизвестные в этом уравнении без всяких делений. Сделаем это:

c=17-5a-8b-2t

Это говорит нам о том, что какие бы не были a,b,t, всё равно c останется целым числом.

Вспоминая, что c+d=t справедливо говорить, что d=t-c. А подставив вместо c полученный выше результат получим:

d=t-c=t-(17-5a-8b-2t) = 5a+8b+3t-17

Тут мы также видим, что что какие бы не были a,b,t, всё равно d останется целым числом.

Итак, мы выразили c и d через a,b,t (свободные переменные). Осталось только записать это в систему:

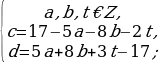
Попробуем найти частное решение исходного уравнения, положив, к примеру, что a=1; b=2; t=3:

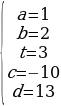
Подставим в исходное уравнение:

5*1+8*2+3*(-10)+2*13=17

17=17

Уравнение решено верно.

Задачи на составление диофантовых уравнений:

Задача 1.

Решение.

Пусть a, b и c – число подстриженных женщин, мужчин и детей соответственно. Тогда по условию задачи имеем систему:

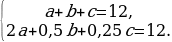
Домножим второе уравнение системы на 4, будем иметь:

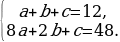
Вычтем из второго уравнения первое, получим, что b = 36 – 7a ≤ 0.

Подставим выражение для b в первое уравнение исходной системы, получим, что c = 6a – 24 ≤ 0.

Таким образом, имеем систему:

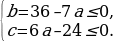
Так как a, b и c – целые неотрицательные числа, то из уравнений системы следует, что

a ≤ 36/7 (5 целых и 1/7) и a ≤4. Значит, a = 4 или a = 5.

Таким образом, возможны два варианта ответа: 5 женщин, 1 мужчина, 6 детей или 4 женщины и 8 мужчин.

Задача 2.

Решение.

Обозначив число попаданий каждого стрелка a и b, составим систему уравнений:

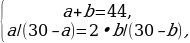
где a и b – натуральные числа.

В результате решения системы, например, способом подстановки, получим, что a = 24 и b = 20.

Ответ: 24 и 20.

Задача 3.

Решение.

В данной задаче за переменную легче взять не величину, про которую спрашивают в задаче, т.е. количество девочек, а количество столов. Задачи на целые числа

Пусть x штук столов. Тогда девочек по две можно усадить за (x – 3) стола, т.е. девочек 2(x – 3) = 2x – 6 человек.

С другой стороны, девочек можно рассадить так: за двумя столами сидят девочки (6 человек), а за оставшимися (x – 2) столами – по одной девочке. Таким образом, число девочек равно

6 + (x – 2) = x + 4.

Из уравнения

2x – 6 = x + 4 находим, что x = 10.

Девочек x + 4 = 14.

Ответ: 14 девочек.

Задача 4.

Решение.

Пусть x – единичное количество шаров, когда в первой коробке 15x, во второй 19x, x кратно 7 · 5. Так как 15 на 7 не делится, а 19 – простое число, то x = 7 · 5y = 35y.

По условию 15x · 4/7

Подстановкой убеждаемся, что y = 3. Тогда 15x = 15 · 35 · 3 = 1575, 19x = 1995.

Ответ: 1575, 1995.

Задача 5.

Решение.

Пусть в стороне квадрата укладывается x шаров. Тогда на стороне треугольника укладывается (x + 2) шара.

Число всех шаров в первом случае равно x2, а во втором 1 + 2 + 3 + … + (x + 2).

Последнее выражение представляет собой сумму арифметической прогрессии, поэтому ее можно записать так:

1 + 2 + 3 + … + (x + 2) = (1 + (x + 2)) · (x + 2))/2 = ((x + 3)(x + 2))/2.

Значит, ((x + 3)(x + 2))/2 = x2.

Решив полученное уравнение, найдем, что x = 6.

Следовательно, всего шаров было 62 = 36.

Ответ: 36 шаров.

Задачи в целых числах:

Задача 1.

Решение

Число студентов всегда выражается целым числом. Значит, нам надо найти такое натуральное число меньшее 50 и одновременно делящееся на 7, 3, 2. Единственно возможным таким числом будет число 42.

Решение можно оформить так: пусть x – число студентов. Тогда по условию задачи имеем х/7 – студентов получили оценку «5»; х/3 – студентов получили оценку «4»; х/2 – студентов получили оценку «3». Так как x должен одновременно делиться на 7, 3, 2, то таким числом, меньшим 50, будет число 42.

Решение этой задачи можно оформить и так:

1/7+1/3+1/2=(6+14+21)/42=41/42

Числитель дроби – число 41 показывает, какое количество студентов получили оценки «5», «4», «3», а знаменатель – число 42 показывает общее количество студентов. И отсюда можно заключить, что оценку «2» получил 1 студент.

Ответ: 1 студент получил оценку «2».

Задача 2.

Решение

Пусть Алексей купил х пирожков, а Володя – у. Тогда Иван купил 2х пирожков. Получаем смешанную систему, составленную из уравнения и неравенства:

Так как х

4х

Отсюда следует, что 4x13

Решая эту систему неравенств, получаем

2+3/

Тогда х = 3, 2х = 6. Найдем у:

3х + у = 13, 9 + у = 13, у = 4.

Проверим еще, выполняется ли неравенство:

х

Ответ: Алексей – 3 пирожка, Володя – 4 пирожка, Иван – 6 пирожков.

Задача 3.

Решение

Пусть х – средний возраст обучающегося, у – количество обучающихся.

Запишем уравнение, которое мы составим по условию задачи (читателю следует объяснить, как оно составлено).

((xy+x+24)/(y+1))+20 = x+24

Так как у + 1 не равно 0, то мы можем обе части уравнения умножить на это выражение. Будем иметь

ху + х + 24 + 20у + 20 = ху + 24у + х + 24,

4у = 20.

у = 5.

Ответ: 5 обучающихся.

Задача* (из Демоверсии профильного ЕГЭ по математике.

Решение:

1. Пусть, в школе №1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал 19 баллов и перешёл в школу №2. Тогда средний балл в школе №1 уменьшился в 10 раз.

2. Пусть, в школе №2 писали тест m учащихся, средний балл равен B, а перешедший в неё учащийся набрал u баллов. Тогда получаем:

u=0,9(m+1)B-mB; 10u=(9-m)B.

Если B=7, то (9-m)B не делится на 10, а 10u делится на 10. Но это не возможно, поскольку 10u=(9-m)B.

1. Пусть, в школе №1 средний балл равняется А. Тогда получаем:

u=(9-m)A-0,9(8-m)A; 10u=(18-m)A=(9-m)B.

Заметим, что если B=1 или В=3, то 10u=(9-m)B не делится на 10. Если В =2 или В=4, то m=4. В пером случае 14А=10, а во втором 14А=20. Значит, ни один из этих случаев не возможен.

При В=5, m=3, тогда получаем u=3 и A=2. Этот случай реализуется, например, если в школе №1 писали тест 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла; в школе №2 писали тест 3 учащихся и каждый набрал по 5 баллов, а у перешедшего из одной школы в другую учащегося – 3 балла.

Ответ: а) да; б) нет; в) 5.

Примеры заданий на применение разных алгоритмов (с ответами)

Задача 1. Вовочка купил ручки по 8 рублей и карандаши по 5 рублей. Причем за все карандаши он заплатил на 19 рублей больше, чем за все ручки. Сколько ручек и сколько карандашей купил Вовочка?

Ответ: куплено 7 карандашей и 8 ручек, то есть (7,2) – частное решение и у = 2 + 5n, х = 7 + 8n, где nє Z – общее решение.

Задача 2. Куплены фломастеры по 7 рублей и карандаши по 4 рубля за штуку, всего на сумму 53 рубля. Сколько куплено фломастеров и карандашей?

Ответ: (-53; 106) – частное решение, х=4n-53, у=-7n+106 – общие решения, при n=14, х=3, у=8, то есть куплено 3 фломастера и 8 карандашей.

Задача 3. на планете С в ходу два вида монет: по 16 тугриков и по 27 тугриков. Можно ли с их помощью купить товар, ценой в 1 тугрик?

Ответ: например, заплатить 3 монеты по 27 тугриков и получить сдачу 5 монет по 16 тугриков.

Задача 4. Шехерезада рассказывает свои сказки великому правителю. Всего она должна рассказать 1001 сказку. Сколько ночей потребуется Шехерезаде, чтобы рассказать все свои сказки, если в какие-то ночи она будет рассказывать по 3 сказки, а в какие-то по 5?

Ответ: 2 ночи по три сказки и 199 ночей по 5 сказок - всего 201 ночь.

Задача 5. В дневнике у Вовочки по математике только пятерки и четверки, причем пятерок больше. Сумма всех Вовочкиных оценок по математике равна 47. Сколько Вовочка получил пятерок и сколько четверок?

Ответ: Вовочка получил 7 пятерок и 4 четверки.

Задача 6.

Прах Диофанта гробница покоит; дивись ей и камень

Мудрым искусством его скажет усопшего век.

Волей богов шестую часть жизни он прожил ребенком.

И половину шестой встретил с пушком на щеках.

Только минула седьмая, с подругой он обручился.

С нею, пять лет, проведя, сына дождался мудрец;

Только полжизни отцовской возлюбленный сын его прожил.

Отнят он был у отца ранней могилой своей.

Дважды два года родитель оплакивал тяжкое горе,

Тут и увидел предел жизни печальной своей.

Ответ: Диофант прожил 84 года

Теория

Разберем метод решения относительно одного неизвестного.

Задача: В каталоге картинной галереи всего 96 картин. На каких-то страницах расположено 4 картины, а на каких-то 6. Сколько страниц каждого вида есть в каталоге?

Решение. Пусть х – количество страниц с четырьмя картинами, у – количество страниц с шестью картинами, тогда по условию этой задачи можно составить уравнение:

4x+6y=96.

Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. В нашем случае это 4х, то есть:

4х=96-6у.

Делим все уравнение на этот коэффициент:

4х=96-6у | :4;

х=(96-6у):4.

Остатки при делении на 4: 1,2,3. Подставим вместо у эти числа.

Если у=1, то х=(96-6∙1):4=90:4 - Не походит, решение не в целых числах.

Если у=2, то х=(96-6∙2):4=21 – Подходит.

Если у=3, то х=(96-6∙3):4=78:4 - Не походит, решение не в целых числах.

Итак, частным решением является пара (21;2), а это значит, что на 21 странице расположено по 4 картины, а на 2 страницах по 6 картин.

Ответ: на 21 странице расположено по 4 картины, а на 2 страницах по 6 картин.

Разберем метод решения с использованием алгоритма Евклида.

Задача: В магазине продаётся шоколад двух видов: молочный и горький. Весь шоколад хранится в коробках. Молочного шоколада на складе имеется 7 коробок, а горького 4. Известно, что горького шоколада было на одну плитку больше. Сколько плиток шоколада находятся в коробках каждого вида?

Решение. Пусть х – количество плиток молочного шоколада в одной коробке, у – количество плиток горького шоколада в одной коробке, тогда по условию этой задачи можно составить уравнение:

4у-7х=1.

Решим это уравнение, используя алгоритм Евклида.

у-7х=1;

Выразим 7=4∙1+3, = 3=7-4∙1.

Выразим 4=3∙1+1, =

1=4-3∙1=4-(7-4∙1)=4-7+4∙1=4∙2-7∙1=1.

Итак, получается х=1; у=2.

А это значит, что молочный шоколад лежит в коробке по 1 штуке, а горький по 2 штуки.

Ответ: молочный шоколад лежит в коробке по 1 штуке, а горький по 2 штуки.