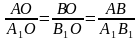Билет №1
1 вопрос: дайте определение многоугольника, вершины, стороны, диагонали и периметра многоугольника. Запишите формулу суммы углов выпуклого многоугольника.
Определение. Многоугольником называют фигуру, составленную из отрезков так, что:
смежные отрезки не лежат на одной прямой
несмежные не имеют общих точек
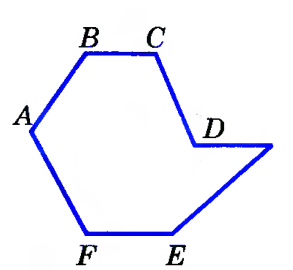
Вершинами называются точки: А, В, С, D, E, F.
Сторонами многоугольника называются отрезки: AB, BC, CD, DE, ЕF, FA.
Диагональю многоугольника называется отрезок, соединяющий две любые не соседние вершины.
Периметром многоугольника называется сумма длин всех сторон.
Сумма углов выпуклого многоугольника равна (n-2) 180°
180°
2 вопрос: докажите теорему о средней линни
Не изучено
3 вопрос:
Не изучено
4 вопрос: периметр прямоугольника равен 56, а диагональ равна 20. Найдите площадь этого прямоугольника.

Билет №2
1 вопрос: дайте определение и свойства параллелограмма.
Определение. Параллелограмм – это четырехугольник, у которого противоположные стороны попарно – параллельны.
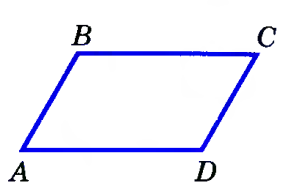
Свойства параллелограмма:
1° В параллелограмме противоположные углы равны. В параллелограмме противоположные стороны равны.
2° Диагонали параллелограмма точкой пересечения делится пополам.
3° В параллелограмме сумма углов прилежащих к одной стороне равна 180°.
4° Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
2 вопрос: доказать свойство медиан треугольника
| Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины |
| 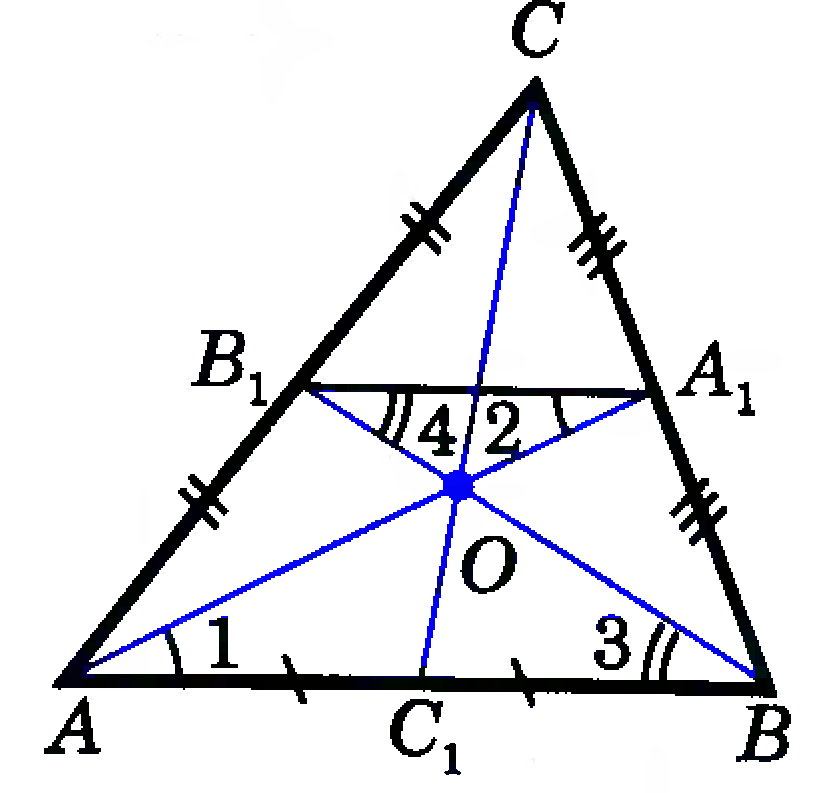
| Дано: ∆АВС, О - точка пересечения медиан АА₁ и ВВ₁; А₁В₁ - средняя линия ∆АВС. Доказать: точка О пересечение медиан АА₁ и ВВ₁ делит каждую из них в отношении 2:1, считая от вершины.
|
Доказательство:
Отрезок А₁В₁ параллелен стороне АВ, поэтому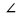 1 =
1 = 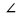 2 ;
2 ; 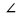 3 =
3 = 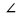 4 (как накрест лежащие углы при пересечении параллельных прямых АВ и А₁В₁.).
4 (как накрест лежащие углы при пересечении параллельных прямых АВ и А₁В₁.).
Следовательно, треугольники АОВ и А₁ОВ₁ подобны по двум углам, и, значит, их стороны пропорциональны: 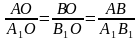
Но АВ=2 А₁В₁, поэтому АО=2 А₁О и ВО= 2
А₁О и ВО= 2 В₁О.
В₁О.
Таким образом, точка О пересечение медиан АА₁ и ВВ₁ делит каждую из них в отношении 2:1, считая от вершины.
Аналогично доказывается, что точка пересечения медиан ВВ₁ и СС₁ делит каждую из них в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О.
Итак, все три медианы треугольника АВС пересекаются в точке О и делятся ею в отношении 2:1, считая от вершины.
Теорема доказана.
3 вопрос: не изучено
4 вопрос: не изучено.








 180°
180°


 1 =
1 =