162
СВОЙСТВА МОДЕЛЕЙ
ПОНЯТЬ
В предыдущих главах мы рассказывали о том как строить модели. В этой главе мы будем сравнивать модели друг с другом и с объектом моделирования.
Итак, вы уже знаете, что построив модель, мы создаем некоторый новый объект, который находится в определенных отношениях к исходному объекту. Этот новый объект – модель, в свою очередь, сам может быть объектом моделирования и т.д. При этом следует заметить, что каждый объект может иметь много моделей. Таким образом, получается неограниченное множество объектов, в котором некоторые из объектов являются моделями других объектов. Нашей ближайшей задачей является изучение свойств этого множества и отношений, существующих между его элементами.
В множестве объектов и моделей теоретически возможны отношения между:
а) объектом и другим объектом;
б) объектом и его моделью;
в) объектом и моделью другого объекта;
г) моделью и моделируемым объектом;
д) моделью и другим объектом;
е) моделью и другой моделью того же моделируемого объекта;
ж) моделью и моделью другого объекта.
Пункты а),в),д),ж) не представляют для нас интереса.
Пункты б), г) формально можно объединить в один, поскольку модель можно рассматривать как новый объект, а объект можно рассматривать как модель своей модели (см. ниже). Содержательно же мы будем разделять отношения между объектом и его моделью и между разными моделями одного объекта.
На этом этапе целесообразно ввести понятие "наблюдателя". Наблюдетель, в отличие от субъекта познания, введенного в первой главе, сам не строит моделей, а просто "живет" в множестве объектов и созданных моделей, различным образом соотнося себя с ним.
Теоретически у наблюдателя существуют следующие возможности по исследованию этого множества:
а) наблюдателю одновременно доступен и объект, и его модель;
б) наблюдателю доступна модель, но недоступен объект;
в) наблюдателю доступен объект, но недоступна модель;
г) наблюдателю не доступен ни объект, ни его модель.
Последний случай выводит нас за границы всякого познания и поэтому в дальнейшем не рассматривается.
Случай в) требует особого разговора и обсуждается ниже.
В случае б) необходимо понять, как не зная самого объекта оценивать его модель.
В случае а) можно корректно рассматривать свойства отношений, существующих между объектом и моделями, а именно:
1) свойства двуместного отношения "х является моделью y", позволяющего определенным образом отграничить объекты моделирования от объектов–моделей;
2) свойства двуместных отношений, выражающие различные степени "похожести" объектов: объекта моделирования на его модель и объекта-модель на другой объект-модель, относящийся к тому же самому исходному объекту.
Начнем с изучения свойств отношения "х является моделью у".
Самое главное свойство модели - быть подобной объекту моделирования в некотором отношении, обусловленном целями моделирования.
ЗАМЕЧАНИЕ. Для краткости изложения иногда мы будем опускать словосочетание "в некотором отношении, обусловленном целями моделирования", говоря о подобии модели объекту, но это уточнение важно, и всегда подразумевается, когда мы говорим о подобии.
В математике отношение "быть подобным" уточняется через свойства симметричности, рефлексивности, транзитивности.
Отношение называется симметричным, если оно остается справедливым при перестановке объектов. Например, отношения "х брат у", "прямая х параллельна прямой у", "х современник у".
Формально свойство симметичности можно записать так: aRb àbRa, где a и b – объекты; R – отношение; à - знак операции логического следования (если…, то…).
Отношение называется транзитивным (от лат. transitivus – переходный), если оно переносимо с одних пар объектов на другие через "транзитный" элемент. Например, "х больше у и у больше z, следовательно, x больше z", "а=b и b=c, следовательно, a=c", "треугольник 1 подобен треугольнику 2, а треугольник 2 подобен треугольнику 3, следовательно, треугольник 1 подобен треугольнику 3".
Схема отношения транзитивности такова: aRb & bRc à aRc, где & - знак операции логического умножения (логическое "и", одновременность); b – транзитный элемент.
Отношение называет рефлексивным (от ср.-век. лат. reflexivus – букв. повернутый назад), если оно справедливо по отношению к самому себе (или к паре тождественных объектов). Например, “а=а”, “а не больше а”. Заметим, что очень мало отношений, которые в действительности являются рефлексивными, например, все отношения строгого порядка - “быть больше”, “быть ближе” и т.п. - нерефлексивны. Свойство рефлексивности в большей степени необходимо для построения научных теорий. Формально это можно записать как справедливость aRa.
Рассмотрим на примерах, как эти свойства проявляются в моделировании. Покажем, что для отношения “x является моделью y” справедливы все эти свойства.
Симметричность. Поскольку модель в самом общем смысле - это что-то "подобное" в некотором выбранном отношении данному объекту, то и сам объект в том же отношении "подобен" модели. Ранее уже говорилось, что построенную модель можно рассматривать как объект. Тогда "исходный" объект можно рассматривать как модель этого "нового" объекта. Схематично это можно изобразить так:
И сходный объект Модель исходного объекта
сходный объект Модель исходного объекта
М одель нового объекта Новый объект
одель нового объекта Новый объект
ПРИМЕР
Настоящий автомобиль можно рассматривать как модель игрушечной машинки. Реальную вьюгу можно расматривать как модель к строкам А.С.Пушкина "Буря мглою небо кроет, вихри снежные крутя, то как зверь она завоет, то заплачет как дитя..."
То есть сам объект можно рассматривать как модель его модели.
Транзитивность.
ПРИМЕР
Представьте себе, что по фотографии человека Вы делаете словесное описание его внешности. Поскольку фотографию можно рассматривать как модель внешнего облика человека, то словесное описание изображения на фотографии есть не что иное, как модель модели. Но это словесное описание можно расссматривать и как модель самой внешности человека.
То есть модель модели является моделью исходного объекта.
Рефлексивность.
Она означает, что отношение (в нашем случае "быть подобным") применимо к самому объекту. Это свойство по отношению к моделированию означает, что точная копия объекта может выступать его моделью. Другими словами, сам объект является точнейшей моделью самого себя.
Перейдем к изучению свойств отношений "похожести".
Дадим следующие определения.
Любой объект исследования можно рассматривать как систему, состоящую из некоторого набора взаимосвязных элементов, образующих в некотором отношении единое целое.
Две системы (в нашем случае объект исследования и его модель или две модели одного и того же объекта) называются изоморфными, если между ними существует взаимно-однозначное соответствие: каждому элементу одной системы соответствует элемент другой и наоборот.
Каждый объект, как известно, рассматривается ними в трех аспектах: с точки зрения внешнего вида, структуры и поведения, поэтому по отношению к моделированию можно говорить об изоморфизме (взаимно-однозначном соответствии) систем по внешнему виду, по структуре и по поведению.
Модель и объект (модель и модель) называются изоморфными, если между ними можно установить отношение изоморфизма.
Если в данном определении требование взаимной однозначности заменить более слабым требованием однозначного соответствия систем (соответствия только в одну сторону), то такое отношение называется отношением гомоморфизма или просто гомоморфизмом.
Итак, две системы называются гомоморфными, если между ними существует однозначное соответствие: каждому элементу одной системы соответствует элемент другой, но не наоборот.
Гомоморфизм, как и изоморфизм, предполагает сохранение в модели всех определенных на объекте исследования свойств и отношений. Однако здесь требование взаимно-однозначного соответствия заменяется требованием однозначного соответствия: каждому элементу одной системы соответствует элемент второй системы, но не каждому элементу второй системы соответствует элемент первой.
В общем случае обеспечение изоморфизма модели и объекта исследования по всем аспектам моделирования может быть не только трудновыполнимым, но и излишним, поскольку сложность модели при этом может оказаться настолько значительной, что не будет возможным никакое упрощение решаемой задачи. Поэтому для исследования объекта достоточно построить изомофную (или гомоморфную) модель либо по внешнему виду, либо по структуре, либо по поведению.
Что касается отношений изоморфизма или гомоморфизма, существующих между разными моделями одного и того же объекта, то с их помощью можно, например, упорядочить модели по степени отражения в них информации о моделируемом объекте: изомофные модели хотя, как правило, по форме отличаются друг от друга, но дают об объекте одну и ту же информацию. Если же мы имеем несколько уточняющих друг друга моделей, то между ними можно установить отношение гомоморфизма.
ПРИМЕР
Пусть имеются две цветные фотографии одного и того же объекта, сделанные из одной и той же точки, но на фотопленках разного качества. И есть еще черно-белая фотография того же объекта, сделанного из той же точки. Несмотря на то, что одна цветная фотография может отличаться от другой несколько иной цветовой гаммой, тем не менее цвета, различимые на одной фотографии будут различаться и на другой фотографии и каждому оттенку цвета одной фотографии соответствует свой оттенок на другой фотографии.
В этом случае можно говорить об изоморфизме двух моделей по внешнему виду. Что касается черно-белой фотографии, то на ней разные цвета объекта фотографирования могут передаваться одним и тем же оттенком серого. В этом случае можно сказать, что между цветной и черно-белой фотографией существует отношение гомоморфизма.
ПРИМЕР
Отметки, полученные вами по разным школьным предметам, являются моделью вашей успеваимости. Надеемся, что все полученные вами отметки проставлены в вашем дневнике. Они же есть в соответствующих графах школьного журнала. Таким образом мы имеет две модели структуры одного и того же объекта – вашей успеваемости. Теоретически они должны быть изоморфны. В аттестате о среднем образовании также будут проставлены отметки по предметам, которые вы изучали. Но они отражают только часть отметок, полученных вами за годы обучения. Поэтому эта модель находится в отношении гомоморфизма с предыдущими.
ПРИМЕР
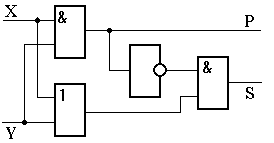
Смоделировать работу такого элементарного устройства компьютера, как сумматор двоичных кодов можно с помощью таблицы истинности, структурных формул или функциональной схемы (рис. 3.1.1). Все эти модели изоморфны по отношению друг к другу.
| X | Y | P | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
P= X & Y

S = (X & Y) & (X V Y)
Рис. 3.1.1 Таблица истинности, структурные формулы и функциональная схема полусумматора
Отношения изоморфизма и гомоморфизма хорошо демонстрируется на примере моделирования действительных чисел точками числовой прямой.
ПРИМЕР
Если на прямой линии выбрать точку и назвать ее началом координат (точкой 0), а также выбрать длину единичного отрезка, отмерить его от начала координат в выбраном направлении и поставить точку 1, то для каждой точки Х полученного отрезка можно определить ее расстояние от начала координат, то есть поставить в соответствие некоторое действительное число от 0 до 1. В свою очередь, каждому действительному числу из интервала [0, 1] можно поставить в соответствие точку на нашем отрезке. Говорят, что существует взаимно однозначное соответствие этих двух математических объектов.




0 х 1
Рис.3.1.1. Моделирование действительных чисел от 0 до 1 с помощью отрезка прямой.
Если использовать формулу для пересчета значения х:
X1 = a + (b - a) * x или x = (X1 - a) / (b-a)
то получим взаимно однозначное соответствие между действительными числами из интервалов хО [0, 1] и Х1 О [a, b]

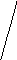





a X1 b




0 x 1
Рис. 3.1.2. Моделирование действительных чисел из интервала [a,b] с помощью отрезка прямой.
Свойство гомоморфизма можно продемонстрировать на примере округления числовых значений. Когда при вычислениях мы округляем результат до заданного количества знаков, мы нарушаем требование взаимно однозначного соответствия.
ПРИМЕР
При решении уравнения вы можете получить, например, значение корня равное 5,256 или 5,311, или 5,299, или 5. 3001. При округлении с точностью до одного знака после запятой все они преобразуются к числу 5,3. Восстановить по округленному значению, каким же было исходное число до округления невозможно. Это пример гомоморфных моделей.
5 ,256
,256
5 ,311
,311
5

 ,299 5,3
,299 5,3
5,3001
5,345
Понятно, что множество действительных чисел, множество рациональных чисел и множество целых чисел являются гомоморфными моделями тех значений, которые могут принимать переменные величины в реальном физическом процессе.
В общем случае построить гомоморфную, а тем более изоморфную модель природных и социальных событий, явлений, процессов не представляется возможным. Для этого было бы необходимо выделить все составляющие их элементы, и все связи между ними, и все закономерности их поведения.
ПРИМЕР
Попробуйте представить себе модель поверхности земного шара - географическую карту, которая бы отражала все особенности рельефа Земного шара. Или построить модель, отражающую все возможные колебания спроса и предложения на все товары и все порождающие их причины, чтобы установить объективную систему цен. Или модель, в которой объясняется происхождение и видоизменение всех слов русского языка.
А существуют ли вообще объекты, для которых можно построить изоморфную модель? Да, это объекты, которые мы знаем досконально. А так знать мы можем только те объекты, которые мы сами сконструировали и создали. В процессе своей жизни человек создает много объектов, как материальных, так и информационных. В отличие от природных, такие объекты будем называть конструктивными.
ПРИМЕР
Одежда, сшитая для взрослого человека, является конструктивным объектом. Для него вполне можно построить изоморфную модель, например, одежду того же фасона, но уже сшитую для ребенка.
Скворечник является конструктивным объектом. Его информационной моделью являются чертежи. Между моделью и объектом в этом случае можно установить отношение изоморфизма.
Математическая модель задачи - также конструктивный объект. Его гомоморфной моделью является алгоритм решения задачи, построенный в точном соответствии с этой моделью.
Программа, написанная на языке программирования в точном соответствии с алгоритмом, заданном блок-схемой, является его изоморфной моделью.
Очевидно, что информационные модели являются конструктивными объектами.
ПРИМЕЧАНИЕ. Понятие конструктивного объекта является одним из основных понятий современной математики. Как писал А.Н.Колмогоров "Во всем современном математическом мышлении большое место занимает различие между "конструктивным" и "неконструктивным", а А.П.Ершов включал понятие конструктивного объекта в число основных понятий программирования. Но смысл понятия “конструктивный объект” в математике несколько иной. (= понятию конечного объекта)
Для чего вообще нужно выяснять, существует ли между объектом и его моделью отношение изоморфизма (гомоморфизма)? Что нам может дать это знание?
Дело в том, что информация, полученная при изучении изоморфной модели, полностью аналогична той, которую мы можем получить, изучая сам объект моделирования. Поэтому от изучения объекта (что может быть по каким-то причинам невозможным или нецелесообразным) мы можем без потери информации перейти к изучению модели.
Кроме того, если модель изоморфна объекту, то он может быть однозначно восстановлен по его модели.
Заметим также, что две разные, но изоморфные друг другу модели одного и того же объекта дают одинаковую информацию о нем (при этом модели могут быть совсем не изоморфны объекту).
Построение гомоморфной модели позволяет “свернуть” доступную нам информацию об исследуемом объекте (содержащую, вообще говоря, кроме действительно необходимых для уяснения сути дела сведений массу второстепенных, мало существенных, а то и случайных данных) в гораздо более компактную (но в то же время более “емкую”), удобозримую и удобообрабатываемую форму.
ЗНАТЬ
Построив модель, мы создаем некоторый новый объект, который находится в определенных отношениях к исходному объекту.
Отношения между объектом и его моделями характеризуются рядом свойств, наиболее важными из которых являются:
а) свойства двуместного отношения "х является моделью y", позволяющего определенным образом отграничить объекты моделирования от объектов – моделей;
б) свойства двуместных отношений, выражающие различные степени "похожести" объектов: объекта моделирования на его модель и объекта-модель на другой объект-модель, относящийся к тому же самому исходному объекту.
Самое главное свойство модели - быть подобной объекту моделирования в некотором отношении, обусловленном целями моделирования. В математике отношение подобия уточняется через свойства симметричности, рефлексивности, транзитивности.
Отношение, существующее между двумя объектами (обозначим их, например, а и b, а само отношение R), называется двуместным.
Двуместное отношение называется симметричными, если из справедливости соотношения aRb следует справедливость соотношения bRa.
Двуместное отношение R назвыается транзитивным, если из справедливости соотношений аRb и bRc следует справедливость соотношения aRc.
Двуместное отношение R называется рефлексивным, если справедливо сотношение aRa.
Для отношения “x является моделью y” справедливы все эти свойства.
Симметричность. Исходный объект можно рассматривать как модель его модели.
Транзитивность. Если для модели объекта построена модель, то она тоже является моделью исходного объекта.
Рефлексивность. Объект является точнейшей моделью самого себя.
Любой объект исследования можно рассматривать как систему, состоящую из некоторого набора взаимосвязных элементов, образующих в некотором отношении единое целое.
Две системы называются изоморфными, если между ними существует взаимно-однозначное соответствие: каждому элементу одной системы соответствует элемент другой и наоборот.
Две системы называются гомоморфными, если между ними существует однозначное соответствие: каждому элементу одной системы соответствует элемент другой, но не наоборот.
По отношению к моделированию можно говорить об изоморфизме и гомоморфизме следующих систем:
Построить изоморфную (гомоморфную) модель можно только для конструктивных объектов.
Под конструктивными объектами будем понимать объекты созданные человеком (в отличие от природных и социальных объектов).
Знание того, что некоторая модель является изоморфной моделью объекта позволяет:
Две разные, но изоморфные друг другу модели одного и того же объекта дают одинаковую информацию о нем.
Построение гомоморфной модели позволяет “свернуть” доступную нам информацию об исследуемом объекте в гораздо более компактную, удобозримую и удобообрабатываемую форму.
УМЕТЬ
ЗАДАНИЕ 1
Заметим, что, как правило, модель изоморфна объекту в каком-то отношении. Например, фотография дома является изоморфной моделью дома и план дома также изоморфная модель дома. Правомерен ли вопрос: что больше похоже на дом - фотография или план дома? Можно ли сказать, что одна модель "более изоморфна", чем другая? Не вернее ли будет сказать, что в одном отношении на дом больше похожа его фотография, а в другом - план? Сформулируйте эти отношения.
ОТВЕТ: Фотография изоморфна дому относительно взаимного расположения (на некоторых плоскостях проекции) всех видимых деталей, т.е. относительно внешнего вида, а план - относительно важнейших конструктивных деталей, в том числе и невидимых снаружи, т.е. относительно структуры.
ЗАДАНИЕ 2
В предыдущем параграфе по условию задачи составлялась таблица, по таблице строился граф, метод решения задачи отражался в математической модели, а расчетные формулы переводились в алгоритм и затем в программу. Определите, какие из данных моделей изоморфны.
ОТВЕТ. Алгоритм и программа являются изоморфными моделями решения задачи, а граф и соответствующая ему таблица – изоморфные модели условия задачи.
ЗАДАНИЕ 3
При решении алгебраических задачи, ее условия представляются в виде формул, которые затем могут быть тождественно преобразованы в другие формулы. Все они будут изоморфными моделями условия задачи. Докажите это, пользуясь определением понятия “изоморфизм”.
ЗАДАНИЕ 4
Рассмотрите отношения, существующие между:
а) постановкой задачи;
б) математической моделью задачи;
в) алгоритмом ее решения;
г) программой, написанной в точном соответствии с алгоритмом.
Какие из этих объектов находятся в отношении изоморфизма, а какие - в отношении гомоморфизма?
Верно ли, что математическая модель и алгоритм гомоморфны друг другу? Ответ обоснуйте.
Любая ли программа, написанная в соответствии с алгоритмом, изоморфна ему? Ответ обоснуйте.
ЗАДАНИЕ 5
Даны несколько моделей-изображений одного и того же объекта (кошки). Какие из этих моделей являются изоморфными, а какие – гомоморфными?
Попытайтесь по этим моделям составить представление о самом объекте.
Рис. 3.1.3. Изображения кошек
ЗАДАНИЕ 6
Определите, какие из следующих моделей являются гомоморфными, а какие изоморфными:
фотоснимок слона с сидящей на его хоботе мухой в 1:200 натуральной величины (объект моделирования - слон с мухой);
отсканированный рисунок, хранящийся во внешней памяти компьютера (объект моделирования - исходный рисунок);
отсканированный текст, подвергшийся обработке с помощью программы оптического распознавания символов (объект моделирования - исходный текст);
сборочный чертеж изделия (объект моделирования - само изделие);
объектный код программы - машинный вариант программы, полученный в результате работы транслятора (объект моделирования - текст программы на языке программирования высокого уровня).
ЗАДАНИЕ 7
Интерфейс системы Windows позволяет пользователю управлять ее работой с помощью:
- пиктограмм;
- ниспадающего меню;
- меню "горячих клавиш".
Можно ли сказать, что модели поведения пользователя, предусмотренные разработчиками системы в каждом из этих случаев, являются гомоморфными или они все-таки изоморфны друг другу?
ЗАДАНИЕ 8
Рассмотрите и охарактеризуйте свойства отношений “объект-модель” и “модель - модель” для следующих объектов: новелла Проспера Мериме “...”, опера Бизе “Кармен”, балет Р.Щедрина “Кармен-сюита” с точки зрения симметричности, рефлексивности, транзитивности, изоморфизма и гомоморфизма.
ВОПРОСЫ - ПРОБЛЕМЫ
1. Все ли информационные модели являются конструктивными? Можете ли вы придумать пример информационной неконструктивной модели?
2. Две модели одного и того же объекта, построенные исходя из разных целей, могут быть совершенно непохожими друг на друга, хотя каждая из них похожа на модель. В задании 1 таковыми являются план дома и его фотография. То есть похожее на одно и то же не обязательно похоже друг на друга. Заметим, в математике подобное отношение называют отношением толерантности или отношением ослабленного подобия.
Как вы думаете, какое свойство (симметричность, рефлексивность, транзитивность) нарушается в этом случае?
3. Проинтерпретируйте мысль замечательного русского философа П.А.Флоренского, что сделанные предметы блестят, а рожденные – мерцают.
РАСШИРЬ СВОЙ КРУГОЗОР
Вернемся к поставленной выше проблеме: рассмотрим ситуацию, когда наблюдателю доступен объект, но недоступна модель и построить ее невозможно. Каким образом в этом случае он может получить информацию об этом объекте?
Вопрос может показаться надуманным, поскольку, имея в распоряжении объект, вы уже не нуждаетесь ни в какой модели.
Тем не менее вопрос вполне правомерен, поскольку, как мы уже говорили выше, научное познание может высветить только какую-то грань объекта, построив его модель. Но именно моделью мы и не располагаем и проблема состоит в том, чтобы познать объект сразу, во всей его полноте. Здесь уже речь идет не о научном познании, а о каком-то ином, “немодельном” способе раскрытия сути объекта. Эта проблема очень ясно осознана в богословии.
Действительно, Бог – этот такой “объект”, который невозможно познать, построив его модель. Парадокс состоит в том, что человек, с одной стороны, не может познать сущность Бога ( как, впрочем и сущность другого человека), с другой стороны – при внимательном взгляде он может увидеть Божественные проявления в жизни.
В православном учении существует способ разрешения этого противоречия и установления связи совершенного и здешнего бытия. Это знаменитый тезис византийского богослова XIV века св. Григория Паломы о божественном энергетизме. Суть его состоит в том, что здешнее бытие причастно божественному, не по сути а по "энергиям" – иначе говоря путем свободного соединения своих энергий (устремлений, воли) с божественными энергиями, "благодатью". На Руси это издревне называлось "стяжанием благодати". "Православный энергетизм" – глубинаая основа православной духовности в Византии и на Руси. Его можно увидеть и в деяниях С.Радонежского, творениях А.Рублева и многих других.
ИНТЕРЕСНЫЙ ФАКТ
Известный специалист по массовой культуре профессор Умберто Эко показал, что все романы Я.Флеминга о Джеймсе Бонде, агенте 007 построены по одной и той же схеме (модели):
М. действует и дает задание Бонду;
Злодей действует и предстает перед Бондом:
Бонд движется и объявляет первый шах Злодею или Злодей делает первый шах Бонду;
Женщина движется и показывается перед Бондом;
Злодей захватывает Бонда (вместе или без Женщины);
Злодей пытает Бонда (вместе или без Женщины);
Бонд бьет Злодея (убивает его, или убивает его представителей или помогает убить их)
Бонд получает в награду Женщину, которую потом теряет.
Постройте по этой информационной модели новый объект - собственный рассказ о похождениях Джеймса Бонда.
Заметим, кстати, что сам У.Эко воплотил результаты своих исследований в романе "Имя розы", который пользовался колоссальным успехом.







 сходный объект Модель исходного объекта
сходный объект Модель исходного объекта
 одель нового объекта Новый объект
одель нового объекта Новый объект 







 ,256
,256  ,311
,311