10 способів розв’язування квадратних рівнянь (додаток №6 до проекту "Квадратні рівняння")

10 способів розв’язуванння квадратних рівнянь

Історія розвитку квадратних рівнянь

Квадратні рівняння у Стародавньому Вавілоні

Необхідність розв'язувати рівняння не тільки першого, але і другоїго степеня ще в давнину була викликана потребою розв'язувати задачі, пов'язані із знаходженням площ земельних ділянок та земляними роботами військового характеру, а також з розвитком астрономії і самої математики. Квадратні рівняння вміли розв'язувати близько 2000 років до нашої ери вавілоняни. Застосовуючи сучасні алгебраїчні записи, можна сказати, що в їх клинописних текстах зустрічаються, крім неповних, і такі, наприклад, повні квадратні рівняння:

Правило розв'язування цих рівнянь, викладене у вавилонських текстах, збігається з сучасним, проте невідомо, яким чином дійшли вавілоняни до цього правила. Майже всі знайдені досі клинописні тексти наводячи тільки завдання з розв'язками, викладеними у вигляді рецептів, без вказівок щодо того, яким чином вони були знайдені. Незважаючи на високий рівень розвитку алгебри у Вавілонії, в клинописних текстах відсутні поняття від'ємного числа і загальні методи розв'язання квадратних рівнянь.

Як складав і розв’язував Діофант

квадратні рівняння

РІВНЯННЯ:

«Знайти два числа, знаючи, що їх сума дорівнює 20, а добуток 96»

Діофант міркує таким чином: з умови задачі випливає, що шукані числа не рівні, оскільки якби вони рівні, то їх добуток дорівнював б не 96, а 100. Таким чином, одне з них буде більше половини їх суми , тобто 10+X , інше ж менше, тобто . 10-X .

Різниця між ними 2 Х

Звідси Х=2 . Одне з шуканих чисел дорівнює 12, інше 8. Розв’язок Х = -2 для Діофанта не існує, так як грецька математика знала тільки додатні числа.

Або ж:

0 Одна з задач відомого індійського математика XІІ ст. Бхаскари Обезьянок резвых стая Всласть поевши, развлекалась. Их в квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам… Стали прыгать повисая… Сколько было обезьянок Ты скажи мне, в этой стае?. Відповідно умови задачі рівняння: Баскара пише у вигляді: Доповнив ліву частину до квадрата, " width="640"

Квадратні рівняння в Індії

Задачі на квадратні рівняння зустрічаються і в астрономічному трактаті «Ариабхаттиам», складеному в 499 р. індійським математиком і астрономом Ариабхаттою. Інший індійський учений, Брахмагупта, виклав загальне правило розв'язання квадратних рівнянь, зведених до єдиної канонічної формі: ax ²+bx=c, a0

Одна з задач відомого індійського математика XІІ ст. Бхаскари

Обезьянок резвых стая

Всласть поевши, развлекалась.

Их в квадрате часть восьмая

На поляне забавлялась.

А двенадцать по лианам…

Стали прыгать повисая…

Сколько было обезьянок

Ты скажи мне, в этой стае?.

Відповідно умови задачі рівняння:

Баскара пише у вигляді:

Доповнив ліву частину до квадрата,

Квадратні рівняння в Стародавній Азії

х 2 +10 х = 39

Ось як розв’язував це рівняння середньоазійський вчений аль-Хорезмі:

Він писав : "Правило таке:

поділи кількість коренів навпіл, 10:2

отримайте в цій задачі п’ять, 5

помнож на це на рівне йому, буде двадцять п’ять, 5·5=25

додай це до тридцяти дев’яти, 25+39

буде шістьдесят чотири, 64

добудь з цього корінь, буде вісім , 8

І відніми з цього половину кількості коренів, тобто п’ять, 8-5

залишиться 3

це буде корінь квадрата , який ти шукав."

А другий корінь ? Другий корінь не знаходили, бо від’ємні числа не були відомі.

Квадратні рівняння в Європі XIII-XVII ст.

Загальне правило розв'язування квадратних рівнянь, приведених до єдиного канонічного виду х²+вх+с=0 , було сформульовано в Європі лише в 1544 р. Штифелем.         

.

Формули розв'язування квадратних рівнянь в Європі були вперше викладені у 1202 р. італійським математиком Леонардом Фібоначчі.  

Отримання формули розв'язування квадратного рівняння у загальному вигляді є у Вієта, однак Вієт визнавав тільки додатні корені. Лише в 17 ст. завдяки працям Декарта, Ньютона та інших вчених спосіб розв'язування квадратних рівнянь набуває сучасного вигляду

Про теорему Вієта

Теорема, що виражає зв'язок між коефіцієнтами квадратного рівняння та його коренями, що носить ім'я Вієта, їм була сформульована вперше в 1591 р. Наступним чином: «Якщо B+D, помножене на А-А , дорівнює BD, то А дорівнює В і дорівнює D». Щоб зрозуміти Вієта, слід пам'ятати, що А, як і всяка голосна буква , означала у нього невідоме (наше х), голосні ж B,D - коефіцієнти при невідомому .

На мові сучасної алгебри вищенаведена формулювання Вієта означає :

Якщо зведене квадратне рівняння x 2 +px+q=0 має дійсні корені, то їх сума дорівнює -p , а добуток дорівнює q , тобто x 1 + x 2 = -p , x 1 x 2 = q

(сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому з протилежним знаком, а добуток коренів - вільному члену).

Метод розкладання на множники

звести квадратне рівняння загального вигляду до виду:

А(х)·В(х)=0,

де А(х) і В(х) – многочлени відносно х.

Мета:

• Винесення спільного множника за дужки;
• Використання формул скороченого множення;
• Спосіб групування.

Способи:

Приклад:

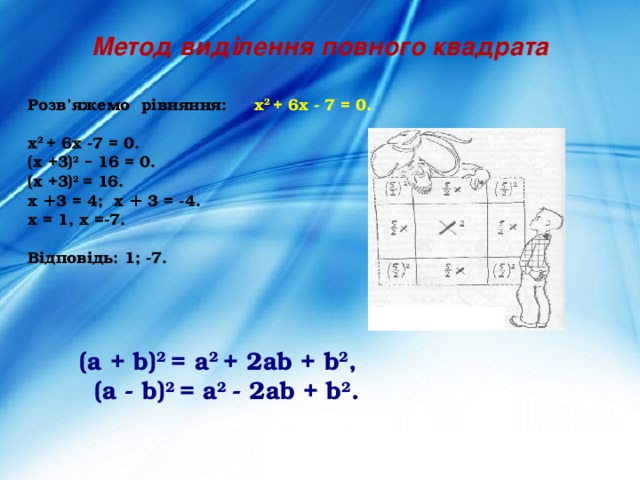
Метод виділення повного квадрата

Розв’яжемо рівняння: х 2 + 6х - 7 = 0.

х 2 + 6х -7 = 0.

(х +3) 2 – 16 = 0.

(х +3) 2 = 16.

х + 3 = 4; х + 3 = -4.

х = 1, х =-7.

Відповідь: 1; -7.

(a + b) 2 = a 2 + 2ab + b 2 ,

(a - b) 2 = a 2 - 2ab + b 2 .

0, Якщо D ЯкщоD Коренів не має " width="640"

Розв’язування квадратних рівнянь за формулою

ax 2 +bx+c=0

Вираз називають дискримінантом квадратного рівняня .

Корені квадратного рівняння:

Якщо D0,

Якщо D

ЯкщоD

Коренів не має

Розв’язування рівнянь за теоремою Вієта

x 1 і х 2 – корені рівняння

Наприклад :

Х 2 + 3Х – 10 = 0

Х 1 ·Х 2 = – 10, значить корені мають різні

знаки

Х 1 + Х 2 = – 3, значить більший по модулю

корінь - від’ємний

підбором знаходимо корені: Х 1 = – 5, Х 2 = 2

0, за оберненою теоремою Вієта, отримуємо корені: 5;6, далі повертаємось до коренів даного рівняння: 2,5; 3. Відповідь: 2,5; 3. " width="640"

Розв’язування рівнянь способом «перекидання»

Розв’яжіть рівняння : 2х 2 - 11х +15 = 0.

Перекинемо коефіцієнт 2 до вільного члена

у 2 - 11у +30= 0.

D0, за оберненою теоремою Вієта, отримуємо корені: 5;6,

далі повертаємось до коренів даного рівняння: 2,5; 3.

Відповідь: 2,5; 3.

Властивості коефіцієнтів квадратного рівняння

Якщо в квадратному рівнянні a+b+c=0, то один з коренів дорівнює 1, а

другий за теоремою Вієта дорівнює с/а

Якщо в квадратному рівнянні a+c=b, то то один з коренів дорівнює (-1),

другий за теоремою Вієта дорівнює (-с/а)

Приклад :

137х 2 + 20х – 157 = 0.

a = 137, b = 20, c = -157.

a + b+ c = 137 + 20 – 157 =0.

x 1 = 1,

Відповідь: 1;

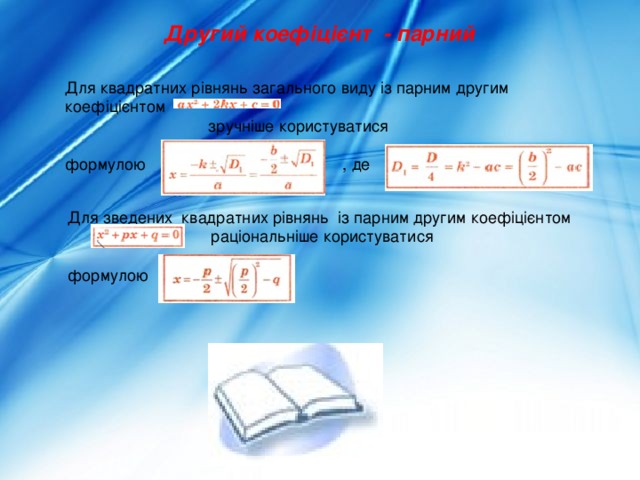
Другий коефіцієнт - парний

Для квадратних рівнянь загального виду із парним другим коефіцієнтом

зручніше користуватися

формулою , де

Для зведених квадратних рівнянь із парним другим коефіцієнтом

раціональніше користуватися

формулою

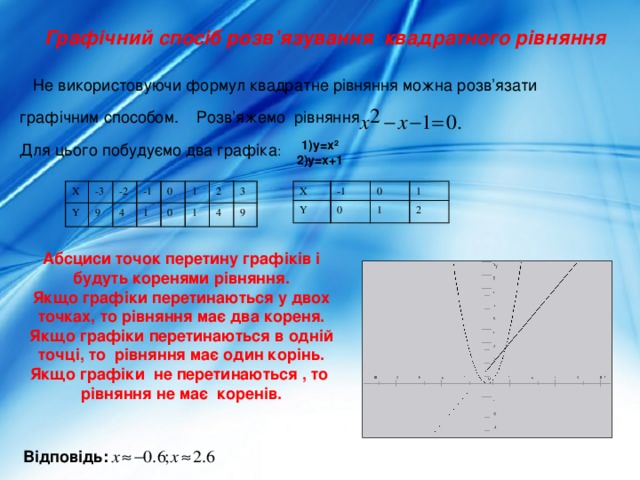
Графічний спосіб розв’язування квадратного рівняння

Не використовуючи формул квадратне рівняння можна розв’язати

графічним способом. Розв’яжемо рівняння

Для цього побудуємо два графіка :

1)y=x² 2)y=x+1

X

-1

Y

0

0

1

1

2

X

Y

-3

9

-2

4

-1

1

0

1

0

1

2

4

3

9

Абсциси точок перетину графіків і будуть коренями рівняння.

Якщо графіки перетинаються у двох точках, то рівняння має два кореня.

Якщо графіки перетинаються в одній точці, то рівняння має один корінь.

Якщо графіки не перетинаються , то рівняння не має коренів.

Відповідь:

Розв’язування квадратних рівнянь за допомогою циркуля і лінійки

Корені квадратного рівняння ах 2 + bх + с = 0 ( а ≠ 0) можна розглядати

як абсциси точок перетину кола з центром Q( - ; ), що

проходяить через точку A(О; 1), з вісію Ох .

Розв’язування квадратних рівнянь за допомогою

номограми

Це старий та незаслужено забутий спосіб розв’язування квадратних рівнянь , розміщений на с.83 «Чотиризначні математичні таблиці» Брадіс В.М.

Таблиця XXII. Номограма для розв’язування квадратного рів-

няння

Ця номограма дозволяє, не розв’язуючи квадратного рівняння, за його коефіцієнтами визнвчити корені рівняння.

Для рівняння

номограма дає корені

Геометричний спосіб розв’язування

квадратних рівнянь

В давнину, коли геометрія була більш розвинена, ніж алгебра, квадратні

рівняння розв’язували не алгебраїчно, а геометрично.

Ось, наприклад, як стародавні греки розв’язували рівняння

або

Вираз та

геометрично представляють собою один і тот самий квадрат, а дане рівняння

одне і теж саме рівняння.

Звідки й отримуємо, що , або

 

 

Висновки

• дані прийоми розв’язування заслуговують уваги, оскільки вони не всі відображені в шкільних підручниках математики;

• оволодіння цими прийомами допоможе учням економити час і ефективно розв’язувати рівняння;

• потреба у швидкому розв’язуванні обумовлена застосуванням тестової системи на ДПА та ЗНО.