Բազմությունները որպես հիմնական մաթեմատիկական հասկացություններ

    Մաթեմատիկայի դպրոցական դասընթացի գիտական հիմունքները Աղավնի Գրիգորյան

Բազմությունները  մաթեմատիկայի  ֆունդամենտալ հասկացություններից են

Բազմության և նրա տարրերի հասկացությունները մաթեմատիկայում սկզբնական (նախնական) հասկացություններ են: Բազմությունը կարող է ընկալվել որպես առարկաների (օբյեկտների) հավաքածու (համախմբություն):

Բազմությունները, սովորաբար, նշանակում են մեծատառերով՝ A, B, C, X,, իսկ նրանց տարրերը՝ փոքրատառերով՝ a,b, c, x և այլն:

N, Z, Q, R տառերով նշանակվում են, համապատասխանաբար, բնական, ամբողջ, ռացիոնալ, իրական թվերի բազմությունները:

a օբյեկտը A բազմության տարր է, գրառվում է այս- պես` a∈ A և կարդացվում՝ «a -ն պատկանում է A բազմությանը» կամ « a -ն գտնվում է A բազմության մեջ»: b∉ A (կամ b ∈ A ) գրառումը նշանակում է` b -ն չի պատկանում A բազմությանը (կամ` b -ն A բազմության տարր չէ):

Տարբերվում են վերջավոր և անվերջ բազմություններ: Վերջավոր է կոչվում այն բազմությունը, որը բաղկացած է վերջավոր թվով տարրերից: Եթե բազմությունը վերջավոր չէ, ապա այն ան- վանում են անվերջ բազմություն:

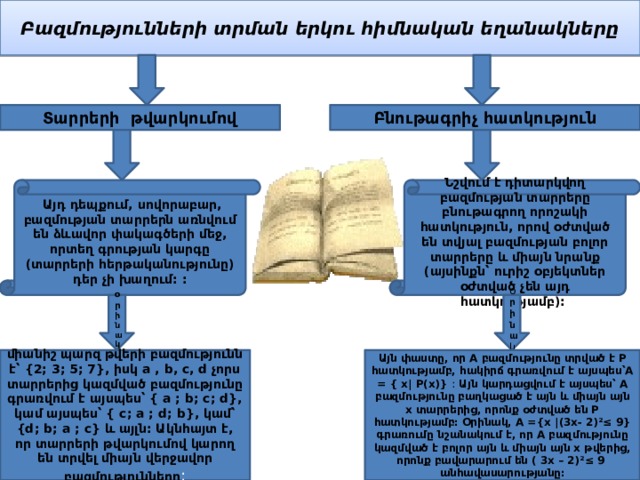
Բազմությունների տրման երկու հիմնական եղանակները

Բնութագրիչ հատկություն

Տարրերի թվարկումով

Այդ դեպքում, սովորաբար, բազմության տարրերն առնվում են ձևավոր փակագծերի մեջ, որտեղ գրության կարգը (տարրերի հերթականությունը) դեր չի խաղում: :

Նշվում է դիտարկվող բազմության տարրերը բնութագրող որոշակի հատկություն, որով օժտված են տվյալ բազմության բոլոր տարրերը և միայն նրանք (այսինքն՝ ուրիշ օբյեկտներ օժտված չեն այդ հատկությամբ):

օր ինակ

օ րինա կ

միանիշ պարզ թվերի բազմությունն է՝ {2; 3; 5; 7}, իսկ a , b, c, d չորս տարրերից կազմված բազմությունը գրառվում է այսպես՝ { a ; b; c; d}, կամ այսպես՝ { c; a ; d; b}, կամ՝ {d; b; a ; c} և այլն: Ակնհայտ է, որ տարրերի թվարկումով կարող են տրվել միայն վերջավոր բազմությունները :

Այն փաստը, որ A բազմությունը տրված է P հատկությամբ, հակիրճ գրառվում է այսպես՝A = { x | P(x)} : Այն կարդացվում է այսպես՝ A բազմությունը բաղկացած է այն և միայն այն x տարրերից, որոնք օժտված են P հատկությամբ: Օրինակ, A ={x |(3x- 2)²≤ 9} գրառումը նշանակում է, որ A բազմությունը կազմված է բոլոր այն և միայն այն x թվերից, որոնք բավարարում են ( 3x – 2)²≤ 9 անհավասարությանը:

Ոչ մի տարր չպարունակող բազմությունն անվանում են դատարկ բազմություն. այն նշանակվում է ∅ պայմանանշանով: A և B բազմությունները կոչվում են հավասար , եթե նրանք կազմված են միևնույն տարրերից: Այդ դեպքում գրում են` A = B : Օրինակ, եթե A ={2,5,8} և B ={5,8,2}, ապա A = B , իսկ եթե C ={0,1,5} և D ={0,1,5,9} , ապա C ≠ D :

Եթե A բազմության յուրաքանչյուր տարր պատկանում է նաև B բազմությանը, ապա A բազմությունը կոչվում է B բազմության ենթաբազմություն:

Օրինակ՝

Յուրաքանչյուր վագր գիշատիչ կենդանի է, յուրաքանչյուր ամբողջ թիվ պատկանում է ռացիոնալ թվերի բազմությանը, յուրաքանչյուր զուգահեռագիծ պատկանում է բոլոր քառանկյունների բազմությանը, [1; 3] հատվածի ցանկացած կետ (0; 4) միջակայքի կետ է: Այն փաստը, որ A բազմությունը B բազմության ենթաբազմություն է, գրառվում է այսպես` A ⊂ B կամ B ⊃ A : Այդ դեպքում ասում են` A բազմությունը պարունակվում է B բազմությունում կամ B բազմությունը պարունակում է A բազմությունը:

օրինակ

երեք տարր պարունակող { a, b , c }բազմության բոլոր ենթաբազմությունները: Դրանք են` դատարկ բազմությունը{Ø} , մեկական տարր պարունակող ենթաբազմությունները` {a}, {b} ,{c}երկուական տարր պարունակողները` {a,b}, {a,c}, {b,c}և երեքական տարր պարունակողները, որը միակն է՝ տրված բազմությունը` {a,b,c}: Այսպիսով, երեք տարր պարունակող բազմության ենթաբազմությունների թիվը 8-ն է: Ընդհանուր դեպքում ճիշտ է հետևյալ պնդումը. տարրերից կազմված բազմության բոլոր ենթաբազմությունների թիվը հավասար է 2ⁿ :

. Գործողություններ բազմությունների հետ

Բազմությունների հատումը: Բազմությունը, որը կազմված է բոլոր այն (և միայն այն) տարրերից, որոնք պատկանում են A և B բազմություններից յուրաքանչյուրին, կոչվում է A և Bբազմությունների հատում և նշանակվում է`A ∩ B :

Օրինակ՝A ={0; 3; 5; 7} ,B{1;3;5;8} A∩ B ={3; 5};

Z∩R= Z; (0;4] և [0;2] միջակայքերի հատումը [0;2];

Բոլոր ուղղանկյունների բազմության և բոլոր շեղանկյունների բազմության հատումը

բոլոր քառակուսիների բազմությունն է: Հատումը դատարկ է՝ A∩B=Ø: Օրինակ՝բոլոր պարզ թվերի բազմության և 4-ի բազմապատիկ թվերի բազմության հատումը դատարկ է :

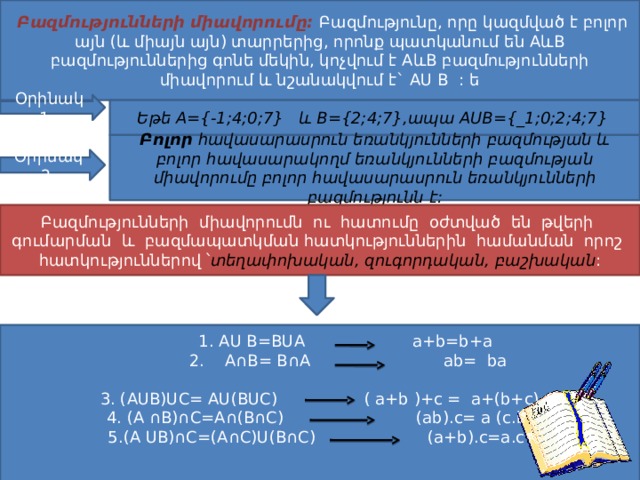
Բազմությունների միավորումը: Բազմությունը, որը կազմված է բոլոր այն (և միայն այն) տարրերից, որոնք պատկանում են AևB բազմություններից գոնե մեկին, կոչվում է AևB բազմությունների միավորում և նշանակվում է` AU B : ե

Օրինակ 1.

Եթե A={-1;4;0;7} և B={2;4;7},ապա AUB={_1;0;2;4;7}

Բոլոր հավասարասրուն եռանկյունների բազմության և բոլոր հավասարակողմ եռանկյունների բազմության միավորումը բոլոր հավասարասրուն եռանկյունների բազմությունն է:

Օրինակ 2.

Բազմությունների միավորումն ու հատումը օժտված են թվերի գումարման և բազմապատկման հատկություններին համանման որոշ հատկություններով ՝ տեղափոխական, զուգորդական, բաշխական :

1. AU B =BUA a+b=b+a

2. A∩B= B∩A ab= ba

3. (AUB)UC= AU(BUC) ( a+b )+c = a+(b+c)

4. (A ∩B)∩C=A∩(B∩C) (ab).c= a (c.b)

5.(A UB)∩C=(A∩C)U(B∩C) (a+b).c=a.c+ b.c

• ։

Խնդիր՝

Դպրոցի 45 աշակերտ ստացան մեդալներ հետևյալ 3 մրցույթներում՝պար,նկարչություն, երաժշտություն:Պարի մրցույթում մեդալ ստացան 36 աշակերտ,նկարչության մրցույթում՝12 աշակերտ,իսկ երաժշտության մրցույթում ՝ 18 աշակերտ:4 աշակերտ՝բոլոր երեք մրցույթներում մեդալ ստացան:Քանի՞ աշակերտ ստացան մեդալ ճիշտ երկու մրցույթում:

լուծում

Դիցուք 1 շրջանը այն մարդկանց բազմությունն է, ովքեր պարի մրցույթում մեդալ են ստացել, 2 շրջանագիծը այն մարդկանցը՝ ովքեր նկարչության մրցույթում մեդալ են ստացել, իսկ 3-ը՝ ովքեր երաժշտության մրցույթում մեդալ են ստացել:  

a + b + c + d + e + f + g =45

a + d + g + f =36

b + d + g + e =12

c + e + g + f =18

g =4

{a+b+c+d+e+f+g=45 a+d+g+f=36 b+d+g+e=12 c+e+g+f=18 g=4

Երկրորդ , երրորդ և չորրորդ հավասարումների գումարից հանելով առաջին հավասարումը , կստանանք   d+e+f+2g=36+12+18 − 45=21 , հաշվի առնելով , որ   g =4 , կստանանք d+e+f 2g= 36+12+18-45=21,հաշվի առնելով,որ g=4, կստանանք d+ e+f=13: Պատ՝ 13

Բազմությունների տարբերություն

• յան լրացումն է մինչև բազմությունը: Ն

Ենթաբազմության լրացում

Բազմությունը, որը կազմված է A բազմության բոլոր այն տարրերից (և միայն դրանցից), որոնք չեն պատկանում B բազմությանը, կոչվում է և բազմությունների տարբերություն և նշանակվում է` A\B: Նկարում ուրվագծորեն պատկերված են այնպիսի և բազմություններ, որտեղ B-ն A-ի ենթաբազմություն է: Գծապատված պատկերը բազմության լրացումն է մինչև A բազմությունը:

A

B

Օրինակ՝ Եթե A={1;3;5;7},B={5;7;8;9;10},ապա A\B={1;3} ,B\A={8;9;10}

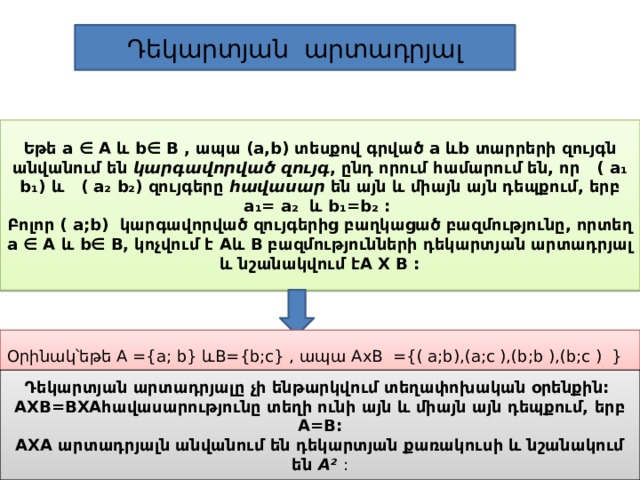
Դեկարտյան արտադրյալ

Եթե a ∈ A և b∈ B , ապա (a,b) տեսքով գրված a ևb տարրերի զույգն անվանում են կարգավորված զույգ , ընդ որում համարում են, որ ( a₁ b₁) և ( a₂ b₂) զույգերը հավասար են այն և միայն այն դեպքում, երբ a₁= a₂ և b₁=b₂ :

Բոլոր ( a;b) կարգավորված զույգերից բաղկացած բազմությունը, որտեղ a ∈ A և b∈ B, կոչվում է Aև B բազմությունների դեկարտյան արտադրյալ և նշանակվում էA X B :

Օրինակ՝եթե A ={a; b} և B={b;c} , ապա AxB ={( a;b),(a;c ),(b;b ),(b;c ) }

Դեկարտյան արտադրյալը չի ենթարկվում տեղափոխական օրենքին:

AXB=BXAհավասարությունը տեղի ունի այն և միայն այն դեպքում, երբ A=B:

AXA արտադրյալն անվանում են դեկարտյան քառակուսի և նշանակում են A² :

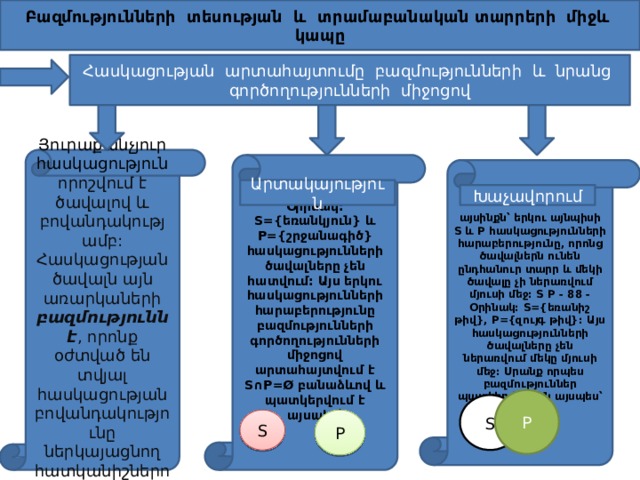
Բազմությունների տեսության և տրամաբանական տարրերի միջև կապը

Հասկացության արտահայտումը բազմությունների և նրանց գործողությունների միջոցով

Յուրաքանչյուր հասկացություն որոշվում է ծավալով և բովանդակությամբ: Հասկացության ծավալն այն առարկաների բազմությունն է , որոնք օժտված են տվյալ հասկացության բովանդակությունը ներկայացնող հատկանիշներով:

Օրինակ: S={եռանկյուն} և P={շրջանագիծ} հասկացությունների ծավալները չեն հատվում: Այս երկու հասկացությունների հարաբերությունը բազմությունների գործողությունների միջոցով արտահայտվում է S ∩P=Ø բանաձևով և պատկերվում է այսպես՝

այսինքն՝ երկու այնպիսի S և P հասկացությունների հարաբերությունը, որոնց ծավալներն ունեն ընդհանուր տարր և մեկի ծավալը չի ներառվում մյուսի մեջ: S P - 88 - Օրինակ: S={եռանիշ թիվ}, P={զույգ թիվ}: Այս հասկացությունների ծավալները չեն ներառվում մեկը մյուսի մեջ: Սրանք որպես բազմություններ պատկերվում են այսպես՝

Արտակայություն

Խաչավորում

P

S

S

P

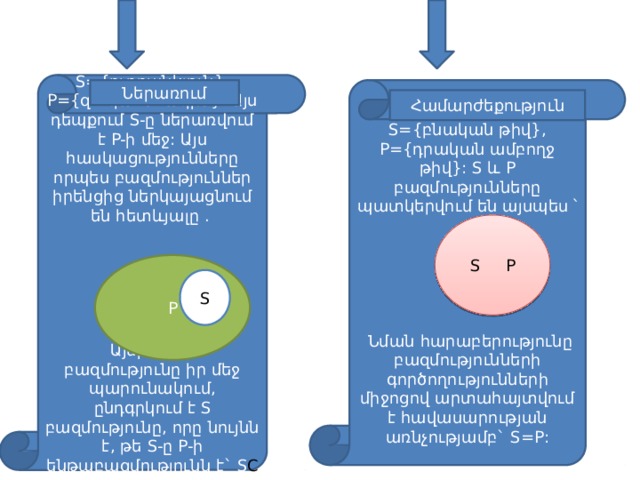
S={ուղղանկյուն}, P={զուգահեռագիծ}: Այս դեպքում S-ը ներառվում է P-ի մեջ: Այս հասկացությունները որպես բազմություններ իրենցից ներկայացնում են հետևյալը .

Այսինքն` P բազմությունը իր մեջ պարունակում, ընդգրկում է S բազմությունը, որը նույնն է, թե S-ը P-ի ենթաբազմությունն է` S С P:

Ներառում

S={բնական թիվ}, P={դրական ամբողջ թիվ}: S և P բազմությունները պատկերվում են այսպես ՝

Նման հարաբերությունը բազմությունների գործողությունների միջոցով արտահայտվում է հավասարության առնչությամբ` S=P:

Համարժեքություն

S P

P

S

Դատողությունների կառուցվածքներում կապերն ու առնչությունները բազմությունների ու նրանց գործողությունների հետ

1. Ընդհանուր հաստատական - բոլոր S-երը P են: Սա նշանակում է, որ եթե ունենք S և P բազմություններ, ապա S բազմության բոլոր տարրերը միաժամանակ տարր են նաև P բազմության համար:

2. Մասնավոր հաստատական - որոշ S-եր P են: Այս դատողությունը ըստ բազմությունների տեսության նշանակում է, որ գոյություն ունեն S բազմության տարրեր, որոնք պատկանում են P-ին:

3. Ընդհանուր ժխտական - բոլոր S-եր P չեն: Այս հարաբերությունը՝ որպես բազմությունների միջև առնչություն արտահայտվում է հետևյալ կապով. S∩P=Ø

4. Մասնավոր ժխտական - որոշ S-եր P չեն: Այս դատողությունը բազմությունների լեզվով գրվում է հետևյալ տեսքով. S\P≠ Ø

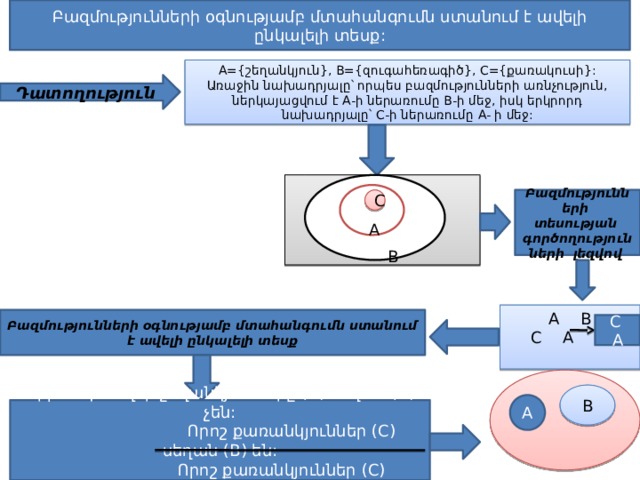
Բազմությունների օգնությամբ մտահանգումն ստանում է ավելի ընկալելի տեսք:

A={շեղանկյուն}, B={զուգահեռագիծ}, C={քառակուսի}: Առաջին նախադրյալը՝ որպես բազմությունների առնչություն, ներկայացվում է A-ի ներառումը B-ի մեջ, իսկ երկրորդ նախադրյալը՝ C-ի ներառումը A- ի մեջ:

Դատողություն

B

A

C

Բազմությունների տեսության գործողությունների լեզվով

A B

С A

Բազմությունների օգնությամբ մտահանգումն ստանում է ավելի ընկալելի տեսք

C A

C

B

A

Օրինակ . Բոլոր շեղանկյունները (A) սեղան (B) չեն:

Որոշ քառանկյուններ (C) սեղան (B) են:

Որոշ քառանկյուններ (C) շեղանկյուն (A) չեն

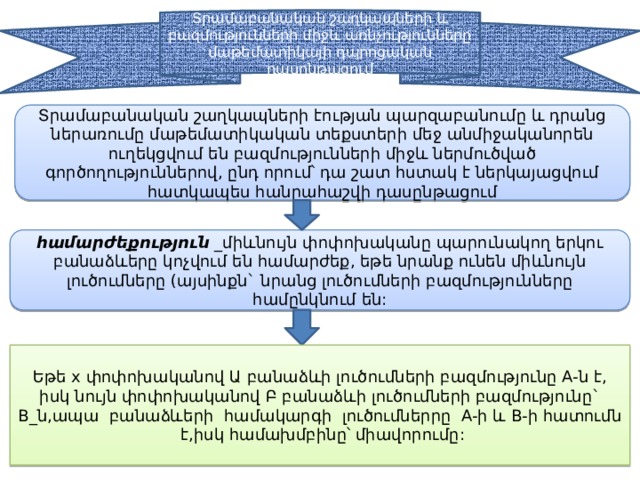
Տրամաբանական շաղկապների և բազմությունների միջև առնչությունները մաթեմատիկայի դպրոցական դասընթացում

Տրամաբանական շաղկապների էության պարզաբանումը և դրանց ներառումը մաթեմատիկական տեքստերի մեջ անմիջականորեն ուղեկցվում են բազմությունների միջև ներմուծված գործողություններով, ընդ որում՝ դա շատ հստակ է ներկայացվում հատկապես հանրահաշվի դասընթացում

համարժեքություն _միևնույն փոփոխականը պարունակող երկու բանաձևերը կոչվում են համարժեք, եթե նրանք ունեն միևնույն լուծումները (այսինքն` նրանց լուծումների բազմությունները համընկնում են:

Եթե x փոփոխականով Ա բանաձևի լուծումների բազմությունը A-ն է, իսկ նույն փոփոխականով Բ բանաձևի լուծումների բազմությունը` B_ն,ապա բանաձևերի համակարգի լուծումներրը A-ի և B-ի հատումն է,իսկ համախմբինը՝ միավորումը:

դասընթացում բանաձևերի համախումբ անվանվում է այդ բանաձևերի տրամաբանական գումարը, որն արտահայտվում է «կամ» շաղկապով (դա հենց դիզյունկցիան է), իսկ բանաձևերի համակարգ` այդ բանաձևերի տրամաբանական արտադրյալը, որն արտահայտվում է «և» շաղկապով (դա կոնյունկցիան է)

Դասընթացում տրամաբանական շաղկապների կապը բազմությունների գործողությունների հետ դիտարկվում է ոչ միայն տեսական ձևակերպումների մակարդակով, այլև խնդիրների ու վարժությունների` հետևողականորեն մշակված համակարգով:

օրինակ

Շնորհակալություն